Ev › Işık ve cam › Eşitsizlikte bir modül nasıl kaldırılır? Modülo Denklemler

Eşitsizlikte bir modül nasıl kaldırılır? Modülo Denklemler

Eşitsizlikleri çevrimiçi çözme

Eşitsizlikleri çözmeden önce denklemlerin nasıl çözüldüğünü iyi anlamak gerekir.

Eşitsizliğin katı () veya katı olmayan (≤, ≥) olması fark etmez, ilk adım eşitsizlik işaretini eşitlik (=) ile değiştirerek denklemi çözmektir.

Bir eşitsizliği çözmenin ne anlama geldiğini açıklayın?

Denklemleri inceledikten sonra öğrencinin kafasında şu resim belirir: Denklemin her iki bölümünün de aynı değerleri aldığı değişkenin bu tür değerlerini bulmanız gerekir. Başka bir deyişle eşitliğin sağlandığı tüm noktaları bulun. Her şey doğru!

Eşitsizliklerden bahsederken eşitsizliğin geçerli olduğu aralıkları (bölümleri) bulmak anlamına gelir. Eşitsizlikte iki değişken varsa çözüm artık aralıklar değil, düzlemdeki bazı alanlar olacaktır. Üç değişkendeki eşitsizliğin çözümü ne olur tahmin edin?

Eşitsizlikler nasıl çözülür?

Aralık yöntemi (diğer adıyla aralık yöntemi), eşitsizlikleri çözmenin evrensel bir yolu olarak kabul edilir; bu, verilen eşitsizliğin karşılanacağı tüm aralıkların belirlenmesinden oluşur.

Eşitsizliğin türüne girmeden, bu durumda öz değil, karşılık gelen denklemin çözülmesi ve köklerinin belirlenmesi ve ardından bu çözümlerin sayısal eksende belirtilmesi gerekir.

Bir eşitsizliğin çözümünü yazmanın doğru yolu nedir?

Eşitsizliğin çözümü için aralıkları belirlediğinizde çözümün kendisini doğru bir şekilde yazmanız gerekir. Önemli bir nüans var - aralıkların sınırları çözüme dahil mi?

Burada her şey basit. Denklemin çözümü ODZ'yi sağlıyorsa ve eşitsizlik katı değilse, aralığın sınırı eşitsizliğin çözümüne dahil edilir. Aksi halde hayır.

Her aralık dikkate alındığında eşitsizliğin çözümü, aralığın kendisi veya bir yarım aralık (sınırlarından biri eşitsizliği karşıladığında) veya bir parça (sınırlarıyla birlikte bir aralık) olabilir.

Önemli nokta

Bir eşitsizliğin çözümünün yalnızca aralıklar, yarım aralıklar ve dilimler olabileceğini düşünmeyin. Hayır, çözüme bireysel noktalar da dahil edilebilir.

Örneğin, |x|≤0 eşitsizliğinin tek bir çözümü vardır: 0 noktası.

Ve |x| eşitsizliği

Eşitsizlik hesaplayıcısı ne işe yarar?

Eşitsizlik hesaplayıcısı doğru nihai cevabı verir. Çoğu durumda sayısal bir eksen veya düzlemin gösterimi verilmiştir. Aralıkların sınırlarının çözüme dahil edilip edilmediğini görebilirsiniz; noktalar dolu veya delinmiş olarak görüntülenir.

Çevrimiçi eşitsizlik hesaplayıcısı sayesinde denklemin köklerini doğru bulup bulmadığınızı kontrol edebilir, sayı doğrusunda işaretleyebilir ve aralıklardaki (ve sınırlardaki) eşitsizlik koşullarını kontrol edebilirsiniz.

Cevabınız hesap makinesinin cevabından farklıysa, kesinlikle çözümünüzü tekrar kontrol etmeniz ve yapılan hatayı belirlemeniz gerekir.

Bir insan ne kadar çok anlarsa, anlama arzusu da o kadar güçlü olur

Thomas Aquinas

Aralık yöntemi, modülü içeren herhangi bir denklemi çözmenizi sağlar. Bu yöntemin özü, sayısal ekseni birkaç bölüme (aralıklara) bölmektir ve ekseni, modüllerdeki ifadelerin sıfırlarına bölmek gerekir. Daha sonra, ortaya çıkan bölümlerin her birinde, herhangi bir alt modül ifadesi ya pozitif ya da negatiftir. Bu nedenle modüllerin her biri eksi işaretiyle veya artı işaretiyle genişletilebilir. Bu eylemlerden sonra, yalnızca elde edilen basit denklemlerin her birini söz konusu aralıkta çözmek ve elde edilen cevapları birleştirmek kalır.

Bu yöntemi belirli bir örnek üzerinde ele alalım.

|x + 1| + |2x – 4| – |x + 3| = 2x - 6.

1) Modüllerdeki ifadelerin sıfırlarını bulun. Bunu yapmak için bunları sıfıra eşitliyoruz ve ortaya çıkan denklemleri çözüyoruz.

x + 1 = 0 2x – 4 = 0 x + 3 = 0

x = -1 2x = 4 x = -3

2) Ortaya çıkan noktaları koordinat çizgisi üzerinde istenilen sıraya göre düzenleyin. Tüm ekseni dört bölüme ayıracaklar.

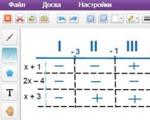
3) Ortaya çıkan bölümlerin her birinde modüllerdeki ifadelerin işaretlerini belirleyelim. Bunu yapmak için, ilgilendiğimiz aralıklardan herhangi bir sayıyı bunların yerine koyarız. Hesaplama sonucu pozitif bir sayı ise tabloya "+", sayı negatif ise "-" koyarız. Bu şu şekilde resimlenebilir:

4) Şimdi tablodaki işaretlerle modülleri açarak dört aralığın her birinde denklemi çözeceğiz. Yani, ilk aralığı düşünün:

I aralığı (-∞; -3). Üzerinde tüm modüller "-" işaretiyle açılır. Aşağıdaki denklemi elde ederiz:

-(x + 1) - (2x - 4) - (-(x + 3)) \u003d 2x - 6. Ortaya çıkan denklemde parantezleri daha önce açarak benzer terimler sunuyoruz:

X - 1 - 2x + 4 + x + 3 = 2x - 6

Alınan cevap dikkate alınan aralığa dahil edilmediğinden son cevaba yazılmasına gerek yoktur.

II aralığı [-3; -1). Tabloda bu aralıkta "-", "-", "+" işaretleri vardır. Orijinal denklemin modüllerini şu şekilde ortaya çıkarıyoruz:

-(x + 1) - (2x - 4) - (x + 3) = 2x - 6. Parantezleri genişleterek basitleştirin:

X - 1 - 2x + 4 - x - 3 \u003d 2x - 6. Ortaya çıkan denklemde aşağıdakileri sunuyoruz:

x = 6/5. Ortaya çıkan sayı, söz konusu aralığa ait olmadığı için orijinal denklemin kökü değildir.

III aralığı [-1; 2). Orijinal denklemin modüllerini üçüncü sütundaki şekildeki işaretlerle açıyoruz. Şunu elde ederiz:

(x + 1) - (2x - 4) - (x + 3) = 2x - 6. Parantezlerden kurtulun, x değişkenini içeren terimleri denklemin sol tarafına, x'i içermeyen terimleri sağa taşıyın . Sahip olacaklar:

x + 1 - 2x + 4 - x - 3 = 2x - 6

2 sayısı dikkate alınan aralığa dahil değildir.

IV aralığı

Basit bir ifadeyle modül “eksisi olmayan bir sayıdır”. Ve bu dualitede (bir yerde orijinal sayıyla hiçbir şey yapmanıza gerek yok, ancak bir yerde bazı eksileri kaldırmanız gerekiyor) ve acemi öğrenciler için tüm zorluk yatıyor.

Bir de geometrik tanımı var. Bunu bilmek de faydalıdır, ancak buna yalnızca geometrik yaklaşımın cebirsel yaklaşımdan daha uygun olduğu karmaşık ve bazı özel durumlarda başvuracağız (spoiler: bugün değil).

Tanım. Gerçek çizgi üzerinde $a$ noktası işaretlensin. Daha sonra $\left| modülü x-a \right|$, bu doğru üzerindeki $x$ noktasından $a$ noktasına olan mesafedir.

Bir resim çizerseniz şöyle bir şey elde edersiniz:

Grafiksel modül tanımı

Öyle ya da böyle, temel özelliği modülün tanımından hemen çıkar: bir sayının modülü her zaman negatif olmayan bir değerdir. Bu gerçek, bugünkü hikayemizin tamamında kırmızı bir iplik olacak.

Eşitsizliklerin çözümü. Aralık Yöntemi

Şimdi eşitsizliklerle ilgilenelim. Birçoğu var ama şimdi görevimiz en azından en basitini çözebilmek. Doğrusal eşitsizliklere ve aralık yöntemine indirgenenler.

Bu konuyla ilgili iki büyük dersim var (bu arada, çok, ÇOK faydalı - çalışmanızı tavsiye ederim):

Eşitsizlikler için aralık yöntemi (özellikle videoyu izleyin);
Kesirli-rasyonel eşitsizlikler çok hacimli bir derstir, ancak ondan sonra hiçbir sorunuz olmayacak.

Bütün bunları biliyorsanız, “eşitsizlikten denkleme geçelim” sözü sizde belli belirsiz kendinizi duvara karşı öldürme isteği uyandırmıyorsa hazırsınız: dersin ana konusuna cehenneme hoş geldiniz. :)

1. "Modül fonksiyondan küçük" formundaki eşitsizlikler

Bu, modüllerde en sık karşılaşılan görevlerden biridir. Formdaki bir eşitsizliği çözmek gerekir:

\[\sol| f\sağ| \ltg\]

Her şey $f$ ve $g$ fonksiyonları gibi davranabilir, ancak bunlar genellikle polinomlardır. Bu tür eşitsizliklere örnekler:

Hepsi şemaya göre tam anlamıyla tek satırda çözüldü:

\[\sol| f\sağ| \lt g\Rightarrow -g \lt f \lt g\quad \left(\Rightarrow \left\( \begin(align) & f \lt g, \\ & f \gt -g \\\end(align) \doğru doğru)\]

Modülden kurtulduğumuzu görmek kolaydır, ancak bunun yerine çifte eşitsizlik (veya aynı şey olan iki eşitsizlik sistemi) elde ederiz. Ancak bu geçiş, olası tüm sorunları kesinlikle hesaba katar: Modülün altındaki sayı pozitifse yöntem işe yarar; negatifse hala çalışıyor; ve $f$ veya $g$ yerine en yetersiz fonksiyonla bile yöntem hala işe yarayacaktır.

Doğal olarak şu soru ortaya çıkıyor: daha kolay değil mi? Ne yazık ki yapamazsınız. Modülün bütün amacı budur.

Ama bu kadar felsefe yeter. Birkaç problemi çözelim:

Görev. Eşitsizliği çözün:

\[\sol| 2x+3\sağ| \ltx+7\]

Çözüm. Yani, "modül küçüktür" biçiminde klasik bir eşitsizliğimiz var - dönüştürülecek hiçbir şey bile yok. Algoritmaya göre çalışıyoruz:

\[\begin(hizala) & \left| f\sağ| \lt g\Rightarrow -g \lt f \lt g; \\ & \sol| 2x+3\sağ| \lt x+7\Rightarrow -\left(x+7 \right) \lt 2x+3 \lt x+7 \\\end(align)\]

Başında "eksi" bulunan parantezleri açmak için acele etmeyin: aceleniz nedeniyle hücum hatası yapmanız oldukça olasıdır.

\[-x-7 \lt 2x+3 \lt x+7\]

\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(align) \right.\]

\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \right.\]

\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \right.\]

Sorun iki temel eşitsizliğe indirgenmiştir. Çözümlerini paralel gerçek çizgiler üzerinde not ediyoruz:
Birçok şeyin kesişimi
Bu kümelerin kesişimi cevap olacaktır.

Cevap: $x\in \left(-\frac(10)(3);4 \right)$

Görev. Eşitsizliği çözün:

\[\sol| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0\]

Çözüm. Bu görev biraz daha zordur. Başlangıç olarak ikinci terimi sağa kaydırarak modülü izole ediyoruz:

\[\sol| ((x)^(2))+2x-3 \sağ| \lt -3\sol(x+1 \sağ)\]

Açıkçası, yine "modül daha az" şeklinde bir eşitsizliğimiz var, bu yüzden zaten bilinen algoritmaya göre modülden kurtuluyoruz:

\[-\left(-3\left(x+1 \right) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \right)\]

Şimdi dikkat: Birisi tüm bu parantezlerle benim biraz sapık olduğumu söyleyecektir. Ama bir kez daha hatırlatıyorum ki asıl amacımız Eşitsizliği doğru bir şekilde çözün ve cevabı alın. Daha sonra, bu derste anlatılan her şeye mükemmel bir şekilde hakim olduğunuzda, kendinizi istediğiniz gibi saptırabilirsiniz: parantezleri açın, eksileri ekleyin vb.

Ve yeni başlayanlar için soldaki çift eksiden kurtuluyoruz:

\[-\left(-3\left(x+1 \right) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\sol(x+1\sağ)\]

Şimdi çift eşitsizlikteki tüm parantezleri açalım:

Çifte eşitsizliğe geçelim. Bu sefer hesaplar daha ciddi olacak:

\[\left\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(hizala) \sağ.\]

\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( hizala)\sağ.\]

Her iki eşitsizlik de karedir ve aralık yöntemiyle çözülür (bu yüzden şunu söylüyorum: ne olduğunu bilmiyorsanız, modülleri henüz ele almamak daha iyidir). Birinci eşitsizlikteki denkleme geçiyoruz:

\[\begin(align) & ((x)^(2))+5x=0; \\ & x\sol(x+5 \sağ)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\bit(hizala)\]

Gördüğünüz gibi çıktının, temel olarak çözülmüş, tamamlanmamış bir ikinci dereceden denklem olduğu ortaya çıktı. Şimdi sistemin ikinci eşitsizliğiyle ilgilenelim. Burada Vieta teoremini uygulamanız gerekir:

\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\bit(hizala)\]

Elde edilen sayıları iki paralel çizgi üzerinde işaretliyoruz (ilk eşitsizlik için ayrı, ikincisi için ayrı):
Yine bir eşitsizlik sistemini çözdüğümüz için, gölgeli kümelerin kesişimiyle ilgileniyoruz: $x\in \left(-5;-2 \right)$. Cevap bu.
Cevap: $x\in \left(-5;-2 \right)$

Bu örneklerden sonra çözüm şemasının çok net olduğunu düşünüyorum:

Diğer tüm terimleri eşitsizliğin karşı tarafına taşıyarak modülü izole edin. Böylece $\left| biçiminde bir eşitsizlik elde ederiz. f\sağ| \ltg$.
Yukarıda anlatıldığı gibi modülden kurtularak bu eşitsizliği çözün. Bir noktada, çifte eşitsizlikten, her biri zaten ayrı ayrı çözülebilen iki bağımsız ifadeden oluşan bir sisteme geçmek gerekli olacaktır.
Son olarak, geriye yalnızca bu iki bağımsız ifadenin çözümlerini çaprazlamak kalıyor - işte bu kadar, nihai cevabı alacağız.

Modülün fonksiyondan büyük olduğu aşağıdaki türdeki eşitsizlikler için benzer bir algoritma mevcuttur. Ancak birkaç ciddi "ama" var. Şimdi bu “ama”lardan bahsedeceğiz.

2. "Modül fonksiyondan büyüktür" şeklindeki eşitsizlikler

Şuna benziyorlar:

\[\sol| f\sağ| \gitmeliyim\]

Öncekine benzer mi? Anlaşılan. Bununla birlikte, bu tür görevler tamamen farklı bir şekilde çözülmektedir. Resmi olarak şema aşağıdaki gibidir:

\[\sol| f\sağ| \gt g\Rightarrow \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(align) \right.\]

Başka bir deyişle iki durumu ele alıyoruz:

İlk önce modülü görmezden geliyoruz - olağan eşitsizliği çözüyoruz;
Daha sonra aslında eksi işaretiyle modülü açıyoruz ve ardından eşitsizliğin her iki kısmını da işaretiyle -1 ile çarpıyoruz.

Bu durumda seçenekler köşeli parantezle birleştirilir; İki gereksinimin birleşimine sahibiz.

Tekrar dikkat edin: önümüzde bir sistem değil, bir bütün var, bu nedenle cevapta kümeler kesişmiyor, birleşiyor. Bu önceki paragraftan temel bir farktır!

Genel olarak birçok öğrencinin birleşimler ve kesişimlerle ilgili kafa karışıklığı vardır, o yüzden gelin bu konuya son kez bakalım:

"∪" bir birleştirme işaretidir. Aslında bu, bize İngilizce dilinden gelen ve "Birlik" kelimesinin kısaltması olan stilize edilmiş bir "U" harfidir, yani. "Dernekler".
"∩" kesişim işaretidir. Bu saçmalık herhangi bir yerden gelmedi, sadece "∪" harfine karşıt olarak ortaya çıktı.

Hatırlamayı daha da kolaylaştırmak için, gözlük yapmak için bu işaretlere bacaklar ekleyin (şimdi beni uyuşturucu bağımlılığını ve alkolizmi teşvik etmekle suçlamayın: bu dersi ciddi şekilde çalışıyorsanız, o zaman zaten bir uyuşturucu bağımlısısınız demektir):

Kümelerin kesişimi ve birleşimi arasındaki fark

Rusçaya çevrildiğinde bu şu anlama gelir: birlik (koleksiyon) her iki gruptan da öğeler içerir, bu nedenle her birinden daha az değildir; ancak kesişim (sistem) yalnızca hem birinci kümede hem de ikinci kümede bulunan öğeleri içerir. Bu nedenle kümelerin kesişimi hiçbir zaman kaynak kümelerden büyük değildir.

Yani daha mı netleşti? Bu harika. Hadi uygulamaya geçelim.

Görev. Eşitsizliği çözün:

\[\sol| 3x+1 \sağ| \gt 5-4x\]

Çözüm. Şemaya göre hareket ediyoruz:

\[\sol| 3x+1 \sağ| \gt 5-4x\Rightarrow \left[ \begin(align) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \right) \\\end(align) \ Sağ.\]

Her bir nüfus eşitsizliğini çözüyoruz:

\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \right.\]

\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \right.\]

\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(align) \right.\]

Ortaya çıkan her kümeyi sayı doğrusunda işaretliyoruz ve sonra bunları birleştiriyoruz:
Setlerin birliği
Açıkçası cevap $x\in \left(\frac(4)(7);+\infty \right)$

Cevap: $x\in \left(\frac(4)(7);+\infty \right)$

Görev. Eşitsizliği çözün:

\[\sol| ((x)^(2))+2x-3 \sağ| \gtx\]

Çözüm. Kuyu? Hayır, hepsi aynı. Modüllü bir eşitsizlikten iki eşitsizlik kümesine geçiyoruz:

\[\sol| ((x)^(2))+2x-3 \sağ| \gt x\Rightarrow \left[ \begin(align) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\end(hizala) \sağ.\]

Her eşitsizliği çözüyoruz. Maalesef orada kökler pek iyi olmayacak:

\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\ &D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\bit(hizala)\]

İkinci eşitsizlikte de biraz oyun var:

\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\ &D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\bit(hizala)\]

Şimdi bu sayıları her eşitsizlik için bir eksen olmak üzere iki eksende işaretlememiz gerekiyor. Ancak noktaları doğru sırayla işaretlemeniz gerekir: sayı ne kadar büyük olursa nokta o kadar sağa kayar.

Ve burada bir kurulum bekliyoruz. $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ sayılarıyla her şey açıksa (birincinin payındaki terimler) kesir ikincinin payındaki terimlerden küçüktür, dolayısıyla toplam da daha küçüktür), $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt) sayılarıyla (21))(2)$ da herhangi bir zorluk olmayacak (pozitif bir sayı açıkça daha negatif), ancak son çiftte her şey o kadar basit değil. Hangisi daha büyük: $\frac(-3+\sqrt(21))(2)$ veya $\frac(-1+\sqrt(13))(2)$? Sayı doğrusu üzerindeki noktaların dizilişi ve aslında cevap bu sorunun cevabına bağlı olacaktır.

Öyleyse karşılaştıralım:

\[\begin(matrix) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matrix)\]

Kökü izole ettik, eşitsizliğin her iki tarafında da negatif olmayan sayılar elde ettik, böylece her iki tarafın karesini alma hakkına sahip olduk:

\[\begin(matrix) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(matrix)\]

Bence bu hiç de akıllıca değil $4\sqrt(13) \gt 3$, yani $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$, son olarak eksenlerdeki noktalar şu şekilde düzenlenecektir:
Çirkin kökler vakası
Size bir kümeyi çözdüğümüzü hatırlatmama izin verin, dolayısıyla cevap taralı kümelerin kesişimi değil, birleşimi olacaktır.

Cevap: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty\right)$

Gördüğünüz gibi şemamız hem basit görevlerde hem de çok zor görevlerde harika çalışıyor. Bu yaklaşımdaki tek "zayıf nokta", irrasyonel sayıları doğru bir şekilde karşılaştırmanız gerektiğidir (ve inanın bana: bunlar sadece kökler değildir). Ancak karşılaştırma sorularına ayrı (ve çok ciddi bir ders) ayrılacaktır. Ve devam ediyoruz.

3. Negatif olmayan "kuyruk"lu eşitsizlikler

Böylece en ilginç olana ulaştık. Bunlar formdaki eşitsizliklerdir:

\[\sol| f\sağ| \gt\sol| g\sağ|\]

Genel olarak konuşursak, şimdi konuşacağımız algoritma sadece modül için geçerlidir. Solda ve sağda negatif olmayan ifadelerin garanti edildiği tüm eşitsizliklerde işe yarar:

Bu görevlerle ne yapmalı? Sadece hatırlıyorum:

Kuyrukları negatif olmayan eşitsizliklerde her iki taraf da herhangi bir doğal güce yükseltilebilir. Hiçbir ek kısıtlama olmayacak.

Her şeyden önce kare almayla ilgileneceğiz - modülleri ve kökleri yakar:

\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f. \\\bit(hizala)\]

Bunu karenin kökünü almakla karıştırmayın:

\[\sqrt(((f)^(2))))=\left| f \sağ|\ne f\]

Bir öğrenci bir modülü kurmayı unuttuğunda sayısız hata yapıldı! Ancak bu tamamen farklı bir hikaye (bunlar irrasyonel denklemler gibi), bu yüzden şimdi buna girmeyeceğiz. Birkaç sorunu daha iyi çözelim:

Görev. Eşitsizliği çözün:

\[\sol| x+2 \sağ|\ge \sol| 1-2x \sağ|\]

Çözüm. Hemen iki şeyi fark ederiz:

Bu katı olmayan bir eşitsizliktir. Sayı doğrusu üzerindeki noktalar işaretlenecektir.

Eşitsizliğin her iki tarafı da açıkça negatif değildir (bu modülün bir özelliğidir: $\left| f\left(x \right) \right|\ge 0$).

Bu nedenle, modülden kurtulmak için eşitsizliğin her iki tarafının karesini alabiliriz ve sorunu olağan aralık yöntemini kullanarak çözebiliriz:

\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\left(x+2 \right))^(2))\ge ((\left(2x-1 \right))^(2)). \\\bit(hizala)\]

Son adımda biraz hile yaptım: Modülün paritesini kullanarak terimlerin sırasını değiştirdim (aslında $1-2x$ ifadesini -1 ile çarptım).

\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ sağ)\sağ)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(align)\]

Aralık yöntemiyle çözüyoruz. Eşitsizlikten denkleme geçelim:

\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\bit(hizala)\]

Bulunan kökleri sayı doğrusunda işaretliyoruz. Bir kez daha: Orijinal eşitsizlik katı olmadığından tüm noktalar gölgelidir!
Modül işaretinden kurtulma
Özellikle inatçı olanlar için hatırlatmama izin verin: Denkleme geçmeden önce yazılan son eşitsizliğin işaretlerini alıyoruz. Ve aynı eşitsizlikte gerekli olan alanları boyuyoruz. Bizim durumumuzda bu $\left(x-3 \right)\left(3x+1 \right)\le 0$.

Tamam artık her şey bitti. Sorun çözüldü.

Cevap: $x\in \left[ -\frac(1)(3);3 \right]$.

Görev. Eşitsizliği çözün:

\[\sol| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \sağ|\]

Çözüm. Her şeyi aynı yapıyoruz. Yorum yapmayacağım - sadece eylemlerin sırasına bakın.

Karesini alalım:

\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \right| \right))^(2))\le ((\left(\left) | ((x)^(2))+3x+4 \sağ| \sağ))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))\le ((\left(((x)^(2))+3x+4 \sağ))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))-((\left(((x)^(2))+3x+4 \ sağ))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x) ^(2))+x+1+((x)^(2))+3x+4 \right)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(align)\]

Aralık yöntemi:

\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ Sağ ok x=-1,5; \\ & 2((x)^(2))+4x+5=0\Rightarrow D=16-40 \lt 0\Rightarrow \varnothing . \\\bit(hizala)\]

Sayı doğrusunda tek bir kök vardır:
Cevap tam bir aralıktır
Cevap: $x\in \left[ -1.5;+\infty \right)$.

Son görevle ilgili küçük bir not. Öğrencilerimden birinin doğru bir şekilde belirttiği gibi, bu eşitsizlikteki her iki alt modül ifadesi de açıkça pozitiftir, dolayısıyla sağlığa zarar vermeden modül işareti atlanabilir.

Ancak bu zaten tamamen farklı bir düşünce düzeyi ve farklı bir yaklaşımdır - buna koşullu olarak sonuçların yöntemi denilebilir. Onun hakkında - ayrı bir derste. Şimdi bugünkü dersin son kısmına geçelim ve her zaman işe yarayan evrensel bir algoritmayı ele alalım. Önceki tüm yaklaşımlar güçsüz olsa bile. :)

4. Seçeneklerin numaralandırılması yöntemi

Peki ya tüm bu hileler işe yaramazsa? Eşitsizlik negatif olmayan kuyruklara inmiyorsa, modülü izole etmek imkansızsa, hiç değilse acı-üzüntü-özlem?

Sonra tüm matematiğin "ağır topları" sahneye çıkıyor - numaralandırma yöntemi. Modül ile ilgili eşitsizliklerle ilgili olarak şöyle görünür:

Tüm alt modül ifadelerini yazın ve bunları sıfıra eşitleyin;
Ortaya çıkan denklemleri çözün ve bulunan kökleri bir sayı doğrusu üzerinde işaretleyin;
Düz çizgi, her modülün sabit bir işarete sahip olduğu ve dolayısıyla açık bir şekilde genişlediği çeşitli bölümlere bölünecektir;
Bu bölümlerin her birinde eşitsizliği çözün (güvenilirlik için paragraf 2'de elde edilen sınır köklerini ayrı ayrı değerlendirebilirsiniz). Sonuçları birleştirin - cevap bu olacak. :)

Peki nasıl? Zayıf? Kolayca! Sadece uzun bir süre için. Pratikte görelim:

Görev. Eşitsizliği çözün:

\[\sol| x+2 \sağ| \lt\sol| x-1 \sağ|+x-\frac(3)(2)\]

Çözüm. Bu saçmalık $\left| gibi eşitsizliklerden ibaret değil f\sağ| \lt g$, $\left| f\sağ| \gt g$ veya $\left| f\sağ| \lt\sol| g \right|$, o halde devam edelim.

Alt modül ifadelerini yazıyoruz, bunları sıfıra eşitliyoruz ve kökleri buluyoruz:

\[\begin(align) & x+2=0\Rightarrow x=-2; \\ & x-1=0\Sağ ok x=1. \\\bit(hizala)\]

Toplamda, sayı doğrusunu üç bölüme ayıran iki kökümüz var ve bu bölümde her modül benzersiz bir şekilde ortaya çıkıyor:
Sayı doğrusunu alt modüler fonksiyonların sıfırlarına bölme
Her bölümü ayrı ayrı ele alalım.

1. $x \lt -2$ olsun. O zaman her iki alt modül ifadesi de negatiftir ve orijinal eşitsizlik şu şekilde yeniden yazılır:

\[\begin(align) & -\left(x+2 \right) \lt -\left(x-1 \right)+x-1,5 \\ & -x-2 \lt -x+1+ x-1,5 \\ & x \gt 1,5 \\\end(align)\]

Oldukça basit bir kısıtlamamız var. Bunu $x \lt -2$ şeklindeki orijinal varsayımla kesiştirelim:

\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1,5 \\\end(align) \right.\Rightarrow x\in \varnothing \]

Açıkçası, $x$ değişkeni aynı anda -2'den küçük ama 1,5'tan büyük olamaz. Bu alanda herhangi bir çözüm bulunmamaktadır.

1.1. Sınır durumunu ayrıca ele alalım: $x=-2$. Bu sayıyı orijinal eşitsizliğin yerine koyalım ve kontrol edelim: geçerli mi?

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=-2) ) \\ & 0 \lt \left| -3 \right|-2-1,5; \\ & 0 \lt 3-3.5; \\ & 0 \lt -0,5\Rightarrow \varnothing . \\\bit(hizala)\]

Açıkçası hesaplama zinciri bizi yanlış eşitsizliğe sürükledi. Bu nedenle orijinal eşitsizlik de yanlıştır ve cevaba $x=-2$ dahil edilmemiştir.

2. Şimdi $-2 \lt x \lt 1$ olsun. Sol modül zaten bir "artı" ile açılacak, ancak sağdaki modül hala "eksi" ile açılacak. Sahibiz:

\[\begin(align) & x+2 \lt -\left(x-1 \right)+x-1,5 \\ & x+2 \lt -x+1+x-1,5 \\& x \lt - 2,5 \\\bitiş(hizalama)\]

Yine orijinal gereksinimle kesişiyoruz:

\[\left\( \begin(align) & x \lt -2,5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]

Ve yine boş çözüm kümesi, çünkü hem -2,5'tan küçük hem de -2'den büyük sayılar yoktur.

2.1. Ve yine özel bir durum: $x=1$. Orijinal eşitsizliği yerine koyarsak:

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=1)) \\ & \sol| 3\sağ| \lt\sol| 0 \right|+1-1,5; \\ & 3 \lt -0,5; \\ & 3 \lt -0,5\Rightarrow \varnothing . \\\bit(hizala)\]

Önceki "özel duruma" benzer şekilde, $x=1$ sayısı cevaba açıkça dahil edilmemiştir.

3. Satırın son parçası: $x \gt 1$. Burada tüm modüller artı işaretiyle genişletilir:

\[\begin(align) & x+2 \lt x-1+x-1,5 \\ & x+2 \lt x-1+x-1,5 \\ & x \gt 4,5 \\ \end(align)\ ]

Ve yine bulunan kümeyi orijinal kısıtlamayla kesiştiriyoruz:

\[\left\( \begin(align) & x \gt 4,5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4,5;+\infty \Sağ)\]

Nihayet! Cevap olacak aralığı bulduk.

Cevap: $x\in \left(4,5;+\infty \right)$

Son olarak, gerçek sorunları çözerken sizi aptalca hatalardan kurtarabilecek bir not:

Eşitsizliklerin modüllerle çözümleri genellikle sayı doğrusu aralıkları ve segmentleri üzerinde sürekli kümelerdir. İzole noktalar çok daha nadirdir. Ve daha da nadiren, çözümün sınırlarının (bölümün sonu) söz konusu aralığın sınırıyla çakıştığı görülür.

Bu nedenle, eğer sınırlar (o çok “özel durumlar”) cevaba dahil edilmezse, o zaman bu sınırların solunda-sağında kalan alanlar da neredeyse kesinlikle cevaba dahil edilmeyecektir. Ve tam tersi: sınıra tepki olarak girildi, bu da etrafındaki bazı bölgelerin de tepki vereceği anlamına geliyor.

Çözümlerinizi kontrol ederken bunu aklınızda bulundurun.

eşitsizlik çözümü modunda çevrimiçi çözüm hemen hemen her eşitsizlik çevrimiçi. Matematiksel çevrimiçi eşitsizlikler matematik çözmek için. Hızlıca bulun eşitsizlik çözümü modunda çevrimiçi. Www.site sitesi bulmanızı sağlar çözüm neredeyse verilen her şey cebirsel, trigonometrik veya çevrimiçi aşkın eşitsizlik. Matematiğin hemen hemen her bölümünü farklı aşamalarda çalışırken, kişinin çevrimiçi eşitsizlikler. Hemen yanıt almak ve en önemlisi doğru yanıt almak için bunu yapmanıza olanak tanıyan bir kaynağa ihtiyacınız var. www.site'ye teşekkürler çevrimiçi eşitsizliği çöz birkaç dakika sürecektir. Matematik çözerken www.sitenin temel avantajı çevrimiçi eşitsizlikler- verilen yanıtın hızı ve doğruluğudur. Site her türlü sorunu çözebilir cebirsel eşitsizlikler çevrimiçi, trigonometrik eşitsizlikler çevrimiçi, aşkın eşitsizlikler çevrimiçi, Ve eşitsizlikler modda bilinmeyen parametrelerle çevrimiçi. eşitsizlikler güçlü bir matematiksel aygıt olarak hizmet eder çözümler pratik görevler. Yardımla matematiksel eşitsizliklerİlk bakışta kafa karıştırıcı ve karmaşık görünebilecek olguları ve ilişkileri ifade etmek mümkündür. bilinmeyen miktarlar eşitsizlikler problemi formüle ederek bulunabilir. matematiksel formdaki dil eşitsizlikler Ve karar vermek modda alınan görev çevrimiçi www.site web sitesinde. Herhangi cebirsel eşitsizlik, trigonometrik eşitsizlik veya eşitsizlikler kapsamak transandantal kolayca özellikleri karar vermekçevrimiçi olun ve doğru cevabı alın. Doğa bilimlerini inceleyen kişi kaçınılmaz olarak şu ihtiyaçla karşılaşır: eşitsizliklerin çözümü. Bu durumda cevabın doğru olması ve modda hemen alınması gerekir. çevrimiçi. Bu nedenle, matematiksel eşitsizlikleri çevrimiçi çözme için vazgeçilmez hesap makineniz olacak www.site sitesini öneriyoruz. cebirsel eşitsizlikleri çevrimiçi çözme, trigonometrik eşitsizlikler çevrimiçi, Ve aşkın eşitsizlikler çevrimiçi veya eşitsizlikler bilinmeyen parametrelerle Çeşitli intravol çözümlerin bulunmasına ilişkin pratik problemler için matematiksel eşitsizlikler kaynak www.. Çözme çevrimiçi eşitsizlikler kendiniz, alınan cevabı kullanarak kontrol etmeniz yararlı olacaktır. eşitsizliklerin çevrimiçi çözümü www.site web sitesinde. Eşitsizliği doğru yazmak ve anında elde etmek gerekir. çevrimiçi çözüm, bundan sonra geriye yalnızca cevabı eşitsizliğe yönelik çözümünüzle karşılaştırmak kalır. Cevabı kontrol etmek bir dakikadan fazla sürmeyecek, yeterli çevrimiçi eşitsizliği çöz ve cevapları karşılaştırın. Bu, hatalardan kaçınmanıza yardımcı olacaktır karar ve cevabı zamanında düzeltin çevrimiçi eşitsizlikleri çözme herhangi biri cebirsel, trigonometrik, aşkın veya eşitsizlik bilinmeyen parametrelerle