O problema B15 é o estudo de uma função usando uma derivada. Investigação de uma função usando uma derivada Investigação de uma função usando uma derivada

No problema B15 propõe-se investigar a função dada pela fórmula dos extremos. Este é um problema padrão em cálculo e sua complexidade varia muito dependendo da função em questão: alguns deles são resolvidos literalmente verbalmente, enquanto outros requerem reflexão séria.

Antes de aprender os métodos de solução, é necessário dominar alguns termos da área de análise matemática. Assim, no problema B15, é necessário encontrar as seguintes quantidades usando a derivada:

1. Pontos de máximo local (mínimo) - o valor da variável em que a função atinge seu valor máximo (menor). Esses pontos também são chamados de pontos extremos.
2. O máximo (mínimo) global da função é o valor máximo (menor) da função sob as restrições especificadas. Outro nome são extremos globais.

Neste caso, os extremos globais geralmente não são procurados em todo o domínio da definição da função, mas apenas em um determinado segmento. É importante compreender que o extremo global e o valor da função no ponto extremo nem sempre coincidem. Vamos explicar isso com um exemplo específico:

Tarefa. Encontre o ponto mínimo e o valor mínimo da função y = 2x 3 − 3x 2 − 12x + 1 no segmento [−3; 3].

Primeiro encontramos o ponto mínimo, para o qual calculamos a derivada:
y' = (2x 3 - 3x 2 - 12x + 1)' = 6x 2 - 6x - 12.

Vamos encontrar os pontos críticos resolvendo a equação y' = 0. Obtemos a equação quadrática padrão:
y' = 0 ⇒ 6x 2 - 6x - 12 = 0 ⇒ ... ⇒ x 1 = -1, x 2 = 2.

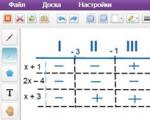
Marcamos esses pontos na linha de coordenadas, adicionamos os sinais da derivada e das restrições - as extremidades do segmento:

A escala da imagem não importa. O mais importante é marcar os pontos na sequência correta. É sabido pelo curso de matemática escolar que no ponto mínimo a derivada muda de sinal de menos para mais. A leitura vai sempre da esquerda para a direita - na direção do semieixo positivo. Portanto, existe apenas um ponto mínimo: x = 2.

Agora vamos encontrar o valor mínimo da função no segmento [−3; 3]. É alcançado no ponto mínimo (então se torna o ponto mínimo global) ou no final do segmento. Observe que no intervalo (2; 3) a derivada é positiva em todos os lugares, o que significa que y(3) > y(2), portanto a extremidade direita do intervalo pode ser ignorada. Restam apenas os pontos x = −3 (extremidade esquerda do segmento) e x = 2 (ponto mínimo). Nós temos:
y(−3) = 2(−3) 3 − 3(−3) 2 − 12(−3) + 1 = −44;
y(2) = 2*2 3 - 3*2 2 - 12*2 + 1 = -19.

Assim, o menor valor da função é alcançado no final do segmento e é igual a −44.

Resposta: xmin = 2; ymin = −44

Do raciocínio acima decorre um fato importante, que muitas pessoas esquecem. A função assume o valor máximo (mínimo), não necessariamente no ponto extremo. Às vezes, esse valor é alcançado no final do segmento, e a derivada ali não precisa ser igual a zero.

Esquema de resolução de problemas B15

Se no problema B15 for necessário encontrar o valor máximo ou mínimo da função f(x) no intervalo, realizamos as seguintes ações:

1. Resolva a equação f'(x) = 0. Se não houver raízes, pule a terceira etapa e vá direto para a quarta.
2. Do conjunto de raízes resultante, exclua tudo o que estiver fora do segmento. Os números restantes serão denotados por x 1 , x 2 , ..., x n - como regra, serão poucos.
3. Substitua as extremidades do segmento e os pontos x 1 , x 2 , ..., x n na função original. Obtemos um conjunto de números f (a), f (b), f (x 1), f (x 2), ..., f (x n), dos quais selecionamos o maior ou menor valor - este será a resposta.

Um pequeno esclarecimento sobre o apagamento das raízes quando coincidem com as extremidades do segmento. Eles também podem ser riscados, pois na quarta etapa as extremidades do segmento ainda são substituídas na função - mesmo que a equação f’(x) = 0 não tivesse soluções.

Tarefa. Encontre o valor máximo da função y = x 3 + 3x 2 − 9x − 7 no segmento [−5; 0].

Primeiro, vamos encontrar a derivada: y' = (x 3 + 3x 2 - 9x - 7)' = 3x 2 + 6x - 9.

Então resolvemos a equação: y’ = 0 ⇒ 3x 2 + 6x − 9 = 0 ⇒ ... ⇒ x = −3; x = 1.

Risque a raiz x = 1 porque ela não pertence ao intervalo [−5; 0].

Resta calcular o valor da função nas extremidades do segmento e no ponto x = −3:
y(−5) = (−5) 3 + 4 (−5) 2 − 9 (−5) − 7 = −12;
y(−3) = (−3) 3 + 4 (−3) 2 − 9 (−3) − 7 = 20;
y(0) = 0 3 + 4 0 2 − 9 0 − 7 = −7.

Obviamente, o maior valor é 20 - é alcançado no ponto x = −3.

Agora considere o caso em que é necessário encontrar o ponto máximo ou mínimo da função f(x) no intervalo . Se o segmento não for especificado, a função é considerada no seu domínio de definição. Em qualquer caso, o esquema de solução é o seguinte:

1. Encontre a derivada da função: f'(x).
2. Resolva a equação f’(x) = 0. Se a derivada for uma função racional fracionária, descobrimos adicionalmente quando seu denominador é zero. Vamos denotar as raízes obtidas x 1 , x 2 , ..., x n .
3. Marque x 1 , x 2 , ..., x n na linha de coordenadas e coloque os sinais que a derivada assume entre esses números. Se for fornecido um segmento, marque-o e risque tudo o que estiver fora dele.
4. Entre os restantes pontos, procuramos aquele em que o sinal da derivada muda de menos para mais (este é o ponto mínimo) ou de mais para menos (ponto mínimo). Deve haver apenas um desses pontos - esta será a resposta.

Um leitor atento certamente notará que para algumas funções esse algoritmo não funciona. Na verdade, existe toda uma classe de funções para as quais encontrar pontos extremos requer cálculos mais complexos. No entanto, tais funções não são encontradas no exame de matemática.

Preste atenção na colocação dos sinais entre os pontos x 1 , x 2 , ..., x n . Lembre-se: ao passar por uma raiz de multiplicidade par, o sinal da derivada não muda. Ao procurar pontos extremos, os sinais são sempre vistos da esquerda para a direita, ou seja, ao longo do eixo numérico.

Tarefa. Encontre o ponto máximo de uma função

no segmento [−8; 8].

Vamos encontrar a derivada:

Como esta é uma função racional fracionária, igualamos a derivada e seu denominador a zero:
y' = 0 ⇒ x 2 − 25 = 0 ⇒ ... ⇒ x = 5; x = −5;
x 2 \u003d 0 ⇒ x \u003d 0 (a raiz da segunda multiplicidade).

Vamos marcar os pontos x = −5, x = 0 e x = 5 na linha de coordenadas, organizar os sinais e limites:

Obviamente, apenas um ponto x = −5 permanece dentro do segmento, no qual o sinal da derivada muda de mais para menos. Este é o ponto máximo.

Mais uma vez, vamos explicar como os pontos extremos diferem dos próprios extremos. Os pontos extremos são os valores das variáveis ​​​​nos quais a função assume o maior ou o menor valor. Os extremos são os valores das próprias funções, máximo ou mínimo em alguma de suas vizinhanças.

Além de polinômios comuns e funções racionais fracionárias, os seguintes tipos de expressões ocorrem no Problema B15:

1. funções irracionais,
2. funções trigonométricas,
3. funções exponenciais,
4. Funções logarítmicas.

Via de regra, não há problemas com funções irracionais. Os demais casos merecem ser considerados com mais detalhes.

Funções trigonométricas

A principal dificuldade das funções trigonométricas é que, ao resolver equações, surge um número infinito de raízes. Por exemplo, a equação sin x = 0 tem raízes x = πn, onde n ∈ Z. Bem, como marcá-los na linha de coordenadas se existem infinitos números desse tipo?

A resposta é simples: você precisa substituir valores específicos de n. Na verdade, nos problemas B15 com funções trigonométricas há sempre uma restrição - um segmento. Portanto, para começar, tomamos n = 0 e depois aumentamos n até que a raiz correspondente “voe” além do segmento. Da mesma forma, diminuindo n, muito em breve obteremos uma raiz menor que o limite inferior.

É fácil mostrar que não existem no segmento outras raízes além das obtidas no processo considerado. Consideremos agora este processo com exemplos concretos.

Tarefa. Encontre o ponto máximo da função y = sin x − 5x sin x − 5cos x + 1 pertencente ao intervalo [−π/3; π/3].

Calcule a derivada: y’ = (sen x − 5x sin x − 5cos x + 1)’ = ... = cos x − 5x cos x = (1 − 5x) cos x.

Então resolvemos a equação: y’ = 0 ⇒ (1 − 5x) cos x = 0 ⇒ ... ⇒ x = 0,2 ou x = π/2 + πn, n ∈ Z.

Com a raiz x = 0,2, tudo fica claro, mas a fórmula x = π / 2 + πn requer processamento adicional. Substituiremos diferentes valores de n, começando em n = 0.

n = 0 ⇒ x = π/2. Mas π/2 > π/3, então a raiz x = π/2 não está incluída no segmento original. Além disso, quanto maior n, maior x, portanto não faz sentido considerar n > 0.

n = −1 ⇒ x = − π/2. Mas −π/2< −π/3 - этот корень тоже придется отбросить. А вместе с ним - и все корни для n < −1.

Acontece que no intervalo [−π/3; π/3] reside apenas na raiz x = 0,2. Marcamos junto com sinais e limites na linha de coordenadas:

Para ter certeza de que a derivada à direita de x = 0,2 é realmente negativa, basta substituir o valor x = π/4 em y’. Apenas notamos que no ponto x = 0,2, a derivada muda de sinal de mais para menos e, portanto, este é o ponto máximo.

Tarefa. Encontre o maior valor da função y = 4tg x − 4x + π − 5 no intervalo [−π/4; π/4].

Calcule a derivada: y’ = (4tg x − 4x + π − 5)’ = 4/cos 2x − 4.

Então resolvemos a equação: y’ = 0 ⇒ 4/cos 2x − 4 = 0 ⇒ ... ⇒ x = πn, n ∈ Z.

Extraímos as raízes desta fórmula substituindo n específico, começando em n = 0:
n = 0 ⇒ x = 0. Essa raiz nos convém.
n = 1 ⇒ x = π. Mas π > π/4, então a raiz x = π e os valores n > 1 devem ser riscados.
n = −1 ⇒ x = −π. Mas π< −π/4, поэтому x = π и n < −1 тоже вычеркиваем.

De toda a variedade de raízes, resta apenas uma: x = 0. Portanto, calculamos o valor da função para x = 0, x = π/4 e x = −π/4.
y(0) = 4tg 0 − 4 0 + π − 5 = π − 5;
y(π/4) = 4tg (π/4) − 4 π/4 + π − 5 = −1;
y(π/4) = 4tg (−π/4) − 4 (−π/4) + π − 5 = ... = 2π − 9.

Agora observe que π = 3,14...< 4, поэтому π − 5 < 4 − 5 = −1 и 2π − 9 < 8 − 9 = −1. Получается одно положительное число и два отрицательных. Мы ищем наибольшее - очевидно, это y = −1.

Observe que no último problema foi possível não comparar os números entre si. Na verdade, dos números π - 5, 1 e 2π - 9, apenas um pode ser escrito na folha de respostas. Na verdade, como escrever na forma, digamos, o número π? Mas de jeito nenhum. Esta é uma característica importante da primeira parte do exame de matemática, que simplifica muito a solução de muitos problemas. E não funciona só no B15.

Às vezes, ao estudar uma função, surgem equações que não têm raízes. Neste caso, o problema torna-se ainda mais simples, pois resta considerar apenas as extremidades do segmento.

Tarefa. Encontre o menor valor da função y = 7sin x − 8x + 5 no intervalo [−3π/2; 0].

Primeiro encontramos a derivada: y’ = (7sin x − 8x + 5)’ = 7cos x − 8.

Vamos tentar resolver a equação: y' = 0 ⇒ 7cos x − 8 = 0 ⇒ cos x = 8/7. Mas os valores de cos x sempre estão no intervalo [−1; 1] e 8/7 > 1. Portanto, não há raízes.

Se não houver raízes, nada precisa ser riscado. Passamos para a última etapa - calculamos o valor da função:
y(−3π/2) = 7sen (−3π/2) − 8 (−3π/2) + 5 = ... = 12π + 12;
y(0) = 7sen 0 − 8 0 + 5 = 5.

Como o número 12π + 12 não pode ser escrito na folha de respostas, resta apenas y = 5.

funções exponenciais

De um modo geral, uma função exponencial é uma expressão da forma y = a x , onde a > 0. Mas no Problema B15, apenas ocorrem funções da forma y = e x e, no caso extremo, y = e kx + b. A razão é que as derivadas destas funções são muito fáceis de calcular:

1. (e x)" = e x . Nada mudou.
2. (e kx + b)" = k e kx + b. Um fator igual ao coeficiente da variável x é simplesmente adicionado. Este é um caso especial da derivada de uma função complexa.

Todo o resto é absolutamente padrão. É claro que as funções reais nos problemas B15 parecem mais severas, mas o esquema de solução não muda com isso. Consideremos alguns exemplos, destacando apenas os pontos principais da solução - sem raciocínios e comentários minuciosos.

Tarefa. Encontre o menor valor da função y = (x 2 − 5x + 5)e x − 3 no intervalo [−1; 5].

Derivada: y’ = ((x 2 − 5x + 5)e x − 3)’ = ... = (x 2 − 3x)e x − 3 = x(x − 3)e x − 3 .

Encontre as raízes: y' = 0 ⇒ x(x − 3)e x − 3 = 0 ⇒ ... ⇒ x = 0; x=3.

Ambas as raízes estão no intervalo [−1; 5]. Resta encontrar o valor da função em todos os pontos:
y(−1) = ((−1) 2 − 5 (−1) + 5)e − 1 − 3 = ... = 11 e −4 ;
y(0) = (0 2 − 5 0 + 5)e 0 − 3 = ... = 5 e −3 ;
y(3) = (3 2 − 5 3 + 5)e 3 − 3 = ... = −1;
y(5) = (5 2 − 5 5 + 5)e 5 − 3 = ... = 5 e 2 .

Dos quatro números obtidos, apenas y = −1 pode ser escrito na forma. Além disso, este é o único número negativo - será o menor.

Tarefa. Encontre o valor máximo da função y = (2x − 7) e 8 − 2x no segmento .

Derivada: y’ = ((2x − 7) e 8 − 2x)’ = ... = (16 − 4x) e 8 − 2x = 4(4 − x) e 8 − 2x .

Encontramos as raízes: y' = 0 ⇒ 4(4 − x) e 8 − 2x = 0 ⇒ x = 4.

A raiz x = 4 pertence ao segmento . Estamos procurando valores de função:
y(0) = (2 0 − 7)e 8 − 2 0 = ... = −7 e 8 ;
y(4) = (2 4 − 7)e 8 − 2 4 = ... = 1;
y(6) = (2 6 − 7)e 8 − 2 6 = ... = 5 e −4 .

Obviamente, apenas y = 1 pode servir como resposta.

Funções logarítmicas

Por analogia com funções exponenciais, apenas logaritmos naturais ocorrem no problema B15, pois sua derivada é facilmente calculada:

1. (lnx)' = 1/x;
2. (ln(kx + b))' = k/(kx + b). Em particular, se b = 0, então (ln(kx))' = 1/x.

Assim, a derivada será sempre uma função racional fracionária. Resta apenas igualar esta derivada e seu denominador a zero e então resolver as equações resultantes.

Para encontrar o valor máximo ou mínimo de uma função logarítmica, lembre-se que o logaritmo natural se torna um número "normal" apenas em pontos da forma e n . Por exemplo, ln 1 \u003d ln e 0 \u003d 0 é um zero logarítmico e, na maioria das vezes, a solução é reduzida a ele. Em outros casos, é impossível “remover” o sinal do logaritmo.

Tarefa. Encontre o menor valor da função y = x 2 − 3x + ln x no segmento .

Consideramos a derivada:

Encontramos os zeros da derivada e seu denominador:
y' = 0 ⇒ 2x 2 − 3x + 1 = 0 ⇒ ... ⇒ x = 0,5; x = 1;
x = 0 - não há nada para decidir.

Dos três números x = 0, x = 0,5 e x = 1, apenas x = 1 está dentro do segmento, e o número x = 0,5 é o seu fim. Nós temos:
y(0,5) = 0,5 2 − 3 0,5 + ln 0,5 = ln 0,5 − 1,25;
y(1) = 1 2 − 3 1 + log 1 = −2;
y(5) = 5 2 − 3 5 + ln 5 = 10 + ln 5.

Dos três valores obtidos, apenas y = −2 não contém o sinal do logaritmo - esta será a resposta.

Tarefa. Encontre o maior valor da função y = ln(6x) − 6x + 4 no segmento .

Calculamos a derivada:

Descobrimos quando a derivada ou seu denominador é igual a zero:
y' = 0 ⇒ 1 − 6x = 0 ⇒ x = 1/6;
x = 0 - já decidido.

Riscamos o número x = 0, pois está fora do segmento. Consideramos o valor da função nas extremidades do segmento e no ponto x = 1/6:
y(0,1) = ln(6 0,1) − 6 0,1 + 4 = ln 0,6 + 3,4;
y(1/6) = log(6 1/6) − 6 1/6 + 4 = log 1 + 3 = 3;
y(3) = ln(6 3) − 6 3 + 4 = ln 18 − 14.

Obviamente, apenas y = 3 pode atuar como resposta - os demais valores contêm o sinal do logaritmo e não podem ser anotados na folha de respostas.

O ponto é chamado ponto máximo (mínimo) função , se existe uma vizinhança do ponto tal que para toda essa vizinhança a desigualdade ().

Os pontos máximo e mínimo de uma função são chamados de pontos. extremo (Fig. 25).

Teorema 3.9 (condição necessária para a existência de pontos extremos) . Em pontos críticos do 1º tipo, a derivada da função também

é zero ou não existe

Os pontos críticos do 1º tipo são geralmente chamados simplesmente de pontos críticos.

Os pontos críticos nos quais a derivada de uma função é igual a zero são chamados pontos de estacionariedade . Os pontos críticos nos quais uma função é contínua, mas não diferenciável, são chamados pontos de canto . Por exemplo, uma função em um ponto é contínua, mas não possui derivada, pois neste ponto um número infinito de tangentes pode ser traçado ao gráfico da função (Fig. 26). Este caso pode ser considerado como uma confirmação de que a afirmação inversa do Teorema 3.3 é falsa.

A função é chamada aumentando em algum intervalo, se neste intervalo o maior valor do argumento corresponde ao maior valor da variável, e minguante se o valor maior do argumento corresponder ao valor menor da variável.

Para futuras pesquisas, os pontos críticos são colocados em um eixo numérico, que é dividido por esses pontos em intervalos, após os quais são verificadas as seguintes condições suficientes.

Teorema 3.10 (condição suficiente para uma função aumentar e diminuir). Se uma função é derivável em algum intervalo e sua derivada é positiva (negativa), então a função é crescente (decrescente) neste intervalo

Teorema 3.11 (condição suficiente para a existência de pontos extremos de uma função). Se a função é contínua e diferenciável em alguma vizinhança do ponto crítico, e ao passar por ela a derivada muda de sinal de mais para menos, então o ponto é um ponto de máximo; se de menos para mais, então o ponto é o ponto mínimo da função

Aqueles pontos críticos da função para os quais a condição suficiente não é satisfeita permanecem simplesmente pontos críticos do primeiro tipo.

Os pontos críticos de 1º tipo, nos quais não existe derivada, são divididos em duas classes:

são pontos nos quais a função é contínua (quando o Teorema 3.11 é satisfeito para eles, a função tem um extremo “agudo” nesses pontos), estes são canto pontos;

são os pontos em que a função sofre uma descontinuidade (passam sempre para a classe dos pontos críticos de 2º tipo).

Mas o estudo realizado desta forma não dá resposta a uma questão muito importante: como a função aumenta (diminui) - convexa ou côncava? A resposta a esta questão é dada por um estudo mais aprofundado da função usando a segunda derivada. Vamos dar uma série de definições necessárias.

A função é chamada convexo (côncavo) em algum intervalo, se a tangente desenhada ao gráfico da função em cada ponto desse intervalo estiver acima (abaixo) do gráfico da função.

Os pontos que separam as áreas de convexidade das áreas de concavidade de uma função são chamados de pontos de inflexão (Fig. 27).

Teorema 3.12 (condição necessária para a existência de pontos de inflexão). Em pontos críticos de 2º tipo, a segunda derivada da função é zero ou não existe

Para futuras pesquisas, pontos críticos de 2º tipo são colocados em um eixo numérico, que é dividido por esses pontos em intervalos, após os quais são verificadas as seguintes condições suficientes.

Teorema 3.13 (condição suficiente para convexidade e concavidade de uma função). Se uma função é duas vezes diferenciável em algum intervalo e sua segunda derivada é positiva (negativa), então a função é côncava (convexa) neste intervalo

Aqueles pontos críticos da função para os quais a condição suficiente não é satisfeita permanecem simplesmente pontos críticos do segundo tipo.

Os pontos críticos de 2º tipo, nos quais não existe a segunda derivada, são divididos em duas classes:

- pontos nos quais a função é contínua, são os chamados pontos de inflexão "afiados" - nesses pontos, um número infinito de tangentes pode ser traçado ao gráfico da função (Fig. 28);

são os pontos em que a função sofre uma descontinuidade (nos pontos de descontinuidade de 2º tipo, o gráfico da função possui uma assíntota vertical).

Para a enumeração final dos pontos extremos e de inflexão da função, é necessário encontrar suas ordenadas e, a seguir, escrever os pontos indicados com duas coordenadas.

Perguntas para auto-exame.

1. Quais pontos são chamados de pontos extremos (máximo e mínimo) de uma função?

2. Qual função é chamada de crescente (decrescente)?

3. Quais são as condições necessárias e suficientes para a existência de pontos extremos de uma função?

4. Qual é a condição suficiente para o aumento (diminuição) de uma função?

5. Quais pontos são chamados de pontos de inflexão de uma função?

6. Qual função é chamada de convexa (côncava)?

7. Quais são as condições necessárias e suficientes para a existência de pontos de inflexão de uma função?

8. Qual é a condição suficiente para a convexidade (concavidade) de uma função?

O objetivo da lição: Ensinar a realizar um estudo de funções; plotá-los.

Forma: aula de conversação.

Métodos: diálogo, recursos visuais e slides.

Equipamento: TIC, tabelas.

Durante as aulas

I. Verificando o dever de casa.

Professor: - Pessoal! Você fez seu dever de casa "Pontos críticos de uma função, máximos e mínimos". Defina o ponto crítico de uma função.

Aluno: - Um ponto crítico é um ponto interno do domínio de definição, no qual a derivada é igual a zero ou não existe.

Professor: - Como encontrar pontos críticos?

Aluno: - 1

) Encontre a derivada da função;

2) Resolva a equação: f "(x) = 0. As raízes desta equação são pontos críticos.

Professor: - Encontre os pontos críticos das funções:

a)f(x)= 4 - 2x + 7x 2

b) f (x) \u003d 4x - x 3/3

a) 1) Encontre a derivada desta função:

f "(x)= (4 - 2x + 7x 2)" = -2+14x

2) Resolva a equação f "(x) = 0<=>-2+14x=0<=>x=1/7

3) Como a equação f "(x) \u003d 0 tem uma raiz, então esta função tem um ponto crítico x \u003d 1/7.

b) 1) Encontre a derivada desta função: f "(x) \u003d 4 - x 2

2) Resolva a equação: f "(x) = 0<=>4 - x 2 = 0<=>x=2 ou x=-2

3) Como a equação f "(x) \u003d 0 tem duas raízes, então esta função tem dois pontos críticos x 1 \u003d 2 e x 2 \u003d -2.

II.trabalho oral.

Professor: - Pessoal! Vamos repetir as principais questões necessárias para estudar um novo tema. Para fazer isso, considere tabelas com figuras ( Anexo 1).

Indique os pontos em que o aumento da função é substituído por uma diminuição. Como são chamados esses pontos?

Aluno: - Na figura a) - o ponto K é o ponto máximo, na figura b) - o ponto M é o ponto máximo.

Professor: - Quais são os pontos mínimos da função.

Aluno: - Ponto K na figura c) ed) - o ponto mínimo da função.

Professor: - Quais pontos podem ser pontos extremos da função?

Aluno: - Os pontos críticos podem ser pontos extremos de uma função.

Professor: - Quais são as condições necessárias que você conhece?

Aluno: - Existe o teorema de Fermat. Condição necessária para um extremo: Se o ponto x 0 é o ponto extremo da função f e neste ponto existe uma derivada f ", então é igual a zero: f" (x) \u003d 0.

Professor: - Encontre os pontos críticos para a função:

uma)f(x) = | x |

b) f(x) = 2x + | x |

Aluno: - Considere a função f(x) = | x | ( aplicação 2). Esta função não tem derivada em 0. Portanto, 0 é um ponto crítico. Obviamente, a função tem um mínimo no ponto 0.

Aluno: - Considere a função f(x) = 2x + | x | ( apêndice 3). O gráfico mostra que no ponto 0 esta função não tem extremo. Neste ponto, a função também não tem derivada.

Na verdade, se assumirmos que a função f tem uma derivada em 0, então f(x) - 2x também tem uma derivada em 0. Mas f(x) - 2x = | x |, e a função | x | no ponto 0 não é diferenciável, ou seja, chegamos a uma contradição.

Isso significa que a função f no ponto 0 não tem derivada.

Professor: - Do teorema de Fermat segue-se que ao encontrar pontos extremos, é necessário encontrar pontos críticos. Mas a partir dos exemplos considerados fica claro que para que este ponto crítico seja um ponto extremo, é necessária alguma condição adicional.

Quais são as condições suficientes para a existência de um extremo em um ponto que você conhece?

Estudante: - Sinal da função máxima: Se a função f é contínua no ponto x 0, e f "(x)> 0 no intervalo (a; x 0) e f "(x)<0 на интервале (х 0 ; в), то точка х 0 является точкой максимума функции f.

Ou seja, se no ponto x 0 a derivada muda de sinal de mais para menos, então x 0 é o ponto máximo.

Estudante: - Sinal de mínimo: Se a função f é contínua no ponto x 0, e f "(x)<0 на интервале (а;х 0) и f "(x) >0 no intervalo (x 0 ; c), então o ponto x 0 é o ponto mínimo da função f.

Ou seja, se no ponto x 0 a derivada muda de sinal de menos para mais, então x 0 é o ponto mínimo.

Professor: - E qual algoritmo para encontrar os pontos extremos de uma função você conhece.

O aluno explica o algoritmo para estudar a função f para um extremo usando a derivada ( anexo 4) e encontra os pontos extremos da função:

f (x) \u003d x 4 -2x 2

D (f) =IR e f é contínua em toda a reta real, como uma função racional inteira.

2. f "(x) \u003d 4x 3 -4x \u003d 4x (x + 1) (x-1).

3.f"(x)=0<=>x= -1 V x=0 V x=1.

Fig.1 (sinais f ")

Como f é contínuo em pontos críticos, da Figura 1 ( anexo 5) pode-se observar que -1 e 1 são os pontos mínimos, e 0 é o ponto máximo da função f.

f min \u003d f (-1) \u003d f (1) \u003d -1, f max \u003d f (0) \u003d 0.

Professor: - Pessoal! Vamos relembrar o algoritmo para encontrar intervalos de monotonicidade da função f.

O aluno lembra o algoritmo para encontrar intervalos de monotonicidade da função f ( anexo 6).

Professor: - Encontre os intervalos de aumento e diminuição da função f dados pela fórmula

f (x) \u003d x 3 -12x

Solução:

1. Como f(x) é um polinômio, então D (f) =IR.

2. A função f é diferenciável em toda a reta real e f "(x) \u003d 3x 2 -12 \u003d 3 (x + 2) (x-2).

3. Apenas zeros de f "(x) podem ser pontos críticos da função f.

f"(x)=0<=>x \u003d -2 V x \u003d 2.

D (f) \ (-2; 2) \u003d (-; -2) U (-2; 2) U (2; +).

Fig.2 (sinais f ").

Encontre os domínios de definição e os valores da função f dada.

Descubra se a função possui características que facilitam o estudo, ou seja, é a função f:

a) par ou ímpar;

b) periódico.

3. Calcule as coordenadas dos pontos de intersecção do gráfico com os eixos coordenados.

4. Encontre intervalos de constância da função f.

5. Descubra em quais intervalos a função f aumenta e em quais diminui.

6. Encontre pontos extremos (máximo ou mínimo) e calcule os valores de f nesses pontos.

7. Investigue o comportamento da função f na vizinhança de pontos característicos que não estão incluídos no domínio de definição.

8. Faça um gráfico da função.

Este diagrama é ilustrativo.

Considerando tudo isso, examinamos a função: f (x) \u003d 3x 5 -5x 3 +2 e construímos seu gráfico.

Vamos fazer a pesquisa da seguinte forma:

D (f ") =IR, já que f (x) é um polinômio.

A função f não é par nem ímpar, porque

f (-x)= 3(-x) 5 -5(-x) 3 +2 = -3x 5 +5x 3 +2= -(3x 5 -5x 3 -2) f(x)

Encontre as coordenadas dos pontos de intersecção do gráfico com os eixos coordenados:

a) com o eixo 0X, para isso resolvemos a equação: 3x 5 -5x 3 +2 = 0.

O método de seleção pode encontrar uma das raízes (x = 1). Outras raízes só podem ser encontradas aproximadamente. Portanto, para esta função não encontraremos os demais pontos de intersecção do gráfico com o eixo das abcissas e intervalos de sinal constante.

b) com eixo 0Y: f(0)=2

Ponto A (0; 2) - o ponto de intersecção do gráfico da função com o eixo 0Y.

Notamos que não encontraremos intervalos de constância de sinal.

Encontre os intervalos de aumento e diminuição da função

a) f "(x) \u003d 15x 4 -15x 2 \u003d 15x 2 (x 2 -1)

D (f ") \u003d IR, portanto não há pontos críticos dos quais f "(x) não existe.

b) f "(x) \u003d 0 se x 2 (x 2 -1) \u003d 0<=>x = -1 V x = 0 V x = 1.

c) Obtemos três pontos críticos, eles dividem a linha de coordenadas em quatro intervalos. Vamos determinar o sinal da derivada nestes intervalos:

Fig.3 (sinais f")

4. Corrigindo um novo tópico. Solução de problemas.

Professor: - Explore a função e construa seu gráfico: f (x) \u003d x 4 -2x 2 -3.

Aluno: - 1) D (f) =R.

2) f (-x) \u003d (-x) 4 -2 (-x) 2 -3 \u003d x 4 -2x 2 -3; f(-x) = f(x),

portanto, a função f é par. Pode ser estudado no intervalo em que a função aumenta de - a -4, portanto, a equação f (x) \u003d 0 não tem raízes neste intervalo.

b) No intervalo [-1; 2] a equação também não tem raízes, pois neste intervalo a função diminui de -4 a -31.

c) No intervalo e diminui em [-∞;-1].

Pontos extremos: x min = -1

Extremos da função: y min =y(-1)=1-2= -1

Capítulo III. Pesquisa funcional.

3.1. Esquema geral de estudo de funções.

Ao examinar uma função, você precisa conhecer o esquema geral de pesquisa:

1) D(y) – domínio de definição (intervalo da variável x)

2) E(y) – área do valor x (intervalo da variável y)

3) Tipo de função: função par, ímpar, periódica ou geral.

4) Pontos de intersecção do gráfico da função com os eixos Ohi Oy (se possível).

5) Intervalos de constância de sinal:

a) a função assume um valor positivo: f(x)>0

b) valor negativo: f(x)<0.

6) Intervalos de monotonicidade da função:

a) aumentar;

b) diminuir;

c) constância (f=const).

7) Pontos extremos (pontos mínimos e máximos)

8) Extremos da função (valor da função nos pontos mínimo e máximo)

9) Pontos adicionais.

Eles podem ser obtidos para traçar a função com mais precisão.

Deve-se notar que os extremos da função f nem sempre coincidem com os valores máximo e mínimo da função.

3.2. Sinal de funções crescentes e decrescentes.

Se você construir um gráfico de uma função usando alguns de seus pontos escolhidos arbitrariamente, conectando-os com uma linha suave, mesmo com um número muito grande de pontos selecionados aleatoriamente, pode acontecer que o gráfico construído desta forma seja muito diferente do gráfico de uma determinada função.

Se, ao estudar uma função, usarmos a derivada e encontrarmos os chamados pontos de "referência", ou seja, pontos de quebra, pontos máximos e mínimos, intervalos de monotonicidade da função, então mesmo com um pequeno número desses pontos de “referência”, teremos a ideia correta do gráfico da função.

Antes de passar aos exemplos, darei as definições e teoremas necessários.

Definição de monotonicidade de uma função em um intervalo A função y \u003d f (x) é chamada crescente no intervalo, se para quaisquer pontos x 1 e x 2 deste intervalo da condição x 1<х 2 следует, что f(x 1)f(x 2), então a função é chamada decrescente neste intervalo.

Critério suficiente para a monotonicidade de uma função em um intervalo. Teorema: se uma função tem uma derivada positiva (negativa) em cada ponto de um intervalo, então a função aumenta (diminui) neste intervalo.

Este teorema é aceito em livros escolares sem prova.

A interpretação geométrica do teorema é muito simples, se lembrarmos que f '(x) \u003d tgα, α é a inclinação da tangente ao gráfico da função em um determinado ponto x. Se, por exemplo, f ‘(x)> 0 em todos os pontos de um determinado intervalo, então a tangente ao gráfico com o eixo das abcissas forma ângulos agudos, o que significa que f (x) também aumenta com x. Se f'(x)<0, то касательная с осью абсцисс образуют тупой угол, а значит, с ростом х функция f(x) убывает. Поскольку эти рассуждения основаны лишь на наглядных геометрических представлениях, они не являются доказательством теоремы.

3.3. Pontos críticos da função, máximos e mínimos.

Determinação de pontos extremos de uma função . Seja x 0 um ponto interior do domínio da função f(x). Então, se existe tal δ - vizinhança ] x 0 - δ, x 0 + δ [ pontos x 0 , que para todo x desta vizinhança a desigualdade f(x)≤f(x 0) é satisfeita (a desigualdade f (x)≥f (x 0)), o ponto x 0 é chamado de ponto máximo (ponto mínimo) desta função.

Os pontos máximo-mínimo são pontos internos do domínio da função.

Um critério necessário para a existência de um extremo de uma função diferenciável .

Teorema de Fermat.

Se x 0 é um ponto extremo da função f (x) e neste ponto existe uma derivada, então é igual a zero: f '(x 0) \u003d 0.

Este teorema não é uma condição suficiente para a existência de um extremo de uma função diferenciável: se em algum ponto x 0 a derivada desaparece, então ainda não se segue que no ponto x 0 a função tenha um extremo.

Definição de pontos críticos de uma função . Os pontos internos do domínio de uma função, nos quais sua derivada é igual a zero ou não existe, são chamados de pontos críticos da função.

Condições suficientes para a existência de um extremo .

Teorema 1. Se a função f (x) é contínua no ponto x 0, f '(x)> 0 no intervalo e f '(x)<0 на интервале , то х 0 является точкой максимума функции f(x).

Teorema 2. Se a função f (x) é contínua no ponto x 0, f ‘(x)<0 на интервале и f ‘(x)>0 no intervalo, então x 0 é o ponto mínimo da função f(x).

Para encontrar os pontos extremos de uma função, é necessário encontrar seus pontos críticos e para cada um deles verificar o cumprimento de condições extremas suficientes.

3.4. Os maiores e menores valores da função.

Regras para encontrar os maiores e menores valores das funções no intervalo. Para encontrar os maiores e menores valores de uma função diferenciável em um determinado intervalo, você precisa encontrar todos os pontos críticos que estão dentro do intervalo, calcular os valores da função nesses pontos e nas extremidades de o intervalo e escolha o maior e o menor de todos os valores da função obtidos desta forma.

Capítulo IV. Exemplos de aplicação da derivada ao estudo de uma função.

Exemplo 11. Explore a função y=x 3 +6x 2 +9x e construa um gráfico.

2) Defina o tipo de função:

y(-x)=(-x) 3 +6(-x) 2 +9(-x)=-x+6x 2 -9x função geral.

x=0 ou x2 +6x+9=0

D=0, a equação tem uma raiz.

(0;0) e (-3;0) - pontos de intersecção com o eixo x.

você'=(x 3 +6x 2 +9x)'=3x 2 +12x+9

você' = 0, ou seja, 3x 2 +12x+9=0 reduzir em 3

D>0, a equação tem 2 raízes.

x 1,2 \u003d (-b±√D) / 2a, x 1 \u003d (-4 + 2) / 2, x 2 \u003d (-4-2) / 2

0
-4

x=-4, y’=3*16-48+9=9>0

x=-2, y’=12-24+9=-3<0

x=0, y'=0+0+9=9>0

7) Encontre x min e x max:

8) Encontre os extremos da função:

ymin=y(-1)=-1+6-9=-4

ymáx=y(-3)=-27+54-27=0

9) Vamos construir um gráfico da função:

10) Pontos adicionais:

y(-4)=-64+96-36=-4

Exemplo 12. Explore a função y=x 2 /(x-2) e construa um gráfico

y=x 2 /(x-2)=x+2+4/(x-2)

Vamos encontrar as assíntotas da função:

x≠ 2, x=2 – assíntota vertical

y=x+2 é a assíntota oblíqua, porque

Vamos encontrar o domínio de definição.

2) Vamos definir o tipo de função.

y(-x)=(-x) 2 /(-x-2)=x 2 /(-x-2), função geral.

3) Encontre os pontos de intersecção com os eixos.

Oy: x=0, y=0 (0;0) – ponto de intersecção com o eixo y.

x=0 ou x=2 (2;0) – ponto de intersecção com o eixo x

4) Encontre a derivada da função:

y'=(2x(x-2)-x 2)/(x-2) 2 =(2x 2 -4x-x 2)/(x-2) 2 =(x(x-4))/(x -2) 2 \u003d (x 2 -4x) / (x-2) 2

5) Defina pontos críticos:

x 2 -4x=0 x(x-4)=0

y'=0, (x 2 -4x)/(x-2) 2 =0<=> <=>

(x-2) 2 ≠ 0 x≠ 2

x 2 -4x=0, e (x-2) 2 ≠ 0, ou seja, x≠ 2

6) Denotamos os pontos críticos na reta coordenada e determinamos o sinal da função.

0 8

x=-1, y’=(1+4)/9=5/9>0

x=1, y’=(1-4)/1=-3<0

x=3, y'=(9-12)/1=-3<0

x=5, y’=(25-20)/9=5/9>0

7) Encontre os pontos mínimo e máximo da função:

8) Encontre os extremos da função:

ymin=y(4)=16/2=8

9) Vamos construir um gráfico da função:

10) Pontos adicionais:

y(-3)=9/-5=-1,8 y(3)=9/1=9

y(1)=1/-1=-1 y(6)=36/4=9

Exemplo 13 Explore a função y=(6(x-1))/(x 2 +3) e construa um gráfico. 1) Encontre o domínio da função:

2) Defina o tipo de função:

y(-x)=(6(-x-1))/(x 2 +3)=-(6(x+1))/(x 2 -3) é uma função geral.

3) Encontre os pontos de intersecção com os eixos:

O y: x=0, y=(6(0-1))/(0+3)=-2, (0;-2) – ponto de intersecção com o eixo y.

(6(x-1))/(x 2 +3)=0

O x: y=0,<=>

4) Encontre a derivada da função:

y'=(6(x-1)/(x 2 +3))'=6(x 2 +3-2x 2 +2x)/(x 2 +2) 2 =-6(x+1)(x -3)/(x 2 +3) 2

5) Defina pontos críticos:

você' = 0, ou seja, -6(x+1)(x-3)/(x 2 +3) 2 =0

y’=0, se x 1 =-1 ou x 2 =3, então x=-1 e x=3, pontos críticos.

6) Denotamos os pontos críticos na reta coordenada e determinamos o sinal da função:

-3 2

x=-2, y’=-6(-2+1)(-2-3)/(4+3) 2 =-30/49<0

x=0, y’=-6(0+1)(0-3)/(0+3) 2 =2>0

x=4, y’=-6(4+1)(4-3)/(16+3) 2=-30/361<0

7) Encontre os pontos mínimo e máximo:

8) Encontre os extremos da função:

ymin=y(-1)=(6(-1-1))/(1+3)=-12/4=-3

y máx =y(3)=(6(3-1))/(9+3)=12/12=1

9) Vamos construir um gráfico da função:

10) Pontos adicionais:

y(-3)=(6(-3-1))/(9+3)=-24/12=-2

y(6)=(6(6-1))/(36+3)=30/39=10/13≈ 0,77

Exemplo 14 Explore a função y=xlnx e construa seu gráfico:

1) Encontre o domínio da função:

D(y)=R + (somente valores positivos)

2) Defina o tipo de função:

y(-x)=-xlnx - forma geral.

3) Encontre os pontos de intersecção com os eixos:

O y , mas x≠ 0, portanto não há pontos de intersecção com o eixo y.

Boi: y=0, ou seja, xlnx=0

x=0 ou lnx=0

(1;0) - ponto de intersecção com o eixo x

4) Encontre a derivada da função:

y'=x' ln x + x(ln x)'=ln x +1

5) Defina pontos críticos:

y'=0, ou seja, lnx +1=0

y'=0 , se x=1/e , então x=1/e é um ponto crítico.

6) Denotamos os pontos críticos na reta coordenada e determinamos o sinal da função:

1/e

x=1/(2e); y'=log(2e) -1 +1=1-ln(2e)=1-ln e=-ln 2<0

x=2e; y'=ln(2e)+1=ln 2+ln e+1=ln 2+2>0

7) 1/e é o ponto mínimo da função.

8) Encontre os extremos da função:

y min \u003d y (1 / e) \u003d 1 / e ln e -1 \u003d -1 / e (≈ -0,4).

9) Vamos construir um gráfico da função:

Conclusão.

Muitos cientistas e filósofos trabalharam neste tópico. Há muitos anos surgiram estes termos: função, gráfico, estudo de função, e sobreviveram até hoje, adquirindo novos recursos e características.

Escolhi esse tema porque foi muito interessante para mim percorrer esse caminho de pesquisa sobre função. Parece-me que muitas pessoas estariam interessadas em aprender mais sobre a função, suas propriedades e transformações. Feito este ensaio, sistematizei minhas habilidades e reabasteci meu estoque de conhecimento sobre o tema.

Quero aconselhar a todos que estudem este tema mais profundamente.

Bibliografia.

1. Bashmakov, M.I. Álgebra e o início da análise - M.: Educação, 1992.

2. Glaser, G.I. História da matemática na escola - M.: Educação, 1983.

3. Gusev, V.A. Matemática: Materiais de referência.- M.: Educação, 1888.

4. Dorofeev, G.V. Manual de matemática para candidatos a universidades - M.: Nauka, 1974.

5. Zorin, V.V. Manual de matemática para candidatos a universidades - M.: Ensino Superior, 1980.

6. Kolmogorov A.N. Álgebra e os primórdios da análise.- M.: Iluminismo, 1993.