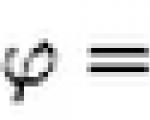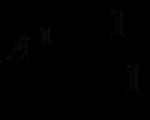Como resolver equações. Resolvendo equações lineares com exemplos

Na fase de preparação para a prova final, os alunos do ensino médio precisam aprimorar seus conhecimentos sobre o tema “Equações Exponenciais”. A experiência dos últimos anos indica que tais tarefas causam certas dificuldades aos alunos. Portanto, os alunos do ensino médio, independente do nível de preparação, precisam dominar cuidadosamente a teoria, memorizar as fórmulas e compreender o princípio de resolução de tais equações. Tendo aprendido a lidar com esse tipo de tarefas, os graduados poderão contar com notas altas ao passar no exame de matemática.

Prepare-se para o exame junto com Shkolkovo!

Ao repetir os materiais abordados, muitos alunos se deparam com o problema de encontrar as fórmulas necessárias para resolver as equações. Nem sempre um livro escolar está à mão e a seleção das informações necessárias sobre um tema na Internet leva muito tempo.

O portal educacional Shkolkovo convida os alunos a utilizar nossa base de conhecimento. Estamos implementando um método completamente novo de preparação para o teste final. Estudando em nosso site, você poderá identificar lacunas de conhecimento e prestar atenção justamente nas tarefas que causam maiores dificuldades.

Os professores de "Shkolkovo" recolheram, sistematizaram e apresentaram todo o material necessário para a aprovação no exame da forma mais simples e acessível.

As principais definições e fórmulas são apresentadas na seção “Referencial Teórico”.

Para uma melhor assimilação do material, recomendamos que você pratique as tarefas. Revise cuidadosamente os exemplos de equações exponenciais com soluções apresentadas nesta página para compreender o algoritmo de cálculo. Depois disso, prossiga com as tarefas da seção “Catálogos”. Você pode começar com as tarefas mais fáceis ou ir direto para a resolução de equações exponenciais complexas com várias incógnitas ou. A base de dados de exercícios do nosso site é constantemente complementada e atualizada.

Aqueles exemplos com indicadores que lhe causaram dificuldades podem ser adicionados aos “Favoritos”. Assim você pode encontrá-los rapidamente e discutir a solução com o professor.

Para passar no exame, estude no portal Shkolkovo todos os dias!

Atribuição de serviço. A calculadora matricial foi projetada para resolver sistemas de equações lineares de forma matricial (veja um exemplo de resolução de problemas semelhantes).

Instrução. Para uma solução online, você deve selecionar o tipo de equação e definir a dimensão das matrizes correspondentes. onde A, B, C são matrizes dadas, X é a matriz desejada. Equações matriciais da forma (1), (2) e (3) são resolvidas através da matriz inversa A -1 . Se a expressão A X - B = C for dada, então é necessário primeiro somar as matrizes C + B e encontrar uma solução para a expressão A X = D , onde D = C + B . Se a expressão A*X = B 2 for dada, então a matriz B deve primeiro ser elevada ao quadrado.

Também é recomendável familiarizar-se com as operações básicas com matrizes.

Exemplo 1. Exercício. Encontre uma solução para uma equação matricial
Solução. Indicar:
Então a equação matricial será escrita na forma: A·X·B = C.
O determinante da matriz A é detA=-1
Como A é uma matriz não singular, existe uma matriz inversa A -1 . Multiplique ambos os lados da equação à esquerda por A -1: Multiplique ambos os lados desta equação à esquerda por A -1 e à direita por B -1: A -1 A X B B -1 = A -1 C B -1 . Como A A -1 = B B -1 = E e E X = X E = X, então X = A -1 C B -1

Matriz inversa A -1:
Encontre a matriz inversa B -1 .
Matriz de transposição B T:
Matriz inversa B -1:
Procuramos a matriz X pela fórmula: X = A -1 C B -1

Responder:

Exemplo #2. Exercício. Resolver equação matricial
Solução. Indicar:
Então a equação matricial será escrita na forma: A X = B.
O determinante da matriz A é detA=0
Como A é uma matriz degenerada (o determinante é 0), portanto, a equação não tem solução.

Exemplo #3. Exercício. Encontre uma solução para uma equação matricial
Solução. Indicar:
Então a equação matricial será escrita na forma: X·A = B.
O determinante da matriz A é detA=-60
Como A é uma matriz não singular, existe uma matriz inversa A -1 . Multiplique à direita ambos os lados da equação por A -1: X A A -1 = B A -1 , a partir do qual descobrimos que X = B A -1
Encontre a matriz inversa A -1 .
Matriz transposta AT:
Matriz inversa A -1:
Procuramos a matriz X pela fórmula: X = B A -1


Resposta: >

para resolver matemática. Encontre rapidamente solução de equação matemática no modo on-line. O site www.site permite resolva a equação quase qualquer dado algébrico, trigonométrico ou equação transcendental on-line. Ao estudar quase qualquer seção da matemática em diferentes estágios, é preciso decidir equações on-line. Para obter uma resposta imediata e, o mais importante, uma resposta precisa, você precisa de um recurso que permita fazer isso. Graças a www.site resolver equações on-line levará alguns minutos. A principal vantagem do www.site na resolução matemática equações on-line- é a velocidade e precisão da resposta emitida. O site é capaz de resolver qualquer equações algébricas on-line, equações trigonométricas on-line, equações transcendentais on-line, e equações com parâmetros desconhecidos no modo on-line. Equações servir como um poderoso aparato matemático soluções tarefas práticas. Com ajuda equações matemáticasé possível expressar fatos e relações que à primeira vista podem parecer confusos e complexos. quantidades desconhecidas equações pode ser encontrado formulando o problema em matemático linguagem na forma equações E decidir a tarefa recebida no modo on-line no site www.site. Qualquer equação algébrica, equação trigonométrica ou equações contendo transcendental apresenta você facilmente decidir on-line e obtenha a resposta certa. Estudando as ciências naturais, inevitavelmente encontramos a necessidade resolvendo equações. Neste caso, a resposta deve ser precisa e deve ser recebida imediatamente na modalidade on-line. Portanto, para resolver equações matemáticas on-line recomendamos o site www.site, que se tornará sua calculadora indispensável para resolver equações algébricas on-line, equações trigonométricas on-line, e equações transcendentais on-line ou equações com parâmetros desconhecidos. Para problemas práticos de encontrar as raízes de vários equações matemáticas recurso www.. Resolvendo equações on-line você mesmo, é útil verificar a resposta recebida usando solução on-line de equações no site www.site. É necessário escrever a equação corretamente e obter instantaneamente solução on-line, após o que resta apenas comparar a resposta com a sua solução da equação. Verificar a resposta não levará mais de um minuto, o suficiente resolver a equação on-line e compare as respostas. Isso irá ajudá-lo a evitar erros em decisão e corrija a resposta a tempo resolvendo equações on-line qualquer algébrico, trigonométrico, transcendente ou a equação com parâmetros desconhecidos.

Neste vídeo analisaremos todo um conjunto de equações lineares que são resolvidas usando o mesmo algoritmo - por isso são chamadas de mais simples.

Para começar, vamos definir: o que é uma equação linear e qual delas deve ser chamada de mais simples?

Uma equação linear é aquela em que existe apenas uma variável, e apenas no primeiro grau.

A equação mais simples significa a construção:

Todas as outras equações lineares são reduzidas às mais simples usando o algoritmo:

1. Colchetes abertos, se houver;
2. Mova os termos que contêm uma variável para um lado do sinal de igual e os termos sem variável para o outro;
3. Traga termos semelhantes à esquerda e à direita do sinal de igual;
4. Divida a equação resultante pelo coeficiente da variável $x$ .

Claro, este algoritmo nem sempre ajuda. O fato é que às vezes, depois de todas essas maquinações, o coeficiente da variável $x$ acaba sendo igual a zero. Neste caso, duas opções são possíveis:

1. A equação não tem solução alguma. Por exemplo, quando você obtém algo como $0\cdot x=8$, ou seja, à esquerda está zero e à direita está um número diferente de zero. No vídeo abaixo, veremos vários motivos pelos quais essa situação é possível.
2. A solução são todos os números. O único caso em que isso é possível é quando a equação foi reduzida à construção $0\cdot x=0$. É bastante lógico que não importa quanto $x$ substituamos, ainda assim resultará “zero é igual a zero”, ou seja, igualdade numérica correta.

E agora vamos ver como tudo funciona usando o exemplo de problemas reais.

Exemplos de resolução de equações

Hoje tratamos de equações lineares, e apenas das mais simples. Em geral, uma equação linear significa qualquer igualdade que contenha exatamente uma variável e vai apenas até o primeiro grau.

Tais construções são resolvidas aproximadamente da mesma maneira:

1. Primeiro de tudo, você precisa abrir os parênteses, se houver (como no nosso último exemplo);
2. Então traga semelhantes
3. Finalmente, isole a variável, ou seja, tudo o que está relacionado com a variável - os termos em que ela está contida - é transferido para um lado, e tudo o que fica sem ela é transferido para o outro lado.

Então, via de regra, é necessário trazer os semelhantes em cada lado da igualdade resultante, e depois disso resta apenas dividir pelo coeficiente em “x”, e obteremos a resposta final.

Em teoria, isso parece bom e simples, mas na prática, mesmo estudantes experientes do ensino médio podem cometer erros ofensivos em equações lineares bastante simples. Normalmente, erros são cometidos ao abrir colchetes ou ao contar "mais" e "menos".

Além disso, acontece que uma equação linear não tem nenhuma solução, ou então a solução é toda a reta numérica, ou seja, qualquer número. Analisaremos essas sutilezas na lição de hoje. Mas começaremos, como você já entendeu, pelas tarefas mais simples.

Esquema para resolver equações lineares simples

Para começar, deixe-me escrever mais uma vez todo o esquema para resolver as equações lineares mais simples:

1. Expanda os parênteses, se houver.
2. Variáveis ​​isoladas, ou seja, tudo que contém “x” é transferido para um lado, e sem “x” - para o outro.
3. Apresentamos termos semelhantes.
4. Dividimos tudo pelo coeficiente em “x”.

Claro que esse esquema nem sempre funciona, tem certas sutilezas e truques, e agora vamos conhecê-los.

Resolvendo exemplos reais de equações lineares simples

Tarefa nº 1

Na primeira etapa, somos obrigados a abrir os colchetes. Mas eles não estão neste exemplo, então pulamos esta etapa. Na segunda etapa, precisamos isolar as variáveis. Observação: estamos falando apenas de termos individuais. Vamos escrever:

Damos termos semelhantes à esquerda e à direita, mas isso já foi feito aqui. Portanto, passamos para o quarto passo: dividir por um fator:

\[\frac(6x)(6)=-\frac(72)(6)\]

Aqui temos a resposta.

Tarefa #2

Nesta tarefa podemos observar os colchetes, então vamos expandi-los:

Tanto à esquerda quanto à direita vemos aproximadamente a mesma construção, mas vamos agir de acordo com o algoritmo, ou seja, variáveis ​​sequestradoras:

Aqui estão alguns como:

Em que raízes isso funciona? Resposta: para qualquer. Portanto, podemos escrever que $x$ é qualquer número.

Tarefa #3

A terceira equação linear já é mais interessante:

\[\esquerda(6-x \direita)+\esquerda(12+x \direita)-\esquerda(3-2x \direita)=15\]

Existem vários colchetes aqui, mas eles não são multiplicados por nada, apenas têm sinais diferentes na frente deles. Vamos decompô-los:

Realizamos a segunda etapa já conhecida por nós:

\[-x+x+2x=15-6-12+3\]

Vamos calcular:

Realizamos a última etapa - dividimos tudo pelo coeficiente em "x":

\[\frac(2x)(x)=\frac(0)(2)\]

Coisas para lembrar ao resolver equações lineares

Se ignorarmos tarefas muito simples, gostaria de dizer o seguinte:

• Como eu disse acima, nem toda equação linear tem solução - às vezes simplesmente não há raízes;
• Mesmo que existam raízes, o zero pode entrar entre elas - não há nada de errado com isso.

Zero é o mesmo número que o resto, você não deve discriminá-lo de alguma forma ou presumir que, se obtiver zero, você fez algo errado.

Outra característica está relacionada à expansão dos parênteses. Atenção: quando há um “menos” na frente deles, nós o removemos, mas entre colchetes mudamos os sinais para oposto. E então podemos abri-lo de acordo com algoritmos padrão: obteremos o que vimos nos cálculos acima.

Compreender este simples fato irá ajudá-lo a evitar cometer erros estúpidos e prejudiciais no ensino médio, quando tais ações são um dado adquirido.

Resolvendo equações lineares complexas

Vamos passar para equações mais complexas. Agora as construções ficarão mais complicadas e uma função quadrática aparecerá ao realizar várias transformações. Porém, não se deve ter medo disso, pois se, segundo a intenção do autor, resolvermos uma equação linear, então no processo de transformação todos os monômios contendo uma função quadrática serão necessariamente reduzidos.

Exemplo 1

Obviamente, o primeiro passo é abrir os colchetes. Vamos fazer isso com muito cuidado:

Agora vamos considerar a privacidade:

\[-x+6((x)^(2))-6((x)^(2))+x=-12\]

Aqui estão alguns como:

Obviamente, esta equação não tem solução, então na resposta escrevemos o seguinte:

\[\variedade \]

ou sem raízes.

Exemplo #2

Realizamos os mesmos passos. Primeiro passo:

Vamos mover tudo com variável para a esquerda e sem ela - para a direita:

Aqui estão alguns como:

Obviamente, esta equação linear não tem solução, então escrevemos assim:

\[\varnada\],

ou sem raízes.

Nuances da solução

Ambas as equações estão completamente resolvidas. No exemplo dessas duas expressões, mais uma vez garantimos que mesmo nas equações lineares mais simples, nem tudo pode ser tão simples: pode haver um, ou nenhum, ou infinitos. No nosso caso, consideramos duas equações, em ambas simplesmente não há raízes.

Mas gostaria de chamar a atenção para outro fato: como trabalhar com colchetes e como expandi-los se houver um sinal de menos na frente deles. Considere esta expressão:

Antes de abrir, é preciso multiplicar tudo por “x”. Atenção: multiplique cada termo individual. Dentro há dois termos - respectivamente, dois termos e é multiplicado.

E somente depois que essas transformações aparentemente elementares, mas muito importantes e perigosas forem concluídas, o colchete pode ser aberto do ponto de vista de que há um sinal de menos depois dele. Sim, sim: só agora, quando as transformações são feitas, lembramos que há um sinal de menos na frente dos colchetes, o que significa que tudo abaixo apenas muda de sinal. Ao mesmo tempo, os próprios colchetes desaparecem e, o mais importante, o “menos” frontal também desaparece.

Fazemos o mesmo com a segunda equação:

Não é por acaso que presto atenção a estes pequenos fatos aparentemente insignificantes. Porque resolver equações é sempre uma sequência de transformações elementares, onde a incapacidade de realizar ações simples com clareza e competência faz com que alunos do ensino médio venham até mim e aprendam a resolver equações tão simples novamente.

É claro que chegará o dia em que você aprimorará essas habilidades até o automatismo. Você não precisa mais realizar tantas transformações a cada vez, você escreverá tudo em uma linha. Mas enquanto você está aprendendo, você precisa escrever cada ação separadamente.

Resolvendo equações lineares ainda mais complexas

O que vamos resolver agora dificilmente pode ser chamado de tarefa mais simples, mas o significado permanece o mesmo.

Tarefa nº 1

\[\esquerda(7x+1 \direita)\esquerda(3x-1 \direita)-21((x)^(2))=3\]

Vamos multiplicar todos os elementos da primeira parte:

Vamos fazer um retiro:

Aqui estão alguns como:

Vamos fazer o último passo:

\[\frac(-4x)(4)=\frac(4)(-4)\]

Aqui está nossa resposta final. E, apesar de no processo de resolução termos coeficientes com função quadrática, eles se anulam mutuamente, o que torna a equação exatamente linear, e não quadrada.

Tarefa #2

\[\esquerda(1-4x \direita)\esquerda(1-3x \direita)=6x\esquerda(2x-1 \direita)\]

Vamos fazer o primeiro passo com cuidado: multiplique cada elemento do primeiro colchete por cada elemento do segundo. No total, quatro novos termos devem ser obtidos após as transformações:

E agora faça com cuidado a multiplicação em cada termo:

Vamos mover os termos com "x" para a esquerda e sem - para a direita:

\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]

Aqui estão termos semelhantes:

Recebemos uma resposta definitiva.

Nuances da solução

A observação mais importante sobre essas duas equações é esta: assim que começamos a multiplicar colchetes em que há mais de um termo, isso é feito de acordo com a seguinte regra: pegamos o primeiro termo do primeiro e multiplicamos por cada elemento do segundo; então pegamos o segundo elemento do primeiro e multiplicamos de forma semelhante por cada elemento do segundo. Como resultado, obtemos quatro termos.

Na soma algébrica

Com o último exemplo, gostaria de lembrar aos alunos o que é uma soma algébrica. Na matemática clássica, por $1-7$ queremos dizer uma construção simples: subtraímos sete de um. Em álgebra, queremos dizer com isso o seguinte: ao número “um” adicionamos outro número, nomeadamente “menos sete”. Esta soma algébrica difere da soma aritmética usual.

Assim que ao realizar todas as transformações, cada adição e multiplicação, você começar a ver construções semelhantes às descritas acima, simplesmente não terá problemas de álgebra ao trabalhar com polinômios e equações.

Concluindo, vejamos mais alguns exemplos que serão ainda mais complexos do que os que acabamos de ver e, para resolvê-los, teremos que expandir um pouco nosso algoritmo padrão.

Resolvendo equações com uma fração

Para resolver tais problemas, mais uma etapa deverá ser adicionada ao nosso algoritmo. Mas primeiro, vou lembrar nosso algoritmo:

1. Abra colchetes.
2. Variáveis ​​separadas.
3. Traga semelhante.
4. Divida por um fator.

Infelizmente, esse algoritmo maravilhoso, apesar de toda a sua eficiência, não é totalmente apropriado quando temos frações diante de nós. E no que veremos a seguir, temos uma fração à esquerda e à direita em ambas as equações.

Como trabalhar neste caso? Sim, é muito simples! Para isso, é necessário adicionar mais uma etapa ao algoritmo, que pode ser executada tanto antes quanto depois da primeira ação, ou seja, livrar-se das frações. Assim, o algoritmo será o seguinte:

1. Livre-se das frações.
2. Abra colchetes.
3. Variáveis ​​separadas.
4. Traga semelhante.
5. Divida por um fator.

O que significa “livrar-se das frações”? E por que é possível fazer isso antes e depois da primeira etapa padrão? Na verdade, no nosso caso, todas as frações são numéricas em termos do denominador, ou seja, em todos os lugares o denominador é apenas um número. Portanto, se multiplicarmos ambas as partes da equação por este número, nos livraremos das frações.

Exemplo 1

\[\frac(\esquerda(2x+1 \direita)\esquerda(2x-3 \direita))(4)=((x)^(2))-1\]

Vamos nos livrar das frações nesta equação:

\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \right)\cdot 4\]

Observação: tudo é multiplicado por “quatro” uma vez, ou seja, só porque você tem dois colchetes não significa que você precisa multiplicar cada um deles por "quatro". Vamos escrever:

\[\esquerda(2x+1 \direita)\esquerda(2x-3 \direita)=\esquerda(((x)^(2))-1 \direita)\cdot 4\]

Agora vamos abri-lo:

Realizamos isolamento de uma variável:

Realizamos a redução de termos semelhantes:

\[-4x=-1\esquerda| :\esquerda(-4 \direita) \direita.\]

\[\frac(-4x)(-4)=\frac(-1)(-4)\]

Recebemos a solução final, passamos para a segunda equação.

Exemplo #2

\[\frac(\esquerda(1-x \direita)\esquerda(1+5x \direita))(5)+((x)^(2))=1\]

Aqui realizamos todas as mesmas ações:

\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]

\[\frac(4x)(4)=\frac(4)(4)\]

Problema resolvido.

Isso, na verdade, é tudo o que eu queria contar hoje.

Pontos chave

As principais conclusões são as seguintes:

• Conhecer o algoritmo para resolução de equações lineares.
• Capacidade de abrir colchetes.
• Não se preocupe se você tiver funções quadráticas em algum lugar, provavelmente, no processo de transformações adicionais, elas serão reduzidas.
• As raízes nas equações lineares, mesmo as mais simples, são de três tipos: uma única raiz, toda a reta numérica é uma raiz, não há nenhuma raiz.

Espero que esta lição ajude você a dominar um tópico simples, mas muito importante para uma maior compreensão de toda a matemática. Se algo não estiver claro, acesse o site, resolva os exemplos ali apresentados. Fique ligado, tem muito mais coisas interessantes esperando por você!