Hur man tar bort en modul i en ojämlikhet. Modulo ekvationer

Att lösa ojämlikheter online

Innan du löser ojämlikheter måste du ha en god förståelse för hur ekvationer löses.

Det spelar ingen roll om ojämlikheten är strikt () eller icke-strikt (≤, ≥), det första steget är att lösa ekvationen genom att ersätta olikhetstecknet med likhet (=).

Låt oss förklara vad det innebär att lösa en ojämlikhet?

Efter att ha studerat ekvationerna får eleven följande bild i huvudet: han behöver hitta värden på variabeln så att båda sidor av ekvationen får samma värden. Med andra ord, hitta alla punkter där jämlikhet gäller. Allt är korrekt!

När vi talar om ojämlikheter menar vi att hitta intervall (segment) som ojämlikheten håller i sig. Om det finns två variabler i olikheten, så blir lösningen inte längre intervaller, utan några områden på planet. Gissa själv vad som blir lösningen på en ojämlikhet i tre variabler?

Hur löser man ojämlikheter?

Ett universellt sätt att lösa ojämlikheter anses vara intervallmetoden (även känd som intervallmetoden), som består i att bestämma alla intervall inom vars gränser en given ojämlikhet kommer att uppfyllas.

Utan att gå in på typen av ojämlikhet, i det här fallet är det inte meningen, du måste lösa motsvarande ekvation och bestämma dess rötter, följt av beteckningen av dessa lösningar på talaxeln.

Hur man korrekt skriver lösningen på en ojämlikhet?

När du har bestämt lösningsintervallen för ojämlikheten måste du skriva ut själva lösningen korrekt. Det finns en viktig nyans - ingår gränserna för intervallen i lösningen?

Allt är enkelt här. Om lösningen till ekvationen uppfyller ODZ och olikheten inte är strikt, så ingår gränsen för intervallet i lösningen till ojämlikheten. Annars nej.

Med tanke på varje intervall kan lösningen på ojämlikheten vara själva intervallet, eller ett halvintervall (när en av dess gränser uppfyller olikheten), eller ett segment - intervallet tillsammans med dess gränser.

Viktig poäng

Tro inte att bara intervall, halvintervall och segment kan lösa ojämlikheten. Nej, lösningen kan även innehålla enskilda punkter.

Till exempel har olikheten |x|≤0 bara en lösning - det här är punkt 0.

Och ojämlikheten |x|

Varför behöver du en ojämlikhetsräknare?

Ojämlikhetsberäknaren ger det korrekta slutsvaret. I de flesta fall tillhandahålls en illustration av en nummeraxel eller ett plan. Det syns om gränserna för intervallen ingår i lösningen eller inte - punkterna visas som skuggade eller punkterade.

Tack vare onlinekalkylatorn för ojämlikhet kan du kontrollera om du hittade ekvationens rötter korrekt, markerade dem på talaxeln och kontrollerade att ojämlikhetsvillkoret uppfylldes på intervallen (och gränserna)?

Om ditt svar skiljer sig från räknarens svar, måste du definitivt dubbelkolla din lösning och identifiera felet.

Ju mer en person förstår, desto starkare är hans önskan att förstå

Thomas av Aquino

Intervallmetoden låter dig lösa alla ekvationer som innehåller en modul. Kärnan i denna metod är att dela upp talaxeln i flera sektioner (intervall), och axeln måste delas med nollorna i uttrycken i modulerna. Sedan, på var och en av de resulterande sektionerna, är varje submodulärt uttryck antingen positivt eller negativt. Därför kan var och en av modulerna öppnas antingen med ett minustecken eller med ett plustecken. Efter dessa åtgärder återstår det bara att lösa var och en av de erhållna enkla ekvationerna på det aktuella intervallet och kombinera de erhållna svaren.

Låt oss titta på den här metoden med ett specifikt exempel.

|x + 1| + |2x – 4| – |x + 3| = 2x - 6.

1) Låt oss hitta nollorna för uttrycken i modulerna. För att göra detta måste vi likställa dem till noll och lösa de resulterande ekvationerna.

x + 1 = 0 2x – 4 = 0 x + 3 = 0

x = -1 2x = 4 x = -3

2) Placera de resulterande punkterna i önskad ordning på koordinatlinjen. De kommer att dela upp hela axeln i fyra sektioner.

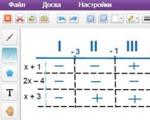
3) Låt oss bestämma för var och en av de resulterande avsnitten tecknen på uttrycken i modulerna. För att göra detta, ersätter vi i dem alla siffror från de intervall som är intressanta för oss. Om resultatet av beräkningen är ett positivt tal sätter vi "+" i tabellen, och om talet är negativt sätter vi "-". Detta kan avbildas så här:

4) Nu ska vi lösa ekvationen på vart och ett av de fyra intervallen, öppna modulerna med tecknen som finns i tabellen. Så låt oss titta på det första intervallet:

I-intervall (-∞; -3). På den öppnas alla moduler med ett "–"-tecken. Vi får följande ekvation:

-(x + 1) - (2x - 4) - (-(x + 3)) \u003d 2x - 6. Vi presenterar liknande termer, efter att tidigare ha öppnat parenteserna i den resulterande ekvationen:

X – 1 – 2x + 4 + x + 3 = 2x – 6

Det mottagna svaret ingår inte i det övervägda intervallet, så det är inte nödvändigt att skriva det i det slutliga svaret.

II-intervall [-3; -1). Vid detta intervall i tabellen finns tecknen "–", "–", "+". Det är exakt hur vi öppnar modulerna i den ursprungliga ekvationen:

-(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Låt oss förenkla genom att öppna parenteserna:

X – 1 – 2x + 4 – x – 3 = 2x – 6. Låt oss presentera liknande i den resulterande ekvationen:

x = 6/5. Det resulterande talet tillhör inte det aktuella intervallet, därför är det inte roten till den ursprungliga ekvationen.

III-intervall [-1; 2). Vi utökar modulerna i den ursprungliga ekvationen med tecknen som visas i den tredje kolumnen i figuren. Vi får:

(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Låt oss ta bort parenteserna och flytta termerna som innehåller variabeln x till vänster sida av ekvationen, och de som inte innehåller x till den rätta. Kommer att ha:

x + 1 – 2x + 4 – x – 3 = 2x – 6

Siffran 2 ingår inte i det aktuella intervallet.

IV intervall

Enkelt uttryckt är en modul ett "tal utan minus." Och det är just i denna dualitet (på vissa ställen behöver du inte göra något med det ursprungliga numret, men på andra måste du ta bort någon form av minus) som är där hela svårigheten ligger för nybörjarelever.

Det finns också en geometrisk definition. Det är också användbart att veta, men vi kommer bara att vända oss till det i komplexa och vissa speciella fall, där det geometriska tillvägagångssättet är bekvämare än det algebraiska (spoiler: inte idag).

Definition. Låt punkten $a$ markeras på talraden. Sedan modulen $\left| x-a \right|$ är avståndet från punkt $x$ till punkt $a$ på denna linje.

Om du ritar en bild får du något sånt här:

Grafisk moduldefinition

På ett eller annat sätt, från definitionen av en modul följer dess nyckelegenskap omedelbart: modulen för ett tal är alltid en icke-negativ storhet. Detta faktum kommer att vara en röd tråd som löper genom hela vår berättelse idag.

Att lösa ojämlikheter. Intervallmetod

Låt oss nu titta på ojämlikheterna. Det finns väldigt många av dem, men vår uppgift nu är att kunna lösa åtminstone de enklaste av dem. De som reducerar till linjära ojämlikheter, samt till intervallmetoden.

Jag har två stora lektioner om detta ämne (förresten, väldigt, MYCKET användbara - jag rekommenderar att du studerar dem):

1. Intervallmetod för ojämlikheter (särskilt titta på videon);
2. Fraktionella rationella ojämlikheter är en mycket omfattande lektion, men efter den kommer du inte att ha några frågor alls.

Om du vet allt detta, om frasen "låt oss gå från ojämlikhet till ekvation" inte får dig att ha en vag önskan att slå dig själv i väggen, så är du redo: välkommen till helvetet till lektionens huvudämne. :)

1. Ojämlikheter i formen "Modul är mindre än funktion"

Detta är ett av de vanligaste problemen med moduler. Det krävs för att lösa en olikhet av formen:

\[\vänster| f\höger| \ltg\]

Funktionerna $f$ och $g$ kan vara vad som helst, men vanligtvis är de polynom. Exempel på sådana ojämlikheter:

\[\begin(align) & \left| 2x+3 \höger| \lt x+7; \\ & \vänster| ((x)^(2))+2x-3 \höger|+3\vänster(x+1 \höger) \lt 0; \\ & \vänster| ((x)^(2))-2\vänster| x \right|-3 \right| \lt 2. \\\end(align)\]

Alla kan lösas bokstavligen på en rad enligt följande schema:

\[\vänster| f\höger| \lt g\Högerpil -g \lt f \lt g\quad \left(\Högerpil \left\( \begin(align) & f \lt g, \\ & f \gt -g \\\end(align) \eller hur)\]

Det är lätt att se att vi gör oss av med modulen, men i gengäld får vi en dubbel olikhet (eller, vilket är samma sak, ett system med två olikheter). Men denna övergång tar hänsyn till absolut alla möjliga problem: om talet under modulen är positivt fungerar metoden; om det är negativt fungerar det fortfarande; och även med den mest otillräckliga funktionen i stället för $f$ eller $g$, kommer metoden fortfarande att fungera.

Naturligtvis uppstår frågan: kunde det inte vara enklare? Tyvärr är det inte möjligt. Detta är hela poängen med modulen.

Dock nog med filosoferandet. Låt oss lösa ett par problem:

Uppgift. Lös ojämlikheten:

\[\vänster| 2x+3 \höger| \lt x+7\]

Lösning. Så vi har framför oss en klassisk ojämlikhet av formen "modulen är mindre" - det finns inte ens något att omvandla. Vi arbetar enligt algoritmen:

\[\begin(align) & \left| f\höger| \lt g\Högerpil -g \lt f \lt g; \\ & \vänster| 2x+3 \höger| \lt x+7\Högerpil -\vänster(x+7 \höger) \lt 2x+3 \lt x+7 \\\end(align)\]

Skynda dig inte för att öppna parentesen som föregås av ett "minus": det är mycket möjligt att du på grund av din brådska kommer att göra ett stötande misstag.

\[-x-7 \lt 2x+3 \lt x+7\]

\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(align) \right.\]

\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \right.\]

\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \right.\]

Problemet reducerades till två elementära ojämlikheter. Låt oss notera deras lösningar på parallella tallinjer:

Skärning av många

Skärningspunkten mellan dessa uppsättningar kommer att vara svaret.

Svar: $x\in \left(-\frac(10)(3);4 \right)$

Uppgift. Lös ojämlikheten:

\[\vänster| ((x)^(2))+2x-3 \höger|+3\vänster(x+1 \höger) \lt 0\]

Lösning. Denna uppgift är lite svårare. Låt oss först isolera modulen genom att flytta den andra termen till höger:

\[\vänster| ((x)^(2))+2x-3 \right| \lt -3\vänster(x+1 \höger)\]

Uppenbarligen har vi återigen en olikhet av formen "modulen är mindre", så vi blir av med modulen med den redan kända algoritmen:

\[-\vänster(-3\vänster(x+1 \höger) \höger) \lt ((x)^(2))+2x-3 \lt -3\vänster(x+1 \höger)\]

Nu uppmärksamhet: någon kommer att säga att jag är lite av en pervers med alla dessa parenteser. Men låt mig återigen påminna er om att vårt huvudmål är rätt lösa ojämlikheten och få svaret. Senare, när du har bemästrat allt som beskrivs i den här lektionen perfekt, kan du pervertera det själv som du vill: öppna parenteser, lägg till minus, etc.

Till att börja med tar vi helt enkelt bort det dubbla minuset till vänster:

\[-\left(-3\left(x+1 \right) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\vänster(x+1 \höger)\]

Låt oss nu öppna alla parenteser i den dubbla olikheten:

Låt oss gå vidare till den dubbla ojämlikheten. Den här gången blir beräkningarna mer seriösa:

\[\vänster\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(align) \right.\]

\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( anpassa till höger.\]

Båda ojämlikheterna är kvadratiska och kan lösas med intervallmetoden (det är därför jag säger: om du inte vet vad detta är, är det bättre att inte ta på moduler ännu). Låt oss gå vidare till ekvationen i den första ojämlikheten:

\[\begin(align) & ((x)^(2))+5x=0; \\ & x\vänster(x+5 \höger)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\end(align)\]

Som du kan se är utdata en ofullständig kvadratisk ekvation, som kan lösas på ett elementärt sätt. Låt oss nu titta på den andra ojämlikheten i systemet. Där måste du tillämpa Vietas teorem:

\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\end(align)\]

Vi markerar de resulterande talen på två parallella linjer (separera för den första olikheten och separera för den andra):

Återigen, eftersom vi löser ett system av ojämlikheter, är vi intresserade av skärningspunkten mellan de skuggade uppsättningarna: $x\in \left(-5;-2 \right)$. Detta är svaret.

Svar: $x\in \left(-5;-2 \right)$

Jag tror att efter dessa exempel är lösningsschemat extremt tydligt:

1. Isolera modulen genom att flytta alla andra termer till motsatt sida av olikheten. Därmed får vi en olikhet av formen $\left| f\höger| \ltg$.
2. Lös denna ojämlikhet genom att bli av med modulen enligt schemat som beskrivs ovan. Vid något tillfälle kommer det att bli nödvändigt att gå från dubbel olikhet till ett system med två oberoende uttryck, som vart och ett redan kan lösas separat.
3. Slutligen, allt som återstår är att skära lösningarna för dessa två oberoende uttryck - och det är det, vi kommer att få det slutliga svaret.

En liknande algoritm finns för olikheter av följande typ, när modulen är större än funktionen. Det finns dock ett par allvarliga "men". Vi ska prata om dessa "men" nu.

2. Ojämlikheter i formen "Modul är större än funktion"

De ser ut så här:

\[\vänster| f\höger| \gtg\]

Liknar den förra? Det verkar. Och ändå löses sådana problem på ett helt annat sätt. Formellt är schemat följande:

\[\vänster| f\höger| \gt g\Högerpil \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(align) \right.\]

Med andra ord, vi överväger två fall:

1. Först ignorerar vi helt enkelt modulen och löser den vanliga ojämlikheten;
2. Sedan utökar vi i huvudsak modulen med minustecknet och multiplicerar sedan båda sidor av olikheten med −1, medan jag har tecknet.

I det här fallet kombineras alternativen med en vinkelhake, d.v.s. Vi har framför oss en kombination av två krav.

Observera igen: detta är inte ett system, utan en helhet, därför i svaret kombineras mängderna snarare än korsar varandra. Detta är en grundläggande skillnad från föregående punkt!

I allmänhet är många studenter helt förvirrade med fackföreningar och korsningar, så låt oss reda ut denna fråga en gång för alla:

• "∪" är ett fackligt tecken. I själva verket är detta en stiliserad bokstav "U", som kom till oss från det engelska språket och är en förkortning för "Union", dvs. "Föreningar".
• "∩" är korsningstecknet. Den här skiten kom inte någonstans ifrån, utan framstod helt enkelt som en motpol till "∪".

För att göra det ännu lättare att komma ihåg, dra bara benen till dessa tecken för att göra glasögon (bara nu inte anklaga mig för att främja drogberoende och alkoholism: om du på allvar studerar den här lektionen, då är du redan en drogmissbrukare):

Skillnad mellan korsning och förening av uppsättningar

Översatt till ryska betyder detta följande: unionen (totaliteten) inkluderar element från båda uppsättningarna, därför är det inte på något sätt mindre än var och en av dem; men skärningspunkten (systemet) inkluderar bara de element som är samtidigt i både den första uppsättningen och den andra. Därför är skärningspunkten mellan mängder aldrig större än källmängderna.

Så det blev tydligare? Det är toppen. Låt oss gå vidare till praktiken.

Uppgift. Lös ojämlikheten:

\[\vänster| 3x+1 \right| \gt 5-4x\]

Lösning. Vi fortsätter enligt schemat:

\[\vänster| 3x+1 \right| \gt 5-4x\Högerpil \vänster[ \begin(align) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \right) \\\end(align) \ höger.\]

Vi löser varje ojämlikhet i befolkningen:

\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \right.\]

\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \right.\]

\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(align) \right.\]

Vi markerar varje resulterande uppsättning på nummerraden och kombinerar dem sedan:

Union av uppsättningar

Det är ganska uppenbart att svaret blir $x\in \left(\frac(4)(7);+\infty \right)$

Svar: $x\in \left(\frac(4)(7);+\infty \right)$

Uppgift. Lös ojämlikheten:

\[\vänster| ((x)^(2))+2x-3 \right| \gt x\]

Lösning. Väl? Ingenting - allt är sig likt. Vi går från en ojämlikhet med en modul till en uppsättning av två olikheter:

\[\vänster| ((x)^(2))+2x-3 \right| \gt x\Högerpil \vänster[ \begin(align) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\end(align) \right.\]

Vi löser alla ojämlikheter. Tyvärr kommer rötterna där inte att vara särskilt bra:

\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\&D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\end(align)\]

Den andra ojämlikheten är också lite vild:

\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\&D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\end(align)\]

Nu måste du markera dessa siffror på två axlar - en axel för varje olikhet. Du måste dock markera punkterna i rätt ordning: ju större nummer, desto längre flyttas punkten åt höger.

Och här väntar ett setup på oss. Om allt är klart med siffrorna $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ (termerna i täljaren för den första bråk är mindre än termerna i täljaren för den andra , så summan är också mindre), med talen $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt (21))(2)$ det kommer inte heller att finnas några svårigheter (positivt tal uppenbarligen mer negativt), sedan med det sista paret är allt inte så klart. Vilket är störst: $\frac(-3+\sqrt(21))(2)$ eller $\frac(-1+\sqrt(13))(2)$? Placeringen av punkter på tallinjerna och faktiskt svaret kommer att bero på svaret på denna fråga.

Så låt oss jämföra:

\[\begin(matris) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matris)\]

Vi isolerade roten, fick icke-negativa tal på båda sidor av ojämlikheten, så vi har rätt att kvadrera båda sidor:

\[\begin(matris) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \ 4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(matris)\]

Jag tror att det är en no brainer att $4\sqrt(13) \gt 3$, så $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$, de sista punkterna på axlarna kommer att placeras så här:

Ett fall av fula rötter

Låt mig påminna dig om att vi löser en uppsättning, så svaret blir en förening, inte en skärningspunkt av skuggade uppsättningar.

Svar: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty \right)$

Som du kan se fungerar vårt schema utmärkt för både enkla och mycket svåra problem. Den enda "svaga punkten" i detta tillvägagångssätt är att du måste jämföra irrationella tal korrekt (och tro mig: det här är inte bara rötter). Men en separat (och mycket allvarlig) lektion kommer att ägnas åt jämförelsefrågor. Och vi går vidare.

3. Ojämlikheter med icke-negativa "svansar"

Nu kommer vi till det mest intressanta. Dessa är ojämlikheter i formen:

\[\vänster| f\höger| \gt\vänster| g\right|\]

Generellt sett är algoritmen som vi kommer att prata om nu endast korrekt för modulen. Det fungerar i alla ojämlikheter där det finns garanterat icke-negativa uttryck till vänster och höger:

Vad ska man göra med dessa uppgifter? Kom bara ihåg:

I ojämlikheter med icke-negativa "svansar" kan båda sidor höjas till vilken naturlig makt som helst. Det kommer inte att finnas några ytterligare begränsningar.

Först och främst kommer vi att vara intresserade av att kvadrera - det bränner moduler och rötter:

\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f. \\\end(align)\]

Förväxla inte detta med att ta roten från en kvadrat:

\[\sqrt(((f)^(2)))=\vänster| f \right|\ne f\]

Otaliga misstag gjordes när en student glömde att installera en modul! Men det här är en helt annan historia (detta är liksom irrationella ekvationer), så vi ska inte gå in på detta nu. Låt oss lösa ett par problem bättre:

Uppgift. Lös ojämlikheten:

\[\vänster| x+2 \right|\ge \left| 1-2x \right|\]

Lösning. Låt oss omedelbart lägga märke till två saker:

1. Detta är inte en strikt ojämlikhet. Punkter på tallinjen kommer att punkteras.
2. Båda sidorna av ojämlikheten är uppenbarligen icke-negativa (detta är en egenskap hos modulen: $\left| f\left(x \right) \right|\ge 0$).

Därför kan vi kvadrera båda sidor av olikheten för att bli av med modulen och lösa problemet med den vanliga intervallmetoden:

\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\left(x+2 \right))^(2))\ge ((\left(2x-1 \right))^(2)). \\\end(align)\]

I det sista steget fuskade jag lite: jag ändrade sekvensen av termer och utnyttjade modulens jämnhet (i själva verket multiplicerade jag uttrycket $1-2x$ med -1).

\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ höger)\höger)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(align)\]

Vi löser med intervallmetoden. Låt oss gå från ojämlikhet till ekvation:

\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\end(align)\]

Vi markerar de hittade rötterna på tallinjen. Än en gång: alla punkter är skuggade eftersom den ursprungliga ojämlikheten inte är strikt!

Att bli av med modultecknet

Låt mig påminna er för de som är särskilt envisa: vi tar tecknen från den senaste ojämlikheten, som skrevs ner innan vi gick vidare till ekvationen. Och vi målar över de ytor som krävs i samma ojämlikhet. I vårt fall är det $\left(x-3 \right)\left(3x+1 \right)\le 0$.

OK det är över nu. Problemet är löst.

Svar: $x\in \left[ -\frac(1)(3);3 \right]$.

Uppgift. Lös ojämlikheten:

\[\vänster| ((x)^(2))+x+1 \höger|\le \vänster| ((x)^(2))+3x+4 \höger|\]

Lösning. Vi gör allt likadant. Jag kommer inte kommentera - titta bara på sekvensen av åtgärder.

Kvadra den:

\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \right| \right))^(2))\le ((\left(\left) | ((x)^(2))+3x+4 \höger| \höger))^(2)); \\ & ((\left(((x)^(2))+x+1 \höger))^(2))\le ((\left(((x)^(2))+3x+4 \höger))^(2)); \\ & ((\vänster(((x)^(2))+x+1 \höger))^(2))-((\vänster(((x)^(2))+3x+4 \ höger))^(2))\le 0; \\ & \vänster(((x)^(2))+x+1-((x)^(2))-3x-4 \höger)\ gånger \\ & \ gånger \vänster(((x) ^(2))+x+1+((x)^(2))+3x+4 \höger)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(align)\]

Intervallmetod:

\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ Högerpil x=-1,5; \\ & 2((x)^(2))+4x+5=0\Högerpil D=16-40 \lt 0\Högerpil \varnothing . \\\end(align)\]

Det finns bara en rot på tallinjen:

Svaret är ett helt intervall

Svar: $x\in \left[ -1.5;+\infty \right)$.

En liten notering om den sista uppgiften. Som en av mina elever korrekt noterade är båda submodulära uttrycken i denna ojämlikhet uppenbarligen positiva, så modultecknet kan utelämnas utan att skada hälsan.

Men det här är en helt annan nivå av tänkande och ett annat förhållningssätt - det kan villkorligt kallas konsekvensmetoden. Om det - i en separat lektion. Låt oss nu gå vidare till den sista delen av dagens lektion och titta på en universell algoritm som alltid fungerar. Även när alla tidigare tillvägagångssätt var maktlösa. :)

4. Metod för uppräkning av alternativ

Tänk om alla dessa knep inte fungerar? Om ojämlikheten inte kan reduceras till icke-negativa svansar, om det är omöjligt att isolera modulen, om det i allmänhet finns smärta, sorg, melankoli?

Sedan kommer det "tunga artilleriet" av all matematik upp på scenen - brute force-metoden. I förhållande till ojämlikheter med modul ser det ut så här:

1. Skriv ut alla submodulära uttryck och sätt dem lika med noll;
2. Lös de resulterande ekvationerna och markera rötterna som finns på en tallinje;
3. Den raka linjen kommer att delas upp i flera sektioner, inom vilka varje modul har ett fast tecken och därför är unikt avslöjat;
4. Lös ojämlikheten på varje sådan sektion (du kan separat överväga rötterna-gränser som erhölls i steg 2 - för tillförlitlighet). Kombinera resultaten - det här kommer att vara svaret. :)

Så hur? Svag? Lätt! Bara under lång tid. Låt oss se i praktiken:

Uppgift. Lös ojämlikheten:

\[\vänster| x+2 \right| \lt \left| x-1 \right|+x-\frac(3)(2)\]

Lösning. Den här skiten kokar inte ner till ojämlikheter som $\left| f\höger| \lt g$, $\left| f\höger| \gt g$ eller $\left| f\höger| \lt \left| g \right|$, så låt oss gå vidare.

Vi skriver ut submoduluttryck, likställer dem med noll och hittar rötterna:

\[\begin(align) & x+2=0\Högerpil x=-2; \\ & x-1=0\Högerpil x=1. \\\end(align)\]

Totalt har vi två rötter som delar upp tallinjen i tre sektioner, inom vilka varje modul avslöjas unikt:

Dela tallinjen med nollor av submodulära funktioner

Låt oss överväga varje avsnitt separat.

1. Låt $x \lt -2$. Då är båda submodulära uttryck negativa, och den ursprungliga olikheten kommer att skrivas om enligt följande:

\[\begin(align) & -\left(x+2 \right) \lt -\left(x-1 \right)+x-1.5 \\ & -x-2 \lt -x+1+ x- 1,5 \\ & x \gt 1,5 \\\end(align)\]

Vi har en ganska enkel begränsning. Låt oss skära det med det initiala antagandet att $x \lt -2$:

\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1,5 \\\end(align) \right.\Rightarrow x\in \varnothing \]

Uppenbarligen kan variabeln $x$ inte samtidigt vara mindre än −2 och större än 1,5. Det finns inga lösningar på detta område.

1.1. Låt oss betrakta gränsfallet separat: $x=-2$. Låt oss bara ersätta detta nummer med den ursprungliga ojämlikheten och kontrollera: är det sant?

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1.5 \right|)_(x=-2) ) \ \ & 0 \lt \left| -3\right|-2-1.5; \\ & 0 \lt 3-3,5; \\ & 0 \lt -0.5\Högerpil \varnothing . \\\end(align)\]

Det är uppenbart att beräkningskedjan har lett oss till en felaktig ojämlikhet. Därför är den ursprungliga olikheten också falsk, och $x=-2$ ingår inte i svaret.

2. Låt nu $-2 \lt x \lt 1$. Den vänstra modulen öppnas redan med ett "plus", men den högra öppnas fortfarande med ett "minus". Vi har:

\[\begin(align) & x+2 \lt -\left(x-1 \right)+x-1.5 \\ & x+2 \lt -x+1+x-1.5 \\& x \lt - 2.5 \\\end(align)\]

Återigen korsar vi det ursprungliga kravet:

\[\left\( \begin(align) & x \lt -2.5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]

Och återigen, den tomma uppsättningen av lösningar, eftersom det inte finns några tal som både är mindre än -2,5 och större än -2.

2.1. Och återigen ett specialfall: $x=1$. Vi ersätter i den ursprungliga ojämlikheten:

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1.5 \right|)_(x=1)) \\ & \vänster| 3\höger| \lt \left| 0\right|+1-1,5; \\ & 3 \lt -0,5; \\ & 3 \lt -0.5\Högerpil \varnothing . \\\end(align)\]

I likhet med det tidigare "specialfallet" är talet $x=1$ uppenbarligen inte inkluderat i svaret.

3. Den sista delen av raden: $x \gt 1$. Här öppnas alla moduler med ett plustecken:

\[\begin(align) & x+2 \lt x-1+x-1,5 \\ & x+2 \lt x-1+x-1,5 \\ & x \gt 4,5 \\ \end(align)\ ]

Och återigen skär vi den hittade uppsättningen med den ursprungliga begränsningen:

\[\left\( \begin(align) & x \gt 4.5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4.5;+\infty \right)\ ]

Till sist! Vi har hittat ett intervall som blir svaret.

Svar: $x\in \left(4,5;+\infty \right)$

Slutligen, en anteckning som kan rädda dig från dumma misstag när du löser verkliga problem:

Lösningar av ojämlikheter med moduler är vanligtvis kontinuerliga uppsättningar på tallinjen - intervall och segment. Isolerade punkter är mycket mindre vanliga. Och ännu mer sällan händer det att lösningens gränser (slutet av segmentet) sammanfaller med gränsen för det aktuella intervallet.

Följaktligen, om gränser (samma "särskilda fall") inte ingår i svaret, kommer områdena till vänster och höger om dessa gränser nästan säkert inte att inkluderas i svaret. Och vice versa: gränsen in i svaret, vilket innebär att vissa områden runt den också kommer att vara svar.

Tänk på detta när du granskar dina lösningar.

ojämlikhetslösning i läge uppkopplad lösning nästan vilken ojämlikhet som helst uppkopplad. Matematisk ojämlikheter på nätet att lösa matematik. Hitta snabbt ojämlikhetslösning i läge uppkopplad. Webbplatsen www.site låter dig hitta lösning nästan vilken som helst algebraisk, trigonometrisk eller transcendental ojämlikhet på nätet. När du studerar nästan vilken gren av matematik som helst i olika stadier måste du bestämma dig ojämlikheter på nätet. För att få ett svar omedelbart, och viktigast av allt ett korrekt svar, behöver du en resurs som låter dig göra detta. Tack vare sajten www.site lösa ojämlikhet online kommer att ta några minuter. Den största fördelen med www.site när man löser matematiska ojämlikheter på nätet- det här är hastigheten och noggrannheten för svaret som tillhandahålls. Sajten kan lösa alla algebraiska ojämlikheter på nätet, trigonometriska ojämlikheter online, transcendentala ojämlikheter på nätet, och ojämlikheter med okända parametrar i läge uppkopplad. Ojämlikheter tjäna som en kraftfull matematisk apparat lösningar praktiska problem. Med hjälpen matematiska ojämlikheter det är möjligt att uttrycka fakta och relationer som vid första anblicken kan verka förvirrande och komplexa. Okända mängder ojämlikheter kan hittas genom att formulera problemet i matematisk språk i formen ojämlikheter Och besluta mottagen uppgift i läge uppkopplad på webbplatsen www.site. Några algebraisk ojämlikhet, trigonometrisk ojämlikhet eller ojämlikheter som innehåller transcendentala funktioner du enkelt kan besluta online och få det exakta svaret. När man studerar naturvetenskap stöter man oundvikligen på behovet lösningar på ojämlikheter. I det här fallet måste svaret vara korrekt och måste erhållas omedelbart i läget uppkopplad. Därför för lösa matematiska ojämlikheter online vi rekommenderar webbplatsen www.site, som kommer att bli din oumbärliga kalkylator för lösa algebraiska ojämlikheter online, trigonometriska ojämlikheter på nätet, och transcendentala ojämlikheter på nätet eller ojämlikheter med okända parametrar. För praktiska problem med att hitta onlinelösningar på olika matematiska ojämlikheter resurs www.. Lösning ojämlikheter på nätet själv är det användbart att kontrollera det mottagna svaret med hjälp av onlinelösning av ojämlikheter på webbplatsen www.site. Du måste skriva ojämlikheten korrekt och omedelbart få onlinelösning, varefter allt som återstår är att jämföra svaret med din lösning på ojämlikheten. Att kontrollera svaret tar inte mer än en minut, det räcker lösa ojämlikhet online och jämför svaren. Detta hjälper dig att undvika misstag beslut och rätta svaret i tid när lösa ojämlikheter online antingen algebraisk, trigonometrisk, transcendentala eller olikhet med okända parametrar.