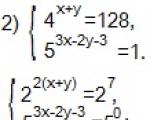सजातीय घातीय असमानताओं को हल करना। घातीय समीकरणों और असमानताओं को हल करना
वह है अनिवार्य घातीय समीकरणों की एक प्रणाली को हल करते समय? निश्चित रूप से, परिवर्तनयह प्रणाली सरल समीकरणों की एक प्रणाली में.
उदाहरण।
समीकरणों की प्रणालियों को हल करें:
आइए व्यक्त करें परके माध्यम से एक्स(2) सिस्टम समीकरण से और इस मान को (1) सिस्टम समीकरण में प्रतिस्थापित करें।
हम परिणामी प्रणाली के वें समीकरण को हल करते हैं (2):
2 x +2 x +2 =10, सूत्र लागू करें: एक एक्स + य=एक एक्स∙ एक य.
2 x +2 x ∙2 2 =10, आइए सामान्य गुणनखंड 2 x को कोष्ठक से बाहर निकालें:
2 x (1+2 2)=10 या 2 x ∙5=10, इसलिए 2 x =2.
2 x =2 1, यहाँ से एक्स=1. आइए समीकरणों की प्रणाली पर वापस लौटें।

उत्तर: (1; 2).
समाधान।
हम (1) समीकरण के बाएँ और दाएँ पक्षों को आधार वाली घातों के रूप में दर्शाते हैं 2 , और (2) समीकरण का दाहिना भाग संख्या की शून्य शक्ति के रूप में है 5 .
यदि समान आधार वाली दो घातें समान हैं, तो इन घातों के घातांक बराबर होते हैं - हम घातांकों को आधारों के साथ बराबर करते हैं 2 और आधार वाले घातांक 5 .
हम जोड़ विधि का उपयोग करके दो चर वाले रैखिक समीकरणों की परिणामी प्रणाली को हल करते हैं।
हम देखतें है एक्स=2और हम इसके स्थान पर इस मान को प्रतिस्थापित करते हैं एक्ससिस्टम के दूसरे समीकरण में।
हम देखतें है पर.
उत्तर: (2; 1.5).

समाधान।
यदि पिछले दो उदाहरणों में हम समान आधारों के साथ दो डिग्री के संकेतकों को बराबर करके एक सरल प्रणाली में चले गए, तो तीसरे उदाहरण में यह ऑपरेशन असंभव है। नए वेरिएबल पेश करके ऐसी प्रणालियों को हल करना सुविधाजनक है। हम वेरिएबल पेश करेंगे यूऔर वी,और फिर वेरिएबल को व्यक्त करें यूके माध्यम से वीऔर हमें चर के लिए एक समीकरण मिलता है वी.
हम सिस्टम के (2) वें समीकरण को हल करते हैं।
वी 2 +63वी-64=0. आइए विएटा के प्रमेय का उपयोग करके जड़ों का चयन करें, यह जानते हुए कि: v 1 +v 2 = -63; वी 1 ∙वी 2 =-64.
हमें मिलता है: वी 1 =-64, वी 2 =1। हम सिस्टम पर लौटते हैं और आपको ढूंढते हैं।

चूँकि घातांकीय फलन का मान सदैव धनात्मक होता है, समीकरण 4 x = -1 और 4 y = -64 कोई समाधान नहीं है.
समीकरणों की प्रणालियों को हल करने की विधियाँ
आरंभ करने के लिए, आइए संक्षेप में याद करें कि समीकरणों की प्रणालियों को हल करने के लिए आम तौर पर कौन सी विधियाँ मौजूद हैं।
अस्तित्व चार मुख्य तरीकेसमीकरणों की प्रणालियों के समाधान:
प्रतिस्थापन विधि: दिए गए समीकरणों में से कोई भी लें और $y$ को $x$ के रूप में व्यक्त करें, फिर $y$ को सिस्टम समीकरण में प्रतिस्थापित किया जाता है, जहां से वेरिएबल $x.$ पाया जाता है, इसके बाद हम आसानी से गणना कर सकते हैं चर $y.$
जोड़ विधि: इस विधि में, आपको एक या दोनों समीकरणों को ऐसी संख्याओं से गुणा करना होगा कि जब आप दोनों को एक साथ जोड़ें, तो एक चर "गायब" हो जाए।
ग्राफ़िकल विधि: सिस्टम के दोनों समीकरणों को निर्देशांक तल पर दर्शाया जाता है और उनके प्रतिच्छेदन का बिंदु पाया जाता है।
नए वेरिएबल पेश करने की विधि: इस विधि में हम सिस्टम को सरल बनाने के लिए कुछ अभिव्यक्तियों को प्रतिस्थापित करते हैं, और फिर उपरोक्त विधियों में से एक का उपयोग करते हैं।
घातांकीय समीकरणों की प्रणाली
परिभाषा 1
घातांकीय समीकरणों से युक्त समीकरणों के निकाय को घातांकीय समीकरणों के निकाय कहा जाता है।
हम उदाहरणों का उपयोग करके घातीय समीकरणों की प्रणालियों को हल करने पर विचार करेंगे।
उदाहरण 1
समीकरणों की प्रणाली को हल करें
चित्र 1।
समाधान।
इस प्रणाली को हल करने के लिए हम पहली विधि का उपयोग करेंगे। सबसे पहले, आइए पहले समीकरण में $y$ को $x$ के रूप में व्यक्त करें।

चित्र 2।
आइए दूसरे समीकरण में $y$ प्रतिस्थापित करें:
\ \ \[-2-x=2\] \ \
उत्तर: $(-4,6)$.
उदाहरण 2
समीकरणों की प्रणाली को हल करें

चित्र तीन।
समाधान।
यह सिस्टम सिस्टम के समतुल्य है

चित्र 4.
आइए समीकरणों को हल करने की चौथी विधि लागू करें। मान लीजिए $2^x=u\ (u >0)$, और $3^y=v\ (v >0)$, हमें मिलता है:

चित्र 5.
आइए हम जोड़ विधि का उपयोग करके परिणामी प्रणाली को हल करें। आइए समीकरण जोड़ें:
\ \
फिर दूसरे समीकरण से हमें वह प्राप्त होता है
प्रतिस्थापन पर लौटने पर, मुझे घातीय समीकरणों की एक नई प्रणाली प्राप्त हुई:
चित्र 6.
हम पाते हैं:
चित्र 7.
उत्तर: $(0,1)$.
घातीय असमानताओं की प्रणाली
परिभाषा 2
घातीय समीकरणों से युक्त असमानताओं की प्रणालियों को घातांकीय असमानताओं की प्रणाली कहा जाता है।
हम उदाहरणों का उपयोग करके घातांकीय असमानताओं की प्रणालियों को हल करने पर विचार करेंगे।
उदाहरण 3
असमानताओं की व्यवस्था को हल करें

आंकड़ा 8।
समाधान:
असमानताओं की यह व्यवस्था व्यवस्था के समतुल्य है

चित्र 9.
पहली असमानता को हल करने के लिए, घातांकीय असमानताओं की तुल्यता पर निम्नलिखित प्रमेय को याद करें:
प्रमेय 1.असमानता $a^(f(x)) >a^(\varphi (x)) $, जहां $a >0,a\ne 1$ दो प्रणालियों के संग्रह के बराबर है
\}