मुख्यपृष्ठ › शरीर › डायओफँटस प्रकल्प आणि त्याचे शोध. गोषवारा: डायओफँटस

डायओफँटस प्रकल्प आणि त्याचे शोध. गोषवारा: डायओफँटस

गुणांक ज्यांचे समाधान पूर्णांकांमध्ये सापडले पाहिजे.

अलेक्झांड्रियाचा डायओफँटस
Διόφαντος ὁ Ἀλεξανδρεύς

जन्मतारीख	आधी नाही आणि नंतर नाहीकिंवा
जन्मस्थान	अलेक्झांड्रिया, इजिप्त
मृत्यूची तारीख	आधी नाही आणि नंतर नाही
देश	प्राचीन रोम
वैज्ञानिक क्षेत्र	संख्या सिद्धांत
म्हणून ओळखले	"बीजगणिताचा जनक"
विकिमीडिया कॉमन्सवर अलेक्झांड्रियाचा डायओफँटस

चरित्र

त्याच्या जीवनातील तपशीलांबद्दल जवळजवळ काहीही माहिती नाही. एकीकडे, डायओफँटसने हायप्सिकल्स (बीसी दुसरे शतक) उद्धृत केले; दुसरीकडे, थिओन ऑफ अलेक्झांड्रिया (सुमारे 350 एडी) डायओफंटसबद्दल लिहितो, ज्यावरून आपण असा निष्कर्ष काढू शकतो की त्याचे जीवन या कालखंडाच्या सीमेत घडले. डायओफँटसच्या जीवनकाळाचे संभाव्य स्पष्टीकरण त्याच्यावर आधारित आहे अंकगणित"सर्वात आदरणीय डायोनिसियस" यांना समर्पित. असे मानले जाते की हा डायोनिसियस दुसरा कोणी नसून अलेक्झांड्रियाचा बिशप डायोनिसियस आहे, जो तिसऱ्या शतकाच्या मध्यभागी राहत होता. n e

हे खालील समीकरण सोडवण्यासारखे आहे:

x = x 6 + x 12 + x 7 + 5 + x 2 + 4 (\displaystyle x=(\frac (x)(6))+(\frac (x)(12))+(\frac (x) (7))+5+(\frac (x)(2))+4)

हे समीकरण देते x = 84 (\displaystyle x=84), म्हणजेच डायओफँटसचे वय 84 वर्षांच्या बरोबरीचे आहे. तथापि, माहितीच्या अचूकतेची पुष्टी केली जाऊ शकत नाही.

अंकगणितडायओफंटा

डायओफँटसचे मुख्य कार्य - अंकगणित 13 पुस्तकांमध्ये. दुर्दैवाने, पहिल्या १३ पुस्तकांपैकी फक्त ६ (किंवा १०, खाली पहा) वाचली आहेत.

पहिल्या पुस्तकाच्या आधी विस्तृत परिचय आहे, ज्यामध्ये डायओफँटसने वापरलेल्या नोटेशनचे वर्णन केले आहे. डायओफँटस अज्ञात "नंबर" म्हणतात ( ἀριθμός ) आणि अक्षराने दर्शविले जाते ς , चौरस अज्ञात - चिन्ह Δ Υ (यासाठी लहान δύναμις - "डिग्री"), अज्ञातचे घन - चिन्ह Κ Υ (यासाठी लहान κύβος - "क्यूब"). अज्ञाताच्या खालील अंशांसाठी विशेष चिन्हे प्रदान केली आहेत, सहाव्या पर्यंत, ज्याला क्यूब-क्यूब म्हणतात, आणि त्यांच्या विरुद्ध अंशांसाठी, वजा सहाव्या पर्यंत.

डायओफँटसमध्ये अतिरिक्त चिन्ह नाही: तो फक्त पदवीच्या उतरत्या क्रमाने एकमेकांच्या पुढे सकारात्मक संज्ञा लिहितो आणि प्रत्येक टर्ममध्ये अज्ञात पदवी प्रथम लिहिली जाते, आणि नंतर संख्यात्मक गुणांक. वजा केलेल्या संज्ञा देखील शेजारी शेजारी लिहिल्या जातात आणि त्यांच्या संपूर्ण गटासमोर उलटे अक्षर Ψ च्या स्वरूपात एक विशेष चिन्ह ठेवले जाते. समान चिन्ह दोन अक्षरांनी दर्शविले जाते ἴσ (यासाठी लहान ἴσος - "समान").

समान संज्ञा आणण्यासाठी एक नियम आणि समीकरणाच्या दोन्ही बाजूंना समान संख्या किंवा अभिव्यक्ती जोडण्यासाठी किंवा वजा करण्याचा नियम तयार करण्यात आला: ज्याला नंतर अल-खोरेझमीने "बीजगणित आणि अल्मुकाबाला" म्हणण्यास सुरुवात केली. चिन्हांचा नियम सादर केला गेला आहे: “वजा बाय प्लस देते वजा”, “वजा करून वजा अधिक देतो”; वजा केलेल्या पदांसह दोन अभिव्यक्तींचा गुणाकार करताना हा नियम वापरला जातो. हे सर्व भौमितिक व्याख्येचा संदर्भ न घेता, सामान्य अटींमध्ये तयार केले आहे.

बहुतेक काम हे निराकरणांसह समस्यांचा संग्रह आहे (सहा वाचलेल्या पुस्तकांमध्ये एकूण 189 आहेत, अरबी भागातील चार - 290), सामान्य पद्धती स्पष्ट करण्यासाठी कुशलतेने निवडले आहेत. मुख्य मुद्दे अंकगणित- अनिश्चित समीकरणांवर सकारात्मक तर्कशुद्ध उपाय शोधणे. डायओफँटस द्वारे परिमेय संख्यांना नैसर्गिक संख्यांप्रमाणेच मानले जाते, जे प्राचीन गणितज्ञांसाठी वैशिष्ट्यपूर्ण नाही.

प्रथम, डायओफँटस दोन अज्ञातांमधील द्वितीय-क्रम समीकरणांच्या प्रणालींचे परीक्षण करतो; हे आधीच ज्ञात असल्यास इतर उपाय शोधण्यासाठी एक पद्धत निर्दिष्ट करते. मग तो उच्च पदवीच्या समीकरणांना समान पद्धती लागू करतो. पुस्तक VI परिमेय बाजूंसह काटकोन त्रिकोणाशी संबंधित समस्यांचे परीक्षण करते.

प्रभाव अंकगणितगणिताच्या विकासासाठी

10 व्या शतकात अंकगणितअरबीमध्ये अनुवादित केले गेले (कुस्ता इब्न लुका पहा), त्यानंतर इस्लामिक देशांतील गणितज्ञांनी (अबू कामिल आणि इतर) डायओफंटसचे काही संशोधन चालू ठेवले. युरोप मध्ये, मध्ये स्वारस्य अंकगणितराफेल बॉम्बेली यांनी हे काम लॅटिनमध्ये अनुवादित करून प्रकाशित केल्यानंतर आणि त्यातून 143 समस्या प्रकाशित केल्यानंतर वाढ झाली. बीजगणित(१५७२). 1621 मध्ये, एक क्लासिक, पूर्णपणे भाष्य केलेले लॅटिन भाषांतर दिसू लागले अंकगणित, Bachet de Meziriac द्वारे अंमलात आणले.

डायओफँटसच्या पद्धतींचा फार मोठा प्रभाव फ्रँकोइस व्हिएट आणि पियरे फर्मॅटवर पडला; तथापि, आधुनिक काळात, अनिश्चित समीकरणे सहसा पूर्णांकांमध्ये सोडवली जातात, परिमेय संख्यांमध्ये नाही, जसे डायओफँटसने केले. जेव्हा पियरे फर्मॅटने बॅचेट डी मेझिरियाक यांनी संपादित केलेले डायओफँटसचे अंकगणित वाचले, तेव्हा तो निष्कर्षापर्यंत पोहोचला की डायओफँटसने विचारात घेतलेल्या समीकरणांपैकी एकाला पूर्णांकांमध्ये कोणतेही निराकरण नव्हते आणि त्याने समासात नमूद केले की त्याला "खरोखरच एक अद्भुत पुरावा सापडला आहे. हे प्रमेय ... तथापि, पुस्तकाचे समास ते समाविष्ट करण्यासाठी खूपच अरुंद आहेत." हे विधान आता फर्मॅटचे शेवटचे प्रमेय म्हणून ओळखले जाते.

20 व्या शतकात, डायओफंटसच्या नावाखाली आणखी चार पुस्तकांचा अरबी मजकूर सापडला. अंकगणित. आय.जी. बाश्माकोवा आणि ई.आय. स्लाव्हुटिन यांनी या मजकुराचे विश्लेषण करून, एक गृहितक मांडले की त्याचा लेखक डायओफँटस नव्हता, परंतु डायओफँटसच्या पद्धतींमध्ये पारंगत भाष्यकार होता, बहुधा हायपेटिया. तथापि, पहिल्या तीन आणि शेवटच्या तीन पुस्तकांतील समस्या सोडवण्याच्या पद्धतीतील महत्त्वाची पोकळी अरबी भाषांतराच्या चार पुस्तकांनी भरून काढली आहे. हे आम्हाला मागील अभ्यासाच्या परिणामांवर पुनर्विचार करण्यास भाग पाडते. . [ ]

डायओफँटसची इतर कामे

डायओफँटसचा ग्रंथ बहुभुज संख्यांबद्दल (Περὶ πολυγώνων ἀριθμῶν ) पूर्णपणे संरक्षित नाही; संरक्षित भागामध्ये, भौमितिक बीजगणित पद्धती वापरून अनेक सहायक प्रमेये काढली जातात.

डायओफँटसच्या कामातून पृष्ठभाग मोजण्याबद्दल (ἐπιπεδομετρικά ) आणि गुणाकार बद्दल (Περὶ πολλαπλασιασμοῦ ) देखील फक्त तुकडे टिकले आहेत.

डायओफँटसचे पुस्तक पोरिझम्समध्ये वापरल्या गेलेल्या काही प्रमेयांवरूनच ज्ञात आहे अंकगणित.

देखील पहा

संग्रह Budé" (2 खंड प्रकाशित: पुस्तके 4 - 7).

संशोधन:

बाश्माकोवा I. G., Slavutin E. I., Rosenfeld B. A. Diophantus च्या "अंकगणित" ची अरबी आवृत्ती // ऐतिहासिक आणि गणितीय अभ्यास. - एम., 1978. - अंक. XXIII. - पृष्ठ 192 - 225.
बाश्माकोवा आय. जी.बीजगणितीय वक्रांचे अंकगणित: (डायोफँटसपासून पॉइन्कारेपर्यंत) // ऐतिहासिक आणि गणितीय अभ्यास. - 1975. - अंक. 20. - पृ. 104 - 124.
बाश्माकोवा आय. जी.डायओफँटस आणि डायओफँटाइन समीकरण. - M.: नौका, 1972 (पुनर्मुद्रण: M.: LKI, 2007). प्रति. त्याच्या वर. इंग्रजी: डायओफंट आणि डायओफँटिशे ग्लेचुंजन. - बेसल; स्टटगार्ट: बिरखौसर, 1974. ट्रान्स. इंग्रजी मध्ये. इंग्रजी: डायओफँटस आणि डायओफँटाइन समीकरण/ अनुवाद. ए. शेनित्झर यांनी एच. ग्रँटच्या संपादकीय सहाय्याने आणि जे. सिल्व्हरमन // द डॉल्सियानी मॅथेमॅटिकल एक्सपोझिशन्सद्वारे अद्यतनित केले. - क्रमांक 20. - वॉशिंग्टन, डीसी: मॅथेमॅटिकल असोसिएशन ऑफ अमेरिका, 1997.
बाश्माकोवा आय. जी.डायओफँटस आणि फर्मॅट: (स्पर्शिका आणि टोकाच्या पद्धतीच्या इतिहासावर) // ऐतिहासिक आणि गणितीय अभ्यास. - एम., 1967. - अंक. VII. - पृष्ठ 185 - 204.
बाश्माकोवा I. G., Slavutin E. I.डायओफँटस ते फर्मेट पर्यंत डायओफँटिन विश्लेषणाचा इतिहास. - एम.: नौका, 1984.
प्राचीन काळापासून 19व्या शतकाच्या सुरुवातीपर्यंत गणिताचा इतिहास. - T. I: सर्वात प्राचीन पासून. नवीन युग सुरू होण्यापूर्वी वेळा. वेळ / एड. ए.पी. युश्केविच. - एम., नौका, 1970.
स्लावुटिन ई. आय.डायओफँटस बीजगणित आणि त्याची उत्पत्ती // ऐतिहासिक आणि गणितीय अभ्यास. - एम., 1975. - अंक. 20. - पृ. 63 - 103.
श्चेत्निकोव्ह ए. आय.अलेक्झांड्रियाच्या “ऑन पॉलीगोनल नंबर्स” या पुस्तकाच्या डायओफँटसला पूर्णपणे बीजगणित म्हणता येईल का? // ऐतिहासिक आणि गणितीय संशोधन. - एम., 2003. - अंक. 8 (43). - पृ. 267 - 277.
हिथ गु. एल.अलेक्झांड्रियाचा डायोफँटस, ग्रीक बीजगणिताच्या इतिहासातील एक अभ्यास. - केंब्रिज, 1910 (रिप्र.: NY, 1964).
नॉर डब्ल्यू. आर. Arithmktikê stoicheiôsis: अलेक्झांड्रियाच्या डायओफंटस आणि हिरोवर // हिस्टोरिया मॅथेमॅटिका. - 20. - 1993. - पृष्ठ 180 - 192.
ख्रिस्टिनिडिस जे.डायओफँटसचा मार्ग: डायओफँटसच्या समाधानाच्या पद्धतीवर काही स्पष्टीकरण // हिस्टोरिया मॅथेमॅटिका. - 34. - 2007. - पृष्ठ 289 - 305.
रशीद आर., हौझेल सी. Les Arithmétiques de Diophante. व्याख्यान इतिहास आणि गणित . - डी ग्रुटर, 2013.

महापालिका शैक्षणिक संस्था

"Lyceum क्रमांक 10" Perm

डायओफँटस. डायओफँटाइन समीकरणे

काम केले

इलिना याना,

11वी वर्गातील विद्यार्थी

पर्यवेक्षक

झोलोतुखिना एल. व्ही.

गणिताचे शिक्षक

पर्म, 2010

परिचय ……………………………………………………………………………….3

1. डायओफँटस ……………………………………………………………………………………………………… 4

2. संख्या आणि चिन्हे………………………………………………………6

3. डायओफँटाइन समीकरण ………………………………………………….. …८

४. उपाय………………………………………………………..१२

निष्कर्ष………………………………………………………………………………….१५

संदर्भ ……………………………………………………… १६

परिचय

आजची शाळकरी मुले विविध समीकरणे सोडवतात. युनिफाइड स्टेट एक्झामिनेशन टास्कच्या भाग क मध्ये डायओफँटाइन समीकरण नावाचे एक मनोरंजक समीकरण आहे. डायओफँटसने आपल्या कामांमध्ये केवळ अनिश्चित समीकरणे परिमेय संख्येत सोडवण्याची समस्या मांडली नाही तर ती सोडवण्याच्या काही सामान्य पद्धतीही दिल्या. आजच्या अकरावीच्या जे विद्यार्थी गणिताची परीक्षा देणार आहेत त्यांच्यासाठी या पद्धती खूप उपयुक्त ठरतील.

डायओफँटसने आर्किमिडीज प्रमाणे गणिताच्या विकासात मोठे योगदान दिले. आर्किमिडीजने हेच केले, उदाहरणार्थ: लंबवर्तुळाचे क्षेत्र, पॅराबोलाचा एक भाग, गोलाची पृष्ठभाग, गोलाची मात्रा आणि इतर शरीरे ठरवताना, त्याने अविभाज्य रकमेची पद्धत आणि उत्तीर्ण होण्याची पद्धत वापरली. मर्यादेपर्यंत, परंतु कोठेही त्याने या पद्धतींचे सामान्य अमूर्त वर्णन दिले नाही. आर्किमिडीजच्या पद्धतींना तिथून वेगळे करण्यासाठी 16व्या आणि 17व्या शतकातील शास्त्रज्ञांना त्याच्या कामांचा काळजीपूर्वक अभ्यास करावा लागला आणि नवीन पद्धतीने त्याची पुनर्रचना करावी लागली. डायओफँटसचीही अशीच परिस्थिती आहे. त्याच्या पद्धती समजल्या गेल्या आणि नवीन समस्यांवर विएथे आणि फर्मेट यांनी लागू केले, म्हणजे. आर्किमिडीजचे निराकरण झाले त्याच वेळी.

1. डायओफँटस

डायओफंटस विज्ञानाच्या इतिहासातील सर्वात कठीण रहस्यांपैकी एक सादर करते. तो केव्हा जगला हे आपल्याला माहीत नाही किंवा त्याच क्षेत्रात काम करणाऱ्या त्याच्या पूर्ववर्तींनाही माहीत नाही. त्याची कार्ये संपूर्ण अभेद्य अंधारात चमकणाऱ्या अग्नीसारखी आहेत. डायओफँटस जगू शकला असता तो कालावधी अर्धा सहस्राब्दी आहे! या मध्यांतराची खालची सीमा कोणत्याही अडचणीशिवाय निश्चित केली जाते: बहुभुज संख्यांवरील त्याच्या पुस्तकात, डायओफँटसने अलेक्झांड्रियाच्या गणितज्ञ हायप्सिकल्सचा वारंवार उल्लेख केला आहे, जो ईसापूर्व दुसऱ्या शतकाच्या मध्यभागी राहत होता. e दुसरीकडे, अलेक्झांड्रियाच्या थिओनच्या टिप्पण्यांमध्ये प्रसिद्ध खगोलशास्त्रज्ञ टॉलेमीच्या “अल्माजेस्ट” मधील, डायओफंटसच्या कार्याचा एक उतारा ठेवला आहे. थिओन चौथ्या शतकाच्या मध्यभागी राहत होता. e हे या मध्यांतराची वरची सीमा निर्धारित करते. तर, 500 वर्षे!

परंतु डायओफंटसचे निवासस्थान सुप्रसिद्ध आहे - हे प्रसिद्ध अलेक्झांड्रिया आहे, हेलेनिस्टिक जगाच्या वैज्ञानिक विचारांचे केंद्र आहे.

डायओफँटसच्या व्यक्तिमत्त्वाबद्दल ज्ञात असलेल्या सर्व गोष्टी संपवण्यासाठी, आम्ही एक कोडी कविता सादर करतो जी आमच्यापर्यंत आली आहे:

Diophantus च्या राख थडग्यात विश्रांती; तिला आश्चर्य वाटले - आणि दगड
मृत व्यक्तीचे वय त्याच्या सुज्ञ कलेतून बोलेल.
देवांच्या इच्छेनुसार, तो लहानपणी त्याच्या आयुष्याचा सहावा भाग जगला.
आणि गालावर फुंकर घालून साडेपाचला भेटलो.
त्याच्या मैत्रिणीशी त्याची एंगेजमेंट होऊन फक्त सातवा दिवस होता.
तिच्याबरोबर पाच वर्षे घालवल्यानंतर ऋषी आपल्या मुलाची वाट पाहू लागले;
त्याच्या वडिलांचा लाडका मुलगा त्याचे अर्धे आयुष्य जगला.
त्याला त्याच्या वडिलांकडून त्याच्या लवकर कबरेने नेले होते.
दोनदा दोन वर्षांनी पालकांनी खूप शोक केला,
इथे मला माझ्या दुःखी आयुष्याची मर्यादा दिसली.

येथून डायओफंटस 84 वर्षे जगला याची गणना करणे सोपे आहे. तथापि, यासाठी तुम्हाला डायओफँटसची कला पारंगत करण्याची गरज नाही! एका अज्ञातासह 1ल्या पदवीचे समीकरण सोडविण्यास सक्षम असणे पुरेसे आहे आणि इजिप्शियन शास्त्री 2 हजार वर्षांपूर्वी हे करण्यास सक्षम होते. e

पण सर्वात रहस्यमय म्हणजे डायओफँटसचे काम. 13 पैकी सहा पुस्तके आमच्यापर्यंत पोहोचली आहेत, जी "अंकगणित" मध्ये एकत्र केली गेली आहेत. या पुस्तकांची शैली आणि सामग्री संख्या सिद्धांत आणि बीजगणितावरील शास्त्रीय प्राचीन कृतींपेक्षा खूप वेगळी आहे, ज्याची उदाहरणे आपल्याला आर्किमिडीज आणि अपोलोनियसच्या कृतींमधून युक्लिडचे घटक, त्याचा डेटा आणि लेमास वरून माहित आहेत. "अंकगणित" हा निःसंशयपणे असंख्य अभ्यासांचा परिणाम होता जो आपल्यासाठी पूर्णपणे अज्ञात राहिला. आम्ही फक्त त्याच्या मुळांबद्दल अंदाज लावू शकतो आणि त्याच्या पद्धती आणि परिणामांची समृद्धता आणि सौंदर्य पाहून आश्चर्यचकित होऊ शकतो.

डायओफँटस द्वारे "अंकगणित" हा समस्यांचा संग्रह आहे (एकूण 189 आहेत), ज्यापैकी प्रत्येक समाधान (किंवा निराकरणाच्या अनेक पद्धती) आणि आवश्यक स्पष्टीकरणांसह सुसज्ज आहे. त्यामुळे, पहिल्या दृष्टीक्षेपात असे दिसते की हे एक सैद्धांतिक काम नाही. तथापि, काळजीपूर्वक वाचन दर्शविते की समस्या काळजीपूर्वक निवडल्या गेल्या आहेत आणि अतिशय विशिष्ट, काटेकोरपणे विचार केलेल्या पद्धतींचे वर्णन करतात. प्राचीन काळातील प्रथेप्रमाणे, पद्धती सामान्य स्वरूपात तयार केल्या जात नाहीत, परंतु समान समस्यांचे निराकरण करण्यासाठी पुनरावृत्ती केली जाते.

2. संख्या आणि चिन्हे

डायओफँटसची सुरुवात मूलभूत व्याख्या आणि अक्षर चिन्हांच्या वर्णनाने होते.

शास्त्रीय ग्रीक गणितामध्ये, ज्याची पूर्णता युक्लिडच्या घटकांमध्ये आढळली, άριJμός - “ ताल" किंवा " arithmos"; म्हणून संख्यांच्या विज्ञानासाठी "अंकगणित" हे नाव) एककांचा संच समजले गेले, म्हणजे पूर्णांक अपूर्णांक किंवा अपरिमेयता यांना संख्या म्हटले गेले नाही. काटेकोरपणे सांगायचे तर, प्रिन्सिपियामध्ये कोणतेही अपूर्णांक नाहीत. एकक अविभाज्य मानले जाते आणि युनिटच्या अपूर्णांकांऐवजी, पूर्णांकांचे गुणोत्तर मानले जाते; अपरिमेयता अतुलनीय विभागांचे गुणोत्तर म्हणून दिसतात, उदाहरणार्थ, आपण आता √2 दर्शवितो ती संख्या शास्त्रीय ग्रीक लोकांसाठी चौरसाच्या कर्णाचे त्याच्या बाजूचे गुणोत्तर होते. निगेटिव्ह आकड्यांची चर्चा नव्हती. त्यांच्यासाठी समतुल्यही नव्हते. डायओफँटसमध्ये आम्हाला पूर्णपणे भिन्न चित्र आढळते.

डायओफँटस एककांचा संच म्हणून संख्येची पारंपारिक व्याख्या देतो, परंतु नंतर त्याच्या समस्या शोधतो सकारात्मक तर्कसंगतउपाय, आणि अशा प्रत्येक सोल्युशनला नंबर म्हणतात (άριJμός - “ ताल »).

पण प्रकरण एवढ्यावरच थांबत नाही. डायओफँटस ने ऋण संख्यांचा परिचय करून दिला: तो त्यांना विशेष संज्ञा λει̃ψις म्हणतो - “ लिपसिस"- λει̃πω - " या क्रियापदापासून व्युत्पन्न लीपो", ज्याचा अर्थ उणीव, उणीव, जेणेकरून या शब्दाचे भाषांतर "अभाव" या शब्दाने केले जाऊ शकते. तसे, विज्ञानाचे प्रसिद्ध रशियन इतिहासकार I. टिमचेन्को हेच करतात. डायओफँटस सकारात्मक संख्येला ΰπαρξις शब्द म्हणतात - “ iparxis”, ज्याचा अर्थ अस्तित्व, अस्तित्व आणि अनेकवचनात या शब्दाचा अर्थ मालमत्ता किंवा मालमत्ता असा होऊ शकतो. अशा प्रकारे, सापेक्ष संख्यांसाठी डायओफँटसची संज्ञा पूर्व आणि युरोपमधील मध्ययुगात वापरल्या जाणाऱ्या शब्दावलीच्या जवळ आहे. बहुधा, हे फक्त ग्रीकमधून अरबी, संस्कृत, लॅटिन आणि नंतर युरोपच्या विविध भाषांमध्ये भाषांतर होते.

लक्षात घ्या की λει̃ψις हा शब्द आहे “ लिपसिस"- "वजाबाकी" असे भाषांतर केले जाऊ शकत नाही, जसे डायओफँटसचे अनेक भाषांतरकार करतात, कारण वजाबाकीच्या कार्यासाठी डायओफँटस पूर्णपणे भिन्न संज्ञा वापरतात, म्हणजे άφελει̃ν - " afelein"किंवा άφαιρει̃ν - " अग्निशमन", जे άφαιρεω - " या क्रियापदावरून आलेले आहेत. afireo"- घेऊन जा. समीकरणे बदलताना, डायओफँटस स्वतः अनेकदा मानक अभिव्यक्ती वापरतो "दोन्ही बाजूंना λει̃ψις जोडा."

डायओफँटसच्या शब्दांचे "सकारात्मक" आणि "नकारात्मक" असे भाषांतर केल्यास आम्ही सत्यापासून विचलित होणार नाही हे वाचकांना पटवून देण्यासाठी आम्ही डायओफँटसच्या मजकुराच्या दार्शनिक विश्लेषणावर तपशीलवार विचार केला आहे.

डायओफँटस सापेक्ष संख्येसाठी चिन्हांचा नियम तयार करतो:

"नकारात्मक द्वारे गुणाकार केलेले ऋण धन देते, तर ऋणाचे धनाने गुणाकार केल्यास ऋण मिळते, आणि ऋणाचे वेगळे चिन्ह हे उलटे आणि लहान केलेले (अक्षर) ψ आहे."

“मी तुम्हाला गुणाकार समजावून सांगितल्यानंतर, प्रस्तावित पदांचे विभाजन देखील स्पष्ट होते; आता अशा संज्ञांच्या बेरीज, वजाबाकी आणि गुणाकाराचा सराव सुरू करणे चांगले होईल. सकारात्मक किंवा तितक्याच सकारात्मक आणि नकारात्मक अशा इतर संज्ञांमध्ये भिन्न गुणांकांसह सकारात्मक आणि नकारात्मक संज्ञा जोडा आणि सकारात्मक आणि इतर नकारात्मक संज्ञांमधून इतर सकारात्मक आणि तितक्याच सकारात्मक आणि नकारात्मक संज्ञा वजा करा.

लक्षात घ्या की डायओफँटस केवळ तर्कसंगत सकारात्मक उपाय शोधत असला तरी, मध्यवर्ती गणनेत तो स्वेच्छेने नकारात्मक संख्या वापरतो.

अशाप्रकारे आपण लक्षात घेऊ शकतो की डायओफँटसने संख्या क्षेत्राचा परिमेय संख्यांच्या क्षेत्रात विस्तार केला ज्यामध्ये अंकगणिताच्या चारही ऑपरेशन्स कोणत्याही अडथळ्याशिवाय करता येतात.

3. डायओफँटाइन समीकरण

व्याख्या - बीजगणितीय समीकरणे किंवा पूर्णांक गुणांकांसह बीजगणितीय समीकरणांची प्रणाली, ज्यामध्ये समीकरणांच्या संख्येपेक्षा जास्त अज्ञात संख्या असते आणि ज्यासाठी पूर्णांक किंवा परिमेय उपाय शोधले जातात.

कुऱ्हाड + द्वारे = 1

कुठे एआणि b- कॉप्राइम पूर्णांक

कॉप्राइम क्रमांकअनेक पूर्णांक जसे की या सर्व संख्यांचे सामाईक भाजक फक्त + 1 आणि - 1 आहेत. मूळ संख्यांच्या जोडीचा सर्वात लहान गुणाकार त्यांच्या गुणाकाराच्या समान असतो.

अनंतपणे अनेक उपाय आहेत:

तर x0आणि y0- एक उपाय, नंतर संख्या

एक्स = x0 + bn

येथे = y0 -एक

(n- कोणतेही पूर्णांक) देखील उपाय असतील.

D. u चे दुसरे उदाहरण.

x2 + y2 = z2

या समीकरणाचे सकारात्मक पूर्णांक उपाय पायांच्या लांबीचे प्रतिनिधित्व करतात एक्स , येथेआणि कर्ण zपूर्णांक बाजूच्या लांबीसह काटकोन त्रिकोणांना पायथागोरियन संख्या म्हणतात.

नैसर्गिक संख्यांचे तिप्पट जसे की ज्या त्रिकोणाच्या बाजूची लांबी या संख्यांच्या प्रमाणात (किंवा समान) असते ती आयताकृती असते.

कॉप्रिम पायथागोरियन संख्यांचे सर्व त्रिगुण सूत्रे वापरून मिळवता येतात

एक्स = m2 - n2

येथे = 2mn

z = m2 + n2

कुठे मीआणि n- पूर्ण संख्या ( मी > n > 0).

हे समीकरण विमानात परिभाषित करते आर 2 बीजगणित वक्रΓ. आम्ही तर्कसंगत उपाय म्हणू (2) तर्कशुद्ध मुद्दावक्र Γ. पुढील गोष्टींमध्ये, आम्ही अनेकदा भूमितीच्या भाषेचा अवलंब करू, जरी डायओफँटस स्वतः ती कुठेही वापरत नाही. तथापि, भौमितिक भाषा आता गणितीय विचारसरणीचा एवढा अविभाज्य भाग बनली आहे की तिच्या मदतीने अनेक तथ्ये समजणे आणि स्पष्ट करणे सोपे होईल.

सर्व प्रथम, समीकरणांचे काही वर्गीकरण (2) किंवा, जे समान आहे, बीजगणितीय वक्र देणे आवश्यक आहे. सर्वात नैसर्गिक आणि सर्वात लवकर उद्भवणारे क्रमानुसार त्यांचे वर्गीकरण आहे.

त्याची आठवण करून द्या क्रमानेवक्र (2) हा बहुपदीच्या पदांचा कमाल क्रम आहे f (x , y), जेथे पदाचा क्रम येथे अधिकारांची बेरीज म्हणून समजला जातो xआणि y. या संकल्पनेचा भौमितिक अर्थ असा आहे की सरळ रेषा क्रमाच्या वक्रला छेदते nनक्की येथे nगुण बिंदू मोजताना, एखाद्याने, अर्थातच, छेदनबिंदूंच्या गुणाकार, तसेच जटिल आणि "अनंत दूरच्या" बिंदूंचा विचार केला पाहिजे. तर, उदाहरणार्थ, एक वर्तुळ x 2 + y 2 = 1 आणि सरळ x + y= 2 दोन जटिल बिंदूंना छेदतो आणि हायपरबोला x 2 – y 2 = 1 आणि सरळ y =x- अनंताच्या दोन बिंदूंवर, सरळ रेषेसह समान हायपरबोला x=1 मध्ये गुणाकार 2 चा एक समान बिंदू आहे.

तथापि, हेतूंसाठी डायफॅन्टाइन विश्लेषण(हे नाव गणिताच्या क्षेत्राला देण्यात आले होते जे अनिश्चित समीकरणे सोडवण्याच्या समस्यांमधून विकसित झाले होते; तथापि, आता याला अधिक वेळा डायओफँटाइन भूमिती म्हणतात) क्रमानुसार वर्गीकरण खूप खडबडीत असल्याचे दिसून आले.

तांदूळ. १.

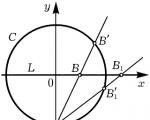
हे एका उदाहरणाने स्पष्ट करू. एक वर्तुळ द्या सी : x 2 + y 2 = 1 आणि परिमेय गुणांक असलेली कोणतीही सरळ रेषा, उदाहरणार्थ, एल : y=0. या वर्तुळाचे तर्कशुद्ध बिंदू आणि रेषा एका-एक पत्रव्यवहारात ठेवता येतात हे दाखवू. हे केले जाऊ शकते, उदाहरणार्थ, याप्रमाणे: बिंदू निश्चित करा ए(0,–1) वर्तुळे आणि प्रत्येक तर्कसंगत बिंदू नियुक्त करा बीसरळ एलबिंदू ब"वर्तुळ सी, चौकात पडलेला सीआणि सरळ एबी(आकृती क्रं 1). की बिंदूचे समन्वय ब"तर्कसंगत असेल, आम्ही वाचकाला ते स्वतः सिद्ध करू देऊ किंवा डायओफँटस कडून तत्सम पुरावा वाचू (तो पुढील परिच्छेदात सादर केला जाईल). साहजिकच, कोणत्याही कोनिक विभागाच्या तर्कसंगत बिंदूंमध्ये समान पत्रव्यवहार स्थापित केला जाऊ शकतो, जर त्यावर किमान एक तर्कशुद्ध बिंदू असेल तर आणि तर्कसंगत रेषा. डायओफँटाइन विश्लेषणाच्या दृष्टिकोनातून आपण वर्तुळ पाहतो सीआणि सरळ एलवेगळे करता येण्यासारखे नाहीत: तर्कसंगत उपायांचे त्यांचे संच समतुल्य आहेत. आणि हे असूनही दोन्ही वक्रांचे ऑर्डर भिन्न आहेत.

बीजगणितीय वक्रांचे वंशानुसार वर्गीकरण अधिक सूक्ष्म आहे, जे फक्त 19व्या शतकात एबेल आणि रिमन यांनी मांडले होते. हे वर्गीकरण वक्र Γ च्या एकवचन बिंदूंची संख्या विचारात घेते.

आपण असे गृहीत धरतो की वक्र Γ च्या समीकरण (2) मध्ये बहुपदी आहे f (x , y) परिमेय संख्यांच्या फील्डवर अपरिवर्तनीय आहे, उदा. ते परिमेय गुणांक असलेल्या बहुपदींच्या उत्पादनामध्ये विस्तारत नाही. ज्ञात आहे, बिंदूवर वक्र Γ ला स्पर्शिकेचे समीकरण पी (x 0 , y 0) होईल

y – y 0 = k (x – x 0),

k = –

fx" (x 0 , y 0)

fy" (x 0 , y 0)

बिंदूवर असल्यास पीव्युत्पन्न fx"किंवा fy"शून्यापेक्षा वेगळे आहे, नंतर उतार kस्पर्शिकेचा एक निश्चित अर्थ आहे (जर fy" (x 0 , y 0) = 0, अ fx" (x 0 , y 0) ≠ 0, नंतर k=∞ आणि स्पर्शिका येथे पीअनुलंब असेल).

बिंदूवर असल्यास पीदोन्ही आंशिक डेरिव्हेटिव्ह नष्ट होतात,

fx" (x 0 , y 0) = 0 आणि fy" (x 0 , y 0) = 0,

नंतर पॉइंट पीम्हणतात विशेष .

उदाहरणार्थ, वक्र येथे y 2 = x 2 + x 3 बिंदू (0, 0) विशेष असेल, कारण त्यात fx" = –2x – 3x 2 आणि fy" = 2yशून्यावर जा.

तांदूळ. 2.

सर्वात सोपा एकवचनी बिंदू दुहेरी आहेत, ज्यावर किमान एक व्युत्पन्न आहे f xx "" , f xy ""आणि f yy ""शून्यापेक्षा वेगळे आहे. अंजीर मध्ये. आकृती 2 दुहेरी बिंदू दर्शविते जेथे वक्र दोन भिन्न स्पर्शिका आहेत. इतर अधिक जटिल एकवचनी बिंदू अंजीर मध्ये दर्शविले आहेत. 3.

तांदूळ. 3.

4. उपाय

नियम 1. जर c ला d ने भाग जात नसेल, तर ax + vy = c समीकरण पूर्णांकांमध्ये कोणतेही निराकरण नाही. N.O.D.(a,b) = d.

नियम 2. coprime a आणि b सह ax + vy = c या समीकरणाचे समाधान शोधण्यासाठी, तुम्हाला प्रथम ax + y = 1 या समीकरणाचे समाधान (X o; y o) शोधणे आवश्यक आहे; CX o, Su o या संख्या ax + vy = c या समीकरणाचे निराकरण करतात.

पूर्णांकांमध्ये समीकरण सोडवा (x,y)

5x - 8y = 19 ... (1)

पहिला मार्ग. निवड पद्धत वापरून विशिष्ट उपाय शोधणे आणि सामान्य समाधान रेकॉर्ड करणे.

आम्हाला माहित आहे की जर N.O.D.(a;b) =1, म्हणजे a आणि b कॉप्राइम संख्या आहेत, नंतर समीकरण (1)

पूर्णांक x आणि y मध्ये समाधान आहे. N.O.D.(5;8) =1. निवड पद्धतीचा वापर करून आम्हाला एक विशिष्ट उपाय सापडतो: X o = 7; y o = 2.

तर, संख्यांची जोडी (7;2) हे समीकरण (1) चे विशिष्ट समाधान आहे.

याचा अर्थ समानता धारण करते: 5 x 7 – 8 x 2 = 19 ... (2)

प्रश्न: एक उपाय दिल्यावर इतर सर्व उपाय कसे लिहायचे?

समीकरण (1) मधून समानता (2) वजा करू आणि मिळवू: 5(x -7) – 8(y - 2) =0.

म्हणून x – 7 = . परिणामी समानतेवरून हे स्पष्ट होते की संख्या (x – 7) पूर्णांक असेल आणि जर (y – 2) 5 ने भाग जात असेल, म्हणजे. y – 2 = 5n, जेथे n काही पूर्णांक आहे. तर, y = 2 + 5n, x = 7 + 8n, जेथे n Z.

अशा प्रकारे, मूळ समीकरणाची सर्व पूर्णांक सोल्यूशन्स खालील स्वरूपात लिहिली जाऊ शकतात:

दुसरा मार्ग . अज्ञातासाठी समीकरण सोडवणे.

आम्ही हे समीकरण सर्वात लहान (मॉड्युलो) गुणांक असलेल्या अज्ञाताच्या संदर्भात सोडवतो. 5x - 8y = 19 x =

5: 0,1,2,3,4 ने भागल्यावर उर्वरित. चला या संख्यांना y ने बदलू.

जर y = 0, तर x = =.

जर y = 1, तर x = =.

जर y = 2, तर x = = = 7 Z.

जर y = 3, तर x = =.

जर y = 4 तर x = =.) निष्कर्ष

दरम्यान, विज्ञानाच्या बहुतेक इतिहासकारांनी, गणितज्ञांच्या विरोधात, आतापर्यंत डायओफँटसच्या कार्यांना कमी लेखले आहे. त्यांच्यापैकी अनेकांचा असा विश्वास होता की डायओफँटस केवळ एकच उपाय शोधण्यापुरते मर्यादित आहे आणि यासाठी कृत्रिम तंत्रे वापरली, भिन्न समस्यांसाठी. पण खरं तर, बहुतेक डायओफँटाइन समीकरणांमध्ये आपण समान समाधान अल्गोरिदम पाहतो.

आज, जसे आपण पाहतो, तेथे अनेक भिन्न उपाय आहेत, ज्याचे अल्गोरिदम लक्षात ठेवणे सोपे आहे. आधी सांगितल्याप्रमाणे, हे समीकरण सहसा युनिफाइड स्टेट परीक्षेच्या टास्क C6 मध्ये आढळते. डायओफँटाइन समीकरणे सोडवण्यासाठी अल्गोरिदमचा अभ्यास केल्याने हे कार्य सोडवण्यास मदत होऊ शकते, जे गुणांची लक्षणीय संख्या आहे.

संदर्भग्रंथ

1. अलेक्झांड्रियाचा डायओफँटस. अंकगणित आणि बहुभुज संख्यांबद्दल एक पुस्तक (प्राचीन ग्रीकमधून आय. एन. वेसेलोव्स्कीचे भाषांतर; संपादन आणि आय. जी. बाश्माकोवा यांच्या टिप्पण्या). एम., "विज्ञान", 1974.

2. B. L. Van der Waerden, Awakening Science (I. N. Veselovsky द्वारे भाषांतर). M., Fizmatgiz, 1959.

3. जी. जी. त्सेटेन, प्राचीन काळातील गणिताचा इतिहास आणि मध्य युग (पी. युश्केविचचे भाषांतर). M.-L., Gostekhizdat, 1932

4. ए.व्ही. वासिलिव्ह, पूर्णांक. पीटर्सबर्ग, १९१९

5. I. V. यशचेन्को, S. A. Shestakov, P. I. Zakharov, Mathematics, Uniified State Examination, MTsNMO, 2010

अलेक्झांड्रियाचा डायओफँटस(प्राचीन ग्रीक Διόφαντος ὁ Ἀλεξανδρεύς ; lat डायओफँटस) हा एक प्राचीन ग्रीक गणितज्ञ आहे जो बहुधा 3 व्या शतकात राहत होता. e अनेकदा "बीजगणिताचे जनक" म्हणून संबोधले जाते. "अंकगणित" चे लेखक - अनिश्चित समीकरणांसाठी सकारात्मक तर्कसंगत उपाय शोधण्यासाठी समर्पित पुस्तक. आजकाल, "डायोफँटाइन समीकरणे" चा अर्थ सामान्यतः पूर्णांक गुणांक असलेली समीकरणे असतात, ज्याचे निराकरण पूर्णांकांमध्ये शोधले पाहिजे.

चरित्र [ | ]

लॅटिन भाषांतर अंकगणित (1621)

हे खालील समीकरण सोडवण्यासारखे आहे:

x = x 6 + x 12 + x 7 + 5 + x 2 + 4 (\displaystyle x=(\frac (x)(6))+(\frac (x)(12))+(\frac (x) (7))+5+(\frac (x)(2))+4)

अंकगणितडायओफंटा[ | ]

प्रभाव अंकगणितगणिताच्या विकासासाठी[ | ]

10 व्या शतकात अंकगणितअरबीमध्ये भाषांतरित केले गेले, त्यानंतर इस्लामिक देशांतील गणितज्ञांनी (अबू कामिल आणि इतर) डायओफंटसचे काही संशोधन चालू ठेवले. युरोप मध्ये, मध्ये स्वारस्य अंकगणितराफेल बॉम्बेली यांनी हे काम लॅटिनमध्ये अनुवादित करून प्रकाशित केल्यानंतर आणि त्यातून 143 समस्या प्रकाशित केल्यानंतर वाढ झाली. बीजगणित(१५७२). 1621 मध्ये, एक क्लासिक, पूर्णपणे भाष्य केलेले लॅटिन भाषांतर दिसू लागले अंकगणित, Bachet de Meziriac द्वारे अंमलात आणले.

डायओफँटसची इतर कामे[ | ]

डायओफंटस कोठे राहतात या प्रश्नावरील विभागात लेखकाने विचारले लेरा...सर्वोत्तम उत्तर आहे डायओफँटस - (इ.स. तिसऱ्या शतकाच्या उत्तरार्धात) - प्रसिद्ध प्राचीन ग्रीक गणितज्ञ.
त्याच्या जीवनाबद्दल जवळजवळ कोणतीही माहिती नाही; त्याच्या जन्म आणि मृत्यूच्या तारखा देखील पूर्णपणे विश्वासार्ह नाहीत.
इजिप्शियन शहरात अलेक्झांड्रियामध्ये राहत होते.
डायओफँटसची क्रिया ग्रीसच्या घसरणीशी जुळली, जिंकली - जसे ज्ञात आहे - रोमने.
ग्रीक शास्त्रज्ञांना इजिप्तमध्ये, प्रामुख्याने अलेक्झांड्रियामध्ये आश्रय मिळाला, जो तोपर्यंत जागतिक संस्कृतीचे केंद्र बनला होता.
अलेक्झांड्रियामध्ये एक भव्य ग्रंथालय तयार केले गेले, जे डायओफंटसच्या काळापर्यंत जागतिक संस्कृती आणि मानवतेचे केंद्र बनले होते; तथाकथित लायब्ररी अलेक्झांड्रियामध्ये उद्भवली. म्युझियन (मंदिर किंवा म्यूजचे अभयारण्य), जिथे नैसर्गिक आणि गणितीय विज्ञानातील सर्वात उल्लेखनीय प्रतिनिधींचे क्रियाकलाप केंद्रित होते.
या शास्त्रज्ञांमध्ये डायओफँटस हा एक गणितज्ञ होता, ज्याने सीरियन आणि भारतीय गणितज्ञांशी ओळखीबद्दल धन्यवाद, बॅबिलोनियन लोकांच्या बीजगणित क्षेत्रातील कामगिरी ग्रीक विज्ञानाकडे हस्तांतरित केल्या.

पासून उत्तर अलेक्झांडर[गुरू]
ग्रीसमधील सर्व गणितज्ञ

पासून उत्तर योगदान[नवीन]
तो अलेक्झांड्रियाचा डायओफँटस आहे या वस्तुस्थितीनुसार, तो इसवी सनाच्या तिसऱ्या शतकात अलेक्झांड्रिया (आधुनिक इजिप्तच्या प्रदेशात) राहत होता. बहुधा त्याच्या आयुष्याच्या तारखा: जन्म - 325, मृत्यू - 409 AD

पासून उत्तर ड्रिल[नवीन]
अलेक्झांड्रियाचा डायओफँटस?
प्राचीन रोमन गणितज्ञ
एक प्राचीन ग्रीक गणितज्ञ जो कथितपणे तिसऱ्या शतकात राहत होता. e अनेकदा "बीजगणिताचे जनक" म्हणून संबोधले जाते. "अंकगणित" चे लेखक - अनिश्चित समीकरणांसाठी सकारात्मक तर्कसंगत उपाय शोधण्यासाठी समर्पित पुस्तक. आजकाल, "डायोफँटाइन समीकरणे" चा अर्थ सामान्यतः पूर्णांक गुणांक असलेली समीकरणे असतात, ज्याचे निराकरण पूर्णांकांमध्ये शोधले पाहिजे.

ऑक्टोपसला 8 पाय असतात, तर स्टारफिशला 5 असतात.

एकूण 39 अंगे असल्यास मत्स्यालयात किती सागरी प्राणी आहेत?

अलेक्झांड्रियाचा डायओफँटस हा एक प्राचीन ग्रीक गणितज्ञ आहे जो बहुधा 3 व्या शतकात राहत होता.

त्याच्या जीवनातील तपशीलांबद्दल जवळजवळ काहीही माहिती नाही. एकीकडे, डायओफँटसने हायप्सिकल्स (बीसी दुसरे शतक) उद्धृत केले; दुसरीकडे, थिओन ऑफ अलेक्झांड्रिया (सुमारे 350 एडी) डायओफंटसबद्दल लिहितो, ज्यावरून आपण असा निष्कर्ष काढू शकतो की त्याचे जीवन या कालखंडाच्या सीमेत घडले. डायओफँटसच्या जीवनाच्या काळाचे संभाव्य स्पष्टीकरण या वस्तुस्थितीवर आधारित आहे की त्याचे "अंकगणित" "सर्वात आदरणीय डायोनिसियस" ला समर्पित आहे. असे मानले जाते की हा डायोनिसियस दुसरा कोणी नसून अलेक्झांड्रियाचा बिशप डायोनिसियस आहे, जो तिसऱ्या शतकाच्या मध्यभागी राहत होता. n e

पॅलाटिन अँथॉलॉजीमध्ये एक एपिग्राम-टास्क आहे ज्यावरून आपण असा निष्कर्ष काढू शकतो की डायओफँटस 84 वर्षे जगला:

Diophantus च्या राख थडग्यात विश्रांती; तिला आणि दगडावर आश्चर्य वाटले

मृत व्यक्तीचे वय त्याच्या सुज्ञ कलेतून बोलेल.

देवांच्या इच्छेनुसार, तो लहानपणी त्याच्या आयुष्याचा सहावा भाग जगला.

आणि गालावर फुंकर घालून साडेपाचला भेटलो.

नुकताच सातव्या दिवशी त्याने त्याच्या मैत्रिणीशी लग्न केले.

तिच्याबरोबर पाच वर्षे घालवल्यानंतर ऋषीला मुलगा झाला;

त्याच्या वडिलांचा लाडका मुलगा त्याचे अर्धे आयुष्य जगला.

त्याला त्याच्या वडिलांकडून त्याच्या लवकर कबरेने नेले होते.

दोनदा दोन वर्षांनी पालकांनी खूप शोक केला,

इथे मला माझ्या दुःखी आयुष्याची मर्यादा दिसली.

समीकरणे सोडवण्याच्या आधुनिक पद्धतींचा वापर करून, डायओफँटस किती वर्षे जगला याची गणना करणे शक्य आहे. चला समीकरण तयार करू आणि सोडवू:

या समीकरणाचे समाधान म्हणजे 84 ही संख्या. अशा प्रकारे डायओफँटस 84 वर्षे जगला.

डायओफँटसचे मुख्य काम 13 पुस्तकांमधील "अंकगणित" आहे. दुर्दैवाने, 13 पैकी फक्त पहिली 6 पुस्तकेच टिकली आहेत.

पहिल्या पुस्तकाच्या आधी विस्तृत परिचय आहे, ज्यामध्ये डायओफँटसने वापरलेल्या नोटेशनचे वर्णन केले आहे. डायओफँटस अज्ञाताला "संख्या" (?ριθμ?ς) म्हणतो आणि त्यास ς या अक्षराने सूचित करतो, चिन्हासह अज्ञाताचा वर्ग (δ?ναμις - "डिग्री" साठी लहान). अज्ञाताच्या खालील अंशांसाठी, सहाव्या पर्यंत, ज्याला क्यूब-क्यूब म्हणतात, आणि त्यांच्या विरुद्ध असलेल्या अंशांसाठी विशेष चिन्हे प्रदान केली आहेत. डायओफँटसमध्ये अतिरिक्त चिन्ह नाही: तो फक्त एकमेकांच्या पुढे सकारात्मक संज्ञा लिहितो आणि प्रत्येक टर्ममध्ये प्रथम अज्ञात पदवी लिहिली जाते आणि नंतर संख्यात्मक गुणांक. वजा केलेल्या संज्ञा देखील शेजारी शेजारी लिहिल्या जातात आणि त्यांच्या संपूर्ण गटासमोर उलटे अक्षर Ψ च्या स्वरूपात एक विशेष चिन्ह ठेवले जाते. समान चिन्ह दोन अक्षरांनी दर्शविले जाते ?σ (?σος - "समान" साठी लहान). समान संज्ञा आणण्याचा नियम आणि समीकरणाच्या दोन्ही बाजूंना समान संख्या किंवा अभिव्यक्ती जोडण्याचा किंवा वजा करण्याचा नियम तयार केला गेला: ज्याला नंतर अल-ख्वारीझमीने "अल-जबर आणि अल-मुकाबाला" म्हटले. एक चिन्ह नियम सादर केला गेला आहे: वजा गुणा वजा अधिक देतो; वजा केलेल्या पदांसह दोन अभिव्यक्तींचा गुणाकार करताना हा नियम वापरला जातो. हे सर्व भौमितिक व्याख्येचा संदर्भ न घेता, सामान्य अटींमध्ये तयार केले आहे.

बहुतेक काम हे निराकरणासह समस्यांचा संग्रह आहे (सहा वाचलेल्या पुस्तकांमध्ये एकूण 189 आहेत), सामान्य पद्धती स्पष्ट करण्यासाठी कुशलतेने निवडले आहेत. "अंकगणित" ची मुख्य समस्या म्हणजे अनिश्चित समीकरणांसाठी सकारात्मक तर्कसंगत उपाय शोधणे. डायओफँटस द्वारे परिमेय संख्यांचा अर्थ नैसर्गिक संख्यांप्रमाणेच केला जातो, जो प्राचीन गणितज्ञांसाठी वैशिष्ट्यपूर्ण नाही.

प्रथम, डायओफँटस 2 अज्ञातांमधील द्वितीय क्रम समीकरणांची प्रणाली तपासतो; हे आधीच ज्ञात असल्यास इतर उपाय शोधण्यासाठी एक पद्धत निर्दिष्ट करते. मग तो उच्च पदवीच्या समीकरणांना समान पद्धती लागू करतो.

10 व्या शतकात, "अंकगणित" चे अरबीमध्ये भाषांतर केले गेले, त्यानंतर इस्लामिक देशांतील गणितज्ञांनी (अबू कामिल आणि इतर) डायओफंटसचे काही संशोधन चालू ठेवले. राफेल बॉम्बेलीने व्हॅटिकन लायब्ररीत हे काम शोधून काढल्यानंतर आणि त्यातून 143 समस्या त्याच्या बीजगणितात (1572) प्रकाशित केल्यानंतर युरोपमध्ये अंकगणितात रस वाढला. 1621 मध्ये, "अंकगणित" चे क्लासिक, पूर्णपणे भाष्य केलेले लॅटिन भाषांतर दिसू लागले, जे बॅचेट डी मेझिरियाक यांनी केले. डायओफँटसच्या पद्धतींचा फ्रँकोइस व्हिएट आणि पियरे फर्मॅटवर मोठा प्रभाव होता; गॉस आणि यूलरच्या अभ्यासासाठी प्रारंभ बिंदू म्हणून काम केले. तथापि, आधुनिक काळात, अनिश्चित समीकरणे सामान्यतः पूर्ण संख्येत सोडवली जातात, आणि परिमेय समीकरणांमध्ये नाही, जसे डायओफँटसने केले.

20 व्या शतकात, डायओफंटसच्या नावाखाली, अंकगणिताच्या आणखी 4 पुस्तकांचा अरबी मजकूर सापडला. गणिताच्या काही इतिहासकारांनी, या मजकुराचे विश्लेषण केल्यावर, त्यांचे लेखक डायओफँटस नव्हते, परंतु बहुधा हायपेटिया, डायओफँटसच्या पद्धतींमध्ये पारंगत भाष्यकार होते असे गृहितक मांडले.

डायओफँटसचा “ऑन पॉलीगोनल नंबर्स” (Περ? πολυγ?νων ?ριθμ?ν) हा ग्रंथ पूर्णपणे जतन केलेला नाही; संरक्षित भागामध्ये, भौमितिक बीजगणित पद्धती वापरून अनेक सहायक प्रमेये काढली जातात.

डायओफँटसच्या "पृष्ठभागांच्या मोजमापावर" (?πιπεδομετρικ?) आणि "गुणाकारावर" (Περ? πολλαπλασιασμο?) मधील केवळ तुकडे जतन केले गेले आहेत.

डायओफँटसचे "पोरिझम्स" हे पुस्तक अंकगणितात वापरल्या जाणाऱ्या काही प्रमेयांवरूनच ओळखले जाते.

आज हे समीकरण फॉर्मचे आहे

कुठे पी- एक पूर्णांक फंक्शन (उदाहरणार्थ, पूर्णांक गुणांक असलेले बहुपद), आणि व्हेरिएबल्स पूर्णांक मूल्ये घेतात, ज्याला प्राचीन ग्रीक गणितज्ञ - डायओफँटिन यांच्या सन्मानार्थ म्हणतात.

बहुधा सर्वात प्रसिद्ध डायओफँटाइन समीकरण आहे

त्याचे उपाय म्हणजे पायथागोरियन ट्रिपलेट: (3; 4; 5), (6; 8; 10), (5; 12; 13), (12; 35; 37)…

डायओफँटाइन समीकरणाच्या पूर्णांकांमध्ये अविघटनशीलतेचा पुरावा

येथे (Fermat's Last theorem) इंग्रजी गणितज्ञ अँड्र्यू वाइल्स यांनी 1994 मध्ये पूर्ण केले.

डायओफँटाइन समीकरणाचे दुसरे उदाहरण म्हणजे पेलचे समीकरण

पॅरामीटर कुठे आहे nअचूक चौरस नाही.

हिल्बर्टची दहावी समस्या ही 23 समस्यांपैकी एक आहे जी डेव्हिड हिल्बर्टने 8 ऑगस्ट 1900 रोजी गणितज्ञांच्या दुसऱ्या आंतरराष्ट्रीय काँग्रेसमध्ये मांडली होती. हिल्बर्टच्या अहवालात, दहाव्या समस्येचे सूत्रीकरण सर्वांत लहान आहे:

अनियंत्रित अज्ञात आणि पूर्णांक परिमेय संख्यात्मक गुणांक असलेले डायओफँटाइन समीकरण देऊ द्या. परिमेय पूर्णांकांमध्ये हे समीकरण सोडवता येण्याजोगे आहे की नाही हे निर्धारित करण्यासाठी, मर्यादित संख्येच्या ऑपरेशननंतर, ज्या पद्धतीद्वारे हे शक्य आहे ते दर्शवा.

या समस्येचे अल्गोरिदमिक निराकरण न करता येण्यास सुमारे वीस वर्षे लागली आणि युरी मतियासेविच यांनी 1970 मध्ये पूर्ण केले.

अलेक्झांड्रिया (तिसरे शतक) च्या पप्पसच्या क्रियाकलापांमुळे, प्राचीन शास्त्रज्ञ आणि त्यांच्या कार्यांची माहिती आमच्यापर्यंत पोहोचली आहे. अपोलोनियस नंतर (इ.स.पूर्व दुसऱ्या शतकापासून) प्राचीन विज्ञानात घट सुरू झाली. नवीन खोल कल्पना दिसत नाहीत. 146 बीसी मध्ये. e रोमने ग्रीस ताब्यात घेतला आणि 31 बीसी मध्ये. e - अलेक्झांड्रिया. सामान्य स्तब्धता आणि घसरणीच्या पार्श्वभूमीवर, अलेक्झांड्रियाच्या डायओफंटसची विशाल आकृती, महान प्राचीन गणितज्ञांपैकी शेवटचे, "बीजगणिताचे जनक" स्पष्टपणे उभे आहेत.

खालील गणितीय वस्तूंना डायओफँटसची नावे देण्यात आली आहेत: