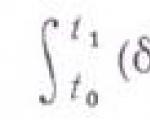Хамгийн бага үйл ажиллагааны зарчим. Гамильтон-Остроградскийн тохиргоо ба фазын орон зайн вариацын зарчим Хавтгай долгионы томъёо
ГАМИЛТОН - ОСТРОГРАДСКИЙН ЗАРЧИМ
Тогтмол үйл ажиллагааны зарчим - ерөнхий интеграл сонгодог механикийн вариацын зарчим,суулгасан У.
Гамильтоныг хамгийн тохиромжтой суурин холболтоор хязгаарласан голономик системд зориулсан, мөн М.В.Остроградскийн стационар бус холболтоор ерөнхийлсөн. Г-ын хэлснээр - О.
Системийн анхны болон эцсийн байрлал, хөдөлгөөний хугацаа нь бодит хөдөлгөөнийхтэй ижил байдаг кинематик боломжтой ижил төстэй хөдөлгөөнүүдтэй харьцуулахад хөдөлгөөнгүй утгатай байна. Энд Т -кинетик, U-боломжит эрчим хүч, L-T-UСистемийн Лагранж функц. Зарим тохиолдолд үнэн нь зөвхөн функциональ суурин цэгтэй тохирдоггүй S,гэхдээ бас хамгийн бага ач холбогдол өгдөг. Тиймээс Г.-О. ихэвчлэн дууддаг хамгийн бага үйл ажиллагааны зарчим. Боломжит бус идэвхтэй хүчний хувьд Fvүйл ажиллагааны хөдөлгөөнгүй байх нөхцөл d S = 0-ийг нөхцөлөөр сольсон
Гэрэл.: Хамилтон В., Шинжлэх ухааныг ахиулах Британийн нийгэмлэгийн 4-р хурлын тайлан, Л., 1835, х. 513-18; Остроградску М., "Мем де 1" Акад. des Sci. де Санкт-Петербург", 1850, т. 8, дугаар 3, х. 33-48.
В.В.Румянцев.
Математикийн нэвтэрхий толь бичиг. - М .: Зөвлөлтийн нэвтэрхий толь бичиг. I. M. Виноградов. 1977-1985 он.
Бусад толь бичгүүдээс "ГАМИЛТОН - ОСТРОГРАДЫН ЗАРЧИМ" гэж юу байдгийг харна уу:
Фишерийн зарчим бол байгаль дээрх амьд организмын зүйлийн зонхилох хүйсийн харьцаа яагаад ойролцоогоор 1:1 байдгийг тайлбарласан хувьслын загвар юм; аль ген нь аль аль хүйсийн илүү бодгаль үйлдвэрлэх ...... Wikipedia
Хамилтон (мөн зүгээр л Гамильтоны зарчим), илүү нарийвчлалтай үйл ажиллагааны тогтворгүй байдлын зарчим, хөдөлгөөнгүй (ихэвчлэн туйлширсан, ихэвчлэн тогтсон уламжлалтай холбоотой) хайх замаар физик системийн хөдөлгөөний тэгшитгэлийг олж авах арга ... ... Википедиа
Гюйгенсийн дагуу долгионы хугарал ... Википедиа
Шинжлэх ухааны арга зүйд аливаа шинэ шинжлэх ухааны онол нь хуучин, сайн шалгагдсан онолын дэргэд үүнтэй огт зөрчилддөггүй, харин зарим хэт ойртсон байдлаар (тусгай тохиолдол) ижил үр дагаврыг өгдөг гэсэн мэдэгдэл байдаг. Жишээлбэл, хууль ... ... Википедиа
Цаг хугацааны салангид хяналтын процесст зориулсан Понтрягины дискрет дээд зарчим. Ийм процессын хувьд төгсгөлийн ялгавартай операторыг дифференциалаар солих замаар олж авсан тасралтгүй аналогийн хувьд төгсгөлтэй ялгавартай оператор ажиллахгүй байж болно... ... Математик нэвтэрхий толь бичиг
Эсвэл механик болон математик физикийн хувьд Гамильтоны зарчим нь хөдөлгөөний дифференциал тэгшитгэлийг олж авахад үйлчилдэг. Энэ зарчим нь ямар ч хүчинд өртөхөөс үл хамааран бүх материаллаг системд хамаарна; Эхлээд бид үүнийг илэрхийлэх болно ... Нэвтэрхий толь бичиг Ф.А. Брокхаус ба И.А. Эфрон
Квантын постулат. физикийн давхцлыг шаарддаг механик . сонгодог үр дүнтэй их квант тоонуудын хязгаарлах тохиолдолд үр дагавар. онолууд. S. p.-д энэ квант баримт илчлэгдсэн. нөлөөлөл нь зөвхөн бичил биетийг авч үзэхэд чухал ач холбогдолтой, үед ... ... Физик нэвтэрхий толь бичиг
Гамильтоны вариацын зарчим- Hamiltono variacinis principas statusas T sritis fizika atitikmenys: engl. Hamilton variation зарчим vok. Hamiltonsches Variationsprinzip, n rus. Гамильтоны вариацын зарчим, m pranc. principe variationnel d’Hamilton, m … Физикос терминų žodynas
Их квант тоонуудын хязгаарлагдмал тохиолдолд түүний физик үр дагавар нь сонгодог онолын үр дүнтэй давхцахыг шаарддаг квант механикийн постулат (Квантын механикийг үзнэ үү). S. p.-д баримт илэрч байна ... ... Зөвлөлтийн агуу нэвтэрхий толь бичиг
- (долгионы механик), бичил бөөмс (элементүүд, атомууд, молекулууд, атомын цөмүүд) ба тэдгээрийн системүүд (жишээлбэл, талстууд), түүнчлэн бөөмсийг тодорхойлдог хэмжигдэхүүнүүдийн хоорондын хамаарлыг тодорхойлох арга, хөдөлгөөний хууль тогтоомжийг тодорхойлдог онол. системүүд, физик хэмжээ ...... Физик нэвтэрхий толь бичиг
Энэ нэр томъёо нь өөр утгатай, Үйлдэл (физик)-г үзнэ үү. Үйлдлийн хэмжээ L2MT−1 Физик дэх үйлдэл нь скаляр физик хэмжигдэхүүн бөгөөд ... Wikipedia
Номууд
- Эдийн засгийн тогтолцооны хөдөлгөөний зарчим. Монограф, Куснер Юрий Семенович, Царев Игорь Геннадьевич. Эдийн засгийн системийн хөдөлгөөний үндсэн тэгшитгэлийг аналитик хэлбэрээр танилцуулж, түүний хөдөлгөөнийг зохицуулах хангалттай аргуудыг олох асуудлыг шийдсэн. Математикийн төхөөрөмжийг ашигласан ...
Бүх интеграл ба зарим дифференциал зарчмуудын үндэс суурь нь механик системийн бодит хөдөлгөөн нь тодорхой физик хэмжигдэхүүнд туйлшрал өгдөг гэсэн байр суурь юм. Энэ байр суурийг математикийн томъёололд оруулахын тулд өмнөх шигээ бодит хөдөлгөөнтэй зэрэгцэн сайтар тодорхойлсон шаардлагад захирагдах боломжтой хөдөлгөөнүүдийн багцыг харгалзан үзэх шаардлагатай.
Интеграл зарчмуудын томъёолол нь тохиргооны орон зайд хийгддэг. Эрх чөлөөний зэрэгтэй системийн хувьд ерөнхий координат гэдгийг санаарай 
, тухайн агшинд системийн тохиргоог тодорхойлох 
, харгалзах хэсэгт декартын координат гэж тооцогдоно 
-хэмжээст орон зай нь тохиргооны орон зай юм. Цаг хугацаа өнгөрөхөд механик системийн төлөв байдал өөрчлөгдөж, энэ системийг төлөөлж буй цэг нь тодорхой муруйг дүрсэлдэг. Системийн хөдөлгөөнийг энэ муруйн дагуух дүрслэх цэгийн хөдөлгөөн гэж үзэх нь тохиромжтой. Цаг хугацаа 
Үүнийг харгалзан үзэх нь параметр бөгөөд траекторийн цэг бүр нь нэг буюу хэд хэдэн утгатай тохирно 
.
Хэрэв бид тухайн агшин бүрт тохиргооны зам дээр системийн байрлалыг сонирхож байгаа бол 
, дараа нь та өөр тэнхлэг нэмэх хэрэгтэй 
.
Дараа нь бид бодож байгаа системийн хөдөлгөөний "олон хэмжээст график"-ийг авах болно. Мөн олон хэмжээст графикийн тодорхой хавтгай дээрх проекцийг судалж болно 
(Зураг 2.7). Зураг дээр А, Бнь агшин дахь төлөөлөх цэгийн проекц юм 
Тэгээд 
Үүний дагуу хатуу шугам нь бодит байдлыг, тасархай шугам нь төсөөлж болох хөдөлгөөнүүдийн нэгийг илэрхийлдэг.
Интеграл зарчим нь системийн бодит хөдөлгөөн нь хязгаарлагдмал (хязгааргүй биш!) хугацааны туршид хэрхэн явагддаг тухай мэдэгдэл юм. 
.
Тухайн үед хүртэл систем ямар байсан 
,
бид сонирхохгүй байна. Гэвч цаг хугацааны эхний болон эцсийн мөчүүд тогтсон л бол тухайн цаг мөчид төсөөлж болох бүх хөдөлгөөнтэй механик систем гэж үздэг. 
цэгээр дамждаг А, яг одоо 
- IN;
Эдгээр цэгүүд нь системийн бодит хөдөлгөөн дэх анхны болон эцсийн байрлалтай тохирч байна.
Механик системийн хөдөлгөөний талаархи хамгийн ерөнхий томъёоллыг хамгийн бага үйл ажиллагааны зарчим гэж нэрлэдэг (үүнийг Гамильтон-Остроградскийн зарчим гэж нэрлэдэг):
-аас хугацааны интервал дахь механик системийн бодит хөдөлгөөн
өмнө
үйл ажиллагааны функц гэж нэрлэгддэг интеграл
ба тэнцүү
, (60.7)
Хаана
-- Тухайн механик системийн лагранж нь экстремумтай (хамгийн бага). Хувьсагч
энэ нь ялгаатай биш юм.
Өөрөөр хэлбэл, бодит хөдөлгөөний үед үйл ажиллагааны өөрчлөлт тэг байх ёстой
(61.7)
бүх тохиргооны замналыг үе үе гэж үзвэл 
Тэгээд 
бодит хөдөлгөөний эхлэл ба төгсгөлийн цэгүүдээр дамжин өнгөрөх, i.e.
Энэ зарчим нь D'Alembert-ийн дифференциал зарчмаас ялгаатай нь системийн бүхэлдээ хязгаарлагдмал хугацааны хөдөлгөөний тухай мэдэгдлийг агуулсан утгаараа салшгүй юм. 
.
Үнэн хэрэгтээ Лагранжийн тэгшитгэлүүд нь үүнээс үүдэлтэй бөгөөд ингэснээр хамгийн бага үйл ажиллагааны зарчмаас механик системийн бүх динамикийг олж авсан гэж хэлж болно.
Функцуудыг зөвшөөр 
, бодит хөдөлгөөнийг дүрслэх, i.e. 
-эдгээр функцүүд 
доод талтай. Функцуудын багцыг авч үзье 
Хаана 
- функцүүдийн өөрчлөлтүүд 
-тай харьцуулахад бага гэж үздэг 
хүртэлх бүх хугацааны интервалын туршид 
өмнө 
. Түүнээс гадна бүх зүйл 
харилцааг хангах (62.7). Эхний хувилбар гэж нэрлэгддэг зүйлийг тооцоолъё 
, Лагранжийн функц нь ерөнхий координатаас хамаардаг гэдгийг санаарай 
,
ерөнхий хурд 
, мөн цаг хугацаа 
:
Учир нь 
, хоёрдугаар ээлжинд 
хэсгүүдээр нэгтгэж, авч болно
.
Нөхцөл байдлын улмаас (62.7) хэмжээ
алга болж, дурын утгуудын хувьд үлдсэн интеграл нь тэгтэй тэнцүү байх болно 
зөвхөн интегралын нийлбэрийн гишүүн бүр алга болох үед. Тиймээс бид 2-р төрлийн Лагранжийн тэгшитгэлийг олж авна
.
(63.7)
Функцийн экстремумын асуудлыг шийдсэнээр төгсгөлтэй тэгшитгэлийн системийг олж авдаг бөгөөд үүнээс функц экстремаль утгад хүрэх цэгийг олдог гэдгийг санах нь зүйтэй. Энэ тохиолдолд бид 2-р дарааллын дифференциал тэгшитгэлийн системээр өгөгдсөн экстремумын асуудлыг шийдэх функциональ шийдлийг авч үзэж байна. Эдгээр тэгшитгэлээс функцээр тодорхойлогдсон тохиргооны орон зайд шугам олддог 
, энэ үед функц нь хамгийн багадаа хүрдэг. Энэ мөрийг экстремаль гэж нэрлэдэг.
Тодорхой механик загварыг бий болгох ажил нь хөдөлгөөний тэгшитгэлийг эмхэтгэх явдал тул үнэндээ системийн динамик нь нэг функцээр тодорхойлогддогийг бид харж байна - Лагранж, учир нь энэ функц нь асуудлыг шийддэг. Тиймээс системийн Лагранж нь динамикийн асуудлуудтай холбогдуулан судлах шаардлагатай сонирхолтой физик объект юм. Ялангуяа хамгийн бага үйл ажиллагааны зарчмаас харахад функц нь тодорхой байна 
координат ба цаг хугацааны дурын функцын нийт деривативыг нэмэх хүртэл л тодорхойлогдоно. Үүнийг дараах байдлаар ойлгох хэрэгтэй: хөдөлгөөний тэгшитгэлээр тодорхойлогдсон систем нь нэгээс олон Лагранжийн функцтэй тохирч байна. 
.
Үнэхээр байг 
хамааралтай 
харьцаа
(64.7)
,
.
Гэхдээ түүнээс хойш 
,
улмаар функцуудыг ашиглан олж авсан Лагранжийн тэгшитгэлүүд 
Тэгээд 
, ижил. (64.7) хэлбэрийн Лагранжийн функцийг тодорхойлох тодорхой бус байдал нь хөдөлгөөний тэгшитгэлд нөлөөлөхгүй бөгөөд тус бүр нь 
ангиас (64.7) нь системийн динамикийг өвөрмөц байдлаар бүтээх асуудлыг шийддэг.
Лагранжийн тэгшитгэлийн системийн чухал шинж чанар нь тэдгээрийн ковариац юм. Энэ нь ерөнхий координат 4-ийн цэгийн хувиргалтуудын үед Лагранжийн тэгшитгэлүүд хэлбэрээ хадгална гэсэн үг юм
өөрөөр хэлбэл ерөнхий координатыг ашиглах үед 
Лагранжийн тэгшитгэл нь ижил хэлбэртэй байна.
,
ерөнхий координатыг ашиглахтай адил 
:
.
Лагранжийн тэгшитгэл нь хувиргах үед (65.7) ковариант гэдгийг шууд баталцгаая. Барьцгаая 
:
ба дериватив
,
1. Материаллаг цэгийн кинематик. Материаллаг цэг нь геометрийн хувьд математикийн цэгтэй тэнцүү боловч масстай физик объект юм. Кинематик бол хөдөлгөөний шалтгааныг харгалзахгүйгээр биеийн хөдөлгөөний төрлийг судалдаг физикийн салбар юм. Орон зай дахь цэгийн байрлал нь радиус вектороор тодорхойлогддог. Цэгийн радиус вектор нь эхлэл нь координатын системийн эхлэлтэй, төгсгөл нь тухайн цэгтэй давхцдаг вектор юм. r = би x+ j y + к z. Хурд гэдэг нь биеийн нэгж хугацаанд туулсан зай юм v(t) = d r/дт. v(t) = би dx/dt + j dy/dt + к dz/dt. Хурдатгал гэдэг нь хурдны өөрчлөлтийн хурд юм. а=d v/dt = d 2 r/ dt 2 = би d 2 x/dt 2 + j d 2 y/dt 2 + к d 2 z/dt 2 . а = а τ + а n= τ dv/dt + n v 2 /R.
г r = v dt; г v = а dt, тиймээс v = v 0 + ат; r = r 2 – r 1 = v 0т+ а t 2 /2.
2. Материаллаг цэгийн динамик. Ньютоны хуулиуд. Динамикийн үндсэн ойлголтууд нь масс ба хүч гэсэн ойлголт юм. Хүч бол хөдөлгөөний шалтгаан, өөрөөр хэлбэл. хүчний нөлөөн дор бие нь хурдыг олж авдаг. Хүч бол вектор хэмжигдэхүүн юм. Масс нь биеийн инерцийн хэмжүүр юм. Масс ба хурдны үржвэрийг импульс гэж нэрлэдэг х= м v. Материаллаг цэгийн өнцгийн импульс нь вектор юм Л = r * х. Материаллаг цэгт үйлчлэх хүчний моментийг вектор гэнэ М = r * Ф. Хэрэв бид өнцгийн импульсийн илэрхийлэлийг ялгаж үзвэл: d Л/ dt = d r/dt* х + r*г х/дт. Үүнийг харгалзан үзэхэд d r/dt= vТэгээд vЗэрэгцээ х, бид d Л/dt= М.Ньютоны хуулиуд.Ньютоны 1-р хуулинд бие махбодь дээр бусад хүч үйлчлэхгүй эсвэл тэдгээрийн үйлдлийг нөхөхөөс бусад тохиолдолд бие нь тайван эсвэл жигд шугаман хөдөлгөөнтэй хэвээр байна гэж заасан. Ньютоны хоёр дахь хууль нь цаг хугацааны явцад импульсийн өөрчлөлт нь тогтмол хэмжигдэхүүн бөгөөд үр дүнтэй хүч d-тэй тэнцүү байна гэж заасан. х/ dt = d / dt (м v) = m d v/dt= Ф.Энэ бол дифференциал хэлбэрээр бичигдсэн Ньютоны хоёр дахь хууль юм. Ньютоны 3-р хууль нь хоёр биетийн харилцан үйлчлэлд тус бүр нь ижил утгатай боловч эсрэг чиглэлтэй хүчээр нөгөө биедээ үйлчилдэг гэж заасан байдаг. Ф 1 = - Ф 2 .
3. Материаллаг цэгүүдийн системийн динамик. Хамгаалалтын хуулиуд. Материаллаг цэгүүдийн систем нь тэдгээрийн хязгаарлагдмал тооны цуглуулга юм. Системийн цэг бүр нь дотоод (бусад цэгүүдээс) болон гадаад хүчний нөлөөгөөр үйлчилдэг. m масс, r i радиус вектор байг. x i, y i, z i – утас. i-р цэг. Материаллаг цэгүүдийн системийн импульс нь системийг бүрдүүлдэг материаллаг цэгүүдийн импульсийн нийлбэр юм. х= Σ (i=1,n) хби = [ х 1 + х 2 +…+ х n]. Материалын цэгүүдийн системийн өнцгийн импульс нь материалын цэгүүдийн системийг бүрдүүлдэг өнцгийн импульсийн нийлбэр юм. Л = Σ [ Лби ] = Σ [ rби* х i]. Материаллаг цэгүүдийн системд үйлчлэх хүчийг системийн цэгүүдэд үйлчлэх бүх хүчний нийлбэр, түүний дотор системийн цэгүүдийн хоорондын харилцан үйлчлэлийн хүчийг тодорхойлно. Ф = Σ [ Ф i ], хаана Фби = Ф i ’ + Σ(j ≠ i) Ф ji нь i индексээр тодорхойлогдсон системийн материаллаг цэгт үйлчлэх хүч юм. Энэ нь гадны хүчнээс бүрддэг Ф i ’ ба дотоод хүч Σ(i ≠ j) [ Ф ji ], системийн бусад цэгүүдтэй харилцан үйлчлэлийн үр дүнд цэг дээр ажилладаг. Дараа нь: F = Σ (i=1,n) [ Ф i ’] + Σ (i=1,n) Σ(j ≠ i) [ Ф ji]. Ньютоны гуравдугаар хуулийн дагуу Σ (i=1,n) Σ(j ≠ i) [ Ф ji ] = 0, тэгэхээр Ф = Σ [ Фби']. Материаллаг цэгүүдийн системд үйлчлэх хүчний момент нь системийн цэгүүдэд үйлчлэх хүчний моментуудын нийлбэр юм. М= Σ (i) [ М i ] = Σ (i) [ rби* Ф i ] = Σ (i) [ rби* Фби']. Материаллаг цэгүүдийн системийн хувьд хөдөлгөөний тэгшитгэл нь d хэлбэртэй байна х/ dt = Σ = Σ [ Ф i].
Материаллаг цэгүүдийн системийн массын төв нь радиус вектор бүхий төсөөллийн цэг юм Р= 1/м Σ . Түүний хөдөлгөөний хурд В=d Р/дт. Дараа нь хөдөлгөөний тэгшитгэл m d В/dt= Ф. Материаллаг цэгүүдийн системийн моментийн тэгшитгэл d Л/dt= М. Хамгаалалтын хуулиуд.Тусгаарлагдсан систем нь гадны хүчний нөлөөнд автдаггүй системийг хэлнэ. Үүн дотор Ф= 0, тэгэхээр d х/dt = 0. Дараа нь х= const. Тусгаарлагдсан системд гадны хүчний момент М= 0. Иймд d Л/dt = 0 гэсэн үг Л= const. Хоёр байрлалын хооронд шилжихэд материаллаг цэгийн кинетик энергийн өөрчлөлт нь хүчний хийсэн ажилтай тэнцүү байна. m 0 v 2 2 /2 – m 0 v 1 2 /2 = ∫(1,2) Фг лэсвэл m 0 v 2 /2 + E p = const.
4. Төвлөрсөн тэгш хэмтэй талбар дахь хөдөлгөөн. Кеплерийн хуулиуд. Биеийн потенциал энерги нь зөвхөн тодорхой цэг хүртэлх r зайнаас хамаардаг бол талбайг төв гэж нэрлэдэг. Хүч Ф= - ∂U(r)/ ∂ r= - dU/dr r/r бөөмс дээр үйлчилдэг, үнэмлэхүй утгаараа мөн зөвхөн r-ээс хамаардаг ба радиус векторын дагуу цэг бүрт чиглэнэ. Төвийн талбарт шилжих үед талбайн төвтэй харьцуулахад системийн момент хадгалагдана. Нэг хэсэгхэн агшинд М = [r*Р]. M ба r векторууд харилцан перпендикуляр байдаг тул M-ийн тогтмол байдал нь бөөмс хөдөлж байх үед түүний радиус вектор нь үргэлж нэг хавтгайд - M-тэй перпендикуляр хавтгайд үлддэг гэсэн үг юм. Тиймээс, төв талбар дахь бөөмийн траектор нь бүхэлдээ оршдог. нэг онгоц. Үүнд r, φ туйлын координатуудыг оруулсны дараа бид Лагранж функцийг L = m/2 (r 2 (∙) + r 2 φ 2 (∙)) - U (r) хэлбэрээр бичнэ. Энэ функц нь φ координатыг тодорхой агуулаагүй болно. Ийм координатын хувьд харгалзах ерөнхий импульс p i нь хөдөлгөөний интеграл юм. Энэ тохиолдолд ерөнхий импульс p φ = mr 2 φ(∙) нь M z = M моменттэй давхцаж байгаа тул M = mr 2 φ(∙) (1) байна. Төвийн талбар дахь нэг бөөмийн хавтгай хөдөлгөөний хувьд энэ хууль нь энгийн геометрийн тайлбарыг зөвшөөрдөг болохыг анхаарна уу. 1/2 r r d φ илэрхийлэл нь хязгааргүй ойрхон радиустай хоёр вектор болон траекторийн нумын элементээс үүссэн салбарын талбайг илэрхийлнэ. Үүнийг df гэж тэмдэглээд бид бөөмийн моментийг M = 2mf хэлбэрээр бичдэг ба f-ийн уламжлалыг салбарын хурд гэж нэрлэдэг. Тиймээс импульс хадгалагдана гэдэг нь салбарын хурдны тогтвортой байдлыг хэлнэ - ижил хугацаанд хөдөлж буй цэгийн радиус вектор нь тэнцүү талбайг дүрсэлдэг ( Кеплерийн хоёр дахь хууль). (1)-ээс φ(∙)-ийг M-ээр илэрхийлж, энергийн илэрхийлэлд орлуулснаар бид: E = m/2 (r 2 (∙) + r 2 φ 2 (∙)) + U(r) = mr болно. 2 (∙ )/2 + М 2 /2мр 2 + U(r). Эндээс r(∙) = √(2/m (E – U(r)) - M 2 /m 2 r 2) эсвэл хувьсагчдыг салгаж, интегралчилбал: t = ∫dr/√(2/m (E – U() r)) - M 2 / м 2 r 2) + const. Дараа нь (1)-ийг dφ = M 2 /mr 2 dt хэлбэрээр бичиж, энд dt-г орлуулж, интегралдахад бид дараахыг олно: φ = ∫dr (M/r 2)/√(2/m (E – U(r)) ) - M 2 /r 2) + const. Кеплерийн анхны хууль.Гараг бүр эллипс хэлбэрээр эргэдэг бөгөөд нар нэг цэг дээр байрладаг. Кеплерийн гурав дахь хууль.Гаригуудын эргэлтийн оддын үеүүдийн квадратууд нь тэдгээрийн тойрог замуудын хагас том тэнхлэгүүдийн шоо T 1 2 /T 2 2 = a 1 3 / a 2 3 .
5. Материалын цэгүүдийн системийн Лагранжийн функц ба Лагранжийн тэгшитгэл. Хөдөлгөөний интегралууд. Материаллаг цэгүүдийн хаалттай системийг авч үзье. Үүний Лагранж функц нь L = Σ(a) – U(r 1, r 2, …) хэлбэртэй, T = Σ (a) нь кинетик энерги, U нь бөөмсийн харилцан үйлчлэлийн потенциал энерги юм. Тэгвэл d/dt (∂L/∂v a) = ∂L/∂r a хөдөлгөөний тэгшитгэлүүд m a dv a /dt = - ∂U/∂r a хэлбэрийг авна. Эдгээр хөдөлгөөний тэгшитгэлийг Ньютоны тэгшитгэл гэж нэрлэдэг. Вектор Ф a = - ∂U/∂r a-г хүч гэнэ. Хэрэв хөдөлгөөнийг дүрслэхийн тулд цэгүүдийн декарт координат биш, харин дурын ерөнхий координат q i ашигладаг бол Лагранжийн функцийг олж авахын тулд харгалзах хувиргалтыг хийх шаардлагатай: x a = f(q 1, q 2, .., q s) , x a (∙) = Σ(k ) [∂f a /∂q k (∙)] гэх мэт. Эдгээр илэрхийллийг L= 1 / 2 Σ(a) – U функцэд орлуулснаар бид маягтын хүссэн Лагранж функцийг олж авна. L = 1/2 Σ(i,k) – U(q). Хөдөлгөөний интегралууд.Зөвхөн эхний нөхцлөөс хамааран хөдөлгөөний явцад тогтмол утгыг хадгалдаг ерөнхий координатын функцууд байдаг. Тэдгээрийг хөдөлгөөний интеграл гэж нэрлэдэг. Цагийн нэгэн төрлийн байдлаас шалтгаалан dL/ dt = Σ(i) [∂L/∂q i q i (∙)] + Σ(i) [∂L/∂q i (∙) q i (∙∙)]. Лагранжийн тэгшитгэлийн дагуу ∂L/∂q i-г d/dt (∂L/∂q i (∙)) -ээр сольсноор бид dL/dt = Σ(i) эсвэл d/dt (Σ(i) - L) = 0 болно. Эндээс бид энерги гэж нэрлэгддэг E = Σ(i) – L хэмжигдэхүүн өөрчлөгдөхгүй, өөрөөр хэлбэл. хөдөлгөөний интеграл. Хязгааргүй ε дамжуулалттай орон зайн нэгэн төрлийн байдлаас шалтгаалан системийн бүх цэгүүд ε = δr-ээр шилжсэн үед δL = ε Σ(a) [∂L/∂r a ]-тай тэнцэх Лагранжийн функцийн өөрчлөлт тэнцүү байх ёстой. тэг хүртэл, өөрөөр хэлбэл. Σ(a) [∂L/∂r a ] = 0. Лагранжийн тэгшитгэлийг ашиглан бид Σ(a) = d/dt (Σ(a)[ ∂L/∂v a ]) = 0 болно. Дараа нь хэмжигдэхүүн Р= Σ(a)[ ∂L/∂v a ], импульс гэж нэрлэгддэг, өөрчлөгдөөгүй хэвээр байна, өөрөөр хэлбэл. хөдөлгөөний интеграл. δφ өнцгөөр хязгааргүй бага эргэлттэй орон зайн изотропийн улмаас Лагранжийн функцийн өөрчлөлт δL = Σ(a) [∂L/∂r a δ-тэй тэнцүү байна. r a + ∂L/∂v a δ v a ] нь тэгтэй тэнцүү байх ёстой. ∂L/∂-г орлуулсны дараа v a = х a ба ∂L/∂ r a = х a (∙) δφ-ийн дур зоргын улмаас бид d/dt Σ(a) [ rа х a ] = 0. Утга M = Σ(a) [ rа х a ], өнцгийн импульс гэж нэрлэгддэг, тогтмол хэвээр байна, i.e. хөдөлгөөний интеграл.
6. Үнэмлэхүй хатуу биеийн динамик. Инерцийн тензор. Эйлерийн тэгшитгэл. Хатуу бие нь материаллаг цэгүүдийн систем бөгөөд тэдгээрийн хоорондын зай тогтмол байдаг. Хатуу биеийн хөдөлгөөнийг бүрэн дүрслэхийн тулд түүний аль нэг цэгийн хөдөлгөөнөөс гадна энэ цэгийг тойрсон биеийн хөдөлгөөнийг бэхэлгээний цэг болгон мэдэх шаардлагатай. Биеийг О цэг дээр тогтооно. О цэгтэй харьцуулахад m i цэгийн радиус векторыг тэмдэглэнэ. rби, wнь биеийн агшин зуурын өнцгийн хурд, дараа нь өнцгийн импульс юм Л= Σ [ rби * м би v i ] = Σ = wΣ – Σ. Энэ вектор тэгшитгэлийг координатын тэнхлэгүүд дээр гурван проекцын хэлбэрээр бичиж болно L x = w x Σ - Σ ; L y = w y Σ - Σ ; L z = w z Σ - Σ . Үүнийг харгалзан үзвэл ( w r i) = x i w x + y i w y + z i w z бид L x = J xx w x + J xy w y + J xz w z -ийг олж авна; L y = J yx w x + J yy w y + J yz w z ; L x = J zx w x + J zy w y + J zz w z, энд J xx = Σ, J xy = Σ, бусад нь адилхан. J xx , J yy , J zz хэмжигдэхүүнүүдийг тэнхлэгийн инерцийн момент, J xy = J yx, J xz = J zx, J yz = J zy – төвөөс зугтах инерцийн момент гэнэ. J ij хэмжигдэхүүнүүдийн багцыг инерцийн тензор гэнэ. J ii-ийн элементүүдийг диагональ гэж нэрлэдэг. Хэрэв диагональ бус бүх элементүүд тэгтэй тэнцүү бол координатын тэнхлэгүүдтэй давхцаж буй биеийн тэнхлэгүүд нь инерцийн үндсэн тэнхлэгүүд бөгөөд J ii хэмжигдэхүүнүүдийг инерцийн үндсэн моментууд гэж нэрлэдэг. Ийм тензорыг диагональ хэлбэрт оруулдаг.
Эйлерийн тэгшитгэл. Биеийн массын төвийн хөдөлгөөний тэгшитгэл нь m d хэлбэртэй байна v 0 /dt = m d/dt ( w * r 0) = Ф, Хаана r 0 - биеийн массын төвийн радиус вектор, түүний бэхэлгээний цэгээс зурсан. Биетэй холбоотой координатын системийн тэнхлэгүүдийг инерцийн үндсэн тэнхлэгийн дагуу чиглүүлэх нь тохиромжтой. Энэ тохиолдолд өнцгийн импульс энгийн хэлбэрийг авна L 1 = J 1 w 1, L 2 = J 2 w 2, L 3 = J 3 w 3 ба w i нь хөдөлж буй координатын тэнхлэгүүд дээрх өнцгийн хурдны проекцууд юм. биетэй. Ерөнхий томьёог ашиглах d А/dt = ∂ А/∂t + w* А, бид моментийн тэгшитгэлийг дараах байдлаар илэрхийлж болно ∂ Л/∂t + w * Л = М. L x = J x w x , L y = J y w y , L z = J z w z гэдгийг харгалзан бид энэ тэгшитгэлийг хөдөлж буй координатын системийн тэнхлэг дээрх проекцоор дахин бичнэ: J x dw x /dt + (J z - J y) )w y w z = M x , J y dw y /dt + (J x – J z)w z w x = M y , J z dw z /dt + (J y – J x)w x w y = M z . Эдгээр тэгшитгэлийг Эйлерийн тэгшитгэл гэж нэрлэдэг.
7.
Инерциал бус жишиг системтэй харьцуулахад хөдөлгөөн.
NISO бол мууранд байдаг систем юм. бие нь амралттай харьцуулахад хурдатгалтай хөдөлдөг. зохицуулалтын системүүд Энд орон зай, цаг хугацааны нэгэн төрлийн ба изотропийн тухай ойлголтууд биелээгүй, учир нь NISO-ийн үргэлжлэх хугацаа, цар хүрээ өөр өөр байдаг. Түүнчлэн Ньютоны 3-р зарчмын агуулга, хамгаалах зарчмууд алдагдсан. Бүх зүйлийн шалтгаан нь зөвхөн координатын системтэй холбоотой инерцийн хүч юм, муур. биеийн хөдөлгөөнд нөлөөлдөг. ЭНЭ. хурдатгалыг гадны хүч эсвэл инерцийн хүчийг ашиглан өөрчилж болно. F=∑Fi=ma (ISO), F=F(ext.)+Fi=ma′(NISO), энд Fi нь инерцийн хүч, a нь хурдатгал юм. ISO дахь биетүүд, a′-хурдатгал. NISO дахь ижил бие. NISO-д Ньютоны 1-р хууль хангагдаагүй байна! Fi=-m(a′-a), i.e. Инерцийн хүчнүүд Ньютоны 3-р хуульд захирагддаггүй, учир нь тэд богино насалдаг. ISO-аас NISO руу шилжих үед инерцийн хүч алга болдог. Инерци хүч үргэлж зовхины эсрэг чиглэсэн байдаг. гадаад хүч. Инерцийн хүчийг вектороор нэмж болно. ISO-д: v=const, v< dx/dt=Ux=dx′/dt+dv(t)/dt′=U′x+v(t) dUx/dt=d/dt′(U′x+v(t))=dU′x/ dt′+dv(t)/dt′=a x ' + a 0 = a x . NISO нь үнэмлэхүй, харьцангуй болон зөөврийн хурд гэсэн ойлголтуудыг танилцуулж байна: u 0 нь үнэмлэхүй хурд, 0 нь харьцангуй хурдатгал юм. амарч байна зохицуулалтын системүүд u x 0 = v + u x 0 '; a x 0 = a’ + a x ; u x ’ a x - хурд ба хурдатгалын харьцангуй. хөдөлгөөн зохицуулалтын системүүд (харьцангуй); v, a′-хурд ба хурдасгасан. to' хэлнэ. руу, өөрөөр хэлбэл. зөөврийн хурд ба хурдатгал Ерөнхий координат, хурд, цаг хугацааны функц байдаг. 2S хэмжээст орон зайг авч үзье, дараа нь системийн байрлал S = ∫(t 1 , t 2) L(g, g( ), t)dt, L нь Лагранжийн функц; S-үйлдэл. Үйлдлийн функцийг itnegral S=∫ Ldt=0, at cat. Хөдөлгөөний жинхэнэ траекторийн дагуу авч үзвэл систем нь хамгийн бага утгатай байх болно, өөрөөр хэлбэл. S=Smin, δS=0. Тэдгээр. 1-ээс 2 хүртэлх систем нь ийм траекторийн дагуу хөдөлдөг тул түүний үйлдэл хамгийн бага байдаг - Хамилтоны хамгийн бага үйл ажиллагааны зарчим. L = T – U нь системийн кинетик ба боломжит энергийн ялгаа юм. Хамилтоны хэлснээр бодит замнал нь хамгийн бага үйлдэлтэй тохирч байна. Замын замыг олцгооё. Бодит зам нь хамгийн бага зам юм. S-функциональ. Үүнийг олцгооё. δS = 0 эхний өөрчлөлт. δS = ∫(t 1 ,t 2)(Σ[∂L/∂g i δg i ] + Σ[∂L/∂g i ( ) δg i ( )])dt; ∫(t 1 ,t 2) ∂L/∂g i ( ) δg i ( ) dt = ∫(t 1 ,t 2) ∂L/∂g i ( ) dδg i = ∂L/∂g i ( )δg i ( )δg 1 ,t 2) - ∫(t 1 ,t 2) δg i d/dt (∂L/∂g i ( )) dt; Би бие биенээсээ хамааралгүй 9.
Нэг ба олон зэрэглэлийн эрх чөлөө бүхий системийн хэлбэлзэл. Чөлөөт ба албадан чичиргээ
.
Хамгийн энгийн тохиолдол бол систем нь нэг зэрэглэлийн эрх чөлөө юм. Тогтвортой тэнцвэрт байдал нь системийн энэ байрлалд тохирч байна, муур. түүний боломж en. U(q) хамгийн бага байна. Энэ байрлалаас хазайх нь хүчийг бий болгоход хүргэдэг - dU / dq, энэ нь системийг буцааж өгөх хандлагатай байдаг. q 0 - ерөнхий координат. U(q) - U(q0)-ийг зэрэгцүүлэн томруулж, U(q) - U(q0) ≈ k/2 (q - q 0) 2-ыг авъя. Энд k = U’’(q 0) эерэг коэффициент байна. U(q 0) = 0 гэж тэмдэглэе x = q - q 0 - координатын тэнцвэрийн утгаас хазайлт, дараа нь U(x) = kx 2 /2 – потенциал энерги. 1/2a(q) q' 2 =1/2a(q)x' 2 -q = q0 ба a(q0) = m үед кинетик энерги нь нэг хэмжээст хэлбэлзлийг гүйцэтгэдэг системийн Лагранж функцийг олж авна: L = mx 2 (∙) /2 – kx 2 /2. Энэ функцэд тохирох хөдөлгөөний тэгшитгэл нь: mx(∙∙) + kx = 0 эсвэл x(∙∙) + w 2 x = 0, энд w = √(k/m) нь мөчлөгийн хэлбэлзлийн давтамж юм. Эдгээр тэгшитгэлийн шийдэл нь x = a cos(wt + α) бөгөөд a нь хэлбэлзлийн далайц, wt + α нь хэлбэлзлийн үе шат юм. Тэр. системийн хэлбэлзлийн энерги нь E = mx 2 (∙)/2 + kx 2 /2 болно. Албадан чичиргээ.Энэ тохиолдолд систем нь өөрийн боломжит энерги ½ kx 2-ийн зэрэгцээ гадаад талбайн үйлчлэлтэй холбоотой U e (x, m) боломжит энергитэй байдаг. Үүний дагуу ийм системийн Лагранжийн функц нь: L = mx 2 (∙)/2 + kx 2 /2 + x F(t), F(t) нь гадаад хүч юм. Харгалзах хөдөлгөөний түвшин нь mx(∙∙) + kx = F(t), эсвэл x(∙∙) + w 2 x = F(t)/m байх болно. Хэрэв F(t) нь тодорхой давтамжтай γ: F(t) = f cos(γt + β) цаг хугацааны энгийн үечилсэн функц бол хөдөлгөөний тэгшитгэлийн шийдэл нь: X = a cos(wt + α) болно. + f cos(γt + β)/(m(w 2 – γ 2)) a ба α нь эхний нөхцлөөс тодорхойлогдоно. Тэр. хөдөлгөгч хүчний нөлөөн дор систем нь системийн байгалийн давтамж w ба хөдөлгөгч хүчний давтамж - γ гэсэн хоёр хэлбэлзлийн хослолыг илэрхийлсэн хөдөлгөөнийг хийдэг. Олон зэрэглэлийн эрх чөлөө бүхий системийн хэлбэлзэл
.
Хүчтэй. en. U(q i) систем q i =q i 0 үед минимумтай байна. Жижиг шилжилтийг x i = q i - q i 0 оруулж, тэдгээрийн хувьд U-г 2-р эрэмбийн нөхцлүүд хүртэл өргөжүүлснээр бид потенциалыг олж авдаг. энерги: U = 1/2 Σ(i,k) , k ik =k ki . Кинет. en. ийм системийн хувьд 1/2 Σ(i,k) байх болно, энд m ik =m ki . Ийм системийн Лагранжийн тэгшитгэл нь: L = 1/2 Σ(i,k) болно. Дараа нь dL = Σ(i,k) . Бид x k (t) -ийг x k = A k exp(-iwt) хэлбэрээр хайдаг, A k нь тогтмол юм. Үүнийг Лагранжийн тэгшитгэлд орлуулснаар бид шугаман нэгэн төрлийн тэгшитгэлийн системийг олж авна. Σ(k) [(-w 2 m ik +k ik)A k ] = 0 - шинж чанарын тэгшитгэл, энэ нь s өөр үндэстэй w 2 α (α=1,2,….,s) w α - байгалийн давтамж систем . Системийн тодорхой шийдэл нь дараах хэлбэртэй байна: x k = ∆ kα C α exp(-iw α t). Ерөнхий шийдэл нь бүх хэсэгчилсэн шийдүүдийн нийлбэр юм: x k = Σ(α) [∆ kα Q α ], энд Q = Re (C α exp(-iw α t)). 10.
Гамильтоны каноник тэгшитгэл.
Механикийн асуултуудыг судлахдаа ерөнхий координат ба импульсийг ашиглан тайлбарлах нь хэд хэдэн давуу талтай бөгөөд бие даасан хувьсагчийн нэг багцаас нөгөөд шилжих шилжилтийг Лежендре хувиргах замаар хийж болно. Энэ тохиолдолд энэ нь дараах байдалтай байна. Координат ба хурдны функц болох Лагранжийн функцүүдийн нийт дифференциал нь тэнцүү байна: dL = Σ(i) [∂L/∂q i ] + Σ(i) [[∂L/∂q i (∙)]. Энэ илэрхийллийг dL = Σ(i) + Σ(i) гэж бичиж болно. Үүнийг d(Σ(i) – L) = - Σ(i) + Σ(i) хэлбэрээр дахин бичье. Дифференциал тэмдгийн доорх хэмжигдэхүүн нь координат ба моментоор илэрхийлэгдсэн системийн энергийг илэрхийлэх ба түүнийг Гамильтоны функц гэнэ: H(p,q,t) = Σ(i) – L. Дифференциалаас. dH = - Σ(i) + Σ(i) тэгшитгэлийг дагана: q i (∙) = ∂H/∂p i, p i (∙) = - ∂H/∂q i – эдгээр нь Хэмилтоны тэгшитгэлүүд юм. Тэдний энгийн байдал, тэгш хэмийн улмаас тэдгээрийг бас нэрлэдэг. каноник. Пуассон хаалт.Ерөнхий координат, импульс ба цаг хугацааны аливаа F функцийн хугацааны дериватив нь dF/dt = ∂F/∂t + Σ(i) [∂F/∂q i dq i /dt] + Σ(i) [∂F/ байх болно. ∂p i dp i /dt]. Хэмилтоны тэгшитгэлийг ашиглан бид энэ тэгшитгэлийг дараах хэлбэрээр дахин бичиж болно: dF/dt = ∂F/∂t + , энд = Σ(i) [∂F/∂q i ∂H/∂p i - ∂H/∂q i ∂F /∂ p i ] - дуудагдана Пуассон хаалт. Гамильтоны тэгшитгэлийг Пуассон хаалт ашиглан бичиж болох нь ойлгомжтой. 11.
Хамилтон-Жакоби тэгшитгэл
.
Хамгийн бага үйл ажиллагааны зарчмаар бид S = ∫(t 1 ,t 2)Ldt байна. Үйлдлийг (S) жинхэнэ траекторийн дагуух хөдөлгөөнийг тодорхойлдог хэмжигдэхүүн гэж үзье. Лагранжийн тэгшитгэлийг үндэслэн нэг траекториос өөр зам руу ойртож өөр зам руу шилжих үед (нэг эрх чөлөөнд) бид дараахь зүйлийг олж авна: δS = pδq эсвэл дурын тооны эрх чөлөөний градусын хувьд: δS = Σ(i) . Үүнээс үзэхэд координаттай холбоотой үйлдлийн хэсэгчилсэн деривативууд нь харгалзах импульстэй тэнцүү байна: ∂S/∂q i = p i (1). Тодорхойлолтоор dS/dt = L, нөгөө талаас, S-ийг координат ба цаг хугацааны функц гэж үзээд (1) томъёог ашиглан бид: dS/dt = ∂S/∂t + Σ(i) [∂S/ ∂q i q i (∙)] = ∂S/∂t + Σ(i) . Хоёр илэрхийлэлийг харьцуулж үзвэл бид ∂S/∂t = L - Σ(i) эсвэл ∂S/∂t = - H(p,q,t) (2)-ыг авна. (1), (2) томъёог dS = Σ(i) – Hdt гэж хамт бичиж болно. Мөн үйлдэл (S) нь өөрөө S = ∫ (Σ(i) – Hdt) байх болно. H нь t – S(q,t)=S 0 (q) - Et-ээс хамааралгүй байх үед S 0 (q) = Σ(i) [∫p i dq i ] нь богиноссон үйлдэл бөгөөд Et нь H(-ээр солигдоно. p,q) . S(q,t) функц нь тодорхой дифференциалыг хангадаг. ∂S/∂q: ∂S/∂t + H(∂S/∂q 1 ,…, ∂S/∂q s ;q 1 ,… ∂S/∂q деривативуудаар (2) хамааралтай P импульсийг сольж олж авах тэгшитгэл. ,q s ,t) = 0 нь 1-р эрэмбийн хэсэгчилсэн дифференциал тэгшитгэл гэж нэрлэгддэг. Хамилтон-Жакоби тэгшитгэл. Тиймээс гадаад талбар дахь U(x,y,z,t) нэг бөөмийн хувьд энэ нь дараах хэлбэртэй байна: ∂S/∂t + 1/(2м)((∂S/∂x) 2 + (∂S/∂) y) 2 + (∂S/∂z) 2) + U(x,y,z,t) = 0. 12.
Хатуу биет дэх хэв гажилт ба хүчдэл. Young's moduli, shear. Пуассоны харьцаа
.
Гадны хүчний нөлөөгөөр биеийн хэлбэр, эзэлхүүний өөрчлөлтийг деформаци гэнэ. Гадны хүчний нөлөөн дор биеийн хэлбэр өөрчлөгддөг. Байгалийн бүх хэв гажилтыг 3 болгон бууруулж болно мүндсэн хэв гажилт: 1) хурцадмал байдал, шахалт; 2) ээлж; 3) мушгих. Нэг төрлийн ба нэг төрлийн бус хэв гажилт байдаг. Хэрэв бүх хэсгүүд ижил хэв гажсан бол энэ нь нэгэн төрлийн гажигтай.Хэрэв биеийн бүх хэсгүүд жигд бус гажигтай бол энэ нь гетероген гажигтай.Хукийн хууль нь зөвхөн уян хатан хэв гажилтын бүсэд хангагдана. = E’. F/S = E ∆l/l 0 ; F удирдлага = ES∆l/l 0 = kx; k = ES/l 0 ; F удирдлага = ESx/l 0 . Hooke-ийн хууль нь ба хоорондын хамаарлыг тодорхойлдог. k нь уян хатан байдлын коэффициент бөгөөд энэ нь геометрийн хэмжээс, материал, бие нь юугаар хийгдсэнээс хамаарна. И-Янгийн модуль. Янгийн модуль нь биеийг хоёр дахин нэмэгдүүлэхийн тулд нэгж хөндлөн огтлолтой биед үзүүлэх хүчтэй тэнцүү байна. Өөр нэг төрлийн хэв гажилт нь гадаргууг тангенциар хэрэглэх үед ажиглагддаг зүсэлтийн хэв гажилт юм; энэ нь зүсэлтийн хэв гажилтын гадаргуутай параллель байх ба шүргэгч хүчний үйл ажиллагааны дор ажиглагддаг, өөрөөр хэлбэл хүчийг тангенциалаар хийдэг. Ψ~F t /S (шилжүүлэх өнцөг). Ψ = nF t / S; n нь шилжилтийн коэффициент юм. F t = nS. (E>N, E~ 4N). 13.
Шингэн ба хийн механик.
Бүх шингэн ба хийн хувьд нэгтгэх параметр нь: нягт ρ, даралт P=F n /S. Шингэн ба хийд Янгийн модуль явагддаг боловч шилжилтийн модуль |σ|=|P| явагдахгүй, σ нь хүчдэл юм. Хэрэв шингэн (хий) хөдөлгөөнгүй бол бид гидростатик (аэростатик) -тай харьцаж байна. Онцлог хуулиуд: Паскалийн хууль: хий болон шингэнд үүссэн илүүдэл даралтыг бүх чиглэлд жигд дамжуулдаг. Архимедийн зарчим нь шингэн болон хийн аль алинд нь хүчинтэй. Архимедийн хүч үргэлж таталцлын эсрэг ажилладаг. Архимедийн хүч үүсэх болсон шалтгаан нь биед V эзэлхүүн байдагт оршино.Архимедийн зарчим: Шингэн болон хий дотор байрласан биед үргэлж шингэн юмуу хийн шилжсэн жинтэй тэнцэх хүч үйлчилдэг. биеийн хэсгийг дүрж, босоо дээшээ чиглүүлнэ. Хэрэв F A >F Гравитаци бол бие хөвж, харин эсрэгээрээ живдэг. Хэрэв шингэн (хий) урсаж байвал тийрэлтэт тасралтгүй байдлын тэгшитгэлийг эдгээр тэгшитгэлд нэмнэ. Шингэн дэх бөөмийн траекторийг гэнэ. одоогийн шугам. Одоогийн шугамаар хязгаарлагдах зайны хэсгийг дуудна. одоогийн хоолой. Одоогийн хоолой дахь шингэн нь хөдөлгөөнгүй эсвэл тогтворгүй урсаж болно. Гүйдэл гэж нэрлэдэг статик хэрэв хоолойн өгөгдсөн хэсгээр нэгжид гүйдэл байвал. цаг хугацаа өнгөрөхөд ижил хэмжээний шингэн (хий) дамждаг, эс тэгвээс урсгал тогтворгүй болно. Дараах хэлбэрийн гүйдлийн хоолойтой болцгооё: Хэрэв шингэний урсгал хөдөлгөөнгүй бол. Дараа нь нэгж хугацаанд m 1 =m 2 =…=m n, хэрэв шингэн нь шахагдах боломжгүй бол ρ 1 V 1 =ρ 2 V 2 =…; =ρ n V n , ρ 1 Δx 1 = ρ 2 Δx 2 =…; = ρ n Δx n, ρ 1 υ 1 ΔtS 1 =ρ 2 υ 2 ΔtS 2 =…= ρ n υ n ΔtS n, учир нь шингэн нь шахагдах боломжгүй ρ тогтмол υ 1 S 1 =υ…=2 S 2 n S n , υS=const; υ=const/S – тийрэлтэт тасралтгүй байдлын тэгшитгэл. ρ d v/dt = ρ g– grad P – eq. Эйлер - 2-р захиалга. Шингэн ба хийн хувьд Ньютон. Хууль хадгалагдсан Шингэн ба хий дэх энерги. Lv. Бернулли. ID. Нэр Наалдамхай үрэлтийн хүчийг үл тоомсорлож болох шахагдашгүй шингэн. Үрэлтийн хүчний эсрэг ажил хийхэд кинетик энерги дэмий үрдэггүй. Ρυ 2 /2+ρgh + P = const – eq. Бернулли, ρυ 2 /2 – динамик даралт, ρgh – гидростат. Даралт, P - молекулын даралт. Mυ 2 /2 = E K ; mυ 2 /2V= E K /V= ρυ 2 /2. Наалдамхай үрэлтийн хүч F A = - ηΔυΔS/ΔZ 6 π r η υ – Стоксын хүч. Η - коэффициент зуурамтгай чанар, Δυ/ΔZ – grad υ, r – биеийн хэмжээс. Энэ бол наалдамхай үрэлтийн хүчний Ньютоны томъёо юм. Хэрэв шингэнд үрэлтийн хүч байгаа бол id. Шингэн нь наалдамхай болдог. ρ v 1 2 /2 + ρgh 1 + P 1 = ρ v 2 2 /2 + ρgh 2 + P 2; (P 1 – P 2) = ρ(υ 2 2 – υ 1 2)/2. Хэрэв ΔP = 0 бол υ 2 2 – υ 1 2 = 0 байх ба шингэний урсгал байхгүй болно. Хаана P их байна, тэнд хурд байдаг. Гүйдэл бага байна. Хэрэв хөндлөн огтлол S нэмэгдэж байвал P нь нэмэгдэж, υ буурна. Хэрэв гүйдлийн хоолой хэвтээ байрлалтай биш бол υ 2 2 -υ 1 2 =2г (h 1 -h 2); υ = sqrt(2г (h 1 -h 2)) – Торричеллигийн томьёо. Өргөтгөсөн тохируулга ба фазын орон зай дахь механик системийн хөдөлгөөнийг дүрсэлсэн траекторууд нь гайхалтай шинж чанартай байдаг - тэдгээр нь зарим өөрчлөлтийн асуудлын хэт туйлшрал бөгөөд үйл ажиллагааны үйл ажиллагаанд хөдөлгөөнгүй утгыг өгдөг. Өргөтгөсөн тохиргооны орон зайд вариацын асуудлын томъёоллыг авч үзье R"*",тэдгээрийн цэгүүд нь олонлогууд (q, ().
Муруйг y„ = ((q, t): q e Rt e, 5q(/ 0)= 8q(/,) = 0). 8q(/) хувилбар нь C1 ангиллын дурын функц бөгөөд = 0 сегментийн төгсгөлд алга болдог. Үйл ажиллагааны анхны хувилбар Стодорхойлолтын дагуу y = y 0 үед энэ нь тэнцүү байна ба хэсгүүдээр нэгтгэсний дараа хэлбэрийг авдаг Илэрхийлэл (2.3) дахь дотоод нэр томъёо алга болж, учир нь bq k (t 0) = bq k (t y) = 0, - 1.....l, илэрхийлэл нь дөрвөлжин хэлбэртэй байна 0 нь Лагранжийн тэгшитгэлийг (2.1) хангасан бодит траектор учраас интеграл тэмдгийн доорх хаалтанд 0-тэй тэнцүү байна. Иймд хэлбэлзэл 55(y 0) = 0. ? Эсрэг заалт нь бас үнэн юм: хэрэв 65(y*) = 0 хэлбэлзэл нь y* нь тойрог замын хөдөлгөөний ангилалд хамаарах бол y* = y 0 нь бодит замнал болно. Энэхүү мэдэгдлийн хүчинтэй байдал нь эхний өөрчлөлтийн илэрхийлэл (2.3) ба өөрчлөлтийн тооцооны үндсэн леммагаас үүдэлтэй. Энэ тохиолдолд эхний өөрчлөлтийн тэгшитгэлээс тэг хүртэл 6-аас - 1 хүртэлх хувилбаруудын бие даасан байдал, ..., хоёр дахь төрлийн Лагранжийн тэгшитгэлийн хүчинтэй байдал l, энэ нь үнэн гэсэн үг Хэзээ q k = q k *(t), k= 1.....л. Энэ нь y* нь механик системийн бодит замнал гэсэн үг юм. 3.1. Консерватив бус системийн хувьд бодит зам дээр хөдөлгөөнгүй утгад хүрсэн функцийг зааж өгөх боломжгүй юм. Гэсэн хэдий ч, энэ тохиолдолд дараах мэдэгдлүүд тэнцүү байна: Энд q(/) нь бодит замнал юм. Дээрх мэдэгдлүүдийн эхнийх нь консерватив бус системийн хувьд Хамилтон-Остроградскийн вариацын зарчмын агуулгыг бүрдүүлдэг. 3.2. Хэрэв - / 0 зөрүү хангалттай бага байвал үйлдлийн функциональ тогтмол утга нь хамгийн бага болохыг харуулж болно. Энэ нөхцөл байдал нь хэлэлцэж буй зарчмын өөр нэртэй холбоотой - Хамилтон-Остроградын хамгийн бага үйл ажиллагааны зарчим. Дээр авч үзсэн вариацын асуудлыг өргөтгөсөн фазын орон зайд томъёолж болох бөгөөд энэ нь Гамильтоны каноник тэгшитгэлийн интегралчлалын асуудлыг авч үзэхэд чухал ач холбогдолтой юм. Г = ((р + 6р. q + 8q,) гэж тэмдэглэе. I): p, q, 6p. 6q e R",te[r 0 , /,]. Өргөтгөсөн фазын орон зайд 5q(/ 0)= 8q(/|) = 0) муруй ба 8p = 8q = 0 үед Г 0 муруйг Гамильтоны каноник тэгшитгэлийн системийн шийдэл гэж үзье. Бүх цагийн функцууд нь C 1 ангилалд хамаарна. Ийнхүү тойрог замын хөдөлгөөний гэр бүл (G) тодорхойлогдсон бөгөөд үүнд G 0-ийн бодит траектор хамаарах болно (Зураг 46). Лагранж ба Хамилтон функцүүдийн хоорондын холболтыг харгалзан функциональ үйлдэл нь хэлбэрийг авдаг Энд p + 8p, q + 8q үсгийн оронд p, q үсгүүдийг товчилно. Бодит зам дээрх функциональ S[Г]-ийн өөрчлөлтийг тооцоод бид олж авна Хилийн нөхцөлийг харгалзан хэсгүүдээр нэгтгэж, бид олдог Үүнээс үзэхэд p(/), q(f) нь Гамильтоны каноник тэгшитгэлийг (2.4) хангаж байвал 85|Г 0 1 = 0 хэлбэлзэл ба. эсрэгээр хэлбэлзлүүдийн бие даасан байдлын нөхцлөөс 8p(r), 6q(/) тэгшитгэл (2.4) нь вариацын тооцооны үндсэн леммийн дагуу дагана. Ийнхүү системийн фазын орон зайд хамгийн бага үйл ажиллагааны зарчмын үнэн зөвийг нотолсон: тойрог замд өгөгдсөн функциональ үйлдэл 5[Г] (Г|. Бодит зам дээр хөдөлгөөнгүй утгыг авдаг, өөрөөр хэлбэл. 85[Г 0 1 = 0. Цагаан будаа. 46 Би энэ зарчмын талаар анх мэдэхэд ямар нэгэн ид шидийн мэдрэмж төрж байсан. Байгаль нь системийн хөдөлгөөний бүх боломжит замыг нууцлаг байдлаар туулж, хамгийн сайныг нь сонгодог юм шиг санагддаг. Өнөөдөр би физикийн хамгийн гайхалтай зарчмуудын нэг болох хамгийн бага үйлдлийн зарчмын талаар бага зэрэг ярихыг хүсч байна. Гэрэл тусах үед нэг цэгээс нөгөө цэг рүү хамгийн богино хугацаанд хүрэх байдлаар хөдөлдөг. Зураг дээр хамгийн богино зам нь тусгалын өнцөг нь тусгалын өнцөгтэй тэнцүү байх ногоон зам байх болно. Бусад зам, жишээлбэл, улаан, илүү урт байх болно. 1662 онд Пьер Ферма нягт биет дэх гэрлийн хурд, тухайлбал шил, агаараас бага байна гэж үзсэн. Үүнээс өмнө Декартын хувилбарыг ерөнхийд нь хүлээн зөвшөөрсөн бөгөөд үүний дагуу хугарлын зөв хуулийг олж авахын тулд матер дахь гэрлийн хурд агаараас их байх ёстой. Фермагийн хувьд гэрэл нь ховорхон дундаас илүү нягт орчинд илүү хурдан хөдөлж чадна гэсэн таамаглал нь байгалийн бус мэт санагдаж байв. Тиймээс тэрээр бүх зүйл яг эсрэгээрээ байна гэж таамаглаж, гайхалтай зүйлийг нотолсон - энэ таамаглалаар гэрэл хамгийн бага хугацаанд хүрэх газартаа хүрэх байдлаар хугардаг. Эдгээр бүх баримтууд нь байгаль ямар нэгэн оновчтой байдлаар үйлчилдэг, гэрэл, бие нь хамгийн оновчтой байдлаар хөдөлж, аль болох бага хүчин чармайлт гаргадаг болохыг харуулж байна. Гэхдээ эдгээр нь ямар хүчин чармайлт, тэдгээрийг хэрхэн тооцоолох нь нууц хэвээр байв. 1744 онд Маупертуйс "үйлдэл" гэсэн ойлголтыг нэвтрүүлж, бөөмийн жинхэнэ замнал нь түүний үйл ажиллагаа хамгийн бага байдгаараа бусдаас ялгарах зарчмыг томъёолжээ. Гэсэн хэдий ч Маупертуис өөрөө энэ үйлдэл нь юу болох талаар тодорхой тодорхойлолт өгч чадаагүй юм. Хамгийн бага үйл ажиллагааны зарчмын нарийн математик томъёоллыг бусад математикчид - Эйлер, Лагранж аль хэдийн боловсруулсан бөгөөд эцэст нь Уильям Хамилтон өгсөн: Тэгвэл яг товлосон цагтаа зорьсон газраа хүрч, аль болох бага түлш хэрэглэхийн тулд хэрхэн жолоодох ёстой вэ? Та шулуун шугамаар явах хэрэгтэй нь тодорхой байна. Явсан зай ихсэх тусам түлш бага зарцуулагдахгүй. Дараа нь та өөр өөр тактик сонгож болно. Жишээлбэл, та өмнө нь очих газарт хурдан хүрч, цаг нь ирэх хүртэл зүгээр л суугаад хүлээх боломжтой. Жолооны хурд, тиймээс цаг мөч бүрт түлшний зарцуулалт өндөр байх боловч жолоодох хугацаа багасна. Магадгүй шатахууны нийт хэрэглээ тийм ч их биш байх. Эсвэл та жигд, ижил хурдтайгаар жолоодох боломжтой бөгөөд ингэснээр та яарахгүйгээр яг цагтаа ирдэг. Эсвэл замын нэг хэсгийг хурдан жолоодож, арай удаан яв. Хамгийн сайн арга юу вэ? Эндээс харахад хамгийн оновчтой, хэмнэлттэй жолоодлого бол тогтмол хурдтай жолоодох бөгөөд яг товлосон цагтаа зорьсон газартаа хүрэх явдал юм. Өөр ямар ч сонголт илүү их түлш зарцуулна. Та хэд хэдэн жишээ ашиглан өөрөө шалгаж болно. Учир нь шатахууны зарцуулалт хурдны квадратаар нэмэгддэг. Тиймээс хурд нэмэгдэхийн хэрээр түлшний зарцуулалт жолоодох хугацаа багасахаас хурдан нэмэгдэж, нийт түлшний зарцуулалт мөн нэмэгддэг. Тиймээс, хэрэв машин цаг мөч бүрт кинетик энергитэйгээ пропорциональ түлш зарцуулдаг бол яг тогтоосон цагт нэг цэгээс цэг рүү явах хамгийн хэмнэлттэй арга бол жигд, шулуун замаар явах явдал гэдгийг бид олж мэдсэн. биенд үйлчлэх хүч байхгүй үед биеийн хөдөлгөөн.хүч Бусад жолоодлогын арга нь нийт түлшний зарцуулалтыг нэмэгдүүлнэ. Цаг мөч бүрт түлшний зарцуулалт нь машины боломжит энергийг хассан кинетик энергитэй тэнцүү байна (суулгасан төхөөрөмж түлш үйлдвэрлэдэг бөгөөд үүнийг хэрэглэдэггүй тул боломжит энергийг хассан). Одоо машиныг цэгүүдийн хооронд аль болох үр дүнтэй хөдөлгөх бидний даалгавар улам хэцүү болж байна. Энэ тохиолдолд шулуун тэгш хөдөлгөөн нь хамгийн үр дүнтэй биш юм. Бага зэрэг өндөрт гарч, тэнд хэсэг хугацаанд байж, илүү их түлш зарцуулж, дараа нь цэг рүү буух нь илүү оновчтой болох нь харагдаж байна. Нислэгийн траекторийг зөв хийвэл авиралтаас үүдэлтэй нийт түлшний үйлдвэрлэл нь замын уртыг нэмэгдүүлэх, хурдыг нэмэгдүүлэхэд шаардагдах түлшний нэмэлт зардлыг нөхөх болно. Хэрэв та анхааралтай тооцоолж үзвэл автомашины хамгийн хэмнэлттэй арга бол дэлхийн таталцлын талбарт чулуу нисдэгтэй яг ижил траекторийн дагуу, яг ижил хурдтайгаар параболоор нисэх явдал юм. Хөдөлгөөний бүх хугацаанд зарцуулсан түлшний нийт хэмжээний аналог, өөрөөр хэлбэл. Хөдөлгөөний бүх хугацаанд хуримтлагдсан Лагранжийн утгыг "үйлдэл" гэж нэрлэдэг. Хамгийн бага үйл ажиллагааны зарчим нь бие нь үйлдэл (хөдөлгөөний замналаас хамаардаг) хамгийн бага байхаар хөдөлдөг. Үүний зэрэгцээ бид эхний болон эцсийн нөхцөлийг тодорхойлсон гэдгийг мартаж болохгүй, i.e. цаг хугацааны агшинд болон цаг мөчид бие хаана байна. Энэ тохиолдолд бие нь бидний машинд зориулж авч үзсэн нэгэн жигд таталцлын талбарт шилжих албагүй. Бүрэн өөр нөхцөл байдлыг авч үзэж болно. Бие нь уян харимхай туузан дээр хэлбэлзэж, дүүжин дээр эргэлдэж, эсвэл нарны эргэн тойронд нисч чаддаг бөгөөд энэ бүх тохиолдолд "түлшний нийт хэрэглээ" -ийг багасгахын тулд хөдөлдөг. үйлдэл. Хэрэв систем нь хэд хэдэн биеэс бүрддэг бол ийм системийн лагранж нь бүх биеийн нийт кинетик энергийг бүх биеийн нийт потенциал энергийг хассантай тэнцүү байна. Дахин хэлэхэд бүх бие нь нэг дор хөдөлж, ийм хөдөлгөөний үед бүхэл системийн нөлөө бага байх болно. Жишээлбэл, бөмбөг аваад хоосон зайд байрлуулъя. Үүнээс тодорхой зайд бид уян хатан ханыг байрлуулна. Хэсэг хугацааны дараа бөмбөг яг ижил газартаа хүрэхийг хүсч байна гэж бодъё. Эдгээр өгөгдсөн нөхцөлд бөмбөг хоёр өөр аргаар хөдөлж болно. Нэгдүгээрт, энэ нь зүгээр л байрандаа байж болно. Хоёрдугаарт, та үүнийг хана руу түлхэж болно. Бөмбөлөг хана руу нисч, түүнээс үсэрч буцаж ирнэ. Яг зөв цагтаа буцаж ирэх тийм хурдтай түлхэж чадах нь ойлгомжтой. Ийм нөхцөлд хүчинтэй байхын тулд бид хамгийн бага үйл ажиллагааны зарчмыг хэрхэн хадгалах вэ? Бид энэ талаар ярих болно.8. Хэмилтоны вариацын зарчим. (хамгийн бага үйл ажиллагааны зарчим).
;
=0
Бодит зам дээр дараахь тэгшитгэлийг хангасан байх ёстой. 
- Лагранжийн тэгшитгэл (ямар ч i= 1,...S хувьд).
E ба N хоорондын тоон хамаарлыг Пуассоны харьцаагаар тодорхойлно. N = E/(2(1+μ)), энд нь Пуассоны харьцаа юм. μ = |∆d/d 0 |/|∆l/l 0 |. Пуассоны харьцаа нь хурцадмал эсвэл шахалтын үед хөндлөн хэмжээсийн өөрчлөлтийг тодорхойлдог. 0.5.
Суурь
Галилеогийн үеэс эхлэн ямар ч хүчний нөлөөгүй биетүүд шулуун шугамаар, өөрөөр хэлбэл хамгийн богино замаар хөдөлдөг болохыг мэддэг болсон. Гэрлийн цацрагууд мөн шулуун шугамаар дамждаг. 
Үүнийг толины эсрэг талын цацрагийн замыг тусгаснаар батлахад хялбар байдаг. Тэдгээрийг зурган дээр тасархай шугамаар харуулав. 
ACB ногоон зам нь шулуун ACB' болж хувирч байгааг харж болно. Мөн улаан зам нь АХБ' гэсэн тасархай шугам болж хувирдаг бөгөөд энэ нь мэдээж ногооноос урт юм. 
Дахин хэлэхэд, ногоон өнгө нь гэрлийн туяа үнэхээр дамждаг замыг харуулдаг. Улаанаар тэмдэглэгдсэн зам нь хамгийн богино боловч хамгийн хурдан биш, учир нь гэрэл нь шилээр дамжин өнгөрөх урт замтай бөгөөд тэнд удаан байдаг. Хамгийн хурдан зам бол гэрлийн цацрагийн бодит зам юм. 
Математикийн хэлээр хамгийн бага үйлдлийн зарчмыг нэлээд товчхон томъёолсон боловч бүх уншигчид ашигласан тэмдэглэгээний утгыг ойлгодоггүй. Би энэ зарчмыг илүү ойлгомжтой, энгийнээр тайлбарлахыг хичээмээр байна. Чөлөөт бие
Тиймээс, та машинд сууж байгаа бөгөөд яг тэр мөчид танд энгийн даалгавар өгсөн гэж төсөөлөөд үз дээ: цаг мөчид та машинаа цэг рүү жолоодох хэрэгтэй. 
Машины түлш нь үнэтэй бөгөөд мэдээжийн хэрэг та үүнийг аль болох бага зарцуулахыг хүсч байна. Таны машин хамгийн сүүлийн үеийн супер технологиор хийгдсэн бөгөөд хүссэн хэмжээгээрээ хурдасгах эсвэл тоормослох боломжтой. Гэхдээ хурдан явах тусам шатахуун зарцуулдаг байхаар бүтээгдсэн. Түүнээс гадна түлшний зарцуулалт нь хурдны квадраттай пропорциональ байна. Хэрэв та хоёр дахин хурдан жолоодвол ижил хугацаанд 4 дахин их түлш зарцуулна. Шатахууны зарцуулалтад хурдаас гадна тээврийн хэрэгслийн жин нөлөөлдөг нь мэдээж. Манай машин хүнд байх тусмаа шатахуун зарцуулдаг. Манай машины түлшний зарцуулалт цаг мөч бүрт тэнцүү байна, өөрөөр хэлбэл. машины кинетик энергитэй яг тэнцүү байна. Таталцлын талбарт
Одоо машинаа жаахан сайжруулъя. Ямар ч чиглэлд чөлөөтэй нисэх боломжтой тийрэлтэт хөдөлгүүрүүдийг холбоно. Ерөнхийдөө загвар нь ижил хэвээр байсан тул түлшний зарцуулалт дахин машины кинетик энергитэй пропорциональ хэвээр байв. Хэрэв одоо цагт нэг цэгээс нисч, нэг цэгт хүрэх даалгавар өгөгдсөн бол өмнөх шигээ хамгийн хэмнэлттэй арга бол мэдээжийн хэрэг, төгсгөлийн тулд жигд, шулуун шугамаар нисэх явдал юм. яг товлосон цагтаа дээш. Энэ нь гурван хэмжээст орон зай дахь биеийн чөлөөт хөдөлгөөнтэй дахин тохирч байна. 
Гэсэн хэдий ч хамгийн сүүлийн үеийн автомашины загварт ер бусын төхөөрөмж суурилуулсан. Энэ төхөөрөмж нь юу ч бишээс шууд утгаараа түлш үйлдвэрлэж чадна. Гэхдээ загвар нь машин өндөр байх тусам тухайн төхөөрөмж нь ямар ч үед илүү их түлш үйлдвэрлэдэг. Шатахууны үйлдвэрлэл нь тухайн машин байгаа өндөртэй шууд пропорциональ байна. Мөн машин хүнд байх тусам түүн дээр илүү хүчирхэг төхөөрөмж суурилуулж, илүү их түлш үйлдвэрлэдэг бөгөөд үйлдвэрлэл нь машины жинтэй шууд пропорциональ байдаг. Төхөөрөмж нь түлшний үйлдвэрлэл яг тэнцүү байхаар болсон (чөлөөт уналтын хурдатгал хаана байна), өөрөөр хэлбэл. машины боломжит энерги. 
Эндээс тодруулга хийх нь зүйтэй болов уу. Мэдээжийн хэрэг, та чулууг цэгээс онохын тулд олон янзын аргаар шидэж болно. Гэхдээ яг тэр мөчид цэгээсээ хөөрч, яг тэр мөчид нь онох байдлаар шидэх хэрэгтэй. Энэ хөдөлгөөн нь манай машины хувьд хамгийн хэмнэлттэй байх болно. Лагранжийн функц ба хамгийн бага үйлдлийн зарчим
Одоо бид энэ зүйрлэлийг бодит бие махбодид шилжүүлж болно. Биеийн түлшний хэрэглээний түвшингийн аналогийг Лагранж функц эсвэл Лагранж (Лагранжийг хүндэтгэх) гэж нэрлэдэг бөгөөд үсгээр тэмдэглэнэ. Лагранж нь тухайн үед бие нь хэр их "түлш" зарцуулдагийг харуулдаг. Потенциал талбарт хөдөлж буй биеийн хувьд Лагранж нь түүний кинетик энергийг потенциал энергийг хассантай тэнцүү байна. Тийм ч энгийн биш
Ер нь бие дандаа үйлдлийг багасгаж хөдөлдөг гэж би жаахан хуурсан. Энэ нь олон тохиолдолд үнэн боловч үйлдэл нь маш бага биш байх нөхцөл байдлын талаар бодох боломжтой. 
Бөмбөгийг хөдөлгөх хоёр сонголт хоёулаа боломжтой боловч хоёр дахь тохиолдолд үйлдэл нь илүү их байх болно, учир нь энэ бүх хугацаанд бөмбөг тэг бус кинетик энергитэй хөдөлдөг.
