Вакуум дахь Гауссын теорем. Гауссын теоремыг цахилгаан талбайг тооцоолоход ашиглах

Дээр дурдсанчлан, талбайн шугамд перпендикуляр гадаргуугийн нэгжийг цоолох шугамын тоо нь векторын модультай тэнцүү байхаар тийм нягтралтай хүчний шугамыг зурахаар тохиролцсон. Дараа нь суналтын шугамын загвараас зөвхөн чиглэлийг төдийгүй орон зайн янз бүрийн цэгүүд дэх векторын хэмжээг шүүж болно.

Тогтворгүй эерэг цэгийн цэнэгийн талбайн шугамуудыг авч үзье. Эдгээр нь цэнэгээс сунаж, төгсгөлгүй радиаль шугамууд юм. Гүйцэе Нийм шугамууд. Дараа нь хол зайд rцэнэгээс радиустай бөмбөрцгийн нэгж гадаргууг огтолж буй хүчний шугамын тоо r, тэнцүү байх болно. Энэ утга нь зайд байгаа цэгийн цэнэгийн талбайн хүчтэй пропорциональ байна r.Тоо Нтэгш байдлыг хангахын тулд та үргэлж сонгож болно

хаана. Хүчний шугамууд тасралтгүй байдаг тул цэнэгийг хүрээлж буй аль ч хэлбэрийн битүү гадаргууг ижил тооны хүчний шугамууд огтолдог. q.Цэнэгийн тэмдгээс хамааран хүчний шугамууд энэ хаалттай гадаргуу руу орох эсвэл гадагшаа гардаг. Хэрэв гарах мөрүүдийн тоог эерэг, ирж буй мөрүүдийн тоог сөрөг гэж үзвэл модулийн тэмдгийг орхиж, дараахийг бичиж болно.

.

(1.4)

Хүчдэлийн вектор урсгал.Талбай бүхий энгийн дэвсгэр байрлуулцгаая. Талбай нь маш бага байх ёстой бөгөөд ингэснээр түүний бүх цэг дэх цахилгаан орны хүчийг ижил гэж үзэж болно. Сайт руу хэвийн зурж үзье (Зураг 1.17). Энэ нормын чиглэлийг дур зоргоороо сонгодог. Нормаль нь вектортой өнцөг үүсгэдэг. Сонгосон гадаргуугаар дамжин өнгөрөх цахилгаан талбайн хүч чадлын векторын урсгал нь гадаргуугийн талбай ба цахилгаан талбайн хүч чадлын векторын талбайн норм руу проекцын үржвэр юм.

Сайтын норм дээрх векторын проекц хаана байна.

Нэг талбайг цоолж буй талбайн шугамын тоо нь сонгосон талбайн ойролцоох эрчмийн векторын модультай тэнцүү тул гадаргуугаар дамжин өнгөрөх эрчимжилтийн векторын урсгал нь энэ гадаргууг огтолж буй талбайн шугамын тоотой пропорциональ байна. Тиймээс, ерөнхий тохиолдолд талбайн хүч чадлын векторын тухайн талбайгаар дамжин өнгөрөх урсгалыг энэ хэсэгт нэвтэрч буй талбайн шугамын тоотой тэнцэх утга гэж нүдээр тайлбарлаж болно.

.

(1.5)

Хэвийн чиглэлийг сонгох нь нөхцөлт бөгөөд өөр чиглэлд чиглүүлэх боломжтой гэдгийг анхаарна уу. Үүний үр дүнд урсгал нь алгебрийн хэмжигдэхүүн юм: урсгалын тэмдэг нь зөвхөн талбайн тохиргооноос гадна хэвийн вектор ба эрчмийн векторын харьцангуй чиглэлээс хамаарна. Хэрэв эдгээр хоёр вектор хурц өнцөг үүсгэвэл урсгал эерэг, мохоо бол сөрөг байна. Битүү гадаргуугийн хувьд энэ гадаргууг бүрхсэн талбайн гаднах нормыг авах, өөрөөр хэлбэл гаднах хэвийнийг сонгох нь заншилтай байдаг.

Хэрэв талбай нь нэгэн төрлийн бус, гадаргуу нь дур зоргоороо байвал урсгалыг дараах байдлаар тодорхойлно. Гадаргууг бүхэлд нь талбайтай жижиг элементүүдэд хувааж, эдгээр элемент тус бүрээр дамжих хүчдэлийн урсгалыг тооцоолж, дараа нь бүх элементүүдээр дамжих урсгалыг нэгтгэн гаргана.

Тиймээс талбайн хүч нь орон зайн нэг цэг дэх цахилгаан талбайг тодорхойлдог. Эрчим хүчний урсгал нь тухайн цэг дэх талбайн хүч чадлын утгаас хамаарахгүй, харин тухайн талбайн гадаргуу дээрх талбайн тархалтаас хамаарна.

Цахилгаан талбайн шугам нь зөвхөн эерэг цэнэгээр эхэлж, сөрөг цэнэгээр төгсдөг. Тэд сансар огторгуйд эхэлж эсвэл төгсөж чадахгүй. Тиймээс хэрэв тодорхой хаалттай эзэлхүүн дотор цахилгаан цэнэг байхгүй бол энэ эзлэхүүнд орж, гарах шугамын нийт тоо тэг байх ёстой. Хэрэв эзлэхүүн рүү орохоос илүү олон мөр гарч байвал эзлэхүүн дотор эерэг цэнэг байна; Хэрэв гарч ирж буй шугамаас илүү олон шугам байгаа бол дотор нь сөрөг цэнэг байх ёстой. Эзлэхүүн доторх нийт цэнэг тэгтэй тэнцүү эсвэл цахилгаан цэнэггүй үед хээрийн шугамууд түүгээр нэвтэрч, нийт урсгал нь тэг болно.

Эдгээр энгийн санаанууд нь цахилгаан цэнэгийг эзлэхүүн дотор хэрхэн хуваарилахаас хамаардаггүй. Энэ нь эзлэхүүний төв хэсэгт эсвэл эзлэхүүнийг хязгаарлаж буй гадаргуугийн ойролцоо байрлаж болно. Эзлэхүүн нь эзлэхүүн дотор ямар нэгэн байдлаар тархсан хэд хэдэн эерэг ба сөрөг цэнэгийг агуулж болно. Зөвхөн нийт цэнэг нь ирж буй эсвэл гарах хүчдэлийн шугамын нийт тоог тодорхойлно.

(1.4) ба (1.5)-аас харахад цэнэгийг хүрээлсэн дурын хаалттай гадаргуугаар дамжин өнгөрөх цахилгаан орны хүчний векторын урсгалыг харж болно. q,тэнцүү . Хэрэв гадаргуу дотор байгаа бол nцэнэгүүд, тэгвэл талбайн суперпозиция зарчмын дагуу нийт урсгал нь бүх цэнэгийн талбайн хүч чадлын урсгалын нийлбэр байх ба -тэй тэнцүү байх бөгөөд энэ тохиолдолд бид хаагдсан бүх цэнэгийн алгебрийн нийлбэрийг хэлнэ. гадаргуу.

Гауссын теорем. ГауссДурын хаалттай гадаргуугаар дамжин өнгөрөх цахилгаан орны хүч чадлын векторын урсгал нь энэ эзэлхүүний дотор байрлах нийт цэнэгтэй холбоотой байх ёстой гэсэн энгийн баримтыг анх олж мэдсэн.

Гаусс Карл Фридрих (1777-1855)

Германы агуу математикч, физикч, одон орон судлаач, физикийн нэгжийн үнэмлэхүй системийг бүтээгч. Тэрээр цахилгаан статик потенциалын онолыг боловсруулж, цахилгаан статикийн хамгийн чухал теоремыг (Гаусын теорем) нотолсон. Нарийн төвөгтэй оптик системд дүрс бүтээх онолыг бий болгосон. Тэрээр Евклидийн бус геометрийн оршин тогтнох боломжтой гэсэн санааг анх гаргасан хүмүүсийн нэг байв. Нэмж дурдахад Гаусс математикийн бараг бүх салбарт онцгой хувь нэмэр оруулсан.

Сүүлийн хамаарал нь цахилгаан талбайн Гауссын теорем юм: Дурын хаалттай гадаргуугаар дамжин өнгөрөх эрчим хүчний векторын урсгал нь энэ гадаргуугийн дотор байрлах цэнэгийн алгебрийн нийлбэртэй пропорциональ байна.Пропорциональ байдлын коэффициент нь нэгжийн системийн сонголтоос хамаарна.

Гауссын теоремыг Кулоны хууль ба суперпозиция зарчмын үр дүнд олж авсан гэдгийг тэмдэглэх нь зүйтэй. Хэрэв цахилгаан талбайн хүч нь зайны квадраттай урвуу пропорциональ өөрчлөгдөөгүй бол теорем хүчингүй болно. Иймээс Гауссын теорем нь урвуу квадратын хууль ба суперпозицийн зарчим хатуу хангагдсан аливаа талбарт, жишээлбэл, таталцлын талбарт хамаарна. Таталцлын талбайн хувьд талбарыг үүсгэх цэнэгийн үүргийг биеийн масс гүйцэтгэдэг. Битүү гадаргуугаар дамжин өнгөрөх таталцлын талбайн шугамын урсгал нь тухайн гадаргууд агуулагдах нийт масстай пропорциональ байна.

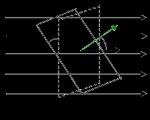
Цэнэглэгдсэн онгоцны талбайн хүч.Хязгааргүй цэнэгтэй хавтгайн цахилгаан орны хүчийг тодорхойлохын тулд Гауссын теоремыг ашиглая. Хэрэв хавтгай нь хязгааргүй бөгөөд жигд цэнэглэгдсэн бол, өөрөөр хэлбэл гадаргуугийн цэнэгийн нягт нь аль ч байршилд ижил байвал аль ч цэг дээрх цахилгаан орны хүчний шугамууд энэ хавтгайд перпендикуляр байна. Үүнийг харуулахын тулд бид хүчдэлийн векторын суперпозиция зарчмыг ашиглана. Хавтгай дээрх цэгийн цэг гэж үзэж болох хоёр энгийн хэсгийг сонгоцгооё А, үүнд талбайн хүчийг тодорхойлох шаардлагатай. Зураг дээрээс харж болно. 1.18, үүссэн хурцадмал байдлын вектор нь хавтгайд перпендикуляр чиглэнэ. Онгоцыг аливаа ажиглалтын цэгийн хувьд ийм хэсгүүдийн хязгааргүй тооны хос болгон хувааж болох тул цэнэглэгдсэн хавтгайн талбайн шугамууд нь хавтгайд перпендикуляр, талбай нь жигд байх нь тодорхой байна (Зураг 1.19). Хэрэв тийм биш байсан бол онгоц өөрөө хөдөлж байх үед орон зайн цэг бүрийн талбар өөрчлөгдөх боловч энэ нь цэнэглэгдсэн системийн тэгш хэмтэй зөрчилддөг (онгоц нь хязгааргүй юм). Эерэг цэнэгтэй онгоцны хувьд хүчний шугамууд хавтгайгаас эхэлж хязгааргүйд төгсдөг бол сөрөг цэнэгтэй онгоцны хувьд хүчний шугамууд хязгааргүйд эхэлж, хавтгайд ордог.

Цагаан будаа. 1.18	Цагаан будаа. 1.19

Хязгааргүй эерэг цэнэгтэй хавтгайн цахилгаан орны хүчийг тодорхойлохын тулд тэнхлэг нь цэнэглэгдсэн хавтгайд перпендикуляр, сууриуд нь параллель, суурийн аль нэг нь талбайн цэгээр дамждаг цилиндрийг огторгуйд оюун ухаанаараа сонгодог. бидний сонирхлыг татдаг (Зураг 1.19). Цилиндр нь цэнэглэгдсэн хавтгайгаас талбайн хэсгийг огтолж, онгоцны янз бүрийн талд байрлах цилиндрийн суурь нь ижил талбайтай байна.

Гауссын теоремын дагуу цилиндрийн гадаргуугаар дамжин өнгөрөх цахилгаан орны хүч чадлын векторын урсгал нь цилиндрийн доторх цахилгаан цэнэгтэй дараах илэрхийлэлээр холбогдоно.

.

Сунгах шугамууд нь зөвхөн цилиндрийн суурьтай огтлолцдог тул цилиндрийн хажуугийн гадаргуугаар урсах урсгал нь тэг байна. Тиймээс цилиндр гадаргуугаар дамжих суналтын векторын урсгал нь зөвхөн цилиндрийн сууриудыг дамжих урсгалуудаас бүрдэх тул

Эрчим хүчний векторын урсгалын сүүлийн хоёр илэрхийлэлийг харьцуулж үзвэл бид олж авна

Эсрэг цэнэгтэй ялтсуудын хоорондох цахилгаан талбайн хүч.Хэрэв ялтсуудын хэмжээс нь тэдгээрийн хоорондох зайнаас ихээхэн давсан бол хавтан тус бүрийн цахилгаан талбарыг хязгааргүй жигд цэнэглэгдсэн хавтгайн талбарт ойрхон гэж үзэж болно. Хавтануудын хоорондох эсрэг цэнэгтэй ялтсуудын цахилгаан талбайн хүч чадлын шугамууд нэг чиглэлд чиглэсэн байдаг (Зураг 1.20) хавтан хоорондын талбайн хүч нь тэнцүү байна.

.

Гаднах орон зайд эсрэг цэнэгтэй ялтсуудын цахилгаан орны хүчний шугамууд нь эсрэг чиглэлтэй байдаг тул эдгээр хавтангийн гадна талд үүссэн цахилгаан орны хүч нь тэг байна. Хүчтэй байдлын хувьд олж авсан илэрхийлэл нь том цэнэгтэй ялтсуудын хувьд эрчимийг тэдгээрийн ирмэгээс хол байрлах цэг дээр тодорхойлоход хүчинтэй байна.

Хязгааргүй урттай жигд цэнэглэгдсэн нимгэн утасны цахилгаан талбайн хүч.Хязгааргүй урттай жигд цэнэглэгдсэн нимгэн утасны цахилгаан орны хүч нь утасны тэнхлэг хүртэлх зайнаас хамаарах хамаарлыг Гауссын теоремоор олъё. Хязгаарлагдмал урттай утасны хэсгийг сонгоцгооё. Хэрэв утас дээрх шугаман цэнэгийн нягт нь , дараа нь сонгосон талбайн цэнэг тэнцүү байна.

$q$ цэгийн цэнэгийн талбарыг авч үзээд эрчмийн векторын ($\overrightarrow(E)$) $S$ хаалттай гадаргуугаар дамжин өнгөрөх урсгалыг олъё. Цэнэг нь гадаргуу дотор байрладаг гэж бид таамаглах болно. Аливаа гадаргуугаар дамжих суналтын векторын урсгал нь суналтын векторын гарах шугамын тоо (хэрэв $q>0$ байвал цэнэгээс эхэлнэ) эсвэл $\overrightarrow(E)$ орж байгаа шугамын тоотой тэнцүү байна. , хэрэв $q \[Ф_E=\frac( q)((\varepsilon )_0)\ \left(1\баруун),\]

энд урсгалын тэмдэг нь цэнэгийн тэмдэгтэй давхцаж байна.

Остроградский-Гаусын теорем интеграл хэлбэрээр

S гадаргуу дотор N цэгийн цэнэг, утгууд $q_1,q_2,\dots q_N.$ байна гэж үзье. Суперпозиция зарчмаас бид бүх N цэнэгийн талбайн хүчийг нийлбэрээр олж болохыг мэдэж байна. цэнэг тус бүрээр үүсгэгдсэн талбайн хүч, Дараа нь:

Тиймээс цэгийн цэнэгийн системийн урсгалын хувьд бид дараахь зүйлийг бичиж болно.

Томъёо (1) ашиглан бид дараахь зүйлийг олж авна.

\[Ф_E=\oint\limits_S(\overrightarrow(E)d\overrightarrow(S))=\frac(1)((\varepsilon )_0)\sum\limits^N_(i=1)(q_i\ )\ зүүн(4\баруун).\]

Тэгшитгэл (4) нь битүү гадаргуугаар дамжин өнгөрөх цахилгаан орны хүч чадлын векторын урсгал нь энэ гадаргуугийн доторх цэнэгийн алгебрийн нийлбэрийг цахилгаан тогтмолд хуваасантай тэнцүү байна. Энэ бол интеграл хэлбэрийн Остроградский-Гаусын теорем юм. Энэ теорем нь Кулоны хуулийн үр дагавар юм. Энэ теоремын ач холбогдол нь янз бүрийн цэнэгийн хуваарилалтын цахилгаан талбарыг энгийнээр тооцоолох боломжийг олгодог.

Остроградский-Гаусын теоремын үр дүнд цэнэгүүд нь энэ гадаргуугаас гадуур байх тохиолдолд эрчим хүчний векторын ($Ф_E$) хаалттай гадаргуугаар дамжин өнгөрөх урсгал тэгтэй тэнцүү байна гэж хэлэх ёстой.

Цэнэгүүдийн салангид байдлыг үл тоомсорлож болох тохиолдолд цэнэгийг эзлэхүүн даяар тараасан тохиолдолд эзэлхүүний цэнэгийн нягт ($\rho $) гэсэн ойлголтыг ашиглана. Энэ нь дараах байдлаар тодорхойлогддог.

\[\rho =\frac(dq)(dV)\зүүн(5\баруун),\]

$dq$ нь цэгтэй төстэй цэнэг, $dV$ нь жижиг хэмжээ юм. ($dV$-ийн талаар дараах тайлбарыг хийх ёстой. Энэ эзэлхүүн нь түүний доторх цэнэгийн нягтыг тогтмол гэж үзэж болохуйц бага боловч цэнэгийн салангид байдал гарч эхлэхгүй байх хангалттай том хэмжээтэй). Хөндий дэх нийт цэнэгийг дараах байдлаар олж болно.

\[\нийлбэр\хязгаар\N_(i=1)(q_i\ )=\int\limits_V(\rho dV)\зүүн(6\баруун).\]

Энэ тохиолдолд бид (4) томъёог дараах хэлбэрээр бичнэ.

\[\oint\limits_S(\overrightarrow(E)d\overrightarrow(S))=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV)\left(7\баруун).\ ]

Дифференциал хэлбэрээр Остроградский-Гаусын теорем

Вектор шинж чанартай аливаа талбарт Остроградский-Гаусын томъёог ашиглан хаалттай гадаргуу дээрх интегралаас эзэлхүүн дэх интеграл руу шилжих ажлыг гүйцэтгэдэг.

\[\oint\limits_S(\overrightarrow(a)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(a)dV\ \left(8\right),\]

Энд $\overrightarrow(a)-$field вектор (манай тохиолдолд энэ нь $\overrightarrow(E)$), $div\overrightarrow(a)=\overrightarrow(\nabla )\overrightarrow(a)=\frac(\ хэсэгчилсэн a_x)(\partial x)+\frac(\partial a_y)(\partial y)+\frac(\partial a_z)(\partial z)$ -- $\overrightarrow(a)$ векторын ялгаа координаттай ( x,y,z) цэг нь вектор талбарыг скаляртай харьцуулдаг. $\overrightarrow(\nabla )=\frac(\partial )(\partial x)\overrightarrow(i)+\frac(\partial )(\partial y)\overrightarrow(j)+\frac(\partial )(\ хэсэгчилсэн z)\overrightarrow(k)$ - ажиглагдах боломжтой оператор. (Манай тохиолдолд $div\overrightarrow(E)=\overrightarrow(\nabla )\overrightarrow(E)=\frac(\partial E_x)(\partial x)+\frac(\partial E_y)(\partial байх болно) y) +\frac(\partial E_z)(\partial z)$) -- хурцадмал векторын зөрүү. Дээрхийг дагаж бид (6) томъёог дараах байдлаар дахин бичнэ.

\[\oint\limits_S(\overrightarrow(E)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(E)dV=\frac(1)((\varepsilon )_0)\int\limits_V( \rho dV)\зүүн(9\баруун).\]

(9) тэгшитгэлийн тэгшитгэл нь дурын эзэлхүүний хувьд хангагдсан бөгөөд энэ нь зөвхөн интегралд байгаа функцүүд орон зайн гүйдэл бүрт тэнцүү байх тохиолдолд л хэрэгжих боломжтой, өөрөөр хэлбэл бид дараахь зүйлийг бичиж болно.

Илэрхийлэл (10) нь дифференциал хэлбэрийн Остроградский-Гаусын теорем юм. Үүний тайлбар нь дараах байдалтай байна: цэнэг нь цахилгаан талбайн эх үүсвэр юм. Хэрэв $div\overrightarrow(E)>0$ бол талбайн эдгээр цэгүүдэд (төлбөр эерэг) бидэнд талбарын эх үүсвэрүүд байна, хэрэв $div\overrightarrow(E) бол

Даалгавар: Цэнэг нь эзлэхүүнд жигд тархсан бөгөөд энэ эзлэхүүнд b талтай куб гадаргууг сонгосон. Энэ нь бөмбөрцөгт бичигдсэн байдаг. Эдгээр гадаргуугаар дамжих хүчдэлийн векторын урсгалын харьцааг ол.

Гауссын теоремоор бол эзэлхүүн дэх цэнэгийн жигд тархалттай битүү гадаргуугаар $\overrightarrow(E)$ эрчмийн векторын урсгал ($Ф_E$) дараахтай тэнцүү байна.

\[Ф_E=\frac(1)((\varepsilon )_0)Q=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV=\frac(\rho )((\varepsilon ) _0)\int\limits_V(dV)=\frac(\rho V)((\varepsilon )_0))\left(1.1\баруун).\]

Тиймээс, хэрэв бөмбөгийг энэ шоо тойруулан дүрсэлсэн бол бид шоо болон бөмбөгний эзлэхүүнийг тодорхойлох хэрэгтэй. Эхлээд кубын эзэлхүүнийг ($V_k$) b тал нь тэнцүү бол:

Бөмбөгний эзэлхүүнийг ($V_(sh)$) томъёогоор олъё.

Энд $D$ нь бөмбөгний диаметр ба (бөмбөг нь шоо тойрон хүрээлэгдсэн тул) шоогийн гол диагональ. Тиймээс бид шоо дөрвөлжингийн диагональыг тал талаас нь илэрхийлэх хэрэгтэй. Хэрэв та Пифагорын теоремыг ашиглавал үүнийг хийхэд хялбар байдаг. Шоогийн диагональыг тооцоолохын тулд, жишээлбэл, (1.5) бид эхлээд квадратын диагональ (шоогийн доод суурь) (1.6) олох хэрэгтэй. Диагональ (1.6) урт нь дараахтай тэнцүү байна.

Энэ тохиолдолд диагональ (1.5) урт нь дараахтай тэнцүү байна.

\[(D=D)_(15)=\sqrt(b^2+((\sqrt(b^2+b^2\ \ \ )))^2)=b\sqrt(3)\ \зүүн (1.5\баруун).\]

Бөмбөлгийн олдсон диаметрийг (1.3) орлуулснаар бид дараахь зүйлийг олж авна.

Одоо бид шоо гадаргуугаар дамжин хурцадмал векторын урсгалыг олж болно, энэ нь тэнцүү байна.

\[Ф_(Эк)=\frac(\rho V_k)((\varepsilon )_0)=\frac(\rho b^3)((\varepsilon )_0)\left(1.7\баруун),\]

бөмбөгний гадаргуугаар:

\[Ф_(Esh)=\frac(\rho V_(sh))((\varepsilon )_0)=\frac(\rho )((\varepsilon )_0)\frac(\sqrt(3))(2) \pi b^3\ \зүүн(1.8\баруун).\]

$\frac(Ф_(Esh))(Ф_(Ek))$ харьцааг олъё:

\[\frac(Ф_(Esh))(Ф_(Ek))=\frac(\frac(с)(\varepsilon_0)\frac(\sqrt(3))(2) \pi b^3)(\frac (сb^3)(\varepsilon_0))=\frac(\pi)(2)\sqrt(3)\\ойролцоогоор 2.7\зүүн(1.9\баруун).\]

Хариулт: Бөмбөгний гадаргуугаар дамжин өнгөрөх урсгал 2.7 дахин их байна.

Даалгавар: Дамжуулагчийн цэнэг түүний гадаргуу дээр байрлаж байгааг батал.

Үүнийг батлахын тулд бид Гауссын теоремыг ашигладаг. Дамжуулагчийн гадаргуугийн ойролцоо байгаа дамжуулагч дахь дурын хэлбэрийн битүү гадаргууг сонгоцгооё (Зураг 2).

Дамжуулагчийн дотор цэнэгүүд байгаа гэж үзье, бид S гадаргуугийн аль ч цэгийн талбайн дивергенцийн Остроградский-Гаусын теоремыг бичнэ.

Энд $\rho нь дотоод цэнэгийн нягт \ $. Гэхдээ дамжуулагч дотор талбар байхгүй, өөрөөр хэлбэл $\overrightarrow(E)=0$, тиймээс $div\overrightarrow(E)=0\to \rho =0$. Дифференциал хэлбэрээр Остроградский-Гаусын теорем нь орон нутгийн шинж чанартай, өөрөөр хэлбэл энэ нь талбайн цэгийн хувьд бичигдсэн байдаг, бид цэгийг тусгай аргаар сонгоогүй тул дамжуулагчийн доторх талбайн аль ч цэг дээр цэнэгийн нягт нь тэг байна.

Кулоны хуультай хослуулан суперпозиция хийх зарчим нь дурын цэнэгийн системийн цахилгаан талбайг тооцоолох түлхүүрийг өгдөг боловч (4.2) томъёог ашиглан талбаруудын шууд нийлбэр нь ихэвчлэн нарийн төвөгтэй тооцоолол шаарддаг. Гэсэн хэдий ч цэнэгийн системийн нэг буюу өөр тэгш хэм байгаа тохиолдолд цахилгаан талбайн урсгалын тухай ойлголтыг нэвтрүүлж, Гауссын теоремыг ашиглавал тооцооллыг ихээхэн хялбаршуулна.

Цахилгаан орны урсгалын тухай ойлголтыг гидродинамикаас электродинамик руу нэвтрүүлсэн. Гидродинамикийн хувьд хоолойгоор дамжин өнгөрөх шингэний урсгал, өөрөөр хэлбэл, нэгж хугацаанд хоолойн хөндлөн огтлолоор дамжин өнгөрөх N шингэний эзэлхүүн нь v ⋅ S-тэй тэнцүү бөгөөд v нь шингэний хурд, S нь хоолойн хөндлөн огтлолын талбай. Хэрэв шингэний хурд хөндлөн огтлолын дагуу харилцан адилгүй байвал N = ∫ S v → ⋅ d S → салшгүй томъёог ашиглах хэрэгтэй. Үнэн хэрэгтээ, хурдны векторт перпендикуляр хурдны талбарт d S жижиг талбайг тодруулцгаая (Зураг ).

Цагаан будаа. 1.4: Шингэний урсгал

Энэ талбайг d t хугацаанд урсах шингэний эзэлхүүн нь v d S d t-тэй тэнцүү байна. Хэрэв платформ урсгал руу хазайсан бол харгалзах эзэлхүүн нь v d S cos θ d t байх болно, энд θ нь хурдны вектор v → ба хэвийн n → платформ d S хүртэлх өнцөг юм. Нэгж хугацаанд d S талбайгаар урсах шингэний эзэлхүүнийг энэ утгыг d t-д хуваах замаар олно. Энэ нь тэнцүү байна v d S cos θ d t , i.e. скаляр үржвэр v → ⋅ d S → хурдны вектор v → талбайн элементийн вектороор d S → = n → d S . d S талбайн n → нормаль нэгж векторыг хоёр шууд эсрэг чиглэлд зурж болно. тэдгээрийн нэгийг болзолт эерэг гэж хүлээн зөвшөөрдөг. Энэ чиглэлд хэвийн n → зурсан байна. Нормаль n → гарч ирэх талбайн талыг гадаад, хэвийн n → орж ирэх талыг дотоод гэж нэрлэдэг. Талбайн элементийн вектор d S → нь гаднах хэвийн n → гадаргуу руу чиглэсэн бөгөөд хэмжээ нь d S = ∣ d S → ∣ элементийн талбайтай тэнцүү байна. Хязгаарлагдмал хэмжээстэй S талбайгаар урсах шингэний эзэлхүүнийг тооцоолохдоо түүнийг хязгааргүй жижиг талбай болгон хөгжүүлэх шаардлагатай d S , дараа нь бүхэл бүтэн S гадаргуу дээрх ∫ S v → ⋅ d S → интегралыг тооцоолно.

∫ S v → ⋅ d S → гэх мэт илэрхийллүүд физик, математикийн олон салбаруудад байдаг. Тэдгээрийг v → векторын шинж чанараас үл хамааран S гадаргуугаар дамжин өнгөрөх v → векторын урсгал гэж нэрлэдэг. Электродинамикийн хувьд интеграл

N = ∫ S E → ⋅ d S →

(5.1)

Энэ ойлголттой ямар ч бодит урсгал холбоогүй ч дурын S гадаргуугаар дамжин өнгөрөх цахилгаан орны хүчний E → урсгал гэж нэрлэдэг.

E → векторыг геометрийн нийлбэрээр илэрхийлнэ гэж үзье

E → = ∑ j E → j .

Энэ тэгшитгэлийг скаляраар d S →-ээр үржүүлээд интеграл болгосноор бид олж авна

N = ∑ j N j .

Энд N j нь ижил гадаргуугаар дамжин өнгөрөх E → j векторын урсгал юм. Тиймээс, цахилгаан талбайн хүч чадлын суперпозиция зарчмаас харахад ижил гадаргуугаар дамжин өнгөрөх урсгалууд алгебрийн дагуу нэмэгддэг.

Гауссын теорем нь дурын битүү гадаргуугаар дамжин өнгөрөх E → векторын урсгал нь энэ гадаргуугийн дотор байрлах бүх бөөмийн Q цэнэгийг 4 π-ээр үржүүлсэнтэй тэнцүү байна.

Бид теоремийн баталгааг гурван үе шаттайгаар явуулна.

1. Нэг цэгийн цэнэгийн q цахилгаан орны урсгалыг тооцоолж эхэлцгээе (Зураг ). Хамгийн энгийн тохиолдолд интегралын гадаргуу S нь бөмбөрцөг бөгөөд цэнэг нь түүний төвд байх үед Гауссын теоремын хүчинтэй байдал бараг тодорхой болно. Бөмбөрцгийн гадаргуу дээр цахилгаан орны хүч нь

E → = q r → ∕ r 3

тогтмол хэмжигдэхүүн, хаа сайгүй гадаргуу дээр хэвийн чиглэгддэг тул цахилгаан талбайн урсгал нь E = q ∕ r 2 бүтээгдэхүүн ба бөмбөрцгийн талбай S = 4 π r 2 хэмжээтэй тэнцүү байна. Тиймээс N = 4 π q байна. Энэ үр дүн нь цэнэгийг тойрсон гадаргуугийн хэлбэрээс үл хамаарна. Үүнийг батлахын тулд бид гадаад хэвийн n → түүн дээр тохируулсан хангалттай жижиг хэмжээтэй гадаргуугийн дурын талбайг сонгоно. Зураг дээр. нэг ийм сегментийг хэт том хэмжээтэй (тодорхой болгох үүднээс) харуулсан байна.

Энэ талбараар дамжин өнгөрөх E → векторын урсгал нь d N = E → ⋅ d S → = E cos θ d S -тэй тэнцүү байна.

Энд θ нь E → чиглэл ба гадаад нормаль n → d S талбай хүртэлх өнцөг юм. Үнэмлэхүй утгаараа E = q ∕ r 2 , d S cos θ ∕ ​​r 2 нь хатуу өнцгийн d Ω = d S ∣ cos θ ∣ ∕ r 2 элемент байх тул доороос d S талбай харагдах болно. цэнэгийн байрлаж буй цэг,

D N = ± q d Ω .

Энд нэмэх ба хасах тэмдэг нь cos θ тэмдэгтэй тохирч байна, тухайлбал: хэрэв вектор E → гадаад хэвийн n → чиглэлтэй хурц өнцөг үүсгэвэл хасах тэмдэг, өөрөөр хэлбэл нэмэх тэмдгийг авна.

2. Одоо зарим сонгосон V эзлэхүүнийг хамарсан хязгаарлагдмал S гадаргууг авч үзье. Энэ эзэлхүүний хувьд S гадаргуугийн аль ч элементийн хэвийн болон эсрэг талын хоёр чиглэлийн алийг нь гаднах гэж үзэхийг үргэлж тодорхойлох боломжтой. Гаднах хэвийн хэмжээ нь V хэмжээнээс гадагш чиглэсэн байна. Сегментүүдийг нэгтгэн дүгнэхэд бид N = q Ω гэсэн тэмдэгтэй байна, энд Ω нь q цэнэгийн байрлаж буй цэгээс S гадаргуу харагдах хатуу өнцөг юм. Хэрэв S гадаргуу хаалттай байвал q цэнэг S дотор байгаа тохиолдолд Ω = 4 π болно. Үгүй бол Ω = 0. Сүүлийн мэдэгдлийг тодруулахын тулд бид Зураг дээр дахин хандаж болно. .

Хаалттай гадаргуугийн сегментүүдээр ижил тэгш өнцөгт тулгуурласан, гэхдээ эсрэг чиглэлд чиглэсэн урсгалууд бие биенээ үгүйсгэдэг нь тодорхой байна. Хэрэв цэнэг нь битүү гадаргуугаас гадуур байвал гадагш чиглэсэн сегментийн хувьд дотогшоо чиглэсэн харгалзах сегмент байх нь ойлгомжтой.

3. Эцэст нь суперпозиция зарчмыг ашиглан Гауссын теоремын эцсийн томъёололд хүрнэ (). Үнэн хэрэгтээ цэнэгийн системийн талбар нь тус тусад нь цэнэг тус бүрийн талбайн нийлбэртэй тэнцүү боловч зөвхөн хаалттай гадаргуу дотор байрлах цэнэгүүд теоремын баруун талд тэгээс өөр хувь нэмэр оруулдаг (). Энэ нь нотлох баримтыг гүйцээнэ.

Макроскопийн биетүүдэд цэнэгийн тээвэрлэгчдийн тоо маш их байдаг тул цэнэгийн нягтын тухай ойлголтыг нэвтрүүлж, тасралтгүй тархалт хэлбэрээр бөөмсийн салангид чуулгад дүрслэхэд тохиромжтой. Тодорхойлолтоор цэнэгийн нягтрал ρ нь Δ V хэмжээ нь физикийн хувьд хязгааргүй бага утгатай байх үед хязгаар дахь Δ Q ∕ Δ V харьцаа юм.

Энд баруун талын интеграци нь S гадаргуугаар хаагдсан V эзлэхүүн дээр явагдана.

Гауссын теорем нь E → векторын гурван бүрэлдэхүүн хэсгийн нэг скаляр тэгшитгэлийг өгдөг тул цахилгаан орныг тооцоолоход энэ теорем дангаараа хангалтгүй юм. Асуудлыг нэг скаляр тэгшитгэл болгон бууруулахын тулд цэнэгийн нягтын тархалтын мэдэгдэж буй тэгш хэм шаардлагатай. Гауссын теорем нь () дахь интеграцийн гадаргууг сонгох боломжтой тохиолдолд талбайг олох боломжийг олгодог бөгөөд ингэснээр цахилгаан орны хүч нь бүх гадаргуу дээр тогтмол байх болно. Хамгийн сургамжтай жишээнүүдийг харцгаая.

▸ Асуудал 5.1

Эзлэхүүнээр жигд цэнэглэгдсэн бөмбөрцгийн талбайг олгадаргуу.

Шийдэл: Цэгэн цэнэгийн цахилгаан орон E → = q r → ∕ r 3 хандлагатай байна хязгааргүй үед r → 0 . Энэ баримт нь санааны үл нийцэх байдлыг харуулж байна энгийн бөөмсийг цэгийн цэнэгээр . Хэрэв төлбөр q хязгаарлагдмал радиустай бөмбөрцгийн эзэлхүүн дээр жигд тархсана, тэгвэл цахилгаан орон нь онцгой шинж чанартай байдаггүй.

Асуудлын тэгш хэмээс харахад цахилгаан орон нь тодорхой байна E → хаа сайгүй радиаль чиглэлтэй, түүний хурцадмал байдал E = E(r) нь зөвхөн r зайнаас хамаарна бөмбөгний төв рүү. Дараа нь цахилгаан орон нь радиустай бөмбөрцөгөөр урсдаг r нь ердөө л 4 π r 2 E-тэй тэнцүү (Зураг ).

Нөгөө талаас нэг бөмбөрцөг доторх цэнэг нь нийт цэнэгтэй тэнцүү байнабөмбөг Q хэрэв r ≥ a. Бөмбөгний цэнэгийг q 4 π-ээр үржүүлсэн 4 π r 2 E-ийг тэнцүүлж үзвэл: E (r) = q ∕ r 2 болно.

Тиймээс гадаад орон зайд цэнэглэгдсэн бөмбөг үүсдэг бүх цэнэг нь түүний төвд төвлөрсөн мэт талбар. Энэ үр дүн нь ямар ч бөмбөрцөг тэгш хэмийн хувьд хүчинтэй цэнэгийн хуваарилалт.

Бөмбөг доторх талбай нь E (r) = Q ∕ r 2, энд Q нь r радиустай хүхрийн доторх цэнэг юм. Хэрэв цэнэг бөмбөгний эзлэхүүнд жигд тархсан бол Q = q (r ∕ a) 3 . Энэ тохиолдолд

E (r) = q r ∕ a 3 = (4 π ∕ 3) ρ r ,

Энд ρ = q ∕ (4 π a 3 ∕ 3) — цэнэгийн нягт. Бөмбөлөг дотор талбар хамгийн дээд хэмжээнээсээ шугаман буурдаг Бөмбөгний гадаргуу дээрх утгууд нь түүний төв хэсэгт тэг болно (Зураг 1). ).

E(r) функц Үүний зэрэгцээ энэ нь хаа сайгүй хязгаарлагдмал бөгөөд үргэлжилдэг.

Хэрэв цэнэгийг бөмбөгний гадаргуу дээр тараасан бол Q = 0, тиймээс бас E = 0. Энэ үр дүн нь бөмбөрцөг дотор байгаа тохиолдолд бас хүчинтэй цэнэгийн хөндий байхгүй, гаднах цэнэгүүд нь бөмбөрцөг хэлбэрээр тархдагтэгш хэмтэй. ▸ Асуудал 5.2

Нэг жигд цэнэглэгдсэн хязгааргүй утасны талбарыг олох; утасны радиус a, нэгж уртын цэнэг ϰ.

▸ Асуудал 5.3

Хязгааргүй шулуун утас ба хязгааргүй уртын талбарыг ол жигд цэнэглэгдсэн цилиндр.

▸ Асуудал 5.4

Хязгааргүй цэнэглэгдсэн хавтгай ба жигд талбайг ол цэнэглэгдсэн хязгааргүй хавтгай давхарга.

Шийдэл: Асуудлын тэгш хэмийн улмаас талбарыг чиглүүлдэг давхаргад хэвийн байх ба зөвхөн зайнаас хамаарна x-аас хавтангийн тэгш хэмийн хавтгай. Талбарыг ашиглан тооцоолох Гауссын теорем, интегралын гадаргууг сонгоход тохиромжтой S in Зурагт үзүүлсэн шиг параллелипипед хэлбэрээр. .

Сүүлчийн үр дүнг хязгаарт хүрэх замаар олж авна a → 0 нэгэн зэрэг цэнэгийн нягтыг нэмэгдүүлэхρ утга нь σ = ρ a байхаар ρ өөрчлөгдөөгүй хэвээр байв. Онгоцны эсрэг талд цахилгаан орны хүч чадал ижил хэмжээтэй боловч эсрэг чиглэлд. Тиймээс дайран өнгөрөхдөө цэнэглэгдсэн онгоц, талбар нь хэмжээгээр огцом өөрчлөгддөг 4 π σ. Хэрэв хавтанг хязгааргүй гэж үзэж болно гэдгийг анхаарна уу хэмжээтэй харьцуулахад зай нь өчүүхэн юм. Асаалттай хавтангийн хэмжээстэй харьцуулахад маш том зай, энэ цэгийн цэнэг шиг ажиллах ба түүний талбай буцаж багасдаг зайны квадраттай пропорциональ байна.

Хүчний шугам (хүчдэлийн шугам) ашиглан цахилгаан статик талбайг тодорхой дүрсэлж болно. Цахилгаан шугамЦэг бүр дэх шүргэгч нь E суналтын вектортой давхцдаг муруй гэж нэрлэдэг.

Хүчний шугам нь ердийн ойлголт бөгөөд үнэндээ байдаггүй. Нэг сөрөг ба нэг эерэг цэнэгийн талбайн шугамыг Зураг дээр үзүүлэв. 5 нь эерэг цэнэгээс ирж байгаа эсвэл сөрөг цэнэг рүү явж буй радиаль шулуун шугамууд юм.

Талбайн нийт эзэлхүүн дэх талбайн шугамын нягт ба чиглэл өөрчлөгдөөгүй хэвээр байвал ийм электростатик талбарыг нэгэн төрлийн гэж үзнэ (шугамын тоо нь талбайн хүч E-тэй тэнцүү байх ёстой).

Тэдэнд перпендикуляр ">dS" гэж тэмдэглэгдсэн талбайн шугамын тоог тодорхойлно электростатик талбайн хүч чадлын векторын урсгал:

томъёо" src="http://hi-edu.ru/e-books/xbook785/files/17-1.gif" border="0" align="absmiddle" alt="- E векторын хэвийн n-ийн чиглэлд dS сайт руу чиглэсэн проекц (Зураг 6).

Үүний дагуу дурын хаалттай S гадаргуугаар дамжин өнгөрөх E векторын урсгал

mark">S нь зөвхөн хэмжээ төдийгүй урсгалын тэмдэг нь өөрчлөгдөж болно:

1) томъёогоор" src="http://hi-edu.ru/e-books/xbook785/files/17-4.gif" border="0" align="absmiddle" alt="

3)"> сонгохдоо төв хэсэгт q цэгийн цэнэг байгаа бөмбөрцөг S гадаргуугаар Е векторын урсгалыг олъё.

Энэ тохиолдолд ">E ба n" тэмдэг нь бөмбөрцөг гадаргуугийн бүх цэгүүдэд давхцдаг.

Цэгэн цэнэгийн талбайн хүчийг харгалзан томьёо" src="http://hi-edu.ru/e-books/xbook785/files/18-2.gif" border="0" align="absmiddle" " alt="(! LANG:бид авдаг

томъёо" src="http://hi-edu.ru/e-books/xbook785/files/Fe.gif" border="0" align="absmiddle" alt="- цэнэгийн тэмдгээс хамаарч алгебрийн хэмжигдэхүүн. Жишээлбэл, q үед<0 линии Е направлены к заряду и противоположны направлению внешней нормали n ..gif" border="0" align="absmiddle" alt="цэнэгийн эргэн тойронд q дурын хэлбэртэй байна. Мэдээжийн хэрэг, гадаргуу нь ">E, S гадаргуутай адил. Иймээс дурын гадаргуугаар дамжин өнгөрөх Е векторын урсгал нь томъёо юм" src="http://hi-edu.ru/e-books/xbook785/ файлууд/Fe.gif" хүрээ ="0" align="absmiddle" alt=".

Хэрэв цэнэг нь хаалттай гадаргуугийн гадна талд байрладаг бол хаалттай хэсэгт хэдэн шугам орох нь тодорхой тоогоор гарах болно. Үүний үр дүнд Е векторын урсгал тэгтэй тэнцүү байх болно.

Хэрэв цахилгаан орон нь цэгийн цэнэгийн системээр үүсгэгдсэн болтомъёо" src="http://hi-edu.ru/e-books/xbook785/files/18-4.gif" border="0" align="absmiddle" alt="

Энэ томъёо нь Гауссын теоремын математик илэрхийлэл юм. Дурын хаалттай гадаргуугаар вакуум дахь цахилгаан орны хүч чадлын вектор Е-ийн урсгал нь түүний бүрхсэн цэнэгийн алгебрийн нийлбэрийг 1-т хуваасантай тэнцүү байна.томъёо" src="http://hi-edu.ru/e-books/xbook785/files/18-6.gif" border="0" align="absmiddle" alt="

Тайлбарыг дуусгахын тулд Гауссын теоремыг интеграл харилцаанд биш харин орон зайн өгөгдсөн цэг дэх талбайн параметрүүдэд тулгуурлан орон нутгийн хэлбэрээр танилцуулъя. Үүнийг хийхийн тулд дифференциал оператор - векторын ялгаа, - ашиглахад тохиромжтой.

томъёо" src="http://hi-edu.ru/e-books/xbook785/files/nabla.gif" border="0" align="absmiddle" alt="("набла") -

томъёо" src="http://hi-edu.ru/e-books/xbook785/files/19-1.gif" border="0" align="absmiddle" alt="

Математикийн шинжилгээнд Гаусс-Остроградскийн теоремыг мэддэг: хаалттай гадаргуугаар дамжин өнгөрөх векторын урсгал нь энэ гадаргуугаар хязгаарлагдах эзэлхүүн дэх түүний дифференциалын интегралтай тэнцүү байна.

томъёо" src="http://hi-edu.ru/e-books/xbook785/files/ro.gif" border="0" align="absmiddle" alt=":

томъёо" src="http://hi-edu.ru/e-books/xbook785/files/19-4.gif" border="0" align="absmiddle" alt="

Энэ илэрхийлэл нь орон нутгийн (дифференциал) хэлбэрээр Гауссын теорем юм.

Гауссын теорем (2.2) нь янз бүрийн электростатик талбайн хүчийг тодорхойлох боломжийг олгодог. Гауссын теоремыг хэрэглэх хэд хэдэн жишээг авч үзье.

1. Тооцоолъё Нэг жигд цэнэглэгдсэн бөмбөрцөг гадаргуугаас үүссэн цахилгаан статик орон.

R радиустай бөмбөрцөг гадаргуу нь жигд тархсан q цэнэгийг авч явдаг гэж үзье, өөрөөр хэлбэл. гадаргуугийн цэнэгийн нягт нь хаа сайгүй ижил тэмдэгтэй байна ">r >R бөмбөрцгийн төвөөс эхлэн бид оюун ухаанаараа цэнэглэгдсэн бөмбөрцөгт тэгш хэмтэй шинэ бөмбөрцөг S гадаргууг бүтээдэг. Гауссын теоремын дагуу.

томъёо" src="http://hi-edu.ru/e-books/xbook785/files/20-1.gif" border="0" align="absmiddle" alt="

R радиустай цэнэглэгдсэн бөмбөрцгийн гадаргуу дээр байрлах цэгүүдийн хувьд аналогиар бид дараахь зүйлийг бичиж болно.

Сонголт">цэнэглэгдсэн бөмбөрцөг дотор байгаа, дотор нь цахилгаан цэнэг агуулаагүй тул урсгалын тэмдэг">E = 0 байна.

Хэрэв бид Германы эрдэмтэн К.Гауссын (1777-1855) нээсэн теоремыг хэрэглэвэл цахилгаан цэнэгийн системийн талбайн хүчийг электростатик талбайн суперпозиция зарчмыг ашиглан тооцоолох ажлыг ихээхэн хялбаршуулж болох бөгөөд энэ нь цахилгаан цэнэгийн урсгалыг тодорхойлдог. дурын хаалттай гадаргуугаар дамжин өнгөрөх цахилгаан орны хүч чадлын вектор.

Хаалттай гадаргуугаар дамжин өнгөрөх эрчмийн векторын урсгалын тодорхойлолтоос түүний төвд байрлах Q цэгийн цэнэгийг хамарсан r радиустай бөмбөрцөг гадаргуугаар дамжин өнгөрөх эрчим векторын урсгал нь тэнцүү байна (Зураг 1)

Энэ үр дүн нь дурын хэлбэрийн хаалттай гадаргууд хүчинтэй байна. Үнэн хэрэгтээ, хэрэв та бөмбөрцөгийг (Зураг 1) дур мэдэн хаалттай гадаргууд оруулбал бөмбөрцөгт нэвтэрч буй хурцадмал байдлын шугам бүр энэ гадаргуугаар дамжин өнгөрөх болно.

Хэрэв ямар нэгэн хэлбэрийн битүү гадаргуу нь цэнэгийг бүрхсэн бол (Зураг 2) ямар ч хурцадмал шугам гадаргуутай огтлолцох үед энэ нь түүнд орох эсвэл гарах болно. Урсгалыг тооцоолохдоо хурцадмал шугамууд гадаргуугаас гарах тохиолдолд урсгал нь эерэг, гадаргуу руу орж буй шугамуудад сөрөг байна.Хэрэв битүү гадаргуу нь цэнэгийг хүрээгүй бол урсгал нь нэг огтлолцол хүртэл буурдаг. , тэгвэл түүгээр дамжин өнгөрөх урсгал нь тэг байх тул гадаргуу руу орох суналтын шугамын тоо түүнээс гарах суналтын шугамын тоотой хэрхэн тэнцүү байна.

Энэ нь дурын хэлбэртэй гадаргуугийн хувьд битүү бөгөөд Q цэгийн цэнэгийг агуулж байвал векторын урсгалыг илэрхийлнэ гэсэн үг. Э Q/ε 0-тэй тэнцүү байх болно, өөрөөр хэлбэл.

Урсгалын тэмдэг нь Q цэнэгийн тэмдэгтэй давхцдаг.

n цэнэгийг тойрсон дурын гадаргуугийн ерөнхий тохиолдлыг судалъя. Суперпозиция, хурцадмал байдлын зарчмыг ашиглан Эбүх цэнэгийн үүсгэсэн талбар нь эрчмийн нийлбэртэй тэнцүү байна Э битөлбөр тус бүрээр тус тусад нь үүсгэсэн талбарууд. Тийм ч учраас

(1)-ийн дагуу нийлбэрийн тэмдгийн доор гарч буй интеграл бүр нь Q i /ε 0-тэй тэнцүү байна. гэсэн үг,

(2)

Формула (2) илэрхийлнэ Вакуум дахь электростатик талбайн Гауссын теорем: дурын хаалттай гадаргуугаар вакуум дахь цахилгаан статик талбайн хүч чадлын векторын урсгал нь энэ гадаргуу дотор агуулагдах цэнэгийн алгебрийн нийлбэрийг ε 0-д хуваасантай тэнцүү байна. Энэ теоремыг дурын шинж чанартай вектор талбайн хувьд математикийн аргаар Оросын математикч М.В.Остроградский (1801-1862), дараа нь түүнээс үл хамааран электростатик талбайтай холбоотой К.Гаусс олж авсан.

Ерөнхий тохиолдолд цахилгаан цэнэгийг тодорхой эзэлхүүний нягтралтай ρ=dQ/dV хуваарилах боломжтой бөгөөд энэ нь орон зайн өөр өөр газар өөр өөр байдаг. Дараа нь тодорхой V эзэлхүүнийг хамарсан хаалттай гадаргуугийн S дотор агуулагдах нийт цэнэг,

(3)

Томъёо (3) ашиглан Гауссын теоремыг (2) дараах байдлаар бичиж болно.

Хүчдэлийн векторын эргэлт нь нэг эерэг цэнэгийг L хаалттай зам дагуу хөдөлгөхөд цахилгаан хүчний хийсэн ажил юм.

(13.18)

Хаалттай гогцооны дагуух электростатик талбайн хүчний ажил тэг (боломжийн хүчний ажил) тул хаалттай гогцооны дагуух электростатик талбайн хүч чадлын эргэлт тэг байна.

Цахилгаан статик талбайн боломж.Консерватив хүчний талбарыг зөвхөн вектор функцээр тайлбарлахаас гадна түүний цэг бүрт тохиромжтой скаляр хэмжигдэхүүнийг тодорхойлох замаар энэ талбайн эквивалент тайлбарыг олж авч болно. Электростатик талбайн хувьд энэ хэмжигдэхүүн байна электростатик талбайн потенциал, туршилтын цэнэгийн боломжит энергийн харьцаагаар тодорхойлогддог qэнэ цэнэгийн хэмжээнд,  = В P / q, үүнээс үүдэн потенциал нь талбайн өгөгдсөн цэг дэх нэгж эерэг цэнэгийн эзэмшиж буй потенциал энергитэй тоон хувьд тэнцүү байна. Потенциалыг хэмжих нэгж нь вольт (1 В) юм.

Цэгийн цэнэгийн талбайн боломж Qдиэлектрик тогтмол  нэгэн төрлийн изотроп орчинд:

Суперпозиция зарчим.Потенциал нь скаляр функц бөгөөд үүнд суперпозиция зарчим хүчинтэй. Тэгэхээр цэгийн цэнэгийн системийн талбайн потенциалын хувьд Q 1, Q 2, Q nбидэнд байгаа

,

Хаана r i-  потенциалтай талбайн цэгээс цэнэг хүртэлх зай Q i. Хэрэв цэнэгийг орон зайд дур мэдэн хуваарилсан бол

,

Хаана r- анхан шатны эзлэхүүнээс хол байх d x,d y,d zзааж өгөх ( x, y, z), боломж нь тодорхойлогдсон газар; В- цэнэг тархсан орон зайн эзэлхүүн.

Цахилгаан орны хүчний боломж ба ажил.Потенциалын тодорхойлолт дээр үндэслэн цэгийн цэнэгийг хөдөлгөх үед цахилгаан талбайн хүчний хийсэн ажил болохыг харуулж болно. qталбайн нэг цэгээс нөгөө цэг хүртэл энэ цэнэгийн хэмжээ ба замын эхний ба эцсийн цэгүүдийн боломжит зөрүүний үржвэртэй тэнцүү байна. A = q (     
Хэрэв боломжит энергитэй зүйрлэвэл цахилгаан цэнэгүүдээс хязгааргүй алслагдсан цэгүүдэд - талбайн эх үүсвэрүүд потенциал тэг байна гэж үзвэл цэнэгийг хөдөлгөх үед цахилгаан талбайн хүчний ажил. q 1 цэгээс хязгааргүй хүртэл гэж төлөөлж болно А   q  1 .
Тиймээс цахилгаан статик талбайн өгөгдсөн цэг дэх потенциал нь Нэгж эерэг цэгийн цэнэгийг талбайн өгөгдсөн цэгээс хязгааргүй алслагдсан цэг рүү шилжүүлэх үед цахилгаан талбайн хүчний хийсэн ажилтай тоон хувьд тэнцүү физик хэмжигдэхүүн:  = А  / q.
Зарим тохиолдолд цахилгаан орны потенциалыг илүү тодорхой тодорхойлсон байдаг нэгж эерэг цэгийн цэнэгийг хязгааргүйгээс өгөгдсөн цэг рүү шилжүүлэх үед цахилгаан талбайн хүчний эсрэг гадны хүчний ажилтай тоон хувьд тэнцүү физик хэмжигдэхүүн. Сүүлийн тодорхойлолтыг дараах байдлаар бичих нь тохиромжтой.

Орчин үеийн шинжлэх ухаан, технологид, ялангуяа бичил сансарт тохиолдох үзэгдлийг дүрслэхдээ ажил, энергийн нэгж гэж нэрлэдэг. электрон вольт(eV). Энэ нь 1 В потенциалын зөрүүтэй хоёр цэгийн хооронд электроны цэнэгтэй тэнцүү цэнэгийг хөдөлгөхөд хийсэн ажил: 1 эВ = 1.6010  C1 V = 1.6010  J.

Эквипотенциал гадаргуу- статик цахилгаан орон эсвэл Ньютоны таталцлын талбар гэх мэт аливаа боломжит вектор талбарт хамаарах ойлголт. Өгөгдсөн потенциал талбайн скаляр потенциал тогтмол утгыг (потенциал түвшний гадаргуу) авах гадаргууг эквипотенциал гадаргуу гэнэ. Өөр нэг ижил төстэй тодорхойлолт нь аль ч цэгийн талбайн шугамтай ортогональ гадаргуу юм.

Цахилгаан статик дахь дамжуулагчийн гадаргуу нь эквипотенциал гадаргуу юм. Үүнээс гадна эквипотенциал гадаргуу дээр дамжуулагчийг байрлуулах нь электростатик талбайн тохиргоог өөрчлөхгүй. Энэ баримтыг зургийн аргад ашигладаг бөгөөд энэ нь нарийн төвөгтэй тохиргооны хувьд электростатик талбайг тооцоолох боломжийг олгодог.

(Хөдөлгөөнгүй) таталцлын талбайд хөдөлгөөнгүй шингэний түвшинг эквипотенциал гадаргуугийн дагуу тогтооно. Тодруулбал, далай тэнгисийн түвшин дэлхийн таталцлын талбайн эквипотенциал гадаргуугийн дагуу өнгөрдөг гэж ойролцоогоор хэлж болно. Дэлхийн гадаргуу хүртэл үргэлжилсэн далай тэнгисийн гадаргуугийн хэлбэрийг геоид гэж нэрлэдэг бөгөөд геодезид чухал үүрэг гүйцэтгэдэг. Тиймээс геоид нь таталцлын болон төвөөс зугтах бүрэлдэхүүн хэсгээс бүрдэх таталцлын эквипотенциал гадаргуу юм.