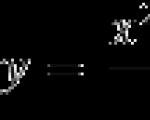ปัญหา B15 - ตรวจสอบฟังก์ชันโดยใช้อนุพันธ์ของมัน การศึกษาฟังก์ชันโดยใช้อนุพันธ์ของมัน การศึกษาฟังก์ชันโดยใช้อนุพันธ์ของมัน

ปัญหา B15 เสนอให้ตรวจสอบฟังก์ชันที่ระบุโดยสูตรสำหรับเอ็กซ์ตรีม นี่เป็นปัญหาแคลคูลัสมาตรฐาน และความยากของมันจะแตกต่างกันไปมากขึ้นอยู่กับฟังก์ชันที่เป็นปัญหา บางปัญหาสามารถแก้ไขได้ด้วยวาจา ในขณะที่บางปัญหาต้องใช้การคิดอย่างจริงจัง

ก่อนที่จะศึกษาวิธีการแก้ปัญหา คุณต้องเข้าใจคำศัพท์บางคำจากสาขาการวิเคราะห์ทางคณิตศาสตร์เสียก่อน ดังนั้น ในปัญหา B15 คุณต้องหาปริมาณต่อไปนี้โดยใช้อนุพันธ์:

1. จุดสูงสุด (ต่ำสุด) ในพื้นที่ - ค่าของตัวแปรที่ฟังก์ชันถึงค่าสูงสุด (น้อยที่สุด) จุดดังกล่าวเรียกอีกอย่างว่าจุดสุดขั้ว
2. ค่าสูงสุด (ต่ำสุด) โดยรวมของฟังก์ชันคือค่าที่ใหญ่ที่สุด (น้อยที่สุด) ของฟังก์ชันภายใต้ข้อจำกัดที่ระบุ อีกชื่อหนึ่งคือความสุดขั้วระดับโลก

ในกรณีนี้ โดยทั่วไปแล้วจะค้นหาค่า extrema โดยรวมไม่เกินขอบเขตคำจำกัดความทั้งหมดของฟังก์ชัน แต่จะค้นหาเฉพาะบางส่วนเท่านั้น สิ่งสำคัญคือต้องเข้าใจว่าค่าสุดขั้วโกลบอลและค่าของฟังก์ชันที่จุดสุดขั้วไม่ตรงกันเสมอไป เรามาอธิบายเรื่องนี้ด้วยตัวอย่างเฉพาะ:

งาน. ค้นหาจุดต่ำสุดและค่าต่ำสุดของฟังก์ชัน y = 2x 3 − 3x 2 − 12x + 1 ในช่วงเวลา [−3; 3].

อันดับแรก เราจะหาจุดต่ำสุดซึ่งเราคำนวณอนุพันธ์:
y’ = (2x 3 − 3x 2 − 12x + 1)’ = 6x 2 − 6x − 12

มาหาจุดวิกฤตด้วยการแก้สมการ y’ = 0 เราได้สมการกำลังสองมาตรฐาน:
y’ = 0 ⇒ 6x 2 − 6x − 12 = 0 ⇒ ... ⇒ x 1 = −1, x 2 = 2

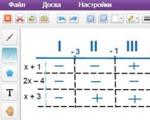
ทำเครื่องหมายจุดเหล่านี้บนเส้นพิกัด เพิ่มเครื่องหมายอนุพันธ์และข้อ จำกัด - ส่วนท้ายของส่วน:

ขนาดของภาพไม่สำคัญ สิ่งที่สำคัญที่สุดคือการทำเครื่องหมายจุดต่างๆ ในลำดับที่ถูกต้อง จากหลักสูตรคณิตศาสตร์ของโรงเรียน เรารู้ว่าที่จุดต่ำสุด อนุพันธ์จะเปลี่ยนเครื่องหมายจากลบเป็นบวก การนับจะนับจากซ้ายไปขวาเสมอ - ในทิศทางของครึ่งแกนบวก ดังนั้นจึงมีจุดต่ำสุดเพียงจุดเดียว: x = 2

ทีนี้ลองหาค่าต่ำสุดของฟังก์ชันในช่วงเวลา [−3; 3]. สามารถทำได้ที่จุดต่ำสุด (จากนั้นจะกลายเป็นจุดต่ำสุดโดยรวม) หรือที่ส่วนท้ายของส่วน โปรดทราบว่าในช่วง (2; 3) อนุพันธ์จะเป็นค่าบวกทุกจุด ซึ่งหมายความว่า y(3) > y(2) ดังนั้นจึงสามารถละเว้นปลายด้านขวาของเซกเมนต์ได้ จุดเดียวที่เหลืออยู่คือ x = −3 (จุดสิ้นสุดด้านซ้ายของส่วน) และ x = 2 (จุดต่ำสุด) เรามี:
y(−3) = 2(−3) 3 − 3(−3) 2 − 12(−3) + 1 = −44;
y(2) = 2*2 3 − 3*2 2 − 12*2 + 1 = −19

ดังนั้น ค่าที่น้อยที่สุดของฟังก์ชันจะเกิดขึ้นที่ส่วนท้ายของเซกเมนต์และเท่ากับ −44

คำตอบ: xmin = 2; ยินมิน = −44

จากเหตุผลข้างต้นทำให้เกิดข้อเท็จจริงสำคัญที่หลายคนลืมไป ฟังก์ชันรับค่าสูงสุด (ต่ำสุด) โดยไม่จำเป็นต้องอยู่ที่จุดสุดขั้ว บางครั้งค่านี้ถึงจุดสิ้นสุดของเซ็กเมนต์ และอนุพันธ์ไม่จำเป็นต้องเท่ากับศูนย์

โครงการแก้ไขปัญหา B15

หากในปัญหา B15 คุณต้องค้นหาค่าสูงสุดหรือต่ำสุดของฟังก์ชัน f(x) ในช่วงเวลา ให้ทำตามขั้นตอนต่อไปนี้:

1. แก้สมการ f’(x) = 0 หากไม่มีราก ให้ข้ามขั้นตอนที่สามแล้วตรงไปยังขั้นตอนที่สี่
2. จากชุดรากที่ได้ ให้ขีดฆ่าทุกอย่างที่อยู่นอกเซกเมนต์ออก ให้เราแสดงตัวเลขที่เหลือ x 1, x 2, ..., xn - ตามกฎแล้วจะมีไม่กี่ตัว
3. ลองแทนที่ส่วนท้ายของส่วนและจุด x 1, x 2, ..., xn ลงในฟังก์ชันดั้งเดิม เราได้ชุดตัวเลข f(a), f(b), f(x 1), f(x 2), ..., f(x n) ซึ่งเราเลือกค่าที่ใหญ่ที่สุดหรือเล็กที่สุด - นี่จะเป็น คำตอบ.

คำอธิบายสั้นๆ เกี่ยวกับการขีดฆ่ารากเมื่อรากเหล่านั้นตรงกับจุดสิ้นสุดของเซ็กเมนต์ ยังสามารถขีดฆ่าออกได้ เนื่องจากในขั้นตอนที่สี่ ส่วนปลายของเซ็กเมนต์ยังคงถูกแทนที่ในฟังก์ชัน แม้ว่าสมการ f’(x) = 0 จะไม่มีคำตอบก็ตาม

งาน. ค้นหาค่าที่ใหญ่ที่สุดของฟังก์ชัน y = x 3 + 3x 2 − 9x − 7 ในช่วงเวลา [−5; 0].

ก่อนอื่น มาหาอนุพันธ์: y’ = (x 3 + 3x 2 − 9x − 7)’ = 3x 2 + 6x − 9

จากนั้นเราก็แก้สมการ: y’ = 0 ⇒ 3x 2 + 6x − 9 = 0 ⇒ ... ⇒ x = −3; x = 1

เราขีดฆ่าราก x = 1 เนื่องจากมันไม่อยู่ในเซกเมนต์ [−5; 0].

ยังคงคำนวณค่าของฟังก์ชันที่ส่วนท้ายของส่วนและที่จุด x = −3:
y(−5) = (−5) 3 + 4·(−5) 2 − 9·(−5) − 7 = −12;
y(−3) = (−3) 3 + 4·(−3) 2 − 9·(−3) − 7 = 20;
y(0) = 0 3 + 4 0 2 − 9 0 − 7 = −7

แน่นอนว่าค่าที่ใหญ่ที่สุดคือ 20 ซึ่งทำได้ที่จุด x = −3

ตอนนี้ให้พิจารณากรณีนี้เมื่อคุณต้องการหาจุดสูงสุดหรือต่ำสุดของฟังก์ชัน f(x) บนเซกเมนต์ หากไม่ได้ระบุเซ็กเมนต์ ฟังก์ชันจะถือว่าอยู่ในขอบเขตของคำจำกัดความ ไม่ว่าในกรณีใด วิธีแก้ไขจะเป็นดังนี้:

1. ค้นหาอนุพันธ์ของฟังก์ชัน: f’(x)
2. แก้สมการ f’(x) = 0 ถ้าอนุพันธ์เป็นฟังก์ชันตรรกยะเศษส่วน เราจะทราบเพิ่มเติมว่าตัวส่วนเป็นศูนย์เมื่อใด ให้เราแสดงถึงรากผลลัพธ์ x 1 , x 2 , ..., x n .
3. ทำเครื่องหมาย x 1, x 2, ..., xn บนเส้นพิกัดแล้วจัดเรียงเครื่องหมายที่อนุพันธ์ใช้ระหว่างตัวเลขเหล่านี้ หากมีการกำหนดส่วนไว้ ให้ทำเครื่องหมายและขีดฆ่าทุกสิ่งที่อยู่ด้านนอกออก
4. ในบรรดาจุดที่เหลือ เรากำลังมองหาจุดที่มีเครื่องหมายของอนุพันธ์เปลี่ยนจากลบเป็นบวก (นี่คือจุดต่ำสุด) หรือจากบวกเป็นลบ (จุดต่ำสุด) ควรมีจุดดังกล่าวเพียงจุดเดียว - นี่จะเป็นคำตอบ

ผู้อ่านที่มีวิจารณญาณอาจสังเกตเห็นว่าสำหรับบางฟังก์ชันอัลกอริทึมนี้ใช้ไม่ได้ อันที่จริง มีฟังก์ชันทั้งคลาสที่การค้นหาจุดสุดขั้วต้องใช้การคำนวณที่ซับซ้อนกว่า อย่างไรก็ตาม ฟังก์ชันดังกล่าวไม่พบในการสอบ Unified State ในวิชาคณิตศาสตร์

ให้ความสนใจอย่างระมัดระวังกับการวางป้ายระหว่างจุด x 1, x 2, ..., x n ข้อควรจำ: เมื่อผ่านรากของการคูณเลขคู่ เครื่องหมายของอนุพันธ์จะไม่เปลี่ยนแปลง เมื่อมองหาจุดที่สูงที่สุด ป้ายต่างๆ จะถูกมองจากซ้ายไปขวาเสมอ เช่น ในทิศทางของแกนจำนวน

งาน. ค้นหาจุดสูงสุดของฟังก์ชัน

ในส่วน [−8; 8].

มาหาอนุพันธ์กัน:

เนื่องจากนี่คือฟังก์ชันเศษส่วนเชิงตรรกศาสตร์ เราจึงถือว่าอนุพันธ์และส่วนเป็นศูนย์:
y’ = 0 ⇒ x 2 − 25 = 0 ⇒ ... ⇒ x = 5; x = −5;
x 2 = 0 ⇒ x = 0 (รากหลายหลากที่สอง)

ลองทำเครื่องหมายจุด x = −5, x = 0 และ x = 5 บนเส้นพิกัด ป้ายสถานที่ และขอบเขต:

แน่นอนว่าเหลือเพียงจุดเดียวภายในเซ็กเมนต์ x = −5 ซึ่งเครื่องหมายของอนุพันธ์เปลี่ยนจากบวกเป็นลบ นี่คือจุดสูงสุด

ให้เราอธิบายอีกครั้งว่าจุดสุดขั้วแตกต่างจากจุดสุดขีดอย่างไร จุดสุดขีดคือค่าของตัวแปรที่ฟังก์ชันรับค่าที่ใหญ่ที่สุดหรือน้อยที่สุด Extrema คือค่าของฟังก์ชันเอง สูงสุดหรือต่ำสุดในบางพื้นที่ใกล้เคียง

นอกจากพหุนามปกติและฟังก์ชันเศษส่วนแบบตรรกยะแล้ว นิพจน์ประเภทต่อไปนี้ยังพบได้ในปัญหา B15:

1. ฟังก์ชันที่ไม่ลงตัว
2. ฟังก์ชันตรีโกณมิติ
3. ฟังก์ชันเลขชี้กำลัง
4. ฟังก์ชันลอการิทึม

ตามกฎแล้วจะไม่มีปัญหาเกิดขึ้นกับฟังก์ชันที่ไม่ลงตัว กรณีที่เหลือควรพิจารณารายละเอียดเพิ่มเติม

ฟังก์ชันตรีโกณมิติ

ปัญหาหลักของฟังก์ชันตรีโกณมิติคือเมื่อแก้สมการจะมีรากจำนวนอนันต์เกิดขึ้น ตัวอย่างเช่น สมการ sin x = 0 มีราก x = πn โดยที่ n ∈ Z จะทำเครื่องหมายบนเส้นพิกัดได้อย่างไรหากมีตัวเลขดังกล่าวมากมายนับไม่ถ้วน?

คำตอบนั้นง่าย: คุณต้องแทนที่ค่าเฉพาะของ n อันที่จริงในปัญหา B15 ที่มีฟังก์ชันตรีโกณมิติจะมีข้อจำกัดอยู่เสมอ - ส่วน ดังนั้นในการเริ่มต้นเราใช้ n = 0 แล้วเพิ่ม n จนกระทั่งรูท "แมลงวัน" ที่สอดคล้องกันเกินขอบเขตของเซ็กเมนต์ ในทำนองเดียวกัน เมื่อลด n เราก็จะได้รากที่น้อยกว่าขอบเขตล่างในไม่ช้า

มันง่ายที่จะแสดงให้เห็นว่าไม่มีรากอื่นใดนอกจากที่ได้รับในกระบวนการพิจารณา อยู่ในเซ็กเมนต์ ให้เราพิจารณากระบวนการนี้โดยใช้ตัวอย่างที่เฉพาะเจาะจง

งาน. ค้นหาจุดสูงสุดของฟังก์ชัน y = sin x − 5x·sin x − 5cos x + 1 ซึ่งอยู่ในเซ็กเมนต์ [−π/3; พาย/3].

เราคำนวณอนุพันธ์: y’ = (sin x − 5x sin x − 5cos x + 1)’ = ... = cos x − 5x cos x = (1 − 5x) cos x

จากนั้นเราแก้สมการ: y’ = 0 ⇒ (1 − 5x) cos x = 0 ⇒ ... ⇒ x = 0.2 หรือ x = π/2 + πn, n ∈ Z

ทุกอย่างชัดเจนด้วยราก x = 0.2 แต่สูตร x = π/2 + πn ต้องมีการประมวลผลเพิ่มเติม เราจะแทนที่ค่าต่างๆ ของ n โดยเริ่มจาก n = 0

n = 0 ⇒ x = π/2 แต่ π/2 > π/3 ดังนั้นราก x = π/2 จะไม่รวมอยู่ในส่วนเดิม นอกจากนี้ ยิ่ง n มากเท่าใด x ก็จะยิ่งมากขึ้น ดังนั้นจึงไม่มีเหตุผลที่จะต้องพิจารณา n > 0

n = −1 ⇒ x = − π/2 แต่ −π/2< −π/3 - этот корень тоже придется отбросить. А вместе с ним - и все корни для n < −1.

ปรากฎว่าในช่วงเวลา [−π/3; π/3] อยู่กับราก x = 0.2 เท่านั้น ทำเครื่องหมายพร้อมกับเครื่องหมายและขอบเขตบนเส้นพิกัด:

เพื่อให้แน่ใจว่าอนุพันธ์ทางขวาของ x = 0.2 เป็นลบจริงๆ ก็เพียงพอที่จะแทนค่า x = π/4 ไปเป็น y’ เราจะสังเกตง่ายๆ ว่า ณ จุด x = 0.2 อนุพันธ์จะเปลี่ยนเครื่องหมายจากบวกเป็นลบ ดังนั้นนี่คือจุดสูงสุด

งาน. จงหาค่าที่ใหญ่ที่สุดของฟังก์ชัน y = 4tg x − 4x + π − 5 ในช่วงเวลา [−π/4; พาย/4].

เราคำนวณอนุพันธ์: y’ = (4tg x − 4x + π − 5)’ = 4/cos 2x − 4

จากนั้นเราแก้สมการ: y’ = 0 ⇒ 4/cos 2x − 4 = 0 ⇒ ... ⇒ x = πn, n ∈ Z

ให้เราแยกรากออกจากสูตรนี้โดยการแทนที่ n เฉพาะ โดยเริ่มจาก n = 0:
n = 0 ⇒ x = 0 รูตนี้เหมาะกับเรา
n = 1 ⇒ x = π แต่ π > π/4 ดังนั้นจะต้องขีดฆ่าราก x = π และค่า n > 1 ออก
n = −1 ⇒ x = −π แต่ π< −π/4, поэтому x = π и n < −1 тоже вычеркиваем.

จากความหลากหลายของรากทั้งหมด เหลือเพียงรากเดียวเท่านั้น: x = 0 ดังนั้นเราจึงคำนวณค่าของฟังก์ชันสำหรับ x = 0, x = π/4 และ x = −π/4
y(0) = 4tg 0 − 4 0 + π − 5 = π − 5;
y(π/4) = 4tg (π/4) − 4 π/4 + π − 5 = −1;
y(π/4) = 4tg (−π/4) − 4 (−π/4) + π − 5 = ... = 2π − 9

ตอนนี้สังเกตว่า π = 3.14...< 4, поэтому π − 5 < 4 − 5 = −1 и 2π − 9 < 8 − 9 = −1. Получается одно положительное число и два отрицательных. Мы ищем наибольшее - очевидно, это y = −1.

โปรดทราบว่าในปัญหาที่แล้วไม่สามารถเปรียบเทียบตัวเลขด้วยกันได้ ท้ายที่สุดแล้ว ตัวเลข π − 5, 1 และ 2π − 9 สามารถเขียนได้เพียงตัวเดียวในแบบฟอร์มคำตอบ แน่นอนจะเขียนอย่างไรพูดตัวเลขπบนแบบฟอร์ม? แต่ไม่มีทาง นี่เป็นคุณลักษณะที่สำคัญของส่วนแรกของการสอบ Unified State ในวิชาคณิตศาสตร์ ซึ่งช่วยให้การแก้ปัญหาต่างๆ ง่ายขึ้นอย่างมาก และใช้งานได้ไม่เพียงแต่ใน B15 เท่านั้น

บางครั้งเมื่อศึกษาฟังก์ชัน สมการจะเกิดขึ้นโดยไม่มีราก ในกรณีนี้ งานจะง่ายขึ้น เนื่องจากต้องพิจารณาเพียงส่วนท้ายของส่วนเท่านั้น

งาน. จงหาค่าที่น้อยที่สุดของฟังก์ชัน y = 7sin x − 8x + 5 ในช่วงเวลา [−3π/2; 0].

ก่อนอื่น เราหาอนุพันธ์: y’ = (7sin x − 8x + 5)’ = 7cos x − 8

ลองแก้สมการ: y’ = 0 ⇒ 7cos x − 8 = 0 ⇒ cos x = 8/7 แต่ค่าของ cos x จะอยู่ในช่วง [−1; 1] และ 8/7 > 1 ดังนั้นจึงไม่มีราก

หากไม่มีรากก็ไม่จำเป็นต้องขีดฆ่าสิ่งใดเลย มาดูขั้นตอนสุดท้ายกัน - คำนวณค่าของฟังก์ชัน:
y(−3π/2) = 7ซิน (−3π/2) − 8·(−3π/2) + 5 = ... = 12π + 12;
y(0) = 7ซิน 0 − 8 0 + 5 = 5

เนื่องจากไม่สามารถเขียนเลข 12π + 12 ลงในกระดาษคำตอบได้ จึงเหลือเพียง y = 5

ฟังก์ชันเลขชี้กำลัง

โดยทั่วไปแล้ว ฟังก์ชันเลขชี้กำลังคือนิพจน์ที่อยู่ในรูปแบบ y = a x โดยที่ a > 0 แต่ในปัญหา B15 จะมีเพียงฟังก์ชันในรูปแบบ y = e x และในกรณีที่รุนแรง y = e kx + b เหตุผลก็คืออนุพันธ์ของฟังก์ชันเหล่านี้คำนวณได้ง่ายมาก:

1. (e x)" = e x ไม่มีอะไรเปลี่ยนแปลง
2. (e kx + b)" = k·e kx + b เพียงบวกตัวประกอบเท่ากับสัมประสิทธิ์ของตัวแปร x นี่เป็นกรณีพิเศษของอนุพันธ์ของฟังก์ชันเชิงซ้อน

ทุกสิ่งทุกอย่างเป็นมาตรฐานอย่างแน่นอน แน่นอนว่าการทำงานจริงในปัญหา B15 ดูรุนแรงกว่า แต่ไม่ได้เปลี่ยนรูปแบบการแก้ปัญหา ลองดูตัวอย่างบางส่วน โดยเน้นเฉพาะประเด็นหลักของการแก้ปัญหา โดยไม่ต้องให้เหตุผลหรือแสดงความคิดเห็นอย่างละเอียด

งาน. ค้นหาค่าที่น้อยที่สุดของฟังก์ชัน y = (x 2 − 5x + 5)e x − 3 ในช่วงเวลา [−1; 5].

อนุพันธ์: y' = ((x 2 − 5x + 5)e x − 3)' = ... = (x 2 − 3x)e x − 3 = x(x − 3)e x − 3

ค้นหาราก: y’ = 0 ⇒ x(x − 3)e x − 3 = 0 ⇒ ... ⇒ x = 0; x=3.

รากทั้งสองอยู่บนส่วน [−1; 5]. ยังคงต้องหาค่าของฟังก์ชันทุกจุด:
y(−1) = ((−1) 2 − 5·(−1) + 5)e − 1 − 3 = ... = 11·e −4 ;
y(0) = (0 2 − 5 0 + 5)e 0 − 3 = ... = 5 อี −3 ;
y(3) = (3 2 − 5 3 + 5)e 3 − 3 = ... = −1;
y(5) = (5 2 − 5 5 + 5)e 5 − 3 = ... = 5 e 2

จากตัวเลขทั้งสี่ที่ได้ มีเพียง y = −1 เท่านั้นที่สามารถเขียนลงในแบบฟอร์มได้ นอกจากนี้ นี่เป็นจำนวนลบเพียงตัวเดียว - มันจะน้อยที่สุด

งาน. ค้นหาค่าสูงสุดของฟังก์ชัน y = (2x − 7) e 8 − 2x บนเซกเมนต์นั้น

อนุพันธ์: y’ = ((2x − 7) e 8 − 2x)’ = ... = (16 − 4x) e 8 − 2x = 4(4 − x) e 8 − 2x

เราหารากได้: y' = 0 ⇒ 4(4 − x) e 8 − 2x = 0 ⇒ x = 4

ราก x = 4 เป็นของกลุ่ม เรากำลังมองหาค่าฟังก์ชัน:
y(0) = (2 0 − 7)e 8 − 2 0 = ... = −7 e 8 ;
y(4) = (2 4 − 7)e 8 − 2 4 = ... = 1;
y(6) = (2 6 − 7)e 8 − 2 6 = ... = 5 e −4

แน่นอนว่ามีเพียง y = 1 เท่านั้นที่สามารถใช้เป็นคำตอบได้

ฟังก์ชันลอการิทึม

โดยการเปรียบเทียบกับฟังก์ชันเลขชี้กำลังในปัญหา B15 จะพบเฉพาะลอการิทึมธรรมชาติเท่านั้นเนื่องจากอนุพันธ์ของพวกมันนั้นคำนวณได้ง่าย:

1. (lnx)' = 1/x;
2. (ln(kx + b))’ = k/(kx + b) โดยเฉพาะอย่างยิ่ง ถ้า b = 0 ดังนั้น (ln(kx))’ = 1/x

ดังนั้นอนุพันธ์จะเป็นฟังก์ชันเศษส่วนเสมอ สิ่งที่เหลืออยู่คือการเทียบอนุพันธ์นี้และตัวส่วนให้เป็นศูนย์ แล้วแก้สมการผลลัพธ์

หากต้องการค้นหาค่าสูงสุดหรือต่ำสุดของฟังก์ชันลอการิทึม โปรดจำไว้ว่า: ลอการิทึมธรรมชาติจะกลายเป็นตัวเลข "ปกติ" ที่จุดของรูปแบบ e n เท่านั้น ตัวอย่างเช่น ln 1 = ln e 0 = 0 เป็นศูนย์ลอการิทึม และส่วนใหญ่แล้วคำตอบจะออกมาเป็นค่านั้น ในกรณีอื่นๆ เป็นไปไม่ได้ที่จะ "ลบ" เครื่องหมายของลอการิทึม

งาน. ค้นหาค่าที่น้อยที่สุดของฟังก์ชัน y = x 2 − 3x + ln x บนเซ็กเมนต์

เราคำนวณอนุพันธ์:

เราค้นหาศูนย์ของอนุพันธ์และตัวส่วน:
y’ = 0 ⇒ 2x 2 − 3x + 1 = 0 ⇒ ... ⇒ x = 0.5; x = 1;
x = 0 - ไม่มีอะไรต้องตัดสินใจที่นี่

จากตัวเลขทั้งสามตัว x = 0, x = 0.5 และ x = 1 มีเพียง x = 1 เท่านั้นที่อยู่ในเซ็กเมนต์ และตัวเลข x = 0.5 คือจุดสิ้นสุด เรามี:
y(0.5) = 0.5 2 − 3 0.5 + ln 0.5 = ln 0.5 − 1.25;
y(1) = 1 2 − 3 1 + ln 1 = −2;
y(5) = 5 2 − 3 5 + ln 5 = 10 + ln 5

จากค่าทั้งสามที่ได้รับมีเพียง y = −2 เท่านั้นที่ไม่มีเครื่องหมายลอการิทึม - นี่จะเป็นคำตอบ

งาน. จงหาค่าสูงสุดของฟังก์ชัน y = ln(6x) − 6x + 4 บนเซ็กเมนต์นั้น

เราคำนวณอนุพันธ์:

เราพบว่าเมื่ออนุพันธ์หรือส่วนของมันมีค่าเท่ากับศูนย์:
y’ = 0 ⇒ 1 − 6x = 0 ⇒ x = 1/6;
x = 0 - ตัดสินใจแล้ว

เราขีดฆ่าตัวเลข x = 0 เนื่องจากมันอยู่นอกส่วน เราคำนวณค่าของฟังก์ชันที่ส่วนท้ายของส่วนและที่จุด x = 1/6:
y(0.1) = ln(6 0.1) − 6 0.1 + 4 = ln 0.6 + 3.4;
y(1/6) = ln(6 1/6) − 6 1/6 + 4 = ln 1 + 3 = 3;
y(3) = ln(6 3) − 6 3 + 4 = ln 18 − 14

เห็นได้ชัดว่ามีเพียง y = 3 เท่านั้นที่สามารถทำหน้าที่เป็นคำตอบได้ - ค่าที่เหลือมีเครื่องหมายลอการิทึมและไม่สามารถเขียนลงในกระดาษคำตอบได้

ประเด็นนี้เรียกว่า จุดสูงสุด (ขั้นต่ำ) ฟังก์ชั่นถ้ามีย่านใกล้เคียงจุดที่สำหรับทุกคนในละแวกนี้มีความไม่เท่าเทียมกัน ().

จุดสูงสุดและต่ำสุดของฟังก์ชันเรียกว่าจุด สุดขั้ว (รูปที่ 25)

ทฤษฎีบท 3.9 (เงื่อนไขที่จำเป็นสำหรับการมีอยู่ของจุดสุดขั้ว) . ที่จุดวิกฤตของชนิดที่ 1 อนุพันธ์ของฟังก์ชันอย่างใดอย่างหนึ่ง

เป็นศูนย์หรือไม่มีอยู่

จุดวิกฤตประเภทที่ 1 มักเรียกง่ายๆ ว่าจุดวิกฤติ

จุดวิกฤติที่อนุพันธ์ของฟังก์ชันเท่ากับศูนย์เรียกว่า จุดคงที่ . จุดวิกฤติที่ฟังก์ชันต่อเนื่องแต่ไม่สามารถหาอนุพันธ์ได้จะถูกเรียก จุดมุม . ตัวอย่างเช่น ฟังก์ชัน ณ จุดหนึ่งมีความต่อเนื่อง แต่ไม่มีอนุพันธ์ เนื่องจาก ณ จุดนี้ สามารถวาดแทนเจนต์จำนวนอนันต์ลงบนกราฟของฟังก์ชันได้ (รูปที่ 26) กรณีนี้ถือได้ว่าเป็นการยืนยันว่าการสนทนาของทฤษฎีบท 3.3 เป็นเท็จ

ฟังก์ชันนี้เรียกว่า เพิ่มขึ้น ในช่วงเวลาหนึ่ง หากในช่วงเวลานี้ ค่าอาร์กิวเมนต์ที่มากกว่าจะสอดคล้องกับค่าที่มากกว่าของตัวแปร และ ลดลง ถ้าค่าที่มากกว่าของอาร์กิวเมนต์สอดคล้องกับค่าที่น้อยกว่าของตัวแปร

สำหรับการวิจัยเพิ่มเติม จุดวิกฤตจะถูกวางไว้บนแกนตัวเลข ซึ่งแบ่งตามจุดเหล่านี้ออกเป็นระยะๆ หลังจากนั้นจะมีการตรวจสอบเงื่อนไขที่เพียงพอต่อไปนี้

ทฤษฎีบท 3.10 (เงื่อนไขเพียงพอสำหรับฟังก์ชันการเพิ่มและลด)หากในช่วงเวลาหนึ่งฟังก์ชันสามารถหาอนุพันธ์ได้และอนุพันธ์ของมันคือค่าบวก (ลบ) ฟังก์ชันในช่วงเวลานี้จะเพิ่มขึ้น (ลดลง)

ทฤษฎีบท 3.11 (เงื่อนไขที่เพียงพอสำหรับการมีอยู่ของจุดปลายสุดของฟังก์ชัน)ถ้าฟังก์ชันมีความต่อเนื่องและหาอนุพันธ์ได้ในพื้นที่ใกล้เคียงของจุดวิกฤติ และเมื่อผ่านฟังก์ชันนั้น อนุพันธ์จะเปลี่ยนเครื่องหมายจากบวกเป็นลบ จุดนั้นจะเป็นจุดสูงสุด ถ้าจากลบถึงบวก จุดนั้นคือจุดต่ำสุดของฟังก์ชัน

จุดวิกฤตของฟังก์ชันที่ไม่เป็นไปตามเงื่อนไขที่เพียงพอนั้น ยังคงเป็นเพียงจุดวิกฤตประเภทที่ 1 เท่านั้น

จุดวิกฤตของประเภทที่ 1 ซึ่งไม่มีอนุพันธ์จะถูกแบ่งออกเป็นสองประเภท:

– จุดที่ฟังก์ชันต่อเนื่องกัน (หากทฤษฎีบท 3.11 เป็นไปตามนั้น ฟังก์ชันที่จุดเหล่านี้จะมีปลายสุด "คม") ได้แก่ มุม คะแนน;

– จุดที่ฟังก์ชันประสบความไม่ต่อเนื่อง (จะข้ามไปยังระดับของจุดวิกฤติประเภทที่ 2 เสมอ)

แต่การศึกษาที่ดำเนินการในลักษณะนี้ไม่ได้ตอบคำถามที่สำคัญมาก: ฟังก์ชั่นเพิ่มขึ้น (ลดลง) - นูนหรือเว้าได้อย่างไร? คำตอบสำหรับคำถามที่ได้รับคือการศึกษาฟังก์ชันเพิ่มเติมโดยใช้อนุพันธ์อันดับสอง ให้เราให้คำจำกัดความที่จำเป็นจำนวนหนึ่ง

ฟังก์ชันนี้เรียกว่า นูน (เว้า) ในช่วงเวลาหนึ่ง ถ้าแทนเจนต์ที่ลากไปยังกราฟของฟังก์ชันในแต่ละจุดของช่วงเวลานี้อยู่เหนือ (ด้านล่าง) กราฟของฟังก์ชัน

จุดที่แยกพื้นที่นูนออกจากพื้นที่เว้าของฟังก์ชันเรียกว่าจุดของมัน จุดเปลี่ยน (รูปที่ 27)

ทฤษฎีบท 3.12 (เงื่อนไขที่จำเป็นสำหรับการมีอยู่ของจุดเปลี่ยนเว้า). ที่จุดวิกฤตของชนิดที่ 2 อนุพันธ์อันดับสองของฟังก์ชันจะเป็นศูนย์หรือไม่มีอยู่จริง

สำหรับการวิจัยเพิ่มเติม จุดวิกฤตของประเภทที่ 2 จะถูกวางไว้บนแกนตัวเลข ซึ่งแบ่งตามจุดเหล่านี้ออกเป็นระยะๆ หลังจากนั้นจึงตรวจสอบเงื่อนไขที่เพียงพอต่อไปนี้

ทฤษฎีบท 3.13 (เงื่อนไขที่เพียงพอสำหรับการนูนและความเว้าของฟังก์ชัน)ถ้าในช่วงเวลาหนึ่ง ฟังก์ชันสามารถหาอนุพันธ์ได้สองเท่าและอนุพันธ์อันดับสองเป็นค่าบวก (ลบ) ฟังก์ชันในช่วงเวลานี้จะเว้า (นูน)

จุดวิกฤตของฟังก์ชันที่ไม่เป็นไปตามเงื่อนไขที่เพียงพอนั้น ยังคงเป็นเพียงจุดวิกฤตของชนิดที่ 2

จุดวิกฤตของประเภทที่ 2 ซึ่งไม่มีอนุพันธ์อันดับสองแบ่งออกเป็นสองประเภท:

– จุดที่ฟังก์ชันต่อเนื่องคือจุดที่เรียกว่าจุดเปลี่ยนแบบ "แหลม" - ณ จุดดังกล่าวสามารถวาดแทนเจนต์จำนวนอนันต์ไปที่กราฟของฟังก์ชัน (รูปที่ 28)

– จุดที่ฟังก์ชันเกิดความไม่ต่อเนื่อง (ที่จุดความไม่ต่อเนื่องของชนิดที่ 2 กราฟของฟังก์ชันจะมีเส้นกำกับแนวตั้ง)

สำหรับการแสดงรายการจุดปลายสุดและจุดเปลี่ยนเว้าของฟังก์ชันขั้นสุดท้าย จำเป็นต้องค้นหาพิกัดของมัน จากนั้นจดจุดที่ระบุด้วยพิกัดสองจุด

คำถามทดสอบตัวเอง

1. จุดใดที่เรียกว่าจุดสุดขีด (สูงสุดและต่ำสุด) ของฟังก์ชัน

2. ฟังก์ชันใดเรียกว่าเพิ่ม (ลดลง)?

3. อะไรคือเงื่อนไขที่จำเป็นและเพียงพอสำหรับการดำรงอยู่ของจุดสุดขั้วของฟังก์ชัน?

4. เงื่อนไขที่เพียงพอสำหรับการเพิ่ม (ลดลง) ของฟังก์ชันคืออะไร?

5. จุดใดที่เรียกว่าจุดเปลี่ยนเว้าของฟังก์ชัน?

6. ฟังก์ชันใดเรียกว่านูน (เว้า)?

7. อะไรคือเงื่อนไขที่จำเป็นและเพียงพอสำหรับการดำรงอยู่ของจุดเปลี่ยนเว้าของฟังก์ชัน?

8. เงื่อนไขที่เพียงพอสำหรับความนูน (เว้า) ของฟังก์ชันคืออะไร?

วัตถุประสงค์ของบทเรียน:เพื่อสอนการศึกษาฟังก์ชัน สร้างกราฟของพวกเขา

รูปร่าง:บทเรียนการสนทนา

วิธีการ:บทสนทนา อุปกรณ์ช่วยการมองเห็น และสไลด์

อุปกรณ์:ไอซีที, ตาราง.

ในระหว่างเรียน

I. ตรวจการบ้าน

ครู: - พวก! คุณมีการบ้าน "จุดสำคัญของฟังก์ชัน, ค่าสูงสุดและค่าต่ำสุด" กำหนดจุดวิกฤติของฟังก์ชัน

นักศึกษา: - จุดวิกฤติคือจุดภายในของโดเมนของคำจำกัดความซึ่งอนุพันธ์มีค่าเท่ากับศูนย์หรือไม่มีอยู่จริง

ครู: - จะหาจุดวิกฤติได้อย่างไร?

นักเรียน: - 1

) ค้นหาอนุพันธ์ของฟังก์ชัน

2) แก้สมการ: f "(x) = 0 รากของสมการนี้คือจุดวิกฤต

ครู: - ค้นหาจุดวิกฤตของฟังก์ชัน:

ก) ฉ(x)= 4 - 2x + 7x 2

ข) ฉ(x)= 4x - x 3 /3

ก) 1) ค้นหาอนุพันธ์ของฟังก์ชันนี้:

ฉ "(x)= (4 - 2x + 7x 2)" = -2+14x

2) แก้สมการ f "(x)=0<=>-2+14x =0<=>x=1/7

3) เนื่องจากสมการ f "(x) = 0 มีหนึ่งรูต ฟังก์ชันนี้จึงมีจุดวิกฤตหนึ่งจุด x = 1/7

b) 1) ค้นหาอนุพันธ์ของฟังก์ชันนี้: f "(x)= 4 - x 2

2) แก้สมการ: f "(x)=0<=>4 - x 2 = 0<=>x = 2 หรือ x = -2

3) เนื่องจากสมการ f "(x) = 0 มีสองราก ฟังก์ชันนี้จึงมีจุดวิกฤตสองจุด x 1 = 2 และ x 2 = -2

ครั้งที่สองงานช่องปาก.

ครู: - พวก! ให้เราทำซ้ำคำถามพื้นฐานที่จำเป็นเพื่อศึกษาหัวข้อใหม่ เมื่อต้องการทำเช่นนี้ ให้พิจารณาตารางที่มีรูปภาพ ( ภาคผนวก 1).

ระบุจุดที่ฟังก์ชันเพิ่มขึ้นและลดลง จุดเหล่านี้เรียกว่าอะไร?

นักศึกษา: - ในรูป a) - จุด K คือจุดสูงสุด ในรูป b) - จุด M คือจุดสูงสุด

ครู: - ตั้งชื่อจุดต่ำสุดของฟังก์ชัน

นักเรียน: - จุด K ในรูปที่ c) และ d) คือจุดต่ำสุดของฟังก์ชัน

ครู: - จุดใดที่สามารถเป็นจุดปลายสุดของฟังก์ชันได้?

นักศึกษา: - จุดวิกฤตอาจเป็นจุดสุดขั้วของฟังก์ชันได้

ครู: - คุณรู้เงื่อนไขที่จำเป็นอะไรบ้าง?

นักเรียน: - มีทฤษฎีบทของแฟร์มาต์ เงื่อนไขที่จำเป็นสำหรับภาวะสุดขั้ว:หากจุด x 0 เป็นจุดปลายสุดของฟังก์ชัน f และ ณ จุดนี้ มีอนุพันธ์ f " ดังนั้นจะเท่ากับศูนย์: f "(x) = 0

ครู: - ค้นหาจุดวิกฤตของฟังก์ชัน:

ก) ฉ(x) = | x |

ข) ฉ(x) = 2x + | x |

นักศึกษา: - พิจารณาฟังก์ชัน f(x) = | x | ( ภาคผนวก 2). ฟังก์ชันนี้ไม่มีอนุพันธ์ที่ 0 ซึ่งหมายความว่า 0 เป็นจุดวิกฤต แน่นอนว่า ณ จุดที่ 0 ฟังก์ชันจะมีค่าต่ำสุด

นักศึกษา: - พิจารณาฟังก์ชัน f(x) = 2x + | x | ( ภาคผนวก 3). กราฟแสดงให้เห็นว่า ณ จุดที่ 0 ฟังก์ชันนี้ไม่มีจุดสิ้นสุด ณ จุดนี้ฟังก์ชันไม่มีอนุพันธ์

ที่จริงแล้ว ถ้าเราสมมุติว่าฟังก์ชัน f มีอนุพันธ์ที่จุด 0 แล้ว f(x) - 2x ก็มีอนุพันธ์ที่ 0 เช่นกัน แต่ f(x) - 2x = | x | และฟังก์ชัน | x | ที่จุด 0 ไม่สามารถหาอนุพันธ์ได้ กล่าวคือ เรามาถึงจุดขัดแย้งแล้ว

ซึ่งหมายความว่าฟังก์ชัน f ที่จุด 0 ไม่มีอนุพันธ์

ครู: - จากทฤษฎีบทของแฟร์มาต์ เป็นไปตามว่าเมื่อค้นหาจุดสุดขั้ว คุณจะต้องค้นหาจุดวิกฤต แต่จากตัวอย่างที่พิจารณา เห็นได้ชัดว่าเพื่อให้จุดวิกฤตินี้เป็นจุดสุดขั้ว จำเป็นต้องมีเงื่อนไขเพิ่มเติมบางประการ

คุณรู้เงื่อนไขที่เพียงพอสำหรับการดำรงอยู่ของภาวะสุดขั้ว ณ จุดใดจุดหนึ่งหรือไม่?

นักเรียน: - เครื่องหมายสูงสุดของฟังก์ชัน: ถ้าฟังก์ชัน f ต่อเนื่องกันที่จุด x 0 และ f "(x)> 0 ในช่วงเวลา (a; x 0) และ f "(x)<0 на интервале (х 0 ; в), то точка х 0 является точкой максимума функции f.

นั่นคือ ถ้า ณ จุด x 0 อนุพันธ์เปลี่ยนเครื่องหมายจากบวกเป็นลบ แล้ว x 0 คือจุดสูงสุด

นักเรียน: - ป้ายขั้นต่ำ: ถ้าฟังก์ชัน f ต่อเนื่องกันที่จุด x 0 และ f "(x)<0 на интервале (а;х 0) и f "(x) >0 ในช่วงเวลา (x 0 ; b) ดังนั้นจุด x 0 คือจุดต่ำสุดของฟังก์ชัน f

นั่นคือ ถ้า ณ จุด x 0 อนุพันธ์เปลี่ยนเครื่องหมายจากลบเป็นบวก แล้ว x 0 คือจุดต่ำสุด

ครู: - คุณรู้อัลกอริทึมอะไรในการค้นหาจุดสุดขั้วของฟังก์ชัน

นักเรียนอธิบายอัลกอริทึมสำหรับศึกษาฟังก์ชัน f ถึงสุดขีดโดยใช้อนุพันธ์ ( ภาคผนวก 4) และค้นหาจุดปลายสุดของฟังก์ชัน:

ฉ (x) \u003d x 4 -2x 2

D (f) =IR และ f ต่อเนื่องกันบนเส้นจำนวนทั้งหมด เช่นเดียวกับฟังก์ชันตรรกยะทั้งหมด

2. ฉ "(x) = 4x 3 -4x = 4x (x+1)(x-1)

3.f"(x)=0<=>x \u003d -1 V x \u003d 0 V x \u003d 1

รูปที่ 1 (เครื่องหมาย ฉ ")

เนื่องจาก f มีความต่อเนื่องที่จุดวิกฤต ดังนั้นจากรูปที่ 1 ( ภาคผนวก 5) เห็นได้ชัดว่า -1 และ 1 เป็นจุดต่ำสุด และ 0 คือจุดสูงสุดของฟังก์ชัน f

ฉ นาที = ฉ (-1) = ฉ (1) = -1, ฉสูงสุด = ฉ (0) =0

ครู: - พวก! จำอัลกอริทึมสำหรับค้นหาช่วงเวลาของความน่าเบื่อของฟังก์ชัน f

นักเรียนจำอัลกอริทึมสำหรับการค้นหาช่วงเวลาของความน่าเบื่อของฟังก์ชัน f ( ภาคผนวก 6).

ครู: - ค้นหาช่วงเวลาของการเพิ่มขึ้นและลดลงของฟังก์ชัน f ที่กำหนดโดยสูตร

ฉ (x) \u003d x 3 -12x

สารละลาย:

1. เนื่องจาก f(x) เป็นพหุนาม ดังนั้น D (f) =IR

2. ฟังก์ชัน f สามารถหาอนุพันธ์ได้บนเส้นจำนวนทั้งหมด และ f "(x)= 3x 2 -12 = 3 (x+2) (x-2)

3. จุดวิกฤตของฟังก์ชัน f ต้องเป็นศูนย์ของ f "(x) เท่านั้น

ฉ"(x)=0<=>x \u003d -2 V x \u003d 2

ง (ฉ)\ (-2; 2)= (-; -2) ยู (-2; 2) ยู (2; +)

รูปที่ 2 (เครื่องหมาย ฉ ")

ค้นหาโดเมนของคำจำกัดความและค่าของฟังก์ชันนี้ f

ค้นหาว่าฟังก์ชันมีคุณสมบัติที่เอื้อต่อการค้นคว้าหรือไม่ นั่นคือ ฟังก์ชัน f:

ก) คู่หรือคี่;

ข) เป็นระยะ

3. คำนวณพิกัดของจุดตัดของกราฟด้วยแกนพิกัด

4. ค้นหาช่วงเวลาของเครื่องหมายคงที่ของฟังก์ชัน f

5. ค้นหาว่าช่วงใดที่ฟังก์ชัน f เพิ่มขึ้นและลดลงในช่วงใด

6. ค้นหาจุดสุดขั้ว (สูงสุดหรือต่ำสุด) และคำนวณค่า f ที่จุดเหล่านี้

7. ตรวจสอบพฤติกรรมของฟังก์ชัน f ในบริเวณใกล้เคียงกับจุดคุณลักษณะที่ไม่รวมอยู่ในขอบเขตของคำจำกัดความ

8. สร้างกราฟของฟังก์ชัน

แผนภาพนี้เป็นเพียงตัวอย่างเท่านั้น

เมื่อคำนึงถึงทั้งหมดที่กล่าวไว้แล้ว มาตรวจสอบฟังก์ชันกัน: f(x) = 3x 5 -5x 3 +2 และสร้างกราฟของมัน

เรามาศึกษาตามโครงการที่ระบุ:

D (f ") =IR เนื่องจาก f (x) เป็นพหุนาม

ฟังก์ชัน f ไม่เป็นคู่หรือคี่ เนื่องจาก

ฉ (-x)= 3(-x) 5 -5(-x) 3 +2 = -3x 5 +5x 3 +2= -(3x 5 -5x 3 -2) ฉ(x)

มาหาพิกัดของจุดตัดของกราฟกับแกนพิกัด:

ก) ด้วยแกน 0X เพื่อแก้สมการนี้: 3x 5 -5x 3 +2 = 0

เมื่อใช้วิธีการเลือก คุณสามารถค้นหาหนึ่งในราก (x = 1) รากอื่น ๆ สามารถพบได้ประมาณเท่านั้น ดังนั้น สำหรับฟังก์ชันนี้ เราจะไม่พบจุดตัดที่เหลือของกราฟกับแกนแอบซิสซาและช่วงของเครื่องหมายคงที่

b) ด้วยแกน 0У: f(0)=2

จุด A (0; 2) คือจุดตัดของกราฟฟังก์ชันที่มีแกน 0Y

เราสังเกตว่าเราจะไม่พบช่วงความคงที่ของเครื่องหมาย

ลองหาช่วงเวลาของฟังก์ชันเพิ่มขึ้นและลดลง

ก) ฉ "(x)= 15x 4 -15x 2 = 15x 2 (x 2 -1)

D (f ") =IR ดังนั้นจึงไม่มีจุดวิกฤติที่ไม่มี f "(x)

ข) ฉ "(x) = 0 ถ้า x 2 (x 2 -1) = 0<=>x = -1 โวลต์ x = 0 โวลต์ x = 1

c) เราได้จุดวิกฤตสามจุด โดยแบ่งเส้นพิกัดออกเป็นสี่ช่วง ให้เรากำหนดสัญญาณของอนุพันธ์ในช่วงเวลาเหล่านี้:

รูปที่ 3 (เครื่องหมาย ฉ ")

IV. กำลังปักหมุดหัวข้อใหม่ การแก้ปัญหา.

ครู: - สำรวจฟังก์ชันและสร้างกราฟ: f (x) = x 4 -2x 2 -3

นักเรียน: - 1) D (f) = R.

2) ฉ(-x)= (-x) 4 -2(-x) 2 -3 = x 4 -2x 2 -3; ฉ(-x)= ฉ(x)

หมายความว่าฟังก์ชัน f เป็นเลขคู่ การศึกษาสามารถทำได้ในช่วงเวลาที่ฟังก์ชันเพิ่มขึ้นจาก - ถึง -4 ดังนั้นในช่วงเวลานี้ สมการ f (x) = 0 จึงไม่มีราก

b) ในช่วงเวลา [-1; 2] สมการยังไม่มีราก เนื่องจากในช่วงเวลานี้ ฟังก์ชันจะลดลงจาก -4 เป็น -31

c) ตามช่วงเวลาและลดลง [-∞;-1]

จุดสุดขั้ว: x นาที = -1

ฟังก์ชันสุดขั้ว: y min =y(-1)=1-2= -1

บทที่ 3 การวิจัยฟังก์ชัน

3.1. รูปแบบทั่วไปสำหรับการศึกษาฟังก์ชั่น

เมื่อตรวจสอบฟังก์ชัน คุณจำเป็นต้องรู้แผนการวิจัยทั่วไป:

1) D(y) – โดเมนของคำจำกัดความ (ช่วงการเปลี่ยนแปลงของตัวแปร x)

2) E(y) – พื้นที่ของค่า x (พื้นที่การเปลี่ยนแปลงของตัวแปร y)

3) ประเภทของฟังก์ชัน: ฟังก์ชันคู่ คี่ เป็นระยะ หรือทั่วไป

4) จุดตัดกันของกราฟฟังก์ชันกับแกน Ohi O (ถ้าเป็นไปได้)

5) ช่วงเวลาของความสม่ำเสมอของสัญญาณ:

ก) ฟังก์ชันรับค่าบวก: f(x)>0

b) ค่าลบ: f(x)<0.

6) ช่วงเวลาของความน่าเบื่อของฟังก์ชัน:

ก) เพิ่มขึ้น;

ข) ลดลง;

c) ความคงตัว (f=const)

7) คะแนนสูงสุด (คะแนนต่ำสุดและสูงสุด)

8) ฟังก์ชั่น extrema (ค่าฟังก์ชั่นที่จุดต่ำสุดและสูงสุด)

9) คะแนนเพิ่มเติม

สามารถนำมาใช้เพื่อพล็อตกราฟฟังก์ชันได้แม่นยำยิ่งขึ้น

ควรสังเกตว่า extrema ของฟังก์ชัน f ไม่ตรงกับค่าที่ใหญ่ที่สุดและเล็กที่สุดของฟังก์ชันเสมอไป

3.2. สัญญาณของฟังก์ชันที่เพิ่มขึ้นและลดลง

หากคุณสร้างกราฟของฟังก์ชันโดยใช้จุดที่เลือกแบบสุ่มบางจุด เชื่อมต่อพวกมันด้วยเส้นเรียบ แม้ว่าจะมีจุดสุ่มเลือกจำนวนมากมาก ก็อาจกลายเป็นว่ากราฟที่สร้างขึ้นในลักษณะนี้จะแตกต่างอย่างมากจาก กราฟของฟังก์ชันที่กำหนด

หากคุณใช้อนุพันธ์เมื่อศึกษาฟังก์ชันและค้นหาจุดที่เรียกว่า "อ้างอิง" เช่น จุดพัก จุดสูงสุดและต่ำสุด ช่วงเวลาของความน่าเบื่อของฟังก์ชัน จากนั้นถึงแม้จะมีจุด "อ้างอิง" จำนวนน้อย เราก็จะได้แนวคิดที่ถูกต้องเกี่ยวกับกราฟของฟังก์ชัน

ก่อนที่จะมาดูตัวอย่าง ฉันจะให้คำจำกัดความและทฤษฎีบทที่จำเป็นก่อน

การหาค่าความน่าเบื่อของฟังก์ชันในช่วงเวลาหนึ่ง กล่าวกันว่าฟังก์ชัน y=f(x) เพิ่มขึ้นในช่วงเวลาหนึ่ง ถ้าจุดใดๆ x 1 และ x 2 ของช่วงเวลานี้จากเงื่อนไข x 1<х 2 следует, что f(x 1)f(x 2) แล้วฟังก์ชันนี้จะลดลงในช่วงเวลานี้

สัญญาณที่เพียงพอของความน่าเบื่อของฟังก์ชันในช่วงเวลา ทฤษฎีบท: หากฟังก์ชันมีอนุพันธ์ที่เป็นค่าบวก (ลบ) ในแต่ละจุดของช่วงเวลา ฟังก์ชันนั้นจะเพิ่มขึ้น (ลดลง) ในช่วงเวลานี้

ทฤษฎีบทนี้ได้รับการยอมรับโดยไม่มีการพิสูจน์ในตำราเรียนของโรงเรียน

การตีความทางเรขาคณิตของทฤษฎีบทนั้นง่ายมาก ถ้าเราจำได้ว่า f ’(x)=tgα, α คือความชันของเส้นสัมผัสกันกับกราฟของฟังก์ชันที่จุดที่กำหนด x ตัวอย่างเช่น หาก f ‘ (x)>0 ในทุกจุดของช่วงเวลาหนึ่ง ค่าแทนเจนต์ของกราฟที่มีแกนแอบซิสซาจะทำให้เกิดมุมแหลม ซึ่งหมายความว่าเมื่อ x เพิ่มขึ้น f(x) จะเพิ่มขึ้นด้วย ถ้าฉ ' (x)<0, то касательная с осью абсцисс образуют тупой угол, а значит, с ростом х функция f(x) убывает. Поскольку эти рассуждения основаны лишь на наглядных геометрических представлениях, они не являются доказательством теоремы.

3.3. จุดวิกฤตของฟังก์ชัน ค่าสูงสุดและค่าต่ำสุด

การหาจุดปลายสุดของฟังก์ชัน . ให้ x 0 เป็นจุดภายในจากโดเมนของนิยามของฟังก์ชัน f(x) จากนั้น หากมี δ - ย่านใกล้เคียง ] x 0 - δ, x 0 + δ [ ชี้ x 0 โดยที่ x ทั้งหมดจากย่านนี้จะมีอสมการ f(x)≤f(x 0) (อสมการ f(x) )≥f (x 0)) จุด x 0 เรียกว่าจุดสูงสุด (จุดต่ำสุด) ของฟังก์ชันนี้

จุดสูงสุดและต่ำสุดคือจุดภายในของขอบเขตคำจำกัดความของฟังก์ชัน

สัญญาณที่จำเป็นของการมีอยู่ของฟังก์ชันเชิงอนุพันธ์ที่มีอยู่ .

ทฤษฎีบทของแฟร์มาต์

หาก x 0 เป็นจุดปลายสุดของฟังก์ชัน f(x) และ ณ จุดนี้อนุพันธ์มีอยู่ มันจะเท่ากับศูนย์: f ’(x 0) = 0

ทฤษฎีบทนี้ไม่ใช่เงื่อนไขที่เพียงพอสำหรับการมีอยู่ของส่วนปลายสุดของฟังก์ชันหาอนุพันธ์ได้: หาก ณ จุดใดจุดหนึ่ง x 0 อนุพันธ์หายไป แสดงว่าฟังก์ชันนั้นมีปลายสุดที่จุด x 0 ตามมา

การหาจุดวิกฤตของฟังก์ชัน . จุดภายในของโดเมนของคำจำกัดความของฟังก์ชันซึ่งมีอนุพันธ์เท่ากับศูนย์หรือไม่มีอยู่เรียกว่าจุดวิกฤตของฟังก์ชัน

เงื่อนไขที่เพียงพอสำหรับการดำรงอยู่ของสุดขั้ว .

ทฤษฎีบท 1 หากฟังก์ชัน f(x) ต่อเนื่องกันที่จุด x 0, f ‘(x)>0 ในช่วงเวลาและ f ‘(x)<0 на интервале , то х 0 является точкой максимума функции f(x).

ทฤษฎีบท 2 ถ้าฟังก์ชัน f(x) ต่อเนื่องกันที่จุด x 0, f ‘(x)<0 на интервале и f ‘(x)>0 ในช่วงเวลา จากนั้น x 0 คือจุดต่ำสุดของฟังก์ชัน f(x)

ในการค้นหาจุดสูงสุดของฟังก์ชัน คุณต้องค้นหาจุดวิกฤตและตรวจสอบว่าแต่ละจุดตรงตามเงื่อนไขเพียงพอสำหรับจุดสุดขั้วหรือไม่

3.4. ค่าที่ใหญ่ที่สุดและเล็กที่สุดของฟังก์ชัน

กฎสำหรับการค้นหาค่าฟังก์ชันที่ใหญ่ที่สุดและน้อยที่สุดในช่วงเวลา ในการค้นหาค่าที่ใหญ่ที่สุดและเล็กที่สุดของฟังก์ชันที่สามารถหาอนุพันธ์ได้ในช่วงเวลาหนึ่ง คุณจะต้องค้นหาจุดวิกฤตทั้งหมดที่อยู่ในช่วงเวลานั้น คำนวณค่าของฟังก์ชันที่จุดเหล่านี้และที่จุดสิ้นสุดของช่วงเวลา และเลือกค่าที่ใหญ่ที่สุดและเล็กที่สุดจากค่าทั้งหมดของฟังก์ชันที่ได้รับในลักษณะนี้

บทที่สี่ ตัวอย่างการใช้อนุพันธ์ในการศึกษาฟังก์ชัน

ตัวอย่างที่ 11 สำรวจฟังก์ชัน y=x 3 +6x 2 +9x แล้ววาดกราฟ

2) กำหนดประเภทของฟังก์ชัน:

y(-x)=(-x) 3 +6(-x) 2 +9(-x)=-x+6x 2 -9x ฟังก์ชันของรูปแบบทั่วไป

x=0 หรือ x 2 +6x+9=0

D=0 สมการมีหนึ่งรูท

(0;0) และ (-3;0) คือจุดตัดกับแกน x

y'=(x 3 +6x 2 +9x)'=3x 2 +12x+9

y'=0 เช่น 3x 2 +12x+9=0 ลดลง 3

D>0 สมการมี 2 ราก

x 1,2 =(-b±√D)/2a, x 1 =(-4+2)/2, x 2 =(-4-2)/2

0
-4

x=-4, y’=3*16-48+9=9>0

x=-2, y’=12-24+9=-3<0

x=0, y’=0+0+9=9>0

7) ค้นหา x นาที และ x สูงสุด:

8) ค้นหาจุดสุดขีดของฟังก์ชัน:

y นาที =y(-1)=-1+6-9=-4

y สูงสุด =y(-3)=-27+54-27=0

9) มาสร้างกราฟของฟังก์ชันกันดีกว่า:

10) คะแนนเพิ่มเติม:

ญ(-4)=-64+96-36=-4

ตัวอย่างที่ 12 สำรวจฟังก์ชัน y=x 2 /(x-2) และวาดกราฟ

y=x 2 /(x-2)=x+2+4/(x-2)

ลองหาเส้นกำกับของฟังก์ชัน:

x≠ 2, x=2 – เส้นกำกับแนวตั้ง

y=x+2 – เส้นกำกับเฉียง เนื่องจาก

ลองหาโดเมนของคำจำกัดความกัน

2) เรามากำหนดประเภทของฟังก์ชันกัน

y(-x)=(-x) 2 /(-x-2)=x 2 /(-x-2) ซึ่งเป็นฟังก์ชันที่มีรูปแบบทั่วไป

3) ค้นหาจุดตัดกับแกน

Oy: x=0, y=0 (0;0) – จุดตัดกับแกน y

x=0 หรือ x=2 (2;0) – จุดตัดกับแกน x

4) ค้นหาอนุพันธ์ของฟังก์ชัน:

y'=(2x(x-2)-x 2)/(x-2) 2 =(2x 2 -4x-x 2)/(x-2) 2 =(x(x-4))/(x -2) 2 =(x 2 -4x)/(x-2) 2

5) เรามาพิจารณาประเด็นสำคัญ:

x 2 -4x=0 x(x-4)=0

y’=0, (x 2 -4x)/(x-2) 2 =0<=> <=>

(x-2) 2 ≠ 0 x≠ 2

x 2 -4x=0 และ (x-2) 2 ≠ 0 เช่น x≠ 2

6) ให้เรากำหนดจุดวิกฤตบนเส้นพิกัดและกำหนดสัญลักษณ์ของฟังก์ชัน

0 8

x=-1, y’=(1+4)/9=5/9>0

x=1, y’=(1-4)/1=-3<0

x=3, y’=(9-12)/1=-3<0

x=5, y’=(25-20)/9=5/9>0

7) ค้นหาจุดต่ำสุดและสูงสุดของฟังก์ชัน:

8) ค้นหาจุดสุดขีดของฟังก์ชัน:

ymin=y(4)=16/2=8

9) มาสร้างกราฟของฟังก์ชันกันดีกว่า:

10) คะแนนเพิ่มเติม:

y(-3)=9/-5=-1.8 y(3)=9/1=9

y(1)=1/-1=-1 y(6)=36/4=9

ตัวอย่างที่ 13 สำรวจฟังก์ชัน y=(6(x-1))/(x 2 +3) และสร้างกราฟ 1) ค้นหาโดเมนของคำจำกัดความของฟังก์ชัน:

2) กำหนดประเภทของฟังก์ชัน:

y(-x)=(6(-x-1))/(x 2 +3)=-(6(x+1))/(x 2 -3) เป็นฟังก์ชันที่มีรูปแบบทั่วไป

3) ค้นหาจุดตัดกับแกน:

O y: x=0, y=(6(0-1))/(0+3)=-2, (0;-2) – จุดตัดกับแกน y

(6(x-1))/(x 2 +3)=0

O x: y=0,<=>

4) ค้นหาอนุพันธ์ของฟังก์ชัน:

y'=(6(x-1)/(x 2 +3))'=6(x 2 +3-2x 2 +2x)/(x 2 +2) 2 =-6(x+1)(x -3)/(x 2 +3) 2

5) เรามาพิจารณาประเด็นสำคัญ:

y'=0 เช่น -6(x+1)(x-3)/(x 2 +3) 2 =0

y’=0 ถ้า x 1 =-1 หรือ x 2 =3 แล้ว x=-1 และ x=3 คือจุดวิกฤต

6) ให้เราแสดงจุดวิกฤตบนเส้นพิกัดและกำหนดสัญลักษณ์ของฟังก์ชัน:

-3 2

x=-2, y’=-6(-2+1)(-2-3)/(4+3) 2 =-30/49<0

x=0, y’=-6(0+1)(0-3)/(0+3) 2 =2>0

x=4, y’=-6(4+1)(4-3)/(16+3) 2 =-30/361<0

7) ค้นหาจุดต่ำสุดและสูงสุด:

8) ค้นหาจุดสุดขีดของฟังก์ชัน:

y นาที =y(-1)=(6(-1-1))/(1+3)=-12/4=-3

y สูงสุด =y(3)=(6(3-1))/(9+3)=12/12=1

9) มาสร้างกราฟของฟังก์ชันกันดีกว่า:

10) คะแนนเพิ่มเติม:

y(-3)=(6(-3-1))/(9+3)=-24/12=-2

y(6)=(6(6-1))/(36+3)=30/39=10/13µ 0.77

ตัวอย่างที่ 14 สำรวจฟังก์ชัน y=xlnx แล้วลงจุด:

1) ค้นหาโดเมนของคำจำกัดความของฟังก์ชัน:

D(y)=R + (ค่าบวกเท่านั้น)

2) กำหนดประเภทของฟังก์ชัน:

y(-x)=-xlnx - รูปแบบทั่วไป

3) ค้นหาจุดตัดกับแกน:

โอ้ y แต่ x≠ 0 ซึ่งหมายความว่าไม่มีจุดตัดกับแกน y

O x: y=0 นั่นคือ xlnx=0

x=0 หรือ lnx=0

(1;0) – จุดตัดกับแกน x

4) ค้นหาอนุพันธ์ของฟังก์ชัน:

y'=x' ln x + x(ln x)'=ln x +1

5) เรามาพิจารณาประเด็นสำคัญ:

y'=0 เช่น lnx +1=0

y’=0 ถ้า x=1/e แล้ว x=1/e เป็นจุดวิกฤต

6) ให้เราแสดงจุดวิกฤตบนเส้นพิกัดและกำหนดสัญลักษณ์ของฟังก์ชัน:

1/จ

x=1/(2e); y'=บันทึก(2e) -1 +1=1-ln(2e)=1-ln อี=-ln 2<0

x=2e; y'=ln(2e)+1=ln 2+ln อี+1=ln 2+2>0

7) 1/e – จุดต่ำสุดของฟังก์ชัน

8) ค้นหาจุดสุดขีดของฟังก์ชัน:

y min \u003d y (1 / e) \u003d 1 / e ln e -1 \u003d -1 / e (γ -0.4)

9) มาสร้างกราฟของฟังก์ชันกันดีกว่า:

บทสรุป.

นักวิทยาศาสตร์และนักปรัชญาหลายคนทำงานในหัวข้อนี้ เมื่อหลายปีก่อนคำเหล่านี้ถือกำเนิดขึ้น: ฟังก์ชัน กราฟ การศึกษาฟังก์ชัน และยังคงได้รับการอนุรักษ์ไว้ ทำให้ได้รับคุณลักษณะและลักษณะเฉพาะใหม่ๆ

ฉันเลือกหัวข้อนี้เพราะฉันสนใจที่จะศึกษาเส้นทางการวิจัยเกี่ยวกับการทำงานนี้มาก สำหรับฉันดูเหมือนว่าหลายคนจะสนใจที่จะเรียนรู้เพิ่มเติมเกี่ยวกับฟังก์ชัน คุณสมบัติ และการแปลงของมัน เมื่อเขียนเรียงความนี้เสร็จ ฉันได้จัดระบบทักษะและเพิ่มพูนความรู้เกี่ยวกับหัวข้อนี้

ฉันอยากจะสนับสนุนให้ทุกคนศึกษาหัวข้อนี้เพิ่มเติม

บรรณานุกรม.

1. บาชมาคอฟ, มิ.ย. พีชคณิตกับจุดเริ่มต้นของการวิเคราะห์ - อ.: การศึกษา, 2535.

2. เกลเซอร์, G.I. ประวัติศาสตร์คณิตศาสตร์ในโรงเรียน - อ.: การศึกษา, 2526.

3. กูเซฟ วี.เอ. คณิตศาสตร์: เอกสารอ้างอิง - อ.: การศึกษา, 2431.

4. Dorofeev, G.V. คู่มือคณิตศาสตร์สำหรับผู้เข้ามหาวิทยาลัย - อ.: เนากา, 2517.

5. โซริน, V.V. คู่มือคณิตศาสตร์สำหรับผู้เข้ามหาวิทยาลัย - ม.: อุดมศึกษา, 2523.

6. โคลโมโกรอฟ เอ.เอ็น. พีชคณิตและจุดเริ่มต้นของการวิเคราะห์ - อ.: การศึกษา, 2536.