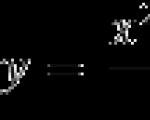บ้าน › แสงและกระจก › วิธีลบโมดูลในความไม่เท่าเทียมกัน สมการโมดูโล่

วิธีลบโมดูลในความไม่เท่าเทียมกัน สมการโมดูโล่

การแก้ปัญหาความไม่เท่าเทียมกันทางออนไลน์

ก่อนที่จะแก้อสมการ จำเป็นต้องเข้าใจวิธีการแก้สมการให้ดีเสียก่อน

ไม่สำคัญว่าอสมการจะเข้มงวด () หรือไม่เข้มงวด (≤, ≥) ขั้นตอนแรกคือการแก้สมการโดยแทนที่เครื่องหมายอสมการด้วยความเท่าเทียมกัน (=)

อธิบายว่าการแก้ปัญหาความไม่เท่าเทียมกันหมายความว่าอย่างไร

หลังจากศึกษาสมการแล้ว นักเรียนมีภาพต่อไปนี้ในหัว: คุณต้องค้นหาค่าดังกล่าวของตัวแปรที่สมการทั้งสองส่วนใช้ค่าเดียวกัน กล่าวอีกนัยหนึ่ง ให้ค้นหาจุดทั้งหมดที่มีความเท่าเทียมกัน ทุกอย่างถูกต้อง!

เมื่อพูดถึงความไม่เท่าเทียมกัน หมายถึงการค้นหาช่วงเวลา (ส่วน) ที่ความไม่เท่าเทียมกันมีอยู่ หากมีตัวแปรสองตัวในอสมการ ผลเฉลยจะไม่ใช่ช่วงเวลาอีกต่อไป แต่จะเป็นบางพื้นที่บนระนาบ ลองทายซิว่าอะไรคือคำตอบของความไม่เท่าเทียมกันในตัวแปรทั้งสาม?

จะแก้ไขความไม่เท่าเทียมกันได้อย่างไร?

วิธีการกำหนดช่วงเวลา (หรือที่รู้จักในชื่อวิธีการเว้นช่วงเวลา) ถือเป็นวิธีสากลในการแก้ไขความไม่เท่าเทียมกัน ซึ่งประกอบด้วยการกำหนดช่วงเวลาทั้งหมดที่จะบรรลุถึงความไม่เท่าเทียมกันที่กำหนด

ในกรณีนี้นี่ไม่ใช่สาระสำคัญโดยไม่ต้องคำนึงถึงประเภทของอสมการ แต่จำเป็นต้องแก้สมการที่เกี่ยวข้องและกำหนดรากของมันตามด้วยการกำหนดวิธีแก้ปัญหาเหล่านี้บนแกนตัวเลข

วิธีที่ถูกต้องในการเขียนคำตอบของอสมการคืออะไร?

เมื่อคุณได้กำหนดช่วงเวลาในการแก้อสมการแล้ว คุณต้องเขียนคำตอบให้ถูกต้องด้วยตัวมันเอง มีความแตกต่างที่สำคัญ - ขอบเขตของช่วงเวลารวมอยู่ในการแก้ปัญหาหรือไม่?

ทุกอย่างเรียบง่ายที่นี่ หากการแก้สมการเป็นไปตาม ODZ และอสมการไม่เข้มงวด ขอบเขตของช่วงจะรวมอยู่ในคำตอบของอสมการด้วย มิฉะนั้นไม่มี

เมื่อพิจารณาแต่ละช่วงเวลา วิธีแก้ปัญหาความไม่เท่าเทียมกันอาจเป็นช่วงนั้นเอง หรือช่วงครึ่งเวลา (เมื่อขอบเขตใดขอบเขตหนึ่งเป็นไปตามความไม่เท่าเทียมกัน) หรือการแบ่งส่วน - ช่วงเวลาร่วมกับขอบเขตของมัน

จุดสำคัญ

อย่าคิดว่าเฉพาะช่วงเวลา ช่วงเวลาครึ่งเวลา และการแบ่งส่วนเท่านั้นที่จะสามารถแก้ปัญหาความไม่เท่าเทียมกันได้ ไม่ได้ สามารถรวมคะแนนแต่ละคะแนนไว้ในโซลูชันได้เช่นกัน

ตัวอย่างเช่น อสมการ |x|≤0 มีวิธีแก้ปัญหาเพียงวิธีเดียว - จุด 0

และอสมการ |x|

เครื่องคำนวณอสมการมีไว้เพื่ออะไร?

เครื่องคำนวณอสมการจะให้คำตอบสุดท้ายที่ถูกต้อง ในกรณีนี้ ในกรณีส่วนใหญ่ จะมีการแสดงภาพประกอบของแกนตัวเลขหรือระนาบ คุณสามารถดูได้ว่าขอบเขตของช่วงเวลารวมอยู่ในโซลูชันหรือไม่ - จุดต่างๆ จะแสดงเต็มหรือเจาะ

ด้วยเครื่องคำนวณอสมการออนไลน์ คุณสามารถตรวจสอบว่าคุณพบรากของสมการถูกต้องหรือไม่ ทำเครื่องหมายไว้บนเส้นจำนวน และตรวจสอบเงื่อนไขอสมการในช่วงเวลา (และขอบเขต) หรือไม่

หากคำตอบของคุณแตกต่างจากคำตอบของเครื่องคิดเลข คุณจะต้องตรวจสอบวิธีแก้ปัญหาของคุณอีกครั้งและระบุข้อผิดพลาดที่เกิดขึ้น

ยิ่งบุคคลเข้าใจมากเท่าไร ความปรารถนาที่จะเข้าใจก็จะยิ่งมากขึ้นเท่านั้น

โทมัส อไควนัส

วิธีช่วงเวลาช่วยให้คุณสามารถแก้สมการใดๆ ที่มีโมดูลัสได้ สาระสำคัญของวิธีนี้คือการแบ่งแกนตัวเลขออกเป็นหลายส่วน (ช่วงเวลา) และจำเป็นต้องแบ่งแกนด้วยศูนย์ของนิพจน์ในโมดูล จากนั้น ในแต่ละส่วนที่เป็นผลลัพธ์ นิพจน์โมดูลย่อยใดๆ จะเป็นค่าบวกหรือค่าลบ ดังนั้น แต่ละโมดูลสามารถขยายได้ด้วยเครื่องหมายลบหรือเครื่องหมายบวก หลังจากการกระทำเหล่านี้ ยังคงเป็นเพียงการแก้สมการง่าย ๆ แต่ละสมการที่ได้รับในช่วงเวลาที่พิจารณาและรวมคำตอบที่ได้รับ

ลองพิจารณาวิธีนี้กับตัวอย่างที่เฉพาะเจาะจง

|x + 1| + |2x – 4| – |x + 3| = 2x - 6.

1) ค้นหาศูนย์ของนิพจน์ในโมดูล ในการทำเช่นนี้ เราทำให้มันเท่ากันกับศูนย์ และแก้สมการผลลัพธ์

x + 1 = 0 2x – 4 = 0 x + 3 = 0

x = -1 2x = 4 x = -3

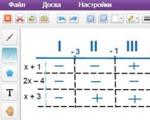
2) จัดเรียงจุดผลลัพธ์ตามลำดับที่ต้องการบนเส้นพิกัด พวกเขาจะแบ่งแกนทั้งหมดออกเป็นสี่ส่วน

3) เรามาพิจารณาแต่ละส่วนที่เป็นผลจากสัญญาณของนิพจน์ในโมดูล ในการทำเช่นนี้เราจะแทนที่ตัวเลขใด ๆ จากช่วงที่เราสนใจ หากผลลัพธ์ของการคำนวณเป็นจำนวนบวก เราจะใส่ "+" ลงในตาราง และหากตัวเลขเป็นลบ เราก็จะใส่ "-" สามารถนึกภาพได้ดังนี้:

4) ตอนนี้เราจะแก้สมการในแต่ละช่วงเวลาทั้งสี่โดยเปิดโมดูลด้วยเครื่องหมายที่อยู่ในตาราง ดังนั้น ให้พิจารณาช่วงแรก:

ฉันช่วงเวลา (-∞; -3) โมดูลทั้งหมดจะเปิดขึ้นโดยมีเครื่องหมาย "-" เราได้รับสมการต่อไปนี้:

-(x + 1) - (2x - 4) - (-(x + 3)) \u003d 2x - 6 เรานำเสนอคำศัพท์ที่คล้ายกันโดยก่อนหน้านี้ได้เปิดวงเล็บในสมการผลลัพธ์:

X - 1 - 2x + 4 + x + 3 = 2x - 6

คำตอบที่ได้รับจะไม่รวมอยู่ในช่วงเวลาที่พิจารณา จึงไม่จำเป็นต้องเขียนลงในคำตอบสุดท้าย

ช่วงที่สอง [-3; -1) ในช่วงเวลานี้ในตารางจะมีเครื่องหมาย "-", "-", "+" นี่คือวิธีที่เราเปิดเผยโมดูลของสมการดั้งเดิม:

-(x + 1) - (2x - 4) - (x + 3) = 2x - 6 ลดความซับซ้อนโดยขยายวงเล็บ:

X - 1 - 2x + 4 - x - 3 \u003d 2x - 6 เรานำเสนอในสมการผลลัพธ์ต่อไปนี้:

x = 6/5. จำนวนผลลัพธ์ไม่อยู่ในช่วงที่พิจารณา ดังนั้นจึงไม่ใช่รากของสมการดั้งเดิม

ช่วงที่สาม [-1; 2). เราเปิดโมดูลของสมการดั้งเดิมด้วยเครื่องหมายที่อยู่ในรูปในคอลัมน์ที่สาม เราได้รับ:

(x + 1) - (2x - 4) - (x + 3) = 2x - 6 นำวงเล็บออก ย้ายพจน์ที่มีตัวแปร x ไปด้านซ้ายของสมการ และไม่มี x ไปทางขวา . จะมี:

x + 1 - 2x + 4 - x - 3 = 2x - 6

หมายเลข 2 ไม่รวมอยู่ในช่วงเวลาที่พิจารณา

ช่วงเวลา IV

พูดง่ายๆ ก็คือ โมดูลัสคือ "ตัวเลขที่ไม่มีเครื่องหมายลบ" และมันอยู่ในความเป็นคู่นี้ (โดยที่คุณไม่จำเป็นต้องทำอะไรกับหมายเลขเดิม แต่บางแห่งคุณต้องลบเครื่องหมายลบออก) และความยากลำบากทั้งหมดสำหรับนักเรียนมือใหม่ก็อยู่

นอกจากนี้ยังมีคำจำกัดความทางเรขาคณิตด้วย การรู้ก็มีประโยชน์เช่นกัน แต่เราจะอ้างอิงถึงมันเฉพาะในกรณีที่ซับซ้อนและบางกรณีพิเศษเท่านั้น ซึ่งวิธีการทางเรขาคณิตนั้นสะดวกกว่าวิธีพีชคณิต (สปอยเลอร์: ไม่ใช่วันนี้)

คำนิยาม. ให้จุด $a$ ถูกกำหนดไว้บนเส้นจริง จากนั้นโมดูล $\left| x-a \right|$ คือระยะห่างจากจุด $x$ ถึงจุด $a$ บนเส้นนี้

หากคุณวาดภาพคุณจะได้สิ่งนี้:

คำจำกัดความของโมดูลกราฟิก

ไม่ทางใดก็ทางหนึ่ง คุณสมบัติหลักของมันจะตามมาจากคำจำกัดความของโมดูลทันที: โมดูลัสของตัวเลขจะเป็นค่าที่ไม่เป็นลบเสมอ. ความจริงข้อนี้จะกลายเป็นด้ายแดงที่พาดผ่านเรื่องราวทั้งหมดของเราในวันนี้

การแก้ปัญหาความไม่เท่าเทียมกัน วิธีการเว้นวรรค

ทีนี้มาจัดการกับความไม่เท่าเทียมกันกัน มีพวกมันมากมาย แต่งานของเราตอนนี้คือต้องสามารถแก้ไขอย่างน้อยที่สุดก็ง่ายที่สุด สิ่งที่ลดลงเป็นอสมการเชิงเส้นเช่นเดียวกับวิธีการของช่วงเวลา

ฉันมีบทเรียนสำคัญสองบทในหัวข้อนี้ (อย่างไรก็ตาม มีประโยชน์มาก - ฉันแนะนำให้ศึกษา):

วิธีช่วงเวลาสำหรับความไม่เท่าเทียมกัน (โดยเฉพาะดูวิดีโอ)
อสมการแบบเศษส่วน-ตรรกยะเป็นบทเรียนที่กว้างขวางมาก แต่หลังจากนั้น คุณจะไม่มีคำถามใดๆ เลย

หากคุณรู้ทั้งหมดนี้หากวลี "เปลี่ยนจากความไม่เท่าเทียมกันไปสู่สมการ" ไม่ได้ทำให้คุณอยากฆ่าตัวตายชิดกำแพงอย่างคลุมเครือแสดงว่าคุณพร้อมแล้ว: ยินดีต้อนรับสู่หัวข้อหลักของบทเรียน ยินดีต้อนรับสู่นรก :)

1. ความไม่เท่าเทียมกันของรูปแบบ "โมดูลน้อยกว่าฟังก์ชัน"

นี่เป็นหนึ่งในงานที่พบบ่อยที่สุดในโมดูล จำเป็นต้องแก้ไขความไม่เท่าเทียมกันของแบบฟอร์ม:

\[\ซ้าย| ฉ\ขวา| \ltg\]

อะไรก็ตามที่ทำหน้าที่เป็นฟังก์ชัน $f$ และ $g$ ได้ แต่โดยปกติแล้วจะเป็นพหุนาม ตัวอย่างของความไม่เท่าเทียมกันดังกล่าว:

พวกเขาทั้งหมดได้รับการแก้ไขอย่างแท้จริงในบรรทัดเดียวตามแบบแผน:

\[\ซ้าย| ฉ\ขวา| \lt g\Rightarrow -g \lt f \lt g\quad \left(\ลูกศรขวา \left\( \begin(align) & f \lt g, \\ & f \gt -g \\\end(align) \right.\right)\]

มันง่ายที่จะเห็นว่าเรากำจัดโมดูลออกไป แต่กลับกลายเป็นความไม่เท่าเทียมกันสองเท่า (หรือซึ่งเป็นสิ่งเดียวกัน นั่นคือระบบของความไม่เท่าเทียมกันสองประการ) แต่การเปลี่ยนแปลงนี้คำนึงถึงปัญหาที่อาจเกิดขึ้นทั้งหมด: หากตัวเลขใต้โมดูลเป็นบวก วิธีการนี้ก็ใช้งานได้ หากเป็นลบก็ยังใช้งานได้ และถึงแม้จะมีฟังก์ชันที่ไม่เพียงพอที่สุดแทนที่ $f$ หรือ $g$ วิธีการก็ยังใช้งานได้

โดยธรรมชาติแล้วคำถามก็เกิดขึ้น: มันไม่ง่ายกว่าเหรอ? น่าเสียดายที่คุณไม่สามารถทำได้ นี่คือจุดรวมของโมดูล

แต่พอเป็นปรัชญาแล้ว มาแก้ไขปัญหาสองสามข้อกัน:

งาน. แก้ความไม่เท่าเทียมกัน:

\[\ซ้าย| 2x+3\ขวา| \ltx+7\]

สารละลาย. ดังนั้นเราจึงมีความไม่เท่าเทียมกันแบบคลาสสิกของรูปแบบ "โมดูลน้อยกว่า" - ไม่มีอะไรจะแปลงด้วยซ้ำ เราทำงานตามอัลกอริทึม:

\[\begin(align) & \left| ฉ\ขวา| \lt g\ลูกศรขวา -g \lt f \lt g; \\ & \ซ้าย| 2x+3\ขวา| \lt x+7\ลูกศรขวา -\left(x+7 \right) \lt 2x+3 \lt x+7 \\\end(align)\]

อย่ารีบเปิดวงเล็บที่มี "ลบ" นำหน้า: ค่อนข้างเป็นไปได้ว่าคุณจะทำผิดพลาดที่น่ารังเกียจเนื่องจากการเร่งรีบ

\[-x-7 \lt 2x+3 \lt x+7\]

\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(align) \right.\]

\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \right.\]

\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \right.\]

ปัญหาลดลงเหลือความไม่เท่าเทียมกันเบื้องต้นสองประการ เราสังเกตวิธีแก้ปัญหาของพวกเขาบนเส้นจริงคู่ขนาน:
ทางแยกของหลาย ๆ คน
จุดตัดของเซตเหล่านี้จะเป็นคำตอบ

คำตอบ: $x\in \left(-\frac(10)(3);4 \right)$

งาน. แก้ความไม่เท่าเทียมกัน:

\[\ซ้าย| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0\]

สารละลาย. งานนี้ยากขึ้นเล็กน้อย ขั้นแรก เราแยกโมดูลโดยเลื่อนเทอมที่สองไปทางขวา:

\[\ซ้าย| ((x)^(2))+2x-3 \right| \lt -3\left(x+1 \right)\]

เห็นได้ชัดว่าเรามีความไม่เท่าเทียมกันของรูปแบบ "โมดูลน้อยกว่า" อีกครั้งดังนั้นเราจึงกำจัดโมดูลตามอัลกอริทึมที่ทราบอยู่แล้ว:

\[-\left(-3\left(x+1 \right) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \right)\]

ตอนนี้โปรดทราบ: บางคนจะบอกว่าฉันเป็นคนนิสัยไม่ดีกับวงเล็บพวกนี้ แต่ฉันขอเตือนคุณอีกครั้งว่าเป้าหมายหลักของเราคือ แก้ความไม่เท่าเทียมกันให้ถูกต้องแล้วได้คำตอบ. ต่อมา เมื่อคุณเชี่ยวชาญทุกสิ่งที่อธิบายไว้ในบทเรียนนี้อย่างสมบูรณ์แบบแล้ว คุณสามารถบิดเบือนตัวเองได้ตามที่คุณต้องการ: เปิดวงเล็บเหลี่ยม เพิ่มข้อเสีย ฯลฯ

อันดับแรก เราแค่กำจัดเครื่องหมายลบสองเท่าทางด้านซ้าย:

\[-\left(-3\left(x+1 \right) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\ซ้าย(x+1\ขวา)\]

ทีนี้มาเปิดวงเล็บทั้งหมดในอสมการสองเท่ากัน:

มาดูอสมการสองเท่ากัน. คราวนี้การคำนวณจะจริงจังกว่านี้:

\[\left\( \begin(จัดแนว) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(จัดตำแหน่ง) \right.\]

\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( จัดตำแหน่ง)\right.\]

อสมการทั้งสองเป็นรูปสี่เหลี่ยมจัตุรัสและแก้ไขได้โดยวิธีช่วงเวลา (นั่นคือเหตุผลที่ฉันพูดว่า: ถ้าคุณไม่รู้ว่ามันคืออะไร จะยังไม่ดีกว่าที่จะไม่เข้าร่วมโมดูล) เราส่งผ่านไปยังสมการในอสมการแรก:

\[\begin(align) & ((x)^(2))+5x=0; \\ & x\ซ้าย(x+5 \ขวา)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\end(จัดแนว)\]

อย่างที่คุณเห็นผลลัพธ์กลายเป็นสมการกำลังสองที่ไม่สมบูรณ์ซึ่งแก้ไขได้ในเบื้องต้น ทีนี้มาจัดการกับอสมการที่สองของระบบกัน ที่นั่นคุณต้องใช้ทฤษฎีบทของ Vieta:

\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\end(จัดแนว)\]

เราทำเครื่องหมายตัวเลขที่ได้รับบนเส้นคู่ขนานสองเส้น (แยกสำหรับความไม่เท่าเทียมกันแรกและแยกจากที่สอง):
อีกครั้ง เนื่องจากเรากำลังแก้ระบบอสมการ เราจึงสนใจจุดตัดของเซตสีเทา: $x\in \left(-5;-2 \right)$ นี่คือคำตอบ
คำตอบ: $x\in \left(-5;-2 \right)$

ฉันคิดว่าหลังจากตัวอย่างเหล่านี้ รูปแบบการแก้ปัญหามีความชัดเจนมาก:

แยกโมดูลโดยการย้ายพจน์อื่นๆ ทั้งหมดไปไว้ฝั่งตรงข้ามของอสมการ ดังนั้นเราจึงได้ความไม่เท่าเทียมกันของรูปแบบ $\left| ฉ\ขวา| \ltg$.
แก้ไขความไม่เท่าเทียมกันนี้ด้วยการกำจัดโมดูลตามที่อธิบายไว้ข้างต้น เมื่อถึงจุดหนึ่ง จำเป็นต้องย้ายจากความไม่เท่าเทียมกันสองเท่าไปเป็นระบบที่มีนิพจน์อิสระสองตัว ซึ่งแต่ละนิพจน์สามารถแก้ไขได้แยกกันอยู่แล้ว
ท้ายที่สุด เหลือเพียงการข้ามคำตอบของนิพจน์อิสระทั้งสองนี้ - เท่านั้นเอง เราก็จะได้คำตอบสุดท้าย

อัลกอริธึมที่คล้ายกันมีอยู่สำหรับอสมการประเภทต่อไปนี้ เมื่อโมดูลัสมากกว่าฟังก์ชัน อย่างไรก็ตาม มี "แต่" ที่ร้ายแรงอยู่สองสามประการ เราจะพูดถึง "แต่" เหล่านี้ตอนนี้

2. ความไม่เท่าเทียมกันของรูปแบบ "โมดูลมีค่ามากกว่าฟังก์ชัน"

พวกเขามีลักษณะเช่นนี้:

\[\ซ้าย| ฉ\ขวา| \gt ก\]

คล้ายกับครั้งก่อน? มันดูเหมือน. อย่างไรก็ตามงานดังกล่าวได้รับการแก้ไขด้วยวิธีที่แตกต่างไปจากเดิมอย่างสิ้นเชิง อย่างเป็นทางการโครงการมีดังนี้:

\[\ซ้าย| ฉ\ขวา| \gt g\ลูกศรขวา \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(align) \right.\]

กล่าวอีกนัยหนึ่ง เราจะพิจารณาสองกรณี:

อันดับแรก เราเพียงเพิกเฉยต่อโมดูล - เราแก้ไขความไม่เท่าเทียมกันตามปกติ
จากนั้น ที่จริงแล้ว เราเปิดโมดูลด้วยเครื่องหมายลบ จากนั้นเราก็คูณทั้งสองส่วนของอสมการด้วย −1 ด้วยเครื่องหมาย

ในกรณีนี้ ตัวเลือกจะรวมกับวงเล็บเหลี่ยม เช่น เรามีข้อกำหนดสองประการรวมกัน

โปรดทราบอีกครั้ง: ตรงหน้าเราไม่ใช่ระบบ แต่เป็นระบบรวม ในคำตอบ เซตต่างๆ จะรวมกัน ไม่ถูกตัดกัน. นี่เป็นความแตกต่างพื้นฐานจากย่อหน้าก่อนหน้า!

โดยทั่วไปแล้ว นักเรียนหลายคนมีความสับสนอย่างมากกับสหภาพแรงงานและทางแยก ดังนั้น เรามาดูปัญหานี้กันสักครั้ง:

"∪" เป็นเครื่องหมายการต่อกัน อันที่จริงนี่คือตัวอักษรเก๋ "U" ซึ่งมาจากภาษาอังกฤษและเป็นคำย่อของ "Union" เช่น "สมาคม".
"∩" คือป้ายสี่แยก เรื่องไร้สาระนี้ไม่ได้มาจากไหน แต่แค่ปรากฏเป็นการต่อต้าน "∪"

เพื่อให้จำง่ายยิ่งขึ้น เพียงเพิ่มขาบนป้ายเหล่านี้เพื่อทำแว่นตา (อย่ากล่าวหาว่าฉันส่งเสริมการติดยาและโรคพิษสุราเรื้อรังในขณะนี้: หากคุณกำลังศึกษาบทเรียนนี้อย่างจริงจัง แสดงว่าคุณติดยาแล้ว):

ความแตกต่างระหว่างจุดตัดและการรวมกันของเซต

เมื่อแปลเป็นภาษารัสเซียหมายถึงสิ่งต่อไปนี้: สหภาพ (คอลเลกชัน) มีองค์ประกอบจากทั้งสองชุดดังนั้นจึงไม่น้อยไปกว่าแต่ละชุด แต่จุดตัด (ระบบ) จะรวมเฉพาะองค์ประกอบที่อยู่ในชุดแรกและชุดที่สองเท่านั้น ดังนั้นจุดตัดกันของเซตจึงไม่มากกว่าเซตต้นทาง

มันเลยชัดเจนขึ้น? เป็นสิ่งที่ดี. เรามาฝึกกันต่อ

งาน. แก้ความไม่เท่าเทียมกัน:

\[\ซ้าย| 3x+1 \ขวา| \gt 5-4x\]

สารละลาย. เราดำเนินการตามโครงการ:

\[\ซ้าย| 3x+1 \ขวา| \gt 5-4x\ลูกศรขวา \left[ \begin(align) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \right) \\\end(align) \ ขวา.\]

เราแก้ปัญหาความไม่เท่าเทียมกันของประชากรแต่ละกลุ่ม:

\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \right.\]

\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \right.\]

\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(align) \right.\]

เราทำเครื่องหมายแต่ละชุดผลลัพธ์บนเส้นจำนวน จากนั้นจึงรวมเข้าด้วยกัน:
ยูเนี่ยนของชุด
แน่นอนว่าคำตอบคือ $x\in \left(\frac(4)(7);+\infty \right)$

คำตอบ: $x\in \left(\frac(4)(7);+\infty \right)$

งาน. แก้ความไม่เท่าเทียมกัน:

\[\ซ้าย| ((x)^(2))+2x-3 \right| \gtx\]

สารละลาย. ดี? ไม่ มันเหมือนกันหมด เราผ่านจากความไม่เท่าเทียมกันด้วยโมดูลัสไปสู่ชุดของอสมการสองประการ:

\[\ซ้าย| ((x)^(2))+2x-3 \right| \gt x\ลูกศรขวา \left[ \begin(align) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\end(จัดตำแหน่ง) \right.\]

เราแก้ไขแต่ละความไม่เท่าเทียมกัน น่าเสียดายที่รากนั้นไม่ค่อยดีนัก:

\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\ &D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2) \\\end(จัดแนว)\]

ในความไม่เท่าเทียมกันประการที่สอง ยังมีเกมอีกเล็กน้อย:

\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\ &D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2) \\\end(จัดแนว)\]

ตอนนี้เราต้องทำเครื่องหมายตัวเลขเหล่านี้บนสองแกน - หนึ่งแกนสำหรับอสมการแต่ละอัน อย่างไรก็ตาม คุณต้องทำเครื่องหมายจุดตามลำดับที่ถูกต้อง ยิ่งตัวเลขมาก จุดก็จะเลื่อนไปทางขวามากขึ้น

และที่นี่เรากำลังรอการตั้งค่า ถ้าทุกอย่างชัดเจนด้วยตัวเลข $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ (เงื่อนไขในตัวเศษของตัวแรก เศษส่วนจะน้อยกว่าพจน์ในตัวเศษของวินาที ดังนั้นผลรวมจึงน้อยกว่าด้วย) โดยมีตัวเลข $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt (21))(2)$ ก็จะไม่มีปัญหาเช่นกัน (จำนวนบวกเป็นลบมากกว่าอย่างเห็นได้ชัด) แต่สำหรับคู่สุดท้าย ทุกอย่างไม่ง่ายเลย อันไหนใหญ่กว่า: $\frac(-3+\sqrt(21))(2)$ หรือ $\frac(-1+\sqrt(13))(2)$? การจัดเรียงคะแนนบนเส้นจำนวน และจริงๆ แล้วคำตอบจะขึ้นอยู่กับคำตอบของคำถามนี้

ลองเปรียบเทียบกัน:

\[\begin(เมทริกซ์) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ วี -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(เมทริกซ์)\]

เราแยกรากออก ได้จำนวนที่ไม่เป็นลบทั้งสองข้างของอสมการ ดังนั้นเราจึงมีสิทธิ์ยกกำลังสองทั้งสองข้าง:

\[\begin(เมทริกซ์) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(เมทริกซ์)\]

ฉันคิดว่ามันไม่ใช่เรื่องง่ายที่ $4\sqrt(13) \gt 3$ ดังนั้น $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$ ในที่สุดจุดบนแกนจะถูกจัดเรียงดังนี้:
กรณีรากน่าเกลียด
ฉันขอเตือนคุณว่าเรากำลังแก้เซต ดังนั้นคำตอบจะเป็นการรวมกันของเซต ไม่ใช่จุดตัดของเซตที่แรเงา

คำตอบ: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty\right)$

อย่างที่คุณเห็น โครงการของเราใช้งานได้ดีทั้งกับงานง่ายๆ และงานที่ยากมาก “จุดอ่อน” เพียงอย่างเดียวในแนวทางนี้คือคุณต้องเปรียบเทียบจำนวนอตรรกยะให้ถูกต้อง (และเชื่อฉันเถอะว่าสิ่งเหล่านี้ไม่ได้เป็นเพียงรากเท่านั้น) แต่บทเรียนแยกต่างหาก (และจริงจังมาก) จะเน้นไปที่คำถามในการเปรียบเทียบ และเราก็เดินหน้าต่อไป

3. อสมการกับ "ก้อย" ที่ไม่เป็นลบ

ดังนั้นเราจึงได้สิ่งที่น่าสนใจที่สุด นี่คือความไม่เท่าเทียมกันของแบบฟอร์ม:

\[\ซ้าย| ฉ\ขวา| \gt\ซ้าย| ก\ขวา|\]

โดยทั่วไปแล้ว อัลกอริธึมที่เรากำลังจะพูดถึงตอนนี้เป็นจริงสำหรับโมดูลเท่านั้น มันใช้ได้กับความไม่เท่าเทียมกันทั้งหมด โดยรับประกันว่านิพจน์ที่ไม่เป็นลบทางซ้ายและขวา:

จะทำอย่างไรกับงานเหล่านี้? เพียงจำไว้ว่า:

ในอสมการที่มีหางที่ไม่เป็นลบ ทั้งสองฝ่ายสามารถยกขึ้นเป็นพลังธรรมชาติใดก็ได้ จะไม่มีข้อจำกัดเพิ่มเติม

ก่อนอื่นเราจะสนใจเรื่องการยกกำลังสอง - มันเผาโมดูลและรูท:

\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f \\\end(จัดแนว)\]

อย่าสับสนกับการหารากของกำลังสอง:

\[\sqrt(((f)^(2)))=\left| ฉ \right|\ne ฉ\]

เกิดข้อผิดพลาดนับไม่ถ้วนเมื่อนักเรียนลืมติดตั้งโมดูล! แต่นี่เป็นเรื่องราวที่แตกต่างไปจากเดิมอย่างสิ้นเชิง (สมการไร้เหตุผล) ดังนั้นเราจะไม่พูดถึงมันในตอนนี้ มาแก้ไขปัญหาสองสามข้อกันดีกว่า:

งาน. แก้ความไม่เท่าเทียมกัน:

\[\ซ้าย| x+2 \right|\ge \left| 1-2x \ขวา|\]

สารละลาย. เราสังเกตเห็นสองสิ่งทันที:

นี่คือความไม่เท่าเทียมกันที่ไม่เข้มงวด จุดบนเส้นจำนวนจะถูกเจาะออก

เห็นได้ชัดว่าความไม่เท่าเทียมกันทั้งสองด้านไม่เป็นลบ (นี่คือคุณสมบัติของโมดูล: $\left| f\left(x \right) \right|\ge 0$)

ดังนั้นเราจึงสามารถยกกำลังสองของความไม่เท่าเทียมกันทั้งสองด้านเพื่อกำจัดโมดูลัสและแก้ไขปัญหาโดยใช้วิธีช่วงเวลาปกติ:

\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\left(x+2 \right))^(2))\ge ((\left(2x-1 \right))^(2)) \\\end(จัดแนว)\]

ในขั้นตอนสุดท้าย ฉันโกงนิดหน่อย: ฉันเปลี่ยนลำดับของพจน์ โดยใช้ความเท่าเทียมกันของโมดูลัส (อันที่จริง ฉันคูณนิพจน์ $1-2x$ ด้วย −1)

\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ ขวา)\right)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(align)\]

เราแก้ด้วยวิธีช่วงเวลา เรามาเปลี่ยนจากอสมการไปสู่สมการกัน:

\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3) \\\end(จัดแนว)\]

เราทำเครื่องหมายรากที่พบบนเส้นจำนวน อีกครั้ง: ทุกจุดถูกแรเงาเพราะอสมการเดิมไม่เข้มงวด!
การกำจัดสัญญาณโมดูล
ฉันขอเตือนคุณสำหรับคนที่ดื้อรั้นเป็นพิเศษ: เรานำสัญญาณจากความไม่เท่าเทียมกันครั้งล่าสุดซึ่งเขียนไว้ก่อนที่จะไปสู่สมการ และเราทาสีทับพื้นที่ที่ต้องการในความไม่เท่าเทียมกันเดียวกัน ในกรณีของเรา นี่คือ $\left(x-3 \right)\left(3x+1 \right)\le 0$

โอเค ตอนนี้ทุกอย่างจบลงแล้ว แก้ไขปัญหา.

คำตอบ: $x\in \left[ -\frac(1)(3);3 \right]$.

งาน. แก้ความไม่เท่าเทียมกัน:

\[\ซ้าย| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \right|\]

สารละลาย. เราทำทุกอย่างเหมือนกัน ฉันจะไม่แสดงความคิดเห็น - แค่ดูลำดับของการกระทำ

ลองยกกำลังสอง:

\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \right| \right))^(2))\le ((\left(\left) | ((x)^(2))+3x+4 \right| \right))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))\le ((\left(((x)^(2))+3x+4 \ขวา))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))-((\left(((x)^(2))+3x+4 \ ขวา))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x) ^(2))+x+1+((x)^(2))+3x+4 \right)\เลอ 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(align)\]

วิธีการเว้นวรรค:

\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ ลูกศรขวา x=-1.5; \\ & 2((x)^(2))+4x+5=0\Rightarrow D=16-40 \lt 0\ลูกศรขวา \varnothing \\\end(จัดแนว)\]

มีเพียงรากเดียวบนเส้นจำนวน:
คำตอบคือทั้งช่วง
คำตอบ: $x\in \left[ -1.5;+\infty \right)$.

บันทึกเล็กๆ น้อยๆ เกี่ยวกับงานสุดท้าย ตามที่นักเรียนคนหนึ่งของฉันระบุไว้อย่างถูกต้อง นิพจน์ย่อยทั้งสองในความไม่เท่าเทียมกันนี้เป็นค่าบวกอย่างเห็นได้ชัด ดังนั้นจึงสามารถละเครื่องหมายโมดูลัสได้โดยไม่เป็นอันตรายต่อสุขภาพ

แต่นี่เป็นระดับการคิดที่แตกต่างไปจากเดิมอย่างสิ้นเชิงและเป็นแนวทางที่แตกต่างออกไปซึ่งสามารถเรียกได้ว่าเป็นวิธีการแห่งผลที่ตามมาอย่างมีเงื่อนไข เกี่ยวกับเขา - ในบทเรียนแยกต่างหาก ตอนนี้เรามาดูส่วนสุดท้ายของบทเรียนวันนี้กันดีกว่าและพิจารณาอัลกอริธึมสากลที่ใช้งานได้เสมอ แม้ว่าวิธีการก่อนหน้านี้ทั้งหมดจะไร้พลังก็ตาม :)

4. วิธีการแจกแจงตัวเลือก

จะเกิดอะไรขึ้นถ้าเทคนิคเหล่านี้ไม่ได้ผล? หากความไม่เท่าเทียมกันไม่ลดลงจนกลายเป็นส่วนหางที่ไม่เป็นลบ หากไม่สามารถแยกโมดูลออกได้ หากเจ็บปวด - เศร้า - โหยหา?

จากนั้น "ปืนใหญ่" ของคณิตศาสตร์ทั้งหมดก็เข้าสู่ฉาก - วิธีการแจงนับ ในเรื่องความไม่เท่าเทียมกับโมดูลัส มีลักษณะดังนี้:

เขียนนิพจน์ submodule ทั้งหมดและจัดให้เป็นศูนย์
แก้สมการผลลัพธ์และทำเครื่องหมายรากที่พบบนเส้นจำนวนหนึ่งเส้น
เส้นตรงจะแบ่งออกเป็นหลายส่วน โดยแต่ละโมดูลจะมีป้ายตายตัวและขยายออกไปอย่างชัดเจน
แก้ไขความไม่เท่าเทียมกันในแต่ละส่วนดังกล่าว (คุณสามารถพิจารณารากของขอบเขตที่ได้รับในย่อหน้าที่ 2 แยกกัน - เพื่อความน่าเชื่อถือ) รวมผลลัพธ์ - นี่จะเป็นคำตอบ :)

แล้วยังไงล่ะ? อ่อนแอ? อย่างง่ายดาย! เป็นเวลานานเท่านั้น มาดูในทางปฏิบัติ:

งาน. แก้ความไม่เท่าเทียมกัน:

\[\ซ้าย| x+2 \ขวา| \lt\ซ้าย| x-1 \right|+x-\frac(3)(2)\]

สารละลาย. เรื่องไร้สาระนี้ไม่ได้เดือดลงไปถึงความไม่เท่าเทียมเช่น $\left| ฉ\ขวา| \lt g$, $\left| ฉ\ขวา| \gt g$ หรือ $\left| ฉ\ขวา| \lt\ซ้าย| g \right|$ งั้นไปต่อเลย

เราเขียนนิพจน์ submodule จัดให้เป็นศูนย์และค้นหาราก:

\[\begin(align) & x+2=0\ลูกศรขวา x=-2; \\ & x-1=0\ลูกศรขวา x=1 \\\end(จัดแนว)\]

โดยรวมแล้ว เรามีรากสองอันที่แบ่งเส้นจำนวนออกเป็นสามส่วน โดยภายในแต่ละโมดูลจะถูกเปิดเผยโดยไม่ซ้ำกัน:
การแยกเส้นจำนวนด้วยศูนย์ของฟังก์ชันย่อย
พิจารณาแต่ละส่วนแยกกัน

1. ให้ $x \lt -2$. จากนั้นนิพจน์ submodule ทั้งสองจะเป็นค่าลบ และความไม่เท่าเทียมกันดั้งเดิมจะถูกเขียนใหม่ดังนี้:

\[\begin(align) & -\left(x+2 \right) \lt -\left(x-1 \right)+x-1,5 \\ & -x-2 \lt -x+1+ x-1.5 \\ & x \gt 1.5 \\\end (จัดแนว)\]

เรามีข้อจำกัดที่ค่อนข้างง่าย ลองตัดมันด้วยสมมติฐานเดิมที่ว่า $x \lt -2$:

\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1,5 \\\end(align) \right.\Rightarrow x\in \varnothing \]

แน่นอนว่าตัวแปร $x$ ต้องไม่น้อยกว่า −2 พร้อมกันแต่มากกว่า 1.5 ไม่มีวิธีแก้ปัญหาในพื้นที่นี้

1.1. ลองพิจารณากรณีขอบเขตแยกกัน: $x=-2$ ลองแทนตัวเลขนี้ลงในอสมการเดิมแล้วตรวจดูว่ามันอยู่หรือเปล่า?

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=-2) ) \\ & 0 \lt \left| -3 \ขวา|-2-1.5; \\ & 0 \lt 3-3.5; \\ & 0 \lt -0,5\ลูกศรขวา \varnothing \\\end(จัดแนว)\]

แน่นอนว่าห่วงโซ่การคำนวณนำเราไปสู่ความไม่เท่าเทียมกันที่ผิด ดังนั้น อสมการดั้งเดิมจึงเป็นเท็จเช่นกัน และ $x=-2$ จะไม่รวมอยู่ในคำตอบ

2. ตอนนี้ ให้ $-2 \lt x \lt 1$. โมดูลด้านซ้ายจะเปิดขึ้นโดยมี "บวก" อยู่แล้ว แต่โมดูลด้านขวายังคงมี "ลบ" เรามี:

\[\begin(align) & x+2 \lt -\left(x-1 \right)+x-1.5 \\ & x+2 \lt -x+1+x-1.5 \\& x \lt - 2.5 \\\end(จัดตำแหน่ง)\]

เราตัดกับข้อกำหนดเดิมอีกครั้ง:

\[\left\( \begin(align) & x \lt -2,5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]

และขอย้ำอีกครั้งว่าชุดคำตอบว่าง เนื่องจากไม่มีตัวเลขใดที่ทั้งน้อยกว่า −2.5 และมากกว่า −2

2.1. และอีกครั้งเป็นกรณีพิเศษ: $x=1$ เราแทนที่ความไม่เท่าเทียมกันดั้งเดิม:

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=1)) \\ & \ซ้าย| 3\ขวา| \lt\ซ้าย| 0 \ขวา|+1-1.5; \\ & 3 \lt -0.5; \\ & 3 \lt -0,5\ลูกศรขวา \varnothing \\\end(จัดแนว)\]

เช่นเดียวกับ "กรณีพิเศษ" ก่อนหน้านี้ ตัวเลข $x=1$ ไม่ได้รวมอยู่ในคำตอบอย่างชัดเจน

3. ส่วนสุดท้ายของบรรทัด: $x \gt 1$ ที่นี่โมดูลทั้งหมดจะถูกขยายด้วยเครื่องหมายบวก:

\[\begin(จัดตำแหน่ง) & x+2 \lt x-1+x-1.5 \\ & x+2 \lt x-1+x-1.5 \\ & x \gt 4.5 \\ \end(align)\ ]

และอีกครั้งที่เราตัดกันเซตที่พบด้วยข้อจำกัดเดิม:

\[\left\( \begin(align) & x \gt 4,5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4,5;+\infty \ขวา)\]

ในที่สุด! เราพบช่วงเวลาซึ่งจะเป็นคำตอบ

คำตอบ: $x\in \left(4,5;+\infty \right)$

สุดท้ายนี้ มีหมายเหตุหนึ่งที่อาจช่วยคุณจากความผิดพลาดโง่ๆ เมื่อแก้ไขปัญหาจริง:

คำตอบของอสมการด้วยโมดูลมักจะถูกกำหนดอย่างต่อเนื่องบนเส้นจำนวน - ช่วงเวลาและเซ็กเมนต์ จุดที่แยกออกมานั้นหายากกว่ามาก และยิ่งไม่ค่อยเกิดขึ้นที่ขอบเขตของการแก้ปัญหา (จุดสิ้นสุดของส่วน) ตรงกับขอบเขตของช่วงที่พิจารณา

ดังนั้น หากขอบเขต (ซึ่งเรียกว่า "กรณีพิเศษ") ไม่ได้รวมอยู่ในคำตอบ พื้นที่ทางซ้าย-ขวาของขอบเขตเหล่านี้ก็แทบจะไม่รวมอยู่ในคำตอบด้วย และในทางกลับกัน: ชายแดนเข้ามาตอบโต้ ซึ่งหมายความว่าบางพื้นที่รอบๆ ก็จะมีการตอบโต้ด้วย

โปรดคำนึงถึงสิ่งนี้เมื่อคุณตรวจสอบวิธีแก้ปัญหาของคุณ

การแก้ปัญหาความไม่เท่าเทียมกันอยู่ในโหมด ออนไลน์ สารละลายความไม่เท่าเทียมกันเกือบทุกประการ ออนไลน์. คณิตศาสตร์ ความไม่เท่าเทียมกันทางออนไลน์เพื่อแก้คณิตศาสตร์ ค้นหาอย่างรวดเร็ว การแก้ปัญหาความไม่เท่าเทียมกันอยู่ในโหมด ออนไลน์. เว็บไซต์ www.site ช่วยให้คุณค้นหา สารละลายเกือบทุกอย่างที่ได้รับ พีชคณิต, ตรีโกณมิติหรือ ความไม่เท่าเทียมกันที่เหนือธรรมชาติทางออนไลน์. เมื่อเรียนคณิตศาสตร์เกือบทุกส่วนในระยะต่างๆ เราต้องตัดสินใจ ความไม่เท่าเทียมกันทางออนไลน์. หากต้องการได้รับคำตอบทันที และที่สำคัญที่สุดคือคำตอบที่แม่นยำ คุณต้องมีทรัพยากรที่ช่วยให้คุณดำเนินการนี้ได้ ขอขอบคุณข้อมูลจาก www.site แก้ปัญหาความไม่เท่าเทียมกันทางออนไลน์จะใช้เวลาไม่กี่นาที ข้อได้เปรียบหลักของ www.site เมื่อแก้โจทย์คณิต ความไม่เท่าเทียมกันทางออนไลน์- คือความเร็วและความแม่นยำของการตอบกลับที่ออก เว็บไซต์สามารถแก้ปัญหาใดๆ อสมการพีชคณิตออนไลน์, อสมการตรีโกณมิติออนไลน์, ความไม่เท่าเทียมเหนือธรรมชาติออนไลน์, และ ความไม่เท่าเทียมกันด้วยพารามิเตอร์ที่ไม่รู้จักในโหมด ออนไลน์. ความไม่เท่าเทียมกันทำหน้าที่เป็นเครื่องมือทางคณิตศาสตร์อันทรงพลัง โซลูชั่นงานภาคปฏิบัติ ด้วยความช่วยเหลือ อสมการทางคณิตศาสตร์เป็นไปได้ที่จะแสดงข้อเท็จจริงและความสัมพันธ์ที่อาจดูสับสนและซับซ้อนเมื่อมองแวบแรก ปริมาณที่ไม่รู้จัก ความไม่เท่าเทียมกันสามารถพบได้โดยการกำหนดปัญหาใน ทางคณิตศาสตร์ภาษาในรูปแบบ ความไม่เท่าเทียมกันและ ตัดสินใจงานที่ได้รับในโหมด ออนไลน์บนเว็บไซต์ www.site. ใดๆ ความไม่เท่าเทียมกันทางพีชคณิต, อสมการตรีโกณมิติหรือ ความไม่เท่าเทียมกันซึ่งประกอบด้วย เหนือธรรมชาตินำเสนอคุณได้อย่างง่ายดาย ตัดสินใจออนไลน์และรับคำตอบที่ถูกต้อง การศึกษาวิทยาศาสตร์ธรรมชาติย่อมต้องเผชิญกับความต้องการอย่างหลีกเลี่ยงไม่ได้ การแก้ปัญหาความไม่เท่าเทียมกัน. ในกรณีนี้คำตอบจะต้องแม่นยำและต้องได้รับทันทีในโหมด ออนไลน์. ดังนั้นเพื่อ แก้อสมการทางคณิตศาสตร์ออนไลน์เราขอแนะนำเว็บไซต์ www.site ซึ่งจะกลายเป็นเครื่องคิดเลขที่ขาดไม่ได้ของคุณ แก้อสมการพีชคณิตออนไลน์, อสมการตรีโกณมิติออนไลน์, และ ความไม่เท่าเทียมเหนือธรรมชาติออนไลน์หรือ ความไม่เท่าเทียมกันด้วยพารามิเตอร์ที่ไม่รู้จัก สำหรับปัญหาเชิงปฏิบัติในการหาคำตอบอินทราโวลต่างๆ อสมการทางคณิตศาสตร์ทรัพยากร www.. การแก้ปัญหา ความไม่เท่าเทียมกันทางออนไลน์ตัวคุณเองจะมีประโยชน์ในการตรวจสอบคำตอบที่ได้รับโดยใช้ การแก้ปัญหาความไม่เท่าเทียมกันออนไลน์บนเว็บไซต์ www.site. มีความจำเป็นต้องเขียนความไม่เท่าเทียมกันอย่างถูกต้องและรับทันที โซลูชั่นออนไลน์หลังจากนั้นก็เหลือเพียงการเปรียบเทียบคำตอบกับคำตอบของคุณกับอสมการเท่านั้น การตรวจสอบคำตอบจะใช้เวลาไม่เกินหนึ่งนาทีก็เพียงพอแล้ว แก้ปัญหาความไม่เท่าเทียมกันทางออนไลน์และเปรียบเทียบคำตอบ ซึ่งจะช่วยให้คุณหลีกเลี่ยงข้อผิดพลาดได้ การตัดสินใจและแก้ไขคำตอบให้ทันเวลา การแก้ไขความไม่เท่าเทียมกันทางออนไลน์ทั้ง พีชคณิต, ตรีโกณมิติ, พ้นหรือ ความไม่เท่าเทียมกันด้วยพารามิเตอร์ที่ไม่รู้จัก