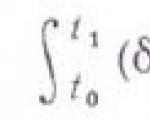Das Prinzip der geringsten Aktion. Hamilton-Ostrogradsky-Variationsprinzip in Konfigurations- und Phasenräumen. Formel für ebene Wellen
HAMILTON-OSTROGRAD-PRINZIP
Prinzip der stationären Wirkung, - allgemeines Integral Variationsprinzip der klassischen Mechanik, gegründet von W.
Hamilton für holonome Systeme, die durch ideale stationäre Beschränkungen eingeschränkt sind, und von M. V. Ostrogradskii auf instationäre Beschränkungen verallgemeinert. Laut G. - O.
hat einen stationären Wert im Vergleich zu nahen kinematisch möglichen Bewegungen, bei denen die Anfangs- und Endpositionen des Systems und die Bewegungszeit mit denen der tatsächlichen Bewegung übereinstimmen. Hier T - kinetisch, U- potenzielle Energie, L-T-U die Lagrange-Funktion des Systems. In manchen Fällen entspricht true nicht nur einem stationären Punkt des Funktionals S, gibt ihm aber auch den kleinsten Wert. Daher hat G. -O. n. oft genannt. das Prinzip der geringsten Wirkung. Bei nicht potentiellen Wirkkräften F v Stationaritätsbedingung für die Aktion d S= 0 wird durch die Bedingung ersetzt
Zündete.: Hamilton W., Report of the Fourth Meeting of the British Association for the Advancement of Science, L., 1835, p. 513-18; Ostrogradsku M., „Mem. de 1“ Acad. des Sci. de St-Petershourg“, 1850, Bd. 8, Nr. 3, S. 33-48.
V. V. Rumjanzew.
Mathematische Enzyklopädie. - M.: Sowjetische Enzyklopädie. I. M. Winogradow. 1977-1985.
Sehen Sie, was das „HAMILTON-OSTROGRAD-PRINZIP“ in anderen Wörterbüchern ist:
Das Fisher-Prinzip ist ein Evolutionsmodell, das erklärt, warum in der Natur das Geschlechterverhältnis der Arten lebender Organismen von etwa 1:1 vorherrscht; in denen Gene für die Produktion von mehr Individuen beiderlei Geschlechts ... ... Wikipedia
Hamilton (auch nur das Hamilton-Prinzip), genauer gesagt das Prinzip der Stationarität der Wirkung, ist eine Methode zur Ermittlung der Bewegungsgleichungen eines physikalischen Systems durch die Suche nach einem stationären (oft extremen, meist in Verbindung mit der etablierten Tradition ... ... Wikipedia
Wellenbrechung nach Huygens ... Wikipedia
In der Methodologie der Wissenschaft ist die Aussage, dass jede neue wissenschaftliche Theorie bei Vorhandensein einer alten, gut getesteten Theorie nicht in völligem Widerspruch dazu steht, sondern in einer einschränkenden Näherung (Sonderfall) die gleichen Konsequenzen liefert. Zum Beispiel das Gesetz ... ... Wikipedia
Diskretes Pontryagin-Maximumprinzip für zeitdiskrete Regelprozesse. Für einen solchen Prozess ist M. p. möglicherweise nicht erfüllt, obwohl für sein kontinuierliches Analogon, das durch Ersetzen des Finite-Differenzen-Operators durch einen Differentialoperator erhalten wird ... ... Mathematische Enzyklopädie
Oder die Anfänge von Hamilton in der Mechanik und der mathematischen Physik dienen dazu, Differentialgleichungen der Bewegung zu erhalten. Dieses Prinzip erstreckt sich auf alle materiellen Systeme, welchen Kräften sie auch immer ausgesetzt sein mögen; Zuerst werden wir es so ausdrücken ... Enzyklopädisches Wörterbuch F.A. Brockhaus und I.A. Efron
Quantum postulieren. Mechanik, die das Zusammentreffen ihrer physikalischen Elemente erfordert. Konsequenzen im Grenzfall großer Quantenzahlen mit den Ergebnissen der Klassik. Theorien. In S. p., die Tatsache, dass das Quantum. Effekte sind nur bei der Betrachtung von Mikroobjekten von Bedeutung, wenn ... ... Physische Enzyklopädie
Hamiltons Variationsprinzip- Hamiltono variacinis principas statusas T sritis fizika atitikmenys: engl. Hamilton-Variationsprinzip vok. Hamiltonsches Variationsprinzip, n rus. Hamiltons Variationsprinzip, m pranc. Hauptvariante d'Hamilton, m … Fizikos terminų žodynas
Ein Postulat der Quantenmechanik (siehe Quantenmechanik), das die Übereinstimmung seiner physikalischen Konsequenzen im Grenzfall großer Quantenzahlen (siehe Quantenzahlen) mit den Ergebnissen der klassischen Theorie erfordert. In S. p. zeigt sich die Tatsache, dass ... ... Große sowjetische Enzyklopädie
- (Wellenmechanik), eine Theorie, die die Beschreibungsmethode und die Bewegungsgesetze von Mikropartikeln (Elem. h c, Atome, Moleküle, Atomkerne) und ihrer Systeme (z. B. Kristalle) sowie die Beziehung von Größen festlegt Charakterisierung von Teilchen und Systemen, mit physikalischen Größen, ... ... Physische Enzyklopädie
Dieser Begriff hat andere Bedeutungen, siehe Aktion (Physik). Aktionsdimension L2MT−1 Aktion ist in der Physik eine skalare physikalische Größe, die ... Wikipedia
Bücher
- Bewegungsprinzipien des Wirtschaftssystems. Monographie, Kusner Yuri Semenovich, Tsarev Igor Gennadievich. Die Grundgleichungen der Bewegung eines Wirtschaftssystems werden in analytischer Form dargestellt und das Problem gelöst, geeignete Methoden zur Steuerung seiner Bewegung zu finden. Mathematik wird verwendet...
Die Idee, die allen Integralprinzipien und einigen Differentialprinzipien zugrunde liegt, ist die Position, dass die reale Bewegung eines mechanischen Systems einer physikalischen Größe Extremalität verleiht. Zur mathematischen Formulierung dieses Satzes ist es nach wie vor notwendig, neben der realen Bewegung auch die Gesamtheit der denkbaren Bewegungen in Betracht zu ziehen und sie ganz bestimmten Anforderungen zu unterwerfen.
Die Formulierung der Integralprinzipien erfolgt im Konfigurationsraum. Denken Sie daran, dass für ein System mit Freiheitsgraden die verallgemeinerten Koordinaten gelten 
, die die Konfiguration des Systems zum jeweiligen Zeitpunkt bestimmen 
, werden im entsprechenden als kartesische Koordinaten behandelt 
-dimensionaler Raum, der der Konfigurationsraum ist. Im Laufe der Zeit ändert sich der Zustand des mechanischen Systems und der Punkt, der dieses System darstellt, beschreibt eine bestimmte Kurve. Es ist zweckmäßig, die Bewegung des Systems als die Bewegung des repräsentativen Punktes entlang dieser Kurve zu betrachten. Zeit 
Unter dieser Betrachtung handelt es sich um einen Parameter, und jeder Punkt der Flugbahn entspricht einem oder mehreren Werten 
.
Wenn wir uns für die Position des Systems auf der Konfigurationsbahn zu jedem Zeitpunkt interessieren 
, dann müssen Sie eine weitere Achse hinzufügen 
.
Dann erhalten wir einen „mehrdimensionalen Graphen“ der Bewegung des betrachteten Systems. Man kann beispielsweise auch die Projektionen eines multivariaten Graphen auf bestimmte Ebenen untersuchen 
(Abb. 2.7). Auf dem Bild A, B sind die Projektionen des repräsentativen Punktes zu den jeweiligen Zeitpunkten 
Und 
dementsprechend stellt die durchgezogene Linie die reale, die gestrichelte Linie eine der denkbaren Bewegungen dar.
Das Integralprinzip ist eine Aussage darüber, wie die reale Bewegung des Systems über ein endliches (nicht unendlich kleines!) Zeitintervall abläuft 
.
Was war mit dem System vor dem Moment der Zeit? 
,
wir sind nicht interessiert. Da aber der Anfangs- und Endzeitpunkt festgelegt sind, geht man davon aus, dass das mechanische System für alle denkbaren Bewegungen im jeweiligen Zeitmoment verantwortlich ist 
geht durch einen Punkt A, In dem Moment 
- IN;
Diese Punkte entsprechen den Anfangs- und Endpositionen des Systems in seiner tatsächlichen Bewegung.
Die allgemeinste Formulierung der Position zur Bewegung mechanischer Systeme ist im sogenannten Prinzip der geringsten Wirkung enthalten (es wird auch Hamilton-Ostrogradsky-Prinzip genannt):
Die reale Bewegung des mechanischen Systems im Zeitintervall von
Vor
ist so, dass das Integral die Aktionsfunktion genannt wird
und gleich
, (60.7)
Wo
-- Lagrangefunktion des gegebenen mechanischen Systems, hat ein Extremum (Minimum). Variable
es variiert nicht.
Mit anderen Worten: Während einer realen Bewegung sollte die Variation der Aktion gleich Null sein
(61.7)
vorausgesetzt, dass alle Konfigurations-Trajektorien zu den jeweiligen Zeitpunkten vorliegen 
Und 
durch den Start- und Endpunkt der realen Bewegung gehen, d.h.
Dieses Prinzip ist im Gegensatz zum Differentialprinzip von d'Alembert in dem Sinne integral, dass es eine Aussage über die Bewegung des Gesamtsystems über einen endlichen Zeitraum enthält. 
.
Tatsächlich ergeben sich daraus die Lagrange-Gleichungen, man kann also sagen, dass man aus dem Prinzip der geringsten Wirkung die gesamte Dynamik eines mechanischen Systems erhält.
Lassen Sie die Funktionen 
, beschreiben Sie die reale Bewegung, d.h. 
welche Funktionen für welche 
hat ein Minimum. Betrachten Sie die Menge der Funktionen 
Wo 
- Funktionsvariationen 
, die im Vergleich zu klein sein dürften 
während des gesamten Zeitintervalls von 
Vor 
. Darüber hinaus alle 
erfüllen Beziehungen (62.7). Wir berechnen die sogenannte erste Variation 
, wobei zu berücksichtigen ist, dass die Lagrange-Funktion von den verallgemeinerten Koordinaten abhängen kann 
,
verallgemeinerte Geschwindigkeiten 
, und Zeit 
:
Weil das 
, die zweite Amtszeit in 
kann durch Teile integriert werden, um zu erhalten
.
Aufgrund der Bedingungen (62,7) ist die Summe
verschwindet und das verbleibende Integral ist für beliebige Werte gleich Null 
nur wenn jeder Term der Summe des Integranden verschwindet. Somit erhalten wir die Lagrange-Gleichungen 2. Art
.
(63.7)
Es ist nützlich, sich daran zu erinnern, dass man aus der Lösung des Problems für das Extremum einer Funktion ein System endlicher Gleichungen erhält, aus dem der Punkt ermittelt wird, an dem die Funktion ein Extremum erreicht. In diesem Fall handelt es sich um ein Funktional, die Lösung eines Extremumproblems, das durch ein System von Differentialgleichungen 2. Ordnung gegeben ist. Aus diesen Gleichungen ergibt sich eine Gerade im Konfigurationsraum, gegeben durch die Funktionen 
wo das Funktionale sein Minimum erreicht. Diese Linie wird als Extremal bezeichnet.
Da die Aufgabe bei der Konstruktion des einen oder anderen mechanischen Modells darin besteht, die Bewegungsgleichungen aufzustellen, sehen wir, dass die Dynamik des Systems tatsächlich durch eine Funktion bestimmt wird – die Lagrange-Funktion, da diese Funktion das Problem löst. Somit ist die Lagrangefunktion des Systems ein interessantes physikalisches Objekt, dessen Untersuchung im Zusammenhang mit den Problemen der Dynamik notwendig ist. Insbesondere lässt sich aus dem Prinzip der geringsten Wirkung erkennen, dass die Funktion 
ist nur bis zur Addition der Gesamtableitung einer beliebigen Funktion von Koordinaten und Zeit definiert. Dies ist so zu verstehen, dass das durch seine Bewegungsgleichungen definierte System mehr als einer Lagrange-Funktion entspricht 
.
In der Tat, lass es sein 
verknüpft mit 
Verhältnis
(64.7)
,
.
Aber seit 
,
und folglich die mit den Funktionen erhaltenen Lagrange-Gleichungen 
Und 
, Dasselbe. Die Mehrdeutigkeit der Definition der Lagrange-Funktion der Form (64.7) hat keinen Einfluss auf die Bewegungsgleichungen und zwar auf alle 
aus der Klasse (64.7) löst das Problem, die Dynamik des Systems eindeutig zu konstruieren.
Eine wichtige Eigenschaft des Systems der Lagrange-Gleichungen ist ihre Kovarianz. Dies bedeutet, dass die Lagrange-Gleichungen unter Punkttransformationen verallgemeinerter Koordinaten ihre Form behalten 4
d. h. bei Verwendung verallgemeinerter Koordinaten 
Die Lagrange-Gleichungen haben die gleiche Form:
,
wie bei der Verwendung verallgemeinerter Koordinaten 
:
.
Lassen Sie uns direkt beweisen, dass die Lagrange-Gleichungen bezüglich der Transformation (65.7) kovariant sind. Lass uns bauen 
:
und Derivate
,
1. Kinematik eines materiellen Punktes. Unter einem materiellen Punkt versteht man ein physikalisches Objekt, das geometrisch einem mathematischen Punkt entspricht, aber Masse besitzt. Kinematik ist ein Zweig der Physik, der die Bewegungsarten von Körpern untersucht, ohne die Bewegungsursachen zu berücksichtigen. Die Position eines Punktes im Raum wird durch einen Radiusvektor charakterisiert. Der Radiusvektor eines Punktes ist ein Vektor, dessen Anfang mit dem Ursprung des Koordinatensystems und dessen Ende mit dem betrachteten Punkt zusammenfällt. R = ich x + J y + k z. Geschwindigkeit ist die Strecke, die ein Körper pro Zeiteinheit zurücklegt. v(t) = d R/dt. v(t) = ich dx/dt + J dy/dt + k dz/dt. Beschleunigung ist die Geschwindigkeitsänderungsrate. A=d v/dt = d2 R/dt2= ich d2x/dt2 + J d 2 y/dt 2 + k d 2 z/dt 2 . A = A τ + A n= τ dv/dt + N v2/R.
D R = v dt; D v = A dt also v = v 0 + A T; R = R 2 – R 1 = v 0 t + A t2/2.
2. Dynamik eines materiellen Punktes. Newtons Gesetze. Die Grundbegriffe der Dynamik sind der Begriff Masse und Kraft. Kraft ist die Ursache der Bewegung, d.h. Unter dem Einfluss der Körperkraft gewinnen sie an Geschwindigkeit. Kraft ist eine Vektorgröße. Die Masse ist ein Maß für die Trägheit eines Körpers. Das Produkt aus Masse und Geschwindigkeit nennt man Impuls. P= m v. Der Drehimpuls eines materiellen Punktes ist der Vektor L = R * P. Das auf einen materiellen Punkt wirkende Kraftmoment wird Vektor genannt M = R * F. Wenn wir den Ausdruck für den Drehimpuls differenzieren, erhalten wir: d L/dt=d R/dt* P + R*D P/dt. In Anbetracht dessen, dass d R/dt= v Und v parallel P, wir bekommen d L/dt= M.Newtons Gesetze. Das erste Newtonsche Gesetz besagt, dass ein Körper einen Ruhezustand oder eine gleichmäßige geradlinige Bewegung beibehält, wenn keine anderen Kräfte auf ihn einwirken oder ihre Wirkung kompensiert wird. Das zweite Newtonsche Gesetz besagt, dass die Impulsänderung über die Zeit ein konstanter Wert ist und gleich der wirkenden Kraft d ist P/ dt = d / dt (m v) = md v/dt= F.Dies ist Newtons zweites Gesetz in Differentialform. Newtons drittes Gesetz besagt, dass bei der Wechselwirkung zweier Körper jeder von ihnen mit der gleichen Größe, aber entgegengesetzter Richtung, Kraft auf den anderen einwirkt. F 1 = - F 2 .
3. Dynamik des Systems materieller Punkte. Naturschutzgesetze. Das System materieller Punkte ist die Gesamtheit ihrer endlichen Anzahl. Jeder Punkt des Systems wird durch interne (von anderen Punkten) und externe Kräfte beeinflusst. Sei m die Masse, r i der Radiusvektor. x i , y i , z i - Schnur. i-ter Punkt. Der Impuls eines Systems materieller Punkte ist die Summe der Impulse der materiellen Punkte, aus denen das System besteht: P= Σ (i=1,n) P ich = [ P 1 + P 2 +…+ P N]. Der Drehimpuls eines Systems materieller Punkte ist die Summe der Impulsmomente, aus denen das System materieller Punkte besteht: L = Σ [ L ich ] = Σ [ R ich * P ich ]. Die auf ein System materieller Punkte wirkende Kraft ist definiert als die Summe aller auf die Punkte des Systems wirkenden Kräfte, einschließlich der Wechselwirkungskräfte zwischen den Punkten des Systems: F = Σ [ F Ich wo F ich = F i' + Σ(j ≠ i) F ji ist die Kraft, die auf den materiellen Punkt des Systems wirkt, angegeben durch den Index i. Es besteht aus einer äußeren Kraft F i ’ und innere Kraft Σ(i ≠ j) [ F ji ], die als Ergebnis der Interaktion mit anderen Punkten des Systems auf den Punkt einwirkt. Dann gilt: F = Σ (i=1,n) [ F i ’] + Σ (i=1,n) Σ(j ≠ i) [ F ji]. Nach Newtons drittem Gesetz Σ (i=1,n) Σ(j ≠ i) [ F ji ] = 0, also F = Σ [ F ich']. Das auf ein System materieller Punkte wirkende Kraftmoment ist die Summe der auf die Punkte des Systems wirkenden Kraftmomente M= Σ (i) [ M i ] = Σ (i) [ R ich * F i ] = Σ (i) [ R ich * F ich']. Für ein System materieller Punkte hat die Bewegungsgleichung die Form d P/ dt = Σ = Σ [ F ich ].
Der Massenschwerpunkt eines Systems materieller Punkte ist ein imaginärer Punkt mit einem Radiusvektor R= 1/mΣ . Die Geschwindigkeit seiner Bewegung V=d R/dt. Dann ist die Bewegungsgleichung m d V/dt= F. Die Momentengleichung für das System materieller Punkte d L/dt= M. Naturschutzgesetze. Ein isoliertes System ist eines, das nicht von äußeren Kräften beeinflusst wird. In ihr F= 0, also d P/dt = 0. Dann P= konst. In einem isolierten System das Moment äußerer Kräfte M= 0. Daher ist d L/dt = 0, was bedeutet L= konst. Die Änderung der kinetischen Energie eines materiellen Punktes, wenn er sich zwischen zwei Positionen bewegt, ist gleich der von der Kraft geleisteten Arbeit. m 0 v 2 2 /2 – m 0 v 1 2 /2 = ∫(1,2) F D l oder m 0 v 2 /2 + E p \u003d const.
4. Bewegung in einem zentralsymmetrischen Feld. Keplers Gesetze. Das Feld heißt zentral, wenn die potentielle Energie des darin befindlichen Körpers nur vom Abstand r zu einem bestimmten Fixpunkt abhängt. Gewalt F= - ∂U(r)/ ∂ R= - dU/dr R/r, der auf das Teilchen einwirkt, hängt im absoluten Wert ebenfalls nur von r ab und ist auf jeden Punkt entlang des Radiusvektors gerichtet. Bei Bewegung im Zentralfeld bleibt das Moment des Systems relativ zur Feldmitte erhalten. Für einen Teilchenmoment M = [R*R]. Da die Vektoren M und r senkrecht zueinander stehen, bedeutet die Konstanz von M, dass bei Bewegung des Teilchens sein Radiusvektor immer in derselben Ebene bleibt – der Ebene senkrecht zu M. Somit liegt die Flugbahn des Teilchens vollständig im Zentralfeld in einer Ebene. Indem wir darin die Polarkoordinaten r, φ einführen, schreiben wir die Lagrange-Funktion in der Form L = m/2 (r 2 (∙) + r 2 φ 2 (∙)) - U(r). Diese Funktion enthält nicht explizit die Koordinate φ. Für eine solche Koordinate ist der ihr entsprechende verallgemeinerte Impuls p i das Integral der Bewegung. In diesem Fall fällt der verallgemeinerte Impuls p φ = mr 2 φ(∙) mit dem Moment M z = M zusammen, sodass M = mr 2 φ(∙) (1). Beachten Sie, dass dieses Gesetz für eine ebene Bewegung eines Teilchens in einem zentralen Feld eine einfache geometrische Interpretation zulässt. Der Ausdruck 1/2 r r d φ ist die Fläche des Sektors, der durch zwei unendlich nahe Radiusvektoren und ein Bogenelement der Flugbahn gebildet wird. Mit df bezeichnen wir den Impuls des Teilchens in der Form M = 2mf, wobei die Ableitung f als Sektorgeschwindigkeit bezeichnet wird. Daher bedeutet Impulserhaltung die Konstanz der Sektorgeschwindigkeit – für gleiche Zeiträume beschreibt der Radiusvektor eines sich bewegenden Punktes gleiche Flächen ( Keplers zweites Gesetz). Wenn wir φ(∙) durch M aus (1) ausdrücken und in den Ausdruck für Energie einsetzen, erhalten wir: E = m/2 (r 2 (∙) + r 2 φ 2 (∙)) + U(r) = mr 2 (∙ )/2 + M 2 /2mr 2 + U(r). Daher r(∙) = √(2/m (E – U(r)) - M 2 /m 2 r 2) oder, Variablen trennen und integrieren: t = ∫dr/√(2/m (E – U( r)) - M 2 /m 2 r 2) + konst. Wenn wir (1) weiter als dφ = M 2 /mr 2 dt schreiben, dt hier einsetzen und integrieren, finden wir: φ = ∫dr (M/r 2)/√(2/m (E – U(r)) - M 2 /r 2) + konst. Keplers erstes Gesetz. Jeder Planet dreht sich in einer Ellipse, in einem seiner Brennpunkte befindet sich die Sonne. Keplers drittes Gesetz. Die Quadrate der Sternperioden der Planeten werden als Kuben der großen Halbachsen ihrer Umlaufbahnen T 1 2 /T 2 2 = a 1 3 /a 2 3 in Beziehung gesetzt.
5. Die Lagrange-Funktion und die Lagrange-Gleichungen eines Systems materieller Punkte. Integrale der Bewegung. Betrachten Sie ein geschlossenes System materieller Punkte. Die Lagrange-Funktion dafür hat die Form L = Σ(a) – U(r 1 , r 2 , …), wobei T = Σ (a) die kinetische Energie und U die potentielle Energie der Teilchenwechselwirkung ist. Dann nehmen die Bewegungsgleichungen d/dt (∂L/∂v a) = ∂L/∂r a die Form m a dv a /dt = - ∂U/∂r a an. Diese Bewegungsgleichungen werden Newtonsche Gleichungen genannt. Vektor F a = - ∂U/∂r a heißt Kraft. Wenn zur Beschreibung der Bewegung nicht kartesische Koordinaten von Punkten verwendet werden, sondern beliebige verallgemeinerte Koordinaten q i , dann ist es zum Erhalten der Lagrange-Funktion notwendig, die entsprechende Transformation durchzuführen: x a = f(q 1 , q 2 , .., q s) , x a (∙) = Σ(k ) [∂f a /∂q k (∙)] usw. Wenn wir diese Ausdrücke in die Funktion L= 1 / 2 Σ(a) – U einsetzen, erhalten wir die gewünschte Lagrange-Funktion der Form L = 1/2 Σ(i,k) – U(q). Integrale der Bewegung. Es gibt solche Funktionen verallgemeinerter Koordinaten, die während der Bewegung konstante Werte behalten, abhängig nur von den Anfangsbedingungen. Man nennt sie Bewegungsintegrale. Aufgrund der Homogenität der Zeit ist dL/ dt = Σ(i) [∂L/∂q i q i (∙)] + Σ(i) [∂L/∂q i (∙) q i (∙∙)]. Wenn wir ∂L/∂q i gemäß den Lagrange-Gleichungen durch d/dt (∂L/∂q i (∙)) ersetzen, erhalten wir dL/dt = Σ(i) oder d/dt (Σ(i) - L) = 0 . Dies zeigt, dass sich die Größe E = Σ(i) – L, Energie genannt, nicht ändert, d. h. Bewegungsintegral. Aufgrund der Homogenität des Raumes bei einem unendlich kleinen Transfer ε, wenn alle Punkte des Systems um ε = δr verschoben werden, ist die Änderung der Lagrange-Funktion gleich δL = ε Σ(a) [∂L/∂r a ], muss gleich Null sein, d.h. Σ(a) [∂L/∂r a ] = 0. Mit den Lagrange-Gleichungen erhalten wir Σ(a) = d/dt (Σ(a)[ ∂L/∂v a ]) = 0. Dann ist die Menge R= Σ(a)[ ∂L/∂v a ], genannt Impuls, bleibt unverändert, d.h. Bewegungsintegral. Aufgrund der Isotropie des Raumes bei einer unendlich kleinen Drehung um den Winkel δφ ist die Änderung der Lagrange-Funktion gleich δL = Σ(a) [∂L/∂r a δ R a + ∂L/∂v a δ v a] muss Null sein. Die Änderung ∂L/∂ vornehmen v a = P a und ∂L/∂ R a = P a (∙) angesichts der Beliebigkeit von δφ erhalten wir d/dt Σ(a) [ R A P a ] = 0. Der Wert М = Σ(a) [ R A P a ], genannt Drehimpuls, bleibt konstant, d.h. Bewegungsintegral.
6. Dynamik eines absolut starren Körpers. Trägheitstensor. Euler-Gleichungen. Ein starrer Körper ist ein System materieller Punkte, deren Abstand zwischen ihnen konstant bleibt. Für eine vollständige Beschreibung der Bewegung eines starren Körpers ist es zusätzlich zur Bewegung eines seiner Punkte erforderlich, die Bewegung des Körpers in der Nähe dieses Punktes als Fixpunkt zu kennen. Der Körper sei am Punkt O fixiert. Wir bezeichnen den Radiusvektor des Punktes m i in Bezug auf O R ich , w ist die momentane Winkelgeschwindigkeit des Körpers, dann der Drehimpuls L= Σ [ R ich*bin ich v i ] = Σ = wΣ - Σ . Diese Vektorgleichheit kann als drei Projektionen auf die Koordinatenachsen L x = w x Σ - Σ geschrieben werden; L y = w y Σ - Σ ; L z = w z Σ - Σ . Angesichts dessen ( w R i) = x i w x + y i w y + z i w z wir erhalten L x = J xx w x + J xy w y + J xz w z ; L y = J yx w x + J yy w y + J yz w z ; L x = J zx w x + J zy w y + J zz w z , wobei J xx = Σ , J xy = Σ , andere sind ähnlich. Die Werte J xx , J yy , J zz heißen axiale Trägheitsmomente und J xy = J yx , J xz = J zx , J yz = J zy heißen Zentrifugalträgheitsmomente. Die Wertemenge J ij wird Trägheitstensor genannt. Die Elemente von J ii heißen Diagonale. Wenn alle außerdiagonalen Elemente gleich Null sind, dann sagt man, dass die mit den Koordinatenachsen zusammenfallenden Achsen des Körpers die Hauptträgheitsachsen sind und die Größen J ii die Hauptträgheitsmomente genannt werden. Ein solcher Tensor wird auf eine Diagonalform reduziert.
Euler-Gleichungen. Die Bewegungsgleichung des Körperschwerpunktes hat die Form m d v 0 /dt = md/dt ( w * R 0) = F, Wo R 0 ist der Radiusvektor des Massenschwerpunkts des Körpers, gezeichnet vom Punkt seiner Befestigung. Es ist zweckmäßig, die Achsen des mit dem Körper verbundenen Koordinatensystems entlang der Hauptträgheitsachsen auszurichten. In diesem Fall nimmt der Drehimpuls eine einfache Form an: L 1 = J 1 w 1 , L 2 = J 2 w 2 , L 3 = J 3 w 3 , und w i sind die Projektionen der Winkelgeschwindigkeit auf die sich gemeinsam bewegenden Koordinatenachsen mit dem Körper. Mit der allgemeinen Formel d A/dt = ∂ A/∂t + w* A können wir die Momentengleichung wie folgt darstellen: ∂ L/∂t + w * L = M. Unter Berücksichtigung der Tatsache, dass L x = J x w x , L y = J y w y , L z = J z w z , schreiben wir diese Gleichung in Projektionen auf die Achsen des sich bewegenden Koordinatensystems um: J x dw x /dt + (J z - J y )w y w z = M x , J y dw y /dt + (J x – J z)w z w x = M y , J z dw z /dt + (J y – J x)w x w y = M z . Diese Gleichungen werden Euler-Gleichungen genannt.
7.
Bewegung relativ zu nicht trägen Bezugssystemen.
NISO ist ein System, in dem Der Körper bewegt sich mit Beschleunigung relativ zur Ruhe. Koordinatensystem. Hier werden die Konzepte der Homogenität und Isotropie von Raum und Zeit nicht erfüllt, weil Dauer und Länge in NISO variieren. Darüber hinaus geht der Inhalt des 3. Newtonschen Gesetzes und der Erhaltungssätze verloren. Der Grund für alles sind die Trägheitskräfte, die nur mit dem Koordinatensystem, der Katze, verbunden sind. beeinflussen die Bewegung des Körpers. DAS. Die Beschleunigung kann durch eine äußere Kraft oder durch Trägheit verändert werden. F=∑Fi=ma (ISO), F=F(ext.)+Fi=ma′(NISO), wobei Fi die Trägheitskraft und a die Beschleunigung ist. Körper in IFR, a′-accel. das gleiche Gremium in NISO. In NISO ist das 1. Newtonsche Gesetz nicht erfüllt! Fi=-m(a′-a), d.h. Trägheitskräfte gehorchen nicht Newtons 3. Z-Nun, weil sie sind von kurzer Dauer. Beim Übergang von ISO zu NISO verschwinden die Trägheitskräfte. Trägheit Kräfte sind immer gegen die Augenlider gerichtet. äußere Kräfte. Die Trägheitskräfte können vektoriell addiert werden. In ISO: v=const, v< dx/dt=Ux=dx′/dt+dv(t)/dt′=U′x+v(t) dUx/dt=d/dt′(U′x+v(t))=dU′x/ dt′+dv(t)/dt′=a x ' + a 0 = a x . Die Konzepte der absoluten, relativen und translatorischen Geschwindigkeiten werden in NISO eingeführt: u 0 – absolute Geschwindigkeit, a 0 – relative Beschleunigung. ruhend Koordinatensystem. u x 0 \u003d v + u x 0 ’; a x 0 \u003d a ' + a x; u x ’ a x – relative Geschwindigkeit und Beschleunigung. Bewegung Koordinatensystem. (relativ) ; v, a′-Geschwindigkeit. und beschleunigt. k′ bezieht sich. k, d.h. tragbare Geschwindigkeit und Beschleunigung Es gibt eine Funktion der verallgemeinerten Koordinaten, Geschwindigkeit und Zeit. Betrachten Sie einen 2S-dimensionalen Raum, dann ist die Position des Systems S = ∫(t 1 , t 2) L(g, g( ), t)dt, L die Lagrange-Funktion; S-Aktion. Die Funktion der Aktion heißt itnegral S=∫ Ldt=0, mit der Katze. entlang der wahren Bewegungsbahn genommen, wird das System einen minimalen Wert haben, d.h. S=Smin, δS=0. Diese. Das System von 1 nach 2 bewegt sich auf einer solchen Flugbahn, dass seine Wirkung minimal ist – Hamiltons Prinzip der geringsten Wirkung. L = T – U ist die Differenz zwischen der kinetischen und potentiellen Energie des Systems. Nach Hamilton entspricht die reale Flugbahn der minimalen Aktion. Finden wir eine Flugbahn. Die tatsächliche Flugbahn ist die minimale Flugbahn. S-funktional. Finden wir die Mindestanzahl. δS = 0 erste Variante. δS = ∫(t 1 ,t 2)(Σ[∂L/∂g i δg i ] + Σ[∂L/∂g i ( ) δg i ( )])dt; ∫(t 1 ,t 2) ∂L/∂g i ( ) δg i ( ) dt = ∫(t 1 ,t 2) ∂L/∂g i ( ) dδg i = ∂L/∂g i ( )δg i (t 1 ,t 2) - ∫(t 1 ,t 2) δg i d/dt (∂L/∂g i ( )) dt; δg i sind nicht voneinander abhängig 9.
Schwingungen von Systemen mit einem und mehreren Freiheitsgraden. Freie und erzwungene Vibrationen
.
Der einfachste Fall liegt vor, wenn das System einen Freiheitsgrad hat. Ein stabiles Gleichgewicht entspricht einer solchen Lage des Systems, in der Katze. ihr Potenzial. de. U(q) hat ein Minimum. Eine Abweichung von dieser Position führt zum Entstehen einer Kraft – dU/dq –, die dazu neigt, das System zurückzubringen. q 0 - verallgemeinerte Koordinate. Wir erweitern U(q) - U(q0) in Potenzen und erhalten U(q) - U(q0) ≈ k / 2 (q - q 0) 2 wobei k \u003d U '' (q 0) ein positiver Koeffizient ist . U(q 0) \u003d 0, wir bezeichnen x \u003d q - q 0 - die Abweichung der Koordinate vom Gleichgewichtswert, dann ist U (x) \u003d kx 2 / 2 potentielle Energie. 1/2a(q) q' 2 =1/2a(q)x' 2 -kinetische Energie bei q = q0 und a(q0) = m erhalten wir die Lagrange-Funktion für ein System, das eindimensionale Schwingungen ausführt: L = mx 2 (∙) /2 – kx 2 /2. Die dieser Funktion entsprechende Bewegungsgleichung lautet: mx(∙∙) + kx = 0 oder x(∙∙) + w 2 x = 0, wobei w = √(k/m) die zyklische Schwingungsfrequenz ist. Die Lösung für diese ur-th ist x = a cos (wt + α), wobei a die Amplitude der Schwingungen und wt + α die Phase der Schwingungen ist. Das. die Energie des schwingenden Systems beträgt E = mx 2 (∙)/2 + kx 2 /2. Erzwungene Vibrationen. In diesem Fall verfügt das System neben seiner eigenen potentiellen Energie ½ kx 2 auch über eine potentielle Energie U e (x, m), die mit der Wirkung eines externen Feldes verbunden ist. Dementsprechend lautet die Lagrange-Funktion eines solchen Systems: L = mx 2 (∙)/2 + kx 2 /2 + x F(t), wobei F(t) eine äußere Kraft ist. Die entsprechende Bewegungsgleichung lautet mx(∙∙) + kx = F(t) oder x(∙∙) + w 2 x = F(t)/m. Wenn F(t) eine einfache periodische Funktion der Zeit mit einer bestimmten Frequenz γ ist: F(t) = f cos(γt + β), dann lautet die Lösung der Bewegungsgleichungen: X = a cos(wt + α) + f cos(γt + β)/(m(w 2 – γ 2)) a und α werden aus den Anfangsbedingungen bestimmt. Das. Unter der Wirkung einer Antriebskraft führt das System eine Bewegung aus, die eine Kombination zweier Schwingungen darstellt – mit der Eigenfrequenz des Systems w und mit der Frequenz der Antriebskraft – γ. Schwingungen von Systemen mit vielen Freiheitsgraden
.
Topf. de. Das System U(q i) hat ein Minimum bei q i =q i 0 . Indem wir kleine Verschiebungen x i = q i - q i 0 einführen und U darin mit einer Termgenauigkeit 2. Ordnung erweitern, erhalten wir das Potential. Energie: U = 1/2 Σ(i,k) , k ik =k ki . Kinet. de. für ein solches System ist 1/2 Σ(i,k) , wobei m ik =m ki . Die Lagrange-Gleichung für ein solches System wäre: L = 1/2 Σ(i,k) . Dann ist dL = Σ(i,k) . Wir suchen nach x k (t) in der Form x k \u003d A k exp (-iwt), A k ist eine Konstante. Wenn wir dies in die Lagrange-Gleichung einsetzen, erhalten wir ein System linearer homogener Gleichungen. Σ(k) [(-w 2 m ik +k ik)A k ] = 0 – charakteristische Gleichung, sie hat s verschiedene Wurzeln w 2 α (α=1,2,….,s) w α – Eigenfrequenzen von das System. Eine bestimmte Lösung des Systems hat die Form: x k = ∆ kα C α exp(-iw α t). Die allgemeine Lösung ist die Summe aller besonderen Lösungen: x k = Σ(α) [∆ kα Q α ], wobei Q = Re (C α exp(-iw α t)). 10.
Kanonische Gleichung von Hamilton.
Eine Reihe von Vorteilen bei der Untersuchung mechanischer Fragen liegt in der Beschreibung mit Hilfe verallgemeinerter Koordinaten und Impulse, der Übergang von einem Satz unabhängiger Variablen zu einem anderen kann durch die Legendre-Transformation erfolgen. In diesem Fall kommt es auf Folgendes an. Das Gesamtdifferential der Lagrange-Funktionen als Funktion von Koordinaten und Geschwindigkeiten ist: dL = Σ(i) [∂L/∂q i ] + Σ(i) [[∂L/∂q i (∙)]. Dieser Ausdruck kann als dL = Σ(i) + Σ(i) geschrieben werden. Schreiben wir es in der Form um: d(Σ(i) – L) = - Σ(i) + Σ(i) . Der Wert unter dem Vorzeichen des Differentials ist die Energie des Systems, ausgedrückt in Koordinaten und Impulsen, und wird Hamilton-Funktion genannt: H (p, q, t) = Σ (i) – L. Aus diff. Gleichungen dH = - Σ(i) + Σ(i) folgen den Gleichungen: q i (∙) = ∂H/∂p i , p i (∙) = - ∂H/∂q i sind die Hamiltonschen Gleichungen. Aufgrund ihrer Einfachheit und Symmetrie werden sie auch genannt. kanonisch. Poisson-Klammern. Die Zeitableitung jeder Funktion F verallgemeinerter Koordinaten, Impulse und Zeit ist dF/dt = ∂F/∂t + Σ(i) [∂F/∂q i dq i /dt] + Σ(i) [∂F/∂ p i dpi /dt]. Mithilfe der Hamilton-Gleichungen können wir diese Gleichung in der folgenden Form umschreiben: dF/dt = ∂F/∂t + , wobei = Σ(i) [∂F/∂q i ∂H/∂p i - ∂H/∂q i ∂F /∂ p i ] - aufgerufen. die Poisson-Klammer. Offensichtlich kann die Hamilton-Gleichung mit Poisson-Klammern geschrieben werden. 11.
Hamilton-Jacobi-Gleichung
.
Nach dem Prinzip der kleinsten Wirkung gilt S = ∫(t 1 ,t 2)Ldt. Betrachten Sie die Aktion (S) als eine Größe, die die Bewegung entlang wahrer Flugbahnen charakterisiert. Basierend auf der Lagrange-Gleichung zur Änderung der Aktion beim Übergang von einer Trajektorie zu einer anderen Trajektorie in der Nähe (mit einem Freiheitsgrad) erhalten wir: δS = pδq oder für eine beliebige Anzahl von Freiheitsgraden: δS = Σ(i) . Daraus folgt, dass die partiellen Ableitungen der Wirkung nach den Koordinaten gleich den entsprechenden Impulsen sind: ∂S/∂q i = p i (1). Per Definition ist dS/dt = L, wenn man andererseits S als Funktion von Koordinaten und Zeit betrachtet und Formel (1) verwendet, gilt: dS/dt = ∂S/∂t + Σ(i) [∂S /∂q i q i (∙)] = ∂S/∂t + Σ(i) . Wenn wir beide Ausdrücke vergleichen, erhalten wir ∂S/∂t = L - Σ(i) oder ∂S/∂t = - H(p,q,t) (2). Die Formeln (1), (2) können zusammen geschrieben werden als dS = Σ(i) – Hdt. Und die Aktion (S) selbst wird S = ∫ (Σ(i) – Hdt) sein. Für H unabhängig von t gilt S(q,t)=S 0 (q) - Et, wobei S 0 (q) = Σ(i) [∫p i dq i ] eine verkürzte Aktion ist und Еt durch H(p) ersetzt wird ,q) . Die Funktion S(q,t) erfüllt eine bestimmte Differenz. Gleichung, die wir erhalten, indem wir die Impulse Р in Beziehung (2) durch die Ableitungen ∂S/∂q ersetzen: ∂S/∂t + H(∂S/∂q 1 ,…, ∂S/∂q s ;q 1 ,… ,q s ,t) = 0 heißt eine Gleichung in partiellen Ableitungen 1. Ordnung. Hamilton-Jacobi-Gleichung. Für ein Teilchen in einem externen Feld U(x,y,z,t) hat es also die Form: ∂S/∂t + 1/(2m)((∂S/∂x) 2 + (∂S/∂ y) 2 + (∂S/∂z) 2) + U(x,y,z,t) = 0. 12.
Verformungen und Spannungen in Festkörpern. Elastizitätsmodul, Scherung. Poissonzahl
.
Eine Verformung ist eine Veränderung der Form und des Volumens eines Körpers unter Einwirkung äußerer Kräfte. Unter Einwirkung einer äußeren Kraft verändert sich die Form des Körpers. Alle Verformungen in der Natur können auf 3 reduziert werden M Hauptverformungen: 1) Zug, Druck; 2) Scherung; 3) Torsion. Unterscheiden Sie zwischen homogenen und inhomogenen Verformungen. Wenn alle Teile gleich verformt sind, dann ist dies der Fall gleichmäßig verformt. Wenn sich alle Körperteile unterschiedlich verformen, dann ist dies der Fall inhomogen verformt. Das Hookesche Gesetz ist nur im Bereich der elastischen Verformung erfüllt. = E’. F/S = E ∆l/l 0 ; F-Steuerung = ES∆l/l 0 = kx; k = ES/l 0 ; F-Steuerung \u003d ESx / l 0. Das Hookesche Gesetz definiert die Beziehung zwischen und . k ist der Elastizitätskoeffizient, er hängt von den geometrischen Abmessungen und dem Material ab, aus dem der Körper besteht. E ist der Elastizitätsmodul. Der Elastizitätsmodul ist gleich der Kraft, die auf einen Körper mit einheitlichem Querschnitt ausgeübt werden muss, damit sich sein Körper um das Zweifache vergrößert. Eine andere Art der Verformung ist die Scherverformung. Sie wird beobachtet, wenn die Oberfläche tangential angelegt wird. Sie verläuft parallel zur Scherverformungsfläche, beobachtet unter Einwirkung tangentialer Kräfte, d. h. die Kräfte wirken tangential. Ψ~F t /S (Verschiebungswinkel). Ψ = nF t /S; n ist der Verschiebungsfaktor. F t = nS. (E> N, E~ 4N). 13.
Mechanik von Flüssigkeiten und Gasen.
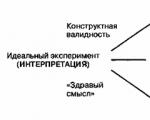
Für alle Flüssigkeiten und Gase ist der einheitliche Parameter: Dichte ρ, Druck P=F n /S. In Flüssigkeiten und Gasen findet der Elastizitätsmodul statt, der Schubmodul |σ|=|P|, σ - Spannung findet jedoch nicht statt. Ist die Flüssigkeit (Gas) bewegungslos, dann handelt es sich um Hydrostatik (Aerostatik). Charakteristische Gesetze: Pascalsches Gesetz: Überdruck, der in Gasen und Flüssigkeiten entsteht, wird in alle Richtungen gleichmäßig übertragen. Zn Archimedes gilt sowohl für Flüssigkeiten als auch für Gase. Die Archimedes-Kraft wirkt immer gegen die Schwerkraft. Der Grund für die Entstehung der Archimedes-Kraft ist das Vorhandensein eines Körpers mit dem Volumen V. Zn Archimedes: Auf einen Körper in einer Flüssigkeit oder einem Gas wirkt immer eine Kraft ein, die dem Gewicht der Flüssigkeit oder des Gases entspricht, das durch den eingetauchten Teil verdrängt wird dem Körper und senkrecht nach oben gerichtet. Wenn F A > F HEAVY, dann schwimmt der Körper, ist es umgekehrt, dann sinkt er. Wenn eine Flüssigkeit (Gas) strömt, wird zu diesen Gleichungen die Strahlkontinuitätsgleichung hinzugefügt. Man nennt die Bewegungsbahn eines Teilchens in einer Flüssigkeit. aktuelle Zeile. Der Teil des Raumes, der von einer aktuellen Linie begrenzt wird, wird aufgerufen. aktuelle Röhre. Die Flüssigkeit im Strömungsrohr kann stationär oder instationär fließen. Der Strom wird aufgerufen Bahnhof wenn durch einen bestimmten Abschnitt der Stromröhre pro Einheit. Im Laufe der Zeit vergeht die gleiche Menge Flüssigkeit (Gas), andernfalls ist die Strömung nicht statisch. Wir haben eine Stromröhre der folgenden Form: Wenn die Flüssigkeitsströmung statisch ist. Dann m 1 =m 2 =…=m n pro Zeiteinheit, wenn die Flüssigkeit inkompressibel ist, dann ρ 1 V 1 =ρ 2 V 2 =…; =ρ n V n , ρ 1 Δx 1 = ρ 2 Δx 2 =…; \u003d ρ n Δx n, ρ 1 υ 1 ΔtS 1 \u003d ρ 2 υ 2 ΔtS 2 =…= ρ n υ n ΔtS n, da die Flüssigkeit inkompressibel ist, ist ρ konstant υ 1 S 1 = υ 2 S 2 =… = υ n S n , υS=const; υ=const/S ist die Strahlkontinuitätsgleichung. p d v/dt = ρ G– Grad P – Gl. Euler - 2. Ordnung. Newton für Flüssigkeiten und Gase. Das Gesetz bleibt erhalten. Energie in Flüssigkeiten und Gasen. Lv. Bernoulli. Ausweis. Naz. Eine inkompressible Flüssigkeit, in der viskose Reibungskräfte vernachlässigbar sind. Kinetische Energie wird nicht für die Arbeit gegen Reibungskräfte aufgewendet. Ρυ 2 /2+ρgh + P = const – Gl. Bernoulli, ρυ 2 /2 – dynamischer Druck, ρgh – Hydrostat. Druck, P – Molekulardruck. Mυ 2 /2 \u003d E K; mυ 2 /2V= E K /V= ρυ 2 /2. Kraft der viskosen Reibung F A = - ηΔυΔS/ΔZ 6 π r η υ – Stokes-Kraft. Η - Koeffizient. Viskosität, Δυ/ΔZ – Grad υ, r – Körperabmessungen. Dies ist Newtons Formel für viskose Reibungskräfte. Wenn in der Flüssigkeit Reibungskräfte vorhanden sind, dann id. Die Flüssigkeit wird zähflüssig. ρ v 1 2 /2 + ρgh 1 + P 1 = ρ v 2 2 /2 + ρgh 2 + P 2 ; (P 1 - P 2) \u003d ρ (υ 2 2 - υ 1 2) / 2. Wenn ΔP = 0, dann ist υ 2 2 - υ 1 2 = 0 und es findet kein Flüssigkeitsfluss statt. Wo P größer ist, ist schnell. Weniger aktuell. Wenn der Querschnitt S zunimmt, dann nimmt P zu und υ ab. Wenn die aktuelle Röhre nicht horizontal liegt, dann υ 2 2 -υ 1 2 \u003d 2g (h 1 -h 2); υ \u003d sqrt (2g (h 1 -h 2)) - Torricellis Formel. Die Trajektorien, die die Bewegungen mechanischer Systeme in erweiterten Konfigurations- und Phasenräumen beschreiben, haben eine bemerkenswerte Eigenschaft – sie sind Extremale eines Variationsproblems und liefern stationäre Werte für das Wirkungsfunktional. Betrachten Sie die Formulierung des Variationsproblems im erweiterten Konfigurationsraum R"*", deren Punkte die Mengen (q, ().
Sei die Kurve yn = ((q, T): q e R t e , 5q(/ 0)= 8q(/,) = 0). Die Variation 8q(/) ist eine beliebige Funktion aus der Klasse C 1, die an den Enden der Strecke = 0 verschwindet. A Die erste Variation des Funktionalen Sy bei y = y 0 ist laut Definition gleich und nimmt nach partieller Integration die Form an Der nicht ganzzahlige Term im Ausdruck (2.3) verschwindet, als bq k (t 0) = bq k (t y) = 0, Zu - 1 ..... l und der Ausdruck im Quadrat Klammern unter dem Integralzeichen ist gleich Null, da y 0 eine reale Trajektorie ist, die die Lagrange-Gleichungen (2.1) erfüllt. Daher ist die Variation 55(y 0) = 0. ? Auch die umgekehrte Aussage gilt: Wenn die Variation 65(y*) = 0 ist, wobei y* zur Klasse der Kreisverkehrtrajektorien gehört, dann ist y* = y 0 eine reale Trajektorie. Die Gültigkeit dieser Aussage ergibt sich aus dem Ausdruck der ersten Variation (2.3) und dem Hauptlemma der Variationsrechnung. In diesem Fall von der Gleichheit bis Null der ersten Variation und die Unabhängigkeit der Variationen 6 k - 1, ..., die Gültigkeit der Lagrange-Gleichungen zweiter Art l, es folgt richtig Wann q k = q k *(t), k= 1....l. Dies bedeutet, dass y* die tatsächliche Trajektorie des mechanischen Systems ist. 3.1. Im Falle eines nichtkonservativen Systems ist es unmöglich, ein Funktional anzugeben, dessen stationärer Wert auf einer realen Trajektorie erreicht wurde. In diesem Fall sind jedoch die folgenden Aussagen äquivalent: wobei q(/) die reale Flugbahn ist. Die erste der obigen Aussagen ist der Inhalt des Hamilton-Ostrogradsky-Variationsprinzips für nichtkonservative Systeme. 3.2. Es kann gezeigt werden, dass der stationäre Wert des Wirkungsfunktionals ein Minimum ist, wenn die Differenz - / 0 klein genug ist. Dieser Umstand hängt mit einem anderen Namen des diskutierten Prinzips zusammen – dem Prinzip der geringsten Wirkung von Hamilton-Ostrogradkogo. Das oben betrachtete Variationsproblem lässt sich im erweiterten Phasenraum formulieren, was sich bei der Betrachtung von Fragen der Integrierbarkeit der kanonischen Gleichungen Hamiltons als wichtig erweist. Bezeichnen mit Г = ((ð + 6ð. q + 8q, ICH): p, q, 6p. 6q e R",te[r 0 , /,]. 5q(/ 0)= 8q(/|) = 0) Kurve im erweiterten Phasenraum und sei für 8p = 8q = 0 die Kurve Г 0 die Lösung des Systems der hamiltonschen kanonischen Gleichungen Alle Zeitfunktionen gehören zur Klasse C 1 . Somit wird eine Familie von Kreisverkehrtrajektorien (Г) definiert, zu der die reale Trajektorie Г 0 gehört (Abb. 46). Das Aktionsfunktional nimmt unter Berücksichtigung des Zusammenhangs zwischen den Lagrange- und Hamilton-Funktionen die Form an Hier werden der Kürze halber die Buchstaben p, q anstelle der Buchstaben p + 8p, q + 8q verwendet. Wenn wir die Variation der Funktion 5[Γ] auf der realen Flugbahn berechnen, erhalten wir: Durch partielle Integration unter Berücksichtigung der Randbedingungen finden wir Daraus folgt, dass die Variation 85|Γ 0 1 = 0 ist, wenn p(/), q(f) die kanonischen Hamilton-Gleichungen (2.4), u erfüllen. im Gegenteil, aus der Bedingung der Unabhängigkeit der Variationen 8p(r), 6q(/) folgen nach dem Hauptlemma der Variationsrechnung die Gleichungen (2.4). Damit wurde die Gültigkeit des Prinzips der kleinsten Wirkung im Phasenraum des Systems bewiesen: Die funktionale Wirkung 5[Г], definiert auf dem Raum der Kreisverkehrtrajektorien (Г|., nimmt auf der realen Trajektorie einen stationären Wert an, d. h. 85 [Г 0 1 = 0. Reis. 46 Als ich zum ersten Mal von diesem Prinzip erfuhr, hatte ich ein Gefühl von Mystik. Es scheint, dass die Natur auf mysteriöse Weise alle möglichen Bewegungsarten des Systems durchsucht und die beste davon auswählt. Heute möchte ich ein wenig über eines der bemerkenswertesten physikalischen Prinzipien sprechen – das Prinzip der geringsten Wirkung. Auch bei der Reflexion bewegt sich Licht so, dass es auf dem kürzesten Weg von einem Punkt zum anderen gelangt. Im Bild ist der kürzeste Weg der grüne Weg, bei dem der Einfallswinkel gleich dem Reflexionswinkel ist. Jeder andere Weg, wie zum Beispiel der rote, ist länger. Im Jahr 1662 schlug Pierre Fermat vor, dass die Lichtgeschwindigkeit in einer dichten Substanz wie Glas geringer sei als in Luft. Zuvor war Descartes die allgemein anerkannte Version, wonach die Lichtgeschwindigkeit in Materie größer sein muss als in Luft, um das korrekte Brechungsgesetz zu erhalten. Für Fermat erschien die Annahme, dass sich Licht in einem dichteren Medium schneller bewegen könnte als in einem verdünnten Medium, unnatürlich. Deshalb ging er davon aus, dass alles genau das Gegenteil sei, und bewies eine erstaunliche Sache: Unter dieser Annahme wird Licht so gebrochen, dass es in kürzester Zeit sein Ziel erreicht. All diese Fakten legen nahe, dass die Natur auf eine rationale Art und Weise handelt, Licht und Körper sich auf die optimalste Art und Weise bewegen und dabei so wenig Aufwand wie möglich aufwenden. Doch was diese Bemühungen waren und wie man sie berechnen sollte, blieb ein Rätsel. Im Jahr 1744 führte Maupertuis das Konzept der „Aktion“ ein und formulierte das Prinzip, nach dem sich die wahre Flugbahn eines Teilchens von jeder anderen dadurch unterscheidet, dass die Wirkung dafür minimal ist. Allerdings konnte Maupertuis selbst nicht klar definieren, was diese Aktion bedeutet. Eine strenge mathematische Formulierung des Prinzips der kleinsten Wirkung wurde von anderen Mathematikern – Euler, Lagrange – entwickelt und schließlich von William Hamilton gegeben: Wie muss man also fahren, um pünktlich am Zielort anzukommen und möglichst wenig Kraftstoff zu verbrauchen? Es ist klar, dass Sie in einer geraden Linie gehen müssen. Mit zunehmender zurückgelegter Strecke wird der Kraftstoffverbrauch genau gleich sein. Und dann können Sie verschiedene Taktiken wählen. Sie können zum Beispiel schnell im Voraus an den Punkt kommen und einfach sitzen und warten, bis die Zeit kommt. Die Fahrgeschwindigkeit und damit der Kraftstoffverbrauch zu jedem Zeitpunkt werden hoch sein, aber auch die Fahrzeit wird verkürzt. Möglicherweise ist der Gesamtkraftstoffverbrauch in diesem Fall nicht so hoch. Oder Sie können gleichmäßig und mit der gleichen Geschwindigkeit vorgehen, sodass Sie ohne Eile genau im richtigen Moment ankommen. Oder man fährt teilweise schnell und teilweise langsamer. Was ist der beste Weg? Es stellt sich heraus, dass die optimalste und wirtschaftlichste Art des Fahrens darin besteht, mit einer konstanten Geschwindigkeit zu fahren, um beispielsweise genau zum vereinbarten Zeitpunkt am Zielort zu sein. Jede andere Option verbraucht mehr Kraftstoff. Anhand einiger Beispiele können Sie es selbst überprüfen. Der Grund dafür ist, dass der Kraftstoffverbrauch mit dem Quadrat der Geschwindigkeit steigt. Daher steigt der Kraftstoffverbrauch mit zunehmender Geschwindigkeit schneller an, als die Fahrzeit abnimmt, und auch der Gesamtkraftstoffverbrauch steigt. Wir haben also herausgefunden, dass, wenn ein Auto zu einem bestimmten Zeitpunkt im Verhältnis zu seiner kinetischen Energie Kraftstoff verbraucht, der wirtschaftlichste Weg, genau zur vereinbarten Zeit von Punkt zu Punkt zu gelangen, darin besteht, gleichmäßig und geradeaus zu fahren Ein Körper bewegt sich, wenn keine Kräfte auf ihn einwirken. Kräfte. Jede andere Fahrweise führt zu einem höheren Gesamtkraftstoffverbrauch. Der Kraftstoffverbrauch zu jedem Zeitpunkt entspricht der kinetischen Energie abzüglich der potenziellen Energie des Autos (abzüglich der potenziellen Energie, da das eingebaute Fahrzeug Kraftstoff produziert und nicht verbraucht). Jetzt besteht unsere Aufgabe darin, das Auto so wirtschaftlich wie möglich zwischen den Punkten zu bewegen, und das wird immer schwieriger. Eine geradlinige, gleichmäßige Bewegung ist in diesem Fall nicht die effektivste. Es stellt sich heraus, dass es optimaler ist, ein wenig aufzusteigen, dort eine Weile zu verweilen, mehr Treibstoff zu entwickeln und dann zum Punkt abzusteigen. Bei korrekter Flugbahn deckt der gesamte Treibstoffverbrauch aufgrund des Steigflugs die zusätzlichen Treibstoffkosten für die Verlängerung der Flugbahn und die Erhöhung der Geschwindigkeit. Bei sorgfältiger Berechnung wäre es für ein Auto am wirtschaftlichsten, in einer Parabel zu fliegen, auf genau derselben Flugbahn und mit genau derselben Geschwindigkeit, wie ein Stein im Schwerefeld der Erde fliegen würde. Ein Analogon zur Gesamtmenge des während der gesamten Bewegungszeit verbrauchten Kraftstoffs, d.h. Der über die gesamte Bewegungszeit akkumulierte Wert der Lagrangefunktion wird als „Aktion“ bezeichnet. Das Prinzip der geringsten Wirkung besteht darin, dass sich der Körper so bewegt, dass die Wirkung (die von der Bewegungsbahn abhängt) minimal ist. Dabei darf man nicht vergessen, dass die Anfangs- und Endbedingungen gegeben sind, d.h. wo sich der Körper zur Zeit und zur Zeit befindet. In diesem Fall muss sich der Körper nicht in einem gleichmäßigen Gravitationsfeld bewegen, was wir für unser Auto berücksichtigt haben. Sie können völlig unterschiedliche Situationen berücksichtigen. Ein Körper kann auf einem Gummiband schwingen, auf einem Pendel schwingen oder um die Sonne fliegen, in all diesen Fällen bewegt er sich so, dass der „Gesamtkraftstoffverbrauch“ minimiert wird, d.h. Aktion. Wenn das System aus mehreren Körpern besteht, ist die Lagrangefunktion eines solchen Systems gleich der gesamten kinetischen Energie aller Körper abzüglich der gesamten potentiellen Energie aller Körper. Und wiederum bewegen sich alle Körper gemeinsam, so dass die Auswirkung auf das gesamte System während dieser Bewegung minimal ist. Nehmen wir zum Beispiel einen Ball und legen ihn in ein leeres Feld. In einiger Entfernung davon haben wir eine elastische Wand angebracht. Nehmen wir an, wir möchten, dass der Ball nach einiger Zeit am selben Ort landet. Unter diesen gegebenen Bedingungen kann sich der Ball auf zwei verschiedene Arten bewegen. Erstens kann er einfach dort bleiben. Zweitens können Sie es in Richtung Wand schieben. Der Ball erreicht die Wand, prallt von ihr ab und kommt zurück. Es ist klar, dass man es mit einer solchen Geschwindigkeit vorantreiben kann, dass es genau zum richtigen Zeitpunkt zurückkehrt. Wie kann das Prinzip der geringsten Aktion gerettet werden, damit es in solchen Situationen gilt? Darüber werden wir in sprechen.8. Hamiltons Variationsprinzip. (Prinzip der geringsten Wirkung).
;
=0
Auf der tatsächlichen Flugbahn muss die folgende Gleichung erfüllt sein: 
- Lagrange-Gleichung (für jedes i= 1,…S).
Die quantitative Beziehung zwischen E und N wird durch die Poissonzahl angegeben. N = E/(2(1+μ)), wobei die Poissonzahl ist. μ = |∆d/d 0 |/|∆l/l 0 |. Die Poissonzahl bestimmt die Änderung der Querabmessungen bei Zug oder Druck. 0,5.
Hintergrund
Seit Galilei ist bekannt, dass sich Körper, auf die keine Kräfte einwirken, geradlinig, also auf dem kürzesten Weg, bewegen. Lichtstrahlen breiten sich auch geradlinig aus. 
Dies lässt sich leicht nachweisen, indem man einfach die Strahlengänge auf die gegenüberliegende Seite des Spiegels reflektiert. Sie sind im Bild gestrichelt dargestellt. 
Es ist zu erkennen, dass der grüne Pfad ACB in eine gerade Linie ACB' übergeht. Und der rote Pfad verwandelt sich in eine gestrichelte Linie ADB‘, die natürlich länger ist als die grüne. 
Auch in der Abbildung zeigt die grüne Farbe den Weg, den der Lichtstrahl tatsächlich zurücklegt. Der rot markierte Weg ist der kürzeste, aber nicht der schnellste, da das Licht im Glas einen längeren Weg zurücklegen muss und seine Geschwindigkeit darin langsamer ist. Am schnellsten ist der tatsächliche Weg des Lichtstrahls. 
In der mathematischen Sprache ist das Prinzip der geringsten Wirkung recht kurz formuliert, aber möglicherweise verstehen nicht alle Leser die Bedeutung der verwendeten Notation. Ich möchte versuchen, dieses Prinzip klarer und einfacher zu erklären. lockerer Körper
Stellen Sie sich also vor, Sie sitzen zu einem bestimmten Zeitpunkt in einem Auto und erhalten zu einem bestimmten Zeitpunkt eine einfache Aufgabe: Zu diesem Zeitpunkt müssen Sie ein Auto zu einem bestimmten Punkt fahren. 
Treibstoff für das Auto ist teuer und natürlich möchte man dafür so wenig wie möglich ausgeben. Ihr Auto ist mit den neuesten Supertechnologien ausgestattet und kann so schnell beschleunigen oder abbremsen, wie Sie möchten. Allerdings ist es so konzipiert, dass es umso mehr Kraftstoff verbraucht, je schneller es fährt. Darüber hinaus ist der Kraftstoffverbrauch proportional zum Quadrat der Geschwindigkeit. Wer doppelt so schnell fährt, verbraucht in der gleichen Zeit viermal mehr Kraftstoff. Neben der Geschwindigkeit wird der Kraftstoffverbrauch natürlich auch von der Masse des Autos beeinflusst. Je schwerer unser Auto ist, desto mehr Kraftstoff verbraucht es. Der Kraftstoffverbrauch unseres Autos beträgt zu jedem Zeitpunkt, d. h. entspricht genau der kinetischen Energie des Autos. Im Bereich der Schwerkraft
Jetzt lasst uns unser Auto ein wenig verbessern. Befestigen wir daran Düsentriebwerke, damit es frei in jede Richtung fliegen kann. Im Allgemeinen blieb die Konstruktion gleich, sodass der Kraftstoffverbrauch wiederum streng proportional zur kinetischen Energie des Autos blieb. Stellt man sich nun die Aufgabe, von einem Punkt zu starten und zum Zeitpunkt t an einem Punkt anzukommen, so ist es natürlich nach wie vor der wirtschaftlichste Weg, gleichmäßig und geradlinig zu fliegen, um den Punkt genau zu erreichen die festgelegte Zeit t. Dies entspricht wiederum der freien Bewegung des Körpers im dreidimensionalen Raum. 
Allerdings wurde im neuesten Modell des Autos ein ungewöhnliches Gerät eingebaut. Dieses Gerät ist in der Lage, Kraftstoff buchstäblich aus dem Nichts zu erzeugen. Aber das Design ist so, dass das Gerät zu jedem Zeitpunkt umso mehr Kraftstoff produziert, je höher das Auto ist. Die Kraftstoffabgabe ist direkt proportional zur Höhe, in der sich das Fahrzeug gerade befindet. Je schwerer das Auto ist, desto leistungsstärker ist das Gerät und desto mehr Kraftstoff produziert es. Die Leistung ist direkt proportional zur Masse des Autos. Es stellte sich heraus, dass die Vorrichtung so beschaffen ist, dass die Kraftstoffabgabe genau gleich ist (wo ist die Beschleunigung im freien Fall), d. h. potentielle Energie des Autos. 
Hier lohnt es sich, eine Erklärung abzugeben. Natürlich ist es auf viele verschiedene Arten möglich, einen Stein von einer Spitze aus so zu werfen, dass er die Spitze trifft. Aber Sie müssen es so werfen, dass es, nachdem es von einem Punkt zu einem bestimmten Zeitpunkt abgeflogen ist, genau zu diesem Zeitpunkt einen Punkt trifft. Es ist diese Bewegung, die für unser Auto am wirtschaftlichsten ist. Die Lagrange-Funktion und das Prinzip der geringsten Wirkung
Jetzt können wir diese Analogie auf reale physische Körper übertragen. Ein Analogon der Intensität des Kraftstoffverbrauchs für Körper wird Lagrange-Funktion oder Lagrange-Funktion (zu Ehren von Lagrange) genannt und mit dem Buchstaben bezeichnet. Der Lagrange-Operator zeigt, wie viel „Treibstoff“ der Körper zu einem bestimmten Zeitpunkt verbraucht. Für einen Körper, der sich in einem Potentialfeld bewegt, ist die Lagrange-Funktion gleich seiner kinetischen Energie minus seiner potentiellen Energie. Nicht so einfach
Tatsächlich habe ich ein wenig geschummelt, indem ich gesagt habe, dass sich Körper immer so bewegen, dass die Aktion minimiert wird. Obwohl dies in sehr vielen Fällen der Fall ist, kann man sich Situationen vorstellen, in denen die Aktion eindeutig nicht minimal ist. 
Beide Bewegungsvarianten des Balls sind möglich, aber im zweiten Fall ist die Wirkung größer, da sich der Ball die ganze Zeit über mit einer kinetischen Energie ungleich Null bewegt.
