Der Satz von Gauß im Vakuum. Anwendung des Gaußschen Theorems zur Berechnung elektrischer Felder

Wie oben erwähnt, wurde vereinbart, die Kraftlinien mit einer solchen Dichte zu zeichnen, dass die Anzahl der Linien, die eine Flächeneinheit senkrecht zu den Linien des Standorts durchdringen, gleich dem Modul des Vektors wäre. Aus dem Muster der Spannungslinien kann man dann nicht nur die Richtung, sondern auch die Größe des Vektors an verschiedenen Punkten im Raum beurteilen.

Betrachten wir die Feldlinien einer stationären positiven Punktladung. Es sind radiale Linien, die von der Ladung ausgehen und im Unendlichen enden. Lasst uns ausführen N solche Zeilen. Dann auf Distanz R von der Ladung, die Anzahl der Kraftlinien, die eine Einheitsoberfläche einer Kugel mit Radius schneiden R, wird gleich sein. Dieser Wert ist proportional zur Feldstärke einer Punktladung in einiger Entfernung R. Nummer N Sie können immer so wählen, dass die Gleichheit gilt

Wo . Da die Kraftlinien kontinuierlich sind, schneidet die gleiche Anzahl von Kraftlinien eine geschlossene Oberfläche beliebiger Form, die die Ladung umschließt Q. Abhängig vom Vorzeichen der Ladung treten die Kraftlinien entweder in diese geschlossene Oberfläche ein oder gehen nach außen. Wenn die Anzahl der ausgehenden Leitungen als positiv und die Anzahl der eingehenden Leitungen als negativ angesehen wird, können wir das Modulzeichen weglassen und schreiben:

.

(1.4)

Spannungsvektorfluss. Lassen Sie uns ein Elementarpad mit der Fläche platzieren. Die Fläche muss so klein sein, dass die elektrische Feldstärke an allen Punkten als gleich angesehen werden kann. Zeichnen wir eine Normale zur Site (Abb. 1.17). Die Richtung dieser Normalen wird willkürlich gewählt. Die Normale bildet mit dem Vektor einen Winkel. Der Fluss des elektrischen Feldstärkevektors durch eine ausgewählte Oberfläche ist das Produkt aus der Oberfläche und der Projektion des elektrischen Feldstärkevektors auf die Flächennormale:

Wo ist die Projektion des Vektors auf die Normale zur Site?

Da die Anzahl der Feldlinien, die einen einzelnen Bereich durchdringen, gleich dem Modul des Intensitätsvektors in der Nähe des ausgewählten Bereichs ist, ist der Fluss des Intensitätsvektors durch die Oberfläche proportional zur Anzahl der Feldlinien, die diese Oberfläche durchqueren. Daher kann im allgemeinen Fall der Fluss des Feldstärkevektors durch das Gebiet visuell als ein Wert interpretiert werden, der der Anzahl der Feldlinien entspricht, die dieses Gebiet durchdringen:

.

(1.5)

Beachten Sie, dass die Wahl der Richtung der Normalen an Bedingungen geknüpft ist; sie kann in die andere Richtung gerichtet sein. Folglich ist der Fluss eine algebraische Größe: Das Vorzeichen des Flusses hängt nicht nur von der Konfiguration des Feldes ab, sondern auch von der relativen Ausrichtung des Normalenvektors und des Intensitätsvektors. Wenn diese beiden Vektoren einen spitzen Winkel bilden, ist der Fluss positiv; wenn er stumpf ist, ist der Fluss negativ. Bei einer geschlossenen Fläche ist es üblich, die Normale außerhalb der von dieser Fläche abgedeckten Fläche zu nehmen, also die äußere Normale zu wählen.

Wenn das Feld inhomogen und die Oberfläche beliebig ist, ist die Strömung wie folgt definiert. Die gesamte Oberfläche muss in kleine Elemente mit Fläche unterteilt werden, die Spannungsflüsse durch jedes dieser Elemente berechnen und dann die Flüsse durch alle Elemente summieren:

Somit charakterisiert die Feldstärke das elektrische Feld an einem Punkt im Raum. Der Intensitätsfluss hängt nicht vom Wert der Feldstärke an einem bestimmten Punkt ab, sondern von der Verteilung des Feldes über die Oberfläche eines bestimmten Gebiets.

Elektrische Feldlinien können nur bei positiven Ladungen beginnen und bei negativen enden. Sie können nicht im Weltraum beginnen oder enden. Wenn also in einem bestimmten geschlossenen Volumen keine elektrische Ladung vorhanden ist, muss die Gesamtzahl der in dieses Volumen ein- und austretenden Leitungen Null sein. Wenn mehr Leitungen das Volumen verlassen als hineingehen, liegt im Inneren des Volumens eine positive Ladung vor; Wenn mehr Leitungen ein- als austreten, muss im Inneren eine negative Ladung vorhanden sein. Wenn die Gesamtladung im Inneren des Volumens gleich Null ist oder keine elektrische Ladung darin vorhanden ist, dringen die Feldlinien durch das Volumen und der Gesamtfluss ist Null.

Diese einfachen Überlegungen hängen nicht davon ab, wie die elektrische Ladung innerhalb des Volumens verteilt ist. Es kann sich in der Mitte des Volumens oder in der Nähe der Oberfläche befinden, die das Volumen begrenzt. Ein Volumen kann mehrere positive und negative Ladungen enthalten, die beliebig innerhalb des Volumens verteilt sind. Nur die Gesamtladung bestimmt die Gesamtzahl der ein- oder ausgehenden Spannungsleitungen.

Wie aus (1.4) und (1.5) ersichtlich ist, erfolgt der Fluss des elektrischen Feldstärkevektors durch eine beliebige geschlossene Oberfläche, die die Ladung umschließt Q, gleich . Wenn es innerhalb der Oberfläche vorhanden ist N Ladungen, dann ist der Gesamtfluss nach dem Prinzip der Feldüberlagerung die Summe der Feldstärkeflüsse aller Ladungen und gleich , wobei wir in diesem Fall die algebraische Summe aller durch die geschlossene Ladung abgedeckten Ladungen meinen Oberfläche.

Satz von Gauß. Gauß war der erste, der die einfache Tatsache entdeckte, dass der Fluss des elektrischen Feldstärkevektors durch eine beliebige geschlossene Oberfläche mit der Gesamtladung in diesem Volumen verbunden sein muss:

Gauß Karl Friedrich (1777–1855)

Großer deutscher Mathematiker, Physiker und Astronom, Schöpfer des absoluten Einheitensystems in der Physik. Er entwickelte die Theorie des elektrostatischen Potentials und bewies den wichtigsten Satz der Elektrostatik (Satz von Gauß). Erstellte eine Theorie zur Konstruktion von Bildern in komplexen optischen Systemen. Er war einer der ersten, der auf die Idee der Möglichkeit der Existenz nichteuklidischer Geometrie kam. Darüber hinaus leistete Gauß herausragende Beiträge zu nahezu allen Bereichen der Mathematik.

Die letzte Beziehung ist der Satz von Gauß für das elektrische Feld: Der Fluss des Intensitätsvektors durch eine beliebige geschlossene Oberfläche ist proportional zur algebraischen Summe der innerhalb dieser Oberfläche befindlichen Ladungen. Der Proportionalitätskoeffizient hängt von der Wahl des Einheitensystems ab.

Es ist zu beachten, dass der Satz von Gauß als Folge des Coulombschen Gesetzes und des Superpositionsprinzips erhalten wird. Wenn sich die elektrische Feldstärke nicht umgekehrt proportional zum Quadrat der Entfernung ändern würde, wäre der Satz ungültig. Daher ist der Satz von Gauß auf alle Felder anwendbar, in denen das umgekehrte Quadratgesetz und das Superpositionsprinzip strikt erfüllt sind, beispielsweise auf das Gravitationsfeld. Im Falle eines Gravitationsfeldes spielen die Massen der Körper die Rolle der Ladungen, die das Feld erzeugen. Der Fluss von Gravitationsfeldlinien durch eine geschlossene Oberfläche ist proportional zur Gesamtmasse, die in dieser Oberfläche enthalten ist.

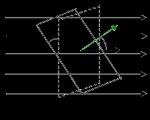
Feldstärke einer geladenen Ebene. Wenden wir den Satz von Gauß an, um die elektrische Feldstärke einer unendlich geladenen Ebene zu bestimmen. Wenn die Ebene unendlich und gleichmäßig geladen ist, das heißt, die Oberflächenladungsdichte ist an jedem Ort gleich, dann stehen die elektrischen Feldstärkelinien an jedem Punkt senkrecht auf dieser Ebene. Um dies zu zeigen, verwenden wir das Superpositionsprinzip für den Spannungsvektor. Wählen wir zwei Elementarabschnitte auf der Ebene aus, die als Punkt für Punkt betrachtet werden können A, bei dem es notwendig ist, die Feldstärke zu bestimmen. Wie aus Abb. ersichtlich ist. 1.18 wird der resultierende Spannungsvektor senkrecht zur Ebene gerichtet sein. Da die Ebene für jeden Beobachtungspunkt in unendlich viele Paare solcher Abschnitte unterteilt werden kann, ist es offensichtlich, dass die Feldlinien der geladenen Ebene senkrecht zur Ebene stehen und das Feld gleichmäßig ist (Abb. 1.19). Wäre dies nicht der Fall, würde sich bei der Bewegung der Ebene entlang sich selbst das Feld an jedem Punkt im Raum ändern, was jedoch der Symmetrie des geladenen Systems widerspricht (die Ebene ist unendlich). Bei einer positiv geladenen Ebene beginnen die Kraftlinien in der Ebene und enden im Unendlichen, während bei einer negativ geladenen Ebene die Kraftlinien im Unendlichen beginnen und in die Ebene eintreten.

Reis. 1.18	Reis. 1.19

Um die elektrische Feldstärke einer unendlichen positiv geladenen Ebene zu bestimmen, wählen wir gedanklich einen Zylinder im Raum aus, dessen Achse senkrecht zur geladenen Ebene steht und dessen Basen parallel dazu sind und eine der Basen durch den Feldpunkt verläuft für uns von Interesse (Abb. 1.19). Der Zylinder schneidet eine Fläche aus der geladenen Ebene aus, und die Basen des Zylinders, die sich auf verschiedenen Seiten der Ebene befinden, haben die gleiche Fläche.

Nach dem Satz von Gauß hängt der Fluss des elektrischen Feldstärkevektors durch die Oberfläche des Zylinders mit der elektrischen Ladung im Zylinder durch den Ausdruck zusammen:

.

Da die Spannungslinien nur die Zylinderböden schneiden, ist der Durchfluss durch die Seitenfläche des Zylinders Null. Daher besteht der Fluss des Spannungsvektors durch die Zylinderoberfläche nur aus den Flüssen durch die Basen des Zylinders.

Wenn wir die letzten beiden Ausdrücke für den Intensitätsvektorfluss vergleichen, erhalten wir:

Elektrische Feldstärke zwischen entgegengesetzt geladenen Platten. Wenn die Abmessungen der Platten den Abstand zwischen ihnen deutlich überschreiten, kann das elektrische Feld jeder der Platten als nahe am Feld einer unendlichen, gleichmäßig geladenen Ebene angesehen werden. Da die elektrischen Feldstärkelinien entgegengesetzt geladener Platten zwischen den Platten in eine Richtung gerichtet sind (Abb. 1.20), ist die Feldstärke zwischen den Platten gleich

.

Im Außenraum haben die elektrischen Feldstärkelinien entgegengesetzt geladener Platten entgegengesetzte Richtungen, daher ist die resultierende elektrische Feldstärke außerhalb dieser Platten Null. Der für die Intensität erhaltene Ausdruck gilt für große geladene Platten, wenn die Intensität an einem Punkt bestimmt wird, der weit von ihren Rändern entfernt liegt.

Elektrische Feldstärke eines gleichmäßig geladenen dünnen Drahtes unendlicher Länge. Lassen Sie uns mithilfe des Gaußschen Theorems die Abhängigkeit der elektrischen Feldstärke eines gleichmäßig geladenen dünnen Drahtes unendlicher Länge vom Abstand zur Drahtachse ermitteln. Wählen wir einen Drahtabschnitt endlicher Länge aus. Wenn die lineare Ladungsdichte auf dem Draht beträgt, dann ist die Ladung des ausgewählten Bereichs gleich.

Betrachten wir das Feld einer Punktladung $q$ und ermitteln wir den Fluss des Intensitätsvektors ($\overrightarrow(E)$) durch die geschlossene Oberfläche $S$. Wir gehen davon aus, dass sich die Ladung innerhalb der Oberfläche befindet. Der Fluss des Spannungsvektors durch eine beliebige Oberfläche ist gleich der Anzahl der ausgehenden Linien des Spannungsvektors (beginnend bei der Ladung, wenn $q>0$) oder der Anzahl der hineingehenden Linien $\overrightarrow(E)$ , wenn $q \[Ф_E=\frac( q)((\varepsilon )_0)\ \left(1\right),\]

wobei das Vorzeichen des Flusses mit dem Vorzeichen der Ladung übereinstimmt.

Ostrogradsky-Gauss-Theorem in Integralform

Nehmen wir an, dass es innerhalb der Oberfläche S N Punktladungen gibt, Werte $q_1,q_2,\dots q_N.$ Aus dem Superpositionsprinzip wissen wir, dass die resultierende Feldstärke aller N Ladungen als Summe von ermittelt werden kann die Feldstärken, die durch jede der Ladungen erzeugt werden, dann ergibt sich:

Daher können wir für den Fluss eines Systems von Punktgebühren schreiben:

Mit Formel (1) erhalten wir Folgendes:

\[Ф_E=\oint\limits_S(\overrightarrow(E)d\overrightarrow(S))=\frac(1)((\varepsilon )_0)\sum\limits^N_(i=1)(q_i\ )\ links(4\rechts).\]

Gleichung (4) bedeutet, dass der Fluss des elektrischen Feldstärkevektors durch eine geschlossene Oberfläche gleich der algebraischen Summe der Ladungen innerhalb dieser Oberfläche geteilt durch die elektrische Konstante ist. Dies ist der Satz von Ostrogradsky-Gauss in integraler Form. Dieser Satz ist eine Folge des Coulombschen Gesetzes. Die Bedeutung dieses Satzes besteht darin, dass er es ermöglicht, elektrische Felder für verschiedene Ladungsverteilungen ganz einfach zu berechnen.

Als Folge des Ostrogradsky-Gauss-Theorems muss gesagt werden, dass der Fluss des Intensitätsvektors ($Ф_E$) durch eine geschlossene Oberfläche für den Fall, dass sich die Ladungen außerhalb dieser Oberfläche befinden, gleich Null ist.

Für den Fall, dass die Diskretion der Ladungen vernachlässigt werden kann, wird das Konzept der volumetrischen Ladungsdichte ($\rho $) verwendet, wenn die Ladung über das Volumen verteilt ist. Es ist definiert als:

\[\rho =\frac(dq)(dV)\left(5\right),\]

Dabei ist $dq$ eine Ladung, die als punktförmig betrachtet werden kann, und $dV$ ist ein kleines Volumen. (Bezüglich $dV$ muss folgende Bemerkung gemacht werden: Dieses Volumen ist klein genug, dass die Ladungsdichte darin als konstant angesehen werden kann, aber groß genug, dass keine Ladungsdiskretität auftritt.) Die Gesamtladung, die sich im Hohlraum befindet, kann wie folgt ermittelt werden:

\[\sum\limits^N_(i=1)(q_i\ )=\int\limits_V(\rho dV)\left(6\right).\]

In diesem Fall schreiben wir Formel (4) in der Form um:

\[\oint\limits_S(\overrightarrow(E)d\overrightarrow(S))=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV)\left(7\right).\ ]

Ostrogradsky-Gauss-Theorem in Differentialform

Verwendung der Ostrogradsky-Gauss-Formel für jedes Feld vektorieller Natur, mit deren Hilfe der Übergang von der Integration über eine geschlossene Fläche zur Integration über ein Volumen durchgeführt wird:

\[\oint\limits_S(\overrightarrow(a)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(a)dV\ \left(8\right),\]

wobei $\overrightarrow(a)-$Feldvektor (in unserem Fall ist es $\overrightarrow(E)$), $div\overrightarrow(a)=\overrightarrow(\nabla )\overrightarrow(a)=\frac(\ partielles a_x)(\partial x)+\frac(\partial a_y)(\partial y)+\frac(\partial a_z)(\partial z)$ – Divergenz des Vektors $\overrightarrow(a)$ am Punkt mit Koordinaten (x,y,z), der ein Vektorfeld auf ein Skalarfeld abbildet. $\overrightarrow(\nabla )=\frac(\partial )(\partial x)\overrightarrow(i)+\frac(\partial )(\partial y)\overrightarrow(j)+\frac(\partial )(\ partielles z)\overrightarrow(k)$ – beobachtbarer Operator. (In unserem Fall ist es $div\overrightarrow(E)=\overrightarrow(\nabla )\overrightarrow(E)=\frac(\partial E_x)(\partial x)+\frac(\partial E_y)(\partial y) +\frac(\partial E_z)(\partial z)$) – Divergenz des Spannungsvektors. Im Anschluss an das oben Gesagte schreiben wir Formel (6) wie folgt um:

\[\oint\limits_S(\overrightarrow(E)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(E)dV=\frac(1)((\varepsilon )_0)\int\limits_V( \rho dV)\left(9\right).\]

Die Gleichungen in Gleichung (9) sind für jedes Volumen erfüllt, und dies ist nur möglich, wenn die Funktionen in den Integranden in jedem Raumstrom gleich sind, das heißt, wir können Folgendes schreiben:

Ausdruck (10) ist der Satz von Ostrogradsky-Gauss in Differentialform. Seine Interpretation lautet wie folgt: Ladungen sind Quellen eines elektrischen Feldes. Wenn $div\overrightarrow(E)>0$, dann haben wir an diesen Punkten des Feldes (Ladungen sind positiv) Feldquellen, wenn $div\overrightarrow(E)

Aufgabe: Die Ladung ist gleichmäßig über das Volumen verteilt; in diesem Volumen wird eine kubische Fläche mit der Seite b gewählt. Es ist in die Kugel eingeschrieben. Ermitteln Sie das Verhältnis der Spannungsvektorflüsse durch diese Flächen.

Nach dem Satz von Gauß ist der Fluss ($Ф_E$) des Intensitätsvektors $\overrightarrow(E)$ durch eine geschlossene Oberfläche mit gleichmäßiger Ladungsverteilung über das Volumen gleich:

\[Ф_E=\frac(1)((\varepsilon )_0)Q=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV=\frac(\rho )((\varepsilon ) _0)\int\limits_V(dV)=\frac(\rho V)((\varepsilon )_0))\left(1.1\right).\]

Daher müssen wir die Volumina des Würfels und der Kugel bestimmen, wenn die Kugel um diesen Würfel herum beschrieben wird. Zunächst das Volumen eines Würfels ($V_k$), wenn seine Seite b gleich ist:

Ermitteln wir das Volumen des Balls ($V_(sh)$) mithilfe der Formel:

Dabei ist $D$ der Durchmesser der Kugel und (da die Kugel den Würfel umschreibt) die Hauptdiagonale des Würfels. Daher müssen wir die Diagonale eines Würfels durch seine Seite ausdrücken. Dies ist einfach, wenn Sie den Satz des Pythagoras verwenden. Um beispielsweise die Diagonale eines Würfels zu berechnen (1.5), müssen wir zunächst die Diagonale des Quadrats (die untere Basis des Würfels) (1.6) ermitteln. Die Länge der Diagonale (1,6) ist gleich:

In diesem Fall ist die Länge der Diagonale (1,5) gleich:

\[(D=D)_(15)=\sqrt(b^2+((\sqrt(b^2+b^2\ \ \ )))^2)=b\sqrt(3)\ \left (1,5\rechts).\]

Wenn wir den gefundenen Durchmesser der Kugel in (1.3) einsetzen, erhalten wir:

Jetzt können wir die Flüsse des Spannungsvektors durch die Oberfläche des Würfels ermitteln, er ist gleich:

\[Ф_(Ek)=\frac(\rho V_k)((\varepsilon )_0)=\frac(\rho b^3)((\varepsilon )_0)\left(1.7\right),\]

durch die Oberfläche der Kugel:

\[Ф_(Esh)=\frac(\rho V_(sh))((\varepsilon )_0)=\frac(\rho )((\varepsilon )_0)\frac(\sqrt(3))(2) \pi b^3\ \left(1.8\right).\]

Finden wir das Verhältnis $\frac(Ф_(Esh))(Ф_(Ek))$:

\[\frac(Ф_(Esh))(Ф_(Ek))=\frac(\frac(с)(\varepsilon_0)\frac(\sqrt(3))(2) \pi b^3)(\frac (сb^3)(\varepsilon_0))=\frac(\pi)(2)\sqrt(3)\ \ca. 2,7\left(1,9\right).\]

Antwort: Der Fluss durch die Kugeloberfläche ist 2,7-mal größer.

Aufgabe: Beweisen Sie, dass sich die Ladung eines Leiters auf seiner Oberfläche befindet.

Um es zu beweisen, verwenden wir den Satz von Gauß. Wählen wir eine geschlossene Oberfläche beliebiger Form im Leiter nahe der Oberfläche des Leiters (Abb. 2).

Nehmen wir an, dass sich im Leiter Ladungen befinden, schreiben wir den Ostrogradsky-Gauss-Satz für die Felddivergenz für jeden Punkt auf der Oberfläche S:

wobei $\rho die Dichte\ $der inneren Ladung ist. Es gibt jedoch kein Feld innerhalb des Leiters, d. h. $\overrightarrow(E)=0$, also $div\overrightarrow(E)=0\to \rho =0$. Der Ostrogradsky-Gauss-Satz in Differentialform ist lokal, das heißt, er ist für einen Feldpunkt geschrieben, wir haben den Punkt nicht auf besondere Weise ausgewählt, daher ist die Ladungsdichte an jedem Punkt im Feld innerhalb des Leiters Null.

Das Superpositionsprinzip in Kombination mit dem Coulombschen Gesetz liefert den Schlüssel zur Berechnung des elektrischen Feldes eines beliebigen Ladungssystems, aber die direkte Summierung der Felder mithilfe der Formel (4.2) erfordert normalerweise komplexe Berechnungen. Wenn jedoch die eine oder andere Symmetrie des Ladungssystems vorliegt, werden die Berechnungen erheblich vereinfacht, wenn wir das Konzept des elektrischen Feldflusses einführen und den Satz von Gauß verwenden.

Das Konzept des elektrischen Feldflusses wurde aus der Hydrodynamik in die Elektrodynamik eingeführt. In der Hydrodynamik ist der Flüssigkeitsfluss durch ein Rohr, d. h. das Flüssigkeitsvolumen N, das pro Zeiteinheit durch einen Rohrquerschnitt fließt, gleich v ⋅ S, wobei v die Geschwindigkeit des Fluids und S ist die Querschnittsfläche des Rohres. Wenn die Flüssigkeitsgeschwindigkeit über den Querschnitt variiert, müssen Sie die Integralformel N = ∫ S v → ⋅ d S → verwenden. Markieren wir tatsächlich einen kleinen Bereich d S im Geschwindigkeitsfeld, senkrecht zum Geschwindigkeitsvektor (Abb. ).

Reis. 1.4: Flüssigkeitsströmung

Das Flüssigkeitsvolumen, das in der Zeit d t durch diesen Bereich fließt, ist gleich v d S d t . Wenn die Plattform zur Strömung geneigt ist, beträgt das entsprechende Volumen v d S cos θ d t , wobei θ der Winkel zwischen dem Geschwindigkeitsvektor v → und der Normalen n → zur Plattform d S ist. Das Flüssigkeitsvolumen, das pro Zeiteinheit durch die Fläche d S fließt, erhält man, indem man diesen Wert durch d t dividiert. Es ist gleich v d S cos θ d t , d. h. Skalarprodukt v → ⋅ d S → Geschwindigkeitsvektor v → durch den Flächenelementvektor d S → = n → d S . Der Einheitsvektor n → normal zur Fläche d S kann in zwei direkt entgegengesetzten Richtungen gezeichnet werden. einer davon wird bedingt als positiv akzeptiert. Die Normale n → wird in diese Richtung gezeichnet. Die Seite der Stelle, aus der die Normale n → hervorgeht, heißt extern, und die Seite, in die die Normale n → eintritt, heißt intern. Der Flächenelementvektor d S → ist entlang der äußeren Normalen n → zur Oberfläche gerichtet und entspricht in seiner Größe der Fläche des Elements d S = ∣ d S → ∣ . Bei der Berechnung des Flüssigkeitsvolumens, das durch eine Fläche S mit endlichen Abmessungen fließt, muss diese in unendlich kleine Flächen d S entwickelt und dann das Integral ∫ S v → ⋅ d S → über die gesamte Fläche S berechnet werden.

Ausdrücke wie ∫ S v → ⋅ d S → kommen in vielen Bereichen der Physik und Mathematik vor. Sie werden als Fluss des Vektors v → durch die Oberfläche S bezeichnet, unabhängig von der Natur des Vektors v →. In der Elektrodynamik das Integral

N = ∫ S E → ⋅ d S →

(5.1)

wird der Fluss der elektrischen Feldstärke E → durch eine beliebige Oberfläche S genannt, obwohl mit diesem Konzept kein wirklicher Fluss verbunden ist.

Nehmen wir an, dass der Vektor E → durch eine geometrische Summe dargestellt wird

E → = ∑ j E → j .

Wenn wir diese Gleichheit skalar mit d S → multiplizieren und integrieren, erhalten wir

N = ∑ j N j .

wobei N j der Fluss des Vektors E → j durch dieselbe Oberfläche ist. Aus dem Prinzip der Überlagerung der elektrischen Feldstärke folgt also, dass sich die Flüsse durch dieselbe Oberfläche algebraisch addieren.

Der Satz von Gauß besagt, dass der Fluss des Vektors E → durch eine beliebige geschlossene Oberfläche gleich der Gesamtladung Q aller innerhalb dieser Oberfläche befindlichen Teilchen multipliziert mit 4 π ist:

Wir werden den Beweis des Satzes in drei Schritten durchführen.

1. Beginnen wir mit der Berechnung des elektrischen Feldflusses einer Punktladung q (Abb. ). Im einfachsten Fall, wenn die Integrationsfläche S eine Kugel ist und sich die Ladung in ihrem Zentrum befindet, ist die Gültigkeit des Satzes von Gauß fast offensichtlich. Auf der Oberfläche der Kugel herrscht die elektrische Feldstärke

E → = q r → ∕ r 3

betragsmäßig konstant und überall senkrecht zur Oberfläche gerichtet, so dass der elektrische Feldfluss einfach gleich dem Produkt E = q ∕ r 2 und der Kugelfläche S = 4 π r 2 ist. Daher ist N = 4 π q. Dieses Ergebnis ist unabhängig von der Form der die Ladung umgebenden Oberfläche. Um dies zu beweisen, wählen wir einen beliebigen Bereich der Oberfläche von ausreichend kleiner Größe mit der darauf eingestellten Richtung der Außennormalen n → aus. In Abb. Ein solches Segment ist (aus Gründen der Übersichtlichkeit) übertrieben groß dargestellt.

Der Fluss des Vektors E → durch diesen Bereich ist gleich d N = E → ⋅ d S → = E cos θ d S ,

wobei θ der Winkel zwischen der Richtung E → und der äußeren Normalen n → zur Fläche d S ist. Da E = q ∕ r 2 und d S cos θ ∕ ​​​​r 2 im absoluten Wert ist, ist das Element des Raumwinkels d Ω = d S ∣ cos θ ∣ ∕ r 2 , unter dem die Fläche d S sichtbar ist der Ort, an dem sich die Ladung befindet,

D N = ± q d Ω .

wobei die Plus- und Minuszeichen dem cos θ-Zeichen entsprechen, nämlich: Sie sollten das Pluszeichen nehmen, wenn der Vektor E → einen spitzen Winkel mit der Richtung der äußeren Normalen n → bildet, andernfalls das Minuszeichen.

2. Betrachten Sie nun eine endliche Oberfläche S, die ein ausgewähltes Volumen V abdeckt. In Bezug auf dieses Volumen ist es immer möglich zu bestimmen, welche der beiden entgegengesetzten Richtungen der Normalen zu einem beliebigen Element der Oberfläche S als extern betrachtet werden soll. Die äußere Normale ist vom Volumen V nach außen gerichtet. Summiert man über Segmente, ergibt sich bis zum Vorzeichen N = q Ω, wobei Ω der Raumwinkel ist, unter dem die Oberfläche S von dem Punkt aus sichtbar ist, an dem sich die Ladung q befindet. Wenn die Oberfläche S geschlossen ist, dann ist Ω = 4 π, vorausgesetzt, dass die Ladung q innerhalb von S liegt. Ansonsten ist Ω = 0. Um die letzte Aussage zu verdeutlichen, können wir noch einmal auf Abb. zurückgreifen. .

Es ist offensichtlich, dass sich die Strömungen durch Segmente einer geschlossenen Fläche, die auf gleichen Raumwinkeln basieren, aber in entgegengesetzte Richtungen weisen, gegenseitig aufheben. Es ist auch offensichtlich, dass, wenn sich die Ladung außerhalb der geschlossenen Oberfläche befindet, es für jedes nach außen gerichtete Segment ein entsprechendes nach innen gerichtetes Segment gibt.

3. Schließlich gelangen wir unter Verwendung des Superpositionsprinzips zur endgültigen Formulierung des Satzes von Gauß (). Tatsächlich ist das Feld eines Ladungssystems gleich der Summe der Felder jeder einzelnen Ladung, aber nur Ladungen, die sich innerhalb der geschlossenen Oberfläche befinden, leisten einen Beitrag ungleich Null zur rechten Seite des Satzes (). Damit ist der Beweis abgeschlossen.

In makroskopischen Körpern ist die Anzahl der Ladungsträger so groß, dass es praktisch ist, ein diskretes Ensemble von Teilchen in Form einer kontinuierlichen Verteilung darzustellen, was das Konzept der Ladungsdichte einführt. Per Definition ist die Ladungsdichte ρ das Verhältnis Δ Q ∕ Δ V im Grenzfall, wenn das Volumen Δ V gegen einen physikalisch verschwindend kleinen Wert tendiert:

wobei die Integration auf der rechten Seite über das von der Fläche S abgeschlossene Volumen V durchgeführt wird.

Der Satz von Gauß liefert eine Skalargleichung für drei Komponenten des Vektors E →, daher reicht dieser Satz allein nicht aus, um das elektrische Feld zu berechnen. Eine bekannte Symmetrie der Ladungsdichteverteilung ist notwendig, damit das Problem auf eine einzige skalare Gleichung reduziert werden kann. Der Satz von Gauß ermöglicht es, das Feld in Fällen zu finden, in denen die Integrationsfläche in () so gewählt werden kann, dass die elektrische Feldstärke E über die gesamte Fläche konstant ist. Schauen wir uns die lehrreichsten Beispiele an.

▸ Aufgabe 5.1

Finden Sie das Feld einer Kugel mit gleichmäßiger Volumenladung oder Oberflächen.

Lösung: Elektrisches Feld einer Punktladung E → = q r → ∕ r 3 tendiert dazu Unendlich bei r → 0 . Diese Tatsache zeigt die Widersprüchlichkeit der Idee Elementarteilchen durch Punktladungen. Wenn die Gebühr Q gleichmäßig über das Volumen einer Kugel mit endlichem Radius verteilt a, dann Das elektrische Feld hat keine Singularitäten.

Aus der Symmetrie des Problems geht hervor, dass das elektrische Feld E → überall ist radial gerichtet, und seine Spannung E = E(r) hängt nur vom Abstand r ab zur Mitte des Balls. Dann fließt das elektrische Feld durch eine Kugel mit Radius r ist einfach gleich 4 π r 2 E (Abb. ).

Andererseits ist die Ladung innerhalb derselben Kugel gleich der Gesamtladung Ball Q, wenn r ≥ a. Wenn wir 4 π r 2 E mit der Ladung q der Kugel multipliziert mit 4 π gleichsetzen, erhalten wir: E (r) = q ∕ r 2 .

So entsteht im Außenraum eine geladene Kugel ein solches Feld, als ob die gesamte Ladung in seinem Zentrum konzentriert wäre. Dieses Ergebnis gilt für jede Kugelsymmetrische Ladungsverteilung.

Das Feld innerhalb des Balls ist E (r) = Q ∕ r 2, wobei Q die Ladung innerhalb des Schwefels mit Radius r ist. Wenn die Ladung gleichmäßig über das Volumen der Kugel verteilt ist, dann Q = q (r ∕ a) 3 . In diesem Fall

E (r) = q r ∕ a 3 = (4 π ∕ 3) ρ r ,

wobei ρ = ​​q ∕ (4 π a 3 ∕ 3) — Ladungsdichte. Im Inneren des Balls nimmt das Feld ausgehend von seinem Maximum linear ab Werte auf der Oberfläche des Balls auf Null in seiner Mitte (Abb. ).

Funktion E(r) zugleich ist es überall endlich und stetig.

Wenn die Ladung über die Oberfläche der Kugel verteilt ist, dann Q = 0 und daher auch E = 0. Dieses Ergebnis gilt auch für den Fall, dass es sich innerhalb einer Kugel befindet Es gibt keinen Ladungshohlraum und äußere Ladungen sind kugelförmig verteilt symmetrisch. ▸ Aufgabe 5.2

Finden Sie das Feld eines gleichmäßig geladenen unendlichen Fadens. Gewinderadius a, Ladung pro Längeneinheit ϰ.

▸ Aufgabe 5.3

Finden Sie das Feld eines unendlich langen geraden Fadens und eines unendlich langen Fadens gleichmäßig geladener Zylinder.

▸ Aufgabe 5.4

Finden Sie das Feld einer unendlich geladenen Ebene und gleichmäßig geladene unendliche flache Schicht.

Lösung: Aufgrund der Symmetrie des Problems ist das Feld gerichtet normal zur Ebene und hängt nur vom Abstand ab x von Symmetrieebene der Platte. Um ein Feld zu berechnen mit Nach dem Satz von Gauß ist es praktisch, die Integrationsfläche zu wählen S in in Form eines Parallelipipeds, wie in Abb. .

Das letzte Ergebnis erhält man durch den Übergang zum Grenzwert ein → 0 bei gleichzeitiger Erhöhung der Ladungsdichteρ, so dass der Wert σ = ρ a ist unverändert geblieben. Auf gegenüberliegenden Seiten des Flugzeugs die elektrische Feldstärke ist betragsmäßig gleich groß, aber entgegengesetzte Richtung. Daher bei der Durchreise geladenen Ebene ändert sich das Feld schlagartig um den Betrag 4 π σ . Beachten Sie, dass die Platte als unendlich betrachtet werden kann, wenn Der Abstand ist im Vergleich zu seiner Größe vernachlässigbar. An Abstände sehr groß im Vergleich zu den Abmessungen der Platte, es wirkt wie eine Punktladung und ihr Feld nimmt zurück proportional zum Quadrat der Entfernung.

Das elektrostatische Feld lässt sich anhand von Kraftlinien (Spannungslinien) anschaulich darstellen. Stromleitungen nennt man Kurven, deren Tangenten in jedem Punkt mit dem Spannungsvektor E zusammenfallen.

Kraftlinien sind ein konventionelles Konzept und existieren nicht wirklich. Die Feldlinien einer einzelnen negativen und einer einzelnen positiven Ladung sind in Abb. dargestellt. 5 sind radiale Geraden, die von einer positiven Ladung ausgehen oder zu einer negativen Ladung führen.

Bleiben Dichte und Richtung der Feldlinien im gesamten Feldvolumen unverändert, gilt ein solches elektrostatisches Feld als homogen (die Anzahl der Linien sollte numerisch gleich der Feldstärke E sein).

Die Anzahl der mit „>dS“ gekennzeichneten Feldlinien, die senkrecht dazu stehen, bestimmt Fluss des elektrostatischen Feldstärkevektors:

Formel" src="http://hi-edu.ru/e-books/xbook785/files/17-1.gif" border="0" align="absmiddle" alt="- Projektion des Vektors E auf die Richtung der Normalen n zum Ort dS (Abb. 6).

Dementsprechend ist der Fluss des Vektors E durch eine beliebige geschlossene Oberfläche S

mark">S kann sich nicht nur die Größe, sondern auch das Vorzeichen des Flusses ändern:

1) mit Formel" src="http://hi-edu.ru/e-books/xbook785/files/17-4.gif" border="0" align="absmiddle" alt="

3) bei Auswahl"> Finden wir den Fluss des Vektors E durch eine sphärische Oberfläche S, in deren Mitte sich eine Punktladung q befindet.

In diesem Fall fallen die Markierungen „>E und n an allen Punkten der Kugeloberfläche zusammen.

Unter Berücksichtigung der Feldstärke einer Punktladung ergibt sich die Formel" src="http://hi-edu.ru/e-books/xbook785/files/18-2.gif" border="0" align="absmiddle " alt="(! SPRACHE:wir bekommen

Formel" src="http://hi-edu.ru/e-books/xbook785/files/Fe.gif" border="0" align="absmiddle" alt="- eine algebraische Größe abhängig vom Vorzeichen der Ladung. Wenn zum Beispiel q<0 линии Е направлены к заряду и противоположны направлению внешней нормали n ..gif" border="0" align="absmiddle" alt="um die Ladung herum hat q eine beliebige Form. Offensichtlich ist die Oberfläche mit „>E“ gekennzeichnet, ebenso wie die Oberfläche S. Daher ist der Fluss des Vektors E durch eine beliebige Oberfläche die Formel „src="http://hi-edu.ru/e-books/xbook785/ files/Fe.gif" border="0" align="absmiddle" alt=".

Befindet sich die Ladung außerhalb der geschlossenen Fläche, dann wird es natürlich davon abhängen, wie viele Linien in die geschlossene Fläche eintreten und diese wieder verlassen. Infolgedessen ist der Fluss des Vektors E gleich Null.

Wenn das elektrische Feld durch ein System von Punktladungen erzeugt wird Formel" src="http://hi-edu.ru/e-books/xbook785/files/18-4.gif" border="0" align="absmiddle" alt="

Diese Formel ist der mathematische Ausdruck des Satzes von Gauß: Der Fluss des elektrischen Feldstärkevektors E im Vakuum durch eine beliebige geschlossene Oberfläche ist gleich der algebraischen Summe der von ihr abgedeckten Ladungen geteilt durch Formel" src="http://hi-edu.ru/e-books/xbook785/files/18-6.gif" border="0" align="absmiddle" alt="

Um die Beschreibung zu vervollständigen, stellen wir den Satz von Gauß auch in einer lokalen Form dar und stützen uns dabei nicht auf Integralbeziehungen, sondern auf die Feldparameter an einem bestimmten Punkt im Raum. Dazu ist es zweckmäßig, den Differentialoperator Vektordivergenz zu verwenden.

Formel" src="http://hi-edu.ru/e-books/xbook785/files/nabla.gif" border="0" align="absmiddle" alt="(„nabla“) –

Formel" src="http://hi-edu.ru/e-books/xbook785/files/19-1.gif" border="0" align="absmiddle" alt="

In der mathematischen Analyse ist der Satz von Gauß-Ostrogradsky bekannt: Der Fluss eines Vektors durch eine geschlossene Oberfläche ist gleich dem Integral seiner Divergenz über das durch diese Oberfläche begrenzte Volumen -

Formel" src="http://hi-edu.ru/e-books/xbook785/files/ro.gif" border="0" align="absmiddle" alt=":

Formel" src="http://hi-edu.ru/e-books/xbook785/files/19-4.gif" border="0" align="absmiddle" alt="

Dieser Ausdruck ist der Satz von Gauß in lokaler (differentieller) Form.

Der Satz von Gauß (2.2) ermöglicht es uns, die Stärken verschiedener elektrostatischer Felder zu bestimmen. Schauen wir uns einige Beispiele für die Anwendung des Satzes von Gauß an.

1. Lassen Sie uns rechnen E elektrostatisches Feld, das durch eine gleichmäßig geladene Kugeloberfläche erzeugt wird.

Nehmen wir an, dass eine Kugeloberfläche mit dem Radius R eine gleichmäßig verteilte Ladung q trägt, d. h. Die Oberflächenladungsdichte ist überall die gleiche Marke „>r >R“ vom Mittelpunkt der Kugel aus konstruieren wir im Geiste eine neue Kugeloberfläche S, symmetrisch zur geladenen Kugel. In Übereinstimmung mit dem Satz von Gauß

Formel" src="http://hi-edu.ru/e-books/xbook785/files/20-1.gif" border="0" align="absmiddle" alt="

Für Punkte, die sich auf der Oberfläche einer geladenen Kugel mit Radius R befinden, können wir analog schreiben:

Auswahl">innerhalb einer geladenen Kugel, enthält keine elektrischen Ladungen in sich, daher ist die Flussmarke">E = 0.

Die Aufgabe, die Feldstärke eines Systems elektrischer Ladungen nach dem Prinzip der Überlagerung elektrostatischer Felder zu berechnen, lässt sich erheblich vereinfachen, wenn wir den vom deutschen Wissenschaftler K. Gauss (1777-1855) entdeckten Satz anwenden, der den Fluss der elektrischer Feldstärkevektor durch eine beliebige geschlossene Oberfläche.

Aus der Definition des Intensitätsvektorflusses durch eine geschlossene Oberfläche ergibt sich, dass der Intensitätsvektorfluss durch eine sphärische Oberfläche mit dem Radius r, die eine Punktladung Q in ihrem Zentrum abdeckt (Abb. 1), gleich ist

Dieses Ergebnis gilt für eine geschlossene Oberfläche beliebiger Form. Wenn man nämlich eine Kugel (Abb. 1) in eine beliebige geschlossene Oberfläche einschließt, dann verläuft jede Spannungslinie, die die Kugel durchdringt, auch durch diese Oberfläche.

Wenn eine geschlossene Oberfläche beliebiger Form eine Ladung umschließt (Abb. 2), tritt eine Spannungslinie, wenn sie die Oberfläche schneidet, entweder in die Oberfläche ein oder verlässt sie. Bei der Berechnung des Flusses reduziert sich eine ungerade Anzahl von Schnittpunkten letztendlich auf einen einzigen Schnittpunkt, da davon ausgegangen wird, dass der Fluss positiv ist, wenn Spannungslinien die Oberfläche verlassen, und negativ für Linien, die in die Oberfläche eindringen. Wenn eine geschlossene Oberfläche keine Ladung umschließt , dann ist der Fluss durch sie Null, also ist die Anzahl der Spannungslinien, die in die Oberfläche eindringen, gleich der Anzahl der Spannungslinien, die sie verlassen.

Dies bedeutet, dass für eine Oberfläche beliebiger Form, wenn sie geschlossen ist und eine Punktladung Q enthält, der Fluss des Vektors E wird gleich Q/ε 0 sein, d.h.

Das Vorzeichen des Flusses stimmt mit dem Vorzeichen der Ladung Q überein.

Betrachten wir den allgemeinen Fall einer beliebigen Oberfläche, die n Ladungen umgibt. Unter Verwendung des Prinzips der Überlagerung, Spannung E Das von allen Ladungen erzeugte Feld ist gleich der Summe der Intensitäten E i Felder, die von jeder Gebühr separat erstellt werden. Deshalb

Gemäß (1) ist jedes der Integrale, die unter dem Summenzeichen erscheinen, gleich Q i /ε 0 . Bedeutet,

(2)

Formel (2) drückt aus Gaußscher Satz für das elektrostatische Feld im Vakuum: Der Fluss des elektrostatischen Feldstärkevektors im Vakuum durch eine beliebige geschlossene Oberfläche ist gleich der algebraischen Summe der in dieser Oberfläche enthaltenen Ladungen geteilt durch ε 0. Dieser Satz wurde mathematisch für ein Vektorfeld beliebiger Natur vom russischen Mathematiker M.V. Ostrogradsky (1801-1862) und dann unabhängig von ihm in Bezug auf das elektrostatische Feld von K. Gauss ermittelt.

Im Allgemeinen können elektrische Ladungen mit einer bestimmten Volumendichte ρ=dQ/dV verteilt sein, die an verschiedenen Orten im Raum unterschiedlich ist. Dann ist die Gesamtladung, die in der geschlossenen Oberfläche S enthalten ist, die ein bestimmtes Volumen V abdeckt,

(3)

Unter Verwendung der Formel (3) kann der Satz von Gauß (2) wie folgt geschrieben werden:

Die Zirkulation des Spannungsvektors ist die Arbeit, die elektrische Kräfte leisten, wenn sie eine einzelne positive Ladung entlang eines geschlossenen Pfades L bewegen

(13.18)

Da die Arbeit der elektrostatischen Feldkräfte entlang eines geschlossenen Kreislaufs Null ist (die Arbeit der potentiellen Feldkräfte), ist daher die Zirkulation der elektrostatischen Feldstärke entlang eines geschlossenen Kreislaufs Null.

Elektrostatisches Feldpotential. Das Feld einer konservativen Kraft kann nicht nur durch eine Vektorfunktion beschrieben werden, sondern eine äquivalente Beschreibung dieses Feldes kann durch die Definition einer geeigneten Skalargröße an jedem seiner Punkte erhalten werden. Für ein elektrostatisches Feld beträgt diese Größe elektrostatisches Feldpotential, definiert als das Verhältnis der potentiellen Energie der Testladung Q zur Größe dieser Ladung,  = W P / Q, woraus folgt, dass das Potential numerisch gleich der potentiellen Energie ist, die eine positive Einheitsladung an einem bestimmten Punkt im Feld besitzt. Die Maßeinheit für das Potenzial ist Volt (1 V).

Punktladungsfeldpotential Q in einem homogenen isotropen Medium mit Dielektrizitätskonstante :

Prinzip der Superposition. Das Potential ist eine Skalarfunktion, für es gilt das Superpositionsprinzip. Also für das Feldpotential eines Systems von Punktladungen Q 1, Q 2, Qn wir haben

,

Wo r i- Abstand vom Feldpunkt mit Potential  zur Ladung Qi. Wenn die Ladung willkürlich im Raum verteilt ist, dann

,

Wo R- Abstand vom Elementarvolumen d X,D j,D z darauf hinweisen ( X, j, z), wobei das Potenzial bestimmt wird; V- das Raumvolumen, in dem die Ladung verteilt ist.

Potenzial und Arbeit elektrischer Feldkräfte. Basierend auf der Definition des Potentials kann gezeigt werden, dass die Arbeit, die die Kräfte des elektrischen Feldes leisten, wenn sie eine Punktladung bewegt Q von einem Punkt des Feldes zum anderen ist gleich dem Produkt aus der Größe dieser Ladung und der Potentialdifferenz am Anfangs- und Endpunkt des Weges, A = q (     
Wenn wir in Analogie zur potentiellen Energie davon ausgehen, dass an Punkten, die unendlich weit von elektrischen Ladungen – Feldquellen – entfernt sind, das Potential Null ist, dann ist die Arbeit der elektrischen Feldkräfte beim Bewegen einer Ladung erforderlich Q von Punkt 1 bis Unendlich kann dargestellt werden als A   Q  1 .
Somit beträgt das Potential an einem bestimmten Punkt des elektrostatischen Feldes physikalische Größe, die numerisch gleich der Arbeit ist, die von den Kräften des elektrischen Feldes geleistet wird, wenn eine positive Punktladungseinheit von einem gegebenen Punkt im Feld zu einem unendlich entfernten Punkt bewegt wird:  = A  / Q.
In einigen Fällen wird das elektrische Feldpotential klarer definiert als eine physikalische Größe, die numerisch der Arbeit äußerer Kräfte gegen die Kräfte des elektrischen Feldes entspricht, wenn eine positive Punktladungseinheit von der Unendlichkeit zu einem bestimmten Punkt bewegt wird. Es ist zweckmäßig, die letzte Definition wie folgt zu schreiben:

In der modernen Wissenschaft und Technik, insbesondere bei der Beschreibung von im Mikrokosmos auftretenden Phänomenen, wird eine Einheit aus Arbeit und Energie bezeichnet Elektronenvolt(eV). Dies ist die Arbeit, die geleistet wird, wenn eine Ladung, die der Ladung eines Elektrons entspricht, zwischen zwei Punkten mit einer Potentialdifferenz von 1 V bewegt wird: 1 eV = 1,6010  C1 V = 1,6010  J

Äquipotentialflächen- ein Konzept, das auf jedes potentielle Vektorfeld anwendbar ist, beispielsweise ein statisches elektrisches Feld oder ein Newtonsches Gravitationsfeld. Eine Äquipotentialfläche ist eine Fläche, auf der das Skalarpotential eines gegebenen Potentialfeldes einen konstanten Wert annimmt (Potentialniveaufläche). Eine andere, äquivalente Definition ist eine Fläche, die an jedem Punkt orthogonal zu den Feldlinien ist.

Die Oberfläche eines Leiters ist in der Elektrostatik eine Äquipotentialfläche. Darüber hinaus ändert die Platzierung eines Leiters auf einer Äquipotentialfläche nicht die Konfiguration des elektrostatischen Feldes. Diese Tatsache wird in der Bildmethode genutzt, die die Berechnung des elektrostatischen Feldes für komplexe Konfigurationen ermöglicht.

In einem (stationären) Gravitationsfeld stellt sich der Pegel einer stationären Flüssigkeit entlang der Äquipotentialfläche ein. Insbesondere lässt sich näherungsweise sagen, dass der Meeresspiegel entlang der Äquipotentialfläche des Schwerefeldes der Erde verläuft. Die Form der Meeresoberfläche, die bis zur Erdoberfläche reicht, wird Geoid genannt und spielt in der Geodäsie eine wichtige Rolle. Das Geoid ist somit eine Äquipotentialfläche der Schwerkraft, bestehend aus einer Gravitations- und einer Zentrifugalkomponente.