home › Body › The Diophantus project and its discoveries. Abstract: Diophantus

The Diophantus project and its discoveries. Abstract: Diophantus

Coefficients whose solutions must be found among integers.

Diophantus of Alexandria
Διόφαντος ὁ Ἀλεξανδρεύς

Date of Birth	no earlier and no later or
Place of Birth	Alexandria, Egypt
Date of death	no earlier and no later
A country	Ancient Rome
Scientific field	number theory
Known as	"father of algebra"
Diophantus of Alexandria at Wikimedia Commons

Biography

Almost nothing is known about the details of his life. On the one hand, Diophantus quotes Hypsicles (2nd century BC); on the other hand, Theon of Alexandria (about 350 AD) writes about Diophantus, from which we can conclude that his life took place within the boundaries of this period. A possible clarification of the life time of Diophantus is based on the fact that he Arithmetic dedicated to “the most venerable Dionysius.” It is believed that this Dionysius is none other than Bishop Dionysius of Alexandria, who lived in the middle of the 3rd century. n. e.

It is equivalent to solving the following equation:

x = x 6 + x 12 + x 7 + 5 + x 2 + 4 (\displaystyle x=(\frac (x)(6))+(\frac (x)(12))+(\frac (x) (7))+5+(\frac (x)(2))+4)

This equation gives x = 84 (\displaystyle x=84), that is, the age of Diophantus is equal to 84 years. However, the accuracy of the information cannot be confirmed.

Arithmetic Diophanta

The main work of Diophantus - Arithmetic in 13 books. Unfortunately, only 6 (or 10, see below) of the first 13 books have survived.

The first book is preceded by an extensive introduction, which describes the notation used by Diophantus. Diophantus calls the unknown “number” ( ἀριθμός ) and is denoted by the letter ς , square unknown - symbol Δ Υ (short for δύναμις - “degree”), the cube of the unknown - symbol Κ Υ (short for κύβος - “cube”). Special signs are provided for the following degrees of the unknown, up to the sixth, called cube-cube, and for their opposite degrees, up to minus the sixth.

Diophantus does not have an addition sign: he simply writes positive terms next to each other in descending order of degree, and in each term the degree of the unknown is first written, and then the numerical coefficient. The subtracted terms are also written side by side, and a special sign in the form of an inverted letter Ψ is placed in front of their entire group. The equal sign is represented by two letters ἴσ (short for ἴσος - “equal”).

A rule for bringing similar terms and a rule for adding or subtracting the same number or expression to both sides of an equation were formulated: what al-Khorezmi later began to call “algebra and almukabala.” The rule of signs has been introduced: “minus by plus gives minus”, “minus by minus gives plus”; This rule is used when multiplying two expressions with subtracted terms. All this is formulated in general terms, without reference to geometric interpretations.

Most of the work is a collection of problems with solutions (there are a total of 189 in the six surviving books, together with the four from the Arabic part - 290), skillfully selected to illustrate general methods. Main issues Arithmetic- finding positive rational solutions to uncertain equations. Rational numbers are treated by Diophantus in the same way as natural numbers, which is not typical for ancient mathematicians.

First, Diophantus examines systems of second-order equations in two unknowns; it specifies a method for finding other solutions if one is already known. Then he applies similar methods to equations of higher degrees. Book VI examines problems related to right triangles with rational sides.

Influence Arithmetic for the development of mathematics

In the 10th century Arithmetic was translated into Arabic (see Kusta ibn Luka), after which mathematicians from Islamic countries (Abu Kamil and others) continued some of Diophantus’s research. In Europe, interest in Arithmetic increased after Raphael Bombelli translated and published this work into Latin, and published 143 problems from it in his Algebra(1572). In 1621, a classic, thoroughly commented Latin translation appeared Arithmetic, executed by Bachet de Meziriac.

Diophantus' methods greatly influenced François Viète and Pierre Fermat; however, in modern times, indefinite equations are usually solved in integers, and not in rational numbers, as Diophantus did. When Pierre Fermat read Diophantus's Arithmetic, edited by Bachet de Mezyriac, he came to the conclusion that one of the equations similar to those considered by Diophantus had no solutions in integers, and noted in the margin that he had found "a truly wonderful proof of this theorem ... however, the margins of the book are too narrow to include it.” This statement is now known as Fermat's Last Theorem.

In the 20th century, the Arabic text of four more books was discovered under the name of Diophantus. Arithmetic. I. G. Bashmakova and E. I. Slavutin, having analyzed this text, put forward a hypothesis that its author was not Diophantus, but a commentator well versed in Diophantus’ methods, most likely Hypatia. However, the significant gap in the methodology for solving problems in the first three and last three books is well filled by four books of Arabic translation. This forces us to reconsider the results of previous studies. . [ ]

Other works of Diophantus

Treatise of Diophantus About polygonal numbers (Περὶ πολυγώνων ἀριθμῶν ) not completely preserved; in the preserved part, a number of auxiliary theorems are derived using geometric algebra methods.

From the works of Diophantus About measuring surfaces (ἐπιπεδομετρικά ) And About multiplication (Περὶ πολλαπλασιασμοῦ ) also only fragments have survived.

Book of Diophantus Porisms known only from a few theorems used in Arithmetic.

Bashmakova I. G., Slavutin E. I., Rosenfeld B. A. Arabic version of “Arithmetic” of Diophantus // Historical and mathematical studies. - M., 1978. - Issue. XXIII. - P. 192 - 225.
Bashmakova I. G. Arithmetic of algebraic curves: (From Diophantus to Poincaré) // Historical and mathematical studies. - 1975. - Issue. 20. - pp. 104 - 124.
Bashmakova I. G. Diophantus and Diophantine equations. - M.: Nauka, 1972 (Reprint: M.: LKI, 2007). Per. On him. language: Diophant und diophantische Gleichungen. - Basel; Stuttgart: Birkhauser, 1974. Trans. in English. language: Diophantus and Diophantine Equations/ Transl. by A. Shenitzer with the editorial assistance of H. Grant and updated by J. Silverman // The Dolciani Mathematical Expositions. - No. 20. - Washington, DC: Mathematical Association of America, 1997.
Bashmakova I. G. Diophantus and Fermat: (On the history of the method of tangents and extrema) // Historical and mathematical studies. - M., 1967. - Issue. VII. - P. 185 - 204.
Bashmakova I. G., Slavutin E. I. History of Diophantine analysis from Diophantus to Fermat. - M.: Nauka, 1984.
History of mathematics from ancient times to the beginning of the 19th century. - T. I: From the most ancient. times before the beginning of the New Age. time / Ed. A. P. Yushkevich. - M., Nauka, 1970.
Slavutin E. I. Diophantus’ algebra and its origins // Historical and mathematical studies. - M., 1975. - Issue. 20. - pp. 63 - 103.
Shchetnikov A. I. Can Diophantus of Alexandria’s book “On Polygonal Numbers” be called purely algebraic? // Historical and mathematical research. - M., 2003. - Issue. 8 (43). - pp. 267 - 277.
Heath Th. L. Diophantus of Alexandria, A Study in the History of Greek Algebra. - Cambridge, 1910 (Repr.: NY, 1964).
Knorr W. R. Arithmktikê stoicheiôsis: On Diophantus and Hero of Alexandria // Historia Mathematica. - 20. - 1993. - P. 180 - 192.
Christianidis J. The way of Diophantus: Some clarifications on Diophantus’ method of solution // Historia Mathematica. - 34. - 2007. - P. 289 - 305.
Rashed R., Houzel C. Les Arithmétiques de Diophante. Lecture historique et mathématique . - De Gruyter, 2013.

Municipal educational institution

"Lyceum No. 10" Perm

Diophantus. Diophantine equations

Done the job

Ilyina Yana,

11th grade student

Supervisor

Zolotukhina L. V.

mathematic teacher

Perm, 2010

Introduction……………………………………………………………………………….3

1. Diophantus………………………………………………………………………………..…4

2. Numbers and symbols………………………………………………………6

3. Diophantine equation……………………………………………..…8

4. Solutions………………………………………………………..12

Conclusion…………………………………………………………………………………15

References………………………………………………………16

Introduction

Today's schoolchildren solve various equations. In Part C of the Unified State Examination tasks there is an interesting equation called the Diophantine equation. In his works, Diophantus not only posed the problem of solving indefinite equations in rational numbers, but also gave some general methods for solving them. These methods will be very useful for today's eleventh graders who are about to take the math exam.

Diophantus made as great a contribution to the development of mathematics as Archimedes. This is what Archimedes did, for example: when determining the areas of an ellipse, a segment of a parabola, the surface of a sphere, the volumes of a sphere and other bodies, he used the method of integral sums and the method of passage to the limit, but nowhere did he give a general abstract description of these methods. Scientists of the 16th and 17th centuries had to carefully study and rearrange his works in a new way in order to isolate the methods of Archimedes from there. The situation is similar with Diophantus. His methods were understood and applied to new problems by Viethe and Fermat, i.e. at the same time when Archimedes was solved.

1. Diophantus

Diophantus presents one of the most difficult mysteries in the history of science. We do not know the time when he lived, nor his predecessors who would have worked in the same field. His works are like a sparkling fire in the midst of complete impenetrable darkness. The period of time when Diophantus could have lived is half a millennium! The lower bound of this interval is determined without difficulty: in his book on polygonal numbers, Diophantus repeatedly mentions the mathematician Hypsicles of Alexandria, who lived in the middle of the 2nd century BC. e. On the other hand, in the comments of Theon of Alexandria to the “Almagest” of the famous astronomer Ptolemy, an excerpt from the work of Diophantus is placed. Theon lived in the middle of the 4th century AD. e. This determines the upper bound of this interval. So, 500 years!

But the place of residence of Diophantus is well known - this is the famous Alexandria, the center of scientific thought of the Hellenistic world.

To exhaust everything known about the personality of Diophantus, we present a riddle poem that has come down to us:

The ashes of Diophantus rest in the tomb; marvel at her - and the stone
The age of the deceased will speak through his wise art.
By the will of the gods, he lived a sixth of his life as a child.
And I met half past five with fluff on my cheeks.
It was only the seventh day when he became engaged to his girlfriend.
After spending five years with her, the sage waited for his son;
His father's beloved son lived only half his life.
He was taken from his father by his early grave.
Twice two years the parent mourned a heavy grief,
Here I saw the limit of my sad life.

From here it is easy to calculate that Diophantus lived 84 years. However, for this you do not need to master the art of Diophantus! It is enough to be able to solve an equation of the 1st degree with one unknown, and Egyptian scribes were able to do this back 2 thousand years BC. e.

But the most mysterious is the work of Diophantus. Six books out of 13 have reached us, which were combined into “Arithmetic”. The style and content of these books differ sharply from classical ancient works on number theory and algebra, examples of which we know from Euclid’s Elements, his Data, and lemmas from the works of Archimedes and Apollonius. "Arithmetic" was undoubtedly the result of numerous studies that remained completely unknown to us. We can only guess about its roots and marvel at the richness and beauty of its methods and results.

“Arithmetic” by Diophantus is a collection of problems (there are 189 in total), each of which is equipped with a solution (or several methods of solution) and the necessary explanations. Therefore, at first glance it seems that it is not a theoretical work. However, a careful reading shows that the problems are carefully selected and serve to illustrate very specific, strictly thought-out methods. As was customary in ancient times, methods are not formulated in a general form, but are repeated to solve similar problems.

2. Numbers and symbols

Diophantus begins with basic definitions and a description of the letter symbols he will use.

In classical Greek mathematics, which found its completion in Euclid’s Elements, under the number άριJμός - “ arrhythmos" or " arithmos"; hence the name “arithmetic” for the science of numbers) was understood as a set of units, i.e. integer. Neither fractions nor irrationality were called numbers. Strictly speaking, there are no fractions in the Principia. The unit is considered indivisible and instead of fractions of a unit, ratios of integers are considered; irrationalities appear as ratios of incommensurable segments, for example, the number we now denote √2 was for the classical Greeks the ratio of the diagonal of a square to its side. There was no talk of negative numbers. There weren't even any equivalents for them. We find a completely different picture in Diophantus.

Diophantus gives the traditional definition of number as a set of units, but later seeks for his problems positive rational solutions, and calls each such solution a number (άριJμός - “ arrhythmos »).

But the matter does not stop there. Diophantus introduces negative numbers: he calls them the special term λει̃ψις - “ leipsis" - derived from the verb λει̃πω - " leipo”, which means to lack, to lack, so that the term itself could be translated by the word “lack”. By the way, this is what the famous Russian historian of science I. Timchenko does. Diophantus calls a positive number the word ΰπαρξις - “ iparxis”, which means existence, being, and in the plural this word can mean property or property. Thus, Diophantus's terminology for relative numbers is close to that used in the Middle Ages in the East and Europe. Most likely, it was simply a translation from Greek into Arabic, Sanskrit, Latin, and then into various languages of Europe.

Note that the term λει̃ψις is “ leipsis" - cannot be translated as "subtracted", as many translators of Diophantus do, because for the operation of subtraction Diophantus uses completely different terms, namely άφελει̃ν - " afelein"or άφαιρει̃ν - " afirerain", which are derived from the verb άφαιρεω - " afireo"- take away. When transforming equations, Diophantus himself often uses the standard expression “add λει̃ψις to both sides.”

We have dwelled in such detail on the philological analysis of Diophantus’s text in order to convince the reader that we will not deviate from the truth if we translate Diophantus’s terms as “positive” and “negative”.

Diophantus formulates the rule of signs for relative numbers:

“a negative multiplied by a negative gives a positive, while a negative multiplied by a positive gives a negative, and the distinguishing sign for a negative is an inverted and shortened (letter) ψ.”

“After I explained multiplication to you, the division of the proposed terms also becomes clear; Now it will be good to start practicing the addition, subtraction and multiplication of such terms. Add positive and negative terms with different coefficients to other terms that are either positive or equally positive and negative, and from positive and other negative terms subtract other positive and equally positive and negative terms.”

Note that although Diophantus seeks only rational positive solutions, in intermediate calculations he willingly uses negative numbers.

We can thus note that Diophantus expanded the number field into a field of rational numbers in which all four operations of arithmetic can be performed without hindrance.

3. Diophantine equation

Definition - algebraic equations or systems of algebraic equations with integer coefficients, having a number of unknowns exceeding the number of equations, and for which integer or rational solutions are sought.

ax + by = 1

Where A And b- coprime integers

Coprime numbers several integers such that the common divisors for all these numbers are only + 1 and - 1. The smallest multiple of a pair of prime numbers is equal to their product.

has infinitely many solutions:

If x0 And y0- one solution, then the numbers

X = x0 + bn

at = y0 -an

(n- any integer) will also be solutions.

Another example of D. u.

x2 + y2 = z2

Positive integer solutions to this equation represent the lengths of the legs X , at and hypotenuse z right triangles with integer side lengths are called Pythagorean numbers.

triples of natural numbers such that a triangle whose side lengths are proportional (or equal) to these numbers is rectangular.

All triplets of coprime Pythagorean numbers can be obtained using the formulas

X = m2 - n2

at = 2mn

z = m2 + n2

Where m And n- whole numbers ( m > n > 0).

This equation defines on the plane R 2 algebraic curveΓ. We will call the rational solution (2) rational point curve Γ. In what follows, we will often resort to the language of geometry, although Diophantus himself does not use it anywhere. However, geometric language has now become such an integral part of mathematical thinking that many facts will be easier to understand and explain with its help.

First of all, it is necessary to give some classification of equations (2) or, which is the same, algebraic curves. The most natural and earliest to arise is their classification by order.

Let us remind you that in order curve (2) is the maximum order of the terms of the polynomial f (x , y), where the order of a term is understood as the sum of powers at x And y. The geometric meaning of this concept is that a straight line intersects a curve of order n exactly at n points. When counting points, one must, of course, take into account the multiplicity of intersection points, as well as complex and “infinitely distant” points. So, for example, a circle x 2 + y 2 = 1 and straight x + y= 2 intersect at two complex points, and the hyperbola x 2 – y 2 = 1 and straight y =x- at two points at infinity, the same hyperbola with a straight line x=1 has one common point of multiplicity 2.

However, for the purposes diophantine analysis(this name was given to the field of mathematics that grew out of the problems of solving indeterminate equations; however, now it is more often called Diophantine geometry) classification by order turned out to be too rough.

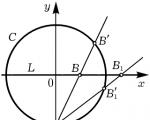
Rice. 1.

Let us explain this with an example. Let a circle be given C : x 2 + y 2 = 1 and any straight line with rational coefficients, for example, L : y=0. Let us show that the rational points of this circle and the line can be put into a one-to-one correspondence. This can be done, for example, like this: fix the point A(0,–1) circles and assign each rational point B straight L point B" circle C, lying at the intersection C and straight AB(Fig. 1). That the coordinates of the point B" will be rational, we will let the reader prove it for himself or read a similar proof from Diophantus (it will be presented in the next paragraph). Obviously, the same correspondence can be established between the rational points of any conic section, if at least one rational point lies on it, and a rational line. We see that from the point of view of Diophantine analysis the circle C and straight L are indistinguishable: their sets of rational solutions are equivalent. And this despite the fact that the orders of both curves are different.

More subtle is the classification of algebraic curves by genus, which was introduced only in the 19th century by Abel and Riemann. This classification takes into account the number of singular points of the curve Γ.

We assume that in equation (2) of the curve Γ the polynomial f (x , y) is irreducible over the field of rational numbers, i.e. it does not expand into a product of polynomials with rational coefficients. As is known, the equation of the tangent to the curve Γ at the point P (x 0 , y 0) will

y – y 0 = k (x – x 0),

k = –

fx" (x 0 , y 0)

fy" (x 0 , y 0)

If at the point P derivative fx" or fy" is different from zero, then the slope k tangent has a very definite meaning (if fy" (x 0 , y 0) = 0, a fx" (x 0 , y 0) ≠ 0, then k=∞ and tangent at P will be vertical).

If at the point P both partial derivatives vanish,

fx" (x 0 , y 0) = 0 and fy" (x 0 , y 0) = 0,

then point P called special .

For example, at the curve y 2 = x 2 + x 3 point (0, 0) will be special, since in it fx" = –2x – 3x 2 and fy" = 2y go to zero.

Rice. 2.

The simplest singular points are double ones, at which at least one of the derivatives f xx "" , f xy "" And f yy "" is different from zero. In Fig. Figure 2 shows a double point where the curve has two different tangents. Other more complex singular points are shown in Fig. 3.

Rice. 3.

4. Solutions

Rule 1. If c is not divisible by d, then the equation ax + vy = c has no solutions in integers. N.O.D.(a,b) = d.

Rule 2. To find a solution to the equation ax + vy = c with coprime a and b, you must first find a solution (X o; y o) to the equation ax + y = 1; the numbers CX o, Su o form a solution to the equation ax + vy = c.

Solve the equation in integers (x,y)

5x - 8y = 19 ... (1)

First way. Finding a particular solution using the selection method and recording the general solution.

We know that if N.O.D.(a;b) =1, i.e. a and b are coprime numbers, then equation (1)

has a solution in integers x and y. N.O.D.(5;8) =1. Using the selection method we find a particular solution: X o = 7; y o =2.

So, the pair of numbers (7;2) is a particular solution to equation (1).

This means that the equality holds: 5 x 7 – 8 x 2 = 19 ... (2)

Question: How, given one solution, write down all the other solutions?

Let us subtract equality (2) from equation (1) and get: 5(x -7) – 8(y - 2) =0.

Hence x – 7 = . From the resulting equality it is clear that the number (x – 7) will be an integer if and only if (y – 2) is divisible by 5, i.e. y – 2 = 5n, where n is some integer. So, y = 2 + 5n, x = 7 + 8n, where n Z.

Thus, all integer solutions of the original equation can be written in the following form:

Second way . Solving an equation for one unknown.

We solve this equation with respect to the unknown that has the smallest (modulo) coefficient. 5x - 8y = 19 x = .

Remainders when divided by 5: 0,1,2,3,4. Let's substitute these numbers for y.

If y = 0, then x = =.

If y = 1, then x = =.

If y = 2, then x = = = 7 Z.

If y = 3, then x = =.

If y = 4 then x = =.) Conclusion

Meanwhile, most historians of science, as opposed to mathematicians, have so far underestimated the works of Diophantus. Many of them believed that Diophantus was limited to finding only one solution and used artificial techniques for this, different for different problems. But in fact, in most Diophantine equations we observe similar solution algorithms.

Today, as we see, there are several different solutions, the algorithms of which are easy to remember. As mentioned earlier, this equation is usually found in task C6 on the Unified State Exam. Studying algorithms for solving Diophantine equations can help in solving this task, which is worth a significant number of points.

Bibliography

1. Diophantus of Alexandria. Arithmetic and a book about polygonal numbers (translation from ancient Greek by I. N. Veselovsky; editing and comments by I. G. Bashmakova). M., “Science”, 1974.

2. B. L. Van der Waerden, Awakening Science (translation by I. N. Veselovsky). M., Fizmatgiz, 1959.

3. G. G. Tseyten, History of mathematics in antiquity and the Middle Ages (translation by P. Yushkevich). M.–L., Gostekhizdat, 1932

4. A. V. Vasiliev, Integer. Petersburg, 1919

5. I. V. Yashchenko, S. A. Shestakov, P. I. Zakharov, Mathematics, Unified State Examination, MTsNMO, 2010

Diophantus of Alexandria(ancient Greek Διόφαντος ὁ Ἀλεξανδρεύς ; lat. Diophantus) is an ancient Greek mathematician who presumably lived in the 3rd century AD. e. Often referred to as the "father of algebra". Author of "Arithmetic" - a book dedicated to finding positive rational solutions to indeterminate equations. Nowadays, “Diophantine equations” usually mean equations with integer coefficients, the solutions of which must be found among integers.

Biography [ | ]

Latin translation Arithmetic (1621)

It is equivalent to solving the following equation:

x = x 6 + x 12 + x 7 + 5 + x 2 + 4 (\displaystyle x=(\frac (x)(6))+(\frac (x)(12))+(\frac (x) (7))+5+(\frac (x)(2))+4)

This equation gives x = 84 (\displaystyle x=84), that is, the age of Diophantus is equal to 84 years. However, the accuracy of the information cannot be confirmed.

Arithmetic Diophanta[ | ]

The main work of Diophantus - Arithmetic in 13 books. Unfortunately, only 6 (or 10, see below) of the first 13 books have survived.

Influence Arithmetic for the development of mathematics[ | ]

In the 10th century Arithmetic was translated into Arabic, after which mathematicians from Islamic countries (Abu Kamil and others) continued some of Diophantus’s research. In Europe, interest in Arithmetic increased after Raphael Bombelli translated and published this work into Latin, and published 143 problems from it in his Algebra(1572). In 1621, a classic, thoroughly commented Latin translation appeared Arithmetic, executed by Bachet de Meziriac.

Other works of Diophantus[ | ]

From the works of Diophantus About measuring surfaces (ἐπιπεδομετρικά ) And About multiplication (Περὶ πολλαπλασιασμοῦ ) also only fragments have survived.

Book of Diophantus Porisms known only from a few theorems used in Arithmetic.

In the section on the question where did Diophantus live asked by the author Lera... the best answer is Diophantus - (late 3rd century AD) - famous ancient Greek mathematician.
There is almost no information about his life; even the dates of his birth and death are not entirely reliable.
Lived in the Egyptian city of Alexandria.
The activity of Diophantus coincided with the decline of Greece, conquered - as is known - by Rome.
Greek scientists found refuge in Egypt, mainly in Alexandria, which by that time had become the center of world culture.
A magnificent library was created in Alexandria, which by the time of Diophantus had become the center of world culture and the humanities; the so-called library arose in Alexandria. Museion (temple or sanctuary of the muses), where the activities of the most outstanding representatives of the natural and mathematical sciences were concentrated.
Among these scientists was Diophantus, a mathematician who, thanks to his acquaintance with Syrian and Indian mathematicians, transferred the achievements of the Babylonians in the field of algebra to Greek science.

Answer from Alexander[guru]
all mathematicians from Greece

Answer from contribute[newbie]
Judging by the fact that he is Diophantus of Alexandria, he lived in Alexandria (in the territory of modern Egypt) in the 3rd century AD. Presumably the dates of his life: born - 325, died - 409 AD

Answer from Drill[newbie]
Diophantus of Alexandria?
Ancient Roman mathematician
An ancient Greek mathematician who supposedly lived in the 3rd century AD. e. Often referred to as the "father of algebra". Author of "Arithmetic" - a book dedicated to finding positive rational solutions to indeterminate equations. Nowadays, “Diophantine equations” usually mean equations with integer coefficients, the solutions of which must be found among integers.

Octopuses have 8 legs, starfish have 5.

How many marine animals are there in the aquarium if there are 39 limbs in total?

Diophantus of Alexandria is an ancient Greek mathematician who presumably lived in the 3rd century AD.

Almost nothing is known about the details of his life. On the one hand, Diophantus quotes Hypsicles (2nd century BC); on the other hand, Theon of Alexandria (about 350 AD) writes about Diophantus, from which we can conclude that his life took place within the boundaries of this period. A possible clarification of the time of Diophantus’s life is based on the fact that his “Arithmetic” is dedicated to “the most venerable Dionysius.” It is believed that this Dionysius is none other than Bishop Dionysius of Alexandria, who lived in the middle of the 3rd century. n. e.

The Palatine Anthology contains an epigram-task from which we can conclude that Diophantus lived 84 years:

The ashes of Diophantus rest in the tomb; marvel at her and the stone

The age of the deceased will speak through his wise art.

By the will of the gods, he lived a sixth of his life as a child.

And I met half past five with fluff on my cheeks.

Just past the seventh day, he got engaged to his girlfriend.

After spending five years with her, the sage had a son;

His father's beloved son lived only half his life.

He was taken from his father by his early grave.

Twice two years the parent mourned a heavy grief,

Here I saw the limit of my sad life.

Using modern methods of solving equations, it is possible to calculate how many years Diophantus lived. Let's create and solve the equation:

The solution to this equation is the number 84. Thus, Diophantus lived 84 years.

The main work of Diophantus is “Arithmetic” in 13 books. Unfortunately, only the first 6 books out of 13 have survived.

The first book is preceded by an extensive introduction, which describes the notation used by Diophantus. Diophantus calls the unknown a “number” (?ριθμ?ς) and denotes it with the letter ς, the square of the unknown with a symbol (short for δ?ναμις - “degree”). Special signs are provided for the following degrees of the unknown, up to the sixth, called the cube-cube, and for the degrees opposite to them. Diophantus does not have an addition sign: he simply writes positive terms next to each other, and in each term the degree of the unknown is first written, and then the numerical coefficient. The subtracted terms are also written side by side, and a special sign in the form of an inverted letter Ψ is placed in front of their entire group. The equal sign is denoted by two letters ?σ (short for ?σος - “equal”). The rule for bringing similar terms and the rule for adding or subtracting the same number or expression to both sides of the equation were formulated: what al-Khwarizmi later came to call “al-jabr and al-muqabala.” A sign rule has been introduced: minus times minus gives plus; This rule is used when multiplying two expressions with subtracted terms. All this is formulated in general terms, without reference to geometric interpretations.

Most of the work is a collection of problems with solutions (there are a total of 189 in the six surviving books), skillfully selected to illustrate general methods. The main problem of "Arithmetic" is finding positive rational solutions to indeterminate equations. Rational numbers are interpreted by Diophantus in the same way as natural numbers, which is not typical for ancient mathematicians.

First, Diophantus examines systems of 2nd order equations in 2 unknowns; it specifies a method for finding other solutions if one is already known. Then he applies similar methods to equations of higher degrees.

In the 10th century, “Arithmetic” was translated into Arabic, after which mathematicians from Islamic countries (Abu Kamil and others) continued some of Diophantus’s research. In Europe, interest in Arithmetic increased after Raphael Bombelli discovered this work in the Vatican Library and published 143 problems from it in his Algebra (1572). In 1621, a classic, thoroughly commented Latin translation of “Arithmetic” appeared, carried out by Bachet de Meziriak. Diophantus' methods had a huge influence on François Viète and Pierre Fermat; served as the starting point for the studies of Gauss and Euler. However, in modern times, indefinite equations are usually solved in whole numbers, and not in rational ones, as Diophantus did.

In the 20th century, under the name of Diophantus, the Arabic text of 4 more books of Arithmetic was discovered. Some historians of mathematics, after analyzing this text, put forward the hypothesis that their author was not Diophantus, but a commentator well versed in Diophantus’ methods, most likely Hypatia.

Diophantus's treatise “On Polygonal Numbers” (Περ? πολυγ?νων ?ριθμ?ν) has not been completely preserved; in the preserved part, a number of auxiliary theorems are derived using geometric algebra methods.

From the works of Diophantus “On the measurement of surfaces” (?πιπεδομετρικ?) and “On multiplication” (Περ? πολλαπλασιασμο?) only fragments have also been preserved.

Diophantus' book "Porisms" is known only from a few theorems used in Arithmetic.

Today the equation is of the form

Where P- an integer function (for example, a polynomial with integer coefficients), and the variables take integer values, called in honor of the ancient Greek mathematician - Diophantine.

Probably the most famous Diophantine equation is

Its solutions are Pythagorean triplets: (3; 4; 5), (6; 8; 10), (5; 12; 13), (12; 35; 37)…

Proof of the unsolvability in integers of the Diophantine equation

at (Fermat's Last Theorem) was completed by English mathematician Andrew Wiles in 1994.

Another example of a Diophantine equation is Pell's equation

where is the parameter n is not an exact square.

Hilbert's tenth problem is one of 23 problems that David Hilbert proposed on August 8, 1900 at the Second International Congress of Mathematicians. In Hilbert's report, the formulation of the tenth problem is the shortest of all:

Let a Diophantine equation with arbitrary unknowns and integer rational numerical coefficients be given. Indicate a method by which it is possible, after a finite number of operations, to determine whether this equation is solvable in rational integers.

Proving the algorithmic unsolvability of this problem took about twenty years and was completed by Yuri Matiyasevich in 1970.

Largely thanks to the activities of Pappus of Alexandria (III century), information about ancient scientists and their works has reached us. After Apollonius (from the 2nd century BC), a decline began in ancient science. No new deep ideas appear. In 146 BC. e. Rome captures Greece, and in 31 BC. e. - Alexandria. Against the background of general stagnation and decline, the gigantic figure of Diophantus of Alexandria, the last of the great ancient mathematicians, the “father of algebra,” stands out sharply.

The following mathematical objects are named after Diophantus: