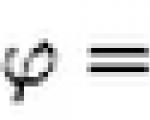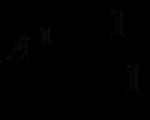Cara menulis persamaan osilasi harmonik. Getaran harmonik dan ciri-cirinya

Jenis getaran yang paling sederhana adalah getaran harmonis- fluktuasi di mana perpindahan titik osilasi dari posisi setimbang berubah seiring waktu menurut hukum sinus atau kosinus.

Jadi, dengan rotasi seragam bola di sekeliling keliling, proyeksinya (bayangan dalam sinar cahaya paralel) melakukan gerakan osilasi harmonik pada layar vertikal (Gbr. 1).

Perpindahan dari posisi setimbang pada getaran harmonik dijelaskan dengan persamaan (disebut hukum kinematik gerak harmonik) berbentuk:

dimana x - perpindahan - nilai yang mencirikan posisi titik osilasi pada waktu t relatif terhadap posisi setimbang dan diukur dengan jarak dari posisi setimbang ke posisi titik pada waktu tertentu; A - amplitudo osilasi - perpindahan maksimum benda dari posisi setimbang; T - periode osilasi - waktu satu osilasi penuh; itu. periode waktu terkecil setelah nilai besaran fisis yang mencirikan osilasi diulang; - tahap awal;

Fase osilasi pada waktu t. Fase osilasi adalah argumen fungsi periodik, yang, untuk amplitudo osilasi tertentu, menentukan keadaan sistem osilasi (perpindahan, kecepatan, percepatan) benda pada setiap saat.

Jika pada saat awal titik osilasi mengalami perpindahan maksimal dari posisi setimbang, maka , dan perpindahan titik dari posisi setimbang berubah menurut hukum

Jika titik osilasi di berada pada posisi setimbang stabil, maka perpindahan titik dari posisi setimbang berubah menurut hukum

Nilai V, kebalikan periode dan sama dengan jumlah osilasi lengkap yang dilakukan dalam 1 s, disebut frekuensi osilasi:

Jika pada waktu t benda melakukan N osilasi penuh, maka

nilai , yang menunjukkan berapa banyak getaran yang dilakukan benda dalam s, disebut frekuensi siklik (melingkar)..

Hukum kinematik gerak harmonik dapat dituliskan sebagai:

Secara grafis, ketergantungan perpindahan suatu titik osilasi terhadap waktu diwakili oleh kosinus (atau sinusoidal).

Gambar 2, a menunjukkan ketergantungan waktu perpindahan titik osilasi dari posisi setimbang untuk kasus tersebut.

Mari kita cari tahu bagaimana kecepatan suatu titik berosilasi berubah seiring waktu. Untuk melakukan ini, kita mencari turunan waktu dari ungkapan ini:

dimana adalah amplitudo proyeksi kecepatan pada sumbu x.

Rumus ini menunjukkan bahwa pada osilasi harmonik, proyeksi kecepatan benda pada sumbu x juga berubah menurut hukum harmonik dengan frekuensi yang sama, dengan amplitudo yang berbeda, dan mendahului fase pencampuran sebesar (Gbr. 2, b) .

Untuk mengetahui ketergantungan percepatan, kita mencari turunan waktu dari proyeksi kecepatan:

dimana adalah amplitudo proyeksi percepatan pada sumbu x.

Untuk osilasi harmonik, proyeksi percepatan mendahului perpindahan fasa sebesar k (Gbr. 2, c).

Demikian pula, Anda dapat membuat grafik ketergantungan

Persamaan Gelombang Harmonik

Persamaan osilasi harmonik menetapkan ketergantungan koordinat benda terhadap waktu

Grafik cosinus mempunyai nilai maksimum pada momen awal, dan grafik sinus mempunyai nilai nol pada momen awal. Jika kita mulai menyelidiki osilasi dari posisi setimbang, maka osilasi akan mengulangi sinusoidal. Jika kita mulai memperhatikan osilasi dari posisi simpangan maksimum, maka osilasi tersebut akan menggambarkan kosinus. Atau osilasi seperti itu dapat dijelaskan dengan rumus sinus dengan fase awal.

Perubahan kecepatan dan percepatan selama osilasi harmonik

Tidak hanya koordinat benda yang berubah terhadap waktu menurut hukum sinus atau kosinus. Namun besaran seperti gaya, kecepatan dan percepatan juga berubah dengan cara yang sama. Gaya dan percepatan maksimum bila benda yang berosilasi berada pada posisi ekstrim dimana perpindahan maksimum, dan sama dengan nol bila benda melewati posisi setimbang. Sebaliknya, kecepatan pada posisi ekstrim sama dengan nol, dan ketika benda melewati posisi setimbang, ia mencapai nilai maksimumnya.

Jika osilasi dijelaskan menurut hukum kosinus

Jika osilasi dijelaskan menurut hukum sinus

Nilai kecepatan dan percepatan maksimum

Setelah menganalisis persamaan ketergantungan v(t) dan a(t), dapat ditebak bahwa nilai maksimum kecepatan dan percepatan diambil jika faktor trigonometri sama dengan 1 atau -1. Ditentukan oleh rumus

Getaran mekanis. Parameter osilasi. Getaran harmonik.

keraguan Suatu proses disebut berulang secara tepat atau kira-kira pada interval tertentu.

Ciri osilasi adalah wajib adanya posisi setimbang yang stabil pada lintasan, di mana jumlah semua gaya yang bekerja pada benda sama dengan nol disebut posisi setimbang.

Pendulum matematika adalah suatu titik material yang digantungkan pada seutas benang tipis, tidak berbobot, dan tidak dapat diperpanjang.

Parameter gerak osilasi.

1. Mengimbangi atau mengoordinasikan (X) - penyimpangan dari posisi setimbang pada suatu waktu tertentu

momen waktu.	[X ]=M

2. Amplitudo ( xm) adalah simpangan maksimum dari posisi setimbang.

[ X M ]=M

3. Periode osilasi ( T) adalah waktu yang diperlukan untuk satu kali osilasi penuh.

[T ]=C.

0 "style="margin-left:31.0pt;border-collapse:collapse">

Pendulum matematika

Pendulum pegas

M

https://pandia.ru/text/79/117/images/image006_26.gif" width="134" height="57 src="> Frekuensi (linier) ( N ) – jumlah osilasi lengkap dalam 1 s.

[n]= Hz

5. Frekuensi siklik ( w ) – jumlah osilasi lengkap dalam 2p sekon, yaitu kira-kira 6,28 s.

w = 2pn ; [w]=0" style="margin-left:116.0pt;border-collapse:collapse">

https://pandia.ru/text/79/117/images/image012_9.jpg" width="90" height="103">

Bayangan di layar berfluktuasi.

Persamaan dan grafik osilasi harmonik.

Getaran harmonik - ini adalah osilasi di mana koordinat berubah seiring waktu sesuai dengan hukum sinus atau kosinus.

https://pandia.ru/text/79/117/images/image014_7.jpg" width="254" height="430 src="> X=XMdosa(w T+j 0 )

X=XMkarena(w T+j 0 )

x - koordinat,

Xm adalah amplitudo osilasi,

w adalah frekuensi siklik,

berat+j 0 = j adalah fase osilasi,

J 0 adalah fase awal osilasi.

https://pandia.ru/text/79/117/images/image016_4.jpg" width="247" height="335 src=">

Grafik berbeda hanya amplitudo

Grafik hanya berbeda dalam periode (frekuensi)

https://pandia.ru/text/79/117/images/image018_3.jpg" width="204" height="90 src=">

Jika amplitudo osilasi tidak berubah seiring waktu, osilasi disebut tidak teredam.

Getaran alami tidak memperhitungkan gesekan, energi mekanik total sistem tetap konstan: E ke + E n = E bulu = konstanta.

Osilasi alami tidak teredam.

Dengan osilasi paksa, energi yang disuplai secara terus menerus atau berkala dari sumber luar mengkompensasi kerugian yang timbul akibat kerja gaya gesekan, dan osilasi dapat tidak teredam.

Energi kinetik dan potensial suatu benda selama getaran berpindah satu sama lain. Ketika simpangan sistem dari posisi setimbang maksimum, energi potensial maksimum, dan energi kinetik nol. Saat melewati posisi setimbang, sebaliknya.

Frekuensi osilasi bebas ditentukan oleh parameter sistem osilasi.

Frekuensi osilasi paksa ditentukan oleh frekuensi gaya luar. Amplitudo osilasi paksa juga bergantung pada gaya eksternal.

resonansi C

Resonansi disebut peningkatan tajam dalam amplitudo osilasi paksa ketika frekuensi aksi gaya eksternal bertepatan dengan frekuensi osilasi alami sistem.

Ketika frekuensi w perubahan gaya bertepatan dengan frekuensi alami w0 osilasi sistem, gaya melakukan kerja positif sepanjang periode, meningkatkan amplitudo osilasi benda. Pada frekuensi lain, dalam satu bagian periode, gaya melakukan kerja positif, dan pada bagian periode lainnya, gaya melakukan kerja negatif.

Pada resonansi, peningkatan amplitudo osilasi dapat menyebabkan kerusakan sistem.

Pada tahun 1905, di bawah serangan satu skuadron kavaleri penjaga, jembatan Mesir yang melintasi Sungai Fontanka di St. Petersburg runtuh.

Osilasi diri.

Osilasi mandiri disebut osilasi tak teredam dalam sistem, yang didukung oleh sumber energi internal tanpa adanya perubahan gaya eksternal.

Berbeda dengan osilasi paksa, frekuensi dan amplitudo osilasi sendiri ditentukan oleh sifat sistem osilasi itu sendiri.

Osilasi sendiri berbeda dari osilasi bebas dalam hal independensi amplitudo dari waktu dan dari dampak awal jangka pendek yang menggairahkan proses osilasi. Sistem osilasi sendiri biasanya dapat dibagi menjadi tiga elemen:

1) sistem osilasi;

2) sumber energi;

3) alat umpan balik yang mengatur aliran energi dari suatu sumber ke dalam sistem osilasi.

Energi yang berasal dari sumber selama suatu periode sama dengan energi yang hilang dalam sistem osilasi dalam waktu yang sama.

Kami mempertimbangkan beberapa sistem yang sangat berbeda secara fisik, dan memastikan bahwa persamaan gerak direduksi ke bentuk yang sama

Perbedaan antara sistem fisik hanya terwujud dalam definisi besaran yang berbeda dan dalam arti fisik yang berbeda dari variabel X: dapat berupa koordinat, sudut, muatan, arus, dll. Perhatikan bahwa dalam kasus ini, sebagai berikut dari struktur persamaan (1.18), besaran selalu berdimensi kebalikan waktu.

Persamaan (1.18) menjelaskan apa yang disebut getaran harmonis.

Persamaan osilasi harmonik (1.18) merupakan persamaan diferensial linier orde kedua (karena mengandung turunan kedua dari variabel X). Linearitas persamaan berarti bahwa

jika ada fungsi x(t) adalah solusi persamaan ini, maka fungsinya Cx(t) juga akan menjadi solusinya ( C adalah konstanta sembarang);

jika berfungsi x 1 (t) Dan x 2 (t) adalah solusi persamaan ini, lalu jumlahnya x 1 (t) + x 2 (t) juga akan menjadi solusi untuk persamaan yang sama.

Teorema matematika juga terbukti, yang menyatakan bahwa persamaan orde kedua memiliki dua solusi independen. Semua solusi lain, berdasarkan sifat linearitasnya, dapat diperoleh sebagai kombinasi liniernya. Mudah untuk memeriksa dengan diferensiasi langsung bahwa fungsi independen dan memenuhi persamaan (1.18). Jadi solusi umum persamaan ini adalah:

Di mana C1,C2 adalah konstanta yang berubah-ubah. Solusi ini juga bisa disajikan dalam bentuk lain. Kami memperkenalkan kuantitasnya

dan tentukan sudutnya sebagai:

Maka solusi umum (1.19) ditulis sebagai

Menurut rumus trigonometri, persamaan dalam tanda kurung adalah

Kami akhirnya tiba di solusi umum persamaan osilasi harmonik sebagai:

Nilai non-negatif A ditelepon amplitudo osilasi, - fase awal osilasi. Seluruh argumen kosinus - kombinasinya - disebut fase osilasi.

Ekspresi (1.19) dan (1.23) benar-benar ekuivalen, sehingga kita dapat menggunakan keduanya demi alasan kesederhanaan. Kedua solusi tersebut merupakan fungsi periodik waktu. Memang sinus dan kosinus bersifat periodik dengan suatu periode . Oleh karena itu, berbagai keadaan sistem yang melakukan osilasi harmonik akan berulang setelah jangka waktu tertentu T*, yang fase osilasinya mendapat kenaikan yang merupakan kelipatan :

Oleh karena itu, berikut ini

Paling sedikit dari waktu-waktu ini

ditelepon periode osilasi (Gbr. 1.8), a - miliknya melingkar (siklik) frekuensi.

Beras. 1.8.

Mereka juga menggunakan frekuensi keraguan

Dengan demikian, frekuensi melingkar sama dengan jumlah osilasi per detik.

Jadi, jika sistem pada waktunya T dicirikan oleh nilai variabelnya x(t), maka, nilai yang sama akan dimiliki variabel tersebut setelah periode waktu tertentu (Gbr. 1.9), yaitu

Nilai yang sama tentu saja akan terulang kembali setelah beberapa saat. 2T, ZT dll.

Beras. 1.9. Periode osilasi

Solusi umum mencakup dua konstanta sembarang ( C 1 , C 2 atau A, A), yang nilainya harus ditentukan oleh dua kondisi awal. Biasanya (walaupun belum tentu) perannya dimainkan oleh nilai awal variabel x(0) dan turunannya.

Mari kita ambil contoh. Biarkan penyelesaian (1.19) persamaan osilasi harmonik menggambarkan gerak bandul pegas. Nilai konstanta sembarang bergantung pada cara kita membuat pendulum keluar dari keseimbangan. Misalnya, kita menarik pegas ke kejauhan dan melepaskan bola tanpa kecepatan awal. Pada kasus ini

Mengganti t = 0 di (1.19), kita menemukan nilai konstanta Dari 2

Solusinya terlihat seperti:

Kecepatan beban ditemukan melalui diferensiasi terhadap waktu

Mengganti di sini T = 0, carilah konstanta Dari 1:

Akhirnya

Dibandingkan dengan (1.23), kita menemukan bahwa adalah amplitudo osilasi, dan fase awalnya sama dengan nol: .

Sekarang kita membuat pendulum keluar dari keseimbangan dengan cara lain. Mari kita pukul bebannya, sehingga memperoleh kecepatan awal, tetapi praktis tidak bergerak selama tumbukan. Kami kemudian memiliki kondisi awal lainnya:

solusi kami sepertinya

Kecepatan beban akan berubah menurut hukum:

Mari kita taruh di sini:

Topik pengkode USE: osilasi harmonik; amplitudo, periode, frekuensi, fase osilasi; getaran bebas, getaran paksa, resonansi.

fluktuasi adalah perubahan keadaan sistem yang berulang sepanjang waktu. Konsep osilasi mencakup fenomena yang sangat luas.

Getaran sistem mekanis, atau getaran mekanis- ini adalah gerakan mekanis suatu benda atau sistem benda, yang dapat diulang dalam waktu dan terjadi di sekitar posisi setimbang. posisi keseimbangan Ini adalah keadaan sistem di mana ia dapat bertahan dalam jangka waktu lama tanpa mengalami pengaruh eksternal.

Misalnya jika pendulum dibelokkan dan dilepaskan, maka osilasi akan dimulai. Posisi setimbang adalah posisi bandul tanpa adanya defleksi. Dalam posisi ini, pendulum, jika tidak disentuh, dapat bertahan tanpa batas waktu. Ketika pendulum berosilasi, ia melewati posisi setimbang berkali-kali.

Segera setelah bandul yang dibelokkan dilepaskan, ia mulai bergerak, melewati posisi setimbang, mencapai posisi ekstrim yang berlawanan, berhenti sejenak di dalamnya, bergerak ke arah yang berlawanan, melewati posisi setimbang lagi dan kembali lagi. Satu hal terjadi ayunan penuh. Proses ini kemudian akan diulangi secara berkala.

Amplitudo osilasi tubuh adalah besarnya deviasi terbesarnya dari posisi setimbang.

Periode osilasi adalah waktu untuk satu osilasi penuh. Kita dapat mengatakan bahwa untuk periode tersebut benda menempuh jalur dengan empat amplitudo.

Frekuensi osilasi adalah kebalikan dari periode: . Frekuensi diukur dalam hertz (Hz) dan menunjukkan berapa banyak osilasi lengkap yang terjadi dalam satu detik.

Getaran harmonik.

Kita asumsikan bahwa posisi benda yang berosilasi ditentukan oleh satu koordinat. Nilainya sesuai dengan posisi kesetimbangan. Tugas utama mekanika dalam hal ini adalah menemukan fungsi yang memberikan koordinat benda pada suatu waktu.

Untuk deskripsi matematis osilasi, wajar jika menggunakan fungsi periodik. Ada banyak fungsi seperti itu, tetapi dua di antaranya - sinus dan kosinus - adalah yang paling penting. Mereka memiliki banyak sifat baik dan berkaitan erat dengan berbagai fenomena fisik.

Karena fungsi sinus dan cosinus diperoleh satu sama lain dengan menggeser argumen sebesar , kita dapat membatasi diri hanya pada salah satu fungsi tersebut. Untuk kepastiannya, kita akan menggunakan kosinus.

Getaran harmonik adalah osilasi yang koordinatnya bergantung pada waktu menurut hukum harmonik:

(1)

Mari kita cari tahu arti besaran yang termasuk dalam rumus ini.

Nilai positif adalah nilai koordinat terbesar dalam nilai absolut (karena nilai maksimum modulus kosinus sama dengan satu), yaitu simpangan terbesar dari posisi kesetimbangan. Oleh karena itu - amplitudo osilasi.

Argumen kosinus disebut fase fluktuasi. Nilai yang sama dengan nilai fasa di disebut fasa awal. Fase awal sesuai dengan koordinat awal benda: .

Nilainya disebut frekuensi siklik. Mari kita cari hubungannya dengan periode dan frekuensi osilasi. Satu osilasi lengkap berhubungan dengan kenaikan fase yang sama dengan radian: , dari mana

(2)

(3)

Frekuensi siklik diukur dalam rad/s (radian per detik).

Sesuai dengan ungkapan (2) dan (3), kita memperoleh dua bentuk lagi pencatatan hukum harmonik (1) :

Grafik fungsi (1), yang menyatakan ketergantungan koordinat terhadap waktu selama osilasi harmonik, ditunjukkan pada Gambar. 1 .

Hukum harmonik bentuk (1) bersifat paling umum. Ini menjawab, misalnya, situasi ketika dua tindakan awal dilakukan secara bersamaan dengan pendulum: mereka membelokkannya dengan jumlah tertentu dan memberinya kecepatan awal. Ada dua kasus khusus yang penting dimana salah satu tindakan ini tidak dilakukan.

Biarkan pendulum ditolak, tetapi kecepatan awalnya tidak dilaporkan (dilepaskan tanpa kecepatan awal). Jelas bahwa dalam kasus ini, kita dapat menempatkannya. Kami mendapatkan hukum kosinus:

Grafik osilasi harmonik dalam hal ini ditunjukkan pada Gambar. 2.

Beras. 2. Hukum kosinus

Sekarang mari kita asumsikan bahwa pendulum tidak dibelokkan, tetapi kecepatan awal diberikan padanya dari posisi setimbang melalui suatu pukulan. Dalam hal ini, Anda dapat memasukkannya. Kami mendapatkan hukum sinus:

Jadwal fluktuasi disajikan pada gambar. 3.

Beras. 3. Hukum sinus

Persamaan osilasi harmonik.

Mari kita kembali ke hukum harmonik umum (1) . Mari kita bedakan persamaan ini:

. (4)

Sekarang kita bedakan persamaan yang dihasilkan (4) :

. (5)

Mari kita bandingkan ekspresi (1) untuk koordinat dan ekspresi (5) untuk proyeksi percepatan. Kita melihat bahwa proyeksi percepatan berbeda dari koordinat hanya dengan faktor :

. (6)

Rasio ini disebut persamaan osilasi harmonik. Itu juga dapat ditulis ulang dalam bentuk ini:

. (7)

Dari sudut pandang matematika, persamaan (7) adalah persamaan diferensial. Solusi persamaan diferensial adalah fungsi (dan bukan bilangan, seperti dalam aljabar biasa).
Jadi, kita dapat membuktikan bahwa:

Penyelesaian persamaan (7) adalah sembarang fungsi berbentuk (1) dengan sembarang ;

Tidak ada fungsi lain yang merupakan solusi persamaan ini.

Dengan kata lain, hubungan (6) , (7) menggambarkan osilasi harmonik dengan frekuensi siklik dan hanya osilasi tersebut. Dua konstanta ditentukan dari kondisi awal - dengan nilai awal koordinat dan kecepatan.

Pendulum pegas.

Pendulum pegas adalah beban yang dipasang pada pegas, yang mampu berosilasi dalam arah horizontal atau vertikal.

Mari kita cari periode osilasi horizontal kecil pendulum pegas (Gbr. 4). Osilasi akan kecil jika besarnya deformasi pegas jauh lebih kecil dari dimensinya. Untuk deformasi kecil, kita dapat menggunakan hukum Hooke. Hal ini akan menyebabkan osilasi menjadi harmonis.

Kami mengabaikan gesekan. Massa mempunyai massa dan konstanta pegas adalah .

Koordinat tersebut sesuai dengan posisi kesetimbangan di mana pegas tidak mengalami deformasi. Oleh karena itu, besarnya deformasi pegas sama dengan modulus koordinat beban.

Beras. 4. Pendulum pegas

Pada arah mendatar, hanya gaya elastis pegas yang bekerja pada beban. Hukum kedua Newton untuk beban yang diproyeksikan pada sumbu adalah:

. (8)

Jika (beban digeser ke kanan seperti pada gambar), maka gaya elastis diarahkan ke arah yang berlawanan, dan . Sebaliknya jika , maka . Tanda dan tandanya selalu berlawanan, sehingga hukum Hooke dapat dituliskan sebagai berikut:

Kemudian relasi (8) berbentuk:

Kami memperoleh persamaan osilasi harmonik dalam bentuk (6) , di mana

Frekuensi siklik osilasi pendulum pegas sama dengan:

. (9)

Dari sini dan dari perbandingan kita mencari periode osilasi horizontal bandul pegas:

. (10)

Jika Anda menggantungkan beban pada pegas, Anda akan mendapatkan pendulum pegas yang berosilasi ke arah vertikal. Dapat ditunjukkan bahwa dalam hal ini rumus (10) juga berlaku untuk periode osilasi.

Pendulum matematika.

Pendulum matematika - ini adalah benda kecil yang digantung pada seutas benang tanpa bobot yang tidak dapat diperpanjang (Gbr. 5). Pendulum matematika dapat berosilasi pada bidang vertikal dalam medan gravitasi.

Beras. 5. Pendulum matematika

Mari kita cari periode osilasi kecil bandul matematika. Panjang benangnya adalah. Hambatan udara diabaikan.

Mari kita tuliskan hukum kedua Newton untuk pendulum:

dan memproyeksikannya ke sumbu:

Jika pendulum menempati posisi seperti pada gambar (yaitu), maka:

Jika pendulum berada di sisi lain dari posisi setimbang (yaitu), maka:

Jadi, untuk setiap posisi pendulum kita mempunyai:

. (11)

Ketika bandul diam pada posisi setimbang, persamaan terpenuhi. Untuk osilasi kecil, bila deviasi pendulum dari posisi setimbang kecil (dibandingkan dengan panjang benang), persamaan perkiraan terpenuhi. Mari kita gunakan dalam rumus (11):

Ini adalah persamaan osilasi harmonik bentuk (6) di mana

Oleh karena itu, frekuensi siklik osilasi bandul matematika adalah:

. (12)

Maka periode osilasi bandul matematika:

. (13)

Perlu diketahui bahwa rumus (13) tidak memasukkan massa beban. Berbeda dengan bandul pegas, periode osilasi bandul matematika tidak bergantung pada massanya.

Getaran bebas dan paksa.

Sistem dikatakan demikian getaran bebas, jika ia dikeluarkan dari posisi setimbang dan kemudian dibiarkan begitu saja. Tidak ada eksternal berkala
Pada saat yang sama, sistem tidak mengalami dampak apa pun, dan tidak ada sumber energi internal yang mendukung osilasi dalam sistem.

Osilasi pegas dan pendulum matematika yang dibahas di atas adalah contoh osilasi bebas.

Frekuensi terjadinya getaran bebas disebut frekuensi alami sistem osilasi. Jadi, rumus (9) dan (12) memberikan frekuensi osilasi alami (siklik) pegas dan pendulum matematika.

Dalam situasi ideal tanpa adanya gesekan, osilasi bebas tidak teredam, yaitu memiliki amplitudo konstan dan berlangsung tanpa batas. Dalam sistem osilasi nyata, gesekan selalu ada, sehingga osilasi bebas secara bertahap meredam (Gbr. 6).

Getaran paksa- ini adalah osilasi yang dilakukan oleh sistem di bawah pengaruh gaya eksternal, yang berubah secara berkala terhadap waktu (yang disebut gaya penggerak).

Mari kita asumsikan bahwa frekuensi osilasi alami sistem adalah , dan gaya penggerak bergantung pada waktu menurut hukum harmonik:

Untuk beberapa waktu, osilasi paksa terjadi: sistem melakukan gerakan kompleks, yang merupakan superposisi dari osilasi paksa dan bebas. Osilasi bebas berangsur-angsur mereda, dan dalam keadaan stabil sistem melakukan osilasi paksa, yang juga menjadi harmonis. Frekuensi osilasi paksa yang stabil bertepatan dengan frekuensinya
kekuatan pendorong (kekuatan eksternal, seolah-olah, memaksakan frekuensinya pada sistem).

Amplitudo osilasi paksa dalam keadaan tunak bergantung pada frekuensi gaya penggerak. Grafik ketergantungan ini ditunjukkan pada Gambar. 7.

Beras. 7. Resonansi

Kita melihat bahwa resonansi terjadi di dekat frekuensi - fenomena peningkatan amplitudo osilasi paksa. Frekuensi resonansi kira-kira sama dengan frekuensi osilasi alami sistem: , dan persamaan ini semakin akurat, semakin sedikit gesekan dalam sistem. Dengan tidak adanya gesekan, frekuensi resonansi bertepatan dengan frekuensi osilasi alami, , dan amplitudo osilasi meningkat hingga tak terhingga pada .