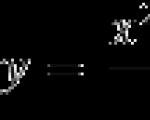Il problema B15 è lo studio di una funzione che utilizza una derivata. Studio di una funzione utilizzando una derivata Studio di una funzione utilizzando una derivata

Nel problema B15 si propone di indagare la funzione data dalla formula degli estremi. Questo è un problema standard nel calcolo infinitesimale e la sua complessità varia notevolmente a seconda della funzione in questione: alcuni di essi vengono risolti letteralmente verbalmente, mentre altri richiedono una riflessione seria.

Prima di apprendere i metodi risolutivi è necessario padroneggiare alcuni termini del campo dell'analisi matematica. Quindi, nel problema B15, è necessario trovare le seguenti quantità utilizzando la derivata:

1. Punti di massimo locale (minimo) - il valore della variabile in cui la funzione raggiunge il suo valore massimo (minimo). Tali punti sono anche chiamati punti estremi.
2. Il massimo (minimo) globale della funzione è il valore massimo (minimo) della funzione con le restrizioni specificate. Un altro nome è estremi globali.

In questo caso, gli estremi globali vengono solitamente ricercati non sull'intero dominio della definizione della funzione, ma solo su un determinato segmento. È importante capire che l'estremo globale e il valore della funzione nel punto estremo non sempre coincidono. Spieghiamolo con un esempio specifico:

Compito. Trova il punto minimo e il valore minimo della funzione y = 2x 3 − 3x 2 − 12x + 1 sul segmento [−3; 3].

Per prima cosa troviamo il punto di minimo, per il quale calcoliamo la derivata:
y' = (2x 3 - 3x 2 - 12x + 1)' = 6x 2 - 6x - 12.

Troviamo i punti critici risolvendo l'equazione y' = 0. Otteniamo l'equazione quadratica standard:
y' = 0 ⇒ 6x 2 - 6x - 12 = 0 ⇒ ... ⇒ x 1 = -1, x 2 = 2.

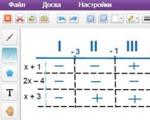
Contrassegniamo questi punti sulla linea delle coordinate, aggiungiamo i segni della derivata e le restrizioni - le estremità del segmento:

La scala dell'immagine non ha importanza. La cosa più importante è segnare i punti nella sequenza corretta. Dal corso di matematica scolastico si sa che nel punto minimo la derivata cambia segno da meno a più. La lettura va sempre da sinistra a destra, nella direzione del semiasse positivo. Esiste quindi un solo punto di minimo: x = 2.

Ora troviamo il valore minimo della funzione sul segmento [−3; 3]. Si raggiunge o nel punto di minimo (diventa quindi il punto di minimo globale), oppure alla fine del segmento. Si noti che sull'intervallo (2; 3) la derivata è ovunque positiva, il che significa che y(3) > y(2), quindi l'estremità destra dell'intervallo può essere ignorata. Rimangono solo i punti x = −3 (estremità sinistra del segmento) e x = 2 (punto minimo). Abbiamo:
y(−3) = 2(−3) 3 − 3(−3) 2 − 12(−3) + 1 = −44;
y(2) = 2*2 3 - 3*2 2 - 12*2 + 1 = -19.

Quindi, il valore più piccolo della funzione viene raggiunto alla fine del segmento ed è uguale a −44.

Risposta: xmin = 2; ymin = −44

Da quanto sopra segue un fatto importante, che molte persone dimenticano. La funzione assume il valore massimo (minimo), non necessariamente nel punto estremo. A volte tale valore viene raggiunto alla fine del segmento e la derivata non deve essere necessariamente uguale a zero.

Schema di risoluzione dei problemi B15

Se nel problema B15 si vuole trovare il valore massimo o minimo della funzione f(x) sull'intervallo , eseguiamo le seguenti azioni:

1. Risolvi l'equazione f'(x) = 0. Se non ci sono radici, salta il terzo passaggio e vai direttamente al quarto.
2. Dall'insieme di radici risultante, elimina tutto ciò che si trova al di fuori del segmento. I numeri rimanenti saranno indicati con x 1 , x 2 , ..., x n - di regola ce ne saranno pochi.
3. Sostituisci gli estremi del segmento e i punti x 1 , x 2 , ..., x n nella funzione originale. Otteniamo un insieme di numeri f (a), f (b), f (x 1), f (x 2), ..., f (x n), da cui selezioniamo il valore più grande o più piccolo - questo sarà la risposta.

Una piccola precisazione sull'eliminazione delle radici quando coincidono con le estremità del segmento. Possono anche essere cancellati, poiché nel quarto passaggio le estremità del segmento vengono comunque sostituite nella funzione, anche se l'equazione f’(x) = 0 non ha soluzioni.

Compito. Trova il valore più grande della funzione y = x 3 + 3x 2 − 9x − 7 sull'intervallo [−5; 0].

Per prima cosa troviamo la derivata: y' = (x 3 + 3x 2 - 9x - 7)' = 3x 2 + 6x - 9.

Quindi risolviamo l’equazione: y’ = 0 ⇒ 3x 2 + 6x − 9 = 0 ⇒ ... ⇒ x = −3; x = 1.

Cancellare la radice x = 1 perché non appartiene all'intervallo [−5; 0].

Resta da calcolare il valore della funzione agli estremi del segmento e nel punto x = −3:
y(−5) = (−5) 3 + 4 (−5) 2 − 9 (−5) − 7 = −12;
y(−3) = (−3) 3 + 4 (−3) 2 − 9 (−3) − 7 = 20;
y(0) = 0 3 + 4 0 2 − 9 0 − 7 = −7.

Ovviamente il valore più grande è 20 e si raggiunge nel punto x = −3.

Consideriamo ora il caso in cui si debba trovare il punto massimo o minimo della funzione f(x) sull'intervallo . Se il segmento non è specificato, la funzione viene considerata nel suo dominio di definizione. In ogni caso lo schema risolutivo è il seguente:

1. Trova la derivata della funzione: f'(x).
2. Risolvi l'equazione f’(x) = 0. Se la derivata è una funzione razionale frazionaria, scopriamo inoltre quando il suo denominatore è zero. Indichiamo le radici ottenute x 1 , x 2 , ..., x n .
3. Segna x 1 , x 2 , ..., x n sulla linea delle coordinate e posiziona i segni che prende la derivata tra questi numeri. Se viene fornito un segmento, contrassegnalo e cancella tutto ciò che si trova al di fuori di esso.
4. Tra i punti rimanenti cerchiamo quello in cui il segno della derivata cambia da meno a più (questo è il punto di minimo) o da più a meno (punto di minimo). Dovrebbe esserci solo uno di questi punti: questa sarà la risposta.

Un lettore attento noterà sicuramente che per alcune funzioni questo algoritmo non funziona. In effetti, esiste un'intera classe di funzioni per le quali la ricerca dei punti estremi richiede calcoli più complessi. Tuttavia, tali funzioni non si trovano nell'esame di matematica.

Presta attenzione al posizionamento dei segni tra i punti x 1 , x 2 , ..., x n . Ricorda: quando si passa per una radice di molteplicità pari, il segno della derivata non cambia. Quando si cercano i punti estremi, i segnali vengono sempre visti da sinistra a destra, cioè lungo l'asse numerico.

Compito. Trovare il punto massimo di una funzione

sull'intervallo [−8; 8].

Troviamo la derivata:

Poiché si tratta di una funzione razionale frazionaria, equiparamo la derivata e il suo denominatore a zero:
y' = 0 ⇒ x 2 − 25 = 0 ⇒ ... ⇒ x = 5; x = −5;
x 2 \u003d 0 ⇒ x \u003d 0 (la radice della seconda molteplicità).

Segniamo i punti x = −5, x = 0 e x = 5 sulla linea delle coordinate, disponiamo i segni e i confini:

Ovviamente all'interno del segmento rimane solo un punto x = −5, in cui il segno della derivata cambia da più a meno. Questo è il punto massimo.

Ancora una volta, spieghiamo in che modo i punti estremi differiscono dagli estremi stessi. I punti estremi sono i valori delle variabili in cui la funzione assume il valore più grande o più piccolo. Gli estremi sono i valori delle funzioni stesse, massimi o minimi in alcuni dei loro dintorni.

Oltre ai polinomi ordinari e alle funzioni razionali frazionarie, nel Problema B15 si trovano i seguenti tipi di espressioni:

1. funzioni irrazionali,
2. funzioni trigonometriche,
3. funzioni esponenziali,
4. Funzioni logaritmiche.

Di norma, non ci sono problemi con le funzioni irrazionali. I restanti casi meritano di essere considerati più in dettaglio.

Funzioni trigonometriche

La principale difficoltà delle funzioni trigonometriche è che quando si risolvono le equazioni si forma un numero infinito di radici. Ad esempio, l'equazione sin x = 0 ha radici x = πn, dove n ∈ Z. Ebbene, come contrassegnarle sulla linea delle coordinate se esistono infiniti numeri simili?

La risposta è semplice: è necessario sostituire valori specifici di n. Infatti, nei problemi B15 con funzioni trigonometriche c'è sempre una restrizione: un segmento. Pertanto, per cominciare, prendiamo n \u003d 0, quindi aumentiamo n finché la radice corrispondente “vola fuori” oltre il segmento. Allo stesso modo, diminuendo n, molto presto otterremo una radice inferiore al limite inferiore.

È facile mostrare che sull'intervallo non esistono radici diverse da quelle ottenute nel processo considerato. Consideriamo ora questo processo con esempi concreti.

Compito. Trovare il punto massimo della funzione y = sin x − 5x sin x − 5cos x + 1 appartenente all'intervallo [−π/3; π/3].

Calcola la derivata: y’ = (sin x − 5x sin x − 5cos x + 1)’ = ... = cos x − 5x cos x = (1 − 5x) cos x.

Quindi risolviamo l’equazione: y’ = 0 ⇒ (1 − 5x) cos x = 0 ⇒ ... ⇒ x = 0,2 oppure x = π/2 + πn, n ∈ Z.

Con la radice x = 0,2 tutto è chiaro, ma la formula x = π / 2 + πn richiede un'ulteriore elaborazione. Sostituiremo diversi valori di n, partendo da n = 0.

n = 0 ⇒ x = π/2. Ma π/2 > π/3, quindi la radice x = π/2 non è inclusa nel segmento originale. Inoltre, maggiore è n, maggiore è x, quindi non ha senso considerare n > 0.

n = −1 ⇒ x = −π/2. Ma −π/2< −π/3 - этот корень тоже придется отбросить. А вместе с ним - и все корни для n < −1.

Risulta che nell'intervallo [−π/3; π/3] si trova solo nella radice x = 0,2. Lo contrassegniamo insieme con segni e confini sulla linea di coordinate:

Per essere sicuri che la derivata a destra di x = 0,2 sia realmente negativa, è sufficiente sostituire il valore x = π/4 in y’. Notiamo solo che nel punto x = 0,2 la derivata cambia segno da più a meno, e quindi questo è il punto di massimo.

Compito. Trovare il valore più grande della funzione y = 4tg x − 4x + π − 5 sull'intervallo [−π/4; π/4].

Calcola la derivata: y’ = (4tg x − 4x + π − 5)’ = 4/cos 2x − 4.

Quindi risolviamo l’equazione: y’ = 0 ⇒ 4/cos 2x − 4 = 0 ⇒ ... ⇒ x = πn, n ∈ Z.

Estraiamo le radici da questa formula sostituendo n specifico, a partire da n = 0:
n = 0 ⇒ x = 0. Questa radice ci si addice.
n = 1 ⇒ x = π. Ma π > π/4, quindi la radice x = π e i valori n > 1 devono essere cancellati.
n = −1 ⇒ x = −π. Ma π< −π/4, поэтому x = π и n < −1 тоже вычеркиваем.

Di tutta la varietà di radici ne rimane solo una: x = 0. Pertanto, calcoliamo il valore della funzione per x = 0, x = π/4 e x = −π/4.
y(0) = 4tg 0 − 4 0 + π − 5 = π − 5;
y(π/4) = 4tg (π/4) − 4 π/4 + π − 5 = −1;
y(π/4) = 4tg (−π/4) − 4 (−π/4) + π − 5 = ... = 2π − 9.

Ora notiamo che π = 3,14...< 4, поэтому π − 5 < 4 − 5 = −1 и 2π − 9 < 8 − 9 = −1. Получается одно положительное число и два отрицательных. Мы ищем наибольшее - очевидно, это y = −1.

Nota che nell'ultimo problema era possibile non confrontare i numeri tra loro. Infatti, dei numeri π - 5, 1 e 2π - 9, solo uno può essere scritto nel foglio delle risposte. In effetti, come scrivere nella forma, ad esempio, il numero π? Ma assolutamente no. Questa è una caratteristica importante della prima parte dell'esame di matematica, che semplifica notevolmente la soluzione di molti problemi. E funziona non solo in B15.

A volte, quando si studia una funzione, emergono equazioni che non hanno radici. In questo caso il problema diventa ancora più semplice, poiché resta da considerare solo le estremità del segmento.

Compito. Trovare il valore più piccolo della funzione y = 7sin x − 8x + 5 sull'intervallo [−3π/2; 0].

Innanzitutto troviamo la derivata: y’ = (7sin x − 8x + 5)’ = 7cos x − 8.

Proviamo a risolvere l'equazione: y' = 0 ⇒ 7cos x − 8 = 0 ⇒ cos x = 8/7. Ma i valori di cos x giacciono sempre nell'intervallo [−1; 1] e 8/7 > 1. Pertanto non ci sono radici.

Se non ci sono radici, non è necessario cancellare nulla. Passiamo all'ultimo passaggio: calcoliamo il valore della funzione:
y(−3π/2) = 7sin (−3π/2) − 8 (−3π/2) + 5 = ... = 12π + 12;
y(0) = 7sen 0 − 8 0 + 5 = 5.

Poiché il numero 12π + 12 non può essere scritto sul foglio delle risposte, rimane solo y = 5.

funzioni esponenziali

In generale, una funzione esponenziale è un'espressione della forma y = a x , dove a > 0. Ma nel problema B15 si verificano solo funzioni della forma y = e x e, nel caso estremo, y = e kx + b. Il motivo è che le derivate di queste funzioni sono molto facili da calcolare:

1. (e x)" = e x . Non è cambiato nulla.
2. (e kx + b)" = k e kx + b. Viene semplicemente aggiunto un fattore uguale al coefficiente della variabile x. Questo è un caso speciale di derivata di una funzione complessa.

Tutto il resto è assolutamente standard. Naturalmente, le funzioni reali nei problemi B15 sembrano più severe, ma lo schema della soluzione non cambia da questo. Consideriamo un paio di esempi, evidenziando solo i punti principali della soluzione, senza ragionamenti e commenti approfonditi.

Compito. Trova il valore più piccolo della funzione y = (x 2 − 5x + 5)e x − 3 sul segmento [−1; 5].

Derivata: y’ = ((x 2 − 5x + 5)e x − 3)’ = ... = (x 2 − 3x)e x − 3 = x(x − 3)e x − 3 .

Trova le radici: y' = 0 ⇒ x(x − 3)e x − 3 = 0 ⇒ ... ⇒ x = 0; x=3.

Entrambe le radici giacciono sull'intervallo [−1; 5]. Resta da trovare il valore della funzione in tutti i punti:
y(−1) = ((−1) 2 − 5 (−1) + 5)e − 1 − 3 = ... = 11 e −4 ;
y(0) = (0 2 − 5 0 + 5)e 0 − 3 = ... = 5 e −3 ;
y(3) = (3 2 − 5 3 + 5)e 3 − 3 = ... = −1;
y(5) = (5 2 − 5 5 + 5)e 5 − 3 = ... = 5 e 2 .

Dei quattro numeri ottenuti, solo y = −1 può essere scritto nella forma. Inoltre, questo è l'unico numero negativo: sarà il più piccolo.

Compito. Trova il valore massimo della funzione y = (2x − 7) e 8 − 2x sul segmento .

Derivata: y’ = ((2x − 7) e 8 − 2x)’ = ... = (16 − 4x) e 8 − 2x = 4(4 − x) e 8 − 2x .

Troviamo le radici: y' = 0 ⇒ 4(4 − x) e 8 − 2x = 0 ⇒ x = 4.

La radice x = 4 appartiene al segmento . Cerchiamo i valori della funzione:
y(0) = (2 0 − 7)e 8 − 2 0 = ... = −7 e 8 ;
y(4) = (2 4 − 7)e 8 − 2 4 = ... = 1;
y(6) = (2 6 − 7)e 8 − 2 6 = ... = 5 e −4 .

Ovviamente solo y = 1 può servire come risposta.

Funzioni logaritmiche

Per analogia con le funzioni esponenziali, nel problema B15 ricorrono solo i logaritmi naturali, poiché la loro derivata si calcola facilmente:

1. (lnx)' = 1/x;
2. (ln(kx + b))' = k/(kx + b). In particolare, se b = 0, allora (ln(kx))' = 1/x.

Pertanto, la derivata sarà sempre una funzione razionale frazionaria. Resta solo da equiparare questa derivata e il suo denominatore a zero, quindi risolvere le equazioni risultanti.

Per trovare il valore massimo o minimo di una funzione logaritmica, ricordiamo che il logaritmo naturale diventa un numero "normale" solo nei punti della forma e n . Ad esempio, ln 1 \u003d ln e 0 \u003d 0 è uno zero logaritmico e molto spesso la soluzione si riduce a esso. In altri casi è impossibile "togliere" il segno del logaritmo.

Compito. Trova il valore più piccolo della funzione y = x 2 − 3x + ln x sul segmento .

Consideriamo la derivata:

Troviamo gli zeri della derivata e il suo denominatore:
y' = 0 ⇒ 2x 2 − 3x + 1 = 0 ⇒ ... ⇒ x = 0,5; x = 1;
x = 0 - non c'è niente da decidere.

Dei tre numeri x = 0, x = 0,5 e x = 1, solo x = 1 si trova all'interno del segmento e il numero x = 0,5 è la sua estremità. Abbiamo:
y(0,5) = 0,5 2 − 3 0,5 + ln 0,5 = ln 0,5 − 1,25;
y(1) = 1 2 − 3 1 + log 1 = −2;
y(5) = 5 2 − 3 5 + ln 5 = 10 + ln 5.

Dei tre valori ottenuti, solo y = −2 non contiene il segno del logaritmo: questa sarà la risposta.

Compito. Trova il valore più grande della funzione y = ln(6x) − 6x + 4 sul segmento .

Calcoliamo la derivata:

Scopriamo quando la derivata o il suo denominatore è uguale a zero:
y' = 0 ⇒ 1 − 6x = 0 ⇒ x = 1/6;
x = 0 - già deciso.

Cancelliamo il numero x = 0, poiché si trova all'esterno del segmento. Consideriamo il valore della funzione agli estremi del segmento e nel punto x = 1/6:
y(0,1) = ln(6 0,1) − 6 0,1 + 4 = ln 0,6 + 3,4;
y(1/6) = log(6 1/6) − 6 1/6 + 4 = log 1 + 3 = 3;
y(3) = ln(6 3) − 6 3 + 4 = ln 18 − 14.

Ovviamente solo y = 3 può fungere da risposta: il resto dei valori contiene il segno del logaritmo e non può essere scritto nel foglio delle risposte.

Il punto è chiamato punto massimo (minimo). funzione , se esiste un tale intorno del punto che per tutto questo intorno vi è disuguaglianza ().

I punti massimo e minimo di una funzione si chiamano punti. estremo (Fig. 25).

Teorema 3.9 (condizione necessaria per l'esistenza dei punti estremi) . Nei punti critici di 1° specie anche la derivata della funzione

è zero o non esiste

I punti critici del 1° tipo sono solitamente chiamati semplicemente punti critici.

Vengono chiamati i punti critici in cui la derivata di una funzione è uguale a zero punti di stazionarietà . Vengono chiamati i punti critici in cui una funzione è continua ma non differenziabile punti d'angolo . Ad esempio, una funzione in un punto è continua, ma non ha una derivata, poiché in questo punto è possibile disegnare un numero infinito di tangenti sul grafico della funzione (Fig. 26). Questo caso può essere considerato come una conferma che l’affermazione contraria al Teorema 3.3 è falsa.

La funzione viene chiamata crescente su un intervallo , se su questo intervallo il valore maggiore dell'argomento corrisponde al valore maggiore della variabile , e calante se il valore maggiore dell'argomento corrisponde al valore minore della variabile.

Per ulteriori ricerche, i punti critici vengono posizionati su un asse numerico, che è diviso da questi punti in intervalli, dopo i quali vengono verificate le seguenti condizioni sufficienti.

Teorema 3.10 (condizione sufficiente affinché una funzione cresca e diminuisca). Se una funzione è differenziabile su un intervallo e la sua derivata è positiva (negativa), allora la funzione è crescente (diminuente) su questo intervallo

Teorema 3.11 (condizione sufficiente per l'esistenza dei punti estremi di una funzione). Se la funzione è continua e differenziabile in qualche intorno del punto critico, e passando per esso la derivata cambia segno da più a meno, allora il punto è un punto massimo; se da meno a più, il punto è il punto minimo della funzione

Quei punti critici della funzione per i quali la condizione sufficiente non è soddisfatta rimangono semplicemente punti critici del primo tipo.

I punti critici del 1° tipo, in cui la derivata non esiste, si dividono in due classi:

sono punti in cui la funzione è continua (quando per essi è soddisfatto il Teorema 3.11, la funzione ha un estremo “apice” in questi punti), questi sono angolo punti;

sono i punti in cui la funzione subisce una discontinuità (passano sempre nella classe dei punti critici di 2° specie).

Ma lo studio condotto in questo modo non fornisce una risposta a una domanda molto importante: come aumenta (diminuisce) la funzione: convessa o concava? La risposta a questa domanda è data da un ulteriore studio della funzione utilizzando la derivata seconda. Diamo alcune definizioni necessarie.

La funzione viene chiamata convesso (concavo) su un certo intervallo, se la tangente tracciata al grafico della funzione in ciascun punto di questo intervallo si trova sopra (sotto) il grafico della funzione.

I punti che separano le aree di convessità dalle aree di concavità di una funzione si chiamano sue punti di flesso (Fig. 27).

Teorema 3.12 (condizione necessaria per l'esistenza dei punti di flesso). Nei punti critici del 2° tipo la derivata seconda della funzione è zero oppure non esiste

Per ulteriori ricerche, i punti critici del 2° tipo vengono posti su un asse numerico, che è diviso da questi punti in intervalli, dopo i quali vengono verificate le seguenti condizioni sufficienti.

Teorema 3.13 (condizione sufficiente per la convessità e la concavità di una funzione). Se una funzione è differenziabile due volte su un certo intervallo e la sua derivata seconda è positiva (negativa), allora la funzione è concava (convessa) su questo intervallo

Quei punti critici della funzione per i quali la condizione sufficiente non è soddisfatta rimangono semplicemente punti critici del secondo tipo.

I punti critici del 2° tipo, in cui la derivata seconda non esiste, si dividono in due classi:

- punti in cui la funzione è continua, questi sono i cosiddetti punti di flesso "forte" - in tali punti si può tracciare un numero infinito di tangenti al grafico della funzione (Fig. 28);

sono i punti in cui la funzione subisce una discontinuità (nei punti di discontinuità di 2° specie il grafico della funzione ha un asintoto verticale).

Per l'enumerazione finale dei punti estremi e di flesso della funzione, è necessario trovare le loro ordinate, quindi scrivere i punti indicati con due coordinate.

Domande per l'autoesame.

1. Quali punti sono chiamati punti estremi (massimo e minimo) di una funzione?

2. Quale funzione si chiama aumento (diminuzione)?

3. Quali sono le condizioni necessarie e sufficienti per l'esistenza dei punti estremi di una funzione?

4. Qual è la condizione sufficiente per l'aumento (diminuzione) di una funzione?

5. Quali punti sono chiamati punti di flesso di una funzione?

6. Quale funzione è chiamata convessa (concava)?

7. Quali sono le condizioni necessarie e sufficienti per l'esistenza dei punti di flesso di una funzione?

8. Qual è la condizione sufficiente per la convessità (concavità) di una funzione?

Lo scopo della lezione: Insegnare come condurre uno studio delle funzioni; tracciarli.

Modulo: lezione di conversazione.

Metodi: dialoghi, supporti visivi e diapositive.

Attrezzatura: ICT, tabelle.

Durante le lezioni

I. Controllo i compiti.

Insegnante: - Ragazzi! Hai fatto i compiti "Punti critici di una funzione, massimi e minimi". Definire il punto critico di una funzione.

Studente: - Un punto critico è un punto interno al dominio di definizione, in cui la derivata o è uguale a zero oppure non esiste.

Insegnante: - Come trovare i punti critici?

Studente: - 1

) Trovare la derivata della funzione;

2) Risolvi l'equazione: f "(x) = 0. Le radici di questa equazione sono punti critici.

Insegnante: - Trovare i punti critici delle funzioni:

a) f(x)= 4 - 2x + 7x 2

b) f (x) \u003d 4x - x 3 / 3

a) 1) Trova la derivata di questa funzione:

f "(x)= (4 - 2x + 7x 2)" = -2+14x

2) Risolvi l'equazione f "(x) = 0<=>-2+14x=0<=>x=1/7

3) Poiché l'equazione f "(x) \u003d 0 ha una radice, allora questa funzione ha un punto critico x \u003d 1/7.

b) 1) Trova la derivata di questa funzione: f "(x) \u003d 4 - x 2

2) Risolvi l'equazione: f "(x) = 0<=>4 -x2 = 0<=>x=2 o x=-2

3) Poiché l'equazione f "(x) \u003d 0 ha due radici, allora questa funzione ha due punti critici x 1 \u003d 2 e x 2 \u003d -2.

II.lavoro orale.

Insegnante: - Ragazzi! Ripetiamo le domande principali necessarie per studiare un nuovo argomento. Per fare ciò, considera le tabelle con figure ( Allegato 1).

Specificare i punti in cui l'aumento della funzione viene sostituito da una diminuzione. Come si chiamano questi punti?

Studente: - Nella figura a) - il punto K è il punto massimo, nella figura b) - il punto M è il punto massimo.

Insegnante: - Quali sono i punti minimi della funzione.

Studente: - Punto K nelle figure c) ed) - il punto minimo della funzione.

Insegnante: - Quali punti possono essere gli estremi della funzione?

Studente: - I punti critici possono essere punti estremi di una funzione.

Insegnante: - Quali sono le condizioni necessarie che conosci?

Studente: - Esiste il teorema di Fermat. Condizione necessaria per un estremo: Se il punto x 0 è il punto estremo della funzione f e in questo punto esiste una derivata f ", allora è uguale a zero: f" (x) \u003d 0.

Docente: - Trovare i punti critici per la funzione:

a) f(x) = | x|

b) f(x) = 2x + | x|

Studente: - Considera la funzione f(x) = | x| ( applicazione 2). Questa funzione non ha derivata in 0. Quindi, 0 è un punto critico. Ovviamente la funzione ha minimo nel punto 0.

Studente: - Considera la funzione f(x) = 2x + | x| ( appendice 3). Il grafico mostra che al punto 0 questa funzione non ha estremi. A questo punto anche la funzione non ha derivata.

Infatti, se assumiamo che la funzione f abbia una derivata in 0, allora anche f(x) - 2x ha una derivata in 0. Ma f(x) - 2x = | x | e la funzione | x| nel punto 0 non è differenziabile, cioè siamo arrivati ​​ad una contraddizione.

Ciò significa che la funzione f nel punto 0 non ha derivata.

Insegnante: - Dal teorema di Fermat consegue che quando si trovano i punti estremi, è necessario trovare i punti critici. Ma dagli esempi considerati è chiaro che affinché questo punto critico sia un punto estremo, sono necessarie alcune condizioni aggiuntive.

Quali sono le condizioni sufficienti per l'esistenza di un estremo in un punto che conosci?

Alunno: - Segno della funzione massima: Se la funzione f è continua nel punto x 0, e f "(x)> 0 sull'intervallo (a; x 0) e f "(x)<0 на интервале (х 0 ; в), то точка х 0 является точкой максимума функции f.

Cioè, se nel punto x 0 la derivata cambia segno da più a meno, allora x 0 è il punto massimo.

Alunno: - Segno di minimo: Se la funzione f è continua nel punto x 0, e f "(x)<0 на интервале (а;х 0) и f "(x) >0 sull'intervallo (x 0 ; c), allora il punto x 0 è il punto di minimo della funzione f.

Cioè, se nel punto x 0 la derivata cambia segno da meno a più, allora x 0 è il punto di minimo.

Insegnante: - E quale algoritmo conosci per trovare i punti estremi di una funzione.

Lo studente spiega l'algoritmo per studiare la funzione f per un estremo utilizzando la derivata ( allegato 4) e trova i punti estremi della funzione:

f (x) \u003d x 4 -2x 2

D (f) =IR e f è continua su tutta la retta reale, come un'intera funzione razionale.

2. f "(x) \u003d 4x 3 -4x \u003d 4x (x + 1) (x-1).

3.f"(x)=0<=>x \u003d -1 Vx \u003d 0 Vx \u003d 1.

Fig.1 (segni f ")

Poiché f è continua nei punti critici, dalla Figura 1 ( allegato 5) si vede che -1 e 1 sono i punti di minimo, e 0 è il punto di massimo della funzione f.

f min \u003d f (-1) \u003d f (1) \u003d -1, f max \u003d f (0) \u003d 0.

Insegnante: - Ragazzi! Ricordiamo l'algoritmo per trovare gli intervalli di monotonicità della funzione f.

Lo studente ricorda l'algoritmo per trovare gli intervalli di monotonicità della funzione f ( allegato 6).

Insegnante: - Trova gli intervalli di aumento e diminuzione della funzione f dati dalla formula

f (x) \u003d x 3 -12x

Soluzione:

1. Poiché f(x) è un polinomio, allora D (f) =IR.

2. La funzione f è differenziabile sull'intera linea reale e f "(x) \u003d 3x 2 -12 \u003d 3 (x + 2) (x-2).

3. Solo gli zeri di f "(x) possono essere punti critici della funzione f.

f"(x)=0<=>x \u003d -2Vx \u003d 2.

D (f) \ (-2; 2) \u003d (-; -2) U (-2; 2) U (2; +).

Fig.2 (segni f ").

Trova i domini di definizione e i valori della funzione data f.

Scopri se la funzione ha caratteristiche che ne facilitano lo studio, ovvero se è la funzione f:

a) pari o dispari;

b) periodico.

3. Calcola le coordinate dei punti di intersezione del grafico con gli assi delle coordinate.

4. Trova gli intervalli di costanza della funzione f.

5. Scopri su quali intervalli la funzione f aumenta e su quali diminuisce.

6. Trova i punti estremi (massimo o minimo) e calcola i valori di f in questi punti.

7. Studiare il comportamento della funzione f nell'intorno di punti caratteristici che non rientrano nel dominio di definizione.

8. Rappresentare graficamente la funzione.

Questo diagramma è illustrativo.

Considerando tutto quanto sopra, esaminiamo la funzione: f (x) \u003d 3x 5 -5x 3 +2 e costruiamo il suo grafico.

Facciamo la ricerca come segue:

D (f ") = IR, poiché f (x) è un polinomio.

La funzione f non è né pari né dispari, perché

f (-x)= 3(-x) 5 -5(-x) 3 +2 = -3x 5 +5x 3 +2= -(3x 5 -5x 3 -2) f(x)

Trova le coordinate dei punti di intersezione del grafico con gli assi delle coordinate:

a) con l'asse 0X, per questo risolviamo l'equazione: 3x 5 -5x 3 +2 = 0.

Il metodo di selezione può trovare una delle radici (x = 1). Altre radici possono essere trovate solo approssimativamente. Pertanto, per questa funzione, non troveremo i restanti punti di intersezione del grafico con l'asse delle ascisse e gli intervalli di segno costante.

b) con asse 0Y: f(0)=2

Punto A (0; 2) - il punto di intersezione del grafico della funzione con l'asse 0Y.

Abbiamo notato che non troveremo intervalli di costanza di segno.

Trova gli intervalli di aumento e diminuzione della funzione

a) f "(x) \u003d 15x 4 -15x 2 \u003d 15x 2 (x 2 -1)

D (f ") \u003d IR, quindi non ci sono punti critici di cui f "(x) non esiste.

b) f "(x) \u003d 0 se x 2 (x 2 -1) \u003d 0<=>x = -1 V x = 0 V x = 1.

c) Otteniamo tre punti critici, dividono la linea delle coordinate in quattro intervalli. Determiniamo il segno della derivata su questi intervalli:

Fig.3 (segni f ")

IV. Correzione di un nuovo argomento. Risoluzione dei problemi.

Insegnante: - Esplora la funzione e costruisci il suo grafico: f (x) \u003d x 4 -2x 2 -3.

Studente: - 1) D (f) =R.

2) f (-x) \u003d (-x) 4 -2 (-x) 2 -3 \u003d x 4 -2x 2 -3; f(-x)= f(x),

quindi la funzione f è pari. Può essere studiato nell'intervallo in cui la funzione aumenta da - a -4, pertanto l'equazione f (x) \u003d 0 non ha radici su questo intervallo.

b) Nell'intervallo [-1; 2] anche l'equazione non ha radici, poiché su questo intervallo la funzione diminuisce da -4 a -31.

c) Sull'intervallo e diminuisce su [-∞;-1].

Punti estremi: x min = -1

Estremi della funzione: y min =y(-1)=1-2= -1

Capitolo III. Ricerca funzionale.

3.1. Schema generale per lo studio delle funzioni.

Quando si esamina una funzione, è necessario conoscere lo schema generale di ricerca:

1) D(y) – dominio di definizione (intervallo della variabile x)

2) E(y) – area del valore x (intervallo della variabile y)

3) Tipo di funzione: funzione pari, dispari, periodica o generale.

4) Punti di intersezione del grafico della funzione con gli assi Ohi Oy (se possibile).

5) Intervalli di costanza del segno:

a) la funzione assume un valore positivo: f(x)>0

b) valore negativo: f(x)<0.

6) Intervalli di monotonicità della funzione:

a) aumentare;

b) diminuzione;

c) costanza (f=const).

7) Punti estremi (punteggio minimo e massimo)

8) Funzione estremi (valore della funzione nei punti minimo e massimo)

9) Punti aggiuntivi.

Possono essere presi per tracciare la funzione in modo più accurato.

Va notato che gli estremi della funzione f non sempre coincidono con i valori massimo e minimo della funzione.

3.2. Segno di funzioni crescenti e decrescenti.

Se costruisci un grafico di una funzione utilizzando alcuni dei suoi punti scelti arbitrariamente, collegandoli con una linea morbida, quindi anche con un numero molto elevato di punti selezionati casualmente, potrebbe risultare che il grafico costruito in questo modo sarà molto diverso dal grafico di una data funzione.

Se, studiando una funzione, usiamo la derivata e troviamo i cosiddetti punti di "riferimento", cioè punti di interruzione, punti di massimo e minimo, intervalli di monotonicità della funzione, quindi anche con un numero limitato di tali punti di “riferimento” otterremo un'idea corretta del grafico della funzione.

Prima di passare agli esempi, fornirò le definizioni e i teoremi necessari.

Definizione di monotonicità di una funzione su un intervallo La funzione y \u003d f (x) viene chiamata crescente nell'intervallo, se per qualsiasi punto x 1 e x 2 di questo intervallo dalla condizione x 1<х 2 следует, что f(x 1)f(x 2), allora la funzione si dice decrescente su questo intervallo.

Un criterio sufficiente per la monotonicità di una funzione in un intervallo. Teorema: se una funzione ha una derivata positiva (negativa) in ogni punto di un intervallo, allora la funzione aumenta (diminuisce) in questo intervallo.

Questo teorema è accettato nei libri di testo scolastici senza dimostrazione.

L'interpretazione geometrica del teorema è molto semplice, se ricordiamo che f '(x) \u003d tgα, α è la pendenza della tangente al grafico della funzione in un dato punto x. Se, ad esempio, f ' (x)> 0 in tutti i punti di un certo intervallo, allora la tangente al grafico con l'asse delle ascisse forma angoli acuti, il che significa che anche f (x) aumenta con x. Se f' (x)<0, то касательная с осью абсцисс образуют тупой угол, а значит, с ростом х функция f(x) убывает. Поскольку эти рассуждения основаны лишь на наглядных геометрических представлениях, они не являются доказательством теоремы.

3.3. Punti critici della funzione, massimi e minimi.

Determinazione dei punti estremi di una funzione . Sia x 0 un punto interno al dominio della funzione f(x). Allora, se esiste un tale intorno δ ] x 0 - δ, x 0 + δ [ punti x 0 , che per tutti gli x di questo intorno la disuguaglianza f(x)≤f(x 0) è soddisfatta (la disuguaglianza f (x)≥f (x 0)), il punto x 0 è chiamato punto massimo (punto minimo) di questa funzione.

I punti massimo-minimo sono punti interni al dominio della funzione.

Un criterio necessario per l'esistenza di un estremo di una funzione differenziabile .

Il teorema di Fermat.

Se x 0 è un punto estremo della funzione f (x) e in questo punto esiste la derivata, allora è uguale a zero: f '(x 0) \u003d 0.

Questo teorema non è una condizione sufficiente per l'esistenza di un estremo di una funzione differenziabile: se in un punto x 0 la derivata si annulla, allora non ne consegue ancora che nel punto x 0 la funzione abbia un estremo.

Definizione dei punti critici di una funzione . I punti interni del dominio di una funzione, in cui la sua derivata è uguale a zero o non esiste, sono detti punti critici della funzione.

Condizioni sufficienti per l'esistenza di un estremo .

Teorema 1. Se la funzione f (x) è continua nel punto x 0, f '(x) > 0 sull'intervallo e f '(x)<0 на интервале , то х 0 является точкой максимума функции f(x).

Teorema 2. Se la funzione f(x) è continua nel punto x 0, f'(x)<0 на интервале и f ‘(x)>0 sull'intervallo, allora x 0 è il punto di minimo della funzione f(x).

Per trovare i punti estremi di una funzione è necessario trovarne i punti critici e per ciascuno di essi verificare il soddisfacimento di sufficienti condizioni estreme.

3.4. I valori più grandi e più piccoli della funzione.

Regole per trovare i valori più grandi e più piccoli delle funzioni nell'intervallo. Per trovare i valori più grandi e più piccoli di una funzione differenziabile in un certo intervallo, è necessario trovare tutti i punti critici che si trovano all'interno dell'intervallo, calcolare i valori della funzione in questi punti e alle estremità di l'intervallo, e scegli il più grande e il più piccolo tra tutti i valori della funzione così ottenuti.

Capitolo IV. Esempi di applicazione della derivata allo studio di una funzione.

Esempio 11. Esplora la funzione y=x 3 +6x 2 +9x e costruisci un grafico.

2) Definire il tipo di funzione:

y(-x)=(-x) 3 +6(-x) 2 +9(-x)=-x+6x 2 -9x funzione generale.

x=0 oppure x2 +6x+9=0

D=0, l'equazione ha una radice.

(0;0) e (-3;0) - punti di intersezione con l'asse x.

y'=(x 3 +6x 2 +9x)'=3x 2 +12x+9

y'=0, cioè 3x 2 +12x+9=0 riduci di 3

D>0, l'equazione ha 2 radici.

x 1,2 \u003d (-b±√D) / 2a, x 1 \u003d (-4 + 2) / 2, x 2 \u003d (-4-2) / 2

0
-4

x=-4, y'=3*16-48+9=9>0

x=-2, y’=12-24+9=-3<0

x=0, y'=0+0+9=9>0

7) Trova x min e x max:

8) Trova gli estremi della funzione:

ymin=y(-1)=-1+6-9=-4

ymax=y(-3)=-27+54-27=0

9) Costruiamo un grafico della funzione:

10) Punti aggiuntivi:

y(-4)=-64+96-36=-4

Esempio 12. Esplora la funzione y=x 2 /(x-2) e costruisci un grafico

y=x2 /(x-2)=x+2+4/(x-2)

Troviamo gli asintoti della funzione:

x≠ 2, x=2 – asintoto verticale

y=x+2 è l'asintoto obliquo, perché

Troviamo il dominio di definizione.

2) Definiamo il tipo di funzione.

y(-x)=(-x) 2 /(-x-2)=x 2 /(-x-2), funzione generale.

3) Trovare i punti di intersezione con gli assi.

Oy: x=0, y=0 (0;0) – punto di intersezione con l'asse y.

x=0 oppure x=2 (2;0) – punto di intersezione con l'asse x

4) Trova la derivata della funzione:

y'=(2x(x-2)-x 2)/(x-2) 2 =(2x 2 -4x-x 2)/(x-2) 2 =(x(x-4))/(x -2) 2 \u003d (x 2 -4x) / (x-2) 2

5) Definire i punti critici:

x2-4x=0x(x-4)=0

y'=0, (x2 -4x)/(x-2)2 =0<=> <=>

(x-2) 2 ≠ 0 x≠ 2

x 2 -4x=0 e (x-2) 2 ≠ 0, cioè x≠ 2

6) Indichiamo i punti critici sulla linea delle coordinate e determiniamo il segno della funzione.

0 8

x=-1, y’=(1+4)/9=5/9>0

x=1, y’=(1-4)/1=-3<0

x=3, y’=(9-12)/1=-3<0

x=5, y’=(25-20)/9=5/9>0

7) Trovare i punti di minimo e massimo della funzione:

8) Trova gli estremi della funzione:

ymin=y(4)=16/2=8

9) Costruiamo un grafico della funzione:

10) Punti aggiuntivi:

y(-3)=9/-5=-1,8 y(3)=9/1=9

y(1)=1/-1=-1 y(6)=36/4=9

Esempio 13 Esplora la funzione y=(6(x-1))/(x 2 +3) e costruisci un grafico. 1) Trova il dominio della funzione:

2) Definire il tipo di funzione:

y(-x)=(6(-x-1))/(x 2 +3)=-(6(x+1))/(x 2 -3) è una funzione generale.

3) Trovare i punti di intersezione con gli assi:

O y: x=0, y=(6(0-1))/(0+3)=-2, (0;-2) – punto di intersezione con l'asse y.

(6(x-1))/(x2 +3)=0

Ox: y=0,<=>

4) Trova la derivata della funzione:

y'=(6(x-1)/(x 2 +3))'=6(x 2 +3-2x 2 +2x)/(x 2 +2) 2 =-6(x+1)(x -3)/(x2+3)2

5) Definire i punti critici:

y'=0, cioè -6(x+1)(x-3)/(x2+3)2 =0

y’=0, se x 1 =-1 oppure x 2 =3, allora x=-1 e x=3, punti critici.

6) Indichiamo i punti critici sulla linea delle coordinate e determiniamo il segno della funzione:

-3 2

x=-2, y'=-6(-2+1)(-2-3)/(4+3) 2 =-30/49<0

x=0, y’=-6(0+1)(0-3)/(0+3) 2 =2>0

x=4, y'=-6(4+1)(4-3)/(16+3) 2=-30/361<0

7) Trova i punti minimo e massimo:

8) Trova gli estremi della funzione:

ymin =y(-1)=(6(-1-1))/(1+3)=-12/4=-3

ymax =y(3)=(6(3-1))/(9+3)=12/12=1

9) Costruiamo un grafico della funzione:

10) Punti aggiuntivi:

y(-3)=(6(-3-1))/(9+3)=-24/12=-2

y(6)=(6(6-1))/(36+3)=30/39=10/13≈ 0,77

Esempio 14 Esplora la funzione y=xlnx e costruisci il suo grafico:

1) Trova il dominio della funzione:

D(y)=R + (solo valori positivi)

2) Definire il tipo di funzione:

y(-x)=-xlnx - forma generale.

3) Trovare i punti di intersezione con gli assi:

O y , ma x≠ 0, quindi non ci sono punti di intersezione con l'asse y.

Bue: y=0 cioè xlnx=0

x=0 o lnx=0

(1;0) - punto di intersezione con l'asse x

4) Trova la derivata della funzione:

y'=x' ln x + x(ln x)'=ln x +1

5) Definire i punti critici:

y'=0, cioè lnx +1=0

y'=0 , se x=1/e , allora x=1/e è un punto critico.

6) Indichiamo i punti critici sulla linea delle coordinate e determiniamo il segno della funzione:

1/e

x=1/(2e); y'=log(2e) -1 +1=1-ln(2e)=1-ln e=-ln 2<0

x=2e; y'=ln(2e)+1=ln 2+ln e+1=ln 2+2>0

7) 1/e è il punto di minimo della funzione.

8) Trova gli estremi della funzione:

y min \u003d y (1 / e) \u003d 1 / e ln e -1 \u003d -1 / e (≈ -0,4).

9) Costruiamo un grafico della funzione:

Conclusione.

Molti scienziati e filosofi hanno lavorato su questo argomento. Molti anni fa sono comparsi questi termini: funzione, grafico, studio della funzione, e sono sopravvissuti fino ai giorni nostri, acquisendo nuove funzionalità e caratteristiche.

Ho scelto questo argomento perché per me è stato molto interessante intraprendere questo percorso di ricerca sulla funzione. Mi sembra che molte persone sarebbero interessate a saperne di più sulla funzione, sulle sue proprietà e trasformazioni. Dopo aver realizzato questo saggio, ho sistematizzato le mie capacità e ho ricostituito il mio bagaglio di conoscenze su questo argomento.

Voglio consigliare a tutti di studiare questo argomento più approfonditamente.

Bibliografia.

1. Bashmakov, M.I. L'algebra e l'inizio dell'analisi - M.: Education, 1992.

2. Glaser, G.I. Storia della matematica a scuola - M.: Education, 1983.

3. Gusev, V.A. Matematica: materiali di riferimento - M.: Educazione, 1888.

4. Dorofeev, G.V. Manuale di matematica per i candidati alle università - M.: Nauka, 1974.

5. Zorin, V.V. Manuale di matematica per i candidati alle università - M.: Scuola superiore, 1980.

6. Kolmogorov A.N. L'algebra e gli inizi dell'analisi.- M.: Enlightenment, 1993.