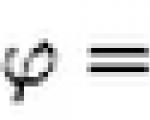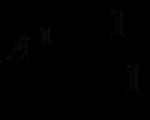Come scrivere l'equazione delle oscillazioni armoniche. Oscillazioni armoniche e loro caratteristiche

Il tipo più semplice di vibrazioni sono vibrazioni armoniche- fluttuazioni in cui lo spostamento del punto oscillante dalla posizione di equilibrio cambia nel tempo secondo la legge del seno o del coseno.

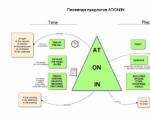
Quindi, con una rotazione uniforme della palla attorno alla circonferenza, la sua proiezione (ombra in raggi di luce paralleli) esegue un movimento oscillatorio armonico su uno schermo verticale (Fig. 1).

Lo spostamento dalla posizione di equilibrio durante le vibrazioni armoniche è descritto da un'equazione (chiamata legge cinematica del moto armonico) della forma:

dove x - spostamento - un valore che caratterizza la posizione del punto oscillante al tempo t rispetto alla posizione di equilibrio e misurato dalla distanza dalla posizione di equilibrio alla posizione del punto in un dato momento; A - ampiezza di oscillazione - lo spostamento massimo del corpo dalla posizione di equilibrio; T - periodo di oscillazione - il tempo di un'oscillazione completa; quelli. il più piccolo periodo di tempo dopo il quale si ripetono i valori delle quantità fisiche che caratterizzano l'oscillazione; - fase iniziale;

La fase dell'oscillazione al tempo t. La fase di oscillazione è un argomento di una funzione periodica che, per una data ampiezza di oscillazione, determina lo stato del sistema oscillatorio (spostamento, velocità, accelerazione) del corpo in qualsiasi momento.

Se nel momento iniziale il punto oscillante è spostato al massimo dalla posizione di equilibrio, allora , e lo spostamento del punto dalla posizione di equilibrio cambia secondo la legge

Se il punto oscillante si trova in una posizione di equilibrio stabile, allora lo spostamento del punto dalla posizione di equilibrio cambia secondo la legge

Il valore V, reciproco del periodo e pari al numero di oscillazioni complete eseguite in 1 s, è chiamato frequenza di oscillazione:

Se nel tempo t il corpo compie N oscillazioni complete, allora

il valore , che indica quante oscillazioni fa il corpo in s, si chiama frequenza ciclica (circolare)..

La legge cinematica del moto armonico può essere scritta come:

Graficamente, la dipendenza dello spostamento di un punto oscillante dal tempo è rappresentata da un coseno (o sinusoide).

La Figura 2, a mostra la dipendenza dal tempo dello spostamento del punto oscillante dalla posizione di equilibrio nel caso .

Scopriamo come cambia la velocità di un punto oscillante nel tempo. Per fare ciò, troviamo la derivata temporale di questa espressione:

dove è l'ampiezza della proiezione della velocità sull'asse x.

Questa formula mostra che durante le oscillazioni armoniche, anche la proiezione della velocità del corpo sull'asse x cambia secondo la legge armonica con la stessa frequenza, con un'ampiezza diversa, ed è in anticipo rispetto alla fase di miscelazione di (Fig. 2, b) .

Per scoprire la dipendenza dell'accelerazione, troviamo la derivata temporale della proiezione della velocità:

dove è l'ampiezza della proiezione dell'accelerazione sull'asse x.

Per le oscillazioni armoniche, la proiezione dell'accelerazione guida lo sfasamento di k (Fig. 2, c).

Allo stesso modo, puoi creare grafici delle dipendenze

Equazione delle onde armoniche

L'equazione dell'oscillazione armonica stabilisce la dipendenza delle coordinate del corpo dal tempo

Il grafico del coseno ha un valore massimo nel momento iniziale e il grafico del seno ha un valore zero nel momento iniziale. Se iniziamo a studiare l'oscillazione dalla posizione di equilibrio, l'oscillazione ripeterà la sinusoide. Se iniziamo a considerare l'oscillazione dalla posizione di massima deviazione, l'oscillazione descriverà il coseno. Oppure tale oscillazione può essere descritta dalla formula del seno con la fase iniziale.

Variazione di velocità e accelerazione durante l'oscillazione armonica

Non solo la coordinata del corpo cambia nel tempo secondo la legge del seno o del coseno. Ma anche quantità come la forza, la velocità e l’accelerazione cambiano in modo simile. La forza e l'accelerazione sono massime quando il corpo oscillante si trova nelle posizioni estreme in cui lo spostamento è massimo, e sono pari a zero quando il corpo passa per la posizione di equilibrio. La velocità, invece, nelle posizioni estreme è pari a zero, e quando il corpo supera la posizione di equilibrio raggiunge il suo valore massimo.

Se l'oscillazione è descritta secondo la legge del coseno

Se l'oscillazione è descritta secondo la legge del seno

Valori massimi di velocità e accelerazione

Dopo aver analizzato le equazioni di dipendenza v(t) e a(t), si può intuire che i valori massimi di velocità e accelerazione vengono presi quando il fattore trigonometrico è pari a 1 o -1. Determinato dalla formula

Vibrazioni meccaniche. Parametri di oscillazione. Vibrazioni armoniche.

esitazione Un processo viene chiamato ripetizione esatta o approssimativa a determinati intervalli.

Una caratteristica delle oscillazioni è la presenza obbligatoria di una posizione di equilibrio stabile sulla traiettoria, in cui la somma di tutte le forze che agiscono sul corpo è uguale a zero è chiamata posizione di equilibrio.

Un pendolo matematico è un punto materiale sospeso su un filo sottile, senza peso e inestensibile.

Parametri del moto oscillatorio.

1. Offset o coordinata (X) - deviazione dalla posizione di equilibrio in un dato

momento del tempo.	[X ]=M

2. Ampiezza ( xm) è la deviazione massima dalla posizione di equilibrio.

[ X M ]=M

3. Periodo di oscillazione ( T) è il tempo impiegato per un'oscillazione completa.

[T ]=C.

0 "style="margin-left:31.0pt;border-collapse:collapse">

Pendolo matematico

Pendolo a molla

M

https://pandia.ru/text/79/117/images/image006_26.gif" larghezza="134" altezza="57 src="> Frequenza (lineare) ( N ) – il numero di oscillazioni complete in 1 s.

[n]= Hz

5. Frequenza ciclica ( w ) – il numero di oscillazioni complete in 2p secondi, cioè circa 6,28 s.

w = 2pn ; [w]=0" style="margin-left:116.0pt;border-collapse:collapse">

https://pandia.ru/text/79/117/images/image012_9.jpg" larghezza="90" altezza="103">

L'ombra sullo schermo fluttua.

Equazione e grafico delle oscillazioni armoniche.

Vibrazioni armoniche - si tratta di oscillazioni in cui la coordinata cambia nel tempo secondo la legge del seno o del coseno.

https://pandia.ru/text/79/117/images/image014_7.jpg" larghezza="254" altezza="430 src="> X=XMpeccato(w T+j 0 )

X=XMcos(w T+j 0 )

x - coordinata,

Xm è l'ampiezza dell'oscillazione,

w è la frequenza ciclica,

peso+j 0 = j è la fase di oscillazione,

J 0 è la fase iniziale delle oscillazioni.

https://pandia.ru/text/79/117/images/image016_4.jpg" larghezza="247" altezza="335 src=">

I grafici sono diversi soltanto ampiezza

I grafici differiscono solo nel periodo (frequenza)

https://pandia.ru/text/79/117/images/image018_3.jpg" larghezza="204" altezza="90 src=">

Se l'ampiezza delle oscillazioni non cambia nel tempo si chiamano oscillazioni non smorzato.

Le vibrazioni naturali non tengono conto dell'attrito, l'energia meccanica totale del sistema rimane costante: E a + E n = E pelliccia = cost.

Le oscillazioni naturali non sono smorzate.

Nelle oscillazioni forzate l'energia fornita continuamente o periodicamente da una fonte esterna compensa le perdite derivanti dal lavoro della forza di attrito e le oscillazioni possono essere non smorzate.

L'energia cinetica e potenziale del corpo durante le vibrazioni si trasmettono l'una nell'altra. Quando la deviazione del sistema dalla posizione di equilibrio è massima, l'energia potenziale è massima e l'energia cinetica è zero. Quando si passa per la posizione di equilibrio, viceversa.

La frequenza delle oscillazioni libere è determinata dai parametri del sistema oscillatorio.

La frequenza delle oscillazioni forzate è determinata dalla frequenza della forza esterna. L'ampiezza delle oscillazioni forzate dipende anche dalla forza esterna.

Risonante C

Risonanza chiamato un forte aumento dell'ampiezza delle oscillazioni forzate quando la frequenza dell'azione di una forza esterna coincide con la frequenza delle oscillazioni naturali del sistema.

Quando la frequenza w della variazione della forza coincide con la frequenza naturale w0 delle oscillazioni del sistema, la forza compie un lavoro positivo durante tutto il periodo, aumentando l'ampiezza delle oscillazioni del corpo. A qualsiasi altra frequenza, durante una parte del periodo, la forza compie un lavoro positivo e durante l'altra parte del periodo un lavoro negativo.

In risonanza, un aumento dell'ampiezza dell'oscillazione può portare alla distruzione del sistema.

Nel 1905, sotto gli zoccoli di uno squadrone di cavalleria delle guardie, il ponte egiziano sul fiume Fontanka a San Pietroburgo crollò.

Autooscillazioni.

Le auto-oscillazioni sono chiamate oscillazioni non smorzate nel sistema, supportate da fonti di energia interne in assenza di cambiamenti di forza esterni.

A differenza delle oscillazioni forzate, la frequenza e l'ampiezza delle auto-oscillazioni sono determinate dalle proprietà del sistema oscillatorio stesso.

Le auto-oscillazioni differiscono dalle oscillazioni libere per l'indipendenza dell'ampiezza dal tempo e dall'impatto iniziale a breve termine che eccita il processo di oscillazioni. Un sistema auto-oscillante può solitamente essere suddiviso in tre elementi:

1) sistema oscillatorio;

2) fonte di energia;

3) un dispositivo di feedback che regola il flusso di energia da una sorgente in un sistema oscillatorio.

L'energia proveniente dalla sorgente in un periodo è uguale all'energia persa nel sistema oscillatorio nello stesso tempo.

Abbiamo considerato diversi sistemi fisicamente completamente diversi e ci siamo assicurati che le equazioni del moto fossero ridotte alla stessa forma

Le differenze tra i sistemi fisici si manifestano solo in diverse definizioni della quantità e in un diverso senso fisico della variabile X: può essere una coordinata, un angolo, una carica, una corrente, ecc. Si noti che in questo caso, come segue dalla struttura stessa dell'equazione (1.18), la quantità ha sempre la dimensione dell'inverso del tempo.

L'equazione (1.18) descrive il cosiddetto vibrazioni armoniche.

L'equazione delle oscillazioni armoniche (1.18) è un'equazione differenziale lineare del secondo ordine (poiché contiene la derivata seconda della variabile X). La linearità dell'equazione significa questo

se qualsiasi funzione x(t)è una soluzione a questa equazione, quindi la funzione Cx(t) sarà anche la sua soluzione ( Cè una costante arbitraria);

se funzioni x1 (t) E x2(t) sono soluzioni di questa equazione, quindi la loro somma x1(t) + x2(t) sarà anche una soluzione della stessa equazione.

Viene inoltre dimostrato un teorema matematico secondo il quale un'equazione del secondo ordine ha due soluzioni indipendenti. Tutte le altre soluzioni, secondo le proprietà della linearità, possono essere ottenute come loro combinazioni lineari. È facile verificare mediante derivazione diretta che le funzioni indipendenti e soddisfano l'equazione (1.18). Quindi la soluzione generale di questa equazione è:

Dove C1,C2 sono costanti arbitrarie. Questa soluzione può essere presentata anche in un'altra forma. Introduciamo la quantità

e definire l'angolo come:

Allora la soluzione generale (1.19) si scrive come:

Secondo le formule trigonometriche, l'espressione tra parentesi è

Finalmente arriviamo a soluzione generale dell'equazione delle oscillazioni armoniche COME:

Valore non negativo UN chiamato ampiezza di oscillazione, - la fase iniziale dell'oscillazione. L'intero argomento del coseno - la combinazione - viene chiamato fase di oscillazione.

Le espressioni (1.19) e (1.23) sono perfettamente equivalenti, quindi possiamo usarle entrambe per ragioni di semplicità. Entrambe le soluzioni sono funzioni periodiche del tempo. In effetti, il seno e il coseno sono periodici con un punto . Pertanto, i vari stati di un sistema che esegue oscillazioni armoniche si ripetono dopo un periodo di tempo T*, per cui la fase di oscillazione riceve un incremento multiplo di :

Ne consegue quindi che

Il meno di questi tempi

chiamato periodo di oscillazione (Fig. 1.8), a - suo circolare (ciclico) frequenza.

Riso. 1.8.

Usano anche frequenza esitazione

Di conseguenza, la frequenza circolare è uguale al numero di oscillazioni per secondi.

Quindi, se il sistema in time T caratterizzato dal valore della variabile x(t), quindi, lo stesso valore, la variabile assumerà dopo un periodo di tempo (Fig. 1.9), cioè

Lo stesso valore, ovviamente, verrà ripetuto dopo un po'. 2T, ZT eccetera.

Riso. 1.9. Periodo di oscillazione

La soluzione generale include due costanti arbitrarie ( C1, C2 O UN, UN), i cui valori dovrebbero essere determinati da due condizioni iniziali. Solitamente (anche se non necessariamente) il loro ruolo è giocato dai valori iniziali della variabile x(0) e il suo derivato.

Facciamo un esempio. Sia la soluzione (1.19) dell'equazione delle oscillazioni armoniche a descrivere il movimento di un pendolo a molla. I valori delle costanti arbitrarie dipendono dal modo in cui abbiamo portato il pendolo fuori equilibrio. Ad esempio, abbiamo allontanato la molla e ha rilasciato la palla senza velocità iniziale. In questo caso

Sostituendo t = 0 nella (1.19) troviamo il valore della costante Dalle 2

La soluzione appare quindi:

La velocità del carico si trova per differenziazione rispetto al tempo

Sostituendo qui T = 0, trova la costante Dall'1:

Finalmente

Confrontando con la (1.23), si trova che è l'ampiezza dell'oscillazione e la sua fase iniziale è pari a zero: .

Ora portiamo il pendolo fuori equilibrio in un altro modo. Colpiamo il carico, in modo che acquisisca una velocità iniziale, ma praticamente non si muova durante l'impatto. Abbiamo allora altre condizioni iniziali:

la nostra soluzione assomiglia

La velocità del carico cambierà secondo la legge:

Mettiamolo qui:

Argomenti del codificatore USE: oscillazioni armoniche; ampiezza, periodo, frequenza, fase delle oscillazioni; vibrazioni libere, vibrazioni forzate, risonanza.

fluttuazioni sono cambiamenti nello stato del sistema che si ripetono nel tempo. Il concetto di oscillazioni copre una gamma molto ampia di fenomeni.

Vibrazioni di sistemi meccanici, o vibrazioni meccaniche- si tratta di un movimento meccanico di un corpo o di un sistema di corpi, che ha ripetibilità nel tempo e avviene in prossimità della posizione di equilibrio. posizione di equilibrio Questo è lo stato del sistema in cui può rimanere per un tempo arbitrariamente lungo senza subire influenze esterne.

Ad esempio, se il pendolo viene deviato e rilasciato, inizieranno le oscillazioni. La posizione di equilibrio è la posizione del pendolo in assenza di deflessione. In questa posizione il pendolo, se lasciato intatto, può rimanere indefinitamente. Quando il pendolo oscilla, passa molte volte la posizione di equilibrio.

Immediatamente dopo che il pendolo deviato è stato rilasciato, ha iniziato a muoversi, ha superato la posizione di equilibrio, ha raggiunto la posizione estrema opposta, si è fermato per un momento, si è mosso nella direzione opposta, ha superato di nuovo la posizione di equilibrio ed è tornato indietro. È successa una cosa pieno svolgimento. Questo processo verrà poi ripetuto periodicamente.

Ampiezza delle oscillazioni del corpo è l'entità della sua massima deviazione dalla posizione di equilibrio.

Periodo di oscillazione è il tempo per un'oscillazione completa. Possiamo dire che durante il periodo il corpo percorre un percorso di quattro ampiezze.

Frequenza di oscillazione è il reciproco del periodo: . La frequenza si misura in hertz (Hz) e indica quante oscillazioni complete si verificano in un secondo.

Vibrazioni armoniche.

Assumeremo che la posizione del corpo oscillante sia determinata da un'unica coordinata. Il valore corrisponde alla posizione di equilibrio. Il compito principale della meccanica in questo caso è trovare una funzione che dia le coordinate del corpo in qualsiasi momento.

Per la descrizione matematica delle oscillazioni è naturale utilizzare funzioni periodiche. Esistono molte funzioni simili, ma due di esse, seno e coseno, sono le più importanti. Hanno molte buone proprietà e sono strettamente correlati a una vasta gamma di fenomeni fisici.

Poiché le funzioni seno e coseno si ottengono l'una dall'altra spostando l'argomento di , possiamo limitarci a una sola di esse. Per chiarezza, useremo il coseno.

Vibrazioni armoniche sono oscillazioni la cui coordinata dipende dal tempo secondo la legge armonica:

(1)

Scopriamo il significato delle quantità incluse in questa formula.

Un valore positivo è il valore di coordinata più grande in valore assoluto (poiché il valore massimo del modulo del coseno è uguale a uno), cioè la deviazione più grande dalla posizione di equilibrio. Pertanto - l'ampiezza delle oscillazioni.

Viene chiamato l'argomento del coseno fase fluttuazioni. Il valore pari al valore della fase a è chiamato fase iniziale. La fase iniziale corrisponde alla coordinata iniziale del corpo: .

Il valore viene chiamato frequenza ciclica. Troviamo la sua connessione con il periodo di oscillazione e la frequenza. Un'oscillazione completa corrisponde ad un incremento di fase pari a radianti: , da cui

(2)

(3)

La frequenza ciclica si misura in rad/s (radianti al secondo).

In accordo con le espressioni (2) e (3), otteniamo altre due forme di registrazione della legge armonica (1):

Il grafico della funzione (1), che esprime la dipendenza della coordinata dal tempo durante le oscillazioni armoniche, è mostrato in Fig. 1 .

La legge armonica della forma (1) è di natura più generale. Risponde, ad esempio, alla situazione in cui due azioni iniziali sono state eseguite contemporaneamente con il pendolo: lo hanno deviato di una certa quantità e gli hanno dato una certa velocità iniziale. Esistono due importanti casi speciali in cui una di queste azioni non è stata eseguita.

Lasciamo che il pendolo venga respinto, ma la velocità iniziale non sia stata segnalata (sono stati rilasciati senza la velocità iniziale). È chiaro che in questo caso , quindi possiamo mettere . Otteniamo la legge del coseno:

Il grafico delle oscillazioni armoniche in questo caso è mostrato in Fig. 2.

Riso. 2. Legge del coseno

Supponiamo ora che il pendolo non sia stato deviato, ma che la velocità iniziale gli sia stata trasmessa dalla posizione di equilibrio mediante un colpo. In questo caso, quindi puoi mettere . Otteniamo la legge del seno:

Il programma di fluttuazioni è presentato in fico. 3 .

Riso. 3. Legge del seno

L'equazione delle oscillazioni armoniche.

Torniamo alla legge armonica generale (1) . Differenziamo questa equazione:

. (4)

Ora differenziamo l'uguaglianza risultante (4):

. (5)

Confrontiamo l'espressione (1) per la coordinata e l'espressione (5) per la proiezione dell'accelerazione. Vediamo che la proiezione dell'accelerazione differisce dalle coordinate solo per il fattore:

. (6)

Questo rapporto è chiamato equazione delle oscillazioni armoniche. Può anche essere riscritto in questa forma:

. (7)

Da un punto di vista matematico, l'equazione (7) lo è equazione differenziale. Le soluzioni delle equazioni differenziali sono funzioni (e non numeri, come nell'algebra ordinaria).
Quindi, possiamo dimostrare che:

La soluzione dell'equazione (7) è qualsiasi funzione della forma (1) con arbitrario ;

Nessun'altra funzione è una soluzione a questa equazione.

In altre parole, le relazioni (6), (7) descrivono oscillazioni armoniche con frequenza ciclica e solo esse. Due costanti sono determinate dalle condizioni iniziali: dai valori iniziali delle coordinate e della velocità.

Pendolo a molla.

Pendolo a molla è un carico fissato su una molla, capace di oscillare in direzione orizzontale o verticale.

Troviamo il periodo delle piccole oscillazioni orizzontali del pendolo a molla (Fig. 4). Le oscillazioni saranno piccole se l'entità della deformazione della molla è molto inferiore alle sue dimensioni. Per piccole deformazioni possiamo usare la legge di Hooke. Ciò farà sì che le oscillazioni siano armoniche.

Trascuriamo l'attrito. La massa ha una massa e la costante della molla è .

La coordinata corrisponde alla posizione di equilibrio in cui la molla non è deformata. Pertanto, l'entità della deformazione della molla è uguale al modulo della coordinata del carico.

Riso. 4. Pendolo a molla

Nella direzione orizzontale, sul carico agisce solo la forza elastica della molla. La seconda legge di Newton per il carico nella proiezione sull'asse è:

. (8)

Se (il carico viene spostato a destra, come in figura), la forza elastica è diretta nella direzione opposta e . Viceversa, se , allora . I segni e sono sempre opposti, quindi la legge di Hooke può essere scritta come segue:

Allora la relazione (8) assume la forma:

Abbiamo ottenuto un'equazione delle oscillazioni armoniche della forma (6) , in cui

La frequenza ciclica di oscillazione di un pendolo a molla è quindi pari a:

. (9)

Da qui e dal rapporto troviamo il periodo delle oscillazioni orizzontali del pendolo a molla:

. (10)

Se appendi un peso a una molla, ottieni un pendolo a molla che oscilla in direzione verticale. Si può dimostrare che in questo caso la formula (10) vale anche per il periodo di oscillazione.

Pendolo matematico.

Pendolo matematico - questo è un piccolo corpo sospeso su un filo inestensibile senza peso (Fig. 5). Un pendolo matematico può oscillare su un piano verticale nel campo di gravità.

Riso. 5. Pendolo matematico

Troviamo il periodo delle piccole oscillazioni del pendolo matematico. La lunghezza del filo è . Si trascura la resistenza dell’aria.

Scriviamo la seconda legge di Newton per il pendolo:

e proiettarlo sull'asse:

Se il pendolo occupa una posizione come in figura (cioè), allora:

Se il pendolo si trova dall'altra parte della posizione di equilibrio (cioè), allora:

Quindi, per qualsiasi posizione del pendolo abbiamo:

. (11)

Quando il pendolo è fermo nella posizione di equilibrio, l’uguaglianza è soddisfatta. Per piccole oscillazioni, quando le deviazioni del pendolo dalla posizione di equilibrio sono piccole (rispetto alla lunghezza del filo), l'uguaglianza approssimativa è soddisfatta. Usiamolo nella formula (11):

Questa è un'equazione delle oscillazioni armoniche della forma (6) in cui

Pertanto, la frequenza ciclica di oscillazione di un pendolo matematico è pari a:

. (12)

Da qui il periodo di oscillazione del pendolo matematico:

. (13)

Si prega di notare che la formula (13) non include la massa del carico. A differenza del pendolo a molla, il periodo di oscillazione di un pendolo matematico non dipende dalla sua massa.

Vibrazioni libere e forzate.

Si dice che il sistema vibrazioni libere, se una volta viene tolto dalla posizione di equilibrio e successivamente lasciato a se stesso. Nessun periodico esterno
Allo stesso tempo, il sistema non subisce alcun impatto e non ci sono fonti interne di energia che supportino le oscillazioni nel sistema.

Le oscillazioni della molla e dei pendoli matematici sopra considerate sono esempi di oscillazioni libere.

Viene chiamata la frequenza alla quale si verificano le vibrazioni libere frequenza naturale sistema oscillatorio. Quindi, le formule (9) e (12) danno le frequenze di oscillazione naturali (cicliche) dei pendoli a molla e matematici.

In una situazione idealizzata in assenza di attrito, le oscillazioni libere non sono smorzate, cioè hanno un'ampiezza costante e durano indefinitamente. Nei sistemi oscillatori reali l'attrito è sempre presente, per cui le oscillazioni libere si smorzano gradualmente (Fig. 6).

Vibrazioni forzate- si tratta di oscillazioni effettuate dal sistema sotto l'influenza di una forza esterna, che cambia periodicamente nel tempo (la cosiddetta forza motrice).

Supponiamo che la frequenza di oscillazione naturale del sistema sia , e che la forza motrice dipenda dal tempo secondo la legge armonica:

Da qualche tempo si instaurano oscillazioni forzate: il sistema esegue un movimento complesso, che è una sovrapposizione di oscillazioni forzate e libere. Le oscillazioni libere si attenuano gradualmente e nello stato stazionario il sistema esegue oscillazioni forzate, che risultano anch'esse armoniche. La frequenza delle oscillazioni forzate costanti coincide con la frequenza
forza motrice (una forza esterna, per così dire, impone la sua frequenza al sistema).

L'ampiezza delle oscillazioni forzate stazionarie dipende dalla frequenza della forza motrice. Il grafico di questa dipendenza è mostrato in Fig. 7.

Riso. 7. Risonanza

Vediamo che la risonanza si verifica vicino alla frequenza, il fenomeno di un aumento dell'ampiezza delle oscillazioni forzate. La frequenza di risonanza è approssimativamente uguale alla frequenza di oscillazione naturale del sistema: , e questa uguaglianza è tanto più precisa quanto minore è l'attrito nel sistema. In assenza di attrito, la frequenza di risonanza coincide con la frequenza di oscillazione naturale, e l'ampiezza dell'oscillazione aumenta all'infinito a .