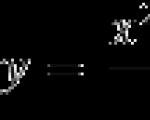casa › Luce e vetro › Come rimuovere un modulo nella disuguaglianza. Equazioni Modulo

Come rimuovere un modulo nella disuguaglianza. Equazioni Modulo

Risolvere le disuguaglianze online

Prima di risolvere le disuguaglianze, è necessario capire bene come si risolvono le equazioni.

Non importa se la disuguaglianza è stretta () o non stretta (≤, ≥), il primo passo è risolvere l'equazione sostituendo il segno di disuguaglianza con l'uguaglianza (=).

Spiegare cosa significa risolvere una disuguaglianza?

Dopo aver studiato le equazioni, lo studente ha in testa la seguente immagine: è necessario trovare tali valori della variabile per i quali entrambe le parti dell'equazione assumono gli stessi valori. In altre parole, trova tutti i punti in cui vale l'uguaglianza. Tutto è corretto!

Quando si parla di disuguaglianze, si intende trovare gli intervalli (segmenti) su cui vale la disuguaglianza. Se nella disuguaglianza ci sono due variabili, la soluzione non saranno più gli intervalli, ma alcune aree del piano. Indovina quale sarà la soluzione della disuguaglianza in tre variabili?

Come risolvere le disuguaglianze?

Il metodo degli intervalli (noto anche come metodo degli intervalli) è considerato un modo universale per risolvere le disuguaglianze, che consiste nel determinare tutti gli intervalli entro i quali verrà soddisfatta la disuguaglianza data.

Senza entrare nel tipo di disuguaglianza, in questo caso non è l'essenza, è necessario risolvere l'equazione corrispondente e determinarne le radici, seguita dalla designazione di queste soluzioni sull'asse numerico.

Qual è il modo corretto di scrivere la soluzione di una disuguaglianza?

Dopo aver determinato gli intervalli per risolvere la disuguaglianza, è necessario scrivere correttamente la soluzione stessa. C'è una sfumatura importante: i confini degli intervalli sono inclusi nella soluzione?

Tutto è semplice qui. Se la soluzione dell'equazione soddisfa l'ODZ e la disuguaglianza non è stretta, il confine dell'intervallo è incluso nella soluzione della disuguaglianza. Altrimenti no.

Considerando ciascun intervallo, la soluzione alla disuguaglianza può essere l'intervallo stesso, o un semiintervallo (quando uno dei suoi confini soddisfa la disuguaglianza), o un segmento - un intervallo insieme ai suoi confini.

Punto importante

Non pensare che solo intervalli, semiintervalli e segmenti possano essere la soluzione ad una disuguaglianza. No, nella soluzione è possibile includere anche singoli punti.

Ad esempio, la disuguaglianza |x|≤0 ha una sola soluzione: il punto 0.

E la disuguaglianza |x|

A cosa serve il calcolatore della disuguaglianza?

Il calcolatore della disuguaglianza fornisce la risposta finale corretta. Nella maggior parte dei casi viene fornita l'illustrazione di un asse o piano numerico. Puoi vedere se i limiti degli intervalli sono inclusi o meno nella soluzione: i punti vengono visualizzati pieni o forati.

Grazie al calcolatore di disuguaglianze online puoi verificare se hai trovato correttamente le radici dell'equazione, segnandole sulla retta numerica e verificando le condizioni di disuguaglianza sugli intervalli (e sui confini)?

Se la tua risposta è diversa da quella della calcolatrice, devi assolutamente ricontrollare la tua soluzione e identificare l'errore commesso.

Più una persona capisce, più forte è il suo desiderio di capire

Tommaso d'Aquino

Il metodo dell'intervallo consente di risolvere qualsiasi equazione contenente il modulo. L'essenza di questo metodo è dividere l'asse numerico in più sezioni (intervalli) ed è necessario dividere l'asse con gli zeri delle espressioni nei moduli. Quindi, su ciascuna delle sezioni risultanti, qualsiasi espressione di sottomodulo è positiva o negativa. Pertanto ciascuno dei moduli può essere espanso con un segno meno o con un segno più. Dopo queste azioni, resta solo da risolvere ciascuna delle semplici equazioni ottenute nell'intervallo in esame e combinare le risposte ottenute.

Consideriamo questo metodo su un esempio specifico.

|x+1| + |2x – 4| – |x + 3| = 2x - 6.

1) Trova gli zeri delle espressioni nei moduli. Per fare ciò, li equiparamo a zero e risolviamo le equazioni risultanti.

x + 1 = 0 2x – 4 = 0 x + 3 = 0

x = -1 2x = 4 x = -3

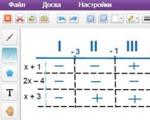
2) Disporre i punti risultanti nell'ordine desiderato sulla linea delle coordinate. Spezzeranno l'intero asse in quattro sezioni.

3) Determiniamo su ciascuna delle sezioni risultanti i segni delle espressioni nei moduli. Per fare ciò, sostituiamo in essi qualsiasi numero dagli intervalli che ci interessano. Se il risultato del calcolo è un numero positivo, inseriamo "+" nella tabella e se il numero è negativo, inseriamo "-". Questo può essere raffigurato in questo modo:

4) Ora risolveremo l'equazione su ciascuno dei quattro intervalli, aprendo i moduli con i segni che sono nella tabella. Consideriamo quindi il primo intervallo:

I intervallo (-∞; -3). Su di esso, tutti i moduli vengono aperti con un segno "-". Otteniamo la seguente equazione:

-(x + 1) - (2x - 4) - (-(x + 3)) \u003d 2x - 6. Presentiamo termini simili, avendo precedentemente aperto le parentesi nell'equazione risultante:

X - 1 - 2x + 4 + x + 3 = 2x - 6

La risposta ricevuta non è compresa nell'intervallo considerato, quindi non è necessario scriverla nella risposta finale.

II intervallo [-3; -1). A questo intervallo nella tabella sono presenti i segni "-", "-", "+". In questo modo riveliamo i moduli dell'equazione originale:

-(x + 1) - (2x - 4) - (x + 3) = 2x - 6. Semplificare espandendo le parentesi:

X - 1 - 2x + 4 - x - 3 \u003d 2x - 6. Presentiamo nell'equazione risultante quanto segue:

x = 6/5. Il numero risultante non appartiene all'intervallo in esame, quindi non è la radice dell'equazione originale.

III intervallo [-1; 2). Apriamo i moduli dell'equazione originale con i segni che sono nella figura nella terza colonna. Noi abbiamo:

(x + 1) - (2x - 4) - (x + 3) = 2x - 6. Elimina le parentesi, sposta i termini che contengono la variabile x sul lato sinistro dell'equazione e che non contengono x sul lato destro . Avrà:

x + 1 - 2x + 4 - x - 3 = 2x - 6

Il numero 2 non è compreso nell'intervallo considerato.

Intervallo IV

In termini semplici, il modulo è “un numero senza meno”. Ed è in questa dualità (da qualche parte non è necessario fare nulla con il numero originale, ma da qualche parte è necessario rimuovere un po 'di meno) e risiede tutta la difficoltà per gli studenti alle prime armi.

C'è anche una definizione geometrica. È anche utile conoscerlo, ma faremo riferimento ad esso solo in casi complessi e in alcuni casi particolari, dove l'approccio geometrico è più conveniente di quello algebrico (spoiler: non oggi).

Definizione. Sia segnato il punto $a$ sulla retta reale. Quindi il modulo $\left| x-a \right|$ è la distanza dal punto $x$ al punto $a$ su questa linea.

Se disegni un'immagine, ottieni qualcosa del genere:

Definizione del modulo grafico

In un modo o nell'altro, la sua proprietà chiave deriva immediatamente dalla definizione del modulo: il modulo di un numero è sempre un valore non negativo. Questo fatto sarà un filo rosso che attraversa tutta la nostra storia oggi.

Soluzione delle disuguaglianze. Metodo di spaziatura

Ora occupiamoci delle disuguaglianze. Ce ne sono moltissimi, ma il nostro compito ora è riuscire a risolvere almeno il più semplice. Quelli che si riducono alle disuguaglianze lineari, nonché al metodo degli intervalli.

Ho due grandi tutorial su questo argomento (tra l'altro, molto, MOLTO utili - consiglio di studiarli):

Il metodo degli intervalli per le disuguaglianze (in particolare guarda il video);
Le disuguaglianze frazionarie-razionali sono una lezione molto voluminosa, ma dopo non avrai più alcuna domanda.

Se sai tutto questo, se la frase “passiamo dalla disuguaglianza all'equazione” non ti fa venire la vaga voglia di ammazzarti contro il muro, allora sei pronto: benvenuto all'inferno nell'argomento principale della lezione. :)

1. Disuguaglianze della forma "Modulo minore di funzione"

Questa è una delle attività più frequenti con i moduli. Occorre risolvere una disuguaglianza della forma:

\[\sinistra| f\giusto| \ltg\]

Qualsiasi cosa può fungere da funzioni $f$ e $g$, ma di solito sono polinomi. Esempi di tali disuguaglianze:

Tutti sono risolti letteralmente in una riga secondo lo schema:

\[\sinistra| f\giusto| \lt g\Rightarrow -g \lt f \lt g\quad \left(\Rightarrow \left\( \begin(align) & f \lt g, \\ & f \gt -g \\\end(align) \giusto giusto)\]

È facile vedere che ci liberiamo del modulo, ma otteniamo invece una doppia disuguaglianza (o, che è la stessa cosa, un sistema di due disuguaglianze). Ma questa transizione tiene conto assolutamente di tutti i possibili problemi: se il numero sotto il modulo è positivo, il metodo funziona; se negativo funziona ancora; e anche con la funzione più inadeguata al posto di $f$ o $g$, il metodo funzionerà comunque.

Naturalmente sorge la domanda: non è più facile? Sfortunatamente non puoi. Questo è il punto centrale del modulo.

Ma basta filosofare. Risolviamo un paio di problemi:

Compito. Risolvi la disuguaglianza:

\[\sinistra| 2x+3\destra| \ltx+7\]

Soluzione. Quindi, abbiamo una disuguaglianza classica della forma "il modulo è inferiore a" - non c'è nemmeno nulla da trasformare. Lavoriamo secondo l'algoritmo:

\[\begin(align) & \left| f\giusto| \lt g\Freccia destra -g \lt f \lt g; \\ & \sinistra| 2x+3\destra| \lt x+7\Rightarrow -\left(x+7 \right) \lt 2x+3 \lt x+7 \\\end(align)\]

Non affrettarti ad aprire le parentesi precedute da un “meno”: è del tutto possibile che a causa della fretta commetterai un errore offensivo.

\[-x-7 \lt 2x+3 \lt x+7\]

\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(align) \right.\]

\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \right.\]

\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \right.\]

Il problema è stato ridotto a due disuguaglianze elementari. Notiamo le loro soluzioni su rette reali parallele:
Intersezione di molti
L'intersezione di questi insiemi sarà la risposta.

Risposta: $x\in \left(-\frac(10)(3);4 \right)$

Compito. Risolvi la disuguaglianza:

\[\sinistra| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0\]

Soluzione. Questo compito è un po' più difficile. Per cominciare isoliamo il modulo spostando il secondo termine verso destra:

\[\sinistra| ((x)^(2))+2x-3 \destra| \lt -3\sinistra(x+1 \destra)\]

Ovviamente, abbiamo ancora una volta una disuguaglianza della forma “il modulo è inferiore”, quindi eliminiamo il modulo secondo l'algoritmo già noto:

\[-\left(-3\left(x+1 \right) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \right)\]

Ora attenzione: qualcuno dirà che sono un po' pervertito con tutte queste parentesi. Ma ancora una volta ti ricordo che il nostro obiettivo principale è Risolvi correttamente la disuguaglianza e ottieni la risposta. Successivamente, quando avrai padroneggiato perfettamente tutto ciò che è descritto in questa lezione, puoi pervertirti come preferisci: aprire parentesi, aggiungere svantaggi, ecc.

E per cominciare, eliminiamo semplicemente il doppio meno a sinistra:

\[-\left(-3\left(x+1 \right) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\sinistra(x+1\destra)\]

Ora apriamo tutte le parentesi nella doppia disuguaglianza:

Passiamo alla doppia disuguaglianza. Questa volta i calcoli saranno più seri:

\[\left\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(allineare) \right.\]

\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( allinea)\destra.\]

Entrambe le disuguaglianze sono quadrate e si risolvono con il metodo degli intervalli (per questo dico: se non sai di cosa si tratta, è meglio non affrontare ancora i moduli). Passiamo all’equazione nella prima disuguaglianza:

\[\begin(align) & ((x)^(2))+5x=0; \\ & x\sinistra(x+5 \destra)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\fine(allinea)\]

Come puoi vedere, il risultato si è rivelato un'equazione quadratica incompleta, che viene risolta in modo elementare. Affrontiamo ora la seconda disuguaglianza del sistema. Lì devi applicare il teorema di Vieta:

\[\begin(align) & ((x)^(2))-x-6=0; \\ & \sinistra(x-3 \destra)\sinistra(x+2 \destra)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\fine(allinea)\]

Contrassegniamo i numeri ottenuti su due rette parallele (separate per la prima disuguaglianza e separate per la seconda):
Ancora una volta, poiché stiamo risolvendo un sistema di disequazioni, siamo interessati all'intersezione degli insiemi ombreggiati: $x\in \left(-5;-2 \right)$. Questa è la risposta.
Risposta: $x\in \left(-5;-2 \right)$

Penso che dopo questi esempi lo schema della soluzione sia molto chiaro:

Isolare il modulo spostando tutti gli altri termini sul lato opposto della disuguaglianza. Si ottiene così una disuguaglianza della forma $\left| f\giusto| \ltg$.
Risolvi questa disuguaglianza eliminando il modulo come descritto sopra. Ad un certo punto sarà necessario passare da una doppia disuguaglianza a un sistema di due espressioni indipendenti, ciascuna delle quali può già essere risolta separatamente.
Infine, resta solo da incrociare le soluzioni di queste due espressioni indipendenti - e basta, otterremo la risposta finale.

Un algoritmo simile esiste per le disuguaglianze del tipo seguente, quando il modulo è maggiore della funzione. Ci sono però un paio di “ma” seri. Parleremo ora di questi “ma”.

2. Disuguaglianze della forma "Il modulo è maggiore della funzione"

Sembrano così:

\[\sinistra| f\giusto| \gt g\]

Simile al precedente? Sembra. Tuttavia, tali compiti vengono risolti in un modo completamente diverso. Formalmente lo schema è il seguente:

\[\sinistra| f\giusto| \gt g\Rightarrow \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(align) \right.\]

In altre parole, consideriamo due casi:

Innanzitutto, ignoriamo semplicemente il modulo: risolviamo la solita disuguaglianza;
Poi, infatti, apriamo il modulo con il segno meno, e poi moltiplichiamo entrambe le parti della disuguaglianza per −1, con un segno.

In questo caso le opzioni vengono combinate con parentesi quadre, ad es. Abbiamo una combinazione di due requisiti.

Prestate ancora attenzione: davanti a noi non c'è un sistema, ma un aggregato, quindi nella risposta gli insiemi sono combinati, non intersecati. Questa è una differenza fondamentale rispetto al paragrafo precedente!

In generale, molti studenti hanno molta confusione con le unioni e le intersezioni, quindi esaminiamo questo problema una volta per tutte:

"∪" è un segno di concatenazione. In realtà, questa è una lettera stilizzata "U", che ci è arrivata dalla lingua inglese ed è l'abbreviazione di "Unione", ad es. "Associazioni".
"∩" è il segno dell'intersezione. Questa schifezza non viene da nessuna parte, ma è apparsa semplicemente come un'opposizione a "∪".

Per renderlo ancora più facile da ricordare, aggiungi semplicemente le gambe a questi segni per creare degli occhiali (non accusarmi di promuovere la tossicodipendenza e l'alcolismo adesso: se stai studiando seriamente questa lezione, allora sei già un tossicodipendente):

Differenza tra intersezione e unione di insiemi

Tradotto in russo, ciò significa quanto segue: l'unione (raccolta) comprende elementi di entrambi gli insiemi, quindi nientemeno che ciascuno di essi; ma l'intersezione (sistema) comprende solo quegli elementi che sono sia nel primo che nel secondo insieme. Pertanto, l'intersezione degli insiemi non è mai maggiore degli insiemi di origine.

Quindi è diventato più chiaro? È grandioso. Passiamo alla pratica.

Compito. Risolvi la disuguaglianza:

\[\sinistra| 3x+1 \destra| \gt 5-4x\]

Soluzione. Agiamo secondo lo schema:

\[\sinistra| 3x+1 \destra| \gt 5-4x\Rightarrow \left[ \begin(align) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \right) \\\end(align) \ Giusto.\]

Risolviamo ogni disuguaglianza della popolazione:

\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \right.\]

\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \right.\]

\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(align) \right.\]

Contrassegniamo ciascun insieme risultante sulla linea numerica e quindi li combiniamo:
Unione di insiemi
Ovviamente la risposta è $x\in \left(\frac(4)(7);+\infty \right)$

Risposta: $x\in \left(\frac(4)(7);+\infty \right)$

Compito. Risolvi la disuguaglianza:

\[\sinistra| ((x)^(2))+2x-3 \destra| \gtx\]

Soluzione. BENE? No, è tutto uguale. Passiamo da una disuguaglianza con modulo ad un insieme di due disuguaglianze:

\[\sinistra| ((x)^(2))+2x-3 \destra| \gt x\Rightarrow \left[ \begin(align) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\end(allineare) \right.\]

Risolviamo ogni disuguaglianza. Sfortunatamente, le radici non saranno molto buone lì:

\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\&D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\fine(allinea)\]

Nella seconda disuguaglianza c’è anche un po’ di gioco:

\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\&D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\fine(allinea)\]

Ora dobbiamo segnare questi numeri su due assi: un asse per ogni disuguaglianza. Tuttavia, è necessario contrassegnare i punti nell'ordine corretto: maggiore è il numero, più il punto si sposta verso destra.

E qui stiamo aspettando una configurazione. Se è tutto chiaro con i numeri $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ (i termini al numeratore del primo frazione sono minori dei termini al numeratore del secondo , quindi anche la somma è più piccola), con i numeri $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt Anche (21))(2)$ non ci saranno difficoltà (un numero positivo ovviamente più negativo), ma con l'ultima coppia non tutto è così semplice. Qual è il valore più grande: $\frac(-3+\sqrt(21))(2)$ o $\frac(-1+\sqrt(13))(2)$? La disposizione dei punti sulle linee numeriche e, di fatto, la risposta dipenderà dalla risposta a questa domanda.

Quindi confrontiamo:

\[\begin(matrix) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matrice)\]

Abbiamo isolato la radice, ottenuto numeri non negativi su entrambi i lati della disuguaglianza, quindi abbiamo il diritto di elevare al quadrato entrambi i lati:

\[\begin(matrix) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \4+4\quadrato(13)+13\vee 21 \\ 4\quadrato(13)\vee 3 \\\end(matrice)\]

Penso che sia un gioco da ragazzi che $4\sqrt(13) \gt 3$, quindi $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$, infine i punti sugli assi verranno disposti così:
Caso di radici brutte
Lascia che ti ricordi che stiamo risolvendo un insieme, quindi la risposta sarà l'unione e non l'intersezione degli insiemi ombreggiati.

Risposta: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty\right)$

Come puoi vedere, il nostro schema funziona alla grande sia per compiti semplici che per quelli molto difficili. L'unico “punto debole” di questo approccio è che è necessario confrontare correttamente i numeri irrazionali (e credetemi: queste non sono solo radici). Ma una lezione a parte (e molto seria) sarà dedicata alle questioni comparative. E andiamo avanti.

3. Disuguaglianze a “code” non negative

Quindi siamo arrivati alla cosa più interessante. Queste sono disuguaglianze della forma:

\[\sinistra| f\giusto| \gt\sinistra| g\giusto|\]

In generale, l'algoritmo di cui parleremo ora vale solo per il modulo. Funziona in tutte le disuguaglianze in cui sono garantite espressioni non negative a sinistra e a destra:

Cosa fare con questi compiti? Ricorda:

Nelle disuguaglianze con code non negative, entrambi i lati possono essere elevati a qualsiasi potenza naturale. Non ci saranno ulteriori restrizioni.

Prima di tutto, saremo interessati alla quadratura: brucia moduli e radici:

\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f. \\\fine(allinea)\]

Basta non confonderlo con la radice del quadrato:

\[\sqrt(((f)^(2)))=\sinistra| f \destra|\ne f\]

Sono stati commessi innumerevoli errori quando uno studente ha dimenticato di installare un modulo! Ma questa è una storia completamente diversa (queste sono, per così dire, equazioni irrazionali), quindi non ne parleremo ora. Risolviamo meglio un paio di problemi:

Compito. Risolvi la disuguaglianza:

\[\sinistra| x+2 \destra|\ge \sinistra| 1-2x \destra|\]

Soluzione. Notiamo subito due cose:

Questa è una disuguaglianza non rigorosa. I punti sulla linea numerica verranno perforati.

Entrambi i lati della disuguaglianza sono ovviamente non negativi (questa è una proprietà del modulo: $\left| f\left(x \right) \right|\ge 0$).

Pertanto, possiamo elevare al quadrato entrambi i lati della disuguaglianza per eliminare il modulo e risolvere il problema utilizzando il consueto metodo dell'intervallo:

\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\left(x+2 \right))^(2))\ge ((\left(2x-1 \right))^(2)). \\\fine(allinea)\]

Nell’ultimo passaggio ho barato un po’: ho cambiato la sequenza dei termini, utilizzando la parità del modulo (ho infatti moltiplicato l’espressione $1-2x$ per −1).

\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ destra)\destra)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(align)\]

Risolviamo con il metodo degli intervalli. Passiamo dalla disuguaglianza all'equazione:

\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\fine(allinea)\]

Contrassegniamo le radici trovate sulla linea numerica. Ancora una volta: tutti i punti sono ombreggiati perché la disuguaglianza originaria non è stretta!
Sbarazzarsi del segno del modulo
Lascia che te lo ricordi per i più testardi: prendiamo i segni dell'ultima disuguaglianza, che è stata scritta prima di passare all'equazione. E dipingiamo sulle aree richieste con la stessa disuguaglianza. Nel nostro caso, questo è $\left(x-3 \right)\left(3x+1 \right)\le 0$.

OK, è tutto finito adesso. Problema risolto.

Risposta: $x\in \left[ -\frac(1)(3);3 \right]$.

Compito. Risolvi la disuguaglianza:

\[\sinistra| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \destra|\]

Soluzione. Facciamo tutto allo stesso modo. Non commenterò: guarda solo la sequenza delle azioni.

Facciamo il quadrato:

\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \right| \right))^(2))\le ((\left(\left | ((x)^(2))+3x+4 \right| \right))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))\le ((\left(((x)^(2))+3x+4 \right))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))-((\left(((x)^(2))+3x+4 \ destra))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x) ^(2))+x+1+((x)^(2))+3x+4 \right)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(align)\]

Metodo di spaziatura:

\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ Freccia destra x=-1,5; \\ & 2((x)^(2))+4x+5=0\Rightarrow D=16-40 \lt 0\Rightarrow \varniente . \\\fine(allinea)\]

C'è solo una radice sulla linea numerica:
La risposta è tutta una serie
Risposta: $x\in \left[ -1.5;+\infty \right)$.

Una piccola nota sull'ultimo compito. Come ha notato accuratamente uno dei miei studenti, entrambe le espressioni dei sottomoduli in questa disuguaglianza sono ovviamente positive, quindi il segno del modulo può essere omesso senza danni alla salute.

Ma questo è già un livello di pensiero completamente diverso e un approccio diverso: può essere condizionatamente chiamato il metodo delle conseguenze. Su di lui - in una lezione separata. E ora passiamo alla parte finale della lezione di oggi e consideriamo un algoritmo universale che funziona sempre. Anche quando tutti gli approcci precedenti erano impotenti. :)

4. Metodo di enumerazione delle opzioni

E se tutti questi trucchi non funzionassero? Se la disuguaglianza non si riduce a code non negative, se è impossibile isolare il modulo, semmai dolore-tristezza-nostalgia?

Poi entra in scena l '"artiglieria pesante" di tutta la matematica: il metodo di enumerazione. Per quanto riguarda le disuguaglianze con il modulo, appare così:

Scrivi tutte le espressioni dei sottomoduli e equiparale a zero;
Risolvi le equazioni risultanti e segna le radici trovate su una linea numerica;
La retta sarà divisa in più tratti, all'interno dei quali ciascun modulo ha un segno fisso e quindi si espande in modo univoco;
Risolvi la disuguaglianza su ciascuna di queste sezioni (puoi considerare separatamente le radici del confine ottenute nel paragrafo 2 - per affidabilità). Combina i risultati: questa sarà la risposta. :)

Ebbene, come? Debole? Facilmente! Solo per molto tempo. Vediamo in pratica:

Compito. Risolvi la disuguaglianza:

\[\sinistra| x+2 \destra| \lt\sinistra| x-1 \destra|+x-\frac(3)(2)\]

Soluzione. Questa schifezza non si riduce a disuguaglianze come $\left| f\giusto| \ltg$, $\sinistra| f\giusto| \gt g$ o $\sinistra| f\giusto| \lt\sinistra| g \right|$, quindi andiamo avanti.

Scriviamo le espressioni del sottomodulo, le equiparamo a zero e troviamo le radici:

\[\begin(align) & x+2=0\Rightarrow x=-2; \\ & x-1=0\Freccia destra x=1. \\\fine(allinea)\]

In totale, abbiamo due radici che dividono la linea numerica in tre sezioni, all'interno delle quali ogni modulo si rivela in modo univoco:
Divisione della retta numerica per zeri di funzioni submodulari
Consideriamo ciascuna sezione separatamente.

1. Sia $x \lt -2$. Quindi entrambe le espressioni del sottomodulo sono negative e la disuguaglianza originale viene riscritta come segue:

\[\begin(align) & -\left(x+2 \right) \lt -\left(x-1 \right)+x-1,5 \\ & -x-2 \lt -x+1+ x-1.5 \\ & x \gt 1.5 \\\end(allineare)\]

Abbiamo un vincolo abbastanza semplice. Intersechiamolo con l'ipotesi originale che $x \lt -2$:

\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1,5 \\\end(align) \right.\Rightarrow x\in \varnothing \]

Ovviamente la variabile $x$ non può essere contemporaneamente inferiore a −2 ma maggiore di 1,5. Non ci sono soluzioni in questo settore.

1.1. Consideriamo separatamente il caso limite: $x=-2$. Sostituiamo semplicemente questo numero nella disuguaglianza originale e controlliamo: vale?

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=-2) ) \\ & 0 \lt \sinistra| -3 \destra|-2-1.5; \\ & 0 \lt 3-3,5; \\ & 0 \lt -0,5\Rightarrow \varniente . \\\fine(allinea)\]

Ovviamente la catena di calcoli ci ha portato alla disuguaglianza sbagliata. Pertanto, anche la disuguaglianza originale è falsa e $x=-2$ non è inclusa nella risposta.

2. Ora sia $-2 \lt x \lt 1$. Il modulo di sinistra si aprirà già con un "più", ma quello di destra avrà ancora un "meno". Abbiamo:

\[\begin(align) & x+2 \lt -\left(x-1 \right)+x-1.5 \\ & x+2 \lt -x+1+x-1.5 \\& x \lt - 2.5 \\\fine(allineare)\]

Ancora una volta ci intersechiamo con il requisito originale:

\[\left\( \begin(align) & x \lt -2,5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]

E ancora, l’insieme vuoto delle soluzioni, poiché non esistono numeri che siano contemporaneamente minori di −2,5 e maggiori di −2.

2.1. E ancora un caso speciale: $x=1$. Sostituiamo nella disuguaglianza originaria:

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=1)) \\ & \sinistra| 3\destra| \lt\sinistra| 0 \destra|+1-1.5; \\ & 3 \lt -0,5; \\ & 3 \lt -0,5\Rightarrow \varniente . \\\fine(allinea)\]

Analogamente al "caso speciale" precedente, il numero $x=1$ chiaramente non è incluso nella risposta.

3. L'ultimo pezzo della riga: $x \gt 1$. Qui tutti i moduli vengono espansi con un segno più:

\[\begin(align) & x+2 \lt x-1+x-1.5 \\ & x+2 \lt x-1+x-1.5 \\ & x \gt 4.5 \\ \end(align)\ ]

E ancora intersechiamo il set trovato con il vincolo originale:

\[\left\( \begin(align) & x \gt 4,5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4,5;+\infty \Giusto)\]

Finalmente! Abbiamo trovato l'intervallo, che sarà la risposta.

Risposta: $x\in \left(4,5;+\infty \right)$

Infine, una nota che potrebbe salvarti da errori stupidi quando risolvi problemi reali:

Le soluzioni di disuguaglianze con moduli sono solitamente insiemi continui sulla linea numerica: intervalli e segmenti. I punti isolati sono molto più rari. E ancora più raramente accade che i confini della soluzione (la fine del segmento) coincidano con il confine dell'intervallo considerato.

Pertanto, se i confini (quelli “casi speciali”) non sono inclusi nella risposta, allora quasi certamente non saranno incluse nella risposta nemmeno le aree a sinistra-destra di questi confini. E viceversa: il confine è entrato in risposta, il che significa che anche alcune aree circostanti saranno risposte.

Tienilo a mente quando controlli le tue soluzioni.

soluzione della disuguaglianza in modalità in linea soluzione quasi ogni data disuguaglianza in linea. Matematico disuguaglianze online per risolvere la matematica. Trova rapidamente soluzione della disuguaglianza in modalità in linea. Il sito www.site ti permette di trovare soluzione quasi ogni dato algebrico, trigonometrico O disuguaglianza trascendente online. Quando si studia quasi ogni sezione della matematica in fasi diverse, bisogna decidere disuguaglianze online. Per ottenere una risposta immediata e, soprattutto, una risposta accurata, hai bisogno di una risorsa che ti consenta di farlo. Grazie a www.sito risolvere la disuguaglianza online ci vorranno alcuni minuti. Il vantaggio principale di www.site nella risoluzione matematica disuguaglianze online- è la velocità e l'accuratezza della risposta emessa. Il sito è in grado di risolvere qualsiasi disuguaglianze algebriche online, disuguaglianze trigonometriche online, disuguaglianze trascendentali online, E disuguaglianze con parametri sconosciuti nella modalità in linea. disuguaglianze fungere da potente apparato matematico soluzioni compiti pratici. Con aiuto disuguaglianze matematicheè possibile esprimere fatti e relazioni che a prima vista possono sembrare confusi e complessi. quantità sconosciute disuguaglianze può essere trovato formulando il problema in matematico linguaggio nella forma disuguaglianze E decidere l'attività ricevuta nella modalità in linea sul sito www.sito. Qualunque disuguaglianza algebrica, disuguaglianza trigonometrica O disuguaglianze contenente trascendentale ti presenta facilmente decidere online e ottieni la risposta giusta. Studiando le scienze naturali ci si imbatte inevitabilmente in questa necessità soluzione delle disuguaglianze. In questo caso, la risposta deve essere precisa e deve essere ricevuta immediatamente nella modalità in linea. Pertanto, per risolvere le disuguaglianze matematiche online ti consigliamo il sito www.site, che diventerà il tuo calcolatore indispensabile risolvere disuguaglianze algebriche online, disuguaglianze trigonometriche online, E disuguaglianze trascendentali online O disuguaglianze con parametri sconosciuti. Per problemi pratici nel trovare soluzioni intravol di vario tipo disuguaglianze matematiche risorsa www.. Risoluzione disuguaglianze online te stesso, è utile controllare la risposta ricevuta utilizzando soluzione online delle disuguaglianze sul sito www.sito. È necessario scrivere correttamente la disuguaglianza e ottenerla immediatamente soluzione in linea, dopodiché resta solo da confrontare la risposta con la tua soluzione alla disuguaglianza. Controllare la risposta non richiederà più di un minuto, abbastanza risolvere la disuguaglianza online e confrontare le risposte. Questo ti aiuterà a evitare errori decisione e correggi la risposta in tempo risolvere le disuguaglianze online O algebrico, trigonometrico, trascendente O disuguaglianza con parametri sconosciuti.