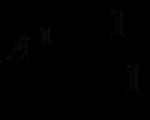Come risolvere equazioni. Risoluzione di equazioni lineari con esempi

Nella fase di preparazione alla prova finale, gli studenti delle scuole superiori devono migliorare le proprie conoscenze sull'argomento "Equazioni esponenziali". L'esperienza degli anni passati indica che tali compiti causano alcune difficoltà agli scolari. Pertanto, gli studenti delle scuole superiori, indipendentemente dal loro livello di preparazione, devono padroneggiare attentamente la teoria, memorizzare le formule e comprendere il principio per risolvere tali equazioni. Avendo imparato ad affrontare questo tipo di compiti, i laureati potranno contare su punteggi elevati nel superare l'esame di matematica.

Preparati per la prova d'esame insieme a Shkolkovo!

Quando si ripetono i materiali trattati, molti studenti si trovano ad affrontare il problema di trovare le formule necessarie per risolvere le equazioni. Non sempre un libro di testo scolastico è a portata di mano e la selezione delle informazioni necessarie su un argomento su Internet richiede molto tempo.

Il portale educativo Shkolkovo invita gli studenti a utilizzare la nostra base di conoscenze. Stiamo implementando un metodo completamente nuovo di preparazione al test finale. Studiando sul nostro sito, sarai in grado di identificare le lacune nella conoscenza e prestare attenzione proprio a quei compiti che causano le maggiori difficoltà.

Gli insegnanti di "Shkolkovo" hanno raccolto, sistematizzato e presentato tutto il materiale necessario per superare con successo l'esame nella forma più semplice e accessibile.

Le principali definizioni e formule sono presentate nella sezione "Riferimenti teorici".

Per una migliore assimilazione del materiale, ti consigliamo di esercitarti con i compiti. Rivedi attentamente gli esempi di equazioni esponenziali con soluzioni presentati in questa pagina per comprendere l'algoritmo di calcolo. Successivamente, procedi con le attività nella sezione "Cataloghi". Puoi iniziare con i compiti più semplici o passare direttamente alla risoluzione di equazioni esponenziali complesse con diverse incognite o . Il database degli esercizi sul nostro sito web viene costantemente integrato e aggiornato.

Gli esempi con indicatori che ti hanno causato difficoltà possono essere aggiunti ai "Preferiti". Quindi puoi trovarli rapidamente e discutere la soluzione con l'insegnante.

Per superare con successo l'esame, studia ogni giorno sul portale Shkolkovo!

Incarico di servizio. Il calcolatore di matrici è progettato per risolvere sistemi di equazioni lineari in modo matriciale (vedere un esempio di risoluzione di problemi simili).

Istruzioni. Per una soluzione online, è necessario selezionare il tipo di equazione e impostare la dimensione delle matrici corrispondenti. dove A, B, C sono matrici date, X è la matrice desiderata. Le equazioni di matrice della forma (1), (2) e (3) vengono risolte attraverso la matrice inversa A -1 . Se è data l'espressione A X - B = C, allora è necessario prima sommare le matrici C + B e trovare una soluzione per l'espressione A X = D , dove D = C + B . Se è data l'espressione A*X = B 2, allora la matrice B deve prima essere quadrata.

Si consiglia inoltre di familiarizzare con le operazioni di base sulle matrici.

Esempio 1. Esercizio. Trovare la soluzione di un'equazione di matrice
Soluzione. Denota:
Quindi l'equazione della matrice verrà scritta nella forma: A·X·B = C.
Il determinante della matrice A è detA=-1
Poiché A è una matrice non singolare, esiste una matrice inversa A -1 . Moltiplica entrambi i lati dell'equazione a sinistra per A -1: Moltiplica entrambi i lati di questa equazione a sinistra per A -1 e a destra per B -1: A -1 A X B B -1 = A -1 C B -1 . Poiché A A -1 = B B -1 = E ed E X = X E = X, allora X = A -1 C B -1

Matrice inversa A -1:
Trova la matrice inversa B -1 .
Matrice trasposta B T:
Matrice inversa B -1:
Cerchiamo la matrice X con la formula: X = A -1 C B -1

Risposta:

Esempio n.2. Esercizio. Risolvere l'equazione della matrice
Soluzione. Denota:
Quindi l'equazione della matrice verrà scritta nella forma: A X = B.
Il determinante della matrice A è detA=0
Poiché A è una matrice degenere (il determinante è 0), l'equazione non ha soluzione.

Esempio n.3. Esercizio. Trovare la soluzione di un'equazione di matrice
Soluzione. Denota:
Quindi l'equazione della matrice verrà scritta nella forma: X·A = B.
Il determinante della matrice A è detA=-60
Poiché A è una matrice non singolare, esiste una matrice inversa A -1 . Moltiplichiamo a destra entrambi i membri dell'equazione per A -1: X A A -1 = B A -1 , da cui troviamo che X = B A -1
Trova la matrice inversa A -1 .
Matrice trasposta A T:
Matrice inversa A -1:
Cerchiamo la matrice X con la formula: X = B A -1


Risposta: >

per risolvere la matematica. Trova rapidamente soluzione di equazioni matematiche in modalità in linea. Il sito web www.site consente risolvere l'equazione quasi ogni dato algebrico, trigonometrico O equazione trascendente online. Quando si studia quasi ogni sezione della matematica in fasi diverse, bisogna decidere equazioni in linea. Per ottenere una risposta immediata e, soprattutto, una risposta accurata, hai bisogno di una risorsa che ti consenta di farlo. Grazie a www.sito risolvere equazioni online ci vorranno alcuni minuti. Il vantaggio principale di www.site nella risoluzione matematica equazioni in linea- è la velocità e l'accuratezza della risposta emessa. Il sito è in grado di risolvere qualsiasi equazioni algebriche online, equazioni trigonometriche online, equazioni trascendenti online, E equazioni con parametri sconosciuti nella modalità in linea. Equazioni fungere da potente apparato matematico soluzioni compiti pratici. Con aiuto equazioni matematicheè possibile esprimere fatti e relazioni che a prima vista possono sembrare confusi e complessi. quantità sconosciute equazioni può essere trovato formulando il problema in matematico linguaggio nella forma equazioni E decidere l'attività ricevuta nella modalità in linea sul sito www.sito. Qualunque equazione algebrica, equazione trigonometrica O equazioni contenente trascendentale ti presenta facilmente decidere online e ottieni la risposta giusta. Studiando le scienze naturali ci si imbatte inevitabilmente in questa necessità risolvere equazioni. In questo caso, la risposta deve essere precisa e deve essere ricevuta immediatamente nella modalità in linea. Pertanto, per risolvere equazioni matematiche online ti consigliamo il sito www.site, che diventerà il tuo calcolatore indispensabile risolvere equazioni algebriche online, equazioni trigonometriche online, E equazioni trascendenti online O equazioni con parametri sconosciuti. Per problemi pratici di trovare le radici di vari equazioni matematiche risorsa www.. Risoluzione equazioni in linea te stesso, è utile controllare la risposta ricevuta utilizzando soluzione online di equazioni sul sito www.sito. È necessario scrivere l'equazione correttamente e ottenerla immediatamente soluzione in linea, dopodiché resta solo da confrontare la risposta con la tua soluzione dell'equazione. Controllare la risposta non richiederà più di un minuto, abbastanza risolvere l'equazione on-line e confrontare le risposte. Questo ti aiuterà a evitare errori decisione e correggi la risposta in tempo risolvere equazioni online O algebrico, trigonometrico, trascendente O l'equazione con parametri sconosciuti.

In questo video analizzeremo tutta una serie di equazioni lineari che vengono risolte utilizzando lo stesso algoritmo: ecco perché sono chiamate le più semplici.

Per cominciare, definiamo: cos'è un'equazione lineare e quale di esse dovrebbe essere definita la più semplice?

Un'equazione lineare è un'equazione in cui esiste una sola variabile e solo di primo grado.

L'equazione più semplice significa la costruzione:

Tutte le altre equazioni lineari sono ridotte a quelle più semplici utilizzando l'algoritmo:

1. Parentesi aperte, se presenti;
2. Sposta i termini che contengono una variabile da un lato del segno di uguale e i termini senza una variabile dall'altro;
3. Porta termini simili a sinistra e a destra del segno di uguale;
4. Dividi l'equazione risultante per il coefficiente della variabile $x$ .

Naturalmente, questo algoritmo non sempre aiuta. Il fatto è che a volte, dopo tutte queste macchinazioni, il coefficiente della variabile $x$ risulta essere pari a zero. In questo caso sono possibili due opzioni:

1. L’equazione non ha alcuna soluzione. Ad esempio, quando ottieni qualcosa come $0\cdot x=8$, cioè a sinistra c'è zero e a destra c'è un numero diverso da zero. Nel video qui sotto, esamineremo diversi motivi per cui questa situazione è possibile.
2. La soluzione sono tutti i numeri. L'unico caso in cui ciò è possibile è quando l'equazione è stata ridotta alla costruzione $0\cdot x=0$. È abbastanza logico che, qualunque sia il $x$ che sostituiamo, risulterà comunque "zero è uguale a zero", cioè corretta uguaglianza numerica.

E ora vediamo come funziona il tutto sull'esempio di problemi reali.

Esempi di risoluzione di equazioni

Oggi ci occupiamo di equazioni lineari, e solo di quelle più semplici. In generale, un'equazione lineare significa qualsiasi uguaglianza che contiene esattamente una variabile e va solo al primo grado.

Tali costruzioni sono risolte più o meno allo stesso modo:

1. Prima di tutto bisogna aprire le parentesi, se presenti (come nel nostro ultimo esempio);
2. Quindi porta simili
3. Infine, isola la variabile, ad es. tutto ciò che è connesso alla variabile - i termini in cui è contenuta - viene trasferito da un lato, e tutto ciò che rimane senza di essa viene trasferito dall'altro.

Quindi, di regola, è necessario portare simili su ciascun lato dell'uguaglianza risultante, dopodiché resta solo da dividere per il coefficiente in "x", e otterremo la risposta finale.

In teoria, sembra carino e semplice, ma in pratica, anche gli studenti più esperti delle scuole superiori possono commettere errori offensivi in ​​equazioni lineari abbastanza semplici. Di solito si commettono errori quando si aprono le parentesi o quando si contano i "più" e i "meno".

Inoltre, accade che un'equazione lineare non abbia alcuna soluzione, o che la soluzione sia l'intera retta numerica, cioè qualsiasi numero. Analizzeremo queste sottigliezze nella lezione di oggi. Ma inizieremo, come hai già capito, con i compiti più semplici.

Schema per la risoluzione di semplici equazioni lineari

Per cominciare, lasciatemi scrivere ancora una volta l'intero schema per risolvere le equazioni lineari più semplici:

1. Espandi le parentesi, se presenti.
2. Isolare le variabili, ad es. tutto ciò che contiene "x" viene trasferito da un lato e senza "x" dall'altro.
3. Presentiamo termini simili.
4. Dividiamo tutto per il coefficiente in "x".

Naturalmente, questo schema non sempre funziona, ha alcune sottigliezze e trucchi, e ora li conosceremo.

Risoluzione di esempi reali di semplici equazioni lineari

Compito n.1

Nel primo passaggio, dobbiamo aprire le parentesi. Ma non sono in questo esempio, quindi saltiamo questo passaggio. Nella seconda fase, dobbiamo isolare le variabili. Nota: stiamo parlando solo di termini individuali. Scriviamo:

Diamo termini simili a sinistra e a destra, ma questo è già stato fatto qui. Procediamo quindi al quarto passaggio: dividiamo per un fattore:

\[\frac(6x)(6)=-\frac(72)(6)\]

Qui abbiamo la risposta.

Compito n.2

In questo compito possiamo osservare le parentesi, quindi espandiamole:

Sia a sinistra che a destra vediamo approssimativamente la stessa costruzione, ma agiamo secondo l'algoritmo, cioè variabili sequestrate:

Eccone alcuni come:

Con quali radici funziona? Risposta: per qualsiasi. Pertanto, possiamo scrivere che $x$ è un numero qualsiasi.

Compito n.3

La terza equazione lineare è già più interessante:

\[\sinistra(6-x \destra)+\sinistra(12+x \destra)-\sinistra(3-2x \destra)=15\]

Ci sono diverse parentesi qui, ma non vengono moltiplicate per nulla, hanno solo segni diversi davanti a loro. Analizziamoli:

Eseguiamo il secondo passo a noi già noto:

\[-x+x+2x=15-6-12+3\]

Calcoliamo:

Eseguiamo l'ultimo passaggio: dividiamo tutto per il coefficiente in "x":

\[\frac(2x)(x)=\frac(0)(2)\]

Cose da ricordare quando si risolvono equazioni lineari

Se ignoriamo compiti troppo semplici, vorrei dire quanto segue:

• Come ho detto sopra, non tutte le equazioni lineari hanno una soluzione: a volte semplicemente non ci sono radici;
• Anche se ci sono radici, in mezzo a loro può entrare zero - non c'è niente di sbagliato in questo.

Lo zero è lo stesso numero del resto, non dovresti in qualche modo discriminarlo o presumere che se ottieni zero, hai fatto qualcosa di sbagliato.

Un'altra caratteristica è legata all'espansione delle parentesi. Nota: quando c'è un "meno" davanti a loro, lo rimuoviamo, ma tra parentesi cambiamo i segni in opposto. E poi possiamo aprirlo secondo algoritmi standard: otterremo ciò che abbiamo visto nei calcoli sopra.

Comprendere questo semplice fatto ti aiuterà a evitare di commettere errori stupidi e dannosi al liceo, quando compiere tali azioni è dato per scontato.

Risoluzione di equazioni lineari complesse

Passiamo ad equazioni più complesse. Ora le costruzioni diventeranno più complicate e quando si eseguono varie trasformazioni apparirà una funzione quadratica. Tuttavia, non dovresti aver paura di questo, perché se, secondo l'intenzione dell'autore, risolviamo un'equazione lineare, nel processo di trasformazione tutti i monomi contenenti una funzione quadratica verranno necessariamente ridotti.

Esempio 1

Ovviamente il primo passo è aprire le parentesi. Facciamolo con molta attenzione:

Ora prendiamo la privacy:

\[-x+6((x)^(2))-6((x)^(2))+x=-12\]

Eccone alcuni come:

Ovviamente questa equazione non ha soluzioni, quindi nella risposta scriviamo quanto segue:

\[\varietà \]

o senza radici.

Esempio n.2

Eseguiamo gli stessi passaggi. Primo passo:

Spostiamo tutto con una variabile a sinistra e senza di essa a destra:

Eccone alcuni come:

Ovviamente questa equazione lineare non ha soluzione, quindi la scriviamo così:

\[\nulla\],

o senza radici.

Sfumature della soluzione

Entrambe le equazioni sono completamente risolte. Usando l'esempio di queste due espressioni, ci siamo ancora una volta assicurati che anche nelle equazioni lineari più semplici tutto possa non essere così semplice: può essercene uno, o nessuno, o infiniti. Nel nostro caso, abbiamo considerato due equazioni, in entrambe semplicemente non ci sono radici.

Ma vorrei attirare la vostra attenzione su un altro fatto: come lavorare con le parentesi e come espanderle se davanti a loro c'è un segno meno. Considera questa espressione:

Prima di aprire, devi moltiplicare tutto per "x". Nota: moltiplicare ogni singolo termine. All'interno ci sono due termini - rispettivamente due termini e viene moltiplicato.

E solo dopo che queste trasformazioni apparentemente elementari, ma molto importanti e pericolose sono state completate, la parentesi può essere aperta dal punto di vista che dietro di essa c'è un segno meno. Sì, sì: solo ora, a trasformazioni completate, ricordiamo che davanti alle parentesi c'è il segno meno, il che significa che tutto quello che sta sotto cambia semplicemente segno. Allo stesso tempo, le parentesi stesse scompaiono e, soprattutto, scompare anche il "meno" anteriore.

Facciamo lo stesso con la seconda equazione:

Non è un caso che presto attenzione a questi piccoli fatti, apparentemente insignificanti. Perché risolvere equazioni è sempre una sequenza di trasformazioni elementari, dove l'incapacità di eseguire azioni semplici in modo chiaro e competente porta al fatto che gli studenti delle scuole superiori vengono da me e imparano di nuovo a risolvere equazioni così semplici.

Naturalmente, arriverà il giorno in cui affinerai queste abilità all'automatismo. Non dovrai più eseguire tante trasformazioni ogni volta, scriverai tutto in una riga. Ma mentre stai solo imparando, devi scrivere ogni azione separatamente.

Risoluzione di equazioni lineari ancora più complesse

Ciò che risolveremo ora difficilmente può essere definito il compito più semplice, ma il significato rimane lo stesso.

Compito n.1

\[\left(7x+1 \right)\left(3x-1 \right)-21((x)^(2))=3\]

Moltiplichiamo tutti gli elementi della prima parte:

Facciamo un ritiro:

Eccone alcuni come:

Facciamo l'ultimo passaggio:

\[\frac(-4x)(4)=\frac(4)(-4)\]

Ecco la nostra risposta finale. E, nonostante il fatto che nel processo di risoluzione avessimo coefficienti con una funzione quadratica, tuttavia, si sono cancellati a vicenda, il che rende l'equazione esattamente lineare, non quadrata.

Compito n.2

\[\sinistra(1-4x \destra)\sinistra(1-3x \destra)=6x\sinistra(2x-1 \destra)\]

Facciamo il primo passo con attenzione: moltiplichiamo ogni elemento della prima parentesi per ogni elemento della seconda. In totale, dopo le trasformazioni si dovrebbero ottenere quattro nuovi termini:

E ora esegui attentamente la moltiplicazione in ciascun termine:

Spostiamo i termini con "x" a sinistra e senza - a destra:

\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]

Ecco termini simili:

Abbiamo ricevuto una risposta definitiva.

Sfumature della soluzione

L'osservazione più importante su queste due equazioni è questa: non appena iniziamo a moltiplicare le parentesi in cui c'è più di un termine, lo facciamo secondo la seguente regola: prendiamo il primo termine dal primo e moltiplichiamo con ciascun elemento dal secondo; quindi prendiamo il secondo elemento dal primo e moltiplichiamo allo stesso modo con ciascun elemento del secondo. Di conseguenza, otteniamo quattro termini.

Sulla somma algebrica

Con l'ultimo esempio vorrei ricordare agli studenti cos'è una somma algebrica. Nella matematica classica, per $1-7$ intendiamo una costruzione semplice: sottraiamo sette da uno. In algebra, con questo intendiamo quanto segue: al numero "uno" aggiungiamo un altro numero, vale a dire "meno sette". Questa somma algebrica differisce dalla solita somma aritmetica.

Non appena esegui tutte le trasformazioni, ogni addizione e moltiplicazione, inizi a vedere costruzioni simili a quelle sopra descritte, semplicemente non avrai problemi in algebra quando lavori con polinomi ed equazioni.

In conclusione, diamo un'occhiata ad un altro paio di esempi che saranno ancora più complessi di quelli che abbiamo appena visto e per risolverli dovremo espandere leggermente il nostro algoritmo standard.

Risoluzione di equazioni con una frazione

Per risolvere tali compiti, sarà necessario aggiungere un ulteriore passaggio al nostro algoritmo. Ma prima ricorderò il nostro algoritmo:

1. Parentesi aperte.
2. Variabili separate.
3. Porta simili.
4. Dividi per un fattore.

Purtroppo, questo meraviglioso algoritmo, nonostante tutta la sua efficienza, non è del tutto appropriato quando abbiamo di fronte le frazioni. E in quello che vedremo di seguito, in entrambe le equazioni abbiamo una frazione a sinistra e una a destra.

Come lavorare in questo caso? Sì, è molto semplice! Per fare ciò, è necessario aggiungere un ulteriore passaggio all'algoritmo, che può essere eseguito sia prima che dopo la prima azione, vale a dire eliminare le frazioni. Pertanto, l’algoritmo sarà il seguente:

1. Sbarazzarsi delle frazioni.
2. Parentesi aperte.
3. Variabili separate.
4. Porta simili.
5. Dividi per un fattore.

Cosa significa "sbarazzarsi delle frazioni"? E perché è possibile farlo sia dopo che prima del primo passaggio standard? Infatti, nel nostro caso, tutte le frazioni sono numeriche in termini di denominatore, cioè ovunque il denominatore è solo un numero. Pertanto, se moltiplichiamo entrambe le parti dell'equazione per questo numero, elimineremo le frazioni.

Esempio 1

\[\frac(\left(2x+1 \right)\left(2x-3 \right))(4)=((x)^(2))-1\]

Eliminiamo le frazioni in questa equazione:

\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \right)\cdot 4\]

Nota: tutto viene moltiplicato per "quattro" una volta, cioè solo perché hai due parentesi non significa che devi moltiplicarle ciascuna per "quattro". Scriviamo:

\[\left(2x+1 \right)\left(2x-3 \right)=\left(((x)^(2))-1 \right)\cdot 4\]

Ora apriamolo:

Eseguiamo l'isolamento di una variabile:

Effettuiamo la riduzione di termini simili:

\[-4x=-1\sinistra| :\sinistra(-4 \destra) \destra.\]

\[\frac(-4x)(-4)=\frac(-1)(-4)\]

Abbiamo ricevuto la soluzione finale, passiamo alla seconda equazione.

Esempio n.2

\[\frac(\left(1-x \right)\left(1+5x \right))(5)+((x)^(2))=1\]

Qui eseguiamo tutte le stesse azioni:

\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]

\[\frac(4x)(4)=\frac(4)(4)\]

Problema risolto.

Questo, infatti, è tutto ciò che volevo dire oggi.

Punti chiave

I risultati principali sono i seguenti:

• Conoscere l'algoritmo per risolvere equazioni lineari.
• Possibilità di aprire parentesi.
• Non preoccuparti se hai funzioni quadratiche da qualche parte, molto probabilmente, nel processo di ulteriori trasformazioni, verranno ridotte.
• Le radici nelle equazioni lineari, anche quelle più semplici, sono di tre tipi: una radice singola, l'intera linea numerica è una radice, non ci sono radici.

Spero che questa lezione ti aiuti a padroneggiare un argomento semplice, ma molto importante per un'ulteriore comprensione di tutta la matematica. Se qualcosa non è chiaro, vai sul sito, risolvi gli esempi lì presentati. Rimanete sintonizzati, ci sono molte altre cose interessanti che vi aspettano!