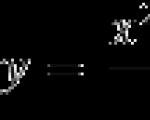B15 uždavinys yra funkcijos tyrimas naudojant išvestinę. Funkcijos tyrimas naudojant išvestinę Funkcijos tyrimas naudojant išvestinę

B15 uždavinyje siūloma ištirti ekstremumo formule pateiktą funkciją. Tai yra standartinė skaičiavimo problema, o jos sudėtingumas labai skiriasi priklausomai nuo nagrinėjamos funkcijos: kai kurios iš jų sprendžiamos pažodžiui žodžiu, o kitos reikalauja rimto mąstymo.

Prieš mokantis sprendimo būdų, būtina įsisavinti kai kuriuos terminus iš matematinės analizės srities. Taigi, B15 uždavinyje, naudojant išvestinę, reikia rasti šiuos dydžius:

1. Vietinio maksimumo (minimalumo) taškai – kintamojo reikšmė, kuriai esant funkcija pasiekia maksimalią (mažiausią) reikšmę. Tokie taškai dar vadinami ekstremumais.
2. Funkcijos visuotinis maksimumas (minimalus) yra maksimali (mažiausia) funkcijos reikšmė pagal nurodytus apribojimus. Kitas pavadinimas – globalūs kraštutinumai.

Šiuo atveju visuotinių ekstremalių paprastai ieškoma ne visoje funkcijos apibrėžimo srityje, o tik tam tikrame segmente. Svarbu suprasti, kad globalus ekstremumas ir funkcijos reikšmė ekstremumo taške ne visada sutampa. Paaiškinkime tai konkrečiu pavyzdžiu:

Užduotis. Raskite funkcijos y = 2x 3 − 3x 2 − 12x + 1 mažiausią tašką ir mažiausią reikšmę atkarpoje [−3; 3].

Pirmiausia randame mažiausią tašką, kuriam apskaičiuojame išvestinę:
y' = (2x 3 - 3x 2 - 12x + 1)' = 6x 2 - 6x - 12.

Raskime kritinius taškus išsprendę lygtį y' = 0. Gauname standartinę kvadratinę lygtį:
y' = 0 ⇒ 6x 2 - 6x - 12 = 0 ⇒ ... ⇒ x 1 = -1, x 2 = 2.

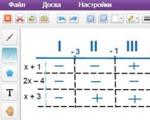
Šiuos taškus pažymime koordinačių tiesėje, pridedame išvestinės ir apribojimų ženklus - atkarpos galus:

Paveikslo mastelis neturi reikšmės. Svarbiausia pažymėti taškus teisinga seka. Iš mokyklinio matematikos kurso žinoma, kad minimaliame taške išvestinė keičia ženklą iš minuso į pliusą. Skaitymas visada vyksta iš kairės į dešinę – teigiamos pusašies kryptimi. Todėl yra tik vienas minimalus taškas: x = 2.

Dabar suraskime mažiausią funkcijos reikšmę segmente [−3; 3]. Jis pasiekiamas arba minimaliame taške (tada jis tampa pasauliniu minimumu), arba atkarpos pabaigoje. Atkreipkite dėmesį, kad intervale (2; 3) išvestinė visur yra teigiama, o tai reiškia, kad y(3) > y(2), todėl dešinės intervalo galo galima nepaisyti. Liko tik taškai x = −3 (kairysis atkarpos galas) ir x = 2 (minimalus taškas). Mes turime:
y(−3) = 2(−3) 3 − 3(−3) 2 − 12(−3) + 1 = −44;
y(2) = 2*2 3 - 3*2 2 - 12*2 + 1 = -19.

Taigi mažiausia funkcijos reikšmė pasiekiama segmento pabaigoje ir lygi –44.

Atsakymas: xmin = 2; ymin = −44

Iš aukščiau pateiktų samprotavimų išplaukia svarbus faktas, kurį daugelis pamiršta. Funkcija įgauna didžiausią (minimalią) reikšmę, nebūtinai kraštutiniame taške. Kartais tokia reikšmė pasiekiama segmento pabaigoje, o ten esanti išvestinė neturi būti lygi nuliui.

Problemų sprendimo schema B15

Jei užduotyje B15 reikia rasti didžiausią arba mažiausią funkcijos f(x) reikšmę intervale , atliekame šiuos veiksmus:

1. Išspręskite lygtį f'(x) = 0. Jei šaknų nėra, trečią žingsnį praleiskite ir eikite tiesiai į ketvirtą.
2. Iš gauto šaknų rinkinio ištrinkite viską, kas yra už segmento ribų. Likę skaičiai bus pažymėti x 1 , x 2 , ..., x n – kaip taisyklė, jų bus mažai.
3. Atkarpos galus ir taškus x 1 , x 2 , ..., x n pakeiskite pradine funkcija. Gauname skaičių aibę f (a), f (b), f (x 1), f (x 2), ..., f (x n), iš kurių pasirenkame didžiausią arba mažiausią reikšmę – tai bus atsakymas.

Šiek tiek paaiškinta apie šaknų ištrynimą, kai jos sutampa su segmento galais. Juos taip pat galima perbraukti, nes ketvirtame žingsnyje atkarpos galai vis tiek pakeičiami į funkciją – net jei lygtis f’(x) = 0 neturėjo sprendinių.

Užduotis. Raskite didžiausią funkcijos y = x 3 + 3x 2 − 9x − 7 reikšmę atkarpoje [−5; 0].

Pirmiausia suraskime išvestinę: y' = (x 3 + 3x 2 - 9x - 7)' = 3x 2 + 6x - 9.

Tada išsprendžiame lygtį: y’ = 0 ⇒ 3x 2 + 6x − 9 = 0 ⇒ ... ⇒ x = −3; x = 1.

Išbraukite šaknį x = 1, nes ji nepriklauso intervalui [−5; 0].

Belieka apskaičiuoti funkcijos reikšmę atkarpos galuose ir taške x = −3:
y(−5) = (−5) 3 + 4 (−5) 2 − 9 (−5) − 7 = −12;
y(−3) = (−3) 3 + 4 (−3) 2 − 9 (−3) − 7 = 20;
y(0) = 0 3 + 4 0 2 − 9 0 − 7 = −7.

Akivaizdu, kad didžiausia reikšmė yra 20 – ji pasiekiama taške x = −3.

Dabar apsvarstykite atvejį, kai reikia rasti didžiausią arba mažiausią funkcijos f(x) tašką intervale . Jei segmentas nenurodytas, funkcija laikoma jos apibrėžimo srityje. Bet kokiu atveju sprendimo schema yra tokia:

1. Raskite funkcijos išvestinę: f'(x).
2. Išspręskite lygtį f’(x) = 0. Jei išvestinė yra trupmeninė racionali funkcija, papildomai išsiaiškiname, kada jos vardiklis lygus nuliui. Gautos šaknys bus pažymėtos x 1 , x 2 , ..., x n .
3. Koordinačių tiesėje pažymėkite x 1 , x 2 , ..., x n ir tarp šių skaičių padėkite ženklus, kuriuos išvestinė ima. Jei nurodytas segmentas, pažymėkite jį ir perbraukite viską, kas yra už jo ribų.
4. Tarp likusių taškų ieškome tokio, kur išvestinės ženklas pasikeičia iš minuso į pliusą (tai yra minimalus taškas) arba iš pliuso į minusą (minimalus taškas). Toks punktas turėtų būti tik vienas – tai bus atsakymas.

Mąstantis skaitytojas tikrai pastebės, kad kai kurioms funkcijoms šis algoritmas neveikia. Tiesą sakant, yra visa klasė funkcijų, kurioms norint rasti ekstremalių taškų reikia sudėtingesnių skaičiavimų. Tačiau matematikos egzamine tokių funkcijų nėra.

Atkreipkite dėmesį į ženklų išdėstymą tarp taškų x 1 , x 2 , ..., x n . Atsiminkite: einant per lyginio dauginio šaknį, išvestinės ženklas nekinta. Ieškant ekstremalių taškų, ženklai visada žiūrimi iš kairės į dešinę, t.y. išilgai skaitinės ašies.

Užduotis. Raskite maksimalų funkcijos tašką

intervale [−8; 8].

Raskime išvestinę:

Kadangi tai yra trupmeninė racionali funkcija, išvestinę ir jos vardiklį prilyginame nuliui:
y' = 0 ⇒ x 2 − 25 = 0 ⇒ ... ⇒ x = 5; x = –5;
x 2 \u003d 0 ⇒ x \u003d 0 (antrojo dauginio šaknis).

Koordinačių tiesėje pažymėkime taškus x = −5, x = 0 ir x = 5, išdėliokime ženklus ir ribas:

Akivaizdu, kad atkarpos viduje lieka tik vienas taškas x = −5, kuriame išvestinės ženklas pasikeičia iš pliuso į minusą. Tai yra maksimalus taškas.

Dar kartą paaiškinkime, kuo ekstremumo taškai skiriasi nuo pačių ekstremalių. Ekstremalūs taškai yra kintamųjų reikšmės, kuriose funkcija įgyja didžiausią arba mažiausią reikšmę. Ekstremalai yra pačių funkcijų reikšmės, maksimalios arba minimalios kai kuriose jų apylinkėse.

Be įprastų daugianarių ir trupmeninių racionaliųjų funkcijų, B15 uždavinyje pasitaiko šių tipų išraiškos:

1. neracionalios funkcijos,
2. trigonometrinės funkcijos,
3. eksponentinės funkcijos,
4. Logaritminės funkcijos.

Paprastai su neracionaliomis funkcijomis problemų nekyla. Likusius atvejus verta apsvarstyti išsamiau.

Trigonometrinės funkcijos

Pagrindinis trigonometrinių funkcijų sunkumas yra tas, kad sprendžiant lygtis atsiranda begalinis šaknų skaičius. Pavyzdžiui, lygtis sin x = 0 turi šaknis x = πn, kur n ∈ Z. Na, kaip jas pažymėti koordinačių tiesėje, jei tokių skaičių yra be galo daug?

Atsakymas paprastas: reikia pakeisti konkrečias n reikšmes. Iš tiesų, problemose B15 su trigonometrinėmis funkcijomis visada yra apribojimas - segmentas. Todėl pirmiausia imame n \u003d 0, o tada didiname n, kol atitinkama šaknis „išskrenda“ už segmento. Panašiai, sumažindami n, labai greitai gausime šaknį, kuri yra mažesnė už apatinę ribą.

Nesunku parodyti, kad šiame intervale nėra kitų šaknų, išskyrus tas, kurios buvo gautos nagrinėjamame procese. Dabar panagrinėkime šį procesą konkrečiais pavyzdžiais.

Užduotis. Raskite funkcijos y = sin x − 5x sin x − 5cos x + 1 maksimalų tašką, priklausantį intervalui [−π/3; π/3].

Apskaičiuokite išvestinę: y’ = (sin x − 5x sin x − 5cos x + 1)’ = ... = cos x − 5x cos x = (1 − 5x) cos x.

Tada išsprendžiame lygtį: y’ = 0 ⇒ (1 − 5x) cos x = 0 ⇒ ... ⇒ x = 0,2 arba x = π/2 + πn, n ∈ Z.

Kai šaknis x = 0,2, viskas aišku, tačiau formulė x = π / 2 + πn reikalauja papildomo apdorojimo. Mes pakeisime skirtingas n reikšmes, pradedant nuo n = 0.

n = 0 ⇒ x = π/2. Bet π/2 > π/3, todėl šaknis x = π/2 į pradinį segmentą neįtraukta. Be to, kuo didesnis n, tuo didesnis x, todėl nėra prasmės laikyti n > 0.

n = −1 ⇒ x = − π/2. Bet −π/2< −π/3 - этот корень тоже придется отбросить. А вместе с ним - и все корни для n < −1.

Pasirodo, intervale [−π/3; π/3] yra tik šaknis x = 0,2. Pažymime jį kartu su ženklais ir ribomis koordinačių linijoje:

Norint įsitikinti, kad išvestinė dešinėje nuo x = 0,2 yra tikrai neigiama, pakanka reikšmę x = π/4 pakeisti y'. Tik pažymime, kad taške x = 0,2 išvestinė keičia ženklą iš pliuso į minusą, todėl tai yra didžiausias taškas.

Užduotis. Raskite didžiausią funkcijos y = 4tg x − 4x + π − 5 reikšmę intervale [−π/4; π/4].

Apskaičiuokite išvestinę: y’ = (4tg x − 4x + π − 5)’ = 4/cos 2x − 4.

Tada išsprendžiame lygtį: y’ = 0 ⇒ 4/cos 2x − 4 = 0 ⇒ ... ⇒ x = πn, n ∈ Z.

Iš šios formulės išskiriame šaknis, pakeisdami specifinį n, pradedant nuo n = 0:
n = 0 ⇒ x = 0. Ši šaknis mums tinka.
n = 1 ⇒ x = π. Bet π > π/4, todėl šaknis x = π ir reikšmės n > 1 turi būti perbrauktos.
n = −1 ⇒ x = −π. Tačiau π< −π/4, поэтому x = π и n < −1 тоже вычеркиваем.

Iš visos šaknų įvairovės lieka tik viena: x = 0. Todėl apskaičiuojame funkcijos reikšmę x = 0, x = π/4 ir x = −π/4.
y(0) = 4tg 0 − 4 0 + π − 5 = π − 5;
y(π/4) = 4tg (π/4) − 4 π/4 + π − 5 = −1;
y(π/4) = 4tg (−π/4) − 4 (−π/4) + π − 5 = ... = 2π − 9.

Dabar atkreipkite dėmesį, kad π = 3,14...< 4, поэтому π − 5 < 4 − 5 = −1 и 2π − 9 < 8 − 9 = −1. Получается одно положительное число и два отрицательных. Мы ищем наибольшее - очевидно, это y = −1.

Atkreipkite dėmesį, kad paskutinėje užduotyje buvo galima nelyginti skaičių tarpusavyje. Iš tikrųjų iš skaičių π - 5, 1 ir 2π - 9 į atsakymų lapą galima įrašyti tik vieną. Iš tiesų, kaip parašyti forma, tarkime, skaičių π? Bet niekaip. Tai svarbi pirmosios matematikos egzamino dalies savybė, labai supaprastinanti daugelio uždavinių sprendimą. Ir tai veikia ne tik B15.

Kartais tiriant funkciją susidaro lygtys, kurios neturi šaknų. Šiuo atveju problema tampa dar paprastesnė, nes lieka atsižvelgti tik į segmento galus.

Užduotis. Raskite mažiausią funkcijos y = 7sin x − 8x + 5 reikšmę intervale [−3π/2; 0].

Pirmiausia randame išvestinę: y’ = (7sin x − 8x + 5)’ = 7cos x − 8.

Pabandykime išspręsti lygtį: y' = 0 ⇒ 7cos x − 8 = 0 ⇒ cos x = 8/7. Tačiau cos x reikšmės visada yra intervale [−1; 1], o 8/7 > 1. Todėl šaknų nėra.

Jei nėra šaknų, tada nieko perbraukti nereikia. Pereiname į paskutinį žingsnį - apskaičiuojame funkcijos reikšmę:
y(−3π/2) = 7sin (−3π/2) − 8 (−3π/2) + 5 = ... = 12π + 12;
y(0) = 7sin 0 − 8 0 + 5 = 5.

Kadangi atsakymų lape negalima įrašyti skaičiaus 12π + 12, lieka tik y = 5.

eksponentinės funkcijos

Paprastai tariant, eksponentinė funkcija yra formos y = a x išraiška, kur a > 0. Tačiau B15 uždavinyje pasitaiko tik y = e x, o kraštutiniu atveju y = e kx + b formos funkcijos. Priežastis ta, kad šių funkcijų išvestis labai lengva apskaičiuoti:

1. (e x)" = e x . Niekas nepasikeitė.
2. (e kx + b)" = k e kx + b. Tiesiog pridedamas koeficientas lygus kintamojo x koeficientui. Tai ypatingas kompleksinės funkcijos išvestinės atvejis.

Visa kita yra visiškai standartinė. Žinoma, tikrosios funkcijos B15 uždaviniuose atrodo sunkesnės, tačiau sprendimo schema nuo to nesikeičia. Panagrinėkime porą pavyzdžių, išryškindami tik pagrindinius sprendimo punktus – be išsamaus samprotavimo ir komentarų.

Užduotis. Raskite mažiausią funkcijos y = (x 2 − 5x + 5)e x − 3 reikšmę atkarpoje [−1; 5].

Išvestinė: y’ = ((x 2 − 5x + 5)e x − 3)’ = ... = (x 2 − 3x)e x − 3 = x(x − 3)e x − 3 .

Raskite šaknis: y' = 0 ⇒ x(x − 3)e x − 3 = 0 ⇒ ... ⇒ x = 0; x=3.

Abi šaknys yra intervale [−1; 5]. Belieka rasti funkcijos reikšmę visuose taškuose:
y(−1) = ((−1) 2 − 5 (−1) + 5)e − 1 − 3 = ... = 11 e −4 ;
y(0) = (0 2 - 5 0 + 5)e 0 - 3 = ... = 5 e -3 ;
y(3) = (3 2 - 5 3 + 5) e 3 - 3 = ... = -1;
y(5) = (5 2 - 5 5 + 5)e 5 - 3 = ... = 5 e 2 .

Iš keturių gautų skaičių į formą galima įrašyti tik y = −1. Be to, tai vienintelis neigiamas skaičius – jis bus mažiausias.

Užduotis. Raskite atkarpoje didžiausią funkcijos y = (2x − 7) e 8 − 2x reikšmę.

Išvestinė: y’ = ((2x − 7) e 8 − 2x)’ = ... = (16 − 4x) e 8 − 2x = 4(4 − x) e 8 − 2x .

Randame šaknis: y' = 0 ⇒ 4(4 − x) e 8 − 2x = 0 ⇒ x = 4.

Šaknis x = 4 priklauso segmentui . Ieškome funkcijų reikšmių:
y(0) = (2 0 - 7) e 8 - 2 0 = ... = -7 e 8 ;
y(4) = (2 4 − 7)e 8 − 2 4 = ... = 1;
y(6) = (2 6 − 7)e 8 − 2 6 = ... = 5 e −4 .

Akivaizdu, kad tik y = 1 gali būti atsakymas.

Logaritminės funkcijos

Analogiškai su eksponentinėmis funkcijomis, uždavinyje B15 atsiranda tik natūralūs logaritmai, nes jų išvestinė yra lengvai apskaičiuojama:

1. (lnx)' = 1/x;
2. (ln(kx + b))' = k/(kx + b). Visų pirma, jei b = 0, tada (ln(kx))' = 1/x.

Taigi išvestinė visada bus trupmeninė racionali funkcija. Belieka tik prilyginti šią išvestinę ir jos vardiklį nuliui, o tada išspręsti gautas lygtis.

Norėdami rasti didžiausią arba mažiausią logaritminės funkcijos reikšmę, atminkite, kad natūralusis logaritmas tampa „normaliu“ skaičiumi tik e n formos taškuose. Pavyzdžiui, ln 1 \u003d ln e 0 \u003d 0 yra logaritminis nulis, ir dažniausiai iki jo redukuojamas sprendimas. Kitais atvejais logaritmo ženklo „nuimti“ neįmanoma.

Užduotis. Raskite atkarpoje mažiausią funkcijos y = x 2 − 3x + ln x reikšmę.

Mes laikome išvestinę:

Randame išvestinės ir jos vardiklio nulius:
y' = 0 ⇒ 2x 2 − 3x + 1 = 0 ⇒ ... ⇒ x = 0,5; x = 1;
x = 0 – nėra ko spręsti.

Iš trijų skaičių x = 0, x = 0,5 ir x = 1 atkarpos viduje yra tik x = 1, o skaičius x = 0,5 yra jo pabaiga. Mes turime:
y(0,5) = 0,5 2 - 3 0,5 + ln 0,5 = ln 0,5 - 1,25;
y(1) = 1 2 - 3 1 + log 1 = -2;
y(5) = 5 2 − 3 5 + ln 5 = 10 + ln 5.

Iš trijų gautų verčių tik y = −2 neturi logaritmo ženklo – tai bus atsakymas.

Užduotis. Raskite atkarpoje didžiausią funkcijos y = ln(6x) − 6x + 4 reikšmę.

Apskaičiuojame išvestinę:

Sužinome, kada išvestinė ar jos vardiklis lygus nuliui:
y' = 0 ⇒ 1 − 6x = 0 ⇒ x = 1/6;
x = 0 – jau nuspręsta.

Nubraukiame skaičių x = 0, nes jis yra už atkarpos ribų. Mes atsižvelgiame į funkcijos reikšmę atkarpos galuose ir taške x = 1/6:
y(0,1) = ln(6 0,1) − 6 0,1 + 4 = ln 0,6 + 3,4;
y(1/6) = log(6 1/6) − 6 1/6 + 4 = log 1 + 3 = 3;
y(3) = ln(6 3) − 6 3 + 4 = ln 18 − 14.

Akivaizdu, kad tik y = 3 gali veikti kaip atsakymas - likusiose reikšmėse yra logaritmo ženklas ir jų negalima užrašyti atsakymų lape.

Taškas vadinamas maksimalus (minimalus) taškas funkcija , jei yra tokia taško kaimynystė, kad visos šios kaimynystės nelygybė ().

Maksimalus ir minimalus funkcijos taškai vadinami taškais. ekstremumas (25 pav.).

3.9 teorema (būtina ekstremumo taškų egzistavimo sąlyga) . Esant kritiniams 1 tipo taškams, funkcijos išvestinė arba

yra nulis arba neegzistuoja

Pirmosios rūšies kritiniai taškai vadinami tiesiog kritiniais taškais.

Vadinami kritiniai taškai, kuriuose funkcijos išvestinė lygi nuliui stacionarumo taškai . Kritiniai taškai, kuriuose funkcija yra ištisinė, bet nediferencijuojama, vadinami kampiniai taškai . Pavyzdžiui, funkcija taške yra ištisinė, bet neturi išvestinės, nes šiame taške funkcijos grafike galima nubrėžti begalinį liestinių skaičių (26 pav.). Šis atvejis gali būti laikomas patvirtinimu, kad priešingas 3.3 teoremos teiginys yra klaidingas.

Funkcija vadinama didėja tam tikru intervalu , jei šiame intervale didesnė argumento reikšmė atitinka didesnę kintamojo reikšmę ir silpsta jei didesnė argumento reikšmė atitinka mažesnę kintamojo reikšmę .

Tolimesniems tyrimams kritiniai taškai dedami ant skaitinės ašies, kuri pagal šiuos taškus padalijama į intervalus, po kurių patikrinamos šios pakankamos sąlygos.

3.10 teorema (pakankama sąlyga funkcijai didėti ir mažėti). Jei funkcija yra diferencijuota tam tikru intervalu, o jos išvestinė yra teigiama (neigiama), tada funkcija šiame intervale didėja (mažėja)

3.11 teorema (pakankama funkcijos ekstremalių taškų egzistavimo sąlyga). Jei funkcija yra ištisinė ir diferencijuojama kurioje nors kritinio taško kaimynystėje, o einant pro jį išvestinė keičia ženklą iš pliuso į minusą, tai taškas yra maksimalus taškas; jei nuo minuso iki pliuso, tai taškas yra mažiausias funkcijos taškas

Tie kritiniai funkcijos taškai, kuriems netenkinama pakankama sąlyga, lieka tiesiog pirmos rūšies kritiniais taškais.

Pirmosios rūšies kritiniai taškai, kuriuose darinys neegzistuoja, skirstomi į dvi klases:

yra taškai, kuriuose funkcija yra tolydi (kai tenkinama 3.11 teorema, funkcija šiuose taškuose turi „aštrią“ ekstremumą), tai yra kampas taškų;

yra taškai, kuriuose funkcija nutrūksta (jie visada patenka į 2-osios rūšies kritinių taškų klasę).

Bet tokiu būdu atliktas tyrimas neduoda atsakymo į labai svarbų klausimą: kaip funkcija didėja (sumažėja) – išgaubta ar įgaubta? Atsakymą į šį klausimą duoda tolesnis funkcijos tyrimas naudojant antrąją išvestinę. Pateiksime keletą būtinų apibrėžimų.

Funkcija vadinama išgaubtas (įgaubtas) tam tikrame intervale, jei funkcijos grafiko liestinė kiekviename šio intervalo taške yra aukščiau (žemiau) funkcijos grafiko.

Taškai, skiriantys funkcijos išgaubimo sritis nuo įgaubimo sričių, vadinami jos vingio taškai (27 pav.).

3.12 teorema (būtina vingio taškų egzistavimo sąlyga). Kritiniuose 2-osios rūšies taškuose antroji funkcijos išvestinė yra lygi nuliui arba jos nėra

Tolimesniems tyrimams antrosios rūšies kritiniai taškai dedami ant skaitinės ašies, kuri pagal šiuos taškus padalijama į intervalus, po kurių patikrinamos šios pakankamos sąlygos.

3.13 teorema (pakankama funkcijos išgaubimo ir įgaubimo sąlyga). Jei funkcija yra du kartus diferencijuojama tam tikru intervalu, o jos antroji išvestinė yra teigiama (neigiama), tada funkcija šiame intervale yra įgaubta (išgaubta)

Tie kritiniai funkcijos taškai, kuriems netenkinama pakankama sąlyga, lieka tiesiog antrosios rūšies kritiniais taškais.

Antrosios rūšies kritiniai taškai, kuriuose antroji išvestinė neegzistuoja, skirstomi į dvi klases:

- taškai, kuriuose funkcija yra ištisinė, tai vadinamieji "aštrūs" vingio taškai - tokiuose taškuose funkcijos grafike galima nubrėžti begalinį liestinių skaičių (28 pav.);

yra taškai, kuriuose funkcija nutrūksta (antrosios rūšies nenutrūkstamumo taškuose funkcijos grafikas turi vertikalią asimptotę).

Norint galutinai surašyti funkcijos ekstremumo ir vingio taškus, reikia rasti jų ordinates, o tada užrašyti nurodytus taškus dviem koordinatėmis.

Klausimai savęs patikrinimui.

1. Kokie funkcijos taškai vadinami ekstremaliais taškais (maksimumu ir minimumu)?

2. Kokia funkcija vadinama didinančia (mažėjančia)?

3. Kokios būtinosios ir pakankamos sąlygos funkcijos ekstremaliems taškams egzistuoti?

4. Kokia yra pakankama funkcijos padidėjimo (sumažėjimo) sąlyga?

5. Kokie taškai vadinami funkcijos vingio taškais?

6. Kokia funkcija vadinama išgaubta (įgaubta)?

7. Kokios būtinosios ir pakankamos sąlygos funkcijos vingio taškams egzistuoti?

8. Kokia yra pakankama funkcijos išgaubtumo (įgaubtumo) sąlyga?

Pamokos tikslas: Išmokyti atlikti funkcijų tyrimą; juos suplanuoti.

Forma: pokalbio pamoka.

Metodai: dialogai, vaizdinės priemonės ir skaidrės.

Įranga: IKT, lentelės.

Per užsiėmimus

I. Namų darbų tikrinimas.

Mokytojas: - Vaikinai! Turėjai namų darbą „Kritiniai funkcijos taškai, maksimumai ir minimumai“. Apibrėžkite kritinį funkcijos tašką.

Mokinys: - Kritinis taškas yra vidinis apibrėžimo srities taškas, kuriame išvestinė arba lygi nuliui, arba neegzistuoja.

Mokytojas: – Kaip rasti kritinius taškus?

Mokinys: - 1

) Raskite funkcijos išvestinę;

2) Išspręskite lygtį: f "(x) = 0. Šios lygties šaknys yra kritiniai taškai.

Mokytojas: - Raskite svarbiausius funkcijų taškus:

a) f(x)= 4 - 2x + 7x 2

b) f (x) \u003d 4x - x 3/3

a) 1) Raskite šios funkcijos išvestinę:

f "(x) = (4 - 2x + 7x 2)" = -2 + 14x

2) Išspręskite lygtį f "(x) = 0<=>-2+14x=0<=>x = 1/7

3) Kadangi lygtis f "(x) \u003d 0 turi vieną šaknį, tada ši funkcija turi vieną kritinį tašką x \u003d 1/7.

b) 1) Raskite šios funkcijos išvestinę: f "(x) \u003d 4 - x 2

2) Išspręskite lygtį: f "(x) = 0<=>4 - x 2 = 0<=>x=2 arba x=-2

3) Kadangi lygtis f "(x) \u003d 0 turi dvi šaknis, tada ši funkcija turi du kritinius taškus x 1 \u003d 2 ir x 2 \u003d -2.

II.žodinis darbas.

Mokytojas: - Vaikinai! Pakartokime pagrindinius klausimus, kurių reikia norint studijuoti naują temą. Norėdami tai padaryti, apsvarstykite lenteles su skaičiais ( 1 priedas).

Nurodykite taškus, kuriuose funkcijos padidėjimas pakeičiamas sumažėjimu. Kaip tie taškai vadinami?

Mokinys: - Paveikslėlyje a) - taškas K yra didžiausias taškas, b) paveiksle - taškas M yra didžiausias taškas.

Mokytojas: - Kokie yra minimalūs funkcijos taškai.

Mokinys: - Taškas K paveikslėlyje c) ir d) - mažiausias funkcijos taškas.

Mokytojas: - Kokie taškai gali būti funkcijos ekstremalūs taškai?

Mokinys: - Kritiniai taškai gali būti funkcijos ekstremalūs taškai.

Mokytojas: – Kokias būtinas sąlygas žinai?

Studentas: - Yra Ferma teorema. Būtina ekstremumo sąlyga: Jei taškas x 0 yra funkcijos f ekstremumo taškas ir šiame taške yra išvestinė f ", tada jis yra lygus nuliui: f" (x) \u003d 0.

Mokytojas: - Raskite svarbiausius funkcijos taškus:

a) f(x) = | x |

b) f(x) = 2x + | x |

Mokinys: - Apsvarstykite funkciją f(x) = | x | ( paraiška 2). Ši funkcija neturi išvestinės ties 0. Vadinasi, 0 yra kritinis taškas. Akivaizdu, kad taške 0 funkcija turi minimumą.

Mokinys: - Apsvarstykite funkciją f(x) = 2x + | x | ( 3 priedas). Grafikas rodo, kad taške 0 ši funkcija neturi ekstremumo. Šiuo metu funkcija taip pat neturi išvestinės.

Iš tiesų, jei darysime prielaidą, kad funkcijos f išvestinė yra 0, tai f(x) - 2x taip pat turi išvestinę, kai yra 0. Tačiau f(x) - 2x = | x | ir funkcija | x | taške 0 nėra diferencijuojamas, t.y. mes priėjome prieštaravimą.

Tai reiškia, kad funkcija f taške 0 neturi išvestinės.

Mokytojas: - Iš Ferma teoremos išplaukia, kad ieškant ekstremalių taškų reikia rasti kritinius taškus. Tačiau iš nagrinėjamų pavyzdžių aišku, kad tam, kad šis kritinis taškas būtų ekstremalus taškas, reikia tam tikrų papildomų sąlygų.

Ar žinote, kokios yra pakankamos sąlygos ekstremumui egzistuoti taške?

Studentas: - Maksimalios funkcijos ženklas: jei funkcija f yra ištisinė taške x 0, o f "(x)> 0 intervale (a; x 0) ir f "(x)<0 на интервале (х 0 ; в), то точка х 0 является точкой максимума функции f.

Tai yra, jei taške x 0 išvestinė keičia ženklą iš pliuso į minusą, tai x 0 yra didžiausias taškas.

Studentas: - Minimalumo ženklas: Jei funkcija f yra ištisinė taške x 0, o f "(x)<0 на интервале (а;х 0) и f "(x) >0 intervale (x 0 ; c), tada taškas x 0 yra mažiausias funkcijos f taškas.

Tai yra, jei taške x 0 išvestinė pakeičia ženklą iš minuso į pliusą, tada x 0 yra mažiausias taškas.

Mokytojas: - O kokį algoritmą funkcijos ekstremaliems taškams rasti tu žinai.

Studentas paaiškina funkcijos f tyrimo ekstremumui algoritmą naudojant išvestinę ( 4 priedas) ir suranda funkcijos kraštutinius taškus:

f (x) \u003d x 4 -2x 2

D (f) =IR ir f yra tolydis visoje realioje tiesėje, kaip visa racionali funkcija.

2. f "(x) \u003d 4x 3 -4x \u003d 4x (x + 1) (x-1).

3.f"(x)=0<=>x \u003d -1 V x \u003d 0 V x \u003d 1.

1 pav (f" ženklai)

Kadangi f yra ištisinis kritiniuose taškuose, iš 1 paveikslo ( 5 priedas) matyti, kad -1 ir 1 yra minimalūs taškai, o 0 yra maksimalus funkcijos f taškas.

f min \u003d f (-1) \u003d f (1) \u003d -1, f max \u003d f (0) \u003d 0.

Mokytojas: - Vaikinai! Prisiminkime funkcijos f monotoniškumo intervalų paieškos algoritmą.

Mokinys prisimena funkcijos f ( () monotoniškumo intervalų paieškos algoritmą 6 priedas).

Mokytojas: - Raskite funkcijos f didėjimo ir mažėjimo intervalus, pateiktus formule

f (x) \u003d x 3 -12x

Sprendimas:

1. Kadangi f(x) yra daugianario, tai D (f) =IR.

2. Funkcija f yra diferencijuojama visoje realioje eilutėje ir f "(x) \u003d 3x 2 -12 \u003d 3 (x + 2) (x-2).

3. Tik f "(x) nuliai gali būti kritiniais funkcijos f taškais.

f"(x)=0<=>x \u003d -2 V x \u003d 2.

D (f) \ (-2; 2) \u003d (-; -2) U (-2; 2) U (2; +).

Fig.2 (ženklai f ").

Raskite pateiktos funkcijos f apibrėžimo ir reikšmių sritis.

Sužinokite, ar funkcija turi ypatybių, kurios palengvina jos tyrimą, ty yra funkcija f:

a) lyginis arba nelyginis;

b) periodiškai.

3. Apskaičiuokite grafiko susikirtimo taškų koordinates su koordinačių ašimis.

4. Raskite funkcijos f pastovumo intervalus.

5. Išsiaiškinkite, kokiais intervalais funkcija f didėja, o kuriais mažėja.

6. Raskite kraštutinius taškus (maksimumą arba minimumą) ir apskaičiuokite f reikšmes šiuose taškuose.

7. Ištirkite funkcijos f elgseną būdingų taškų, neįeinančių į apibrėžimo sritį, kaimynystėje.

8. Nubraižykite funkciją.

Ši diagrama yra iliustracinė.

Atsižvelgdami į visa tai, kas išdėstyta aukščiau, išnagrinėjame funkciją: f (x) \u003d 3x 5 -5x 3 +2 ir sudarome jos grafiką.

Atlikime tyrimą taip:

D (f ") =IR, nes f (x) yra daugianario.

Funkcija f nėra nei lyginė, nei nelyginė, nes

f (-x) = 3 (-x) 5 -5 (-x) 3 +2 = -3x 5 +5x 3 +2 = -(3x 5 -5x 3 -2) f(x)

Raskite grafiko susikirtimo taškų koordinates su koordinačių ašimis:

a) su 0X ašimi sprendžiame lygtį: 3x 5 -5x 3 +2 = 0.

Pasirinkimo metodas gali rasti vieną iš šaknų (x = 1). Kitų šaknų galima rasti tik apytiksliai. Todėl šiai funkcijai likusių grafiko susikirtimo su abscisių ašimi taškų ir pastovaus ženklo intervalų nerasime.

b) su 0Y ašimi: f(0)=2

Taškas A (0; 2) – funkcijos grafiko susikirtimo taškas su 0Y ašimi.

Pažymėjome, kad ženklų pastovumo intervalų nerasime.

Raskite funkcijos didėjimo ir mažėjimo intervalus

a) f "(x) \u003d 15x 4 -15x 2 \u003d 15x 2 (x 2 -1)

D (f ") \u003d IR, todėl nėra kritinių taškų, kurių f "(x) neegzistuotų.

b) f "(x) \u003d 0, jei x 2 (x 2 -1) \u003d 0<=>x = -1 V x = 0 V x = 1.

c) Gauname tris kritinius taškus, jie padalina koordinačių tiesę į keturis intervalus. Nustatykime išvestinės ženklą šiais intervalais:

3 pav (f" ženklai)

IV. Naujos temos taisymas. Problemų sprendimas.

Mokytojas: - Ištirkite funkciją ir sukurkite jos grafiką: f (x) \u003d x 4 -2x 2 -3.

Mokinys: - 1) D (f) =R.

2) f (-x) \u003d (-x) 4 -2 (-x) 2 -3 \u003d x 4 -2x 2 -3; f(-x)= f(x),

vadinasi, funkcija f yra lyginė. Jį galima tirti intervale, kai funkcija didėja nuo - iki -4, todėl lygtis f (x) \u003d 0 šiame intervale neturi šaknų.

b) Ant intervalo [-1; 2] lygtis taip pat neturi šaknų, nes šiame intervale funkcija sumažėja nuo -4 iki -31.

c) Ant intervalo ir mažėja ant [-∞;-1].

Kraštutiniai taškai: x min = -1

Funkcijos ekstremumai: y min =y(-1)=1-2= -1

III skyrius. Funkcijų tyrimas.

3.1. Bendra funkcijų tyrimo schema.

Nagrinėdami funkciją, turite žinoti bendrą tyrimo schemą:

1) D(y) – apibrėžimo sritis (kintamojo x diapazonas)

2) E(y) – x reikšmės sritis (kintamojo y diapazonas)

3) Funkcijos tipas: lyginė, nelyginė, periodinė arba bendroji funkcija.

4) Funkcijos grafiko susikirtimo taškai su Ohi Oy ašimis (jei įmanoma).

5) Ženklo pastovumo intervalai:

a) funkcija įgyja teigiamą reikšmę: f(x)>0

b) neigiama reikšmė: f(x)<0.

6) Funkcijos monotoniškumo intervalai:

a) padidinti;

b) mažėti;

c) pastovumas (f=const).

7) Kraštutiniai taškai (minimalus ir maksimalus taškai)

8) Funkcijos ekstremumai (funkcijos reikšmė minimaliuose ir didžiausiuose taškuose)

9) Papildomi taškai.

Juos galima paimti norint tiksliau nubraižyti funkciją.

Reikėtų pažymėti, kad funkcijos f ekstremumai ne visada sutampa su maksimalia ir mažiausia funkcijos reikšmėmis.

3.2. Didėjančių ir mažėjančių funkcijų požymis.

Jei sukursite funkcijos grafiką naudodami kai kuriuos savavališkai pasirinktus jos taškus, sujungdami juos lygia linija, tada net ir esant labai dideliam atsitiktinai parinktų taškų skaičiui gali pasirodyti, kad taip sudarytas grafikas bus labai skirtingas. iš duotosios funkcijos grafiko.

Jeigu tirdami funkciją panaudosime išvestinę ir rasime vadinamuosius „atskaitos“ taškus, t.y. lūžio taškai, didžiausi ir mažiausi taškai, funkcijos monotoniškumo intervalai, tada net ir su nedideliu tokių „atskaitos“ taškų skaičiumi gausime teisingą funkcijų grafiko idėją.

Prieš pereidamas prie pavyzdžių, pateiksiu reikiamus apibrėžimus ir teoremas.

Funkcijos monotoniškumo intervale apibrėžimas Funkcija y \u003d f (x) vadinama didėjančia intervale, jei bet kuriuose šio intervalo taškuose x 1 ir x 2 iš sąlygos x 1<х 2 следует, что f(x 1)f(x 2), tada funkcija vadinama mažėjančia šiame intervale.

Pakankamas funkcijos monotoniškumo intervale kriterijus. Teorema: jei funkcija turi teigiamą (neigiamą) išvestinę kiekviename intervalo taške, tai funkcija šiame intervale didėja (mažėja).

Ši teorema priimta į mokyklinius vadovėlius be įrodymų.

Geometrinis teoremos aiškinimas yra labai paprastas, jei prisiminsime, kad f '(x) \u003d tgα, α yra funkcijos grafiko liestinės nuolydis duotame taške x. Jei, pavyzdžiui, f ‘ (x)> 0 visuose tam tikro intervalo taškuose, tai grafiko liestinė su abscisių ašimi sudaro aštrius kampus, o tai reiškia, kad f (x) taip pat didėja su x. Jei f' (x)<0, то касательная с осью абсцисс образуют тупой угол, а значит, с ростом х функция f(x) убывает. Поскольку эти рассуждения основаны лишь на наглядных геометрических представлениях, они не являются доказательством теоремы.

3.3. Kritiniai funkcijos taškai, maksimumai ir minimumai.

Funkcijos ekstremalių taškų nustatymas . Tegu x 0 yra funkcijos f(x) srities vidinis taškas. Tada, jei yra tokia δ - kaimynystė ] x 0 - δ, x 0 + δ [ taškai x 0 , kad visiems x iš šios kaimynystės tenkinama nelygybė f(x)≤f(x 0) (nelygybė f (x)≥f (x 0)), taškas x 0 vadinamas didžiausiu šios funkcijos tašku (minimaliu tašku).

Maksimalus-minimalus taškai yra vidiniai funkcijos srities taškai.

Būtinas diferencijuojamos funkcijos ekstremumo egzistavimo kriterijus .

Fermato teorema.

Jei x 0 yra funkcijos f (x) ekstremumo taškas ir šiuo metu išvestinė egzistuoja, tada ji lygi nuliui: f '(x 0) \u003d 0.

Ši teorema nėra pakankama sąlyga diferencijuojamos funkcijos ekstremumui egzistuoti: jeigu kažkuriame x 0 taške išvestinė išnyksta, tai dar neišplaukia, kad taške x 0 funkcija turi ekstremumą.

Funkcijos kritinių taškų apibrėžimas . Funkcijos srities vidiniai taškai, kuriuose jos išvestinė lygi nuliui arba neegzistuoja, vadinami kritiniais funkcijos taškais.

Pakankamos sąlygos egzistuoti ekstremumui .

1 teorema. Jei funkcija f (x) yra ištisinė taške x 0, f '(x)> 0 intervale ir f '(x)<0 на интервале , то х 0 является точкой максимума функции f(x).

2 teorema. Jei funkcija f (x) yra ištisinė taške x 0, f ‘(x)<0 на интервале и f ‘(x)>0 intervale, tada x 0 yra funkcijos f(x) mažiausias taškas.

Norint rasti funkcijos ekstremalinius taškus, būtina rasti jos kritinius taškus ir kiekvienam iš jų patikrinti, ar įvykdomos pakankamos ekstremumo sąlygos.

3.4. Didžiausios ir mažiausios funkcijos reikšmės.

Taisyklės, kaip rasti didžiausią ir mažiausią funkcijų reikšmes intervale. Norėdami rasti didžiausią ir mažiausią funkcijos reikšmes, kurios skiriasi tam tikru intervalu, turite rasti visus kritinius taškus, esančius intervale, apskaičiuoti funkcijos reikšmes šiuose taškuose ir galuose. intervalą ir iš visų tokiu būdu gautų funkcijos reikšmių pasirinkite didžiausią ir mažiausią.

IV skyrius. Išvestinės taikymo funkcijos tyrimui pavyzdžiai.

11 pavyzdys. Išnagrinėkite funkciją y=x 3 +6x 2 +9x ir sukurkite grafiką.

2) Apibrėžkite funkcijos tipą:

y(-x)=(-x) 3 +6(-x) 2 +9(-x)=-x+6x 2 -9x bendroji funkcija.

x=0 arba x2 +6x+9=0

D=0, lygtis turi vieną šaknį.

(0;0) ir (-3;0) – susikirtimo su x ašimi taškai.

y'=(x 3 +6x 2 +9x)'=3x 2 +12x+9

y'=0, t.y. 3x 2 +12x+9=0 sumažinkite 3

D>0, lygtis turi 2 šaknis.

x 1,2 \u003d (-b±√D) / 2a, x 1 \u003d (-4 + 2) / 2, x 2 \u003d (-4-2) / 2

0
-4

x=-4, y’=3*16-48+9=9>0

x=-2, y'=12-24+9=-3<0

x=0, y'=0+0+9=9>0

7) Raskite x min ir x max:

8) Raskite funkcijos kraštutinumą:

ymin=y(-1)=-1+6-9=-4

ymax=y(-3)=-27+54-27=0

9) Sukurkime funkcijos grafiką:

10) Papildomi punktai:

y(-4)=-64+96-36=-4

12 pavyzdys. Išnagrinėkite funkciją y=x 2 /(x-2) ir sukurkite grafiką

y=x 2 /(x-2)=x+2+4/(x-2)

Raskime funkcijos asimptotes:

x≠ 2, x=2 – vertikali asimptotė

y=x+2 yra įstrižinė asimptotė, nes

Raskime apibrėžimo sritį.

2) Apibrėžkime funkcijos tipą.

y(-x)=(-x) 2 /(-x-2)=x 2 /(-x-2), bendroji funkcija.

3) Raskite susikirtimo su ašimis taškus.

Oy: x=0, y=0 (0;0) – susikirtimo su y ašimi taškas.

x=0 arba x=2 (2;0) – susikirtimo su x ašimi taškas

4) Raskite funkcijos išvestinę:

y'=(2x(x-2)-x 2)/(x-2) 2 =(2x 2 -4x-x 2)/(x-2) 2 =(x(x-4))/(x -2) 2 \u003d (x 2 -4x) / (x-2) 2

5) Apibrėžkite kritinius taškus:

x 2 -4x=0 x(x-4)=0

y'=0, (x 2 -4x)/(x-2) 2 =0<=> <=>

(x-2) 2 ≠ 0 x ≠ 2

x 2 -4x=0 ir (x-2) 2 ≠ 0, t.y. x≠ 2

6) Koordinačių tiesėje pažymime kritinius taškus ir nustatome funkcijos ženklą.

0 8

x=-1, y'=(1+4)/9=5/9>0

x=1, y’=(1-4)/1=-3<0

x=3, y’=(9-12)/1=-3<0

x=5, y’=(25-20)/9=5/9>0

7) Raskite funkcijos mažiausią ir didžiausią tašką:

8) Raskite funkcijos kraštutinumą:

ymin=y(4)=16/2=8

9) Sukurkime funkcijos grafiką:

10) Papildomi punktai:

y(-3)=9/-5=-1,8 y(3)=9/1=9

y(1)=1/-1=-1 y(6)=36/4=9

13 pavyzdys Išnagrinėkite funkciją y=(6(x-1))/(x 2 +3) ir sukurkite grafiką. 1) Raskite funkcijos domeną:

2) Apibrėžkite funkcijos tipą:

y(-x)=(6(-x-1))/(x 2 +3)=-(6(x+1))/(x 2 -3) yra bendroji funkcija.

3) Raskite susikirtimo su ašimis taškus:

O y: x=0, y=(6(0-1))/(0+3)=-2, (0;-2) – susikirtimo su y ašimi taškas.

(6(x-1))/(x 2 +3)=0

O x: y=0,<=>

4) Raskite funkcijos išvestinę:

y'=(6(x-1)/(x 2 +3))'=6(x 2 +3-2x 2 +2x)/(x 2 +2) 2 = -6(x+1)(x -3)/(x 2 +3) 2

5) Apibrėžkite kritinius taškus:

y'=0, t.y. -6(x+1)(x-3)/(x 2 +3) 2 =0

y’=0, jei x 1 =-1 arba x 2 =3, tai x=-1 ir x=3, kritiniai taškai.

6) Koordinačių tiesėje pažymime kritinius taškus ir nustatome funkcijos ženklą:

-3 2

x=-2, y'=-6(-2+1)(-2-3)/(4+3)2 =-30/49<0

x=0, y’=-6(0+1)(0-3)/(0+3) 2 =2>0

x=4, y’=-6(4+1)(4-3)/(16+3) 2=-30/361<0

7) Raskite minimalų ir maksimalų taškų skaičių:

8) Raskite funkcijos kraštutinumą:

y min =y(-1)=(6(-1-1))/(1+3)=-12/4=-3

y max =y(3)=(6(3-1))/(9+3)=12/12=1

9) Sukurkime funkcijos grafiką:

10) Papildomi punktai:

y(-3)=(6(-3-1))/(9+3)=-24/12=-2

y(6)=(6(6-1))/(36+3)=30/39=10/13≈ 0,77

14 pavyzdys Išnagrinėkite funkciją y=xlnx ir sukurkite jos grafiką:

1) Raskite funkcijos domeną:

D(y) = R + (tik teigiamos reikšmės)

2) Apibrėžkite funkcijos tipą:

y(-x)=-xlnx – bendroji forma.

3) Raskite susikirtimo su ašimis taškus:

O y , bet x≠ 0, todėl susikirtimo su y ašimi taškų nėra.

Ox: y=0, ty xlnx=0

x=0 arba lnx=0

(1;0) - susikirtimo su x ašimi taškas

4) Raskite funkcijos išvestinę:

y'=x' ln x + x(ln x)'=ln x +1

5) Apibrėžkite kritinius taškus:

y'=0, t.y. lnx +1=0

y'=0 , jei x=1/e , tai x=1/e yra kritinis taškas.

6) Koordinačių tiesėje pažymime kritinius taškus ir nustatome funkcijos ženklą:

1/e

x=1/(2e); y'=log(2e) -1 +1=1-ln(2e)=1-ln e=-ln 2<0

x=2e; y'=ln(2e)+1=ln 2+ln e+1=ln 2+2>0

7) 1/e yra mažiausias funkcijos taškas.

8) Raskite funkcijos kraštutinumą:

y min \u003d y (1 / e) \u003d 1 / e ln e -1 \u003d -1 / e (≈ -0,4).

9) Sukurkime funkcijos grafiką:

Išvada.

Daug mokslininkų ir filosofų dirbo šia tema. Prieš daugelį metų atsirado šie terminai: funkcija, grafikas, funkcijos tyrimas ir jie išliko iki šių dienų, įgavę naujų bruožų ir savybių.

Pasirinkau šią temą, nes man buvo labai įdomu eiti šiuo funkcijų tyrimo keliu. Man atrodo, kad daugeliui žmonių būtų įdomu sužinoti daugiau apie funkciją, jos savybes ir transformacijas. Padaręs šį rašinį, susisteminau savo įgūdžius ir papildžiau žinias šia tema.

Noriu visiems patarti panagrinėti šią temą giliau.

Bibliografija.

1. Bašmakovas, M.I. Algebra ir analizės pradžia.- M .: Išsilavinimas, 1992 m.

2. Glaseris, G.I. Matematikos istorija mokykloje. - M .: Švietimas, 1983 m.

3. Gusevas, V.A. Matematika: informacinė medžiaga.- M .: Išsilavinimas, 1888 m.

4. Dorofejevas, G.V. Matematikos vadovas stojantiesiems į universitetus.- M .: Nauka, 1974 m.

5. Zorinas, V.V. Matematikos vadovas stojantiesiems į universitetus.- M .: Aukštoji mokykla, 1980 m.

6. Kolmogorovas A.N. Algebra ir analizės pradžia.- M.: Švietimas, 1993 m.