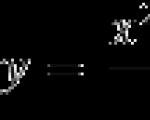ഒരു ഡെറിവേറ്റീവ് ഉപയോഗിച്ച് ഒരു ഫംഗ്ഷനെക്കുറിച്ചുള്ള പഠനമാണ് പ്രശ്നം B15. ഒരു ഡെറിവേറ്റീവ് ഉപയോഗിച്ച് ഒരു ഫംഗ്ഷന്റെ അന്വേഷണം ഒരു ഡെറിവേറ്റീവ് ഉപയോഗിച്ച് ഒരു ഫംഗ്ഷന്റെ അന്വേഷണം

പ്രശ്നം B15-ൽ, എക്സ്ട്രീമുകൾക്കുള്ള ഫോർമുല നൽകുന്ന ഫംഗ്ഷൻ അന്വേഷിക്കാൻ നിർദ്ദേശിക്കപ്പെട്ടിരിക്കുന്നു. ഇത് കാൽക്കുലസിലെ ഒരു സ്റ്റാൻഡേർഡ് പ്രശ്‌നമാണ്, ചോദ്യം ചെയ്യപ്പെടുന്ന പ്രവർത്തനത്തെ ആശ്രയിച്ച് അതിന്റെ സങ്കീർണ്ണത വളരെ വ്യത്യാസപ്പെട്ടിരിക്കുന്നു: അവയിൽ ചിലത് അക്ഷരാർത്ഥത്തിൽ വാക്കാൽ പരിഹരിക്കപ്പെടുന്നു, മറ്റുള്ളവയ്ക്ക് ഗൗരവമായ ചിന്ത ആവശ്യമാണ്.

പരിഹാരത്തിന്റെ രീതികൾ പഠിക്കുന്നതിനുമുമ്പ്, ഗണിതശാസ്ത്ര വിശകലന മേഖലയിൽ നിന്ന് ചില നിബന്ധനകൾ പഠിക്കേണ്ടത് ആവശ്യമാണ്. അതിനാൽ, പ്രശ്നം B15 ൽ, ഡെറിവേറ്റീവ് ഉപയോഗിച്ച് ഇനിപ്പറയുന്ന അളവുകൾ കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്:

1. പ്രാദേശിക പരമാവധി (കുറഞ്ഞത്) പോയിന്റുകൾ - ഫംഗ്ഷൻ അതിന്റെ പരമാവധി (ചെറിയ) മൂല്യത്തിൽ എത്തുന്ന വേരിയബിളിന്റെ മൂല്യം. അത്തരം പോയിന്റുകളെ എക്സ്ട്രീം പോയിന്റുകൾ എന്നും വിളിക്കുന്നു.
2. നിർദ്ദിഷ്‌ട നിയന്ത്രണങ്ങൾക്ക് കീഴിലുള്ള ഫംഗ്‌ഷന്റെ പരമാവധി (ചെറിയ) മൂല്യമാണ് ഫംഗ്‌ഷന്റെ ആഗോള പരമാവധി (മിനിമം). ഗ്ലോബൽ എക്സ്ട്രീംസ് എന്നാണ് മറ്റൊരു പേര്.

ഈ സാഹചര്യത്തിൽ, ഗ്ലോബൽ എക്‌സ്ട്രീമ സാധാരണയായി ഫംഗ്‌ഷൻ നിർവചനത്തിന്റെ മുഴുവൻ ഡൊമെയ്‌നിലും അല്ല, ഒരു പ്രത്യേക വിഭാഗത്തിൽ മാത്രമാണ് അന്വേഷിക്കുന്നത്. ഗ്ലോബൽ എക്‌സ്ട്രീമും എക്‌സ്ട്രീം പോയിന്റിലെ ഫംഗ്‌ഷന്റെ മൂല്യവും എല്ലായ്പ്പോഴും പൊരുത്തപ്പെടുന്നില്ലെന്ന് മനസ്സിലാക്കേണ്ടത് പ്രധാനമാണ്. ഒരു പ്രത്യേക ഉദാഹരണത്തിലൂടെ ഇത് വിശദീകരിക്കാം:

ടാസ്ക്. സെഗ്‌മെന്റിൽ y = 2x 3 - 3x 2 - 12x + 1 എന്ന ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞ പോയിന്റും ഏറ്റവും കുറഞ്ഞ മൂല്യവും കണ്ടെത്തുക [-3; 3].

ആദ്യം, ഞങ്ങൾ ഏറ്റവും കുറഞ്ഞ പോയിന്റ് കണ്ടെത്തുന്നു, അതിനായി ഞങ്ങൾ ഡെറിവേറ്റീവ് കണക്കാക്കുന്നു:
y' = (2x 3 - 3x 2 - 12x + 1)' = 6x 2 - 6x - 12.

y' = 0 എന്ന സമവാക്യം പരിഹരിച്ച് നിർണ്ണായക പോയിന്റുകൾ നമുക്ക് കണ്ടെത്താം. നമുക്ക് സ്റ്റാൻഡേർഡ് ക്വാഡ്രാറ്റിക് സമവാക്യം ലഭിക്കും:
y' = 0 ⇒ 6x 2 - 6x - 12 = 0 ⇒ ... ⇒ x 1 = -1, x 2 = 2.

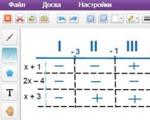
ഞങ്ങൾ ഈ പോയിന്റുകൾ കോർഡിനേറ്റ് ലൈനിൽ അടയാളപ്പെടുത്തുന്നു, ഡെറിവേറ്റീവിന്റെയും നിയന്ത്രണങ്ങളുടെയും അടയാളങ്ങൾ ചേർക്കുക - സെഗ്മെന്റിന്റെ അറ്റങ്ങൾ:

ചിത്രത്തിന്റെ സ്കെയിൽ പ്രശ്നമല്ല. പോയിന്റുകൾ ശരിയായ ക്രമത്തിൽ അടയാളപ്പെടുത്തുക എന്നതാണ് ഏറ്റവും പ്രധാനപ്പെട്ട കാര്യം. സ്‌കൂൾ മാത്തമാറ്റിക്‌സ് കോഴ്‌സിൽ നിന്ന് അറിയപ്പെടുന്നത് മിനിമം പോയിന്റിൽ, ഡെറിവേറ്റീവ് ചിഹ്നം മൈനസിൽ നിന്ന് പ്ലസ് ആയി മാറുന്നു എന്നാണ്. വായന എല്ലായ്പ്പോഴും ഇടത്തുനിന്ന് വലത്തോട്ട് പോകുന്നു - പോസിറ്റീവ് സെമി-അക്ഷത്തിന്റെ ദിശയിൽ. അതിനാൽ, ഒരു മിനിമം പോയിന്റ് മാത്രമേയുള്ളൂ: x = 2.

ഇപ്പോൾ സെഗ്മെന്റിൽ ഫംഗ്ഷന്റെ ഏറ്റവും കുറഞ്ഞ മൂല്യം കണ്ടെത്താം [-3; 3]. ഇത് മിനിമം പോയിന്റിൽ (അപ്പോൾ അത് ആഗോള മിനിമം പോയിന്റായി മാറുന്നു) അല്ലെങ്കിൽ സെഗ്‌മെന്റിന്റെ അവസാനത്തിൽ എത്തിച്ചേരുന്നു. ഇടവേളയിൽ (2; 3) ഡെറിവേറ്റീവ് എല്ലായിടത്തും പോസിറ്റീവ് ആണെന്ന് ശ്രദ്ധിക്കുക, അതായത് y(3) > y(2), അതിനാൽ ഇടവേളയുടെ വലത് അറ്റം അവഗണിക്കാം. പോയിന്റ് x = -3 (സെഗ്‌മെന്റിന്റെ ഇടത് അവസാനം), x = 2 (മിനിമം പോയിന്റ്) എന്നിവ മാത്രമേ അവശേഷിക്കുന്നുള്ളൂ. നമുക്ക് ഉണ്ട്:
y(-3) = 2(-3) 3 - 3(-3) 2 - 12(-3) + 1 = -44;
y(2) = 2*2 3 - 3*2 2 - 12*2 + 1 = -19.

അതിനാൽ, ഫംഗ്‌ഷന്റെ ഏറ്റവും ചെറിയ മൂല്യം സെഗ്‌മെന്റിന്റെ അവസാനത്തിൽ എത്തുന്നു, അത് −44 ന് തുല്യമാണ്.

ഉത്തരം: xmin = 2; ymin = -44

മേൽപ്പറഞ്ഞ ന്യായവാദത്തിൽ നിന്ന് പലരും മറക്കുന്ന ഒരു പ്രധാന വസ്തുത പിന്തുടരുന്നു. ഫംഗ്ഷൻ പരമാവധി (കുറഞ്ഞത്) മൂല്യം എടുക്കുന്നു, എക്സ്ട്രീം പോയിന്റിൽ ആവശ്യമില്ല. ചിലപ്പോൾ സെഗ്‌മെന്റിന്റെ അവസാനത്തിൽ അത്തരമൊരു മൂല്യം എത്തുന്നു, അവിടെയുള്ള ഡെറിവേറ്റീവ് പൂജ്യത്തിന് തുല്യമായിരിക്കണമെന്നില്ല.

പ്രശ്നപരിഹാര പദ്ധതി B15

പ്രശ്നം B15 ആണെങ്കിൽ, ഇടവേളയിൽ f(x) ഫംഗ്‌ഷന്റെ പരമാവധി അല്ലെങ്കിൽ കുറഞ്ഞ മൂല്യം കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്, ഞങ്ങൾ ഇനിപ്പറയുന്ന പ്രവർത്തനങ്ങൾ ചെയ്യുന്നു:

1. f'(x) = 0 എന്ന സമവാക്യം പരിഹരിക്കുക. വേരുകൾ ഇല്ലെങ്കിൽ, മൂന്നാം ഘട്ടം ഒഴിവാക്കി നേരെ നാലാമത്തേതിലേക്ക് പോകുക.
2. തത്ഫലമായുണ്ടാകുന്ന വേരുകളിൽ നിന്ന്, സെഗ്മെന്റിന് പുറത്തുള്ള എല്ലാം ഇല്ലാതാക്കുക. ശേഷിക്കുന്ന സംഖ്യകൾ x 1 , x 2 , ..., x n എന്നിവയാൽ സൂചിപ്പിക്കും - ചട്ടം പോലെ, അവയിൽ കുറച്ച് മാത്രമേ ഉണ്ടാകൂ.
3. സെഗ്‌മെന്റിന്റെ അറ്റങ്ങളും x 1, x 2, ..., x n പോയിന്റുകളും യഥാർത്ഥ ഫംഗ്‌ഷനിലേക്ക് മാറ്റിസ്ഥാപിക്കുക. നമുക്ക് f (a), f (b), f (x 1), f (x 2), ..., f (x n) സംഖ്യകളുടെ ഒരു കൂട്ടം ലഭിക്കുന്നു, അതിൽ നിന്ന് ഞങ്ങൾ ഏറ്റവും വലുതോ ചെറുതോ ആയ മൂല്യം തിരഞ്ഞെടുക്കുന്നു - ഇത് ഉത്തരം.

സെഗ്‌മെന്റിന്റെ അറ്റങ്ങളുമായി പൊരുത്തപ്പെടുമ്പോൾ വേരുകൾ ഇല്ലാതാക്കുന്നതിനെക്കുറിച്ചുള്ള ഒരു ചെറിയ വ്യക്തത. നാലാമത്തെ ഘട്ടത്തിൽ സെഗ്‌മെന്റിന്റെ അറ്റങ്ങൾ ഫംഗ്‌ഷനിലേക്ക് മാറ്റിസ്ഥാപിച്ചിരിക്കുന്നതിനാൽ - f’(x) = 0 എന്ന സമവാക്യത്തിന് പരിഹാരങ്ങൾ ഇല്ലെങ്കിലും.

ടാസ്ക്. സെഗ്‌മെന്റിൽ y = x 3 + 3x 2 - 9x - 7 ഫംഗ്‌ഷന്റെ പരമാവധി മൂല്യം കണ്ടെത്തുക [−5; 0].

ആദ്യം, നമുക്ക് ഡെറിവേറ്റീവ് കണ്ടെത്താം: y' = (x 3 + 3x 2 - 9x - 7)' = 3x 2 + 6x - 9.

അപ്പോൾ നമ്മൾ സമവാക്യം പരിഹരിക്കുന്നു: y' = 0 ⇒ 3x 2 + 6x - 9 = 0 ⇒ ... ⇒ x = -3; x = 1.

x = 1 എന്ന റൂട്ട് ക്രോസ് ചെയ്യുക കാരണം അത് ഇടവേളയിൽ ഉൾപ്പെടുന്നില്ല [−5; 0].

സെഗ്‌മെന്റിന്റെ അറ്റത്തും x = -3 എന്ന പോയിന്റിലും ഫംഗ്‌ഷന്റെ മൂല്യം കണക്കാക്കാൻ ഇത് ശേഷിക്കുന്നു:
y(-5) = (−5) 3 + 4 (-5) 2 - 9 (-5) - 7 = -12;
y(-3) = (−3) 3 + 4 (-3) 2 - 9 (-3) - 7 = 20;
y(0) = 0 3 + 4 0 2 - 9 0 - 7 = -7.

വ്യക്തമായും, ഏറ്റവും വലിയ മൂല്യം 20 ആണ് - ഇത് x = -3 എന്ന പോയിന്റിൽ എത്തുന്നു.

ഇടവേളയിൽ f(x) ഫംഗ്‌ഷന്റെ പരമാവധി അല്ലെങ്കിൽ കുറഞ്ഞ പോയിന്റ് കണ്ടെത്തേണ്ടിവരുമ്പോൾ കേസ് പരിഗണിക്കുക. സെഗ്മെന്റ് വ്യക്തമാക്കിയിട്ടില്ലെങ്കിൽ, ഫംഗ്ഷൻ അതിന്റെ നിർവചന ഡൊമെയ്നിൽ പരിഗണിക്കും. ഏത് സാഹചര്യത്തിലും, പരിഹാര പദ്ധതി ഇപ്രകാരമാണ്:

1. ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക: f'(x).
2. f’(x) = 0 എന്ന സമവാക്യം പരിഹരിക്കുക. ഡെറിവേറ്റീവ് ഒരു ഫ്രാക്ഷണൽ റേഷണൽ ഫംഗ്‌ഷൻ ആണെങ്കിൽ, അതിന്റെ ഡിനോമിനേറ്റർ പൂജ്യമാകുമ്പോൾ ഞങ്ങൾ കണ്ടെത്തും. നമുക്ക് ലഭിച്ച വേരുകൾ സൂചിപ്പിക്കാം x 1 , x 2 , ..., x n .
3. കോർഡിനേറ്റ് ലൈനിൽ x 1 , x 2 , ..., x n അടയാളപ്പെടുത്തുകയും ഈ സംഖ്യകൾക്കിടയിൽ ഡെറിവേറ്റീവ് എടുക്കുന്ന അടയാളങ്ങൾ സ്ഥാപിക്കുകയും ചെയ്യുക. ഒരു സെഗ്‌മെന്റ് നൽകിയിട്ടുണ്ടെങ്കിൽ, അത് അടയാളപ്പെടുത്തുക, അതിന് പുറത്തുള്ളതെല്ലാം ക്രോസ് ചെയ്യുക.
4. ശേഷിക്കുന്ന പോയിന്റുകളിൽ, ഡെറിവേറ്റീവിന്റെ ചിഹ്നം മൈനസിൽ നിന്ന് പ്ലസിലേക്കോ (ഇതാണ് ഏറ്റവും കുറഞ്ഞ പോയിന്റ്) അല്ലെങ്കിൽ പ്ലസിൽ നിന്ന് മൈനസിലേക്കോ (മിനിമം പോയിന്റ്) മാറുന്ന ഒരെണ്ണം ഞങ്ങൾ തിരയുന്നു. അത്തരമൊരു പോയിന്റ് മാത്രമേ ഉണ്ടാകൂ - ഇതായിരിക്കും ഉത്തരം.

ചില ഫംഗ്‌ഷനുകൾക്ക് ഈ അൽഗോരിതം പ്രവർത്തിക്കുന്നില്ല എന്നത് ചിന്തനീയമായ ഒരു വായനക്കാരൻ തീർച്ചയായും ശ്രദ്ധിക്കും. തീർച്ചയായും, എക്സ്ട്രീം പോയിന്റുകൾ കണ്ടെത്തുന്നതിന് കൂടുതൽ സങ്കീർണ്ണമായ കണക്കുകൂട്ടലുകൾ ആവശ്യമായ ഫംഗ്ഷനുകളുടെ ഒരു മുഴുവൻ ക്ലാസ് ഉണ്ട്. എന്നിരുന്നാലും, ഗണിതത്തിലെ പരീക്ഷയിൽ അത്തരം പ്രവർത്തനങ്ങൾ കാണുന്നില്ല.

x 1, x 2, ..., x n എന്നീ പോയിന്റുകൾക്കിടയിൽ അടയാളങ്ങൾ സ്ഥാപിക്കുന്നത് ശ്രദ്ധിക്കുക. ഓർമ്മിക്കുക: ഇരട്ട ഗുണിതത്തിന്റെ ഒരു റൂട്ടിലൂടെ കടന്നുപോകുമ്പോൾ, ഡെറിവേറ്റീവിന്റെ അടയാളം മാറില്ല. എക്സ്ട്രീം പോയിന്റുകൾക്കായി തിരയുമ്പോൾ, അടയാളങ്ങൾ എല്ലായ്പ്പോഴും ഇടത്തുനിന്ന് വലത്തോട്ട് വീക്ഷിക്കപ്പെടുന്നു, അതായത്. സംഖ്യാ അക്ഷത്തിൽ.

ടാസ്ക്. ഒരു ഫംഗ്‌ഷന്റെ പരമാവധി പോയിന്റ് കണ്ടെത്തുക

സെഗ്മെന്റിൽ [-8; 8].

നമുക്ക് ഡെറിവേറ്റീവ് കണ്ടെത്താം:

ഇതൊരു ഫ്രാക്ഷണൽ റേഷണൽ ഫംഗ്‌ഷൻ ആയതിനാൽ, ഞങ്ങൾ ഡെറിവേറ്റീവും അതിന്റെ ഡിനോമിനേറ്ററും പൂജ്യത്തിന് തുല്യമാക്കുന്നു:
y' = 0 ⇒ x 2 - 25 = 0 ⇒ ... ⇒ x = 5; x = -5;
x 2 \u003d 0 ⇒ x \u003d 0 (രണ്ടാമത്തെ ഗുണനത്തിന്റെ റൂട്ട്).

കോർഡിനേറ്റ് ലൈനിൽ x = −5, x = 0, x = 5 എന്നീ പോയിന്റുകൾ അടയാളപ്പെടുത്താം, അടയാളങ്ങളും അതിരുകളും ക്രമീകരിക്കുക:

വ്യക്തമായും, സെഗ്‌മെന്റിനുള്ളിൽ x = -5 എന്ന ഒരു പോയിന്റ് മാത്രമേ അവശേഷിക്കുന്നുള്ളൂ, അതിൽ ഡെറിവേറ്റീവിന്റെ ചിഹ്നം പ്ലസ് മുതൽ മൈനസിലേക്ക് മാറുന്നു. ഇതാണ് പരമാവധി പോയിന്റ്.

എക്സ്ട്രീം പോയിന്റുകൾ എക്സ്ട്രീമയിൽ നിന്ന് എങ്ങനെ വ്യത്യാസപ്പെട്ടിരിക്കുന്നുവെന്ന് ഒരിക്കൽ കൂടി വിശദീകരിക്കാം. ഫംഗ്‌ഷൻ ഏറ്റവും വലുതോ ചെറുതോ ആയ മൂല്യം എടുക്കുന്ന വേരിയബിളുകളുടെ മൂല്യങ്ങളാണ് എക്‌സ്‌ട്രീം പോയിന്റുകൾ. എക്‌സ്‌ട്രീമുകൾ എന്നത് ഫംഗ്‌ഷനുകളുടെ മൂല്യങ്ങളാണ്, അവരുടെ ചില സമീപസ്ഥലങ്ങളിൽ പരമാവധി അല്ലെങ്കിൽ കുറഞ്ഞത്.

സാധാരണ പോളിനോമിയലുകൾക്കും ഫ്രാക്ഷണൽ റേഷണൽ ഫംഗ്ഷനുകൾക്കും പുറമേ, പ്രശ്നം B15 ൽ ഇനിപ്പറയുന്ന തരത്തിലുള്ള പദപ്രയോഗങ്ങൾ സംഭവിക്കുന്നു:

1. യുക്തിരഹിതമായ പ്രവർത്തനങ്ങൾ,
2. ത്രികോണമിതി പ്രവർത്തനങ്ങൾ,
3. എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷനുകൾ,
4. ലോഗരിതമിക് പ്രവർത്തനങ്ങൾ.

ചട്ടം പോലെ, യുക്തിരഹിതമായ പ്രവർത്തനങ്ങളിൽ പ്രശ്നങ്ങളൊന്നുമില്ല. ശേഷിക്കുന്ന കേസുകൾ കൂടുതൽ വിശദമായി പരിഗണിക്കേണ്ടതാണ്.

ത്രികോണമിതി പ്രവർത്തനങ്ങൾ

ത്രികോണമിതി പ്രവർത്തനങ്ങളുടെ പ്രധാന ബുദ്ധിമുട്ട് സമവാക്യങ്ങൾ പരിഹരിക്കുമ്പോൾ, അനന്തമായ എണ്ണം വേരുകൾ ഉണ്ടാകുന്നു എന്നതാണ്. ഉദാഹരണത്തിന്, sin x = 0 എന്ന സമവാക്യത്തിന് x = πn എന്ന വേരുകളുണ്ട്, അവിടെ n ∈ Z. ശരി, അത്തരം സംഖ്യകൾ അനന്തമായി ഉണ്ടെങ്കിൽ അവയെ കോർഡിനേറ്റ് ലൈനിൽ എങ്ങനെ അടയാളപ്പെടുത്താം?

ഉത്തരം ലളിതമാണ്: നിങ്ങൾ n ന്റെ നിർദ്ദിഷ്ട മൂല്യങ്ങൾ മാറ്റിസ്ഥാപിക്കേണ്ടതുണ്ട്. തീർച്ചയായും, ത്രികോണമിതി പ്രവർത്തനങ്ങളുള്ള B15 പ്രശ്നങ്ങളിൽ എല്ലായ്പ്പോഴും ഒരു നിയന്ത്രണമുണ്ട് - ഒരു സെഗ്മെന്റ്. അതിനാൽ, ആരംഭിക്കുന്നതിന്, ഞങ്ങൾ n \u003d 0 എടുക്കുന്നു, തുടർന്ന് അനുബന്ധ റൂട്ട് സെഗ്മെന്റിനപ്പുറത്തേക്ക് "പുറത്തേക്ക് പറക്കുന്നതുവരെ" n വർദ്ധിപ്പിക്കുക. അതുപോലെ, n കുറയ്ക്കുന്നതിലൂടെ, വളരെ വേഗം നമുക്ക് താഴത്തെ പരിധിയേക്കാൾ കുറവുള്ള ഒരു റൂട്ട് ലഭിക്കും.

പരിഗണിക്കപ്പെടുന്ന പ്രക്രിയയിൽ ലഭിച്ചതല്ലാതെ വേരുകളൊന്നും ഇടവേളയിൽ ഇല്ലെന്ന് കാണിക്കുന്നത് എളുപ്പമാണ്. ഇപ്പോൾ നമുക്ക് ഈ പ്രക്രിയയെ വ്യക്തമായ ഉദാഹരണങ്ങൾ ഉപയോഗിച്ച് പരിഗണിക്കാം.

ടാസ്ക്. y = sin x - 5x sin x - 5cos x + 1 എന്ന ഫംഗ്‌ഷന്റെ പരമാവധി പോയിന്റ് കണ്ടെത്തുക [-π/3; π/3].

ഡെറിവേറ്റീവ് കണക്കാക്കുക: y' = (sin x - 5x sin x - 5cos x + 1)' = ... = cos x - 5x cos x = (1 - 5x) cos x.

അപ്പോൾ നമ്മൾ സമവാക്യം പരിഹരിക്കുന്നു: y' = 0 ⇒ (1 - 5x) cos x = 0 ⇒ ... ⇒ x = 0.2 അല്ലെങ്കിൽ x = π/2 + πn, n ∈ Z.

റൂട്ട് x = 0.2 ഉപയോഗിച്ച്, എല്ലാം വ്യക്തമാണ്, എന്നാൽ x = π / 2 + πn ഫോർമുലയ്ക്ക് അധിക പ്രോസസ്സിംഗ് ആവശ്യമാണ്. n = 0 മുതൽ ആരംഭിക്കുന്ന n ന്റെ വ്യത്യസ്ത മൂല്യങ്ങൾ ഞങ്ങൾ മാറ്റിസ്ഥാപിക്കും.

n = 0 ⇒ x = π/2. എന്നാൽ π/2 > π/3, അതിനാൽ x = π/2 എന്ന റൂട്ട് യഥാർത്ഥ സെഗ്മെന്റിൽ ഉൾപ്പെടുത്തിയിട്ടില്ല. കൂടാതെ, വലിയ n, വലുത് x, അതിനാൽ n > 0 പരിഗണിക്കുന്നതിൽ അർത്ഥമില്ല.

n = -1 ⇒ x = - π/2. എന്നാൽ -π/2< −π/3 - этот корень тоже придется отбросить. А вместе с ним - и все корни для n < −1.

ഇടവേളയിൽ [−π/3; π/3] x = 0.2 എന്ന റൂട്ട് മാത്രമാണ്. കോർഡിനേറ്റ് ലൈനിലെ അടയാളങ്ങളും അതിരുകളും ഉപയോഗിച്ച് ഞങ്ങൾ ഇത് അടയാളപ്പെടുത്തുന്നു:

x = 0.2 ന്റെ വലതുവശത്തുള്ള ഡെറിവേറ്റീവ് ശരിക്കും നെഗറ്റീവ് ആണെന്ന് ഉറപ്പാക്കാൻ, x = π/4 എന്ന മൂല്യം y' ആക്കി മാറ്റിയാൽ മതിയാകും. x = 0.2 എന്ന പോയിന്റിൽ, ഡെറിവേറ്റീവ് ചിഹ്നം പ്ലസ് മുതൽ മൈനസ് വരെ മാറ്റുന്നു, അതിനാൽ ഇതാണ് പരമാവധി പോയിന്റ്.

ടാസ്ക്. y = 4tg x - 4x + π - 5 എന്ന ഫംഗ്‌ഷന്റെ ഏറ്റവും വലിയ മൂല്യം [-π/4; π/4].

ഡെറിവേറ്റീവ് കണക്കാക്കുക: y' = (4tg x - 4x + π - 5)' = 4/cos 2x - 4.

അപ്പോൾ നമ്മൾ സമവാക്യം പരിഹരിക്കുന്നു: y' = 0 ⇒ 4/cos 2x - 4 = 0 ⇒ ... ⇒ x = πn, n ∈ Z.

n = 0 മുതൽ ആരംഭിക്കുന്ന നിർദ്ദിഷ്ട n മാറ്റിസ്ഥാപിച്ച് ഞങ്ങൾ ഈ ഫോർമുലയിൽ നിന്ന് വേരുകൾ വേർതിരിച്ചെടുക്കുന്നു:
n = 0 ⇒ x = 0. ഈ റൂട്ട് നമുക്ക് അനുയോജ്യമാണ്.
n = 1 ⇒ x = π. എന്നാൽ π > π/4, അതിനാൽ റൂട്ട് x = π, മൂല്യങ്ങൾ n > 1 എന്നിവ മറികടക്കണം.
n = -1 ⇒ x = -π. എന്നാൽ π< −π/4, поэтому x = π и n < −1 тоже вычеркиваем.

മുഴുവൻ വൈവിധ്യമാർന്ന വേരുകളിൽ, ഒരെണ്ണം മാത്രമേ അവശേഷിക്കുന്നുള്ളൂ: x = 0. അതിനാൽ, x = 0, x = π/4, x = -π/4 എന്നിവയ്‌ക്കായുള്ള ഫംഗ്‌ഷന്റെ മൂല്യം ഞങ്ങൾ കണക്കാക്കുന്നു.
y(0) = 4tg 0 - 4 0 + π - 5 = π - 5;
y(π/4) = 4tg (π/4) - 4 π/4 + π - 5 = -1;
y(π/4) = 4tg (−π/4) - 4 (-π/4) + π - 5 = ... = 2π - 9.

ഇപ്പോൾ ശ്രദ്ധിക്കുക π = 3.14...< 4, поэтому π − 5 < 4 − 5 = −1 и 2π − 9 < 8 − 9 = −1. Получается одно положительное число и два отрицательных. Мы ищем наибольшее - очевидно, это y = −1.

അവസാന പ്രശ്നത്തിൽ അക്കങ്ങൾ പരസ്പരം താരതമ്യം ചെയ്യാതിരിക്കാൻ സാധിച്ചുവെന്നത് ശ്രദ്ധിക്കുക. തീർച്ചയായും, π - 5, 1, 2π - 9 എന്നീ അക്കങ്ങളിൽ നിന്ന് ഉത്തരക്കടലാസിൽ ഒരെണ്ണം മാത്രമേ എഴുതാൻ കഴിയൂ. തീർച്ചയായും, ഫോമിൽ എങ്ങനെ എഴുതാം, പറയുക, നമ്പർ π? പക്ഷേ വഴിയില്ല. ഗണിതശാസ്ത്രത്തിലെ പരീക്ഷയുടെ ആദ്യ ഭാഗത്തിന്റെ ഒരു പ്രധാന സവിശേഷതയാണിത്, ഇത് പല പ്രശ്നങ്ങളുടെയും പരിഹാരം വളരെ ലളിതമാക്കുന്നു. ഇത് ബി 15 ൽ മാത്രമല്ല പ്രവർത്തിക്കുന്നത്.

ചിലപ്പോൾ ഒരു ഫംഗ്ഷൻ പഠിക്കുമ്പോൾ, വേരുകളില്ലാത്ത സമവാക്യങ്ങൾ ഉണ്ടാകുന്നു. ഈ സാഹചര്യത്തിൽ, പ്രശ്നം കൂടുതൽ ലളിതമാകും, കാരണം ഇത് സെഗ്മെന്റിന്റെ അറ്റങ്ങൾ മാത്രം പരിഗണിക്കേണ്ടതുണ്ട്.

ടാസ്ക്. ഫംഗ്‌ഷന്റെ ഏറ്റവും ചെറിയ മൂല്യം y = 7sin x - 8x + 5 ഇടവേളയിൽ കണ്ടെത്തുക [−3π/2; 0].

ആദ്യം നമ്മൾ ഡെറിവേറ്റീവ് കണ്ടെത്തുന്നു: y' = (7sin x - 8x + 5)' = 7cos x - 8.

സമവാക്യം പരിഹരിക്കാൻ ശ്രമിക്കാം: y' = 0 ⇒ 7cos x - 8 = 0 ⇒ cos x = 8/7. എന്നാൽ cos x ന്റെ മൂല്യങ്ങൾ എപ്പോഴും ഇടവേളയിലാണ് [-1; 1], കൂടാതെ 8/7 > 1. അതിനാൽ, വേരുകൾ ഇല്ല.

വേരുകൾ ഇല്ലെങ്കിൽ, ഒന്നും മറികടക്കേണ്ടതില്ല. ഞങ്ങൾ അവസാന ഘട്ടത്തിലേക്ക് കടക്കുന്നു - ഫംഗ്ഷന്റെ മൂല്യം ഞങ്ങൾ കണക്കാക്കുന്നു:
y(-3π/2) = 7sin (−3π/2) - 8 (-3π/2) + 5 = ... = 12π + 12;
y(0) = 7sin 0 - 8 0 + 5 = 5.

ഉത്തരക്കടലാസിൽ 12π + 12 എന്ന സംഖ്യ എഴുതാൻ കഴിയാത്തതിനാൽ, y = 5 മാത്രമേ അവശേഷിക്കുന്നുള്ളൂ.

എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷനുകൾ

പൊതുവായി പറഞ്ഞാൽ, ഒരു എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷൻ എന്നത് y = a x എന്ന ഫോമിന്റെ ഒരു പദപ്രയോഗമാണ്, ഇവിടെ a > 0. എന്നാൽ B15 പ്രശ്‌നത്തിൽ, y = e x എന്ന ഫോമിന്റെ ഫംഗ്‌ഷനുകൾ മാത്രമേ ഉണ്ടാകൂ, കൂടാതെ, y = e kx + b. കാരണം, ഈ ഫംഗ്‌ഷനുകളുടെ ഡെറിവേറ്റീവുകൾ കണക്കാക്കുന്നത് വളരെ എളുപ്പമാണ്:

1. (e x)" = e x. ഒന്നും മാറിയിട്ടില്ല.
2. (e kx + b)" = k e kx + b. വേരിയബിളിന്റെ ഗുണകത്തിന് തുല്യമായ ഒരു ഘടകം ലളിതമായി ചേർത്തിരിക്കുന്നു. ഇത് ഒരു സങ്കീർണ്ണ ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവിന്റെ ഒരു പ്രത്യേക കേസാണ്.

ബാക്കി എല്ലാം തികച്ചും സ്റ്റാൻഡേർഡ് ആണ്. തീർച്ചയായും, B15 പ്രശ്നങ്ങളിലെ യഥാർത്ഥ പ്രവർത്തനങ്ങൾ കൂടുതൽ ഗുരുതരമായി കാണപ്പെടുന്നു, എന്നാൽ പരിഹാര പദ്ധതി ഇതിൽ നിന്ന് മാറില്ല. സമഗ്രമായ ന്യായവാദങ്ങളും അഭിപ്രായങ്ങളും ഇല്ലാതെ - പരിഹാരത്തിന്റെ പ്രധാന പോയിന്റുകൾ മാത്രം എടുത്തുകാണിച്ച് നമുക്ക് രണ്ട് ഉദാഹരണങ്ങൾ പരിഗണിക്കാം.

ടാസ്ക്. സെഗ്‌മെന്റിൽ y = (x 2 - 5x + 5)e x - 3 എന്ന ഫംഗ്‌ഷന്റെ ഏറ്റവും ചെറിയ മൂല്യം കണ്ടെത്തുക [−1; 5].

ഡെറിവേറ്റീവ്: y' = ((x 2 - 5x + 5)e x - 3)' = ... = (x 2 - 3x)e x - 3 = x(x - 3)e x - 3 .

വേരുകൾ കണ്ടെത്തുക: y' = 0 ⇒ x(x - 3)e x - 3 = 0 ⇒ ... ⇒ x = 0; x=3.

രണ്ട് വേരുകളും ഇടവേളയിൽ കിടക്കുന്നു [−1; 5]. എല്ലാ പോയിന്റുകളിലും ഫംഗ്‌ഷന്റെ മൂല്യം കണ്ടെത്താൻ ഇത് ശേഷിക്കുന്നു:
y (-1) = ((-1) 2 - 5 (-1) + 5) e - 1 - 3 = ... = 11 e -4 ;
y(0) = (0 2 - 5 0 + 5)e 0 - 3 = ... = 5 e -3 ;
y(3) = (3 2 - 5 3 + 5)e 3 - 3 = ... = -1;
y(5) = (5 2 - 5 5 + 5)e 5 - 3 = ... = 5 ഇ 2 .

ലഭിച്ച നാല് അക്കങ്ങളിൽ, y = -1 മാത്രമേ ഫോമിൽ എഴുതാൻ കഴിയൂ. കൂടാതെ, ഇത് ഒരേയൊരു നെഗറ്റീവ് സംഖ്യയാണ് - ഇത് ഏറ്റവും ചെറുതായിരിക്കും.

ടാസ്ക്. സെഗ്‌മെന്റിൽ y = (2x - 7) e 8 - 2x എന്ന ഫംഗ്‌ഷന്റെ പരമാവധി മൂല്യം കണ്ടെത്തുക .

ഡെറിവേറ്റീവ്: y' = ((2x - 7) e 8 - 2x)' = ... = (16 - 4x) e 8 - 2x = 4(4 - x) e 8 - 2x .

ഞങ്ങൾ വേരുകൾ കണ്ടെത്തുന്നു: y' = 0 ⇒ 4(4 - x) e 8 - 2x = 0 ⇒ x = 4.

x = 4 എന്ന റൂട്ട് സെഗ്മെന്റിൽ പെടുന്നു. ഞങ്ങൾ ഫംഗ്‌ഷൻ മൂല്യങ്ങൾക്കായി തിരയുന്നു:
y(0) = (2 0 - 7)e 8 - 2 0 = ... = -7 e 8 ;
y(4) = (2 4 - 7)e 8 - 2 4 = ... = 1;
y(6) = (2 6 - 7)e 8 - 2 6 = ... = 5 e -4 .

വ്യക്തമായും, y = 1 ന് മാത്രമേ ഉത്തരമായി വർത്തിക്കാൻ കഴിയൂ.

ലോഗരിതമിക് പ്രവർത്തനങ്ങൾ

എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷനുകളുമായുള്ള സാമ്യം അനുസരിച്ച്, പ്രശ്‌നം B15 ൽ സ്വാഭാവിക ലോഗരിതം മാത്രമേ ഉണ്ടാകൂ, കാരണം അവയുടെ ഡെറിവേറ്റീവ് എളുപ്പത്തിൽ കണക്കാക്കാം:

1. (lnx)' = 1/x;
2. (ln(kx + b))' = k/(kx + b). പ്രത്യേകിച്ചും, b = 0 ആണെങ്കിൽ (ln(kx))' = 1/x.

അങ്ങനെ, ഡെറിവേറ്റീവ് എല്ലായ്പ്പോഴും ഒരു ഫ്രാക്ഷണൽ റേഷണൽ ഫംഗ്ഷൻ ആയിരിക്കും. ഈ ഡെറിവേറ്റീവും അതിന്റെ ഡിനോമിനേറ്ററും പൂജ്യത്തിലേക്ക് തുലനം ചെയ്യുക, തുടർന്ന് ഫലമായുണ്ടാകുന്ന സമവാക്യങ്ങൾ പരിഹരിക്കുക.

ഒരു ലോഗരിഥമിക് ഫംഗ്‌ഷന്റെ പരമാവധി അല്ലെങ്കിൽ കുറഞ്ഞ മൂല്യം കണ്ടെത്താൻ, സ്വാഭാവിക ലോഗരിതം ഒരു "സാധാരണ" സംഖ്യയായി മാറുന്നത് e n എന്ന ഫോമിന്റെ പോയിന്റുകളിൽ മാത്രമാണെന്ന് ഓർമ്മിക്കുക. ഉദാഹരണത്തിന്, ln 1 \u003d ln e 0 \u003d 0 ഒരു ലോഗരിഥമിക് പൂജ്യമാണ്, മിക്കപ്പോഴും പരിഹാരം അതിലേക്ക് ചുരുക്കിയിരിക്കുന്നു. മറ്റ് സന്ദർഭങ്ങളിൽ, ലോഗരിതത്തിന്റെ അടയാളം "നീക്കംചെയ്യുക" അസാധ്യമാണ്.

ടാസ്ക്. സെഗ്‌മെന്റിൽ y = x 2 - 3x + ln x ഫംഗ്‌ഷന്റെ ഏറ്റവും ചെറിയ മൂല്യം കണ്ടെത്തുക.

ഞങ്ങൾ ഡെറിവേറ്റീവ് പരിഗണിക്കുന്നു:

ഡെറിവേറ്റീവിന്റെ പൂജ്യങ്ങളും അതിന്റെ ഡിനോമിനേറ്ററും ഞങ്ങൾ കണ്ടെത്തുന്നു:
y' = 0 ⇒ 2x 2 - 3x + 1 = 0 ⇒ ... ⇒ x = 0.5; x = 1;
x = 0 - തീരുമാനിക്കാൻ ഒന്നുമില്ല.

x = 0, x = 0.5, x = 1 എന്നീ മൂന്ന് സംഖ്യകളിൽ, സെഗ്മെന്റിനുള്ളിൽ x = 1 മാത്രമേ ഉള്ളൂ, x = 0.5 എന്ന സംഖ്യ അതിന്റെ അവസാനമാണ്. നമുക്ക് ഉണ്ട്:
y(0.5) = 0.5 2 - 3 0.5 + ln 0.5 = ln 0.5 - 1.25;
y(1) = 1 2 - 3 1 + ലോഗ് 1 = -2;
y(5) = 5 2 - 3 5 + ln 5 = 10 + ln 5.

ലഭിച്ച മൂന്ന് മൂല്യങ്ങളിൽ, y = -2 ൽ മാത്രം ലോഗരിതം അടയാളം അടങ്ങിയിട്ടില്ല - ഇത് ഉത്തരം ആയിരിക്കും.

ടാസ്ക്. സെഗ്‌മെന്റിൽ y = ln(6x) - 6x + 4 എന്ന ഫംഗ്‌ഷന്റെ ഏറ്റവും വലിയ മൂല്യം കണ്ടെത്തുക.

ഞങ്ങൾ ഡെറിവേറ്റീവ് കണക്കാക്കുന്നു:

ഡെറിവേറ്റീവ് അല്ലെങ്കിൽ അതിന്റെ ഡിനോമിനേറ്റർ പൂജ്യത്തിന് തുല്യമാകുമ്പോൾ ഞങ്ങൾ കണ്ടെത്തുന്നു:
y' = 0 ⇒ 1 - 6x = 0 ⇒ x = 1/6;
x = 0 - ഇതിനകം തീരുമാനിച്ചു.

x = 0 എന്ന സംഖ്യയെ ഞങ്ങൾ മറികടക്കുന്നു, കാരണം അത് സെഗ്മെന്റിന് പുറത്താണ്. സെഗ്‌മെന്റിന്റെ അറ്റത്തും x = 1/6 എന്ന പോയിന്റിലും ഫംഗ്‌ഷന്റെ മൂല്യം ഞങ്ങൾ പരിഗണിക്കുന്നു:
y(0.1) = ln (6 0.1) - 6 0.1 + 4 = ln 0.6 + 3.4;
y(1/6) = ലോഗ് (6 1/6) - 6 1/6 + 4 = ലോഗ് 1 + 3 = 3;
y(3) = ln(6 3) - 6 3 + 4 = ln 18 - 14.

വ്യക്തമായും, y = 3 ന് മാത്രമേ ഉത്തരമായി പ്രവർത്തിക്കാൻ കഴിയൂ - ബാക്കിയുള്ള മൂല്യങ്ങളിൽ ലോഗരിതം അടയാളം അടങ്ങിയിരിക്കുന്നു, ഉത്തരക്കടലാസിൽ എഴുതാൻ കഴിയില്ല.

പോയിന്റ് വിളിക്കുന്നു പരമാവധി (കുറഞ്ഞത്) പോയിന്റ് ഫംഗ്‌ഷൻ, ഈ അയൽപക്കത്തിനെല്ലാം അസമത്വമുള്ള ഒരു അയൽപക്കം ഉണ്ടെങ്കിൽ ().

ഒരു ഫംഗ്‌ഷന്റെ കൂടിയതും കുറഞ്ഞതുമായ പോയിന്റുകളെ പോയിന്റുകൾ എന്ന് വിളിക്കുന്നു. അങ്ങേയറ്റം (ചിത്രം 25).

സിദ്ധാന്തം 3.9 (എക്‌സ്ട്രീം പോയിന്റുകളുടെ നിലനിൽപ്പിന് ആവശ്യമായ വ്യവസ്ഥ) . 1st തരത്തിലുള്ള നിർണായക ഘട്ടങ്ങളിൽ, ഒന്നുകിൽ ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ്

പൂജ്യമാണ് അല്ലെങ്കിൽ നിലവിലില്ല

1-ആം തരത്തിലുള്ള നിർണായക പോയിന്റുകളെ സാധാരണയായി ക്രിട്ടിക്കൽ പോയിന്റുകൾ എന്ന് വിളിക്കുന്നു.

ഒരു ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് പൂജ്യത്തിന് തുല്യമായ നിർണായക പോയിന്റുകളെ വിളിക്കുന്നു നിശ്ചലത പോയിന്റുകൾ . ഒരു ഫംഗ്‌ഷൻ തുടർച്ചയുള്ളതും എന്നാൽ വ്യതിരിക്തമല്ലാത്തതുമായ നിർണ്ണായക പോയിന്റുകളെ വിളിക്കുന്നു കോർണർ പോയിന്റുകൾ . ഉദാഹരണത്തിന്, ഒരു ബിന്ദുവിലെ ഒരു ഫംഗ്‌ഷൻ തുടർച്ചയായാണ്, പക്ഷേ അതിന് ഒരു ഡെറിവേറ്റീവ് ഇല്ല, കാരണം ഈ ഘട്ടത്തിൽ ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്ക് അനന്തമായ ടാൻജന്റുകൾ വരയ്ക്കാനാകും (ചിത്രം 26). സിദ്ധാന്തം 3.3-ലേക്കുള്ള സംഭാഷണ പ്രസ്താവന തെറ്റാണെന്നതിന്റെ സ്ഥിരീകരണമായി ഈ കേസ് കണക്കാക്കാം.

ചടങ്ങിനെ വിളിക്കുന്നു വർദ്ധിച്ചുവരുന്ന ചില ഇടവേളകളിൽ, ഈ ഇടവേളയിൽ ആർഗ്യുമെന്റിന്റെ വലിയ മൂല്യം വേരിയബിളിന്റെ വലിയ മൂല്യവുമായി പൊരുത്തപ്പെടുന്നുവെങ്കിൽ, കൂടാതെ ക്ഷയിക്കുന്നു ആർഗ്യുമെന്റിന്റെ വലിയ മൂല്യം വേരിയബിളിന്റെ ചെറിയ മൂല്യവുമായി പൊരുത്തപ്പെടുന്നുവെങ്കിൽ.

കൂടുതൽ ഗവേഷണത്തിനായി, നിർണായക പോയിന്റുകൾ ഒരു സംഖ്യാ അക്ഷത്തിൽ സ്ഥാപിച്ചിരിക്കുന്നു, ഈ പോയിന്റുകൾ ഇടവേളകളായി തിരിച്ചിരിക്കുന്നു, അതിനുശേഷം ഇനിപ്പറയുന്ന മതിയായ വ്യവസ്ഥകൾ പരിശോധിക്കുന്നു.

സിദ്ധാന്തം 3.10 (ഒരു ഫംഗ്‌ഷൻ കൂട്ടാനും കുറയാനും മതിയായ അവസ്ഥ).ഒരു ഫംഗ്‌ഷൻ ചില ഇടവേളകളിൽ വേർതിരിക്കാവുന്നതും അതിന്റെ ഡെറിവേറ്റീവ് പോസിറ്റീവ് (നെഗറ്റീവ്) ആണെങ്കിൽ, ഈ ഇടവേളയിൽ ഫംഗ്ഷൻ വർദ്ധിക്കുന്നു (കുറയുന്നു).

സിദ്ധാന്തം 3.11 (ഒരു ഫംഗ്ഷന്റെ എക്സ്ട്രീം പോയിന്റുകളുടെ നിലനിൽപ്പിന് മതിയായ വ്യവസ്ഥ).നിർണ്ണായക പോയിന്റിന്റെ ചില അയൽപക്കങ്ങളിൽ ഫംഗ്ഷൻ തുടർച്ചയായതും വ്യത്യാസപ്പെട്ടിരിക്കുന്നതുമാണെങ്കിൽ, അതിലൂടെ കടന്നുപോകുമ്പോൾ, ഡെറിവേറ്റീവ് ചിഹ്നം പ്ലസ് മുതൽ മൈനസിലേക്ക് മാറുകയാണെങ്കിൽ, പോയിന്റ് പരമാവധി പോയിന്റാണ്; മൈനസ് മുതൽ പ്ലസ് വരെയാണെങ്കിൽ, പോയിന്റ് ഫംഗ്ഷന്റെ ഏറ്റവും കുറഞ്ഞ പോയിന്റാണ്

മതിയായ അവസ്ഥ തൃപ്തികരമല്ലാത്ത ഫംഗ്‌ഷന്റെ നിർണായക പോയിന്റുകൾ ആദ്യ തരത്തിലുള്ള നിർണ്ണായക പോയിന്റുകളായി തുടരുന്നു.

ഡെറിവേറ്റീവ് നിലവിലില്ലാത്ത 1-ആം തരത്തിലുള്ള നിർണായക പോയിന്റുകൾ രണ്ട് ക്ലാസുകളായി തിരിച്ചിരിക്കുന്നു:

ഫംഗ്‌ഷൻ തുടർച്ചയായി നടക്കുന്ന പോയിന്റുകളാണ് (സിദ്ധാന്തം 3.11 അവയ്ക്ക് തൃപ്തികരമാകുമ്പോൾ, ഈ പോയിന്റുകളിൽ ഫംഗ്‌ഷന് “മൂർച്ചയുള്ള” തീവ്രതയുണ്ട്), ഇവയാണ് മൂല പോയിന്റുകൾ;

ഫംഗ്‌ഷൻ നിർത്തലാക്കുന്ന പോയിന്റുകളാണ് (അവ എല്ലായ്പ്പോഴും 2-ആം തരത്തിലുള്ള നിർണായക പോയിന്റുകളുടെ ക്ലാസിലേക്ക് കടന്നുപോകുന്നു).

എന്നാൽ ഈ രീതിയിൽ നടത്തിയ പഠനം വളരെ പ്രധാനപ്പെട്ട ഒരു ചോദ്യത്തിന് ഉത്തരം നൽകുന്നില്ല: പ്രവർത്തനം എങ്ങനെ വർദ്ധിക്കുന്നു (കുറയുന്നു) - കുത്തനെയുള്ളതോ കോൺകേവോ? ഈ ചോദ്യത്തിനുള്ള ഉത്തരം രണ്ടാമത്തെ ഡെറിവേറ്റീവ് ഉപയോഗിച്ച് ഫംഗ്ഷനെക്കുറിച്ചുള്ള കൂടുതൽ പഠനത്തിലൂടെയാണ് നൽകുന്നത്. ആവശ്യമായ നിരവധി നിർവചനങ്ങൾ നമുക്ക് നൽകാം.

ചടങ്ങിനെ വിളിക്കുന്നു കുത്തനെയുള്ള (കുത്തനെയുള്ള) ചില ഇടവേളകളിൽ, ഈ ഇടവേളയുടെ ഓരോ പോയിന്റിലും ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്ക് വരച്ച ടാൻജെന്റ് ഫംഗ്‌ഷന്റെ ഗ്രാഫിന് മുകളിൽ (താഴെ) കിടക്കുന്നുണ്ടെങ്കിൽ.

ഒരു ഫംഗ്‌ഷന്റെ കോൺ‌കവിറ്റി ഏരിയകളിൽ നിന്ന് കോൺ‌വെക്‌സിറ്റി ഏരിയകളെ വേർതിരിക്കുന്ന പോയിന്റുകളെ അതിന്റെ വിളിക്കുന്നു ഇൻഫ്ലക്ഷൻ പോയിന്റുകൾ (ചിത്രം 27).

സിദ്ധാന്തം 3.12 (ഇൻഫ്ലക്ഷൻ പോയിന്റുകളുടെ നിലനിൽപ്പിന് ആവശ്യമായ വ്യവസ്ഥ). രണ്ടാം തരത്തിന്റെ നിർണായക പോയിന്റുകളിൽ, ഫംഗ്‌ഷന്റെ രണ്ടാമത്തെ ഡെറിവേറ്റീവ് ഒന്നുകിൽ പൂജ്യമാണ് അല്ലെങ്കിൽ നിലവിലില്ല

കൂടുതൽ ഗവേഷണത്തിനായി, 2-ആം തരത്തിലുള്ള നിർണായക പോയിന്റുകൾ ഒരു സംഖ്യാ അക്ഷത്തിൽ സ്ഥാപിച്ചിരിക്കുന്നു, അത് ഈ പോയിന്റുകളാൽ ഇടവേളകളായി വിഭജിക്കപ്പെടുന്നു, അതിനുശേഷം ഇനിപ്പറയുന്ന മതിയായ വ്യവസ്ഥകൾ പരിശോധിക്കപ്പെടുന്നു.

സിദ്ധാന്തം 3.13 (ഒരു ഫംഗ്‌ഷന്റെ കോൺവെക്‌സിറ്റിക്കും കോൺകാവിറ്റിക്കും മതിയായ അവസ്ഥ).ചില ഇടവേളകളിൽ ഒരു ഫംഗ്‌ഷൻ രണ്ടുതവണ വ്യത്യാസപ്പെട്ടിരിക്കുകയും അതിന്റെ രണ്ടാമത്തെ ഡെറിവേറ്റീവ് പോസിറ്റീവ് (നെഗറ്റീവ്) ആണെങ്കിൽ, ഈ ഇടവേളയിൽ ഫംഗ്‌ഷൻ കോൺകേവ് (കോൺവെക്സ്) ആണ്.

മതിയായ അവസ്ഥ തൃപ്തികരമല്ലാത്ത ഫംഗ്‌ഷന്റെ നിർണായക പോയിന്റുകൾ രണ്ടാമത്തെ തരത്തിലുള്ള നിർണായക പോയിന്റുകളായി തുടരുന്നു.

രണ്ടാമത്തെ ഡെറിവേറ്റീവ് നിലവിലില്ലാത്ത രണ്ടാമത്തെ തരത്തിലുള്ള നിർണായക പോയിന്റുകൾ രണ്ട് ക്ലാസുകളായി തിരിച്ചിരിക്കുന്നു:

- പ്രവർത്തനം തുടർച്ചയായി നടക്കുന്ന പോയിന്റുകൾ, ഇവ "മൂർച്ചയുള്ള" ഇൻഫ്ലക്ഷൻ പോയിന്റുകൾ എന്ന് വിളിക്കപ്പെടുന്നവയാണ് - അത്തരം പോയിന്റുകളിൽ, ഫംഗ്ഷന്റെ ഗ്രാഫിലേക്ക് അനന്തമായ ടാൻജന്റുകൾ വരയ്ക്കാൻ കഴിയും (ചിത്രം 28);

ഫംഗ്‌ഷൻ നിർത്തലാക്കുന്ന പോയിന്റുകളാണ് (രണ്ടാം തരത്തിന്റെ വിച്ഛേദിക്കുന്ന പോയിന്റുകളിൽ, ഫംഗ്‌ഷന്റെ ഗ്രാഫിന് ലംബമായ അസിംപ്റ്റോട്ട് ഉണ്ട്).

ഫംഗ്‌ഷന്റെ എക്‌സ്‌ട്രീം, ഇൻഫ്‌ളക്ഷൻ പോയിന്റുകളുടെ അന്തിമ കണക്കെടുപ്പിനായി, അവയുടെ ഓർഡിനേറ്റുകൾ കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്, തുടർന്ന് സൂചിപ്പിച്ച പോയിന്റുകൾ രണ്ട് കോർഡിനേറ്റുകൾ ഉപയോഗിച്ച് എഴുതുക.

ആത്മപരിശോധനയ്ക്കുള്ള ചോദ്യങ്ങൾ.

1. ഒരു ഫംഗ്‌ഷന്റെ എക്‌സ്‌ട്രീം പോയിന്റുകൾ (പരമാവധി കുറഞ്ഞതും) എന്ന് വിളിക്കപ്പെടുന്ന പോയിന്റുകൾ ഏതാണ്?

2. ഏത് പ്രവർത്തനത്തെ വർദ്ധിപ്പിക്കൽ (കുറയുന്നു) എന്ന് വിളിക്കുന്നു?

3. ഒരു ഫംഗ്ഷന്റെ എക്സ്ട്രീം പോയിന്റുകളുടെ നിലനിൽപ്പിന് ആവശ്യമായതും മതിയായതുമായ വ്യവസ്ഥകൾ എന്തൊക്കെയാണ്?

4. ഒരു ഫംഗ്‌ഷന്റെ വർദ്ധനവിന് (കുറയുന്നതിന്) മതിയായ വ്യവസ്ഥ എന്താണ്?

5. ഒരു ഫംഗ്ഷന്റെ ഇൻഫ്ലക്ഷൻ പോയിന്റുകൾ എന്ന് വിളിക്കുന്ന പോയിന്റുകൾ ഏതാണ്?

6. കോൺവെക്സ് (കോൺകേവ്) എന്ന് വിളിക്കുന്ന ഫംഗ്ഷൻ?

7. ഒരു ഫംഗ്ഷന്റെ ഇൻഫ്ലക്ഷൻ പോയിന്റുകളുടെ നിലനിൽപ്പിന് ആവശ്യമായതും മതിയായതുമായ വ്യവസ്ഥകൾ എന്തൊക്കെയാണ്?

8. ഒരു ഫംഗ്‌ഷന്റെ കോൺവെക്‌സിറ്റിക്ക് (കോൺകാവിറ്റി) മതിയായ അവസ്ഥ എന്താണ്?

പാഠത്തിന്റെ ഉദ്ദേശ്യം:പ്രവർത്തനങ്ങളെക്കുറിച്ച് ഒരു പഠനം എങ്ങനെ നടത്താമെന്ന് പഠിപ്പിക്കാൻ; അവരെ ഗൂഢാലോചന നടത്തുക.

ഫോം:സംഭാഷണ പാഠം.

രീതികൾ:സംഭാഷണം, ദൃശ്യ സഹായികൾ, സ്ലൈഡുകൾ.

ഉപകരണം:ഐസിടി, പട്ടികകൾ.

ക്ലാസുകൾക്കിടയിൽ

I. ഗൃഹപാഠം പരിശോധിക്കുന്നു.

അധ്യാപകൻ: - സുഹൃത്തുക്കളെ! നിങ്ങളുടെ ഗൃഹപാഠം "ഒരു ഫംഗ്‌ഷന്റെ നിർണ്ണായക പോയിന്റുകൾ, മാക്സിമയും മിനിമയും" ഉണ്ടായിരുന്നു. ഒരു ഫംഗ്ഷന്റെ നിർണായക പോയിന്റ് നിർവചിക്കുക.

വിദ്യാർത്ഥി: - ഒരു നിർണായക പോയിന്റ് നിർവചനത്തിന്റെ ഡൊമെയ്‌നിന്റെ ആന്തരിക പോയിന്റാണ്, അതിൽ ഡെറിവേറ്റീവ് പൂജ്യത്തിന് തുല്യമാണ് അല്ലെങ്കിൽ നിലവിലില്ല.

അധ്യാപകൻ: - നിർണായക പോയിന്റുകൾ എങ്ങനെ കണ്ടെത്താം?

വിദ്യാർത്ഥി: - 1

) ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക;

2) സമവാക്യം പരിഹരിക്കുക: f "(x) = 0. ഈ സമവാക്യത്തിന്റെ വേരുകൾ നിർണായക പോയിന്റുകളാണ്.

അധ്യാപകൻ: - ഫംഗ്‌ഷനുകളുടെ നിർണായക പോയിന്റുകൾ കണ്ടെത്തുക:

a) f(x)= 4 - 2x + 7x 2

b) f (x) \u003d 4x - x 3 / 3

a) 1) ഈ ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക:

f "(x)= (4 - 2x + 7x 2)" = -2+14x

2) f "(x) = 0 എന്ന സമവാക്യം പരിഹരിക്കുക<=>-2+14x=0<=>x=1/7

3) f "(x) \u003d 0 എന്ന സമവാക്യത്തിന് ഒരു റൂട്ട് ഉള്ളതിനാൽ, ഈ ഫംഗ്‌ഷന് ഒരു നിർണായക പോയിന്റ് x \u003d 1/7 ഉണ്ട്.

b) 1) ഈ ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക: f "(x) \u003d 4 - x 2

2) സമവാക്യം പരിഹരിക്കുക: f "(x) = 0<=>4 - x 2 = 0<=>x=2 അല്ലെങ്കിൽ x=-2

3) f "(x) \u003d 0 എന്ന സമവാക്യത്തിന് രണ്ട് വേരുകൾ ഉള്ളതിനാൽ, ഈ ഫംഗ്‌ഷന് രണ്ട് നിർണായക പോയിന്റുകൾ x 1 \u003d 2, x 2 \u003d -2 എന്നിവയുണ്ട്.

II.വാക്കാലുള്ള ജോലി.

അധ്യാപകൻ: - സുഹൃത്തുക്കളെ! ഒരു പുതിയ വിഷയം പഠിക്കാൻ ആവശ്യമായ പ്രധാന ചോദ്യങ്ങൾ ആവർത്തിക്കാം. ഇത് ചെയ്യുന്നതിന്, കണക്കുകളുള്ള പട്ടികകൾ പരിഗണിക്കുക ( അനെക്സ് 1).

ഫംഗ്‌ഷന്റെ വർദ്ധനവ് കുറയുന്നതിലൂടെ മാറ്റിസ്ഥാപിക്കുന്ന പോയിന്റുകൾ വ്യക്തമാക്കുക. ഈ പോയിന്റുകളെ എന്താണ് വിളിക്കുന്നത്?

വിദ്യാർത്ഥി: - ചിത്രത്തിൽ a) - പോയിന്റ് K ആണ് പരമാവധി പോയിന്റ്, ചിത്രത്തിൽ b) - പോയിന്റ് M ആണ് പരമാവധി പോയിന്റ്.

അധ്യാപകൻ: - ഫംഗ്ഷന്റെ ഏറ്റവും കുറഞ്ഞ പോയിന്റുകൾ എന്തൊക്കെയാണ്.

വിദ്യാർത്ഥി: - ചിത്രത്തിലെ പോയിന്റ് സി) ഒപ്പം ഡി) - ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞ പോയിന്റ്.

അധ്യാപകൻ: - ഫംഗ്‌ഷന്റെ എക്‌സ്‌ട്രീം പോയിന്റുകൾ ഏതൊക്കെയാണ്?

വിദ്യാർത്ഥി: - ക്രിട്ടിക്കൽ പോയിന്റുകൾ ഒരു ഫംഗ്‌ഷന്റെ എക്‌സ്‌ട്രീം പോയിന്റുകളാകാം.

അധ്യാപകൻ: - ആവശ്യമായ വ്യവസ്ഥകൾ എന്തൊക്കെയാണെന്ന് നിങ്ങൾക്കറിയാമോ?

വിദ്യാർത്ഥി: - ഫെർമാറ്റിന്റെ സിദ്ധാന്തമുണ്ട്. ഒരു തീവ്രതയ്ക്ക് ആവശ്യമായ വ്യവസ്ഥ:പോയിന്റ് x 0 ഫംഗ്‌ഷന്റെ എക്‌സ്‌ട്രീം പോയിന്റ് ആണെങ്കിൽ, ഈ ഘട്ടത്തിൽ ഒരു ഡെറിവേറ്റീവ് f "ഉണ്ടെങ്കിൽ, അത് പൂജ്യത്തിന് തുല്യമാണ്: f" (x) \u003d 0.

ടീച്ചർ: - ഫംഗ്ഷന്റെ നിർണായക പോയിന്റുകൾ കണ്ടെത്തുക:

a) f(x) = | x |

b) f(x) = 2x + | x |

വിദ്യാർത്ഥി: - f(x) = | എന്ന ഫംഗ്‌ഷൻ പരിഗണിക്കുക x | ( അപേക്ഷ 2). ഈ ഫംഗ്‌ഷന് 0-ൽ ഡെറിവേറ്റീവ് ഇല്ല. അതിനാൽ, 0 ഒരു നിർണായക പോയിന്റാണ്. വ്യക്തമായും, ഫംഗ്‌ഷന് പോയിന്റ് 0-ൽ മിനിമം ഉണ്ട്.

വിദ്യാർത്ഥി: - f(x) = 2x + | ഫംഗ്‌ഷൻ പരിഗണിക്കുക x | ( അനുബന്ധം 3). പോയിന്റ് 0-ൽ ഈ ഫംഗ്‌ഷന് ഒരു എക്സ്ട്രീം ഇല്ലെന്ന് ഗ്രാഫ് കാണിക്കുന്നു. ഈ ഘട്ടത്തിൽ, ഫംഗ്‌ഷന് ഒരു ഡെറിവേറ്റീവും ഇല്ല.

തീർച്ചയായും, f ഫംഗ്‌ഷന് 0-ൽ ഒരു ഡെറിവേറ്റീവ് ഉണ്ടെന്ന് ഞങ്ങൾ അനുമാനിക്കുകയാണെങ്കിൽ, f(x) - 2x ന് 0-ലും ഒരു ഡെറിവേറ്റീവ് ഉണ്ട്. എന്നാൽ f(x) - 2x = | x |, കൂടാതെ ഫംഗ്‌ഷൻ | x | പോയിന്റിൽ 0 വ്യത്യാസമില്ല, അതായത്, ഞങ്ങൾ ഒരു വൈരുദ്ധ്യത്തിൽ എത്തിയിരിക്കുന്നു.

ഇതിനർത്ഥം, പോയിന്റ് 0 ലെ f ഫംഗ്‌ഷന് ഡെറിവേറ്റീവ് ഇല്ല എന്നാണ്.

അധ്യാപകൻ: - എക്സ്ട്രീം പോയിന്റുകൾ കണ്ടെത്തുമ്പോൾ, നിങ്ങൾ നിർണായക പോയിന്റുകൾ കണ്ടെത്തേണ്ടതുണ്ടെന്ന് ഫെർമാറ്റിന്റെ സിദ്ധാന്തത്തിൽ നിന്ന് ഇത് പിന്തുടരുന്നു. എന്നാൽ പരിഗണിക്കപ്പെട്ട ഉദാഹരണങ്ങളിൽ നിന്ന് ഈ നിർണായക പോയിന്റ് ഒരു എക്സ്ട്രീം പോയിന്റ് ആകുന്നതിന്, ചില അധിക വ്യവസ്ഥകൾ ആവശ്യമാണെന്ന് വ്യക്തമാണ്.

നിങ്ങൾക്ക് അറിയാവുന്ന ഒരു ഘട്ടത്തിൽ ഒരു തീവ്രതയുടെ നിലനിൽപ്പിന് മതിയായ വ്യവസ്ഥകൾ എന്തൊക്കെയാണ്?

വിദ്യാർത്ഥി: - പരമാവധി പ്രവർത്തനത്തിന്റെ അടയാളം: f എന്ന ഫംഗ്‌ഷൻ x 0 പോയിന്റിലും f "(x)> 0 ഇടവേളയിലും (a; x 0), f "(x) തുടർച്ചയായി ആണെങ്കിൽ<0 на интервале (х 0 ; в), то точка х 0 является точкой максимума функции f.

അതായത്, x 0 എന്ന ബിന്ദുവിൽ ഡെറിവേറ്റീവ് ചിഹ്നം പ്ലസ് മുതൽ മൈനസിലേക്ക് മാറുകയാണെങ്കിൽ, x 0 ആണ് പരമാവധി പോയിന്റ്.

വിദ്യാർത്ഥി: - മിനിമം എന്നതിന്റെ അടയാളം: x 0, f "(x) എന്നീ പോയിന്റുകളിൽ f ഫംഗ്ഷൻ തുടർച്ചയായി ആണെങ്കിൽ<0 на интервале (а;х 0) и f "(x) >ഇടവേളയിൽ 0 (x 0 ; c), തുടർന്ന് x 0 എന്നത് ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞ പോയിന്റാണ്.

അതായത്, x 0 പോയിന്റിൽ ഡെറിവേറ്റീവ് ചിഹ്നം മൈനസിൽ നിന്ന് പ്ലസിലേക്ക് മാറ്റുകയാണെങ്കിൽ, x 0 ആണ് ഏറ്റവും കുറഞ്ഞ പോയിന്റ്.

ടീച്ചർ: - ഒരു ഫംഗ്‌ഷന്റെ എക്‌സ്‌ട്രീം പോയിന്റുകൾ കണ്ടെത്തുന്നതിനുള്ള അൽഗോരിതം എന്താണെന്ന് നിങ്ങൾക്കറിയാം.

ഡെറിവേറ്റീവ് ഉപയോഗിച്ച് ഒരു എക്സ്ട്രീം f ഫംഗ്ഷൻ പഠിക്കുന്നതിനുള്ള അൽഗോരിതം വിദ്യാർത്ഥി വിശദീകരിക്കുന്നു ( അനുബന്ധം 4) കൂടാതെ ഫംഗ്‌ഷന്റെ എക്‌സ്ട്രീം പോയിന്റുകൾ കണ്ടെത്തുന്നു:

f (x) \u003d x 4 -2x 2

D (f) =IR ഉം f ഉം മുഴുവൻ റിയൽ ലൈനിലും ഒരു സമ്പൂർണ്ണ യുക്തിസഹമായ ഫംഗ്‌ഷൻ എന്ന നിലയിൽ തുടർച്ചയായാണ്.

2. f "(x) \u003d 4x 3 -4x \u003d 4x (x + 1) (x-1).

3.f"(x)=0<=>x \u003d -1 V x \u003d 0 V x \u003d 1.

ചിത്രം.1 (അടയാളങ്ങൾ f ")

നിർണ്ണായക പോയിന്റുകളിൽ f തുടർച്ചയായതിനാൽ, ചിത്രം 1 ൽ നിന്ന് ( അനുബന്ധം 5) -1 ഉം 1 ഉം ഏറ്റവും കുറഞ്ഞ പോയിന്റുകളാണെന്നും 0 എന്നത് ഫംഗ്‌ഷന്റെ പരമാവധി പോയിന്റാണെന്നും കാണാൻ കഴിയും.

f മിനിറ്റ് \u003d f (-1) \u003d f (1) \u003d -1, f max \u003d f (0) \u003d 0.

അധ്യാപകൻ: - സുഹൃത്തുക്കളെ! f ഫംഗ്‌ഷന്റെ ഏകതാനതയുടെ ഇടവേളകൾ കണ്ടെത്തുന്നതിനുള്ള അൽഗോരിതം നമുക്ക് ഓർക്കാം.

ഫംഗ്ഷന്റെ ഏകതാനതയുടെ ഇടവേളകൾ കണ്ടെത്തുന്നതിനുള്ള അൽഗോരിതം വിദ്യാർത്ഥി ഓർക്കുന്നു ( അനുബന്ധം 6).

അധ്യാപകൻ: - ഫോർമുല നൽകുന്ന ഫംഗ്ഷൻ f ന്റെ വർദ്ധനവിന്റെയും കുറവിന്റെയും ഇടവേളകൾ കണ്ടെത്തുക

f (x) \u003d x 3 -12x

പരിഹാരം:

1. f(x) ഒരു ബഹുപദമായതിനാൽ, D (f) =IR.

2. ഫംഗ്ഷൻ f എന്നത് മുഴുവൻ യഥാർത്ഥ ലൈനിലും f "(x) \u003d 3x 2 -12 \u003d 3 (x + 2) (x-2) എന്നിവയിലും വ്യത്യസ്തമാണ്.

3. f "(x) ന്റെ പൂജ്യങ്ങൾ മാത്രമേ f ഫംഗ്‌ഷന്റെ നിർണായക പോയിന്റുകളാകൂ.

f"(x)=0<=>x \u003d -2 V x \u003d 2.

D (f) \ (-2; 2) \u003d (-; -2) U (-2; 2) U (2; +).

Fig.2 (അടയാളങ്ങൾ f ").

തന്നിരിക്കുന്ന ഫംഗ്‌ഷന്റെ നിർവചനത്തിന്റെയും മൂല്യങ്ങളുടെയും ഡൊമെയ്‌നുകൾ കണ്ടെത്തുക.

ഫംഗ്‌ഷന് പഠിക്കുന്നത് എളുപ്പമാക്കുന്ന സവിശേഷതകൾ ഉണ്ടോ എന്ന് കണ്ടെത്തുക, അതായത് ഫംഗ്ഷൻ f:

a) ഇരട്ട അല്ലെങ്കിൽ ഒറ്റത്തവണ;

b) ആനുകാലികം.

3. കോർഡിനേറ്റ് അക്ഷങ്ങൾ ഉപയോഗിച്ച് ഗ്രാഫിന്റെ ഇന്റർസെക്ഷൻ പോയിന്റുകളുടെ കോർഡിനേറ്റുകൾ കണക്കാക്കുക.

4. ഫംഗ്‌ഷന്റെ സ്ഥിരതയുടെ ഇടവേളകൾ കണ്ടെത്തുക.

5. ഏത് ഇടവേളകളിലാണ് f ഫംഗ്‌ഷൻ വർദ്ധിക്കുന്നതെന്നും ഏത് സമയത്താണ് കുറയുന്നതെന്നും കണ്ടെത്തുക.

6. എക്സ്ട്രീം പോയിന്റുകൾ (പരമാവധി അല്ലെങ്കിൽ കുറഞ്ഞത്) കണ്ടെത്തി ഈ പോയിന്റുകളിൽ f ന്റെ മൂല്യങ്ങൾ കണക്കാക്കുക.

7. നിർവചനത്തിന്റെ ഡൊമെയ്‌നിൽ ഉൾപ്പെടാത്ത സ്വഭാവസവിശേഷതകളുടെ അയൽപക്കത്തുള്ള f ഫംഗ്‌ഷന്റെ സ്വഭാവം അന്വേഷിക്കുക.

8. ഫംഗ്ഷൻ ഗ്രാഫ് ചെയ്യുക.

ഈ ഡയഗ്രം ചിത്രീകരണമാണ്.

മുകളിൽ പറഞ്ഞവയെല്ലാം പരിഗണിച്ച്, ഞങ്ങൾ ഫംഗ്ഷൻ പരിശോധിക്കുന്നു: f (x) \u003d 3x 5 -5x 3 +2 അതിന്റെ ഗ്രാഫ് നിർമ്മിക്കുക.

നമുക്ക് ഗവേഷണം ഇനിപ്പറയുന്ന രീതിയിൽ നടത്താം:

D (f ") =IR, f (x) ഒരു ബഹുപദമായതിനാൽ.

f ഫംഗ്ഷൻ ഇരട്ടയോ ഒറ്റയോ അല്ല, കാരണം

f (-x)= 3(-x) 5 -5(-x) 3 +2 = -3x 5 +5x 3 +2= -(3x 5 -5x 3 -2) f(x)

കോർഡിനേറ്റ് അക്ഷങ്ങൾ ഉപയോഗിച്ച് ഗ്രാഫിന്റെ ഇന്റർസെക്ഷൻ പോയിന്റുകളുടെ കോർഡിനേറ്റുകൾ കണ്ടെത്തുക:

a) 0X അക്ഷം ഉപയോഗിച്ച്, ഇതിനായി ഞങ്ങൾ സമവാക്യം പരിഹരിക്കുന്നു: 3x 5 -5x 3 +2 = 0.

തിരഞ്ഞെടുക്കൽ രീതിക്ക് റൂട്ടുകളിലൊന്ന് കണ്ടെത്താനാകും (x = 1). മറ്റ് വേരുകൾ ഏകദേശം മാത്രമേ കണ്ടെത്താൻ കഴിയൂ. അതിനാൽ, ഈ പ്രവർത്തനത്തിനായി, അബ്സിസ്സ അച്ചുതണ്ടും സ്ഥിരമായ ചിഹ്നത്തിന്റെ ഇടവേളകളും ഉപയോഗിച്ച് ഗ്രാഫിന്റെ വിഭജനത്തിന്റെ ശേഷിക്കുന്ന പോയിന്റുകൾ ഞങ്ങൾ കണ്ടെത്തുകയില്ല.

b) 0Y അക്ഷത്തിൽ: f(0)=2

പോയിന്റ് A (0; 2) - 0Y അക്ഷത്തോടുകൂടിയ ഫംഗ്ഷൻ ഗ്രാഫിന്റെ വിഭജന പോയിന്റ്.

അടയാള സ്ഥിരതയുടെ ഇടവേളകൾ ഞങ്ങൾ കണ്ടെത്തുകയില്ലെന്ന് ഞങ്ങൾ ശ്രദ്ധിച്ചു.

പ്രവർത്തനത്തിന്റെ വർദ്ധനവിന്റെയും കുറവിന്റെയും ഇടവേളകൾ കണ്ടെത്തുക

a) f "(x) \u003d 15x 4 -15x 2 \u003d 15x 2 (x 2 -1)

D (f ") \u003d IR, അതിനാൽ f "(x) നിലവിലില്ലാത്ത നിർണായക പോയിന്റുകളൊന്നുമില്ല.

b) f "(x) \u003d 0 ആണെങ്കിൽ x 2 (x 2 -1) \u003d 0<=>x = -1 V x = 0 V x = 1.

സി) നമുക്ക് മൂന്ന് നിർണായക പോയിന്റുകൾ ലഭിക്കുന്നു, അവ കോർഡിനേറ്റ് ലൈൻ നാല് ഇടവേളകളായി വിഭജിക്കുന്നു. ഈ ഇടവേളകളിൽ നമുക്ക് ഡെറിവേറ്റീവിന്റെ അടയാളം നിർണ്ണയിക്കാം:

ചിത്രം.3 (അടയാളങ്ങൾ f ")

IV. ഒരു പുതിയ വിഷയം പരിഹരിക്കുന്നു. പ്രശ്നപരിഹാരം.

അധ്യാപകൻ: - ഫംഗ്ഷൻ പര്യവേക്ഷണം ചെയ്ത് അതിന്റെ ഗ്രാഫ് നിർമ്മിക്കുക: f (x) \u003d x 4 -2x 2 -3.

വിദ്യാർത്ഥി: - 1) D (f) =R.

2) f (-x) \u003d (-x) 4 -2 (-x) 2 -3 \u003d x 4 -2x 2 -3; f(-x)= f(x),

അതിനാൽ f ഫംഗ്ഷൻ തുല്യമാണ്. ഫംഗ്ഷൻ - മുതൽ -4 വരെ വർദ്ധിക്കുന്ന ഇടവേളയിൽ ഇത് പഠിക്കാൻ കഴിയും, അതിനാൽ, f (x) \u003d 0 എന്ന സമവാക്യത്തിന് ഈ ഇടവേളയിൽ വേരുകളില്ല.

b) ഇടവേളയിൽ [-1; 2] സമവാക്യത്തിനും വേരുകളില്ല, കാരണം ഈ ഇടവേളയിൽ പ്രവർത്തനം -4 മുതൽ -31 വരെ കുറയുന്നു.

c) ഇടവേളയിലും [-∞;-1] കുറയുകയും ചെയ്യുന്നു.

എക്സ്ട്രീം പോയിന്റുകൾ: x മിനിറ്റ് = -1

ഫംഗ്ഷൻ എക്സ്ട്രീമ: y മിനിറ്റ് =y(-1)=1-2= -1

അധ്യായം III. പ്രവർത്തന ഗവേഷണം.

3.1 പ്രവർത്തനങ്ങളുടെ പഠനത്തിനുള്ള പൊതു പദ്ധതി.

ഒരു ഫംഗ്ഷൻ പരിശോധിക്കുമ്പോൾ, നിങ്ങൾ പൊതുവായ ഗവേഷണ പദ്ധതി അറിയേണ്ടതുണ്ട്:

1) D(y) - നിർവചനത്തിന്റെ ഡൊമെയ്‌ൻ (വേരിയബിളിന്റെ പരിധി x)

2) E(y) - x മൂല്യത്തിന്റെ വിസ്തീർണ്ണം (വേരിയബിളിന്റെ ശ്രേണി)

3) ഫംഗ്‌ഷന്റെ തരം: ഇരട്ട, ഒറ്റ, ആനുകാലിക അല്ലെങ്കിൽ പൊതു പ്രവർത്തനം.

4) ഓഹി ഓയ് (സാധ്യമെങ്കിൽ) അക്ഷങ്ങൾ ഉപയോഗിച്ച് ഫംഗ്ഷന്റെ ഗ്രാഫിന്റെ വിഭജന പോയിന്റുകൾ.

5) ചിഹ്ന സ്ഥിരതയുടെ ഇടവേളകൾ:

a) ഫംഗ്‌ഷൻ ഒരു പോസിറ്റീവ് മൂല്യം എടുക്കുന്നു: f(x)>0

b) നെഗറ്റീവ് മൂല്യം: f(x)<0.

6) ഫംഗ്‌ഷൻ മോണോടോണിസിറ്റിയുടെ ഇടവേളകൾ:

a) വർദ്ധനവ്;

ബി) കുറയുന്നു;

c) സ്ഥിരത (f=const).

7) എക്സ്ട്രീം പോയിന്റുകൾ (കുറഞ്ഞതും കൂടിയതുമായ പോയിന്റുകൾ)

8) ഫംഗ്ഷൻ എക്സ്ട്രീമ (കുറഞ്ഞതും കൂടിയതുമായ പോയിന്റുകളിൽ ഫംഗ്ഷൻ മൂല്യം)

9) അധിക പോയിന്റുകൾ.

ഫംഗ്ഷൻ കൂടുതൽ കൃത്യമായി പ്ലോട്ട് ചെയ്യുന്നതിനായി അവ എടുക്കാം.

ഫംഗ്ഷന്റെ തീവ്രത എല്ലായ്പ്പോഴും ഫംഗ്ഷന്റെ പരമാവധി, കുറഞ്ഞ മൂല്യങ്ങളുമായി പൊരുത്തപ്പെടുന്നില്ല എന്നത് ശ്രദ്ധിക്കേണ്ടതാണ്.

3.2 ഫംഗ്ഷനുകൾ വർദ്ധിക്കുന്നതിന്റെയും കുറയുന്നതിന്റെയും അടയാളം.

നിങ്ങൾ ഒരു ഫംഗ്‌ഷന്റെ ഏകപക്ഷീയമായി തിരഞ്ഞെടുത്ത പോയിന്റുകൾ ഉപയോഗിച്ച് ഒരു ഗ്രാഫ് നിർമ്മിക്കുകയാണെങ്കിൽ, അവയെ ഒരു മിനുസമാർന്ന വരയുമായി ബന്ധിപ്പിച്ച്, ക്രമരഹിതമായി തിരഞ്ഞെടുത്ത പോയിന്റുകളുടെ വളരെ വലിയ സംഖ്യയിൽ പോലും, ഈ രീതിയിൽ നിർമ്മിച്ച ഗ്രാഫ് വളരെ വ്യത്യസ്തമായിരിക്കും. തന്നിരിക്കുന്ന ഫംഗ്ഷന്റെ ഗ്രാഫിൽ നിന്ന്.

ഒരു ഫംഗ്ഷൻ പഠിക്കുമ്പോൾ, ഞങ്ങൾ ഡെറിവേറ്റീവ് ഉപയോഗിക്കുകയും "റഫറൻസ്" പോയിന്റുകൾ എന്ന് വിളിക്കുകയും ചെയ്യുന്നുവെങ്കിൽ, അതായത്. ബ്രേക്ക് പോയിന്റുകൾ, പരമാവധി, മിനിമം പോയിന്റുകൾ, ഫംഗ്‌ഷൻ മോണോടോണിസിറ്റിയുടെ ഇടവേളകൾ, തുടർന്ന് അത്തരം "റഫറൻസ്" പോയിന്റുകളുടെ ഒരു ചെറിയ എണ്ണം പോലും, ഫംഗ്ഷൻ ഗ്രാഫിന്റെ ശരിയായ ആശയം നമുക്ക് ലഭിക്കും.

ഉദാഹരണങ്ങളിലേക്ക് തിരിയുന്നതിനുമുമ്പ്, ആവശ്യമായ നിർവചനങ്ങളും സിദ്ധാന്തങ്ങളും ഞാൻ നൽകും.

ഒരു ഇടവേളയിലെ ഒരു ഫംഗ്‌ഷന്റെ ഏകതാനതയുടെ നിർവ്വചനം x 1 എന്ന അവസ്ഥയിൽ നിന്ന് ഈ ഇടവേളയുടെ ഏതെങ്കിലും പോയിന്റുകൾ x 1 ഉം x 2 ഉം ആണെങ്കിൽ, y \u003d f (x) ഫംഗ്‌ഷനെ ഇടവേളയിൽ വർദ്ധിക്കുന്നത് എന്ന് വിളിക്കുന്നു.<х 2 следует, что f(x 1)f(x 2), അപ്പോൾ ഫംഗ്‌ഷനെ ഈ ഇടവേളയിൽ കുറയുന്നു എന്ന് വിളിക്കുന്നു.

ഒരു ഇടവേളയിലെ ഒരു ഫംഗ്‌ഷന്റെ ഏകതാനതയ്ക്ക് മതിയായ മാനദണ്ഡം. സിദ്ധാന്തം: ഒരു ഫംഗ്‌ഷന് ഒരു ഇടവേളയുടെ ഓരോ പോയിന്റിലും പോസിറ്റീവ് (നെഗറ്റീവ്) ഡെറിവേറ്റീവ് ഉണ്ടെങ്കിൽ, ഈ ഇടവേളയിൽ ഫംഗ്ഷൻ വർദ്ധിക്കുന്നു (കുറയുന്നു).

ഈ സിദ്ധാന്തം തെളിവില്ലാതെ സ്കൂൾ പാഠപുസ്തകങ്ങളിൽ അംഗീകരിക്കപ്പെട്ടിരിക്കുന്നു.

സിദ്ധാന്തത്തിന്റെ ജ്യാമിതീയ വ്യാഖ്യാനം വളരെ ലളിതമാണ്, f '(x) \u003d tgα, α എന്നത് ഒരു നിശ്ചിത പോയിന്റിലെ ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റിന്റെ ചരിവാണ്. ഉദാഹരണത്തിന്, ഒരു നിശ്ചിത ഇടവേളയിലെ എല്ലാ പോയിന്റുകളിലും f ‘ (x)> 0 ആണെങ്കിൽ, abscissa അച്ചുതണ്ടോടുകൂടിയ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റ് മൂർച്ചയുള്ള കോണുകൾ ഉണ്ടാക്കുന്നു, അതായത് f (x) x-നൊപ്പം വർദ്ധിക്കുന്നു. f' (x) ആണെങ്കിൽ<0, то касательная с осью абсцисс образуют тупой угол, а значит, с ростом х функция f(x) убывает. Поскольку эти рассуждения основаны лишь на наглядных геометрических представлениях, они не являются доказательством теоремы.

3.3 ഫംഗ്‌ഷന്റെ നിർണായക പോയിന്റുകൾ, പരമാവധി, മിനിമ.

ഒരു ഫംഗ്ഷന്റെ എക്സ്ട്രീം പോയിന്റുകളുടെ നിർണ്ണയം . f(x) ഫംഗ്‌ഷന്റെ ഡൊമെയ്‌നിൽ നിന്നുള്ള ഒരു ഇന്റീരിയർ പോയിന്റ് x 0 ആയിരിക്കട്ടെ. അപ്പോൾ, അത്തരം ഒരു δ - അയൽപക്കം ഉണ്ടെങ്കിൽ ] x 0 - δ, x 0 + δ [ പോയിന്റ് x 0 , അതായത് ഈ അയൽപക്കത്തിൽ നിന്നുള്ള എല്ലാ x നും അസമത്വം f(x)≤f(x 0) തൃപ്തികരമാണ് (അസമത്വം f(x)≥f (x 0)), x 0 എന്ന പോയിന്റിനെ ഈ ഫംഗ്‌ഷന്റെ പരമാവധി പോയിന്റ് (മിനിമം പോയിന്റ്) എന്ന് വിളിക്കുന്നു.

ഫംഗ്‌ഷന്റെ ഡൊമെയ്‌നിന്റെ ആന്തരിക പോയിന്റുകളാണ് പരമാവധി-മിനിമം പോയിന്റുകൾ.

ഒരു ഡിഫറൻഷ്യബിൾ ഫംഗ്‌ഷന്റെ ഒരു തീവ്രതയുടെ നിലനിൽപ്പിന് ആവശ്യമായ ഒരു മാനദണ്ഡം .

ഫെർമാറ്റിന്റെ സിദ്ധാന്തം.

x 0 എന്നത് f (x) ഫംഗ്‌ഷന്റെ ഒരു എക്‌സ്ട്രീം പോയിന്റാണെങ്കിൽ ഈ ഘട്ടത്തിൽ ഡെറിവേറ്റീവ് നിലവിലുണ്ടെങ്കിൽ, അത് പൂജ്യത്തിന് തുല്യമാണ്: f '(x 0) \u003d 0.

ഈ സിദ്ധാന്തം വ്യതിരിക്തമായ ഒരു ഫംഗ്‌ഷന്റെ ഒരു തീവ്രതയുടെ നിലനിൽപ്പിന് പര്യാപ്തമല്ല: ഏതെങ്കിലും ഘട്ടത്തിൽ x 0 ഡെറിവേറ്റീവ് അപ്രത്യക്ഷമാകുകയാണെങ്കിൽ, x 0 പോയിന്റിൽ ഫംഗ്‌ഷന് ഒരു തീവ്രത ഉണ്ടെന്ന് ഇത് ഇതുവരെ പിന്തുടരുന്നില്ല.

ഒരു ഫംഗ്ഷന്റെ നിർണായക പോയിന്റുകളുടെ നിർവ്വചനം . ഒരു ഫംഗ്‌ഷന്റെ ഡൊമെയ്‌നിന്റെ ആന്തരിക പോയിന്റുകൾ, അതിന്റെ ഡെറിവേറ്റീവ് പൂജ്യത്തിന് തുല്യമായതോ നിലവിലില്ലാത്തതോ ആയ ഫംഗ്‌ഷന്റെ നിർണായക പോയിന്റുകൾ എന്ന് വിളിക്കുന്നു.

ഒരു തീവ്രതയുടെ നിലനിൽപ്പിന് മതിയായ വ്യവസ്ഥകൾ .

സിദ്ധാന്തം 1. f (x) എന്ന ഫംഗ്‌ഷൻ x 0 പോയിന്റിലും f '(x)> 0 ഇടവേളയിലും f '(x) ലും തുടർച്ചയായി ആണെങ്കിൽ<0 на интервале , то х 0 является точкой максимума функции f(x).

സിദ്ധാന്തം 2. f (x) എന്ന ഫംഗ്‌ഷൻ x 0 പോയിന്റിൽ തുടർച്ചയായി ആണെങ്കിൽ, f ‘(x)<0 на интервале и f ‘(x)>ഇടവേളയിൽ 0, പിന്നെ x 0 ആണ് f(x) ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞ പോയിന്റ്.

ഒരു ഫംഗ്‌ഷന്റെ എക്‌സ്‌ട്രീം പോയിന്റുകൾ കണ്ടെത്തുന്നതിന്, അതിന്റെ നിർണായക പോയിന്റുകൾ കണ്ടെത്തുകയും അവയിൽ ഓരോന്നിനും മതിയായ എക്‌സ്‌ട്രീം വ്യവസ്ഥകളുടെ പൂർത്തീകരണം പരിശോധിക്കുകയും ചെയ്യേണ്ടത് ആവശ്യമാണ്.

3.4 പ്രവർത്തനത്തിന്റെ ഏറ്റവും വലുതും ചെറുതുമായ മൂല്യങ്ങൾ.

ഇടവേളയിൽ ഫംഗ്‌ഷനുകളുടെ ഏറ്റവും വലുതും ചെറുതുമായ മൂല്യങ്ങൾ കണ്ടെത്തുന്നതിനുള്ള നിയമങ്ങൾ. ഒരു നിശ്ചിത ഇടവേളയിൽ വ്യത്യാസപ്പെട്ടിരിക്കുന്ന ഒരു ഫംഗ്ഷന്റെ ഏറ്റവും വലുതും ചെറുതുമായ മൂല്യങ്ങൾ കണ്ടെത്തുന്നതിന്, ഇടവേളയ്ക്കുള്ളിൽ കിടക്കുന്ന എല്ലാ നിർണായക പോയിന്റുകളും നിങ്ങൾ കണ്ടെത്തേണ്ടതുണ്ട്, ഈ പോയിന്റുകളിലും അറ്റത്തും ഫംഗ്ഷന്റെ മൂല്യങ്ങൾ കണക്കാക്കുക. ഇടവേള, ഈ രീതിയിൽ ലഭിച്ച ഫംഗ്‌ഷന്റെ എല്ലാ മൂല്യങ്ങളിൽ നിന്നും ഏറ്റവും വലുതും ചെറുതുമായത് തിരഞ്ഞെടുക്കുക.

അധ്യായം IV. ഒരു ഫംഗ്ഷന്റെ പഠനത്തിന് ഡെറിവേറ്റീവ് പ്രയോഗിക്കുന്നതിനുള്ള ഉദാഹരണങ്ങൾ.

ഉദാഹരണം 11. y=x 3 +6x 2 +9x ഫംഗ്‌ഷൻ പര്യവേക്ഷണം ചെയ്‌ത് ഒരു ഗ്രാഫ് നിർമ്മിക്കുക.

2) പ്രവർത്തനത്തിന്റെ തരം നിർവചിക്കുക:

y(-x)=(-x) 3 +6(-x) 2 +9(-x)=-x+6x 2 -9x പൊതു പ്രവർത്തനം.

x=0 അല്ലെങ്കിൽ x2 +6x+9=0

D=0, സമവാക്യത്തിന് ഒരു റൂട്ട് ഉണ്ട്.

(0;0) കൂടാതെ (-3;0) - x-ആക്സിസുമായുള്ള വിഭജനത്തിന്റെ പോയിന്റുകൾ.

y'=(x 3 +6x 2 +9x)'=3x 2 +12x+9

y'=0, അതായത്. 3x 2 +12x+9=0 3 കൊണ്ട് കുറയ്ക്കുക

D>0, സമവാക്യത്തിന് 2 വേരുകളുണ്ട്.

x 1,2 \u003d (-b±√D) / 2a, x 1 \u003d (-4 + 2) / 2, x 2 \u003d (-4-2) / 2

0
-4

x=-4, y'=3*16-48+9=9>0

x=-2, y'=12-24+9=-3<0

x=0, y'=0+0+9=9>0

7) x മിനിറ്റും x പരമാവധിയും കണ്ടെത്തുക:

8) ഫംഗ്‌ഷന്റെ തീവ്രത കണ്ടെത്തുക:

ymin=y(-1)=-1+6-9=-4

ymax=y(-3)=-27+54-27=0

9) നമുക്ക് ഫംഗ്‌ഷന്റെ ഒരു ഗ്രാഫ് നിർമ്മിക്കാം:

10) അധിക പോയിന്റുകൾ:

y(-4)=-64+96-36=-4

ഉദാഹരണം 12. y=x 2 /(x-2) ഫംഗ്‌ഷൻ പര്യവേക്ഷണം ചെയ്‌ത് ഒരു ഗ്രാഫ് നിർമ്മിക്കുക

y=x 2 /(x-2)=x+2+4/(x-2)

ഫംഗ്‌ഷന്റെ അസിംപ്റ്റോട്ടുകൾ നമുക്ക് കണ്ടെത്താം:

x≠ 2, x=2 - ലംബമായ അസിംപ്റ്റോട്ട്

y=x+2 ചരിഞ്ഞ അസിംപ്റ്റോട്ടാണ്, കാരണം

നമുക്ക് നിർവചനത്തിന്റെ ഡൊമെയ്ൻ കണ്ടെത്താം.

2) ഫംഗ്‌ഷന്റെ തരം നിർവചിക്കാം.

y(-x)=(-x) 2 /(-x-2)=x 2 /(-x-2), പൊതു പ്രവർത്തനം.

3) അക്ഷങ്ങൾ ഉപയോഗിച്ച് വിഭജനത്തിന്റെ പോയിന്റുകൾ കണ്ടെത്തുക.

Oy: x=0, y=0 (0;0) - y-ആക്സിസുമായുള്ള വിഭജന പോയിന്റ്.

x=0 അല്ലെങ്കിൽ x=2 (2;0) - x-ആക്സിസുമായുള്ള വിഭജന പോയിന്റ്

4) ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക:

y'=(2x(x-2)-x 2)/(x-2) 2 =(2x 2 -4x-x 2)/(x-2) 2 =(x(x-4))/(x -2) 2 \u003d (x 2 -4x) / (x-2) 2

5) നിർണായക പോയിന്റുകൾ നിർവചിക്കുക:

x 2 -4x=0 x(x-4)=0

y'=0, (x 2 -4x)/(x-2) 2 =0<=> <=>

(x-2) 2 ≠ 0 x≠ 2

x 2 -4x=0, കൂടാതെ (x-2) 2 ≠ 0, അതായത്. x≠ 2

6) കോർഡിനേറ്റ് ലൈനിലെ നിർണായക പോയിന്റുകൾ ഞങ്ങൾ സൂചിപ്പിക്കുകയും ഫംഗ്ഷന്റെ അടയാളം നിർണ്ണയിക്കുകയും ചെയ്യുന്നു.

0 8

x=-1, y'=(1+4)/9=5/9>0

x=1, y'=(1-4)/1=-3<0

x=3, y'=(9-12)/1=-3<0

x=5, y'=(25-20)/9=5/9>0

7) ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞതും കൂടിയതുമായ പോയിന്റുകൾ കണ്ടെത്തുക:

8) ഫംഗ്‌ഷന്റെ തീവ്രത കണ്ടെത്തുക:

ymin=y(4)=16/2=8

9) നമുക്ക് ഫംഗ്‌ഷന്റെ ഒരു ഗ്രാഫ് നിർമ്മിക്കാം:

10) അധിക പോയിന്റുകൾ:

y(-3)=9/-5=-1.8 y(3)=9/1=9

y(1)=1/-1=-1 y(6)=36/4=9

ഉദാഹരണം 13 y=(6(x-1))/(x 2 +3) ഫംഗ്‌ഷൻ പര്യവേക്ഷണം ചെയ്‌ത് ഒരു ഗ്രാഫ് നിർമ്മിക്കുക. 1) ഫംഗ്‌ഷന്റെ ഡൊമെയ്‌ൻ കണ്ടെത്തുക:

2) പ്രവർത്തനത്തിന്റെ തരം നിർവചിക്കുക:

y(-x)=(6(-x-1))/(x 2 +3)=-(6(x+1))/(x 2 -3) എന്നത് ഒരു പൊതു പ്രവർത്തനമാണ്.

3) അക്ഷങ്ങൾ ഉപയോഗിച്ച് വിഭജിക്കുന്ന പോയിന്റുകൾ കണ്ടെത്തുക:

O y: x=0, y=(6(0-1))/(0+3)=-2, (0;-2) - y-ആക്സിസുമായുള്ള വിഭജനത്തിന്റെ പോയിന്റ്.

(6(x-1))/(x 2 +3)=0

O x: y=0,<=>

4) ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക:

y'=(6(x-1)/(x 2 +3))'=6(x 2 +3-2x 2 +2x)/(x 2 +2) 2 =-6(x+1)(x -3)/(x 2 +3) 2

5) നിർണായക പോയിന്റുകൾ നിർവചിക്കുക:

y'=0, അതായത്. -6(x+1)(x-3)/(x 2 +3) 2 =0

y'=0, x 1 =-1 അല്ലെങ്കിൽ x 2 =3 ആണെങ്കിൽ, x=-1, x=3, നിർണായക പോയിന്റുകൾ.

6) കോർഡിനേറ്റ് ലൈനിലെ നിർണായക പോയിന്റുകൾ ഞങ്ങൾ സൂചിപ്പിക്കുകയും ഫംഗ്ഷന്റെ അടയാളം നിർണ്ണയിക്കുകയും ചെയ്യുന്നു:

-3 2

x=-2, y'=-6(-2+1)(-2-3)/(4+3) 2 =-30/49<0

x=0, y'=-6(0+1)(0-3)/(0+3) 2 =2>0

x=4, y'=-6(4+1)(4-3)/(16+3) 2=-30/361<0

7) ഏറ്റവും കുറഞ്ഞതും കൂടിയതുമായ പോയിന്റുകൾ കണ്ടെത്തുക:

8) ഫംഗ്‌ഷന്റെ തീവ്രത കണ്ടെത്തുക:

y മിനിറ്റ് =y(-1)=(6(-1-1))/(1+3)=-12/4=-3

y പരമാവധി =y(3)=(6(3-1))/(9+3)=12/12=1

9) നമുക്ക് ഫംഗ്‌ഷന്റെ ഒരു ഗ്രാഫ് നിർമ്മിക്കാം:

10) അധിക പോയിന്റുകൾ:

y(-3)=(6(-3-1))/(9+3)=-24/12=-2

y(6)=(6(6-1))/(36+3)=30/39=10/13≈ 0.77

ഉദാഹരണം 14 y=xlnx ഫംഗ്‌ഷൻ പര്യവേക്ഷണം ചെയ്‌ത് അതിന്റെ ഗ്രാഫ് നിർമ്മിക്കുക:

1) ഫംഗ്‌ഷന്റെ ഡൊമെയ്‌ൻ കണ്ടെത്തുക:

D(y)=R + (പോസിറ്റീവ് മൂല്യങ്ങൾ മാത്രം)

2) പ്രവർത്തനത്തിന്റെ തരം നിർവചിക്കുക:

y(-x)=-xlnx - പൊതുവായ രൂപം.

3) അക്ഷങ്ങൾ ഉപയോഗിച്ച് വിഭജിക്കുന്ന പോയിന്റുകൾ കണ്ടെത്തുക:

O y, എന്നാൽ x≠ 0, അതിനാൽ y-അക്ഷവുമായി വിഭജന പോയിന്റുകളൊന്നുമില്ല.

കാള: y=0 അതായത് xlnx=0

x=0 അല്ലെങ്കിൽ lnx=0

(1;0) - x-ആക്സിസുമായുള്ള വിഭജന പോയിന്റ്

4) ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക:

y'=x' ln x + x(ln x)'=ln x +1

5) നിർണായക പോയിന്റുകൾ നിർവചിക്കുക:

y'=0, അതായത് lnx +1=0

y'=0 , x=1/e ആണെങ്കിൽ, x=1/e ഒരു നിർണായക പോയിന്റാണ്.

6) കോർഡിനേറ്റ് ലൈനിലെ നിർണായക പോയിന്റുകൾ ഞങ്ങൾ സൂചിപ്പിക്കുകയും ഫംഗ്ഷന്റെ അടയാളം നിർണ്ണയിക്കുകയും ചെയ്യുന്നു:

1/ഇ

x=1/(2e); y'=log(2e) -1 +1=1-ln(2e)=1-ln e=-ln 2<0

x=2e; y'=ln(2e)+1=ln 2+ln e+1=ln 2+2>0

7) ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞ പോയിന്റാണ് 1/e.

8) ഫംഗ്‌ഷന്റെ തീവ്രത കണ്ടെത്തുക:

y മിനിറ്റ് \u003d y (1 / e) \u003d 1 / e ln e -1 \u003d -1 / e (≈ -0.4).

9) നമുക്ക് ഫംഗ്‌ഷന്റെ ഒരു ഗ്രാഫ് നിർമ്മിക്കാം:

ഉപസംഹാരം.

നിരവധി ശാസ്ത്രജ്ഞരും തത്ത്വചിന്തകരും ഈ വിഷയത്തിൽ പ്രവർത്തിച്ചിട്ടുണ്ട്. നിരവധി വർഷങ്ങൾക്ക് മുമ്പ്, ഈ പദങ്ങൾ പ്രത്യക്ഷപ്പെട്ടു: ഫംഗ്ഷൻ, ഗ്രാഫ്, ഫംഗ്ഷന്റെ പഠനം, അവ ഇന്നുവരെ നിലനിൽക്കുന്നു, പുതിയ സവിശേഷതകളും സവിശേഷതകളും നേടിയെടുക്കുന്നു.

പ്രവർത്തനത്തെക്കുറിച്ചുള്ള ഗവേഷണത്തിന്റെ ഈ പാതയിലൂടെ പോകുന്നത് എനിക്ക് വളരെ രസകരമായതിനാൽ ഞാൻ ഈ വിഷയം തിരഞ്ഞെടുത്തു. പ്രവർത്തനത്തെക്കുറിച്ചും അതിന്റെ ഗുണങ്ങളെക്കുറിച്ചും പരിവർത്തനങ്ങളെക്കുറിച്ചും കൂടുതലറിയാൻ പലർക്കും താൽപ്പര്യമുണ്ടെന്ന് എനിക്ക് തോന്നുന്നു. ഈ ഉപന്യാസം തയ്യാറാക്കിയ ശേഷം, ഞാൻ എന്റെ കഴിവുകൾ ചിട്ടപ്പെടുത്തുകയും ഈ വിഷയത്തെക്കുറിച്ചുള്ള എന്റെ അറിവ് നിറയ്ക്കുകയും ചെയ്തു.

ഈ വിഷയം കൂടുതൽ ആഴത്തിൽ പഠിക്കാൻ എല്ലാവരേയും ഉപദേശിക്കാൻ ഞാൻ ആഗ്രഹിക്കുന്നു.

ഗ്രന്ഥസൂചിക.

1. ബാഷ്മാകോവ്, എം.ഐ. ബീജഗണിതവും വിശകലനത്തിന്റെ തുടക്കവും - എം .: വിദ്യാഭ്യാസം, 1992.

2. ഗ്ലേസർ, ജി.ഐ. സ്കൂളിലെ ഗണിതശാസ്ത്ര ചരിത്രം - എം .: വിദ്യാഭ്യാസം, 1983.

3. ഗുസെവ്, വി.എ. ഗണിതം: റഫറൻസ് മെറ്റീരിയലുകൾ - എം .: വിദ്യാഭ്യാസം, 1888.

4. ഡോറോഫീവ്, ജി.വി. സർവ്വകലാശാലകളിലേക്കുള്ള അപേക്ഷകർക്കുള്ള മാത്തമാറ്റിക്സ് മാനുവൽ - എം .: നൗക, 1974.

5. സോറിൻ, വി.വി. സർവ്വകലാശാലകളിലേക്കുള്ള അപേക്ഷകർക്കുള്ള മാത്തമാറ്റിക്സ് മാനുവൽ - എം .: ഹയർ സ്കൂൾ, 1980.

6. കോൾമോഗോറോവ് എ.എൻ. ബീജഗണിതവും വിശകലനത്തിന്റെ തുടക്കവും.- എം.: എൻലൈറ്റൻമെന്റ്, 1993.