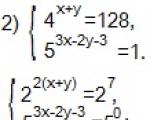എക്‌സ്‌പോണൻഷ്യൽ ക്വാഡ്രാറ്റിക് അസമത്വങ്ങൾ പരിഹരിക്കുന്നു. എക്‌സ്‌പോണൻഷ്യൽ സമവാക്യങ്ങളുടെയും അസമത്വങ്ങളുടെയും സിസ്റ്റങ്ങൾ

എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങൾ സങ്കീർണ്ണവും മനസ്സിലാക്കാൻ കഴിയാത്തതുമായ ഒന്നാണെന്ന് പലരും കരുതുന്നു. അവ പരിഹരിക്കാൻ പഠിക്കുന്നത് മിക്കവാറും ഒരു മികച്ച കലയാണ്, അത് തിരഞ്ഞെടുക്കപ്പെട്ടവർക്ക് മാത്രമേ മനസ്സിലാക്കാൻ കഴിയൂ.

തികഞ്ഞ അസംബന്ധം! എക്സ്പോണൻഷ്യൽ അസമത്വങ്ങൾ എളുപ്പമാണ്. അവ എല്ലായ്പ്പോഴും ലളിതമായി പരിഹരിക്കപ്പെടുന്നു. ശരി, മിക്കവാറും എല്ലായ്‌പ്പോഴും.

ഇന്ന് നമ്മൾ ഈ വിഷയം അകത്തും പുറത്തും നോക്കും. സ്കൂൾ ഗണിതശാസ്ത്രത്തിൻ്റെ ഈ ഭാഗം മനസ്സിലാക്കാൻ തുടങ്ങുന്നവർക്ക് ഈ പാഠം വളരെ ഉപയോഗപ്രദമാകും. ലളിതമായ പ്രശ്നങ്ങളിൽ നിന്ന് ആരംഭിച്ച് കൂടുതൽ സങ്കീർണ്ണമായ പ്രശ്നങ്ങളിലേക്ക് പോകാം. ഇന്ന് കഠിനാധ്വാനമൊന്നും ഉണ്ടാകില്ല, എന്നാൽ നിങ്ങൾ ഇപ്പോൾ വായിക്കുന്നത് എല്ലാത്തരം ടെസ്റ്റുകളിലും സ്വതന്ത്ര ജോലികളിലും അസമത്വങ്ങൾ പരിഹരിക്കാൻ മതിയാകും. നിങ്ങളുടെ ഈ പരീക്ഷയിലും.

എല്ലായ്പ്പോഴും എന്നപോലെ, നമുക്ക് നിർവചനത്തിൽ നിന്ന് ആരംഭിക്കാം. എക്‌സ്‌പോണൻഷ്യൽ അസമത്വം എന്നത് ഒരു എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷൻ ഉൾക്കൊള്ളുന്ന ഏതൊരു അസമത്വവുമാണ്. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, അത് എല്ലായ്പ്പോഴും രൂപത്തിൻ്റെ അസമത്വത്തിലേക്ക് ചുരുക്കാം

\[((എ)^(x)) \gt b\]

$b$ എന്നതിൻ്റെ റോൾ ഒരു സാധാരണ സംഖ്യയായിരിക്കാം, അല്ലെങ്കിൽ അതിലും കഠിനമായ ഒന്നായിരിക്കാം. ഉദാഹരണങ്ങൾ? അതെ, ദയവായി:

\[\ആരംഭിക്കുക(വിന്യസിക്കുക) & ((2)^(x)) \gt 4;\quad ((2)^(x-1))\le \frac(1)(\sqrt(2));\ ക്വാഡ് ((2)^((((x)^(2))-7x+14)) \lt 16; \\ & ((0,1)^(1-x)) \lt 0.01;\quad ((2)^(\frac(x)(2)) \lt ((4)^(\frac (4) )(x))). \\\അവസാനം (വിന്യസിക്കുക)\]

അർത്ഥം വ്യക്തമാണെന്ന് ഞാൻ കരുതുന്നു: ഒരു എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷൻ $((a)^(x))$ ഉണ്ട്, അത് എന്തെങ്കിലുമായി താരതമ്യം ചെയ്യുന്നു, തുടർന്ന് $x$ കണ്ടെത്താൻ ആവശ്യപ്പെടുന്നു. പ്രത്യേകിച്ച് ക്ലിനിക്കൽ കേസുകളിൽ, $x$ എന്ന വേരിയബിളിന് പകരം, അവർക്ക് ചില ഫംഗ്ഷൻ $f\left(x \right)$ നൽകുകയും അതുവഴി അസമത്വത്തെ അൽപ്പം സങ്കീർണ്ണമാക്കുകയും ചെയ്യാം.

തീർച്ചയായും, ചില സന്ദർഭങ്ങളിൽ അസമത്വം കൂടുതൽ രൂക്ഷമായേക്കാം. ഉദാഹരണത്തിന്:

\[((9)^(x))+8 \gt ((3)^(x+2))\]

അല്ലെങ്കിൽ ഇതും:

പൊതുവേ, അത്തരം അസമത്വങ്ങളുടെ സങ്കീർണ്ണത വളരെ വ്യത്യസ്തമായിരിക്കും, പക്ഷേ അവസാനം അവ ഇപ്പോഴും ലളിതമായ നിർമ്മാണത്തിലേക്ക് ചുരുങ്ങുന്നു $((a)^(x)) \gt b$. അത്തരമൊരു നിർമ്മാണം ഞങ്ങൾ എങ്ങനെയെങ്കിലും കണ്ടെത്തും (പ്രത്യേകിച്ച് ക്ലിനിക്കൽ കേസുകളിൽ, ഒന്നും മനസ്സിൽ വരുമ്പോൾ, ലോഗരിതം ഞങ്ങളെ സഹായിക്കും). അതിനാൽ, അത്തരം ലളിതമായ നിർമ്മാണങ്ങൾ എങ്ങനെ പരിഹരിക്കാമെന്ന് ഇപ്പോൾ ഞങ്ങൾ നിങ്ങളെ പഠിപ്പിക്കും.

ലളിതമായ എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങൾ പരിഹരിക്കുന്നു

വളരെ ലളിതമായ ഒരു കാര്യം നോക്കാം. ഉദാഹരണത്തിന്, ഇത്:

\[((2)^(x)) \gt 4\]

വ്യക്തമായും, വലതുവശത്തുള്ള നമ്പർ രണ്ടിൻ്റെ ശക്തിയായി മാറ്റിയെഴുതാം: $4=(2)^(2))$. അതിനാൽ, യഥാർത്ഥ അസമത്വം വളരെ സൗകര്യപ്രദമായ രൂപത്തിൽ മാറ്റിയെഴുതാം:

\[((2)^(x)) \gt ((2)^(2))\]

ഇപ്പോൾ എൻ്റെ കൈകൾ $x \gt 2$ എന്ന ഉത്തരം ലഭിക്കുന്നതിന് ശക്തികളുടെ അടിത്തറയിലെ ഇരുവരെയും "കടക്കാൻ" ചൊറിച്ചിലാണ്. എന്നാൽ എന്തെങ്കിലും മറികടക്കുന്നതിന് മുമ്പ്, നമുക്ക് രണ്ടിൻ്റെ ശക്തികൾ ഓർക്കാം:

\[((2)^(1))=2;\quad ((2)^(2))=4;\quad ((2)^(3))=8;\quad ((2)^( 4))=16;...\]

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, എക്‌സ്‌പോണൻ്റിലെ വലിയ സംഖ്യ, ഔട്ട്‌പുട്ട് നമ്പർ വലുതാണ്. "നന്ദി, ക്യാപ്!" - വിദ്യാർത്ഥികളിൽ ഒരാൾ ആക്രോശിക്കും. ഇത് എന്തെങ്കിലും വ്യത്യസ്തമാണോ? നിർഭാഗ്യവശാൽ, അത് സംഭവിക്കുന്നു. ഉദാഹരണത്തിന്:

\[(\ഇടത്(\frac(1)(2) \വലത്))^(1))=\frac(1)(2);\quad ((\ഇടത്(\frac(1)(2) വലത്))^(2))=\frac(1)(4);\quad ((\ഇടത്(\frac(1)(2) \വലത്))^(3))=\frac(1)(8 );...\]

ഇവിടെയും എല്ലാം യുക്തിസഹമാണ്: വലിയ ഡിഗ്രി, കൂടുതൽ തവണ സംഖ്യ 0.5 സ്വയം ഗുണിക്കുന്നു (അതായത്, പകുതിയായി വിഭജിച്ചിരിക്കുന്നു). അങ്ങനെ, തത്ഫലമായുണ്ടാകുന്ന സംഖ്യകളുടെ ക്രമം കുറയുന്നു, ഒന്നാമത്തെയും രണ്ടാമത്തെയും ശ്രേണി തമ്മിലുള്ള വ്യത്യാസം അടിസ്ഥാനത്തിൽ മാത്രമാണ്:

• ഡിഗ്രിയുടെ അടിസ്ഥാനം $a \gt 1$ ആണെങ്കിൽ, $n$ ഘാതം കൂടുന്നതിനനുസരിച്ച് $((a)^(n))$ എന്ന സംഖ്യയും വർദ്ധിക്കും;
• തിരിച്ചും, $0 \lt a \lt 1$ ആണെങ്കിൽ, $n$ വർദ്ധിക്കുന്നതിനനുസരിച്ച് $((a)^(n))$ എന്ന സംഖ്യ കുറയും.

ഈ വസ്‌തുതകൾ സംഗ്രഹിക്കുന്നതിലൂടെ, എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങളുടെ മുഴുവൻ പരിഹാരവും അടിസ്ഥാനമാക്കിയുള്ള ഏറ്റവും പ്രധാനപ്പെട്ട പ്രസ്താവന ഞങ്ങൾ നേടുന്നു:

$a \gt 1$ ആണെങ്കിൽ, അസമത്വം $((a)^(x)) \gt ((a)^(n))$ അസമത്വത്തിന് തുല്യമാണ് $x \gt n$. $0 \lt a \lt 1$ ആണെങ്കിൽ, അസമത്വം $((a)^(x)) \gt ((a)^(n))$ അസമത്വത്തിന് തുല്യമാണ് $x \lt n$.

മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, അടിസ്ഥാനം ഒന്നിൽ കൂടുതലാണെങ്കിൽ, നിങ്ങൾക്ക് അത് നീക്കംചെയ്യാം - അസമത്വ ചിഹ്നം മാറില്ല. അടിസ്ഥാനം ഒന്നിൽ കുറവാണെങ്കിൽ, അത് നീക്കംചെയ്യാനും കഴിയും, എന്നാൽ അതേ സമയം നിങ്ങൾ അസമത്വ ചിഹ്നം മാറ്റേണ്ടിവരും.

$a=1$, $a\le 0$ എന്നീ ഓപ്ഷനുകൾ ഞങ്ങൾ പരിഗണിച്ചിട്ടില്ല എന്നത് ശ്രദ്ധിക്കുക. കാരണം ഈ സന്ദർഭങ്ങളിൽ അനിശ്ചിതത്വം ഉയർന്നുവരുന്നു. $((1)^(x)) \gt 3$ എന്ന ഫോമിൻ്റെ അസമത്വം എങ്ങനെ പരിഹരിക്കാമെന്ന് നമുക്ക് പറയാം? ഏതൊരു ശക്തിക്കും ഒന്ന് വീണ്ടും ഒന്ന് നൽകും - നമുക്ക് ഒരിക്കലും മൂന്നോ അതിലധികമോ ലഭിക്കില്ല. ആ. പരിഹാരങ്ങളൊന്നുമില്ല.

നെഗറ്റീവ് കാരണങ്ങളാൽ എല്ലാം കൂടുതൽ രസകരമാണ്. ഉദാഹരണത്തിന്, ഈ അസമത്വം പരിഗണിക്കുക:

\[((\ഇടത്(-2 \വലത്))^(x)) \gt 4\]

ഒറ്റനോട്ടത്തിൽ, എല്ലാം ലളിതമാണ്:

ശരിയാണോ? പക്ഷെ ഇല്ല! പരിഹാരം തെറ്റാണെന്ന് ഉറപ്പാക്കാൻ $x$ എന്നതിന് പകരം രണ്ട് ഇരട്ട സംഖ്യകളും രണ്ട് ഒറ്റ സംഖ്യകളും മാറ്റിസ്ഥാപിച്ചാൽ മതിയാകും. ഒന്നു നോക്കൂ:

\[\begin(align) & x=4\Rightarrow ((\left(-2 \right))^(4))=16 \gt 4; \\ & x=5\Rightarrow ((\ഇടത്(-2 \വലത്))^(5))=-32 \lt 4; \\ & x=6\Rightarrow ((\ഇടത്(-2 \വലത്))^(6))=64 \gt 4; \\ & x=7\Rightarrow ((\left(-2 \right))^(7))=-128 \lt 4. \\\ end(align)\]

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, അടയാളങ്ങൾ മാറിമാറി വരുന്നു. എന്നാൽ ഭിന്നശക്തികളും മറ്റ് അസംബന്ധങ്ങളും ഉണ്ട്. ഉദാഹരണത്തിന്, $((\ഇടത്(-2 \വലത്))^(\sqrt(7)))$ (മൈനസ് രണ്ട് മുതൽ ഏഴിൻ്റെ ശക്തി) കണക്കാക്കാൻ നിങ്ങൾ എങ്ങനെയാണ് ഓർഡർ ചെയ്യുന്നത്? ഒരു വഴിയുമില്ല!

അതിനാൽ, വ്യക്തതയ്ക്കായി, എല്ലാ എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങളിലും (കൂടാതെ സമവാക്യങ്ങളും) $1\ne ഒരു \gt 0$ ആണെന്ന് ഞങ്ങൾ അനുമാനിക്കുന്നു. തുടർന്ന് എല്ലാം വളരെ ലളിതമായി പരിഹരിക്കപ്പെടും:

\[((എ)^(x)) \gt ((എ)^(n))\വലത്തോട്ടുള്ള \ഇടത്[ \begin(align) & x \gt n\quad \left(a \gt 1 \right), \\ & x \lt n\quad \left(0 \lt a \lt 1 \right). \\\ അവസാനം (വിന്യസിക്കുക) \വലത്.\]

പൊതുവേ, പ്രധാന നിയമം ഒരിക്കൽ കൂടി ഓർക്കുക: ഒരു എക്‌സ്‌പോണൻഷ്യൽ സമവാക്യത്തിലെ അടിസ്ഥാനം ഒന്നിൽ കൂടുതലാണെങ്കിൽ, നിങ്ങൾക്ക് അത് ലളിതമായി നീക്കംചെയ്യാം; അടിസ്ഥാനം ഒന്നിൽ കുറവാണെങ്കിൽ, അതും നീക്കം ചെയ്യാവുന്നതാണ്, എന്നാൽ അസമത്വത്തിൻ്റെ അടയാളം മാറും.

പരിഹാരങ്ങളുടെ ഉദാഹരണങ്ങൾ

അതിനാൽ, നമുക്ക് കുറച്ച് ലളിതമായ എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങൾ നോക്കാം:

\[\ആരംഭിക്കുക(വിന്യസിക്കുക) & ((2)^(x-1))\le \frac(1)(\sqrt(2)); \\ & ((0,1)^(1-x)) \lt 0.01; \\ & ((2)^(((x)^(2))-7x+14)) \lt 16; \\ & ((0,2)^(1+((x)^(2))))\ge \frac(1)(25). \\\അവസാനം (വിന്യസിക്കുക)\]

എല്ലാ സാഹചര്യങ്ങളിലും പ്രാഥമിക ചുമതല ഒന്നുതന്നെയാണ്: അസമത്വങ്ങളെ ഏറ്റവും ലളിതമായ രൂപത്തിലേക്ക് കുറയ്ക്കുക $((a)^(x)) \gt ((a)^(n))$. ഓരോ അസമത്വത്തിലും നമ്മൾ ഇപ്പോൾ ചെയ്യുന്നത് ഇതാണ്, അതേ സമയം ഞങ്ങൾ ഡിഗ്രികളുടെയും എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷനുകളുടെയും ഗുണങ്ങൾ ആവർത്തിക്കും. അതിനാൽ, നമുക്ക് പോകാം!

\[((2)^(x-1))\le \frac(1)(\sqrt(2))\]

നിങ്ങൾക്ക് ഇവിടെ എന്ത് ചെയ്യാൻ കഴിയും? ശരി, ഇടതുവശത്ത് ഞങ്ങൾക്ക് ഇതിനകം ഒരു സൂചനയുണ്ട് - ഒന്നും മാറ്റേണ്ടതില്ല. എന്നാൽ വലതുവശത്ത് ഒരുതരം വിഡ്ഢിത്തമുണ്ട്: ഒരു ഭിന്നസംഖ്യ, ഡിനോമിനേറ്ററിൽ ഒരു റൂട്ട് പോലും!

എന്നിരുന്നാലും, ഭിന്നസംഖ്യകളും ശക്തികളും ഉപയോഗിച്ച് പ്രവർത്തിക്കുന്നതിനുള്ള നിയമങ്ങൾ നമുക്ക് ഓർമ്മിക്കാം:

\[\begin(align) & \frac(1)(((a)^(n)))=((a)^(-n)); \\ & \sqrt[k](a)=((a)^(\frac(1)(k))). \\\അവസാനം (വിന്യസിക്കുക)\]

എന്താണ് ഇതിനർത്ഥം? ആദ്യം, ഒരു നെഗറ്റീവ് എക്‌സ്‌പോണൻ്റുള്ള ഒരു ശക്തിയാക്കി മാറ്റുന്നതിലൂടെ നമുക്ക് ഭിന്നസംഖ്യയെ എളുപ്പത്തിൽ ഒഴിവാക്കാനാകും. രണ്ടാമതായി, ഡിനോമിനേറ്ററിന് ഒരു റൂട്ട് ഉള്ളതിനാൽ, അതിനെ ഒരു ശക്തിയാക്കി മാറ്റുന്നത് നന്നായിരിക്കും - ഇത്തവണ ഒരു ഫ്രാക്ഷണൽ എക്‌സ്‌പോണൻ്റ് ഉപയോഗിച്ച്.

അസമത്വത്തിൻ്റെ വലതുവശത്ത് തുടർച്ചയായി ഈ പ്രവർത്തനങ്ങൾ പ്രയോഗിച്ച് എന്താണ് സംഭവിക്കുന്നതെന്ന് കാണുക:

\[\frac(1)(\sqrt(2))=(\ഇടത്(\sqrt(2) \വലത്))^(-1))=(\ഇടത്((2)^(\frac( 1)(3))) \വലത്))^(-1))=((2)^(\frac(1)(3)\cdot \left(-1 \right))=((2)^ (-\frac(1)(3)))\]

ഒരു ഡിഗ്രിയെ ഒരു ശക്തിയിലേക്ക് ഉയർത്തുമ്പോൾ, ഈ ഡിഗ്രികളുടെ ഘാതകങ്ങൾ കൂട്ടിച്ചേർക്കപ്പെടുമെന്ന് മറക്കരുത്. പൊതുവേ, എക്‌സ്‌പോണൻഷ്യൽ സമവാക്യങ്ങളോടും അസമത്വങ്ങളോടും കൂടി പ്രവർത്തിക്കുമ്പോൾ, അധികാരങ്ങളുമായി പ്രവർത്തിക്കുന്നതിനുള്ള ഏറ്റവും ലളിതമായ നിയമങ്ങളെങ്കിലും അറിയേണ്ടത് അത്യാവശ്യമാണ്:

\[\begin(align) & ((a)^(x))\cdot ((a)^(y))=((a)^(x+y)); \\ & \frac(((എ)^(x)))(((എ)^(y)))=((എ)^(x-y)); \\ & ((\ഇടത്(((എ)^(x)) \ വലത്))^(y))=((എ)^(x\cdot y)). \\\അവസാനം (വിന്യസിക്കുക)\]

യഥാർത്ഥത്തിൽ, ഞങ്ങൾ അവസാന നിയമം പ്രയോഗിച്ചു. അതിനാൽ, ഞങ്ങളുടെ യഥാർത്ഥ അസമത്വം ഇനിപ്പറയുന്ന രീതിയിൽ മാറ്റിയെഴുതും:

\[((2)^(x-1))\le \frac(1)(\sqrt(2))\Rightarrow ((2)^(x-1))\le ((2)^(-\ frac(1)(3)))\]

ഇപ്പോൾ നമ്മൾ രണ്ടിനെയും അടിത്തട്ടിൽ നിന്ന് ഒഴിവാക്കുന്നു. 2 > 1 മുതൽ, അസമത്വ ചിഹ്നം അതേപടി നിലനിൽക്കും:

\[\begin(align) & x-1\le -\frac(1)(3)\Rightarrow x\le 1-\frac(1)(3)=\frac(2)(3); \\ & x\in \left(-\infty ;\frac(2)(3) \right]. \\\ end(align)\]

അതാണ് പരിഹാരം! പ്രധാന ബുദ്ധിമുട്ട് എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷനിലല്ല, മറിച്ച് യഥാർത്ഥ പദപ്രയോഗത്തിൻ്റെ സമർത്ഥമായ പരിവർത്തനത്തിലാണ്: നിങ്ങൾ അതിനെ ശ്രദ്ധാപൂർവ്വം വേഗത്തിൽ അതിൻ്റെ ലളിതമായ രൂപത്തിലേക്ക് കൊണ്ടുവരേണ്ടതുണ്ട്.

രണ്ടാമത്തെ അസമത്വം പരിഗണിക്കുക:

\[((0.1)^(1-x)) \lt 0.01\]

അങ്ങനെ-അങ്ങനെ. ദശാംശ ഭിന്നസംഖ്യകൾ ഇവിടെ നമ്മെ കാത്തിരിക്കുന്നു. ഞാൻ പലതവണ പറഞ്ഞതുപോലെ, ശക്തികളുള്ള ഏത് പദപ്രയോഗത്തിലും നിങ്ങൾ ദശാംശങ്ങളിൽ നിന്ന് മുക്തി നേടണം - വേഗത്തിലും ലളിതമായും പരിഹാരം കാണാനുള്ള ഒരേയൊരു മാർഗ്ഗമാണിത്. ഇവിടെ ഞങ്ങൾ ഒഴിവാക്കും:

\[\begin(align) & 0.1=\frac(1)(10);\quad 0.01=\frac(1)(100)=((\left(\frac(1)(10) \ right))^ (2)); \\ & ((0,1)^(1-x)) \lt 0,01\Rightarrow ((\ഇടത്(\frac(1)(10) \right))^(1-x)) \lt ( (\ഇടത്(\frac(1)(10) \വലത്))^(2)). \\\അവസാനം (വിന്യസിക്കുക)\]

ഇവിടെയും നമുക്ക് ഏറ്റവും ലളിതമായ അസമത്വമുണ്ട്, കൂടാതെ 1/10 എന്ന അടിത്തറയിൽ പോലും, അതായത്. ഒന്നിൽ കുറവ്. ശരി, ഞങ്ങൾ അടിസ്ഥാനങ്ങൾ നീക്കംചെയ്യുന്നു, ഒരേസമയം "കുറവ്" എന്നതിൽ നിന്ന് "കൂടുതൽ" എന്നതിലേക്ക് അടയാളം മാറ്റുന്നു, നമുക്ക് ലഭിക്കുന്നു:

\[\ആരംഭിക്കുക(അലൈൻ ചെയ്യുക) & 1-x \gt 2; \\ & -x \gt 2-1; \\ & -x \gt 1; \\& x \lt -1. \\\അവസാനം (വിന്യസിക്കുക)\]

ഞങ്ങൾക്ക് അവസാന ഉത്തരം ലഭിച്ചു: $x\in \ഇടത്(-\infty ;-1 \right)$. ദയവായി ശ്രദ്ധിക്കുക: ഉത്തരം കൃത്യമായി ഒരു സെറ്റ് ആണ്, ഒരു സാഹചര്യത്തിലും $x \lt -1$ എന്ന ഫോമിൻ്റെ നിർമ്മാണമല്ല. കാരണം, ഔപചാരികമായി, അത്തരമൊരു നിർമ്മാണം ഒരു സെറ്റല്ല, മറിച്ച് $x$ എന്ന വേരിയബിളുമായി ബന്ധപ്പെട്ട അസമത്വമാണ്. അതെ, ഇത് വളരെ ലളിതമാണ്, പക്ഷേ അത് ഉത്തരമല്ല!

പ്രധാന കുറിപ്പ്. ഈ അസമത്വം മറ്റൊരു വിധത്തിൽ പരിഹരിക്കാൻ കഴിയും - ഒന്നിൽ കൂടുതൽ അടിത്തറയുള്ള ഒരു ശക്തിയിലേക്ക് ഇരുവശങ്ങളെയും ചുരുക്കിക്കൊണ്ട്. ഒന്നു നോക്കൂ:

\[\frac(1)(10)=((10)^(-1))\വലത്താരോ ((\ഇടത്((10)^(-1)) \വലത്))^(1-x)) \ lt ((\ഇടത്(((10)^(-1)) \വലത്))^(2))\Rightarrow ((10)^(-1\cdot \left(1-x \right))) \lt ((10)^(-1\cdot 2))\]

അത്തരമൊരു പരിവർത്തനത്തിന് ശേഷം, നമുക്ക് വീണ്ടും ഒരു എക്‌സ്‌പോണൻഷ്യൽ അസമത്വം ലഭിക്കും, പക്ഷേ 10 > 1 അടിസ്ഥാനം. ഇതിനർത്ഥം നമുക്ക് പത്ത് മറികടക്കാൻ കഴിയും എന്നാണ് - അസമത്വത്തിൻ്റെ അടയാളം മാറില്ല. നമുക്ക് ലഭിക്കുന്നത്:

\[\ആരംഭിക്കുക(അലൈൻ ചെയ്യുക) & -1\cdot \left(1-x \right) \lt -1\cdot 2; \\ & x-1 \lt -2; \\ & x \lt -2+1=-1; \\ & x \lt -1. \\\അവസാനം (വിന്യസിക്കുക)\]

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, ഉത്തരം സമാനമായിരുന്നു. അതേ സമയം, അടയാളം മാറ്റേണ്ടതിൻ്റെ ആവശ്യകതയിൽ നിന്ന് ഞങ്ങൾ സ്വയം രക്ഷപ്പെട്ടു, പൊതുവെ ഏതെങ്കിലും നിയമങ്ങൾ ഓർക്കുക.

\[((2)^(((x)^(2))-7x+14)) \lt 16\]

എന്നിരുന്നാലും, ഇത് നിങ്ങളെ ഭയപ്പെടുത്താൻ അനുവദിക്കരുത്. സൂചകങ്ങളിൽ എന്തുതന്നെയായാലും, അസമത്വം പരിഹരിക്കുന്നതിനുള്ള സാങ്കേതികവിദ്യ അതേപടി തുടരുന്നു. അതിനാൽ, 16 = 2 4 എന്ന് നമുക്ക് ആദ്യം ശ്രദ്ധിക്കാം. ഈ വസ്തുത കണക്കിലെടുത്ത് യഥാർത്ഥ അസമത്വം മാറ്റിയെഴുതാം:

\[\begin(align) & ((2)^(((x)^(2))-7x+14)) \lt ((2)^(4)); \\ & ((x)^(2))-7x+14 \lt 4; \\ & (((x)^(2))-7x+10 \lt 0. \\\ end(align)\]

ഹൂറേ! ഞങ്ങൾക്ക് സാധാരണ ക്വാഡ്രാറ്റിക് അസമത്വം ലഭിച്ചു! അടയാളം എവിടെയും മാറിയിട്ടില്ല, കാരണം അടിസ്ഥാനം രണ്ടാണ് - ഒന്നിനെക്കാൾ വലിയ സംഖ്യ.

നമ്പർ ലൈനിൽ ഒരു ഫംഗ്‌ഷൻ്റെ പൂജ്യങ്ങൾ

$f\left(x \right)=((x)^(2))-7x+10$ എന്ന ഫംഗ്‌ഷൻ്റെ അടയാളങ്ങൾ ഞങ്ങൾ ക്രമീകരിക്കുന്നു - വ്യക്തമായും, അതിൻ്റെ ഗ്രാഫ് ശാഖകളുള്ള ഒരു പരവലയമായിരിക്കും, അതിനാൽ “പ്ലസുകൾ” ഉണ്ടാകും ” വശങ്ങളിൽ. പ്രവർത്തനം പൂജ്യത്തേക്കാൾ കുറവുള്ള മേഖലയിൽ ഞങ്ങൾക്ക് താൽപ്പര്യമുണ്ട്, അതായത്. $x\in \ഇടത്(2;5 \right)$ ആണ് യഥാർത്ഥ പ്രശ്നത്തിനുള്ള ഉത്തരം.

അവസാനമായി, മറ്റൊരു അസമത്വം പരിഗണിക്കുക:

\[((0,2)^(1+((x)^(2)))\ge \frac(1)(25)\]

അടിത്തട്ടിൽ ഒരു ദശാംശ ഭിന്നസംഖ്യയുള്ള ഒരു എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷൻ ഞങ്ങൾ വീണ്ടും കാണുന്നു. നമുക്ക് ഈ ഭിന്നസംഖ്യയെ ഒരു പൊതു ഭിന്നസംഖ്യയിലേക്ക് പരിവർത്തനം ചെയ്യാം:

\[\begin(align) & 0.2=\frac(2)(10)=\frac(1)(5)=((5)^(-1))\Rightarrow \\ & \Rightarrow ((0 ,2 )^(1+((x)^(2)))=(\ഇടത്(((5)^(-1)) \വലത്))^(1+((x)^(2) )) )=((5)^(-1\cdot \left(1+((x)^(2)) \right)))\end(align)\]

ഈ സാഹചര്യത്തിൽ, ഞങ്ങൾ നേരത്തെ നൽകിയ പരാമർശം ഉപയോഗിച്ചു - ഞങ്ങളുടെ തുടർന്നുള്ള പരിഹാരം ലളിതമാക്കുന്നതിന് ഞങ്ങൾ അടിസ്ഥാനം 5 > 1 എന്ന നമ്പറിലേക്ക് ചുരുക്കി. വലതുവശത്തും നമുക്ക് ഇത് ചെയ്യാം:

\[\frac(1)(25)=((\ഇടത്(\frac(1)(5) \വലത്))^(2))=(\ഇടത്((5)^(-1)) \ വലത്))^(2))=((5)^(-1\cdot 2))=((5)^(-2))\]

രണ്ട് പരിവർത്തനങ്ങളും കണക്കിലെടുത്ത് നമുക്ക് യഥാർത്ഥ അസമത്വം മാറ്റിയെഴുതാം:

\[((0,2)^(1+((x)^(2)))\ge \frac(1)(25)\വലത്തോട്ടുള്ള ((5)^(-1\cdot \left(1+) ((x)^(2)) \right)))\ge ((5)^(-2))\]

ഇരുവശത്തുമുള്ള അടിത്തറകൾ ഒന്നുതന്നെയാണ്, ഒന്നിലധികം. വലത്തോട്ടും ഇടത്തോട്ടും മറ്റ് പദങ്ങളൊന്നുമില്ല, അതിനാൽ ഞങ്ങൾ ഫൈവുകൾ "ക്രോസ് ഔട്ട്" ചെയ്യുകയും വളരെ ലളിതമായ ഒരു പദപ്രയോഗം നേടുകയും ചെയ്യുന്നു:

\[\begin(align) & -1\cdot \left(1+((x)^(2)) \right)\ge -2; \\ & -1-((x)^(2))\ge -2; \\ & -((x)^(2))\ge -2+1; \\ & -((x)^(2))\ge -1;\quad \left| \cdot \ഇടത്(-1 \വലത്) \വലത്. \\ & (((x)^(2))\le 1. \\\ end(align)\]

ഇവിടെയാണ് നിങ്ങൾ കൂടുതൽ ശ്രദ്ധിക്കേണ്ടത്. പല വിദ്യാർത്ഥികളും അസമത്വത്തിൻ്റെ ഇരുവശങ്ങളുടെയും വർഗ്ഗമൂല്യം എടുത്ത് $x\le 1\Rightarrow x\in \left(-\infty ;-1 \right]$ പോലെ എന്തെങ്കിലും എഴുതാൻ ഇഷ്ടപ്പെടുന്നു. ഒരു സാഹചര്യത്തിലും ഇത് ചെയ്യാൻ പാടില്ല. , ഒരു കൃത്യമായ ചതുരത്തിൻ്റെ റൂട്ട് ഒരു മോഡുലസ് ആയതിനാൽ, ഒരു സാഹചര്യത്തിലും ഒരു യഥാർത്ഥ വേരിയബിൾ:

\[\sqrt(((x)^(2)))=\ഇടത്| x\വലത്|\]

എന്നിരുന്നാലും, മൊഡ്യൂളുകളിൽ പ്രവർത്തിക്കുന്നത് ഏറ്റവും മനോഹരമായ അനുഭവമല്ല, അല്ലേ? അതിനാൽ ഞങ്ങൾ പ്രവർത്തിക്കില്ല. പകരം, ഞങ്ങൾ എല്ലാ നിബന്ധനകളും ഇടത്തേക്ക് നീക്കുകയും ഇടവേള രീതി ഉപയോഗിച്ച് സാധാരണ അസമത്വം പരിഹരിക്കുകയും ചെയ്യുന്നു:

$\begin(align) & ((x)^(2))-1\le 0; \\ & \ഇടത്(x-1 \right)\left(x+1 \right)\le 0 \\ & ((x)_(1))=1;\quad ((x)_(2)) =-1; \\\ അവസാനം (അലൈൻ) $

ലഭിച്ച പോയിൻ്റുകൾ ഞങ്ങൾ വീണ്ടും നമ്പർ ലൈനിൽ അടയാളപ്പെടുത്തുകയും അടയാളങ്ങൾ നോക്കുകയും ചെയ്യുന്നു:

ദയവായി ശ്രദ്ധിക്കുക: ഡോട്ടുകൾ ഷേഡുള്ളതാണ്

ഞങ്ങൾ കർശനമല്ലാത്ത അസമത്വം പരിഹരിക്കുന്നതിനാൽ, ഗ്രാഫിലെ എല്ലാ പോയിൻ്റുകളും ഷേഡുള്ളതാണ്. അതിനാൽ, ഉത്തരം ഇതായിരിക്കും: $x\in \ഇടത്[ -1;1 \right]$ എന്നത് ഒരു ഇടവേളയല്ല, ഒരു സെഗ്‌മെൻ്റ് ആണ്.

പൊതുവേ, എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങളെക്കുറിച്ച് സങ്കീർണ്ണമായ ഒന്നും തന്നെയില്ലെന്ന് ഞാൻ ശ്രദ്ധിക്കാൻ ആഗ്രഹിക്കുന്നു. ഇന്ന് ഞങ്ങൾ നടത്തിയ എല്ലാ പരിവർത്തനങ്ങളുടെയും അർത്ഥം ഒരു ലളിതമായ അൽഗോരിതത്തിലേക്ക് വരുന്നു:

• ഞങ്ങൾ എല്ലാ ഡിഗ്രികളും കുറയ്ക്കുന്നതിനുള്ള അടിസ്ഥാനം കണ്ടെത്തുക;
• $((a)^(x)) \gt ((a)^(n))$ എന്ന ഫോമിൻ്റെ അസമത്വം ലഭിക്കുന്നതിന് പരിവർത്തനങ്ങൾ ശ്രദ്ധാപൂർവ്വം നടത്തുക. തീർച്ചയായും, $x$, $n$ എന്നീ വേരിയബിളുകൾക്ക് പകരം കൂടുതൽ സങ്കീർണ്ണമായ പ്രവർത്തനങ്ങൾ ഉണ്ടാകാം, എന്നാൽ അർത്ഥം മാറില്ല;
• ഡിഗ്രികളുടെ അടിത്തറകൾ മറികടക്കുക. ഈ സാഹചര്യത്തിൽ, അടിസ്ഥാന $a \lt 1$ ആണെങ്കിൽ അസമത്വ ചിഹ്നം മാറിയേക്കാം.

വാസ്തവത്തിൽ, ഇത് അത്തരം എല്ലാ അസമത്വങ്ങളും പരിഹരിക്കുന്നതിനുള്ള ഒരു സാർവത്രിക അൽഗോരിതം ആണ്. ഈ വിഷയത്തിൽ അവർ നിങ്ങളോട് പറയുന്ന മറ്റെല്ലാം പരിവർത്തനം ലളിതമാക്കുകയും വേഗത്തിലാക്കുകയും ചെയ്യുന്ന പ്രത്യേക സാങ്കേതിക വിദ്യകളും തന്ത്രങ്ങളും മാത്രമാണ്. ഞങ്ങൾ ഇപ്പോൾ ഈ സാങ്കേതികതകളിലൊന്നിനെക്കുറിച്ച് സംസാരിക്കും.

യുക്തിസഹീകരണ രീതി

നമുക്ക് മറ്റൊരു കൂട്ടം അസമത്വങ്ങൾ പരിഗണിക്കാം:

\[\begin(align) & ((\text( )\!\pi\!\!\text( ))^(x+7)) \gt ((\text( )\!\!\pi \!\!\text( ))^(((x)^(2))-3x+2)); \\ & ((\ഇടത്(2\sqrt(3)-3 \വലത്))^(((x)^(2))-2x)) \lt 1; \\ & ((\ഇടത്(\frac(1)(3) \വലത്))^((((x)^(2))+2x)) \gt ((\ഇടത്(\frac(1)(9) \right))^(16-x)); \\ & ((\ഇടത്(3-2\sqrt(2) \വലത്))^(3x-((x)^(2)))) \lt 1. \\\ end(align)\]

അപ്പോൾ അവരുടെ പ്രത്യേകത എന്താണ്? അവർ വെളിച്ചമാണ്. എന്നിരുന്നാലും, നിർത്തുക! സംഖ്യ π ഏതെങ്കിലും ശക്തിയിലേക്ക് ഉയർത്തിയിട്ടുണ്ടോ? എന്ത് വിഡ്ഢിത്തം?

എങ്ങനെ $2\sqrt(3)-3$ എന്ന സംഖ്യയെ ഒരു പവറായി ഉയർത്താം? അല്ലെങ്കിൽ $3-2\sqrt(2)$? പ്രശ്നമുള്ള എഴുത്തുകാർ ജോലിക്ക് ഇരിക്കുന്നതിന് മുമ്പ് വളരെയധികം ഹത്തോൺ കുടിച്ചു.

വാസ്തവത്തിൽ, ഈ ജോലികളിൽ ഭയപ്പെടുത്തുന്ന ഒന്നും തന്നെയില്ല. ഞാൻ നിങ്ങളെ ഓർമ്മിപ്പിക്കട്ടെ: $((a)^(x))$ എന്ന ഫോമിൻ്റെ ഒരു എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷൻ ആണ്, $a$ എന്നത് ഒന്നൊഴികെയുള്ള ഏതൊരു പോസിറ്റീവ് സംഖ്യയുമാണ്. നമ്പർ π പോസിറ്റീവ് ആണ് - ഞങ്ങൾക്ക് അത് ഇതിനകം അറിയാം. $2\sqrt(3)-3$, $3-2\sqrt(2)$ എന്നീ സംഖ്യകളും പോസിറ്റീവ് ആണ് - നിങ്ങൾ അവയെ പൂജ്യവുമായി താരതമ്യം ചെയ്താൽ ഇത് കാണാൻ എളുപ്പമാണ്.

ഈ "ഭയപ്പെടുത്തുന്ന" അസമത്വങ്ങളെല്ലാം മുകളിൽ ചർച്ച ചെയ്ത ലളിതമായവയിൽ നിന്ന് വ്യത്യസ്തമല്ല പരിഹരിക്കപ്പെടുന്നുവെന്ന് ഇത് മാറുന്നു? അവ അതേ രീതിയിൽ പരിഹരിക്കപ്പെടുന്നുണ്ടോ? അതെ, അത് തികച്ചും ശരിയാണ്. എന്നിരുന്നാലും, അവരുടെ ഉദാഹരണം ഉപയോഗിച്ച്, സ്വതന്ത്ര ജോലിയിലും പരീക്ഷകളിലും സമയം ലാഭിക്കുന്ന ഒരു സാങ്കേതികത പരിഗണിക്കാൻ ഞാൻ ആഗ്രഹിക്കുന്നു. യുക്തിസഹീകരണ രീതിയെക്കുറിച്ച് നമ്മൾ സംസാരിക്കും. അതിനാൽ, ശ്രദ്ധ:

$((a)^(x)) \gt ((a)^(n))$ എന്ന ഫോമിൻ്റെ ഏത് എക്‌സ്‌പോണൻഷ്യൽ അസമത്വവും $\left(x-n \right)\cdot \left(a-1 \\) അസമത്വത്തിന് തുല്യമാണ്. വലത്) \gt 0 $.

അതാണ് മൊത്തത്തിലുള്ള രീതി :) മറ്റൊരു തരത്തിലുള്ള കളിയുണ്ടാകുമെന്ന് നിങ്ങൾ കരുതിയോ? ഇതുപോലെ ഒന്നുമില്ല! എന്നാൽ ഒരു വരിയിൽ അക്ഷരാർത്ഥത്തിൽ എഴുതിയിരിക്കുന്ന ഈ ലളിതമായ വസ്തുത നമ്മുടെ ജോലിയെ വളരെയധികം ലളിതമാക്കും. ഒന്നു നോക്കൂ:

\[\begin(matrix) ((\text( )\!\!\pi\!\!\text( ))^(x+7)) \gt ((\text( )\!\pi\ !\!\text( ))^((((x)^(2))-3x+2)) \\ \താഴേക്ക് \\ \ഇടത്(x+7-\left(((x)^(2))) -3x+2 \right) \right)\cdot \left(\text( )\!\!\pi\!\!\text( )-1 \right) \gt 0 \\\end(matrix)\]

അതിനാൽ കൂടുതൽ എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷനുകളൊന്നുമില്ല! അടയാളം മാറുമോ ഇല്ലയോ എന്ന് നിങ്ങൾ ഓർക്കേണ്ടതില്ല. എന്നാൽ ഒരു പുതിയ പ്രശ്‌നം ഉയർന്നുവരുന്നു: \[\left(\text( )\!\!\pi\!\!\text( )-1 \right)\] എന്താണ് ചെയ്യേണ്ടത്? π എന്ന സംഖ്യയുടെ കൃത്യമായ മൂല്യം എന്താണെന്ന് ഞങ്ങൾക്ക് അറിയില്ല. എന്നിരുന്നാലും, ക്യാപ്റ്റൻ വ്യക്തമായ സൂചന നൽകുന്നതായി തോന്നുന്നു:

\[\text( )\!\!\pi\!\!\text( )\ഏകദേശം 3.14... \gt 3\Rightarrow \text( )\!\!\pi\!\!\text( )- 1\gt 3-1=2\]

പൊതുവേ, π യുടെ കൃത്യമായ മൂല്യം നമ്മെ ശരിക്കും ബാധിക്കുന്നില്ല - ഏത് സാഹചര്യത്തിലും $\text( )\!\!\pi\!\!\text( )-1 \gt 2 എന്ന് മനസ്സിലാക്കേണ്ടത് പ്രധാനമാണ്. $, ടി.ഇ. ഇതൊരു പോസിറ്റീവ് സ്ഥിരാങ്കമാണ്, ഇത് അസമത്വത്തിൻ്റെ ഇരുവശങ്ങളെയും നമുക്ക് വിഭജിക്കാം:

\[\ആരംഭിക്കുക(അലൈൻ ചെയ്യുക) & \ഇടത്(x+7-\left(((x)^(2))-3x+2 \right) \right)\cdot \left(\text( )\!\! \pi\!\!\text( )-1 \right) \gt 0 \\ & x+7-\left(((x)^(2))-3x+2 \right) \gt 0; \\ & x+7-((x)^(2))+3x-2 \gt 0; \\ & -((x)^(2))+4x+5 \gt 0;\quad \left| \cdot \ഇടത്(-1 \വലത്) \വലത്. \\ & ((x)^(2))-4x-5 \lt 0; \\ & \left(x-5 \right)\left(x+1 \right) \lt 0. \\\ end(align)\]

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, ഒരു നിശ്ചിത നിമിഷത്തിൽ ഞങ്ങൾക്ക് മൈനസ് ഒന്നായി വിഭജിക്കേണ്ടി വന്നു - അസമത്വത്തിൻ്റെ അടയാളം മാറി. അവസാനം, വിയറ്റയുടെ സിദ്ധാന്തം ഉപയോഗിച്ച് ഞാൻ ക്വാഡ്രാറ്റിക് ട്രൈനോമിയൽ വിപുലീകരിച്ചു - വേരുകൾ $((x)_(1))=5$, $((x)_(2))=-1$ എന്നിവയ്ക്ക് തുല്യമാണെന്ന് വ്യക്തമാണ്. . ക്ലാസിക്കൽ ഇടവേള രീതി ഉപയോഗിച്ച് എല്ലാം പരിഹരിക്കപ്പെടും:

ഇടവേള രീതി ഉപയോഗിച്ച് അസമത്വം പരിഹരിക്കുന്നു

യഥാർത്ഥ അസമത്വം കർശനമായതിനാൽ എല്ലാ പോയിൻ്റുകളും നീക്കംചെയ്യുന്നു. നെഗറ്റീവ് മൂല്യങ്ങളുള്ള മേഖലയിൽ ഞങ്ങൾക്ക് താൽപ്പര്യമുണ്ട്, അതിനാൽ ഉത്തരം $x\in \ഇടത്(-1;5 \right)$ ആണ്. അതാണ് പരിഹാരം :)

നമുക്ക് അടുത്ത ടാസ്ക്കിലേക്ക് പോകാം:

\[((\ഇടത്(2\sqrt(3)-3 \വലത്))^((((x)^(2))-2x)) \lt 1\]

ഇവിടെ എല്ലാം പൊതുവെ ലളിതമാണ്, കാരണം വലതുവശത്ത് ഒരു യൂണിറ്റ് ഉണ്ട്. പൂജ്യം പവറിലേക്ക് ഉയർത്തിയ ഏതൊരു സംഖ്യയും ഒന്നാണെന്ന് ഞങ്ങൾ ഓർക്കുന്നു. ഈ സംഖ്യ ഇടതുവശത്തെ അടിത്തട്ടിൽ യുക്തിരഹിതമായ ഒരു പദപ്രയോഗമാണെങ്കിലും:

\[\ആരംഭിക്കുക(അലൈൻ ചെയ്യുക) & ((\ഇടത്(2\sqrt(3)-3 \വലത്))^(((x)^(2))-2x)) \lt 1=((\ഇടത്(2) \sqrt(3)-3 \വലത്))^(0)); \\ & ((\ഇടത്(2\sqrt(3)-3 \വലത്))^((((x)^(2))-2x)) \lt ((\ഇടത്(2\sqrt(3)-3) \വലത്))^(0)); \\\അവസാനം (വിന്യസിക്കുക)\]

ശരി, നമുക്ക് യുക്തിസഹമാക്കാം:

\[\ആരംഭിക്കുക(വിന്യസിക്കുക) & \ഇടത്(((x)^(2))-2x-0 \right)\cdot \left(2\sqrt(3)-3-1 \right) \lt 0; \\ & \ഇടത്(((x)^(2))-2x-0 \right)\cdot \left(2\sqrt(3)-4 \right) \lt 0; \\ & \left(((x)^(2))-2x-0 \right)\cdot 2\left(\sqrt(3)-2 \right) \lt 0. \\\ end(align)\ ]

അടയാളങ്ങൾ കണ്ടുപിടിക്കുക മാത്രമാണ് അവശേഷിക്കുന്നത്. $2\left(\sqrt(3)-2 \right)$ എന്ന ഘടകം $x$ എന്ന വേരിയബിൾ ഉൾക്കൊള്ളുന്നില്ല - ഇത് ഒരു സ്ഥിരാങ്കം മാത്രമാണ്, അതിൻ്റെ അടയാളം നമ്മൾ കണ്ടെത്തേണ്ടതുണ്ട്. ഇത് ചെയ്യുന്നതിന്, ഇനിപ്പറയുന്നവ ശ്രദ്ധിക്കുക:

\[\begin(matrix) \sqrt(3) \lt \sqrt(4)=2 \\ \Downarrow \\ 2\left(\sqrt(3)-2 \right) \lt 2\cdot \left(2 -2 \right)=0 \\\ end(matrix)\]

രണ്ടാമത്തെ ഘടകം ഒരു സ്ഥിരാങ്കം മാത്രമല്ല, നെഗറ്റീവ് സ്ഥിരാങ്കമാണെന്ന് ഇത് മാറുന്നു! അതിനെ വിഭജിക്കുമ്പോൾ, യഥാർത്ഥ അസമത്വത്തിൻ്റെ അടയാളം വിപരീതമായി മാറുന്നു:

\[\ആരംഭിക്കുക(വിന്യസിക്കുക) & \ഇടത്(((x)^(2))-2x-0 \right)\cdot 2\left(\sqrt(3)-2 \right) \lt 0; \\ & (((x)^(2))-2x-0 \gt 0; \\ & x\left(x-2 \right) \gt 0. \\\ end(align)\]

ഇപ്പോൾ എല്ലാം പൂർണ്ണമായും വ്യക്തമാകും. വലതുവശത്തുള്ള സ്ക്വയർ ട്രൈനോമിയലിൻ്റെ വേരുകൾ: $((x)_(1))=0$, $((x)_(2))=2$. ഞങ്ങൾ അവയെ നമ്പർ ലൈനിൽ അടയാളപ്പെടുത്തുകയും $f\left(x \right)=x\left(x-2 \right)$ എന്ന ഫംഗ്‌ഷൻ്റെ അടയാളങ്ങൾ നോക്കുകയും ചെയ്യുന്നു.

ഞങ്ങൾ സൈഡ് ഇടവേളകളിൽ താൽപ്പര്യമുള്ളപ്പോൾ കേസ്

ഒരു പ്ലസ് ചിഹ്നം കൊണ്ട് അടയാളപ്പെടുത്തിയ ഇടവേളകളിൽ ഞങ്ങൾക്ക് താൽപ്പര്യമുണ്ട്. ഉത്തരം എഴുതുക മാത്രമാണ് അവശേഷിക്കുന്നത്:

നമുക്ക് അടുത്ത ഉദാഹരണത്തിലേക്ക് പോകാം:

\[(\ഇടത്(\frac(1)(3) \വലത്))^(((x)^(2)+2x)) \gt ((\ഇടത്(\frac(1)(9) വലത്))^(16-x))\]

ശരി, എല്ലാം ഇവിടെ പൂർണ്ണമായും വ്യക്തമാണ്: അടിസ്ഥാനങ്ങളിൽ ഒരേ സംഖ്യയുടെ ശക്തികൾ അടങ്ങിയിരിക്കുന്നു. അതിനാൽ, ഞാൻ എല്ലാം ഹ്രസ്വമായി എഴുതാം:

\[\begin(matrix) \frac(1)(3)=((3)^(-1));\quad \frac(1)(9)=\frac(1)(((3)^( 2)))=((3)^(-2)) \\ \താഴേയ്‌ക്ക് \\ ((\ഇടത്(((3)^(-1)) \വലത്))^(((x)^(2) )+2x)) \gt ((\ഇടത്((3)^(-2)) \വലത്))^(16-x)) \\\ end(matrix)\]

\[\ആരംഭിക്കുക(വിന്യസിക്കുക) & ((3)^(-1\cdot \left(((x)^(2))+2x \right)) \gt ((3)^(-2\cdot \ ഇടത് (16-x \ വലത്))); \\ & ((3)^(-((x)^(2))-2x)) \gt ((3)^(-32+2x)); \\ & \left(-((x)^(2))-2x-\left(-32+2x \right) \right)\cdot \left(3-1 \right) \gt 0; \\ & -((x)^(2))-2x+32-2x \gt 0; \\ & -((x)^(2))-4x+32 \gt 0;\quad \left| \cdot \ഇടത്(-1 \വലത്) \വലത്. \\ & (((x)^(2))+4x-32 \lt 0; \\ & \left(x+8 \right)\left(x-4 \right) \lt 0. \\\ end(align)\]

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, പരിവർത്തന പ്രക്രിയയിൽ നമുക്ക് ഒരു നെഗറ്റീവ് സംഖ്യ കൊണ്ട് ഗുണിക്കേണ്ടിവന്നു, അതിനാൽ അസമത്വ ചിഹ്നം മാറി. അവസാനം, ക്വാഡ്രാറ്റിക് ട്രൈനോമിയലിനെ ഫാക്ടർ ചെയ്യാൻ ഞാൻ വീണ്ടും വിയറ്റയുടെ സിദ്ധാന്തം പ്രയോഗിച്ചു. തൽഫലമായി, ഉത്തരം ഇനിപ്പറയുന്നതായിരിക്കും: $x\in \left(-8;4 \right)$ - ഒരു നമ്പർ ലൈൻ വരച്ച് പോയിൻ്റുകൾ അടയാളപ്പെടുത്തി അടയാളങ്ങൾ എണ്ണി ആർക്കും ഇത് സ്ഥിരീകരിക്കാൻ കഴിയും. അതേസമയം, ഞങ്ങളുടെ "സെറ്റിൽ" നിന്ന് അവസാന അസമത്വത്തിലേക്ക് ഞങ്ങൾ നീങ്ങും:

\[((\ഇടത്(3-2\sqrt(2) \right))^(3x-((x)^(2)))) \lt 1\]

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, അടിത്തട്ടിൽ വീണ്ടും ഒരു യുക്തിരഹിതമായ സംഖ്യയുണ്ട്, വലതുവശത്ത് വീണ്ടും ഒരു യൂണിറ്റ് ഉണ്ട്. അതിനാൽ, ഞങ്ങളുടെ എക്‌സ്‌പോണൻഷ്യൽ അസമത്വം ഞങ്ങൾ ഇനിപ്പറയുന്ന രീതിയിൽ മാറ്റിയെഴുതുന്നു:

\[((\ഇടത്(3-2\sqrt(2) \വലത്))^(3x-((x)^(2)))) \lt ((\ഇടത്(3-2\sqrt(2) വലത്))^(0))\]

ഞങ്ങൾ യുക്തിസഹമാക്കൽ പ്രയോഗിക്കുന്നു:

\[\begin(align) & \left(3x-((x)^(2))-0 \right)\cdot \left(3-2\sqrt(2)-1 \right) \lt 0; \\ & \left(3x-((x)^(2))-0 \right)\cdot \left(2-2\sqrt(2) \right) \lt 0; \\ & \left(3x-((x)^(2))-0 \right)\cdot 2\left(1-\sqrt(2) \right) \lt 0. \\\ end(align)\ ]

എന്നിരുന്നാലും, $1-\sqrt(2) \lt 0$, $\sqrt(2)\ഏകദേശം 1,4... \gt 1$ എന്നത് വളരെ വ്യക്തമാണ്. അതിനാൽ, രണ്ടാമത്തെ ഘടകം വീണ്ടും ഒരു നെഗറ്റീവ് സ്ഥിരാങ്കമാണ്, അസമത്വത്തിൻ്റെ ഇരുവശങ്ങളെയും വിഭജിക്കാം:

\[\begin(matrix) \left(3x-((x)^(2))-0 \right)\cdot 2\left(1-\sqrt(2) \right) \lt 0 \\ \Downarrow \ \\ അവസാനം(മാട്രിക്സ്)\]

\[\begin(align) & 3x-((x)^(2))-0 \gt 0; \\ & 3x-((x)^(2)) \gt 0;\quad \left| \cdot \ഇടത്(-1 \വലത്) \വലത്. \\ & (((x)^(2))-3x \lt 0; \\ & x\left(x-3 \right) \lt 0. \\\ end(align)\]

മറ്റൊരു അടിത്തറയിലേക്ക് നീങ്ങുക

എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങൾ പരിഹരിക്കുമ്പോൾ ഒരു പ്രത്യേക പ്രശ്നം "ശരിയായ" അടിസ്ഥാനത്തിനായുള്ള തിരയലാണ്. നിർഭാഗ്യവശാൽ, ഒരു ടാസ്ക്കിലെ ആദ്യ നോട്ടത്തിൽ എന്താണ് അടിസ്ഥാനമായി എടുക്കേണ്ടതെന്നും ഈ അടിസ്ഥാനത്തിൻ്റെ അളവ് അനുസരിച്ച് എന്തുചെയ്യണമെന്നും എല്ലായ്പ്പോഴും വ്യക്തമല്ല.

എന്നാൽ വിഷമിക്കേണ്ട: ഇവിടെ മാന്ത്രികതയോ "രഹസ്യ" സാങ്കേതികവിദ്യയോ ഇല്ല. ഗണിതശാസ്ത്രത്തിൽ, അൽഗോരിതം ചെയ്യാൻ കഴിയാത്ത ഏത് കഴിവും പരിശീലനത്തിലൂടെ എളുപ്പത്തിൽ വികസിപ്പിക്കാൻ കഴിയും. എന്നാൽ ഇതിനായി നിങ്ങൾ വ്യത്യസ്ത തലത്തിലുള്ള സങ്കീർണ്ണതയുടെ പ്രശ്നങ്ങൾ പരിഹരിക്കേണ്ടതുണ്ട്. ഉദാഹരണത്തിന്, ഇതുപോലെ:

\[\ആരംഭിക്കുക(വിന്യസിക്കുക) & ((2)^(\frac(x)(2))) \lt ((4)^(\frac(4)(x))); \\ & ((\ഇടത്(\frac(1)(3) \വലത്))^(\frac(3)(x)))\ge ((3)^(2+x)); \\ & ((\ഇടത്(0,16 \വലത്))^(1+2x))\cdot ((\ഇടത്(6,25 \വലത്))^(x))\ge 1; \\ & ((\left(\frac(27)(\sqrt(3)) \right))^(-x)) \lt ((9)^(4-2x))\cdot 81. \\\ അവസാനം(വിന്യസിക്കുക)\]

ബുദ്ധിമുട്ടുള്ള? ഭീതിദമാണ്? ഒരു കോഴിയെ അസ്ഫാൽറ്റിൽ അടിക്കുന്നതിനേക്കാൾ എളുപ്പമാണ് ഇത്! നമുക്ക് ശ്രമിക്കാം. ആദ്യത്തെ അസമത്വം:

\[((2)^(\frac(x)(2))) \lt ((4)^(\frac(4)(x)))\]

ശരി, ഇവിടെ എല്ലാം വ്യക്തമാണെന്ന് ഞാൻ കരുതുന്നു:

ഞങ്ങൾ യഥാർത്ഥ അസമത്വം മാറ്റിയെഴുതുന്നു, എല്ലാം അടിസ്ഥാന രണ്ടിലേക്ക് ചുരുക്കുന്നു:

\[((2)^(\frac(x)(2))) \lt ((2)^(\frac(8)(x)))\വലത്താരോ \ഇടത്(\frac(x)(2)- \frac(8)(x) \വലത്)\cdot \ഇടത്(2-1 \വലത്) \lt 0\]

അതെ, അതെ, നിങ്ങൾ കേട്ടത് ശരിയാണ്: മുകളിൽ വിവരിച്ച യുക്തിസഹീകരണ രീതി ഞാൻ പ്രയോഗിച്ചു. ഇപ്പോൾ നമ്മൾ ശ്രദ്ധാപൂർവ്വം പ്രവർത്തിക്കേണ്ടതുണ്ട്: നമുക്ക് ഒരു ഫ്രാക്ഷണൽ-റേഷണൽ അസമത്വമുണ്ട് (ഇത് ഡിനോമിനേറ്ററിൽ ഒരു വേരിയബിൾ ഉള്ള ഒന്നാണ്), അതിനാൽ എന്തിനേയും പൂജ്യത്തിലേക്ക് തുല്യമാക്കുന്നതിന് മുമ്പ്, എല്ലാം ഒരു പൊതു വിഭാഗത്തിലേക്ക് കൊണ്ടുവരികയും സ്ഥിരമായ ഘടകത്തിൽ നിന്ന് മുക്തി നേടുകയും വേണം. .

\[\begin(align) & \left(\frac(x)(2)-\frac(8)(x) \right)\cdot \left(2-1 \right) \lt 0; \\ & \ഇടത്(\frac(((x)^(2))-16)(2x) \വലത്)\cdot 1 \lt 0; \\ & \frac(((x)^(2))-16)(2x) \lt 0. \\\ end(align)\]

ഇപ്പോൾ ഞങ്ങൾ സാധാരണ ഇടവേള രീതി ഉപയോഗിക്കുന്നു. ന്യൂമറേറ്റർ പൂജ്യങ്ങൾ: $x=\pm 4$. $x=0$ ആകുമ്പോൾ മാത്രമാണ് ഡിനോമിനേറ്റർ പൂജ്യത്തിലേക്ക് പോകുന്നത്. ആകെ മൂന്ന് പോയിൻ്റുകൾ നമ്പർ ലൈനിൽ അടയാളപ്പെടുത്തേണ്ടതുണ്ട് (അസമത്വ ചിഹ്നം കർശനമായതിനാൽ എല്ലാ പോയിൻ്റുകളും പിൻ ചെയ്‌തിരിക്കുന്നു). നമുക്ക് ലഭിക്കുന്നത്:

കൂടുതൽ സങ്കീർണ്ണമായ കേസ്: മൂന്ന് വേരുകൾ

നിങ്ങൾ ഊഹിക്കുന്നതുപോലെ, ഇടത് വശത്തുള്ള എക്സ്പ്രഷൻ നെഗറ്റീവ് മൂല്യങ്ങൾ എടുക്കുന്ന ഇടവേളകളെ ഷേഡിംഗ് അടയാളപ്പെടുത്തുന്നു. അതിനാൽ, അന്തിമ ഉത്തരത്തിൽ ഒരേസമയം രണ്ട് ഇടവേളകൾ ഉൾപ്പെടും:

യഥാർത്ഥ അസമത്വം കർശനമായതിനാൽ ഇടവേളകളുടെ അറ്റങ്ങൾ ഉത്തരത്തിൽ ഉൾപ്പെടുത്തിയിട്ടില്ല. ഈ ഉത്തരത്തിൻ്റെ കൂടുതൽ പരിശോധന ആവശ്യമില്ല. ഇക്കാര്യത്തിൽ, എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങൾ ലോഗരിതം ഉള്ളതിനേക്കാൾ വളരെ ലളിതമാണ്: ODZ ഇല്ല, നിയന്ത്രണങ്ങളൊന്നുമില്ല, മുതലായവ.

നമുക്ക് അടുത്ത ടാസ്ക്കിലേക്ക് പോകാം:

\[((\ഇടത്(\frac(1)(3) \വലത്))^(\frac(3)(x)))\ge ((3)^(2+x))\]

ഇവിടെയും പ്രശ്‌നങ്ങളൊന്നുമില്ല, കാരണം $\frac(1)(3)=((3)^(-1))$ എന്ന് ഞങ്ങൾക്കറിയാം, അതിനാൽ മുഴുവൻ അസമത്വവും ഇനിപ്പറയുന്ന രീതിയിൽ മാറ്റിയെഴുതാം:

\[\ആരംഭിക്കുക(വിന്യസിക്കുക) & ((\ഇടത്((3)^(-1)) \വലത്))^(\frac(3)(x))\ge ((3)^(2+x) ))\Rightarrow ((3)^(-\frac(3)(x)))\ge ((3)^(2+x)); \\ & \left(-\frac(3)(x)-\left(2+x \right) \right)\cdot \left(3-1 \right)\ge 0; \\ & \left(-\frac(3)(x)-2-x \right)\cdot 2\ge 0;\quad \left| :\ഇടത് (-2 \വലത്) \വലത്. \\ & \frac(3)(x)+2+x\le 0; \\ & \frac(((x)^(2))+2x+3)(x)\le 0. \\\ end(align)\]

ദയവായി ശ്രദ്ധിക്കുക: മൂന്നാമത്തെ വരിയിൽ, നിസ്സാരകാര്യങ്ങളിൽ സമയം പാഴാക്കേണ്ടതില്ലെന്നും എല്ലാം ഉടനടി (−2) കൊണ്ട് ഹരിക്കണമെന്നും ഞാൻ തീരുമാനിച്ചു. മിനുൽ ആദ്യ ബ്രാക്കറ്റിലേക്ക് പോയി (ഇപ്പോൾ എല്ലായിടത്തും പ്ലസ് ഉണ്ട്), രണ്ട് സ്ഥിരമായ ഘടകം ഉപയോഗിച്ച് കുറച്ചു. സ്വതന്ത്രവും പരീക്ഷണാത്മകവുമായ ജോലികൾക്കായി യഥാർത്ഥ കണക്കുകൂട്ടലുകൾ തയ്യാറാക്കുമ്പോൾ നിങ്ങൾ ചെയ്യേണ്ടത് ഇതാണ് - നിങ്ങൾ എല്ലാ പ്രവർത്തനങ്ങളും പരിവർത്തനങ്ങളും നേരിട്ട് വിവരിക്കേണ്ടതില്ല.

അടുത്തതായി, ഇടവേളകളുടെ പരിചിതമായ രീതി പ്രവർത്തിക്കുന്നു. ന്യൂമറേറ്റർ പൂജ്യങ്ങൾ: എന്നാൽ ഒന്നുമില്ല. കാരണം വിവേചനം നെഗറ്റീവ് ആയിരിക്കും. അതാകട്ടെ, $x=0$ - കഴിഞ്ഞ തവണത്തെപ്പോലെ തന്നെ ഡിനോമിനേറ്റർ പുനഃസജ്ജമാക്കും. ശരി, $x=0$ ൻ്റെ വലതുവശത്തുള്ള ഭിന്നസംഖ്യ പോസിറ്റീവ് മൂല്യങ്ങളും ഇടതുവശത്ത് നെഗറ്റീവ് മൂല്യവും എടുക്കുമെന്ന് വ്യക്തമാണ്. നെഗറ്റീവ് മൂല്യങ്ങളിൽ ഞങ്ങൾക്ക് താൽപ്പര്യമുള്ളതിനാൽ, അന്തിമ ഉത്തരം ഇതാണ്: $x\in \ഇടത്(-\infty ;0 \right)$.

\[((\ഇടത്(0.16 \വലത്))^(1+2x))\cdot ((\ഇടത്(6.25 \വലത്))^(x))\ge 1\]

എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങളിലെ ദശാംശ ഭിന്നസംഖ്യകൾ നിങ്ങൾ എന്തുചെയ്യണം? അത് ശരിയാണ്: അവ ഒഴിവാക്കുക, അവയെ സാധാരണക്കാരാക്കി മാറ്റുക. ഇവിടെ ഞങ്ങൾ വിവർത്തനം ചെയ്യും:

\[\begin(align) & 0.16=\frac(16)(100)=\frac(4)(25)\Rightarrow ((\left(0.16 \right))^(1+2x)) =((\ ഇടത് (\frac(4)(25) \വലത്))^(1+2x)); \\ & 6.25=\frac(625)(100)=\frac(25)(4)\വലത്താരോ ((\ഇടത്(6.25 \വലത്))^(x))=(\ഇടത്(\ frac(25) (4)\വലത്))^(x)). \\\അവസാനം (വിന്യസിക്കുക)\]

എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷനുകളുടെ അടിത്തറയിൽ നമുക്ക് എന്താണ് ലഭിച്ചത്? ഞങ്ങൾക്ക് രണ്ട് പരസ്പര വിപരീത സംഖ്യകൾ ലഭിച്ചു:

\[\frac(25)(4)=((\ഇടത്(\frac(4)(25) \വലത്))^(-1))\വലത്താരോ ((\ഇടത്(\frac(25)(4)) \ വലത്))^(x))=(\ഇടത്((\ഇടത്(\frac(4)(25) \വലത്))^(-1)) \right))^(x))=((\\ ഇടത് (\frac(4)(25) \വലത്))^(-x))\]

അതിനാൽ, യഥാർത്ഥ അസമത്വം ഇനിപ്പറയുന്ന രീതിയിൽ മാറ്റിയെഴുതാം:

\[\ആരംഭിക്കുക(വിന്യസിക്കുക) & ((\ഇടത്(\frac(4)(25) \വലത്))^(1+2x))\cdot ((\ഇടത്(\frac(4)(25) \വലത്) )^(-x))\ge 1; \\ & ((\ഇടത്(\frac(4)(25) \വലത്))^(1+2x+\ഇടത്(-x \വലത്)))\ge ((\ഇടത്(\frac(4)(25) \വലത്))^(0)); \\ & ((\ഇടത്(\frac(4)(25) \വലത്))^(x+1))\ge ((\ഇടത്(\frac(4)(25) \വലത്))^(0) ). \\\അവസാനം (വിന്യസിക്കുക)\]

തീർച്ചയായും, ഒരേ അടിത്തറയിൽ ശക്തികളെ ഗുണിക്കുമ്പോൾ, അവയുടെ ഘാതം കൂട്ടിച്ചേർക്കുന്നു, അതാണ് രണ്ടാമത്തെ വരിയിൽ സംഭവിച്ചത്. കൂടാതെ, ഞങ്ങൾ വലതുവശത്തുള്ള യൂണിറ്റിനെ പ്രതിനിധീകരിച്ചു, ബേസ് 4/25-ൽ ഒരു ശക്തിയായി. യുക്തിസഹമാക്കുക മാത്രമാണ് അവശേഷിക്കുന്നത്:

\[(\ഇടത്(\frac(4)(25) \വലത്))^(x+1))\ge ((\ഇടത്(\frac(4)(25) \വലത്))^(0)) \വലത് ആരോ \ഇടത്(x+1-0 \വലത്)\cdot \left(\frac(4)(25)-1 \വലത്)\ge 0\]

ശ്രദ്ധിക്കുക, $\frac(4)(25)-1=\frac(4-25)(25) \lt 0$, അതായത്. രണ്ടാമത്തെ ഘടകം ഒരു നെഗറ്റീവ് സ്ഥിരാങ്കമാണ്, അത് കൊണ്ട് ഹരിക്കുമ്പോൾ, അസമത്വ ചിഹ്നം മാറുന്നു:

\[\begin(align) & x+1-0\le 0\Rightarrow x\le -1; \\ & x\in \ഇടത്(-\infty ;-1 \right]. \\\ end(align)\]

അവസാനമായി, നിലവിലെ "സെറ്റിൽ" നിന്നുള്ള അവസാന അസമത്വം:

\[(\ഇടത്(\frac(27)(\sqrt(3)) \വലത്))^(-x)) \lt ((9)^(4-2x))\cdot 81\]

തത്വത്തിൽ, ഇവിടെ പരിഹാരത്തിൻ്റെ ആശയവും വ്യക്തമാണ്: അസമത്വത്തിൽ ഉൾപ്പെടുത്തിയിരിക്കുന്ന എല്ലാ എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷനുകളും അടിസ്ഥാന “3” ആയി ചുരുക്കണം. എന്നാൽ ഇതിനായി നിങ്ങൾ വേരുകളും ശക്തികളും ഉപയോഗിച്ച് അൽപ്പം ടിങ്കർ ചെയ്യേണ്ടിവരും:

\[\ആരംഭിക്കുക(വിന്യസിക്കുക) & \frac(27)(\sqrt(3))=\frac(((3)^(3)))(((3)^(\frac(1)(3)) ))=((3)^(3-\frac(1)(3)))=((3)^(\frac(8)(3))); \\ & 9=((3)^(2));\quad 81=((3)^(4)). \\\അവസാനം (വിന്യസിക്കുക)\]

ഈ വസ്തുതകൾ കണക്കിലെടുക്കുമ്പോൾ, യഥാർത്ഥ അസമത്വം ഇനിപ്പറയുന്ന രീതിയിൽ മാറ്റിയെഴുതാം:

\[\ആരംഭിക്കുക(അലൈന് ചെയ്യുക) & (\ഇടത്(((3)^(\frac(8)(3))) \വലത്))^(-x)) \lt ((\ഇടത്((3) ^(2))\വലത്))^(4-2x))\cdot ((3)^(4)); \\ & ((3)^(-\frac(8x)(3))) \lt ((3)^(8-4x))\cdot ((3)^(4)); \\ & ((3)^(-\frac(8x)(3))) \lt ((3)^(8-4x+4)); \\ & ((3)^(-\frac(8x)(3))) \lt ((3)^(4-4x)). \\\അവസാനം (വിന്യസിക്കുക)\]

കണക്കുകൂട്ടലുകളുടെ 2-ഉം 3-ഉം വരികൾ ശ്രദ്ധിക്കുക: അസമത്വത്തോടെ എന്തെങ്കിലും ചെയ്യുന്നതിന് മുമ്പ്, പാഠത്തിൻ്റെ തുടക്കം മുതൽ ഞങ്ങൾ സംസാരിച്ച ഫോമിലേക്ക് അത് കൊണ്ടുവരുന്നത് ഉറപ്പാക്കുക: $((a)^(x)) \ lt ((എ)^(n))$. നിങ്ങൾക്ക് ഇടത്തോ വലത്തോ ചില ഇടത് കൈ ഘടകങ്ങൾ, അധിക സ്ഥിരാങ്കങ്ങൾ മുതലായവ ഉള്ളിടത്തോളം, അടിസ്ഥാനങ്ങളുടെ യുക്തിസഹമാക്കൽ അല്ലെങ്കിൽ "ക്രോസ് ഔട്ട്" നടത്താൻ കഴിയില്ല! ഈ ലളിതമായ വസ്തുത മനസ്സിലാക്കുന്നതിൽ പരാജയപ്പെട്ടതിനാൽ എണ്ണമറ്റ ജോലികൾ തെറ്റായി പൂർത്തിയാക്കി. ഞങ്ങൾ എക്‌സ്‌പോണൻഷ്യൽ, ലോഗരിഥമിക് അസമത്വങ്ങൾ വിശകലനം ചെയ്യാൻ തുടങ്ങുമ്പോൾ ഞാൻ തന്നെ എൻ്റെ വിദ്യാർത്ഥികളുമായി ഈ പ്രശ്നം നിരന്തരം നിരീക്ഷിക്കുന്നു.

എന്നാൽ നമുക്ക് നമ്മുടെ ചുമതലയിലേക്ക് മടങ്ങാം. ഇത്തവണ യുക്തിവാദം ഇല്ലാതെ ചെയ്യാൻ ശ്രമിക്കാം. നമുക്ക് ഓർക്കാം: ഡിഗ്രിയുടെ അടിസ്ഥാനം ഒന്നിനെക്കാൾ വലുതാണ്, അതിനാൽ ട്രിപ്പിൾ ലളിതമായി മറികടക്കാൻ കഴിയും - അസമത്വ ചിഹ്നം മാറില്ല. നമുക്ക് ലഭിക്കുന്നത്:

\[\ആരംഭിക്കുക(വിന്യസിക്കുക) & -\frac(8x)(3) \lt 4-4x; \\ & 4x-\frac(8x)(3) \lt 4; \\ & \frac(4x)(3) \lt 4; \\ & 4x \lt 12; \\ & x \lt 3. \\\ end(align)\]

അത്രയേയുള്ളൂ. അന്തിമ ഉത്തരം: $x\in \ഇടത്(-\infty ;3 \right)$.

ഒരു സ്ഥിരതയുള്ള പദപ്രയോഗം വേർതിരിച്ച് ഒരു വേരിയബിൾ മാറ്റിസ്ഥാപിക്കുന്നു

ഉപസംഹാരമായി, നാല് എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങൾ കൂടി പരിഹരിക്കാൻ ഞാൻ നിർദ്ദേശിക്കുന്നു, അവ ഇതിനകം തയ്യാറാകാത്ത വിദ്യാർത്ഥികൾക്ക് വളരെ ബുദ്ധിമുട്ടാണ്. അവരെ നേരിടാൻ, ഡിഗ്രികളുമായി പ്രവർത്തിക്കുന്നതിനുള്ള നിയമങ്ങൾ നിങ്ങൾ ഓർമ്മിക്കേണ്ടതുണ്ട്. പ്രത്യേകിച്ചും, പൊതുവായ ഘടകങ്ങൾ ബ്രാക്കറ്റുകളിൽ നിന്ന് പുറത്തെടുക്കുന്നു.

എന്നാൽ ഏറ്റവും പ്രധാനപ്പെട്ട കാര്യം ബ്രാക്കറ്റുകളിൽ നിന്ന് കൃത്യമായി എന്താണ് എടുക്കാൻ കഴിയുക എന്ന് മനസിലാക്കാൻ പഠിക്കുക എന്നതാണ്. അത്തരമൊരു പദപ്രയോഗത്തെ സ്ഥിരത എന്ന് വിളിക്കുന്നു - ഇത് ഒരു പുതിയ വേരിയബിൾ ഉപയോഗിച്ച് സൂചിപ്പിക്കാം, അങ്ങനെ എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്ഷനിൽ നിന്ന് രക്ഷപ്പെടാം. അതിനാൽ, നമുക്ക് ജോലികൾ നോക്കാം:

\[\begin(align) & ((5)^(x+2))+((5)^(x+1))\ge 6; \\ & ((3)^(x))+((3)^(x+2))\ge 90; \\ & ((25)^(x+1.5))-((5)^(2x+2)) \gt 2500; \\ & ((\left(0.5 \right))^(-4x-8))-((16)^(x+1.5)) \gt 768. \\\ end(align)\]

ആദ്യ വരിയിൽ നിന്ന് തുടങ്ങാം. ഈ അസമത്വം നമുക്ക് പ്രത്യേകം എഴുതാം:

\[((5)^(x+2))+((5)^(x+1))\ge 6\]

ശ്രദ്ധിക്കുക $((5)^(x+2))=((5)^(x+1+1))=((5)^(x+1))\cdot 5$, അതിനാൽ വലത് കൈ വശം മാറ്റിയെഴുതാം:

അസമത്വത്തിൽ $((5)^(x+1))$ ഒഴികെ മറ്റ് എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷനുകളൊന്നും ഇല്ല എന്നത് ശ്രദ്ധിക്കുക. പൊതുവേ, $x$ വേരിയബിൾ മറ്റെവിടെയും ദൃശ്യമാകില്ല, അതിനാൽ നമുക്ക് ഒരു പുതിയ വേരിയബിൾ അവതരിപ്പിക്കാം: $((5)^(x+1))=t$. ഞങ്ങൾക്ക് ഇനിപ്പറയുന്ന നിർമ്മാണം ലഭിക്കുന്നു:

\[\begin(align) & 5t+t\ge 6; \\&6t\ge 6; \\ & t\ge 1. \\\ end(align)\]

ഞങ്ങൾ യഥാർത്ഥ വേരിയബിളിലേക്ക് മടങ്ങുന്നു ($t=(5)^(x+1))$), അതേ സമയം 1=5 0 എന്ന് ഓർക്കുക. നമുക്ക് ഉണ്ട്:

\[\ആരംഭിക്കുക(അലൈൻ ചെയ്യുക) & ((5)^(x+1))\ge ((5)^(0)); \\ & x+1\ge 0; \\ & x\ge -1. \\\അവസാനം (വിന്യസിക്കുക)\]

അതാണ് പരിഹാരം! ഉത്തരം: $x\in \ഇടത്[ -1;+\infty \right)$. നമുക്ക് രണ്ടാമത്തെ അസമത്വത്തിലേക്ക് പോകാം:

\[((3)^(x))+((3)^(x+2))\ge 90\]

ഇവിടെ എല്ലാം ഒന്നുതന്നെ. ശ്രദ്ധിക്കുക $((3)^(x+2))=((3)^(x))\cdot ((3)^(2))=9\cdot ((3)^(x))$ . അപ്പോൾ ഇടതുവശം മാറ്റിയെഴുതാം:

\[\begin(align) & ((3)^(x))+9\cdot ((3)^(x))\ge 90;\quad \left| ((3)^(x))=t\വലത്. \\&t+9t\ge 90; \\ & 10t\ge 90; \\ & t\ge 9\Rightarrow ((3)^(x))\ge 9\Rightarrow ((3)^(x))\ge ((3)^(2)); \\ & x\ge 2\Rightarrow x\in \\ഇടത്[ 2;+\infty \right). \\\അവസാനം (വിന്യസിക്കുക)\]

യഥാർത്ഥ ടെസ്റ്റുകൾക്കും സ്വതന്ത്ര ജോലികൾക്കുമായി നിങ്ങൾ ഒരു പരിഹാരം തയ്യാറാക്കേണ്ടത് ഏകദേശം ഇങ്ങനെയാണ്.

ശരി, കൂടുതൽ സങ്കീർണ്ണമായ എന്തെങ്കിലും ശ്രമിക്കാം. ഉദാഹരണത്തിന്, ഇവിടെ അസമത്വം:

\[((25)^(x+1.5))-((5)^(2x+2)) \gt 2500\]

ഇവിടെ എന്താണ് പ്രശ്നം? ഒന്നാമതായി, ഇടതുവശത്തുള്ള എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷനുകളുടെ അടിസ്ഥാനങ്ങൾ വ്യത്യസ്തമാണ്: 5 ഉം 25 ഉം. എന്നിരുന്നാലും, 25 = 5 2, അതിനാൽ ആദ്യ പദം രൂപാന്തരപ്പെടുത്താം:

\[\begin(align) & ((25)^(x+1.5))=((\ഇടത്((5)^(2)) \വലത്))^(x+1.5))= ((5) ^(2x+3)); \\ & ((5)^(2x+3))=((5)^(2x+2+1))=((5)^(2x+2))\cdot 5. \\\ end(align )\]

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, ആദ്യം ഞങ്ങൾ എല്ലാം ഒരേ അടിത്തറയിലേക്ക് കൊണ്ടുവന്നു, തുടർന്ന് ആദ്യ പദം രണ്ടാമത്തേതിലേക്ക് എളുപ്പത്തിൽ കുറയ്ക്കാൻ കഴിയുമെന്ന് ഞങ്ങൾ ശ്രദ്ധിച്ചു - നിങ്ങൾ എക്സ്പോണൻ്റ് വികസിപ്പിക്കേണ്ടതുണ്ട്. ഇപ്പോൾ നിങ്ങൾക്ക് സുരക്ഷിതമായി ഒരു പുതിയ വേരിയബിൾ അവതരിപ്പിക്കാൻ കഴിയും: $((5)^(2x+2))=t$, കൂടാതെ മുഴുവൻ അസമത്വവും ഇനിപ്പറയുന്ന രീതിയിൽ മാറ്റിയെഴുതും:

\[\begin(align) & 5t-t\ge 2500; \\&4t\ge 2500; \\ & t\ge 625=((5)^(4)); \\ & ((5)^(2x+2))\ge ((5)^(4)); \\ & 2x+2\ge 4; \\&2x\ge 2; \\ & x\ge 1. \\\ end(align)\]

വീണ്ടും, ബുദ്ധിമുട്ടുകളൊന്നുമില്ല! അവസാന ഉത്തരം: $x\in \ഇടത്[ 1;+\infty \right)$. ഇന്നത്തെ പാഠത്തിലെ അവസാന അസമത്വത്തിലേക്ക് പോകാം:

\[((\ഇടത്(0.5 \വലത്))^(-4x-8))-((16)^(x+1.5)) \gt 768\]

നിങ്ങൾ ആദ്യം ശ്രദ്ധിക്കേണ്ട കാര്യം, തീർച്ചയായും, ആദ്യ ശക്തിയുടെ അടിത്തറയിലെ ദശാംശ ഭിന്നസംഖ്യയാണ്. അതിൽ നിന്ന് മുക്തി നേടേണ്ടത് ആവശ്യമാണ്, അതേ സമയം എല്ലാ എക്സ്പോണൻഷ്യൽ ഫംഗ്ഷനുകളും ഒരേ അടിത്തറയിലേക്ക് കൊണ്ടുവരിക - നമ്പർ "2":

\[\begin(align) & 0.5=\frac(1)(2)=(2)^(-1))\Rightarrow ((\left(0.5 \right))^(-4x- 8))= ((\ഇടത്((2)^(-1)) \വലത്))^(-4x-8))=((2)^(4x+8)); \\ & 16=((2)^(4))\വലത്തോട്ടുള്ള ((16)^(x+1.5))=((\ഇടത്((2)^(4)) \വലത്))^( x+ 1.5))=((2)^(4x+6)); \\ & ((2)^(4x+8))-((2)^(4x+6)) \gt 768. \\\ end(align)\]

കൊള്ളാം, ഞങ്ങൾ ആദ്യപടി സ്വീകരിച്ചു-എല്ലാം ഒരേ അടിത്തറയിലേക്ക് നയിച്ചു. ഇപ്പോൾ നിങ്ങൾ ഒരു സ്ഥിരതയുള്ള എക്സ്പ്രഷൻ തിരഞ്ഞെടുക്കേണ്ടതുണ്ട്. ശ്രദ്ധിക്കുക $((2)^(4x+8))=((2)^(4x+6+2))=((2)^(4x+6))\cdot 4$. ഞങ്ങൾ ഒരു പുതിയ വേരിയബിൾ അവതരിപ്പിക്കുകയാണെങ്കിൽ $((2)^(4x+6))=t$, യഥാർത്ഥ അസമത്വം ഇനിപ്പറയുന്ന രീതിയിൽ മാറ്റിയെഴുതാം:

\[\ആരംഭിക്കുക(അലൈൻ ചെയ്യുക) & 4t-t \gt 768; \\ & 3t \gt 768; \\ & t \gt 256=((2)^(8)); \\ & ((2)^(4x+6)) \gt ((2)^(8)); \\ & 4x+6 \gt 8; \\ & 4x \gt 2; \\ & x \gt \frac(1)(2)=0.5. \\\അവസാനം (വിന്യസിക്കുക)\]

സ്വാഭാവികമായും, ചോദ്യം ഉയർന്നേക്കാം: 256 = 2 8 എന്ന് ഞങ്ങൾ എങ്ങനെ കണ്ടെത്തി? നിർഭാഗ്യവശാൽ, ഇവിടെ നിങ്ങൾ രണ്ടിൻ്റെ ശക്തികൾ (അതേ സമയം മൂന്നിൻ്റെയും അഞ്ചിൻ്റെയും ശക്തികൾ) അറിയേണ്ടതുണ്ട്. ശരി, അല്ലെങ്കിൽ 256 നെ 2 കൊണ്ട് ഹരിക്കുക (നിങ്ങൾക്ക് ഹരിക്കാം, കാരണം 256 ഇരട്ട സംഖ്യയായതിനാൽ) നമുക്ക് ഫലം ലഭിക്കുന്നതുവരെ. ഇത് ഇതുപോലെ കാണപ്പെടും:

\[\begin(align) & 256=128\cdot 2= \\ & =64\cdot 2\cdot 2= \\ & =32\cdot 2\cdot 2\cdot 2= \\ & =16\cdot 2 \cdot 2\cdot 2\cdot 2= \\ & =8\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =4\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =(2)^(8)).\ end(align )\]

മൂന്ന് (9, 27, 81, 243 എന്നീ സംഖ്യകൾ അതിൻ്റെ ഡിഗ്രികളാണ്), കൂടാതെ ഏഴ് (49, 343 എന്നീ സംഖ്യകളും ഓർക്കുന്നത് നന്നായിരിക്കും) സമാനമാണ്. ശരി, നിങ്ങൾ അറിഞ്ഞിരിക്കേണ്ട "മനോഹരമായ" ഡിഗ്രികളും അഞ്ചിന് ഉണ്ട്:

\[\begin(align) & ((5)^(2))=25; \\ & ((5)^(3))=125; \\ & ((5)^(4))=625; \\ & ((5)^(5))=3125. \\\അവസാനം (വിന്യസിക്കുക)\]

തീർച്ചയായും, നിങ്ങൾ ആഗ്രഹിക്കുന്നുവെങ്കിൽ, ഈ സംഖ്യകളെല്ലാം പരസ്പരം തുടർച്ചയായി ഗുണിച്ച് നിങ്ങളുടെ മനസ്സിൽ പുനഃസ്ഥാപിക്കാൻ കഴിയും. എന്നിരുന്നാലും, നിങ്ങൾക്ക് നിരവധി എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങൾ പരിഹരിക്കേണ്ടിവരുമ്പോൾ, അടുത്ത ഓരോന്നും മുമ്പത്തേതിനേക്കാൾ ബുദ്ധിമുട്ടുള്ളതാണെങ്കിൽ, നിങ്ങൾ അവസാനമായി ചിന്തിക്കാൻ ആഗ്രഹിക്കുന്നത് ചില സംഖ്യകളുടെ ശക്തികളെക്കുറിച്ചാണ്. ഈ അർത്ഥത്തിൽ, ഈ പ്രശ്നങ്ങൾ ഇടവേള രീതിയിലൂടെ പരിഹരിക്കപ്പെടുന്ന "ക്ലാസിക്കൽ" അസമത്വങ്ങളേക്കാൾ സങ്കീർണ്ണമാണ്.

ഈ വിഷയം പഠിക്കാൻ ഈ പാഠം നിങ്ങളെ സഹായിച്ചുവെന്ന് ഞാൻ പ്രതീക്ഷിക്കുന്നു. എന്തെങ്കിലും വ്യക്തമല്ലെങ്കിൽ, അഭിപ്രായങ്ങളിൽ ചോദിക്കുക. പിന്നെ അടുത്ത പാഠങ്ങളിൽ കാണാം :)

സമവാക്യങ്ങളുടെ സിസ്റ്റങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള രീതികൾ

ആരംഭിക്കുന്നതിന്, സമവാക്യങ്ങളുടെ സിസ്റ്റങ്ങൾ പരിഹരിക്കുന്നതിന് പൊതുവായി നിലനിൽക്കുന്ന രീതികൾ എന്തൊക്കെയാണെന്ന് നമുക്ക് ഹ്രസ്വമായി ഓർമ്മിക്കാം.

നിലവിലുണ്ട് നാല് പ്രധാന വഴികൾസമവാക്യ സംവിധാനങ്ങൾക്കുള്ള പരിഹാരങ്ങൾ:

സബ്‌സ്റ്റിറ്റ്യൂഷൻ രീതി: തന്നിരിക്കുന്ന ഏതെങ്കിലും സമവാക്യങ്ങൾ എടുത്ത് $x$ എന്നതിൻ്റെ അടിസ്ഥാനത്തിൽ $y$ പ്രകടിപ്പിക്കുക, തുടർന്ന് $x.$ എന്ന വേരിയബിൾ കണ്ടെത്തുന്നിടത്ത് നിന്ന് $y$ എന്നത് എളുപ്പത്തിൽ കണക്കാക്കാം $y.$ എന്ന വേരിയബിൾ

കൂട്ടിച്ചേർക്കൽ രീതി: ഈ രീതിയിൽ, നിങ്ങൾ ഒന്നോ രണ്ടോ സമവാക്യങ്ങളെ അത്തരം സംഖ്യകളാൽ ഗുണിക്കേണ്ടതുണ്ട്, നിങ്ങൾ രണ്ടും ഒരുമിച്ച് ചേർക്കുമ്പോൾ, വേരിയബിളുകളിലൊന്ന് "അപ്രത്യക്ഷമാകും."

ഗ്രാഫിക്കൽ രീതി: സിസ്റ്റത്തിൻ്റെ രണ്ട് സമവാക്യങ്ങളും കോർഡിനേറ്റ് തലത്തിൽ ചിത്രീകരിക്കുകയും അവയുടെ വിഭജനത്തിൻ്റെ പോയിൻ്റ് കണ്ടെത്തുകയും ചെയ്യുന്നു.

പുതിയ വേരിയബിളുകൾ അവതരിപ്പിക്കുന്ന രീതി: ഈ രീതിയിൽ ഞങ്ങൾ സിസ്റ്റം ലളിതമാക്കാൻ ചില എക്സ്പ്രഷനുകൾ മാറ്റിസ്ഥാപിക്കുന്നു, തുടർന്ന് മുകളിൽ പറഞ്ഞ രീതികളിൽ ഒന്ന് ഉപയോഗിക്കുക.

എക്സ്പോണൻഷ്യൽ സമവാക്യങ്ങളുടെ സംവിധാനങ്ങൾ

നിർവ്വചനം 1

എക്‌സ്‌പോണൻഷ്യൽ സമവാക്യങ്ങൾ അടങ്ങുന്ന സമവാക്യങ്ങളുടെ സിസ്റ്റങ്ങളെ എക്‌സ്‌പോണൻഷ്യൽ സമവാക്യങ്ങളുടെ സിസ്റ്റങ്ങൾ എന്ന് വിളിക്കുന്നു.

ഉദാഹരണങ്ങൾ ഉപയോഗിച്ച് എക്‌സ്‌പോണൻഷ്യൽ സമവാക്യങ്ങളുടെ സോൾവിംഗ് സിസ്റ്റങ്ങൾ ഞങ്ങൾ പരിഗണിക്കും.

ഉദാഹരണം 1

സമവാക്യങ്ങളുടെ സംവിധാനം പരിഹരിക്കുക

ചിത്രം 1.

പരിഹാരം.

ഈ സംവിധാനം പരിഹരിക്കാൻ ഞങ്ങൾ ആദ്യ രീതി ഉപയോഗിക്കും. ആദ്യം, $x$ എന്നതിൻ്റെ അടിസ്ഥാനത്തിൽ ആദ്യ സമവാക്യത്തിൽ $y$ പ്രകടിപ്പിക്കാം.

ചിത്രം 2.

രണ്ടാമത്തെ സമവാക്യത്തിലേക്ക് $y$ പകരം വയ്ക്കാം:

\ \ \[-2-x=2\] \ \

ഉത്തരം: $(-4,6)$.

ഉദാഹരണം 2

സമവാക്യങ്ങളുടെ സംവിധാനം പരിഹരിക്കുക

ചിത്രം 3.

പരിഹാരം.

ഈ സംവിധാനം സിസ്റ്റത്തിന് തുല്യമാണ്

ചിത്രം 4.

സമവാക്യങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള നാലാമത്തെ രീതി നമുക്ക് പ്രയോഗിക്കാം. $2^x=u\ (u >0)$, $3^y=v\ (v >0)$ എന്നിവ അനുവദിക്കുക, നമുക്ക് ലഭിക്കുന്നത്:

ചിത്രം 5.

സങ്കലന രീതി ഉപയോഗിച്ച് ഫലമായുണ്ടാകുന്ന സിസ്റ്റം നമുക്ക് പരിഹരിക്കാം. നമുക്ക് സമവാക്യങ്ങൾ കൂട്ടിച്ചേർക്കാം:

\ \

അപ്പോൾ രണ്ടാമത്തെ സമവാക്യത്തിൽ നിന്ന് നമുക്ക് അത് ലഭിക്കും

മാറ്റിസ്ഥാപിക്കുന്നതിലേക്ക് മടങ്ങുമ്പോൾ, എനിക്ക് എക്‌സ്‌പോണൻഷ്യൽ സമവാക്യങ്ങളുടെ ഒരു പുതിയ സിസ്റ്റം ലഭിച്ചു:

ചിത്രം 6.

നമുക്ക് ലഭിക്കുന്നത്:

ചിത്രം 7.

ഉത്തരം: $(0,1)$.

എക്സ്പോണൻഷ്യൽ അസമത്വങ്ങളുടെ സംവിധാനങ്ങൾ

നിർവ്വചനം 2

എക്‌സ്‌പോണൻഷ്യൽ സമവാക്യങ്ങൾ അടങ്ങിയ അസമത്വങ്ങളുടെ സിസ്റ്റങ്ങളെ എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങളുടെ സിസ്റ്റങ്ങൾ എന്ന് വിളിക്കുന്നു.

ഉദാഹരണങ്ങൾ ഉപയോഗിച്ച് എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങളുടെ പരിഹാര സംവിധാനങ്ങൾ ഞങ്ങൾ പരിഗണിക്കും.

ഉദാഹരണം 3

അസമത്വങ്ങളുടെ സംവിധാനം പരിഹരിക്കുക

ചിത്രം 8.

പരിഹാരം:

ഈ അസമത്വ സമ്പ്രദായം സിസ്റ്റത്തിന് തുല്യമാണ്

ചിത്രം 9.

ആദ്യത്തെ അസമത്വം പരിഹരിക്കുന്നതിന്, എക്‌സ്‌പോണൻഷ്യൽ അസമത്വങ്ങളുടെ തുല്യതയെക്കുറിച്ചുള്ള ഇനിപ്പറയുന്ന സിദ്ധാന്തം ഓർമ്മിക്കുക:

സിദ്ധാന്തം 1.അസമത്വം $a^(f(x)) >a^(\varphi (x)) $, ഇവിടെ $a >0,a\ne 1$ രണ്ട് സിസ്റ്റങ്ങളുടെ ശേഖരത്തിന് തുല്യമാണ്

\}