lar › Salão › Método gráfico para resolver um sistema de equações. Resolvendo equações, desigualdades, sistemas usando gráficos de funções

Método gráfico para resolver um sistema de equações. Resolvendo equações, desigualdades, sistemas usando gráficos de funções

Apresentação e aula sobre o tema: “Solução gráfica de equações quadráticas”

Materiais adicionais
Caros usuários, não se esqueçam de deixar seus comentários, críticas, desejos! Todos os materiais foram verificados por um programa antivírus.

Auxiliares educacionais e simuladores na loja online Integral para a 8ª série
Potências e raízes Funções e gráficos

Gráficos de funções quadráticas

Na última lição aprendemos como representar graficamente qualquer função quadrática. Com a ajuda de tais funções podemos resolver as chamadas equações quadráticas, que geralmente são escritas da seguinte forma: $ax^2+bx+c=0$,
$a, b, c$ são quaisquer números, mas $a≠0$.
Pessoal, comparem a equação escrita acima com esta: $y=ax^2+bx+c$.
Eles são quase idênticos. A diferença é que em vez de $y$ escrevemos $0$, ou seja, $y=0$. Como então resolver equações quadráticas? A primeira coisa que vem à mente é construir um gráfico da parábola $ax^2+bx+c$ e encontrar os pontos de intersecção deste gráfico com a reta $y=0$. Existem outras soluções. Vejamos eles usando um exemplo específico.

Métodos para resolver funções quadráticas

Exemplo.
Resolva a equação: $x^2+2x-8=0$.

Solução.
Método 1. Vamos traçar a função $y=x^2+2x-8$ e encontrar os pontos de intersecção com a reta $y=0$. O coeficiente de maior grau é positivo, o que significa que os ramos da parábola apontam para cima. Vamos encontrar as coordenadas do vértice:
$x_(c)=-\frac(b)(2a)=\frac(-2)(2)=-1$.
$y_(в)=(-1)^2+2*(-1)-8=1-2-8=-9$.

Tomemos o ponto com coordenadas $(-1;-9)$ como a origem do novo sistema de coordenadas e construamos nele um gráfico da parábola $y=x^2$.

Vemos dois pontos de intersecção. Eles estão marcados com pontos pretos no gráfico. Estamos resolvendo a equação de x, então precisamos escolher as abcissas desses pontos. Eles são iguais a $-4$ e $2$.
Assim, a solução para a equação quadrática $x^2+2x-8=0$ tem duas raízes: $ x_1=-4$ e $x_2=2$.

Método 2. Transforme a equação original na forma: $x^2=8-2x$.
Assim, podemos resolver esta equação da maneira gráfica usual, encontrando a abcissa dos pontos de intersecção dos dois gráficos $y=x^2$ e $y=8-2x$.
Obtivemos dois pontos de intersecção cujas abcissas coincidem com as soluções obtidas no primeiro método, a saber: $x_1=-4$ e $x_2=2$.

Método 3.
Vamos transformar a equação original nesta forma: $x^2-8=-2x$.
Vamos construir dois gráficos $y=x^2-8$ e $y=-2x$ e encontrar seus pontos de intersecção.
O gráfico de $y=x^2-8$ é uma parábola deslocada 8 unidades para baixo.
Obtivemos dois pontos de intersecção, e as abcissas desses pontos são as mesmas dos dois métodos anteriores, a saber: $x_1=-4$ e $x_2=2$.

Método 4.
Vamos selecionar o quadrado perfeito na equação original: $x^2+2x-8=x^2+2x+1-9=(x+1)^2-9$.
Vamos construir dois gráficos das funções $y=(x+1)^2$ e $y=9$. O gráfico da primeira função é uma parábola deslocada uma unidade para a esquerda. O gráfico da segunda função é uma reta paralela ao eixo das abcissas e que passa pela ordenada igual a $9$.
Mais uma vez obtivemos dois pontos de intersecção dos gráficos, e as abcissas desses pontos coincidem com as obtidas nos métodos anteriores $x_1=-4$ e $x_2=2$.

Método 5.
Divida a equação original por x: $\frac(x^2)(x)+\frac(2x)(x)-\frac(8)(x)=\frac(0)(x)$.
$x+2-\frac(8)(x)=0$.
$x+2=\frac(8)(x)$.
Vamos resolver esta equação graficamente, construindo dois gráficos $y=x+2$ e $y=\frac(8)(x)$.
Novamente obtivemos dois pontos de intersecção, e as abcissas desses pontos coincidem com as obtidas acima de $x_1=-4$ e $x_2=2$.

Algoritmo para solução gráfica de funções quadráticas

Pessoal, vimos cinco maneiras de resolver graficamente equações quadráticas. Em cada um desses métodos, as raízes das equações acabaram sendo iguais, o que significa que a solução foi obtida corretamente.

Métodos básicos para resolver graficamente equações quadráticas $ax^2+bx+c=0$, $a, b, c$ - quaisquer números, mas $a≠0$:
1. Construa um gráfico da função $y=ax^2+bx+c$, encontre os pontos de intersecção com o eixo das abcissas, que serão a solução da equação.
2. Construa dois gráficos $y=ax^2$ e $y=-bx-c$, encontre a abcissa dos pontos de intersecção desses gráficos.
3. Construa dois gráficos $y=ax^2+c$ e $y=-bx$, encontre a abcissa dos pontos de intersecção desses gráficos. O gráfico da primeira função será uma parábola deslocada para baixo ou para cima, dependendo do sinal do número c. O segundo gráfico é uma linha reta que passa pela origem.
4. Selecione um quadrado completo, ou seja, traga a equação original para a forma: $a(x+l)^2+m=0$.
Construa dois gráficos da função $y=a(x+l)^2$ e $y=-m$, encontre seus pontos de intersecção. O gráfico da primeira função será uma parábola deslocada para a esquerda ou para a direita, dependendo do sinal do número $l$. O gráfico da segunda função será uma reta paralela ao eixo das abcissas e que cruza o eixo das ordenadas em um ponto igual a $-m$.
5. Divida a equação original por x: $ax+b+\frac(c)(x)=0$.
Converta para o formato: $\frac(c)(x)=-ax-b$.
Construa dois gráficos novamente e encontre seus pontos de intersecção. O primeiro gráfico é uma hipérbole, o segundo gráfico é uma linha reta. Infelizmente, o método gráfico para resolver equações quadráticas nem sempre é uma boa solução. Os pontos de interseção de vários gráficos nem sempre são inteiros ou podem ter números muito grandes na abscissa (ordenada) que não podem ser plotados em uma folha de papel normal.

Vamos demonstrar todos esses métodos mais claramente com um exemplo.

Exemplo.
Resolva a equação: $x^2+3x-12=0$,

Solução.
Vamos traçar a parábola e encontrar as coordenadas dos vértices: $x_(c)=-\frac(b)(2a)=\frac(-3)(2)=-1.5$.
$y_(в)=(-1,5)^2+2*(-1,5)-8=2,25-3-8=-8,75$.
Ao construir tal parábola, surgem imediatamente problemas, por exemplo, na marcação correta do vértice da parábola. Para marcar com precisão a ordenada do vértice, você precisa selecionar uma célula igual a 0,25 unidades de escala. Nessa escala, você precisa descer 35 unidades, o que é inconveniente. Enfim, vamos montar nossa programação.
O segundo problema que encontramos é que o gráfico da nossa função intercepta o eixo x num ponto com coordenadas que não podem ser determinadas com precisão. Uma solução aproximada é possível, mas a matemática é uma ciência exata.
Assim, o método gráfico não é o mais conveniente. Portanto, resolver equações quadráticas requer um método mais universal, que estudaremos nas lições seguintes.

Problemas para resolver de forma independente

1. Resolva a equação graficamente (de todas as cinco maneiras): $x^2+4x-12=0$.
2. Resolva a equação usando qualquer método gráfico: $-x^2+6x+16=0$.

Às vezes, as equações são resolvidas graficamente. Para fazer isso, você precisa transformar a equação de forma que (se ainda não estiver apresentada em uma forma transformada) à esquerda e à direita do sinal de igual haja expressões para as quais você possa desenhar facilmente gráficos de funções. Por exemplo, dada a seguinte equação:
x² – 2x – 1 = 0

Se ainda não estudamos a resolução algébrica de equações quadráticas, podemos tentar fazê-lo por fatoração ou graficamente. Para resolver tal equação graficamente, apresentamos-a desta forma:
x² = 2x + 1

Desta representação da equação segue-se que é necessário encontrar tais valores de x para os quais o lado esquerdo será igual ao direito.

Como você sabe, o gráfico da função y = x² é uma parábola e y = 2x + 1 é uma linha reta. As coordenadas x dos pontos do plano coordenado situados tanto no primeiro gráfico quanto no segundo (ou seja, os pontos de intersecção dos gráficos) são precisamente aqueles valores de x nos quais o lado esquerdo da equação será igual Para a direita. Em outras palavras, as coordenadas x dos pontos de intersecção dos gráficos são as raízes da equação.

Os gráficos podem se cruzar em vários pontos, em um ponto ou nem mesmo se cruzarem. Segue-se que uma equação pode ter várias raízes, ou uma raiz, ou nenhuma.

Vejamos um exemplo mais simples:
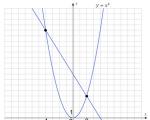
x² – 2x = 0 ou x² = 2x

Vamos desenhar gráficos das funções y = x² e y = 2x:

Como pode ser visto no desenho, a parábola e a reta se cruzam nos pontos (0; 0) e (2; 4). As coordenadas x desses pontos são respectivamente iguais a 0 e 2. Isso significa que a equação x² – 2x = 0 tem duas raízes - x 1 = 0, x 2 = 2.

Vamos verificar isso resolvendo a equação retirando o fator comum dos colchetes:
x² – 2x = 0
x(x – 2) = 0

O zero do lado direito pode ocorrer quando x é 0 ou 2.

A razão pela qual não resolvemos graficamente a equação x² – 2x – 1 = 0 é que na maioria das equações as raízes são números reais (fracionários) e é difícil determinar com precisão o valor de x em um gráfico. Portanto, para a maioria das equações, a solução gráfica não é a melhor. No entanto, o conhecimento deste método proporciona uma compreensão mais profunda da relação entre equações e funções.

>>Matemática: Solução gráfica de equações

Solução gráfica de equações

Vamos resumir nosso conhecimento sobre gráficos funções. Aprendemos como construir gráficos das seguintes funções:

y =b (reta paralela ao eixo x);

y = kx (reta que passa pela origem);

y - kx + m (linha reta);

y = x 2 (parábola).

O conhecimento destes gráficos nos permitirá, se necessário, substituir o analítico modelo geométrico (gráfico), por exemplo, em vez do modelo y = x 2 (que representa uma igualdade com duas variáveis x e y), considere uma parábola no plano coordenado. Em particular, às vezes é útil para resolver equações. Vamos discutir como isso é feito usando vários exemplos.

A. V. Pogorelov, Geometria para 7ª a 11ª séries, Livro didático para instituições educacionais

Conteúdo da lição notas de aula métodos de aceleração de apresentação de aula de suporte tecnologias interativas Prática tarefas e exercícios workshops de autoteste, treinamentos, casos, missões, trabalhos de casa, perguntas para discussão, perguntas retóricas dos alunos Ilustrações áudio, videoclipes e multimídia fotografias, imagens, gráficos, tabelas, diagramas, humor, anedotas, piadas, quadrinhos, parábolas, provérbios, palavras cruzadas, citações Complementos resumos artigos truques para os curiosos berços livros didáticos dicionário básico e adicional de termos outros Melhorando livros didáticos e aulascorrigindo erros no livro didático atualização de um fragmento de um livro didático, elementos de inovação na aula, substituição de conhecimentos desatualizados por novos Somente para professores aulas perfeitas plano de calendário para o ano; recomendações metodológicas; programas de discussão Aulas Integradas

Que haja uma equação quadrática completa: A*x2+B*x+C=0, onde A, B e C são quaisquer números e A não é igual a zero. Este é um caso geral de uma equação quadrática. Existe também uma forma reduzida em que A=1. Para resolver qualquer equação graficamente, você precisa mover o termo de maior grau para outra parte e igualar ambas as partes a alguma variável.

Depois disso, A*x2 permanecerá no lado esquerdo da equação, e B*x-C no lado direito (podemos assumir que B é um número negativo, isso não muda a essência). A equação resultante é A*x2=B*x-C=y. Para maior clareza, neste caso ambas as partes são equiparadas à variável y.

Traçando gráficos e processando resultados

Agora podemos escrever duas equações: y=A*x2 e y=B*x-C. A seguir, você precisa traçar um gráfico de cada uma dessas funções. O gráfico y=A*x2 é uma parábola com um vértice na origem, cujos ramos são direcionados para cima ou para baixo, dependendo do sinal do número A. Se for negativo, os ramos são direcionados para baixo, se positivo, os galhos são direcionados para cima.

O gráfico y=B*x-C é uma linha reta regular. Se C=0, a reta passa pela origem. No caso geral, corta do eixo das ordenadas um segmento igual a C. O ângulo de inclinação desta reta em relação ao eixo das abcissas é determinado pelo coeficiente B. É igual à tangente da inclinação deste ângulo.

Depois que os gráficos forem traçados, verá que eles se cruzam em dois pontos. As coordenadas desses pontos ao longo do eixo x determinam as raízes da equação quadrática. Para determiná-los com precisão, você precisa construir gráficos com clareza e escolher a escala certa.

Outra solução gráfica

Existe outra maneira de resolver graficamente uma equação quadrática. Não é necessário mover B*x+C para o outro lado da equação. Você pode traçar imediatamente a função y=A*x2+B*x+C. Tal gráfico é uma parábola com um vértice em um ponto arbitrário. Este método é mais complicado que o anterior, mas você pode construir apenas um gráfico para...

Primeiro você precisa determinar o vértice da parábola com coordenadas x0 e y0. Sua abcissa é calculada usando a fórmula x0=-B/2*a. Para determinar a ordenada, você precisa substituir o valor da abcissa resultante na função original. Matematicamente, esta afirmação é escrita da seguinte forma: y0=y(x0).

Então você precisa encontrar dois pontos simétricos ao eixo da parábola. Neles, a função original deve desaparecer. Depois disso, você pode construir uma parábola. Os pontos de sua intersecção com o eixo X darão duas raízes da equação quadrática.