Gauss teoremi boşlukta. Gauss teoreminin elektrik alanlarını hesaplamak için uygulanması

Yukarıda belirtildiği gibi, kuvvet çizgilerinin, alanın çizgilerine dik bir yüzey birimini geçen çizgilerin sayısının vektörün modülüne eşit olacağı yoğunlukta çizilmesine karar verildi. Daha sonra, gerilim çizgilerinin deseninden, uzayın çeşitli noktalarındaki vektörün yalnızca yönü değil, aynı zamanda büyüklüğü de değerlendirilebilir.

Durağan bir pozitif nokta yükünün alan çizgilerini ele alalım. Yükten uzanan ve sonsuzda biten radyal çizgilerdir. Hadi gerçekleştirelim N böyle çizgiler. Daha sonra uzaktan R yükten, yarıçaplı bir kürenin birim yüzeyiyle kesişen kuvvet çizgisi sayısı R, eşit olacaktır. Bu değer belirli bir mesafedeki noktasal yükün alan gücüyle orantılıdır. R. Sayı N her zaman eşitliği sağlayacak şekilde seçim yapabilirsiniz

Neresi . Kuvvet çizgileri sürekli olduğundan, aynı sayıda kuvvet çizgisi yükü çevreleyen herhangi bir şekle sahip kapalı bir yüzeyle kesişir. Q. Yükün işaretine bağlı olarak kuvvet çizgileri ya bu kapalı yüzeye girer ya da dışarıya çıkar. Giden satırların sayısı pozitif ve gelen satırların sayısı negatif kabul edilirse modül işaretini atlayıp şunu yazabiliriz:

.

(1.4)

Gerilim vektör akışı. Alanı olan bir temel ped yerleştirelim. Alan o kadar küçük olmalıdır ki, tüm noktalardaki elektrik alan şiddeti aynı kabul edilebilsin. Siteye bir normal çizelim (Şekil 1.17). Bu normalin yönü keyfi olarak seçilir. Normal vektörle açı yapar. Elektrik alan kuvveti vektörünün seçilen bir yüzey boyunca akışı, yüzey alanı ile elektrik alan kuvveti vektörünün alanın normaline izdüşümünün çarpımıdır:

vektörün sahanın normaline izdüşümü nerede.

Tek bir alanı delen alan çizgilerinin sayısı seçilen alanın yakınındaki yoğunluk vektörünün modülüne eşit olduğundan yoğunluk vektörünün yüzey boyunca akışı bu yüzeyden geçen alan çizgilerinin sayısıyla orantılıdır. Bu nedenle, genel durumda, alan şiddeti vektörünün alan boyunca akışı, bu alana giren alan çizgilerinin sayısına eşit bir değer olarak görsel olarak yorumlanabilir:

.

(1.5)

Normalin yönünün seçiminin koşullu olduğunu unutmayın; diğer yöne yönlendirilebilir. Sonuç olarak akış cebirsel bir niceliktir: akışın işareti yalnızca alanın konfigürasyonuna değil aynı zamanda normal vektörün ve yoğunluk vektörünün göreceli yönelimine de bağlıdır. Bu iki vektör dar bir açı oluşturuyorsa akı pozitiftir; genişse akı negatiftir. Kapalı bir yüzey söz konusu olduğunda, bu yüzeyin kapsadığı alanın dışındaki normalin alınması, yani dış normalin seçilmesi adettendir.

Alan homojen değilse ve yüzey keyfi ise akış aşağıdaki gibi tanımlanır. Tüm yüzey alanı olan küçük elemanlara bölünmeli, bu elemanların her birinden geçen gerilim akıları hesaplanmalı ve daha sonra tüm elemanlardan geçen akıların toplamı alınmalıdır:

Böylece alan kuvveti, uzayda bir noktadaki elektrik alanını karakterize eder. Yoğunluk akışı, belirli bir noktadaki alan kuvvetinin değerine değil, alanın belirli bir alanın yüzeyi üzerindeki dağılımına bağlıdır.

Elektrik alan çizgileri yalnızca pozitif yüklerle başlayıp negatif yüklerle bitebilir. Uzayda başlayıp bitemezler. Dolayısıyla belirli bir kapalı hacim içerisinde elektrik yükü yoksa bu hacme giren ve çıkan hatların toplam sayısı sıfır olmalıdır. Hacme girenden daha fazla çizgi ayrılırsa, hacmin içinde pozitif bir yük vardır; Eğer gelen hatlar çıkanlardan daha fazlaysa, o zaman içeride negatif bir yük olmalıdır. Hacim içindeki toplam yük sıfıra eşit olduğunda veya içinde elektrik yükü olmadığında alan çizgileri içinden geçer ve toplam akı sıfırdır.

Bu basit hususlar, elektrik yükünün hacim içinde nasıl dağıldığına bağlı değildir. Hacmin merkezinde veya hacmi sınırlayan yüzeye yakın bir yerde bulunabilir. Bir hacim, hacim içinde herhangi bir şekilde dağıtılmış birçok pozitif ve negatif yük içerebilir. Yalnızca toplam şarj, gelen veya giden gerilim hatlarının toplam sayısını belirler.

(1.4) ve (1.5)'ten görülebileceği gibi, elektrik alan şiddeti vektörünün, yükü çevreleyen rastgele kapalı bir yüzey boyunca akışı Q, eşittir . Yüzeyin içinde varsa N Bu durumda, alan süperpozisyonu ilkesine göre, toplam akı, tüm yüklerin alan kuvvetlerinin akılarının toplamı olacak ve eşit olacaktır; bu durumda, kapalı alan tarafından kapsanan tüm yüklerin cebirsel toplamını kastediyoruz. yüzey.

Gauss teoremi. Gauss Elektrik alanı kuvveti vektörünün rastgele kapalı bir yüzey boyunca akışının, bu hacmin içinde bulunan toplam yük ile ilişkilendirilmesi gerektiği şeklindeki basit gerçeği keşfeden ilk kişi oldu:

Gauss Karl Friedrich (1777–1855)

Büyük Alman matematikçi, fizikçi ve gökbilimci, fizikteki mutlak birimler sisteminin yaratıcısı. Elektrostatik potansiyel teorisini geliştirdi ve elektrostatikin en önemli teoremini (Gauss teoremi) kanıtladı. Karmaşık optik sistemlerde görüntülerin oluşturulmasına yönelik bir teori oluşturuldu. Öklid dışı geometrinin var olma olasılığı fikrine ilk ulaşanlardan biriydi. Ayrıca Gauss'un matematiğin hemen her dalına olağanüstü katkıları olmuştur.

Son ilişki Gauss'un elektrik alanı teoremidir: yoğunluk vektörünün rastgele kapalı bir yüzey boyunca akışı, bu yüzeyin içinde bulunan yüklerin cebirsel toplamı ile orantılıdır Orantılılık katsayısı, birim sisteminin seçimine bağlıdır.

Gauss teoreminin Coulomb yasası ve süperpozisyon ilkesinin bir sonucu olarak elde edildiğine dikkat edilmelidir. Eğer elektrik alan şiddeti mesafenin karesiyle ters orantılı olarak değişmiyorsa teorem geçersiz olacaktır. Bu nedenle Gauss teoremi, ters kare yasasının ve süperpozisyon ilkesinin tam olarak sağlandığı herhangi bir alana, örneğin yerçekimi alanına uygulanabilir. Yerçekimi alanında, alanı oluşturan yüklerin rolü, cisimlerin kütleleri tarafından oynanır. Yerçekimi alanı çizgilerinin kapalı bir yüzey boyunca akışı, o yüzeyin içerdiği toplam kütle ile orantılıdır.

Yüklü bir uçağın alan kuvveti. Sonsuz yüklü bir düzlemin elektrik alan kuvvetini belirlemek için Gauss teoremini uygulayalım. Düzlem sonsuz ve düzgün yüklüyse, yani yüzey yük yoğunluğu herhangi bir yerde aynıysa, herhangi bir noktadaki elektrik alan şiddeti çizgileri bu düzleme diktir. Bunu göstermek amacıyla gerilim vektörü için süperpozisyon ilkesini kullanacağız. Düzlem üzerinde nokta için nokta sayılabilecek iki temel kesit seçelim. A Alan gücünü belirlemenin gerekli olduğu. Olarak Şekil l'de görülebilir. 1.18'de ortaya çıkan gerilim vektörü düzleme dik olarak yönlendirilecektir. Herhangi bir gözlem noktası için düzlem sonsuz sayıda bu tür bölüm çiftlerine bölünebildiğinden, yüklü düzlemin alan çizgilerinin düzleme dik olduğu ve alanın tekdüze olduğu açıktır (Şekil 1.19). Eğer böyle olmasaydı, uçak kendi etrafında hareket ettiğinde uzayın her noktasındaki alan değişirdi, ancak bu durum yüklü sistemin simetrisine aykırıdır (düzlem sonsuzdur). Pozitif yüklü bir düzlemde kuvvet çizgileri düzlemde başlar ve sonsuzda biter, negatif yüklü bir düzlemde ise kuvvet çizgileri sonsuzda başlar ve düzleme girer.

Pirinç. 1.18	Pirinç. 1.19

Sonsuz pozitif yüklü bir düzlemin elektrik alan kuvvetini belirlemek için, uzayda ekseni yüklü düzleme dik, tabanları ona paralel olan ve tabanlardan biri alan noktasından geçen bir silindiri zihinsel olarak seçiyoruz. bizi ilgilendiriyor (Şekil 1.19). Silindir, yüklü düzlemden bir alan keser ve düzlemin farklı taraflarında bulunan silindirin tabanları aynı alana sahiptir.

Gauss teoremine göre, elektrik alan kuvveti vektörünün silindir yüzeyinden akışı silindir içindeki elektrik yüküyle şu ifadeyle ilişkilidir:

.

Gerilme çizgileri silindirin yalnızca tabanlarını kestiği için silindirin yan yüzeyinden geçen akış sıfırdır. Bu nedenle, gerilim vektörünün silindirik yüzey boyunca akısı yalnızca silindirin tabanlarından geçen akılardan oluşacaktır, dolayısıyla,

Yoğunluk vektörü akısı için son iki ifadeyi karşılaştırarak şunu elde ederiz:

Zıt yüklü plakalar arasındaki elektrik alan kuvveti. Plakaların boyutları aralarındaki mesafeyi önemli ölçüde aşarsa, plakaların her birinin elektrik alanının, sonsuz, eşit yüklü bir düzlemin alanına yakın olduğu düşünülebilir. Plakalar arasındaki zıt yüklü plakaların elektrik alan kuvveti çizgileri bir yöne yönlendirildiğinden (Şekil 1.20), plakalar arasındaki alan kuvveti şuna eşittir:

.

Dış uzayda, zıt yüklü plakaların elektrik alan kuvveti çizgileri zıt yönlere sahiptir, dolayısıyla bu plakaların dışında ortaya çıkan elektrik alan kuvveti sıfırdır. Yoğunluk için elde edilen ifade, yoğunluk kenarlarından uzakta bulunan bir noktada belirlendiğinde büyük yüklü plakalar için geçerlidir.

Sonsuz uzunlukta, düzgün yüklü ince bir telin elektrik alan kuvveti. Gauss teoremini kullanarak, sonsuz uzunlukta, düzgün yüklü ince bir telin elektrik alan kuvvetinin tel eksenine olan mesafeye bağımlılığını bulalım. Sonlu uzunlukta bir tel kesiti seçelim. Tel üzerindeki doğrusal yük yoğunluğu ise seçilen alanın yüküne eşit olur.

Bir $q$ nokta yükünün alanını ele alalım ve yoğunluk vektörünün ($\overrightarrow(E)$) $S$ kapalı yüzeyinden akışını bulalım. Yükün yüzeyin içinde bulunduğunu varsayacağız. Gerilim vektörünün herhangi bir yüzey boyunca akısı, gerilim vektörünün dışarı çıkan çizgilerinin sayısına (eğer $q>0$ ise yükten başlayın) veya içeri giren $\overrightarrow(E)$ çizgilerinin sayısına eşittir. , if $q \[Ф_E=\frac( q)((\varepsilon )_0)\ \left(1\right),\]

akının işaretinin yükün işaretiyle çakıştığı yer.

İntegral formda Ostrogradsky-Gauss teoremi

S yüzeyinin içinde N nokta yükü olduğunu varsayalım, değerler $q_1,q_2,\dots q_N.$ Süperpozisyon ilkesinden, tüm N yükün ortaya çıkan alan kuvvetinin toplamı olarak bulunabileceğini biliyoruz. Yüklerin her biri tarafından oluşturulan alan güçleri, o zaman şunlar vardır:

Bu nedenle, noktasal ücret sisteminin akışı için şunu yazabiliriz:

Formül (1)'i kullanarak şunu elde ederiz:

\[Ф_E=\oint\limits_S(\overrightarrow(E)d\overrightarrow(S))=\frac(1)((\varepsilon )_0)\sum\limits^N_(i=1)(q_i\ )\ sol(4\sağ).\]

Denklem (4), elektrik alan kuvveti vektörünün kapalı bir yüzey boyunca akışının, bu yüzeyin içindeki yüklerin cebirsel toplamının elektrik sabitine bölünmesine eşit olduğu anlamına gelir. Bu Ostrogradsky-Gauss teoreminin integral formudur. Bu teorem Coulomb yasasının bir sonucudur. Bu teoremin önemi, çeşitli yük dağılımları için elektrik alanlarının oldukça basit bir şekilde hesaplanmasına olanak sağlamasıdır.

Ostrogradsky-Gauss teoreminin bir sonucu olarak, yüklerin bu yüzeyin dışında olması durumunda yoğunluk vektörünün ($Ф_E$) kapalı bir yüzeyden akısının sıfıra eşit olduğu söylenmelidir.

Yüklerin ayrıklığının göz ardı edilebildiği durumlarda, yükün hacim boyunca dağıldığı durumlarda hacimsel yük yoğunluğu ($\rho $) kavramı kullanılır. Şu şekilde tanımlanır:

\[\rho =\frac(dq)(dV)\left(5\right),\]

burada $dq$ nokta benzeri kabul edilebilecek bir ücrettir, $dV$ küçük bir hacimdir. ($dV$ ile ilgili olarak aşağıdaki açıklamanın yapılması gerekir. Bu hacim, içindeki yük yoğunluğunun sabit kabul edilebileceği kadar küçüktür, ancak yük ayrıklığının ortaya çıkmaya başlamayacağı kadar da büyüktür). Boşluktaki toplam yük şu şekilde bulunabilir:

\[\sum\limits^N_(i=1)(q_i\ )=\int\limits_V(\rho dV)\left(6\right).\]

Bu durumda formül (4)'ü şu şekilde yeniden yazıyoruz:

\[\oint\limits_S(\overrightarrow(E)d\overrightarrow(S))=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV)\left(7\right).\ ]

Diferansiyel formda Ostrogradsky-Gauss teoremi

Kapalı bir yüzey üzerinde entegrasyondan hacim üzerinde entegrasyona geçişin gerçekleştirildiği vektör niteliğindeki herhangi bir alan için Ostrogradsky-Gauss formülünün kullanılması:

\[\oint\limits_S(\overrightarrow(a)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(a)dV\ \left(8\right),\]

burada $\overrightarrow(a)-$field vektörü (bizim durumumuzda $\overrightarrow(E)$), $div\overrightarrow(a)=\overrightarrow(\nabla )\overrightarrow(a)=\frac(\ kısmi a_x)(\partial x)+\frac(\partial a_y)(\partial y)+\frac(\partial a_z)(\partial z)$ -- $\overrightarrow(a)$ vektörünün ıraksaması Bir vektör alanını skaler bir alanla eşleyen koordinatları ( x,y,z) olan nokta. $\overrightarrow(\nabla )=\frac(\partial )(\partial x)\overrightarrow(i)+\frac(\partial )(\partial y)\overrightarrow(j)+\frac(\partial )(\ kısmi z)\overrightarrow(k)$ - gözlemlenebilir operatör. (Bizim durumumuzda $div\overrightarrow(E)=\overrightarrow(\nabla )\overrightarrow(E)=\frac(\partial E_x)(\partial x)+\frac(\partial E_y)(\partial olacaktır) y) +\frac(\partial E_z)(\partial z)$) -- gerilim vektörünün ıraksaması. Yukarıdakileri takiben formül (6)'yı şu şekilde yeniden yazıyoruz:

\[\oint\limits_S(\overrightarrow(E)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(E)dV=\frac(1)((\varepsilon )_0)\int\limits_V( \rho dV)\left(9\right).\]

Denklem (9)'daki eşitlikler herhangi bir hacim için sağlanır ve bu ancak integrallerdeki fonksiyonların uzayın her akımında eşit olması durumunda mümkündür, yani şunu yazabiliriz:

İfade (10), diferansiyel formdaki Ostrogradsky-Gauss teoremidir. Yorumu şu şekildedir: yükler bir elektrik alanının kaynaklarıdır. Eğer $div\overrightarrow(E)>0$ ise, o zaman alanın bu noktalarında (yükler pozitiftir) alan kaynaklarımız vardır, eğer $div\overrightarrow(E)

Atama: Yük hacim boyunca düzgün olarak dağılmıştır; bu hacimde kenarı b olan kübik bir yüzey seçilmiştir. Kürenin içine yazılmıştır. Bu yüzeylerden geçen gerilim vektörü akılarının oranını bulun.

Gauss teoremine göre, $\overrightarrow(E)$ yoğunluk vektörünün hacim üzerinde düzgün yük dağılımına sahip kapalı bir yüzey boyunca akısı ($Ф_E$) şuna eşittir:

\[Ф_E=\frac(1)((\varepsilon )_0)Q=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV=\frac(\rho )((\varepsilon ) _0)\int\limits_V(dV)=\frac(\rho V)((\varepsilon )_0))\left(1.1\right).\]

Dolayısıyla top bu küpün etrafında anlatılıyorsa küpün ve topun hacimlerini belirlememiz gerekir. Başlangıç ​​olarak, b kenarı şuna eşitse küpün hacmi ($V_k$):

Aşağıdaki formülü kullanarak topun hacmini ($V_(sh)$) bulalım:

burada $D$ topun çapıdır ve (top küpün etrafında çevrelendiğinden) küpün ana köşegenidir. Bu nedenle bir küpün köşegenini kendi kenarı cinsinden ifade etmemiz gerekir. Pisagor teoremini kullanırsanız bunu yapmak kolaydır. Bir küpün köşegenini hesaplamak için örneğin (1.5), önce karenin köşegenini (küpün alt tabanını) (1.6) bulmamız gerekir. Köşegenin uzunluğu (1.6) şuna eşittir:

Bu durumda köşegenin uzunluğu (1,5) şuna eşittir:

\[(D=D)_(15)=\sqrt(b^2+((\sqrt(b^2+b^2\ \ \ )))^2)=b\sqrt(3)\ \left (1,5\sağ).\]

Bilyenin bulunan çapını (1.3) yerine koyarsak şunu elde ederiz:

Şimdi küpün yüzeyinden geçen gerilim vektörünün akılarını bulabiliriz, bu şuna eşittir:

\[Ф_(Ek)=\frac(\rho V_k)((\varepsilon )_0)=\frac(\rho b^3)((\varepsilon )_0)\left(1.7\right),\]

topun yüzeyinden:

\[Ф_(Esh)=\frac(\rho V_(sh))((\varepsilon )_0)=\frac(\rho )((\varepsilon )_0)\frac(\sqrt(3))(2) \pi b^3\ \left(1,8\right).\]

$\frac(Ф_(Esh))(Ф_(Ek))$ oranını bulalım:

\[\frac(Ф_(Esh))(Ф_(Ek))=\frac(\frac(с)(\varepsilon_0)\frac(\sqrt(3))(2) \pi b^3)(\frac (сb^3)(\varepsilon_0))=\frac(\pi)(2)\sqrt(3)\ \approx 2,7\left(1,9\right).\]

Cevap: Topun yüzeyinden geçen akı 2,7 kat daha fazladır.

Görev: Bir iletkenin yükünün yüzeyinde bulunduğunu kanıtlayın.

Bunu kanıtlamak için Gauss teoremini kullanıyoruz. İletkenin yüzeyine yakın, iletkende isteğe bağlı şekilde kapalı bir yüzey seçelim (Şekil 2).

İletkenin içinde yüklerin olduğunu varsayalım ve S yüzeyindeki herhangi bir nokta için alan sapması için Ostrogradsky-Gauss teoremini yazıyoruz:

burada $\rho iç yükün yoğunluğu\ $'dır. Ancak iletkenin içinde herhangi bir alan yoktur, yani $\overrightarrow(E)=0$, dolayısıyla $div\overrightarrow(E)=0\to \rho =0$ olur. Diferansiyel formdaki Ostrogradsky-Gauss teoremi yereldir, yani bir alan noktası için yazılmıştır, noktayı özel bir şekilde seçmedik, dolayısıyla iletken içindeki alanın herhangi bir noktasında yük yoğunluğu sıfırdır.

Coulomb yasasıyla birlikte süperpozisyon ilkesi, rastgele bir yük sisteminin elektrik alanını hesaplamanın anahtarını sağlar, ancak alanların formül (4.2) kullanılarak doğrudan toplanması genellikle karmaşık hesaplamalar gerektirir. Bununla birlikte, yük sisteminin belirli bir simetrisinin varlığında, elektrik alanı akışı kavramını tanıtıp Gauss teoremini kullanırsak hesaplamalar önemli ölçüde basitleştirilir.

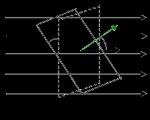
Elektrik alan akışı kavramı, hidrodinamikten elektrodinamiğe tanıtıldı. Hidrodinamikte, bir borudan geçen akışkanın akışı, yani birim zamanda bir borunun kesitinden geçen akışkanın N hacmi v ⋅ S'ye eşittir; burada v akışkanın hızıdır ve S ise borunun kesit alanı. Sıvının hızı kesit boyunca değişiyorsa, N = ∫ S v → ⋅ d S → integral formülünü kullanmanız gerekir. Aslında, hız alanında hız vektörüne dik olan küçük bir dS alanını vurgulayalım (Şekil ).

Pirinç. 1.4: Sıvı akışı

Bu alandan d t zamanında akan sıvının hacmi v d S d t'ye eşittir. Platform akışa eğimliyse, karşılık gelen hacim v d S cos θ d t olacaktır; burada θ, hız vektörü v → ile normal n → platforma d S arasındaki açıdır. Birim zamanda d S alanından akan sıvının hacmi, bu değerin d t'ye bölünmesiyle elde edilir. v d S çünkü θ d t'ye eşittir, yani. skaler çarpım v → ⋅ d S → hız vektörü v → alan eleman vektörüne göre d S → = n → d S . d S alanına normal olan birim vektör n → iki zıt yönde çizilebilir. bunlardan biri şartlı olarak olumlu kabul edilir. Normal n → bu yönde çizilir. Normal n →'nin çıktığı bölgeye dış, normal n →'nin girdiği tarafa ise iç denir. Alan elemanı vektörü d S → dış normal n → boyunca yüzeye yönlendirilir ve büyüklük olarak d S = ∣ d S → ∣ elemanının alanına eşittir. Sonlu boyutlu bir S alanından akan sıvının hacmi hesaplanırken, bunun sonsuz küçük alanlara d S dönüştürülmesi ve ardından tüm S yüzeyi boyunca ∫ S v → ⋅ d S → integralinin hesaplanması gerekir.

∫ S v → ⋅ d S → gibi ifadelere fizik ve matematiğin birçok dalında rastlanır. Bunlar, v → vektörünün doğasından bağımsız olarak, v → vektörünün S yüzeyi boyunca akışı olarak adlandırılır. Elektrodinamikte integral

N = ∫ S E → ⋅ d S →

(5.1)

Bu kavramla hiçbir gerçek akış ilişkilendirilmese de, elektrik alan kuvveti E → rastgele bir S yüzeyi boyunca akışı olarak adlandırılır.

E → vektörünün geometrik bir toplamla temsil edildiğini varsayalım.

E → = ∑ j E → j .

Bu eşitliği d S → ile skaler olarak çarpar ve entegre edersek şunu elde ederiz:

N = ∑j Nj .

burada Nj, E → j vektörünün aynı yüzeyden akışıdır. Böylece, elektrik alan kuvvetinin üst üste binmesi ilkesinden, aynı yüzeyden geçen akıların cebirsel olarak toplandığı sonucu çıkar.

Gauss teoremi, E → vektörünün keyfi bir kapalı yüzey boyunca akısının, bu yüzeyin içinde bulunan tüm parçacıkların toplam Q yükünün 4 π ile çarpımına eşit olduğunu belirtir:

Teoremin ispatını üç aşamada gerçekleştireceğiz.

1. Bir nokta yükü q'nun elektrik alan akısını hesaplayarak başlayalım (Şekil ). En basit durumda, S integrasyon yüzeyi bir küre olduğunda ve yük merkezde olduğunda, Gauss teoreminin geçerliliği neredeyse açıktır. Kürenin yüzeyinde elektrik alan kuvveti

E → = q r → ∕ r 3

büyüklüğü sabittir ve her yerde yüzeye normal olarak yönlendirilir, böylece elektrik alan akısı basitçe E = q ∕ r 2 çarpımına ve S = 4 π r 2 küresinin alanına eşittir. Bu nedenle N = 4 π q. Bu sonuç, yükü çevreleyen yüzeyin şeklinden bağımsızdır. Bunu kanıtlamak için, üzerinde ayarlanan dış normal n → yönü ile yeterince küçük boyutlu yüzeyin keyfi bir alanını seçiyoruz. İncirde. böyle bir bölüm abartılı derecede büyük (netlik sağlamak için) bir boyutta gösterilmiştir.

E → vektörünün bu alandan akışı şuna eşittir: d N = E → ⋅ d S → = E çünkü θ d S ,

burada θ, E → yönü ile dış normal n → arasındaki d S alanına olan açıdır. E = q ∕ r 2 ve d S cos θ ∕ ​​r 2 mutlak değerde olduğundan, altında d S alanının görülebildiği katı açı d Ω = d S ∣ cos θ ∣ ∕ r 2'nin elemanıdır. Yükün bulunduğu nokta,

D N = ± q d Ω .

artı ve eksi işaretleri cos θ işaretine karşılık gelir, yani: E → vektörü dış normal n → yönü ile dar bir açı yapıyorsa artı işaretini, aksi takdirde eksi işaretini almalısınız.

2. Şimdi seçilen V hacmini kaplayan sonlu bir S yüzeyini düşünün. Bu hacme ilişkin olarak, S yüzeyinin herhangi bir elemanına normalin iki zıt yönünden hangisinin dış olarak kabul edilmesi gerektiğini belirlemek her zaman mümkündür. Dış normal V hacminden dışarıya doğru yönlendirilir. Segmentleri özetlersek, işarete kadar N = q Ω elde ederiz; burada Ω, S yüzeyinin q yükünün bulunduğu noktadan görülebildiği katı açıdır. S yüzeyi kapalıysa, q yükünün S'nin içinde olması koşuluyla Ω = 4 π olur. Aksi takdirde Ω = 0. Son ifadeyi açıklığa kavuşturmak için tekrar Şekil 2'ye başvurabiliriz. .

Kapalı bir yüzeyin eşit katı açılara dayanan ancak zıt yönlere bakan bölümlerinden geçen akışların birbirini iptal ettiği açıktır. Ayrıca, eğer yük kapalı yüzeyin dışındaysa, o zaman dışarıya bakan herhangi bir bölüm için içe bakan bir karşılık gelen bölüm olduğu da açıktır.

3. Son olarak süperpozisyon ilkesini kullanarak Gauss teoreminin () son formülasyonuna ulaşıyoruz. Gerçekten de, bir yük sisteminin alanı, her bir yükün ayrı ayrı alanlarının toplamına eşittir, ancak yalnızca kapalı yüzeyin içinde yer alan yükler, teoremin () sağ tarafına sıfırdan farklı bir katkı sağlar. Bu ispatı tamamlar.

Makroskobik cisimlerde, yük taşıyıcılarının sayısı o kadar büyüktür ki, yük yoğunluğu kavramını ortaya koyan ayrı bir parçacık topluluğunu sürekli bir dağılım biçiminde temsil etmek uygundur. Tanım gereği, yük yoğunluğu ρ, hacim Δ V'nin fiziksel olarak sonsuz küçük bir değere yöneldiği limitteki Δ Q ∕ Δ V oranıdır:

burada sağ taraftaki entegrasyon S yüzeyi tarafından kapatılan V hacmi üzerinde gerçekleştirilir.

Gauss teoremi E → vektörünün üç bileşeni için bir skaler denklem verir, dolayısıyla bu teorem tek başına elektrik alanını hesaplamak için yeterli değildir. Sorunun tek bir skaler denkleme indirgenebilmesi için yük yoğunluğu dağılımının bilinen bir simetrisi gereklidir. Gauss teoremi, ()'deki entegrasyon yüzeyinin, elektrik alan kuvveti E'nin tüm yüzey üzerinde sabit olacağı şekilde seçilebildiği durumlarda alanı bulmayı mümkün kılar. En öğretici örneklere bakalım.

▸ Sorun 5.1

Hacim olarak eşit yüklü bir kürenin alanını bulun veya yüzeyler.

Çözüm: Bir nokta yükünün elektrik alanı E → = q r → ∕ r 3 şuna eğilimlidir: sonsuzluk r → 0 . Bu gerçek, fikrin tutarsızlığını göstermektedir. nokta yüklere göre temel parçacıklar. Eğer şarj Q sonlu yarıçaplı bir kürenin hacmi üzerinde eşit olarak dağılmış o zaman elektrik alanının tekilliği yoktur.

Problemin simetrisinden elektrik alanın olduğu açıktır. E → her yer radyal olarak yönlendirilir ve gerilimi E = E(r) yalnızca r mesafesine bağlıdır topun merkezine. Daha sonra elektrik alanı yarıçaplı bir küre boyunca akar r basitçe 4 π r 2 E'ye eşittir (Şek. ).

Öte yandan aynı kürenin içindeki yük toplam yüke eşittir. r ≥ a ise Q topu. 4 π r 2 E'yi topun q yüküne 4 π ile eşitleyerek şunu elde ederiz: E (r) = q ∕ r 2 .

Böylece dış uzayda yüklü bir top oluşur öyle bir alan ki sanki tüm yük merkezde toplanmış gibi. Bu sonuç herhangi bir küresel simetrik durum için geçerlidir. şarj dağıtımı.

Topun içindeki alan E (r) = Q ∕ r 2, burada Q, r yarıçaplı kükürt içindeki yüktür. Yük topun hacmi boyunca eşit olarak dağılmışsa, o zaman S = q (r ∕ a) 3 . Bu durumda

E (r) = q r ∕ a 3 = (4 π ∕ 3) ρ r ,

burada ρ = q ∕ (4 π a 3 ∕ 3) — yük yoğunluğu. Topun içinde alan maksimumdan doğrusal olarak azalır Topun yüzeyindeki değerlerin merkezinde sıfıra kadar (Şek. ).

Fonksiyon E(r) aynı zamanda her yerde sonlu ve süreklidir.

Yük topun yüzeyine dağılmışsa, o zaman Q = 0 ve dolayısıyla E = 0 da. Bu sonuç aynı zamanda küresel bir kürenin içinde olduğu durum için de geçerlidir. yük boşluğu yoktur ve dış yükler küresel olarak dağıtılır simetrik olarak. ▸ Sorun 5.2

Düzgün yüklü sonsuz bir ipliğin alanını bulun; iplik yarıçapı a, birim uzunluk başına yük ϰ.

▸ Sorun 5.3

Sonsuz düz bir ipliğin ve sonsuz uzunluğa sahip bir ipliğin alanını bulun. düzgün yüklü silindir.

▸ Sorun 5.4

Sonsuz yüklü bir düzlemin alanını bulun ve düzgün bir şekilde yüklü sonsuz düz katman.

Çözüm: Problemin simetrisinden dolayı alan yönlendirilir katmana normaldir ve yalnızca mesafeye bağlıdır x'den Plakanın simetri düzlemi. Bir alanı hesaplamak için Gauss teoremi, entegrasyon yüzeyini seçmek uygundur Günah Şekil 2'de gösterildiği gibi paralel boru şeklinde. .

Limite geçilerek son sonuç elde edilir. bir → 0 aynı anda yük yoğunluğunu arttırırkenρ değeri σ = ρ a olacak şekilde değişmeden kaldı. Uçağın karşıt taraflarında elektrik alan kuvveti büyüklük olarak aynıdır, ancak ters yönde. Bu nedenle geçerken yüklü düzlemde alan miktarı kadar aniden değişir 4 π σ . Aşağıdaki durumlarda plakanın sonsuz kabul edilebileceğini unutmayın: boyutuyla karşılaştırıldığında mesafe ihmal edilebilir. Açık mesafeler plakanın boyutlarına göre çok büyük olduğundan noktasal yük gibi davranır ve alanı geriye doğru azalır uzaklığın karesiyle orantılıdır.

Elektrostatik alan, kuvvet çizgileri (gerilme çizgileri) kullanılarak açıkça gösterilebilir. Güç hatları her noktada teğetleri gerilim vektörü E ile çakışan eğrilere eğriler denir.

Kuvvet çizgileri geleneksel bir kavramdır ve gerçekte mevcut değildir. Tek bir negatif ve tek pozitif yükün alan çizgileri Şekil 2'de gösterilmektedir. 5, pozitif bir yükten gelen veya negatif bir yüke giden radyal düz çizgilerdir.

Alanın tüm hacmi boyunca alan çizgilerinin yoğunluğu ve yönü değişmeden kalırsa, böyle bir elektrostatik alanın homojen olduğu kabul edilir (çizgi sayısı sayısal olarak alan kuvveti E'ye eşit olmalıdır).

Onlara dik ">dS" olarak işaretlenen alan çizgilerinin sayısı şunları belirler: elektrostatik alan kuvveti vektörünün akışı:

formül" src = "http://hi-edu.ru/e-books/xbook785/files/17-1.gif" border = "0" align = "absmiddle" alt = "(! LANG:- E vektörünün normal n yönüne dS bölgesine izdüşümü (Şekil 6).

Buna göre, E vektörünün keyfi bir kapalı S yüzeyinden akışı

mark">S akışının yalnızca büyüklüğü değil, işareti de değişebilir:

1)" src="http://hi-edu.ru/e-books/xbook785/files/17-4.gif" border="0" align="absmiddle" alt=" formülüyle)

3)"> seçeneğini seçerken, merkezinde q nokta yükünün bulunduğu küresel bir S yüzeyi boyunca E vektörünün akışını bulalım.

Bu durumda ">E ve n işareti küresel yüzeyin tüm noktalarında çakışmaktadır.

Noktasal yükün alan gücü dikkate alındığında," src="http://hi-edu.ru/e-books/xbook785/files/18-2.gif" border="0" align=absmiddle formülü " alt = "(! LANG:aldık

formül" src = "http://hi-edu.ru/e-books/xbook785/files/Fe.gif" border = "0" align = "absmiddle" alt = "(! LANG:- yükün işaretine bağlı olarak cebirsel bir miktar. Örneğin, ne zaman q<0 линии Е направлены к заряду и противоположны направлению внешней нормали n ..gif" border="0" align="absmiddle" alt="q yükünün etrafında keyfi bir şekil vardır. Açıkçası, yüzey de S yüzeyi gibi ">E olarak işaretlenmiştir. Bu nedenle, E vektörünün rastgele bir yüzeyden akışı" src="http://hi-edu.ru/e-books/xbook785/ formülüdür. files/Fe.gif" border ="0" align="absmiddle" alt=".

Yük kapalı yüzeyin dışında bulunuyorsa, o zaman belli ki kapalı alana kaç hat girecek, aynı sayı oradan ayrılacaktır. Sonuç olarak, E vektörünün akısı sıfıra eşit olacaktır.

Elektrik alanı bir nokta yük sistemi tarafından yaratılıyorsa formül" src = "http://hi-edu.ru/e-books/xbook785/files/18-4.gif" border = "0" align = "absmiddle" alt = "(! LANG:

Bu formül Gauss teoreminin matematiksel ifadesidir: elektrik alanı kuvvet vektörü E'nin vakumda rastgele kapalı bir yüzey boyunca akışı, kapladığı yüklerin cebirsel toplamına bölünerek eşittir formül" src = "http://hi-edu.ru/e-books/xbook785/files/18-6.gif" border = "0" align = "absmiddle" alt = "(! LANG:

Açıklamayı tamamlamak için Gauss teoremini integral ilişkilere değil, uzayda belirli bir noktadaki alan parametrelerine dayanarak yerel bir biçimde sunalım. Bunu yapmak için diferansiyel operatörü - vektör diverjansını, - kullanmak uygundur.

formül" src = "http://hi-edu.ru/e-books/xbook785/files/nabla.gif" border = "0" align = "absmiddle" alt = "(! LANG:(“nabla”) -

formül" src = "http://hi-edu.ru/e-books/xbook785/files/19-1.gif" border = "0" align = "absmiddle" alt = "(! LANG:

Matematiksel analizde Gauss-Ostrogradsky teoremi bilinmektedir: bir vektörün kapalı bir yüzeyden akışı, bu yüzeyle sınırlı hacim üzerindeki diverjansının integraline eşittir -

formül" src = "http://hi-edu.ru/e-books/xbook785/files/ro.gif" border = "0" align = "absmiddle" alt = "(! LANG::

formül" src = "http://hi-edu.ru/e-books/xbook785/files/19-4.gif" border = "0" align = "absmiddle" alt = "(! LANG:

Bu ifade Gauss'un yerel (diferansiyel) formdaki teoremidir.

Gauss teoremi (2.2), çeşitli elektrostatik alanların kuvvetlerini belirlememize olanak tanır. Gauss teoreminin uygulanmasına ilişkin birkaç örneğe bakalım.

1. Hesaplayalım E düzgün yüklü küresel bir yüzey tarafından oluşturulan elektrostatik alan.

R yarıçaplı küresel bir yüzeyin düzgün dağılmış bir q yükünü taşıdığını varsayalım; yüzey yük yoğunluğu kürenin merkezinden itibaren ">r >R her yerde aynı işarete sahipse, zihinsel olarak yüklü küreye simetrik yeni bir küresel S yüzeyi inşa ederiz. Gauss teoremine uygun olarak

formül" src = "http://hi-edu.ru/e-books/xbook785/files/20-1.gif" border = "0" align = "absmiddle" alt = "(! LANG:

R yarıçaplı yüklü bir kürenin yüzeyinde bulunan noktalar için benzetme yoluyla şunu yazabiliriz:

Yüklü bir kürenin içindeki "seçim">, kendi içinde elektrik yükleri içermez, dolayısıyla akı işareti">E = 0.

Elektrostatik alanların üst üste binmesi ilkesini kullanarak bir elektrik yükleri sisteminin alan gücünü hesaplama görevi, Alman bilim adamı K. Gauss (1777-1855) tarafından keşfedilen ve yükün akışını belirleyen teoremi uygularsak büyük ölçüde basitleştirilebilir. keyfi bir kapalı yüzey boyunca elektrik alan kuvveti vektörü.

Kapalı bir yüzey boyunca yoğunluk vektörü akısının tanımından, merkezinde bulunan bir Q nokta yükünü kapsayan r yarıçaplı küresel bir yüzey boyunca yoğunluk vektörü akısı (Şekil 1) şuna eşittir:

Bu sonuç keyfi şekle sahip kapalı bir yüzey için geçerlidir. Aslında, eğer bir küreyi (Şekil 1) isteğe bağlı olarak kapalı bir yüzeye kapatırsanız, o zaman küreye giren her gerilim çizgisi de bu yüzeyden geçecektir.

Herhangi bir şekle sahip kapalı bir yüzey bir yükü çevreliyorsa (Şekil 2), o zaman herhangi bir gerilim çizgisi yüzeyle kesiştiğinde, ya ona girer ya da çıkar. Akıyı hesaplarken, tek sayıdaki kesişmeler sonuçta tek bir kesişim noktasına indirgenir, çünkü gerilim çizgileri yüzeyden ayrılırsa akının pozitif, yüzeye giren çizgiler için ise negatif olduğu varsayılır. o zaman içinden geçen akı sıfırdır, yani yüzeye giren gerilim çizgilerinin sayısı, oradan çıkan gerilim çizgilerinin sayısına nasıl eşit olur.

Bu, keyfi bir şekle sahip bir yüzey için, kapalıysa ve bir Q nokta yükü içeriyorsa, vektörün akışının olduğu anlamına gelir. e Q/ε 0'a eşit olacaktır, yani.

Akının işareti Q yükünün işaretiyle çakışmaktadır.

n yükü çevreleyen rastgele bir yüzeyin genel durumunu inceleyelim. Süperpozisyon ilkesini kullanarak gerilim e Tüm yüklerin oluşturduğu alan, yoğunlukların toplamına eşittir. E ben Her ücretin ayrı ayrı oluşturduğu alanlar. Bu yüzden

(1)'e göre toplam işareti altında görünen integrallerin her biri Q i /ε 0'a eşittir. Araç,

(2)

Formül (2) ifade eder Vakumdaki elektrostatik alan için Gauss teoremi: Elektrostatik alan kuvveti vektörünün vakumda rastgele kapalı bir yüzey boyunca akışı, bu yüzeyin içinde bulunan yüklerin cebirsel toplamının ε 0'a bölünmesine eşittir. Bu teorem, Rus matematikçi M.V. Ostrogradsky (1801-1862) tarafından keyfi nitelikteki bir vektör alanı için matematiksel olarak ve daha sonra elektrostatik alanla ilgili olarak ondan bağımsız olarak K. Gauss tarafından elde edildi.

Genel durumda, elektrik yükleri uzayın farklı yerlerinde farklı olan belirli bir hacim yoğunluğu olan ρ=dQ/dV ile dağıtılabilir. Daha sonra belirli bir V hacmini kaplayan kapalı S yüzeyinin içindeki toplam yük,

(3)

Formül (3) kullanılarak Gauss teoremi (2) şu şekilde yazılabilir:

Gerilim vektörünün dolaşımı, tek bir pozitif yükü kapalı bir L yolu boyunca hareket ettirirken elektrik kuvvetleri tarafından yapılan iştir.

(13.18)

Kapalı bir döngü boyunca elektrostatik alan kuvvetlerinin işi sıfır olduğundan (potansiyel alan kuvvetlerinin işi), dolayısıyla kapalı bir döngü boyunca elektrostatik alan kuvvetinin dolaşımı sıfırdır.

Elektrostatik alan potansiyeli. Korunumlu bir kuvvetin alanı yalnızca bir vektör fonksiyonuyla tanımlanamaz, aynı zamanda bu alanın eşdeğer bir açıklaması, her bir noktasında uygun bir skaler büyüklük tanımlanarak elde edilebilir. Elektrostatik bir alan için bu miktar elektrostatik alan potansiyeli test yükünün potansiyel enerjisinin oranı olarak tanımlanır Q bu yükün büyüklüğüne göre,  = W P / Q Buradan potansiyelin, alanda belirli bir noktada birim pozitif yükün sahip olduğu potansiyel enerjiye sayısal olarak eşit olduğu sonucu çıkar. Potansiyelin ölçüm birimi Volt'tur (1 V).

Nokta yük alanı potansiyeli Q dielektrik sabiti  olan homojen izotropik bir ortamda:

Üstüste binme ilkesi. Potansiyel skaler bir fonksiyondur, süperpozisyon prensibi onun için geçerlidir. Yani bir nokta yük sisteminin alan potansiyeli için Q 1, Q 2, Qn sahibiz

,

Nerede ri- potansiyel  olan alan noktasından yüke olan mesafe Qi. Yük uzayda keyfi olarak dağıtılıyorsa, o zaman

,

Nerede R- temel hacim d'den uzaklık X,D sen,D z işaret etmek ( X, sen, z), potansiyelin belirlendiği yer; V- yükün dağıtıldığı alanın hacmi.

Elektrik alan kuvvetlerinin potansiyeli ve işi. Potansiyelin tanımına dayanarak, bir nokta yükü hareket ettirirken elektrik alan kuvvetlerinin yaptığı işin olduğu gösterilebilir. Q alanın bir noktasından diğerine bu yükün büyüklüğü ile yolun başlangıç ​​ve son noktalarındaki potansiyel farkın çarpımına eşittir, bir = q (     
Potansiyel enerjiye benzeterek, elektrik yüklerinden - alan kaynaklarından sonsuz derecede uzak noktalarda potansiyelin sıfır olduğunu varsayarsak, o zaman bir yükü hareket ettirirken elektrik alan kuvvetlerinin işi Q 1 noktasından sonsuza kadar şu şekilde temsil edilebilir: A   Q  1 .
Böylece, elektrostatik alanın belirli bir noktasındaki potansiyel Bir birim pozitif nokta yükünü alandaki belirli bir noktadan sonsuz uzaklığa hareket ettirirken elektrik alan kuvvetlerinin yaptığı işe sayısal olarak eşit fiziksel miktar:  = A  / Q.
Bazı durumlarda, elektrik alan potansiyeli daha açık bir şekilde şu şekilde tanımlanır: Bir birim pozitif nokta yükünü sonsuzdan belirli bir noktaya hareket ettirirken, dış kuvvetlerin elektrik alanı kuvvetlerine karşı çalışmasına sayısal olarak eşit bir fiziksel miktar. Son tanımı şu şekilde yazmak uygundur:

Modern bilim ve teknolojide, özellikle mikrokozmosta meydana gelen olayları tanımlarken, bir iş ve enerji birimine denir. elektron-volt(eV). Bu, potansiyel farkı 1 V olan iki nokta arasında bir elektronun yüküne eşit bir yükü hareket ettirirken yapılan iştir: 1 eV = 1.6010  C1 V = 1.6010  J

Eş potansiyel yüzeyler- Statik elektrik alanı veya Newton yerçekimi alanı gibi herhangi bir potansiyel vektör alanına uygulanabilen bir kavram. Eşpotansiyel yüzey, belirli bir potansiyel alanın skaler potansiyelinin sabit bir değer aldığı bir yüzeydir (potansiyel seviye yüzeyi). Başka bir eşdeğer tanım, herhangi bir noktada alan çizgilerine dik olan bir yüzeydir.

Elektrostatikte bir iletkenin yüzeyi eş potansiyel bir yüzeydir. Ayrıca eşpotansiyelli bir yüzeye iletken yerleştirmek elektrostatik alanın konfigürasyonunu değiştirmez. Bu gerçek, karmaşık konfigürasyonlar için elektrostatik alanın hesaplanmasına olanak sağlayan görüntü yönteminde kullanılır.

(Sabit) bir yerçekimi alanında, eş potansiyel yüzey boyunca sabit bir sıvının seviyesi belirlenir. Özellikle okyanusların seviyesinin Dünya'nın çekim alanının eşpotansiyel yüzeyi boyunca geçtiği yaklaşık olarak ifade edilebilir. Okyanusların Dünya yüzeyine kadar uzanan yüzeyinin şekline jeoid denir ve jeodezide önemli rol oynar. Jeoid bu nedenle yerçekimi ve merkezkaç bileşeninden oluşan eşpotansiyel bir yerçekimi yüzeyidir.