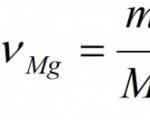Where do the altitudes of a triangle intersect? Everything you need to know about the triangle
Right Triangle Altitude Theorem
If the altitude in a right triangle ABC of length , drawn from the vertex of the right angle, divides the hypotenuse of length and into segments and corresponding to the legs and , then the following equalities are true:
· ![]()
· ![]()
Properties of the bases of altitudes of a triangle
· Reasons heights form a so-called orthotriangle, which has its own properties.
· The circle circumscribed about an orthotriangle is the Euler circle. This circle also contains three midpoints of the sides of the triangle and three midpoints of three segments connecting the orthocenter with the vertices of the triangle.
Another formulation of the last property:
· Euler's theorem for the nine-point circle.
Reasons three heights arbitrary triangle, the midpoints of its three sides ( the foundations of its internal medians) and the midpoints of three segments connecting its vertices with the orthocenter, all lie on the same circle (on nine point circle).
· Theorem. In any triangle, the segment connecting grounds two heights triangle, cuts off a triangle similar to the given one.
· Theorem. In a triangle, the segment connecting grounds two heights triangles lying on two sides antiparallel to a third party with whom he has no common ground. A circle can always be drawn through its two ends, as well as through the two vertices of the third mentioned side.
Other properties of triangle altitudes
· If the triangle versatile (scalene), then it internal the bisector drawn from any vertex lies between internal median and height drawn from the same vertex.
The height of a triangle is isogonally conjugate to the diameter (radius) circumcircle, drawn from the same vertex.
· In an acute triangle there are two heights cut off similar triangles from it.
· In a right triangle height drawn from the vertex of a right angle, splits it into two triangles similar to the original one.
Properties of the minimum altitude of a triangle
The minimum altitude of a triangle has many extreme properties. For example:
· The minimum orthogonal projection of a triangle onto lines lying in the plane of the triangle has a length equal to the smallest of its altitudes.
· The minimum straight cut in the plane through which a rigid triangular plate can be pulled must have a length equal to the smallest of the heights of this plate.
· When two points move continuously along the perimeter of a triangle towards each other, the maximum distance between them during the movement from the first meeting to the second cannot be less than the length of the smallest height of the triangle.
· The minimum height in a triangle always lies inside that triangle.
Basic relationships
·  where is the area of the triangle, is the length of the side of the triangle by which the height is lowered.
where is the area of the triangle, is the length of the side of the triangle by which the height is lowered.
·  where is the product of the sides, the radius of the circumscribed circle
where is the product of the sides, the radius of the circumscribed circle
·  ,
,
where is the radius of the inscribed circle.
Where is the area of the triangle.
where is the side of the triangle to which the height descends.
· Height of an isosceles triangle lowered to the base:

where is the base.
·  - height in an equilateral triangle.
- height in an equilateral triangle.
Medians and altitudes in an equilateral triangle
The medians of a triangle intersect at one point, which divides each of them in a ratio of 2:1, counting from the vertex. This point is called center of gravity triangle. And in equilateral triangles, medians and altitudes are the same thing.

Consider an arbitrary triangle ABC. Let us denote by the letter O the point of intersection of its medians AA1 and BB1 and draw the midline A1B1 of this triangle. The medians of the triangle intersect at one point. The segment A1B1 is parallel to side AB, therefore angles 1 and 2, as well as angles 3 and 4 are equal as crosswise angles at the intersection of parallel lines AB and A1B1 by secants AA1 and BB1. Therefore, triangles AOB and A1OB1 are similar in two angles, and therefore their sides are proportional: AOA1O=BOB1O=ABA1B1. But AB=2⋅A1B1, so AO=2⋅A1O and BO=2⋅B1O. Thus, the intersection point O of the medians AA1 and BB1 divides each of them in a ratio of 2:1, counting from the vertex. Similarly, it is proved that the point of intersection of the medians BB1 and CC1 divides each of them in the ratio 2:1 counting from the vertex, and therefore coincides with the point O. Thus, all three medians of the triangle ABC intersect at the point O and are divided by it in the ratio 2: 1, counting from the top.
The theorem has been proven.

Let's imagine that at the vertices of the angle m₁=1, then at points A₁,B₁,C₁, m₂=2, since they are the midpoints of the sides. And here you can notice that the segments AA₁,BB₁,CC₁, which intersect at one point, are similar to levers with a fulcrum O, where AO-l₁, and OA₁-l₂ (shoulders). And according to the physical formula F₁/F₂=l₁/l₂, where F=m*g, where g-const, and it is reduced accordingly, it turns out m₁/m₂=l₁/l₂ i.e. ½=1/2.
The theorem has been proven.
Orthotriangle
Properties:
· Three altitudes of a triangle intersect at one point, this point is called the orthocenter
· Two adjacent sides of an orthotriangle form equal angles with the corresponding side of the original triangle
The altitudes of a triangle are the bisectors of an orthotriangle
· An orthotriangle is the triangle with the smallest perimeter that can be inscribed within a given triangle (Fagnano problem)
· The perimeter of an orthotriangle is equal to twice the product of the height of the triangle and the sine of the angle from which it originates.
· If points A 1 , B 1 and C 1 on sides BC, AC and AB of acute triangle ABC, respectively, are such that
then is an orthotriangle of triangle ABC.
Orthotriangle cuts off triangles similar to this one

Theorem on the property of bisectors of an orthotriangle

∟ B₁C₁C=∟B₁BC=∟CAA₁=∟CC₁A
CC₁-bisector ∟B₁C₁A
AA₁-bisector ∟B₁A₁C₁
BB₁-bisector ∟A₁B₁C₁
A triangle is a polygon with three sides, or a closed broken line with three links, or a figure formed by three segments connecting three points that do not lie on the same straight line (see Fig. 1).
Basic elements of triangle abc
Peaks – points A, B, and C;
Parties – segments a = BC, b = AC and c = AB connecting the vertices;
Angles – α, β, γ formed by three pairs of sides. Angles are often designated in the same way as vertices, with the letters A, B, and C.
The angle formed by the sides of a triangle and lying in its interior area is called an interior angle, and the one adjacent to it is the adjacent angle of the triangle (2, p. 534).
Heights, medians, bisectors and midlines of a triangle
In addition to the main elements in a triangle, other segments with interesting properties are also considered: heights, medians, bisectors and midlines.
Height
Triangle heights- these are perpendiculars dropped from the vertices of the triangle to opposite sides.
To plot the height, you must perform the following steps:
1) draw a straight line containing one of the sides of the triangle (if the height is drawn from the vertex of an acute angle in an obtuse triangle);
2) from the vertex lying opposite the drawn line, draw a segment from the point to this line, making an angle of 90 degrees with it.


The point where the altitude intersects the side of the triangle is called height base (see Fig. 2).
Properties of triangle altitudes
In a right triangle, the altitude drawn from the vertex of the right angle splits it into two triangles similar to the original triangle.
In an acute triangle, its two altitudes cut off similar triangles from it.
If the triangle is acute, then all the bases of the altitudes belong to the sides of the triangle, and in an obtuse triangle, two altitudes fall on the continuation of the sides.
Three altitudes in an acute triangle intersect at one point and this point is called orthocenter triangle.
Median
Medians(from Latin mediana – “middle”) - these are segments connecting the vertices of the triangle with the midpoints of the opposite sides (see Fig. 3).
To construct the median, you must perform the following steps:
1) find the middle of the side;
2) connect the point that is the middle of the side of the triangle with the opposite vertex with a segment.

Properties of triangle medians
The median divides a triangle into two triangles of equal area.
The medians of a triangle intersect at one point, which divides each of them in a ratio of 2:1, counting from the vertex. This point is called center of gravity triangle.
The entire triangle is divided by its medians into six equal triangles.
Bisector
Bisectors(from Latin bis - twice and seko - cut) are the straight line segments enclosed inside a triangle that bisect its angles (see Fig. 4).
To construct a bisector, you must perform the following steps:
1) construct a ray coming out from the vertex of the angle and dividing it into two equal parts (the bisector of the angle);
2) find the point of intersection of the bisector of the angle of the triangle with the opposite side;
3) select a segment connecting the vertex of the triangle with the intersection point on the opposite side.
Properties of triangle bisectors
The bisector of an angle of a triangle divides the opposite side in a ratio equal to the ratio of the two adjacent sides.
The bisectors of the interior angles of a triangle intersect at one point. This point is called the center of the inscribed circle.
The bisectors of the internal and external angles are perpendicular.
If the bisector of an exterior angle of a triangle intersects the extension of the opposite side, then ADBD=ACBC.
The bisectors of one internal and two external angles of a triangle intersect at one point. This point is the center of one of the three excircles of this triangle.
The bases of the bisectors of two internal and one external angles of a triangle lie on the same straight line if the bisector of the external angle is not parallel to the opposite side of the triangle.
If the bisectors of the external angles of a triangle are not parallel to opposite sides, then their bases lie on the same straight line.
When solving various kinds of problems, both of a purely mathematical and applied nature (especially in construction), it is often necessary to determine the value of the height of a certain geometric figure. How to calculate this value (height) in a triangle?
If we combine 3 points in pairs that are not located on a single line, then the resulting figure will be a triangle. Height is the part of a straight line from any vertex of a figure that, when intersecting with the opposite side, forms an angle of 90°.
Find the height of a scalene triangle
Let us determine the value of the height of a triangle in the case when the figure has arbitrary angles and sides.
Heron's formula
h(a)=(2√(p(p-a)*(p-b)*(p-c)))/a, where
p – half the perimeter of the figure, h(a) – a segment to side a, drawn at right angles to it,
p=(a+b+c)/2 – calculation of the semi-perimeter.
If there is an area of the figure, you can use the relation h(a)=2S/a to determine its height.
Trigonometric functions
To determine the length of a segment that makes a right angle when intersecting with side a, you can use the following relations: if side b and angle γ or side c and angle β are known, then h(a)=b*sinγ or h(a)=c *sinβ.
Where:
γ – angle between side b and a,
β is the angle between side c and a.
Relationship with radius
If the original triangle is inscribed in a circle, you can use the radius of such a circle to determine the height. Its center is located at the point where all 3 heights intersect (from each vertex) - the orthocenter, and the distance from it to the vertex (any) is the radius.
Then h(a)=bc/2R, where:
b, c – 2 other sides of the triangle,
R is the radius of the circle circumscribing the triangle.
Find the height in a right triangle
In this type of geometric figure, 2 sides, when intersecting, form a right angle - 90°. Therefore, if you want to determine the height value in it, then you need to calculate either the size of one of the legs, or the size of the segment forming 90° with the hypotenuse. When designating:
a, b – legs,
c – hypotenuse,
h(c) – perpendicular to the hypotenuse.
You can make the necessary calculations using the following relationships:
- Pythagorean theorem:
a=√(c 2 -b 2),
b=√(c 2 -a 2),
h(c)=2S/c, because S=ab/2, then h(c)=ab/c.
- Trigonometric functions:
a=c*sinβ,
b=c*cosβ,
h(c)=ab/c=с* sinβ* cosβ.
Find the height of an isosceles triangle
This geometric figure is distinguished by the presence of two sides of equal size and a third – the base. To determine the height drawn to the third, distinct side, the Pythagorean theorem comes to the rescue. With notation
a – side,
c – base,
h(c) is a segment to c at an angle of 90°, then h(c)=1/2 √(4a 2 -c 2).


The lesson contains a description of the properties and formulas for finding the height of a triangle, as well as examples of problem solving. If you have not found a solution to a suitable problem - write about it on the forum. Surely the course will be supplemented.
TRIANGLE HEIGHTTriangle height- a perpendicular dropped from the vertex of a triangle, drawn to the side opposite the vertex or to its continuation. Properties triangle heights:
Orthocenter of the triangleAll three altitudes of the triangle (drawn from the three vertices) intersect at one point, which called orthocenter. In order to find the point of intersection of heights, it is enough to draw two heights (two lines intersect only at one point). The location of the orthocenter (point O) is determined by the type of triangle. For an acute triangle, the point of intersection of the altitudes is in the plane of the triangle. (Fig.1). In a right triangle, the point of intersection of the heights coincides with the vertex of the right angle (Fig. 2). For an obtuse triangle, the point of intersection of the heights is located behind the plane of the triangle (Fig. 3). For an isosceles triangle, the median, bisector and altitude drawn to the base of the triangle are the same. In an equilateral triangle, all three “remarkable” lines (altitude, bisector and median) coincide and three “remarkable” points (the points of the orthocenter, the center of gravity and the center of the inscribed and circumscribed circles) are located at the same point of intersection of the “remarkable” lines, i.e. also match. |
HIGH TRIKUTNIKA The height of the tricubitule is descending from the top of the tricubitule perpendicular, drawing on the protidal apex or on its extension. All three heights of the tricubitus (drawing from three vertices) intersect at one point, which is called the orthocenter. In order to find the point of cross-heights, you need to draw two heights (two straight lines cross only at one point). The location of the orthocenter (point O) is determined by the type of tricuputide. In the gostrokutny trikutnik, the point of height crossing is located in the plane of the trikutnik. (Mal.1). In the straight-cut tricut, the point of the height of the cross meets the apex of the straight cut (Mal. 2). In an obtuse-angled tricutnik, the point of the cross-line of the heights is located behind the flatness of the tricutnik (Mal.3). In the isosfemoral tricullus, the median, bisector and height drawn to the base of the tricucutineum are equal. In an equilateral tricube, all three “marked” lines (height, bisector and median) are avoided and three “marked” points (orthocenter points, the center of the line and the center of the inscribed and described keel) are located at the same point of the transfer the mud of the “dirty” lines, so they can also be avoided. |
Formulas for finding the height of a triangle

The figure is shown to make it easier to understand the formulas for finding the height of a triangle. The general rule is that the length of a side is indicated by a small letter opposite the corresponding angle. That is, side a lies opposite angle A.
Height in formulas is denoted by the letter h, the subscript of which corresponds to the side on which it is lowered.
Other designations:
a,b,c- lengths of the sides of the triangle
h a- the height of the triangle drawn to side a from the opposite angle
h b- height drawn to side b
h c- height drawn to side c
R- radius of circumscribed circle
r- radius of the inscribed circle

Explanations for formulas.
The altitude of a triangle is equal to the product of the length of the side adjacent to the angle from which this height is omitted and the sine of the angle between this side and the side to which this height is omitted (Formula 1)
The height of a triangle is equal to the quotient of twice the area of the triangle divided by the length of the side to which this height is lowered (Formula 2)
The height of a triangle is equal to the quotient of dividing the product of the sides adjacent to the angle from which this height is omitted by twice the radius of the circle described around it (Formula 4).
The heights of the sides in a triangle are related to each other in the same proportion as the inverse proportions of the lengths of the sides of the same triangle are related to each other, and also the products of pairs of sides of a triangle that have a common angle are related to each other in the same proportion (Formula 5).
The sum of the reciprocal values of the heights of a triangle is equal to the reciprocal value of the radius of the circle inscribed in such a triangle (Formula 6)
The area of a triangle can be found through the lengths of the altitudes of this triangle (Formula 7)
The length of the side of the triangle by which the height is lowered can be found by applying formulas 7 and 2.
Task on .
In a right triangle ABC (angle C = 90 0) the altitude CD is drawn. Determine CD if AD = 9 cm, BD = 16 cm
Solution.
Triangles ABC, ACD and CBD are similar to each other. This follows directly from the second criterion of similarity (the equality of angles in these triangles is obvious).
Right triangles are the only type of triangle that can be cut into two triangles similar to each other and to the original triangle.
The designations of these three triangles in this order of vertices: ABC, ACD, CBD. Thus, we simultaneously show the correspondence of the vertices. (Vertex A of triangle ABC also corresponds to vertex A of triangle ACD and vertex C of triangle CBD, etc.)
Triangles ABC and CBD are similar. Means:
AD/DC = DC/BD, that is
Problem on applying the Pythagorean theorem.
Triangle ABC is a right triangle. In this case, C is a right angle. From it the height CD = 6 cm is drawn. Difference between segments BD-AD=5 cm.
Find: Sides of triangle ABC.
Solution.
1. Let's create a system of equations according to the Pythagorean theorem
CD 2 +BD 2 =BC 2
CD 2 +AD 2 =AC 2
since CD=6
Since BD-AD=5, then
BD = AD+5, then the system of equations takes the form
36+(AD+5) 2 =BC 2
Let's add the first and second equations. Since the left side is added to the left, and the right side to the right, equality will not be violated. We get:
36+36+(AD+5) 2 +AD 2 =AC 2 +BC 2
72+(AD+5) 2 +AD 2 =AC 2 +BC 2
2. Now, looking at the original drawing of the triangle, according to the same Pythagorean theorem, the equality must be satisfied:
AC 2 +BC 2 =AB 2
Since AB=BD+AD, the equation becomes:
AC 2 +BC 2 =(AD+BD) 2
Since BD-AD=5, then BD = AD+5, then
AC 2 +BC 2 =(AD+AD+5) 2
3. Now let's take a look at the results we obtained when solving the first and second parts of the solution. Namely:
72+(AD+5) 2 +AD 2 =AC 2 +BC 2
AC 2 +BC 2 =(AD+AD+5) 2
They have a common part AC 2 +BC 2. Thus, let's equate them to each other.
72+(AD+5) 2 +AD 2 =(AD+AD+5) 2
72+AD 2 +10AD+25+AD 2 =4AD 2 +20AD+25
2AD 2 -10AD+72=0
In the resulting quadratic equation, the discriminant is equal to D=676, respectively, the roots of the equation are equal:
Since the length of the segment cannot be negative, we discard the first root.
Respectively
AB = BD + AD = 4 + 9 = 13
Using the Pythagorean theorem we find the remaining sides of the triangle:
AC = root of (52)
Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.
Collection and use of personal information
Personal information refers to data that can be used to identify or contact a specific person.
You may be asked to provide your personal information at any time when you contact us.
Below are some examples of the types of personal information we may collect and how we may use such information.
What personal information do we collect:
- When you submit an application on the site, we may collect various information, including your name, phone number, email address, etc.
How we use your personal information:
- The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
- From time to time, we may use your personal information to send important notices and communications.
- We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
- If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.
Disclosure of information to third parties
We do not disclose the information received from you to third parties.
Exceptions:
- If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government authorities in the territory of the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
- In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.
Protection of personal information
We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.
Respecting your privacy at the company level
To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.