home › Salon › Graphical method for solving a system of equations. Solving equations, inequalities, systems using function graphs

Graphical method for solving a system of equations. Solving equations, inequalities, systems using function graphs

Presentation and lesson on the topic: "Graphical solution of quadratic equations"

Additional materials
Dear users, do not forget to leave your comments, reviews, wishes! All materials have been checked by an anti-virus program.

Educational aids and simulators in the Integral online store for grade 8
Powers and roots Functions and graphs

Graphs of Quadratic Functions

In the last lesson we learned how to graph any quadratic function. With the help of such functions we can solve the so-called quadratic equations, which are generally written as follows: $ax^2+bx+c=0$,
$a, b, c$ are any numbers, but $a≠0$.
Guys, compare the equation written above and this: $y=ax^2+bx+c$.
They are almost identical. The difference is that instead of $y$ we wrote $0$, i.e. $y=0$. How then to solve quadratic equations? The first thing that comes to mind is to construct a graph of the parabola $ax^2+bx+c$ and find the points of intersection of this graph with the straight line $y=0$. There are other solutions. Let's look at them using a specific example.

Methods for solving quadratic functions

Example.
Solve the equation: $x^2+2x-8=0$.

Solution.
Method 1. Let's plot the function $y=x^2+2x-8$ and find the points of intersection with the straight line $y=0$. The coefficient of the highest degree is positive, which means the branches of the parabola point upward. Let's find the coordinates of the vertex:
$x_(c)=-\frac(b)(2a)=\frac(-2)(2)=-1$.
$y_(в)=(-1)^2+2*(-1)-8=1-2-8=-9$.

Let us take the point with coordinates $(-1;-9)$ as the origin of the new coordinate system and construct a graph of the parabola $y=x^2$ in it.

We see two points of intersection. They are marked with black dots on the graph. We are solving the equation for x, so we need to choose the abscissas of these points. They are equal to $-4$ and $2$.
Thus, the solution to the quadratic equation $x^2+2x-8=0$ is two roots: $ x_1=-4$ and $x_2=2$.

Method 2. Transform the original equation to the form: $x^2=8-2x$.
Thus, we can solve this equation in the usual graphical way by finding the abscissa of the intersection points of the two graphs $y=x^2$ and $y=8-2x$.
We obtained two intersection points, the abscissas of which coincide with the solutions obtained in the first method, namely: $x_1=-4$ and $x_2=2$.

Method 3.
Let's transform the original equation to this form: $x^2-8=-2x$.
Let's build two graphs $y=x^2-8$ and $y=-2x$ and find their intersection points.
The graph of $y=x^2-8$ is a parabola shifted down 8 units.
We obtained two intersection points, and the abscissas of these points are the same as in the two previous methods, namely: $x_1=-4$ and $x_2=2$.

Method 4.
Let's select the perfect square in the original equation: $x^2+2x-8=x^2+2x+1-9=(x+1)^2-9$.
Let's construct two graphs of the functions $y=(x+1)^2$ and $y=9$. The graph of the first function is a parabola shifted one unit to the left. The graph of the second function is a straight line parallel to the abscissa axis and passing through the ordinate equal to $9$.
Once again we obtained two points of intersection of the graphs, and the abscissas of these points coincide with those obtained in the previous methods $x_1=-4$ and $x_2=2$.

Method 5.
Divide the original equation by x: $\frac(x^2)(x)+\frac(2x)(x)-\frac(8)(x)=\frac(0)(x)$.
$x+2-\frac(8)(x)=0$.
$x+2=\frac(8)(x)$.
Let's solve this equation graphically, construct two graphs $y=x+2$ and $y=\frac(8)(x)$.
Again we got two points of intersection, and the abscissas of these points coincide with those obtained above $x_1=-4$ and $x_2=2$.

Algorithm for graphical solution of quadratic functions

Guys, we looked at five ways to graphically solve quadratic equations. In each of these methods, the roots of the equations turned out to be the same, which means the solution was obtained correctly.

Basic methods for graphically solving quadratic equations $ax^2+bx+c=0$, $a, b, c$ - any numbers, but $a≠0$:
1. Construct a graph of the function $y=ax^2+bx+c$, find the points of intersection with the abscissa axis, which will be the solution to the equation.
2. Construct two graphs $y=ax^2$ and $y=-bx-c$, find the abscissa of the intersection points of these graphs.
3. Construct two graphs $y=ax^2+c$ and $y=-bx$, find the abscissa of the intersection points of these graphs. The graph of the first function will be a parabola, shifted either down or up, depending on the sign of the number c. The second graph is a straight line passing through the origin.
4. Select a complete square, that is, bring the original equation to the form: $a(x+l)^2+m=0$.
Construct two graphs of the function $y=a(x+l)^2$ and $y=-m$, find their intersection points. The graph of the first function will be a parabola shifted either to the left or to the right, depending on the sign of the number $l$. The graph of the second function will be a straight line parallel to the abscissa axis and intersecting the ordinate axis at a point equal to $-m$.
5. Divide the original equation by x: $ax+b+\frac(c)(x)=0$.
Convert to the form: $\frac(c)(x)=-ax-b$.
Construct two graphs again and find their intersection points. The first graph is a hyperbola, the second graph is a straight line. Unfortunately, the graphical method for solving quadratic equations is not always a good solution. The intersection points of various graphs are not always integers or may have very large numbers in the abscissa (ordinate) that cannot be plotted on a regular sheet of paper.

Let us demonstrate all these methods more clearly with an example.

Example.
Solve the equation: $x^2+3x-12=0$,

Solution.
Let's plot the parabola and find the coordinates of the vertices: $x_(c)=-\frac(b)(2a)=\frac(-3)(2)=-1.5$.
$y_(в)=(-1.5)^2+2*(-1.5)-8=2.25-3-8=-8.75$.
When constructing such a parabola, problems immediately arise, for example, in correctly marking the vertex of the parabola. In order to accurately mark the ordinate of the vertex, you need to select one cell equal to 0.25 scale units. At this scale, you need to go down 35 units, which is inconvenient. Anyway, let's build our schedule.
The second problem we encounter is that the graph of our function intersects the x-axis at a point with coordinates that cannot be accurately determined. An approximate solution is possible, but mathematics is an exact science.
Thus, the graphical method is not the most convenient. Therefore, solving quadratic equations requires a more universal method, which we will study in the following lessons.

Problems to solve independently

1. Solve the equation graphically (in all five ways): $x^2+4x-12=0$.
2. Solve the equation using any graphical method: $-x^2+6x+16=0$.

Sometimes equations are solved graphically. To do this, you need to transform the equation so (if it is not already presented in a transformed form) that to the left and right of the equal sign there are expressions for which you can easily draw function graphs. For example, given the following equation:
x² – 2x – 1 = 0

If we have not yet studied solving quadratic equations algebraically, we can try to do this either by factoring or graphically. To solve such an equation graphically, we present it in this form:
x² = 2x + 1

From this representation of the equation it follows that it is necessary to find such values of x for which the left side will be equal to the right.

As you know, the graph of the function y = x² is a parabola, and y = 2x + 1 is a straight line. The x coordinate of the points of the coordinate plane lying both on the first graph and on the second (that is, the points of intersection of the graphs) are precisely those x values at which the left side of the equation will be equal to the right. In other words, the x-coordinates of the intersection points of the graphs are the roots of the equation.

Graphs can intersect at several points, at one point, or not intersect at all. It follows that an equation may have several roots, or one root, or none at all.

Let's look at a simpler example:
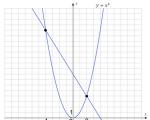
x² – 2x = 0 or x² = 2x

Let's draw graphs of the functions y = x² and y = 2x:

As can be seen from the drawing, the parabola and the straight line intersect at points (0; 0) and (2; 4). The x coordinates of these points are respectively equal to 0 and 2. This means that the equation x² – 2x = 0 has two roots - x 1 = 0, x 2 = 2.

Let's check this by solving the equation by taking the common factor out of brackets:
x² – 2x = 0
x(x – 2) = 0

The zero on the right side can occur either when x is 0 or 2.

The reason why we did not graphically solve the equation x² – 2x – 1 = 0 is that in most equations the roots are real (fractional) numbers, and it is difficult to accurately determine the value of x on a graph. Therefore, for most equations, the graphical solution is not the best. However, knowledge of this method provides a deeper understanding of the relationship between equations and functions.

>>Mathematics: Graphical solution of equations

Graphical solution of equations

Let's summarize our knowledge about graphs functions. We have learned how to build graphs of the following functions:

y =b (straight line parallel to the x axis);

y = kx (line passing through the origin);

y - kx + m (straight line);

y = x 2 (parabola).

Knowledge of these graphs will allow us, if necessary, to replace the analytical model geometric (graphical), for example, instead of the model y = x 2 (which represents an equality with two variables x and y), consider a parabola in the coordinate plane. In particular, it is sometimes useful for solving equations. Let's discuss how this is done using several examples.

A. V. Pogorelov, Geometry for grades 7-11, Textbook for educational institutions

Lesson content lesson notes supporting frame lesson presentation acceleration methods interactive technologies Practice tasks and exercises self-test workshops, trainings, cases, quests homework discussion questions rhetorical questions from students Illustrations audio, video clips and multimedia photographs, pictures, graphics, tables, diagrams, humor, anecdotes, jokes, comics, parables, sayings, crosswords, quotes Add-ons abstracts articles tricks for the curious cribs textbooks basic and additional dictionary of terms other Improving textbooks and lessonscorrecting errors in the textbook updating a fragment in a textbook, elements of innovation in the lesson, replacing outdated knowledge with new ones Only for teachers perfect lessons calendar plan for the year; methodological recommendations; discussion program Integrated Lessons

Let there be a complete quadratic equation: A*x2+B*x+C=0, where A, B and C are any numbers, and A is not equal to zero. This is a general case of a quadratic equation. There is also a reduced form in which A=1. To solve any equation graphically, you need to move the term with the highest degree to another part and equate both parts to some variable.

After this, A*x2 will remain on the left side of the equation, and B*x-C on the right side (we can assume that B is a negative number, this does not change the essence). The resulting equation is A*x2=B*x-C=y. For clarity, in this case both parts are equated to the variable y.

Plotting graphs and processing results

Now we can write two equations: y=A*x2 and y=B*x-C. Next, you need to plot a graph of each of these functions. The graph y=A*x2 is a parabola with a vertex at the origin, the branches of which are directed upward or downward, depending on the sign of the number A. If it is negative, the branches are directed downward, if positive, the branches are directed upward.

The graph y=B*x-C is a regular straight line. If C=0, the line passes through the origin. In the general case, it cuts off a segment equal to C from the ordinate axis. The angle of inclination of this line relative to the abscissa axis is determined by the coefficient B. It is equal to the tangent of the inclination of this angle.

After the graphs are plotted, it will be seen that they intersect at two points. The coordinates of these points along the x-axis determine the roots of the quadratic equation. To accurately determine them, you need to clearly build graphs and choose the right scale.

Another graphical solution

There is another way to solve a quadratic equation graphically. It is not necessary to move B*x+C to the other side of the equation. You can immediately plot the function y=A*x2+B*x+C. Such a graph is a parabola with a vertex at an arbitrary point. This method is more complicated than the previous one, but you can build only one graph to...

First you need to determine the vertex of the parabola with coordinates x0 and y0. Its abscissa is calculated using the formula x0=-B/2*a. To determine the ordinate, you need to substitute the resulting abscissa value into the original function. Mathematically, this statement is written as follows: y0=y(x0).

Then you need to find two points symmetrical to the axis of the parabola. In them, the original function must vanish. After this, you can build a parabola. The points of its intersection with the X axis will give two roots of the quadratic equation.