The extremum point of the function f x. What are extrema of a function: critical points of maximum and minimum
Increasing and decreasing intervals provide very important information about the behavior of a function. Finding them is part of the function exploration and plotting process. In addition, extremum points, at which there is a change from increase to decrease or from decrease to increase, are given special attention when finding the largest and smallest values of the function on a certain interval.
In this article, we will give the necessary definitions, formulate a sufficient test for the increase and decrease of a function on an interval and sufficient conditions for the existence of an extremum, and apply this whole theory to solving examples and problems.
Page navigation.
Increasing and decreasing function on an interval.
Definition of an increasing function.
The function y=f(x) increases on the interval X if for any and 
the inequality is satisfied. In other words, a larger value of the argument corresponds to a larger value of the function.
Decreasing function definition.
The function y=f(x) decreases on the interval X if for any and the inequality 
. In other words, a larger value of the argument corresponds to a smaller value of the function.
REMARK: if the function is defined and continuous at the ends of the interval of increase or decrease (a;b) , that is, at x=a and x=b , then these points are included in the interval of increase or decrease. This does not contradict the definitions of an increasing and decreasing function on the interval X .
For example, from the properties of the basic elementary functions, we know that y=sinx is defined and continuous for all real values of the argument. Therefore, from the increase of the sine function on the interval, we can assert the increase on the interval .
Extremum points, function extrema.
The point is called maximum point function y=f(x) if the inequality is true for all x from its neighborhood. The value of the function at the maximum point is called function maximum and denote .
The point is called minimum point function y=f(x) if the inequality is true for all x from its neighborhood. The value of the function at the minimum point is called function minimum and denote .
The neighborhood of a point is understood as the interval 
, where is a sufficiently small positive number.
The minimum and maximum points are called extremum points, and the function values corresponding to the extremum points are called function extrema.
Do not confuse function extremes with the maximum and minimum values of the function.
On the first picture highest value function on the segment is reached at the maximum point and is equal to the maximum of the function, and in the second figure, the maximum value of the function is reached at the point x=b, which is not the maximum point.
Sufficient conditions for increasing and decreasing functions.
On the basis of sufficient conditions (signs) for the increase and decrease of the function, the intervals of increase and decrease of the function are found.
Here are the formulations of the signs of increasing and decreasing functions on the interval:
- if the derivative of the function y=f(x) is positive for any x from the interval X , then the function increases by X ;
- if the derivative of the function y=f(x) is negative for any x from the interval X , then the function is decreasing on X .
Thus, to determine the intervals of increase and decrease of a function, it is necessary:
Consider an example of finding the intervals of increasing and decreasing functions to clarify the algorithm.
Example.
Find the intervals of increase and decrease of the function .
Solution.
The first step is to find the scope of the function. In our example, the expression in the denominator should not vanish, therefore, .
Let's move on to finding the derivative of the function: 
To determine the intervals of increase and decrease of a function by a sufficient criterion, we solve the inequalities and on the domain of definition. Let us use a generalization of the interval method. The only real root of the numerator is x = 2 , and the denominator vanishes at x=0 . These points divide the domain of definition into intervals in which the derivative of the function retains its sign. Let's mark these points on the number line. By pluses and minuses, we conditionally denote the intervals on which the derivative is positive or negative. The arrows below schematically show the increase or decrease of the function on the corresponding interval. 
Thus, 
And 
.
At the point x=2 the function is defined and continuous, so it must be added to both the ascending and descending intervals. At the point x=0, the function is not defined, so this point is not included in the required intervals.
We present the graph of the function to compare the obtained results with it.
Answer:
The function increases at 
, decreases on the interval (0;2] .
Sufficient conditions for the extremum of a function.
To find the maxima and minima of a function, you can use any of the three extremum signs, of course, if the function satisfies their conditions. The most common and convenient is the first of them.
The first sufficient condition for an extremum.
Let the function y=f(x) be differentiable in a -neighborhood of the point and be continuous at the point itself.
In other words:
Algorithm for finding extremum points by the first sign of the function extremum.
- Finding the scope of the function.
- We find the derivative of the function on the domain of definition.
- We determine the zeros of the numerator, the zeros of the denominator of the derivative, and the points of the domain where the derivative does not exist (all the listed points are called points of possible extremum, passing through these points, the derivative just can change its sign).
- These points divide the domain of the function into intervals in which the derivative retains its sign. We determine the signs of the derivative on each of the intervals (for example, by calculating the value of the derivative of the function at any point of a single interval).
- We select points at which the function is continuous and, passing through which, the derivative changes sign - they are the extremum points.
Too many words, let's consider a few examples of finding extremum points and extremums of a function using the first sufficient condition for the extremum of a function.
Example.
Find the extrema of the function .
Solution.
The scope of the function is the entire set of real numbers, except for x=2 .
We find the derivative: 
The zeros of the numerator are the points x=-1 and x=5 , the denominator goes to zero at x=2 . Mark these points on the number line 
We determine the signs of the derivative on each interval, for this we calculate the value of the derivative at any of the points of each interval, for example, at the points x=-2, x=0, x=3 and x=6 .
Therefore, the derivative is positive on the interval (in the figure we put a plus sign over this interval). Similarly 
Therefore, we put a minus over the second interval, a minus over the third, and a plus over the fourth.
It remains to choose the points at which the function is continuous and its derivative changes sign. These are the extremum points.
At the point x=-1 the function is continuous and the derivative changes sign from plus to minus, therefore, according to the first sign of the extremum, x=-1 is the maximum point, it corresponds to the maximum of the function 
.
At the point x=5 the function is continuous and the derivative changes sign from minus to plus, therefore, x=-1 is the minimum point, it corresponds to the minimum of the function 
.
Graphic illustration.
Answer:
PLEASE NOTE: the first sufficient sign of an extremum does not require the function to be differentiable at the point itself.
Example.
Find extreme points and extrema of a function 
.
Solution.
The domain of the function is the entire set of real numbers. The function itself can be written as: 
Let's find the derivative of the function: 
At the point x=0 the derivative does not exist, since the values of one-sided limits do not coincide when the argument tends to zero: 
At the same time, the original function is continuous at the point x=0 (see the section on investigating a function for continuity): 
Find the values of the argument at which the derivative vanishes: 
We mark all the obtained points on the real line and determine the sign of the derivative on each of the intervals. To do this, we calculate the values of the derivative at arbitrary points of each interval, for example, when x=-6, x=-4, x=-1, x=1, x=4, x=6.
That is, 
Thus, according to the first sign of an extremum, the minimum points are 
, the maximum points are 
.
We calculate the corresponding minima of the function 
We calculate the corresponding maxima of the function 
Graphic illustration.
Answer:
.
The second sign of the extremum of the function.
As you can see, this sign of the extremum of the function requires the existence of a derivative at least up to the second order at the point .
Introduction
In many areas of science and practical activities one often encounters the problem of finding the extremum of a function. The fact is that many technical, economic, etc. processes are modeled by a function or several functions that depend on variables - factors that affect the state of the phenomenon being modeled. It is required to find the extrema of such functions in order to determine the optimal (rational) state, process control. So in the economy, the problems of minimizing costs or maximizing profits are often solved - the microeconomic task of the firm. In this work, we do not consider modeling issues, but consider only algorithms for finding function extrema in the simplest version, when no restrictions are imposed on the variables (unconditional optimization), and the extremum is sought for only one objective function.
EXTREMA OF THE FUNCTION
Consider the graph of a continuous function y=f(x) shown in the figure. Function value at point x 1 will be greater than the values of the function at all neighboring points both to the left and to the right of x 1 . In this case, the function is said to have at the point x 1 max. At the point x The 3 function obviously also has a maximum. If we consider the point x 2 , then the value of the function in it is less than all neighboring values. In this case, the function is said to have at the point x 2 minimum. Similarly for the point x 4 .
Function y=f(x) at the point x 0 has maximum, if the value of the function at this point is greater than its values at all points of some interval containing the point x 0 , i.e. if there is such a neighborhood of the point x 0 , which is for everyone x ≠x 0 , belonging to this neighborhood, we have the inequality f(x) <f(x 0 ) .
Function y=f(x) It has minimum at the point x 0 , if there is such a neighborhood of the point x 0 , what is for everyone x ≠x 0 belonging to this neighborhood, we have the inequality f(x) >f(x0 .
The points at which the function reaches its maximum and minimum are called extremum points, and the values of the function at these points are the extrema of the function.
Let us pay attention to the fact that a function defined on a segment can reach its maximum and minimum only at points contained within the segment under consideration.
Note that if a function has a maximum at a point, this does not mean that at this point the function has the maximum value in the entire domain. In the figure discussed above, the function at the point x 1 has a maximum, although there are points at which the values of the function are greater than at the point x 1 . In particular, f (x 1) < f (x 4) i.e. the minimum of the function is greater than the maximum. From the definition of the maximum, it only follows that this is the most great importance functions at points sufficiently close to the maximum point.
Theorem 1. (A necessary condition for the existence of an extremum.) If a differentiable function y=f(x) has at the point x= x 0 extremum, then its derivative at this point vanishes.
Proof. Let, for definiteness, at the point x 0 the function has a maximum. Then for sufficiently small increments Δ x we have f(x
0
+ Δ x)
Passing in these inequalities to the limit as Δ x→ 0 and taking into account that the derivative f "(x 0) exists, and hence the limit on the left does not depend on how Δ x→ 0, we get: for Δ x → 0 – 0 f" (x 0) ≥ 0 and at Δ x → 0 + 0 f" (x 0) ≤ 0. Since f" (x 0) defines a number, then these two inequalities are compatible only if f" (x 0) = 0.
The proved theorem states that the maximum and minimum points can only be among those values of the argument for which the derivative vanishes.
We have considered the case when a function has a derivative at all points of a certain segment. What happens when the derivative does not exist? Consider examples.
y =|x |.
The function does not have a derivative at a point x=0 (at this point, the graph of the function does not have a definite tangent), but at this point the function has a minimum, since y(0)=0, and for all x ≠ 0y > 0.
has no derivative at x=0, since it goes to infinity when x=0. But at this point, the function has a maximum. 
has no derivative at x=0 because 
at x→0. At this point, the function has neither a maximum nor a minimum. Really, f(x)=0 and at x
<0f(x)
<0, а при x
>0f(x)
>0.
Thus, from the given examples and the formulated theorem it is clear that the function can have an extremum only in two cases: 1) at the points where the derivative exists and is equal to zero; 2) at the point where the derivative does not exist.
However, if at some point x 0 we know that f"(x 0 ) =0, then it cannot be concluded from this that at the point x 0 the function has an extremum.
For example.
.
But point x=0 is not an extremum point, since to the left of this point the function values are located below the axis Ox, and above on the right.
Values of an argument from the domain of a function, for which the derivative of the function vanishes or does not exist, are called critical points .
It follows from the foregoing that the extremum points of a function are among the critical points, and, however, not every critical point is an extremum point. Therefore, to find the extremum of the function, you need to find all the critical points of the function, and then examine each of these points separately for maximum and minimum. For this, the following theorem serves.
Theorem 2. (A sufficient condition for the existence of an extremum.) Let the function be continuous on some interval containing the critical point x 0 , and is differentiable at all points of this interval (except, perhaps, the point itself x 0). If, when passing from left to right through this point, the derivative changes sign from plus to minus, then at the point x = x 0 the function has a maximum. If, when passing through x 0 from left to right, the derivative changes sign from minus to plus, then the function has a minimum at this point.
Thus, if
f"(x)>0 at x <x 0 and f"(x)< 0 at x > x 0 , then x 0 - maximum point;
at x <x 0 and f "(x)> 0 at x > x 0 , then x 0 is the minimum point.
Proof. Let us first assume that when passing through x 0, the derivative changes sign from plus to minus, i.e. for all x close to the point x 0 f "(x)> 0 for x< x 0 , f"(x)< 0 for x > x 0 . Let us apply the Lagrange theorem to the difference f(x) - f(x 0 ) = f "(c)(x- x 0), where c lies between x And x 0 .
Let x< x 0 . Then c< x 0 and f "(c)> 0. That's why f "(c)(x-x 0)< 0 and, therefore,
f(x) - f(x 0 )< 0, i.e. f(x)< f(x 0 ).
Let x > x 0 . Then c> x 0 and f"(c)< 0. Means f "(c)(x-x 0)< 0. That's why f(x) - f(x 0 ) <0,т.е.f(x) < f(x 0 ) .
Thus, for all values x close enough to x 0 f(x) < f(x 0 ) . And this means that at the point x 0 the function has a maximum.
The second part of the minimum theorem is proved similarly.
Let us illustrate the meaning of this theorem in the figure. Let f"(x 1 ) =0 and for any x, close enough to x 1 , the inequalities
f"(x)< 0 at x< x 1 , f "(x)> 0 at x > x 1 .
Then to the left of the point x 1 the function is increasing, and decreasing on the right, therefore, when x = x 1 function goes from increasing to decreasing, that is, it has a maximum.
Similarly, one can consider the points x 2 and x 3 .
Schematically, all of the above can be depicted in the picture:
The rule for studying the function y=f(x) for an extremum
Find the scope of a function f(x).
Find the first derivative of a function f"(x) .
Determine critical points, for this:
find the real roots of the equation f"(x) =0;
find all values x under which the derivative f"(x) does not exist.
Determine the sign of the derivative to the left and right of the critical point. Since the sign of the derivative remains constant between two critical points, it suffices to determine the sign of the derivative at any one point to the left and at one point to the right of the critical point.
Calculate the value of the function at the extremum points.
Before learning how to find the extrema of a function, it is necessary to understand what an extremum is. The most general definition of an extremum is that it is the smallest or largest value of a function used in mathematics on a certain set of a number line or graph. In the place where the minimum is, the extremum of the minimum appears, and where the maximum is, the extremum of the maximum appears. Also in such a discipline as mathematical analysis, local extrema of a function are distinguished. Now let's look at how to find extremums.
Extremes in mathematics are among the most important characteristics of a function, they show its largest and smallest value. The extrema are found mainly at the critical points of the found functions. It is worth noting that it is at the extremum point that the function radically changes its direction. If we calculate the derivative of the extremum point, then, according to the definition, it must be equal to zero or it will be completely absent. Thus, to learn how to find the extremum of a function, you need to perform two sequential tasks:
- find the derivative for the function that needs to be determined by the task;
- find the roots of the equation.
The sequence of finding the extremum
- Write down the function f(x) that is given. Find its first-order derivative f "(x). Equate the resulting expression to zero.
- Now you have to solve the equation that turned out. The resulting solutions will be the roots of the equation, as well as the critical points of the function being defined.
- Now we determine which critical points (maximum or minimum) are the found roots. The next step, after we learned how to find the extremum points of a function, is to find the second derivative of the desired function f "(x). It will be necessary to substitute the values of the found critical points into a specific inequality and then calculate what happens. If this happens, that the second derivative turns out to be greater than zero at the critical point, then it will be the minimum point, and otherwise it will be the maximum point.
- It remains to calculate the value of the initial function at the required maximum and minimum points of the function. To do this, we substitute the obtained values into the function and calculate. However, it should be noted that if the critical point turned out to be a maximum, then the extremum will be maximum, and if it is a minimum, then it will be minimum by analogy.
Algorithm for finding an extremum
To summarize the knowledge gained, let's make a brief algorithm of how to find extremum points.
- We find the domain of the given function and its intervals, which determine exactly on what intervals the function is continuous.
- We find the derivative of the function f "(x).
- We calculate the critical points of the equation y = f (x).
- We analyze the changes in the direction of the function f (x), as well as the sign of the derivative f "(x) where the critical points separate the domain of definition of this function.
- Now we determine whether each point on the graph is a maximum or a minimum.
- We find the values of the function at those points that are extremums.
- We fix the result of this study - extrema and intervals of monotonicity. That's all. Now we have considered how to find an extremum on any interval. If you need to find an extremum on a certain interval of a function, then this is done in a similar way, only the boundaries of the study being performed are necessarily taken into account.
So, we have considered how to find the extremum points of a function. With the help of simple calculations, as well as knowledge about finding derivatives, you can find any extremum and calculate it, as well as graphically designate it. Finding extremes is one of the most important sections of mathematics, both at school and at a higher educational institution, therefore, if you learn how to determine them correctly, then learning will become much easier and more interesting.
From this article, the reader will learn about what an extremum of functional value is, as well as about the features of its use in practice. The study of such a concept is extremely important for understanding the foundations of higher mathematics. This topic is fundamental to a deeper study of the course.
In contact with
What is an extreme?
In the school course, many definitions of the concept of "extremum" are given. This article is intended to give the deepest and clearest understanding of the term for those who are ignorant of the issue. So, the term is understood to what extent the functional interval acquires a minimum or maximum value on a particular set.
The extremum is both the minimum value of the function and the maximum at the same time. There is a minimum point and a maximum point, that is, the extreme values of the argument on the graph. The main sciences in which this concept is used:
- statistics;
- machine control;
- econometrics.
Extreme points play an important role in determining the sequence of a given function. The coordinate system on the graph at its best shows the change in extreme position depending on the change in functionality.
Extrema of the derivative function
There is also such a thing as a "derivative". It is necessary to determine the extremum point. It is important not to confuse the minimum or maximum points with the largest and smallest values. These are different concepts, although they may seem similar.
The value of the function is the main factor in determining how to find the maximum point. The derivative is not formed from the values, but exclusively from its extreme position in one order or another.
The derivative itself is determined based on the data of the extreme points, and not the largest or smallest value. In Russian schools, the line between these two concepts is not clearly drawn, which affects the understanding of this topic in general.
Let's now consider such a thing as a "sharp extremum". To date, there is an acute minimum value and an acute maximum value. The definition is given in accordance with the Russian classification of critical points of a function. The concept of an extremum point is the basis for finding critical points on a chart.
To define such a concept, Fermat's theorem is used. It is the most important in the study of extreme points and gives a clear idea of their existence in one form or another. To ensure extremeness, it is important to create certain conditions for decreasing or increasing on the chart.
To accurately answer the question "how to find the maximum point", you must follow these provisions:
- Finding the exact area of definition on the chart.
- Search for the derivative of a function and an extremum point.
- Solve standard inequalities for the domain of the argument.
- Be able to prove in which functions a point on a graph is defined and continuous.
Attention! The search for a critical point of a function is possible only if there is a derivative of at least the second order, which is ensured by a high proportion of the presence of an extremum point.
Necessary condition for the extremum of the function
In order for an extremum to exist, it is important that there are both minimum points and maximum points. If this rule is observed only partially, then the condition for the existence of an extremum is violated.
Each function in any position must be differentiated in order to identify its new meanings. It is important to understand that the case when a point vanishes is not the main principle of finding a differentiable point.
A sharp extremum, as well as a function minimum, is an extremely important aspect of solving a mathematical problem using extreme values. In order to better understand this component, it is important to refer to the tabular values for the assignment of the functional.
| A complete exploration of meaning | Plotting a Value |
| 1. Determination of points of increase and decrease of values. 2. Finding break points, extremum and intersection with coordinate axes. 3. The process of determining changes in position on the chart. 4. Determination of the index and direction of convexity and convexity, taking into account the presence of asymptotes. 5. Creation of a summary table of the study in terms of determining its coordinates. 6. Finding intervals of increase and decrease of extreme and acute points. 7. Determination of the convexity and concavity of the curve. 8. Building a graph based on the study allows you to find a minimum or maximum. |
The main element, when it is necessary to work with extremums, is the exact construction of its graph. School teachers do not often pay maximum attention to such an important aspect, which is a gross violation of the educational process. The graph is built only on the basis of the results of the study of functional data, the definition of sharp extrema, as well as points on the graph. Sharp extrema of the derivative of a function are displayed on a plot of exact values using the standard procedure for determining asymptotes. |
The extremum point of a function is the point in the function's domain where the value of the function takes on a minimum or maximum value. The function values at these points are called extrema (minimum and maximum) of the function.
Definition. Dot x1 function scope f(x) is called maximum point of the function , if the value of the function at this point is greater than the values of the function at points close enough to it, located to the right and left of it (that is, the inequality f(x0 ) > f(x 0 + Δ x) x1 maximum.
Definition. Dot x2 function scope f(x) is called minimum point of the function, if the value of the function at this point is less than the values of the function at points close enough to it, located to the right and left of it (that is, the inequality f(x0 ) < f(x 0 + Δ x) ). In this case, the function is said to have at the point x2 minimum.
Let's say the point x1 - maximum point of the function f(x) . Then in the interval up to x1 function increases, so the derivative of the function is greater than zero ( f "(x) > 0 ), and in the interval after x1 the function is decreasing, so function derivative less than zero ( f "(x) < 0 ). Тогда в точке x1
Let us also assume that the point x2 - minimum point of the function f(x) . Then in the interval up to x2 the function is decreasing and the derivative of the function is less than zero ( f "(x) < 0 ), а в интервале после x2 the function is increasing and the derivative of the function is greater than zero ( f "(x) > 0 ). In this case also at the point x2 the derivative of the function is zero or does not exist.
Fermat's theorem (a necessary criterion for the existence of an extremum of a function). If point x0 - extremum point of the function f(x) , then at this point the derivative of the function is equal to zero ( f "(x) = 0 ) or does not exist.
Definition. The points at which the derivative of a function is equal to zero or does not exist are called critical points .
Example 1 Let's consider a function.
At the point x= 0 the derivative of the function is equal to zero, therefore, the point x= 0 is the critical point. However, as can be seen on the graph of the function, it increases in the entire domain of definition, so the point x= 0 is not an extremum point of this function.
Thus, the conditions that the derivative of a function at a point is equal to zero or does not exist are necessary conditions for an extremum, but not sufficient, since other examples of functions can be given for which these conditions are satisfied, but the function does not have an extremum at the corresponding point. That's why must have sufficient indications, which make it possible to judge whether there is an extremum at a particular critical point and which one - a maximum or a minimum.
Theorem (the first sufficient criterion for the existence of an extremum of a function). Critical point x0 f(x) , if the derivative of the function changes sign when passing through this point, and if the sign changes from "plus" to "minus", then the maximum point, and if from "minus" to "plus", then the minimum point.
If near the point x0 , to the left and to the right of it, the derivative retains its sign, this means that the function either only decreases or only increases in some neighborhood of the point x0 . In this case, at the point x0 there is no extremum.
So, to determine the extremum points of the function, you need to do the following :
- Find the derivative of a function.
- Equate the derivative to zero and determine the critical points.
- Mentally or on paper, mark the critical points on the numerical axis and determine the signs of the derivative of the function in the resulting intervals. If the sign of the derivative changes from "plus" to "minus", then the critical point is the maximum point, and if from "minus" to "plus", then the critical point is the minimum point.
- Calculate the value of the function at the extremum points.
Example 2 Find extrema of a function 
.
Solution. Let's find the derivative of the function:
Equate the derivative to zero to find the critical points:
.
Since for any values \u200b\u200bof "x" the denominator is not equal to zero, then we equate the numerator to zero:
Got one critical point x= 3 . We determine the sign of the derivative in the intervals delimited by this point:
in the range from minus infinity to 3 - minus sign, that is, the function decreases,
in the range from 3 to plus infinity - a plus sign, that is, the function increases.
That is, point x= 3 is the minimum point.
Find the value of the function at the minimum point:
Thus, the extremum point of the function is found: (3; 0) , and it is the minimum point.
Theorem (the second sufficient criterion for the existence of an extremum of a function). Critical point x0 is the extremum point of the function f(x) , if the second derivative of the function at this point is not equal to zero ( f ""(x) ≠ 0 ), moreover, if the second derivative is greater than zero ( f ""(x) > 0 ), then the maximum point, and if the second derivative is less than zero ( f ""(x) < 0 ), то точкой минимума.
Remark 1. If at a point x0 both the first and second derivatives vanish, then at this point it is impossible to judge the presence of an extremum on the basis of the second sufficient sign. In this case, you need to use the first sufficient criterion for the extremum of the function.
Remark 2. The second sufficient criterion for the extremum of a function is also inapplicable when the first derivative does not exist at the stationary point (then the second derivative does not exist either). In this case, it is also necessary to use the first sufficient criterion for the extremum of the function.
The local nature of the extrema of the function
From the above definitions it follows that the extremum of a function is of a local nature - this is the largest and smallest value of the function compared to the nearest values.
Suppose you consider your earnings in a time span of one year. If in May you earned 45,000 rubles, and in April 42,000 rubles and in June 39,000 rubles, then the May earnings are the maximum of the earnings function compared to the nearest values. But in October you earned 71,000 rubles, in September 75,000 rubles, and in November 74,000 rubles, so the October earnings are the minimum of the earnings function compared to nearby values. And you can easily see that the maximum among the values of April-May-June is less than the minimum of September-October-November.
Generally speaking, a function may have several extrema on an interval, and it may turn out that any minimum of the function is greater than any maximum. So, for the function shown in the figure above, .
That is, one should not think that the maximum and minimum of the function are, respectively, its maximum and minimum values on the entire segment under consideration. At the point of maximum, the function has the greatest value only in comparison with those values that it has at all points sufficiently close to the maximum point, and at the minimum point, the smallest value only in comparison with those values that it has at all points sufficiently close to the minimum point.
Therefore, we can refine the concept of extremum points of a function given above and call the minimum points local minimum points, and the maximum points - local maximum points.
We are looking for the extrema of the function together
Example 3
Solution. The function is defined and continuous on the whole number line. Its derivative 
also exists on the entire number line. Therefore, in this case only those at which , i.e., , whence and . Critical points and divide the entire domain of the function into three intervals of monotonicity: . We select one control point in each of them and find the sign of the derivative at this point.
For the interval, the reference point can be : we find . Taking a point in the interval, we get , and taking a point in the interval, we have . So, in the intervals and , and in the interval . According to the first sufficient sign of an extremum, there is no extremum at the point (since the derivative retains its sign in the interval ), and the function has a minimum at the point (since the derivative changes sign from minus to plus when passing through this point). Find the corresponding values of the function: , and . In the interval, the function decreases, since in this interval , and in the interval it increases, since in this interval.
To clarify the construction of the graph, we find the points of intersection of it with the coordinate axes. When we obtain an equation whose roots and , i.e., two points (0; 0) and (4; 0) of the graph of the function are found. Using all the information received, we build a graph (see at the beginning of the example).
Example 4 Find the extrema of the function and build its graph.
The domain of the function is the entire number line, except for the point, i.e. .
To shorten the study, we can use the fact that this function is even, since 
. Therefore, its graph is symmetrical about the axis Oy and the study can only be performed for the interval .
Finding the derivative 
and critical points of the function:
1) 
;
2) 
,
but the function suffers a break at this point, so it cannot be an extremum point.
Thus, the given function has two critical points: and . Taking into account the parity of the function, we check only the point by the second sufficient sign of the extremum. To do this, we find the second derivative 
and determine its sign at : we get . Since and , then is the minimum point of the function, while 
.
To get a more complete picture of the graph of the function, let's find out its behavior on the boundaries of the domain of definition:
(here the symbol indicates the desire x to zero on the right, and x remains positive; similarly means aspiration x to zero on the left, and x remains negative). Thus, if , then . Next, we find
,
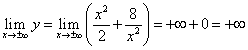those. if , then .
The graph of the function has no points of intersection with the axes. The picture is at the beginning of the example.
We continue to search for extremums of the function together
Example 8 Find the extrema of the function .
Solution. Find the domain of the function. Since the inequality must hold, we obtain from .
Let's find the first derivative of the function:
Let's find the critical points of the function.
