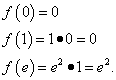The process of finding the smallest and largest values of a function on a segment is reminiscent of a fascinating flight around an object (a graph of a function) on a helicopter with firing from a long-range cannon at certain points and choosing from these points very special points for control shots. Points are selected in a certain way and according to certain rules. By what rules? We will talk about this further.
If the function y = f(x)
continuous on the segment [ a, b] , then it reaches on this segment least
And highest values
. This can either happen in extremum points or at the ends of the segment. Therefore, to find least
And the largest values of the function
, continuous on the interval [ a, b] , you need to calculate its values in all critical points and at the ends of the segment, and then choose the smallest and largest of them.
Let, for example, it is required to determine the maximum value of the function f(x) on the segment [ a, b] . To do this, find all its critical points lying on [ a, b]
.
critical point
is called the point at which function defined, and her derivative is either zero or does not exist. Then you should calculate the values of the function at critical points. And, finally, one should compare the values of the function at critical points and at the ends of the segment ( f(a) And f(b) ). The largest of these numbers will be the largest value of the function on the segment
[a, b]
.
The problem of finding the smallest values of the function
.
We are looking for the smallest and largest values of the function together
Example 1. Find the smallest and largest values of a function 
on the segment [-1, 2]
.
Solution. We find the derivative of this function. Equate the derivative to zero () and get two critical points: and . To find the smallest and largest values of a function on a given segment, it is enough to calculate its values at the ends of the segment and at the point , since the point does not belong to the segment [-1, 2] . These function values are the following: , , . It follows that smallest function value(marked in red on the graph below), equal to -7, is reached at the right end of the segment - at the point , and greatest(also red on the graph), is equal to 9, - at the critical point .
If the function is continuous in a certain interval and this interval is not a segment (but is, for example, an interval; the difference between an interval and a segment: the boundary points of the interval are not included in the interval, but the boundary points of the segment are included in the segment), then among the values of the function there may not be be the smallest and largest. So, for example, the function depicted in the figure below is continuous on ]-∞, +∞[ and does not have the largest value.
However, for any interval (closed, open, or infinite), the following property of continuous functions holds.
Example 4. Find the smallest and largest values of a function on the segment [-1, 3]
.
Solution. We find the derivative of this function as the derivative of the quotient:
.
We equate the derivative to zero, which gives us one critical point: . It belongs to the interval [-1, 3] . To find the smallest and largest values of a function on a given segment, we find its values at the ends of the segment and at the found critical point:
Let's compare these values. Conclusion: equal to -5/13, at the point and the greatest value equal to 1 at the point .
We continue to search for the smallest and largest values of the function together
There are teachers who, on the topic of finding the smallest and largest values of a function, do not give students examples more complicated than those just considered, that is, those in which the function is a polynomial or a fraction, the numerator and denominator of which are polynomials. But we will not limit ourselves to such examples, since among teachers there are lovers of making students think in full (table of derivatives). Therefore, the logarithm and the trigonometric function will be used.
Example 6. Find the smallest and largest values of a function on the segment
.
Solution. We find the derivative of this function as derivative of the product :
We equate the derivative to zero, which gives one critical point: . It belongs to the segment. To find the smallest and largest values of a function on a given segment, we find its values at the ends of the segment and at the found critical point:
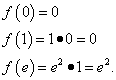
The result of all actions: the function reaches its minimum value, equal to 0, at a point and at a point and the greatest value equal to e² , at the point .
Example 7. Find the smallest and largest values of a function 
on the segment .
Solution. We find the derivative of this function:
Equate the derivative to zero:
The only critical point belongs to the segment . To find the smallest and largest values of a function on a given segment, we find its values at the ends of the segment and at the found critical point:
Conclusion: the function reaches its minimum value, equal to , at the point and the greatest value, equal to , at the point .
In applied extremal problems, finding the smallest (largest) function values, as a rule, is reduced to finding the minimum (maximum). But it is not the minima or maxima themselves that are of greater practical interest, but the values of the argument at which they are achieved. When solving applied problems, an additional difficulty arises - the compilation of functions that describe the phenomenon or process under consideration.
Example 8 A tank with a capacity of 4, having the shape of a parallelepiped with a square base and open at the top, must be tinned. What should be the dimensions of the tank in order to cover it with the least amount of material?
Solution. Let x- base side h- tank height, S- its surface area without cover, V- its volume. The surface area of the tank is expressed by the formula , i.e. is a function of two variables. To express S as a function of one variable, we use the fact that , whence . Substituting the found expression h into the formula for S:
Let us examine this function for an extremum. It is defined and differentiable everywhere in ]0, +∞[ , and
.
We equate the derivative to zero () and find the critical point. In addition, at , the derivative does not exist, but this value is not included in the domain of definition and therefore cannot be an extremum point. So, - the only critical point. Let's check it for the presence of an extremum using the second sufficient criterion. Let's find the second derivative. When the second derivative is greater than zero (). This means that when the function reaches a minimum 
. Because this minimum - the only extremum of this function, it is its smallest value. So, the side of the base of the tank should be equal to 2 m, and its height.
Example 9 From paragraph A, located on the railway line, to the point WITH, at a distance from it l, goods must be transported. The cost of transporting a weight unit per unit distance by rail is equal to , and by highway it is equal to . To what point M lines railway a highway should be built so that the transportation of goods from A V WITH was the most economical AB railroad is assumed to be straight)?
How to find the largest and smallest values of a function on a segment?
For this we follow the well-known algorithm:
1
. We find ODZ functions.
2
. Finding the derivative of a function
3
. Equate the derivative to zero
4
. We find the intervals at which the derivative retains its sign, and from them we determine the intervals of increase and decrease of the function:
If on the interval I the derivative of the function 0" title="f^(prime)(x)>0">, то функция !} increases over this interval.
If on the interval I the derivative of the function , then the function decreases over this interval.
5
. We find maximum and minimum points of the function.
IN the function maximum point, the derivative changes sign from "+" to "-".
IN minimum point of the functionderivative changes sign from "-" to "+".
6
. We find the value of the function at the ends of the segment,
- then we compare the value of the function at the ends of the segment and at the maximum points, and choose the largest of them if you need to find the largest value of the function
- or we compare the value of the function at the ends of the segment and at the minimum points, and choose the smallest of them if you need to find the smallest value of the function
However, depending on how the function behaves on the interval, this algorithm can be significantly reduced.
Consider the function 
. The graph of this function looks like this:
Let's look at some examples of solving problems from open bank assignments for
1 . Task B15 (#26695)
On the cut.
1. The function is defined for all real values of x
Obviously, this equation has no solutions, and the derivative is positive for all values of x. Therefore, the function increases and takes the largest value at the right end of the interval, that is, at x=0.
Answer: 5.
2
. Task B15 (No. 26702)
Find the largest value of a function 
on the segment.
1.ODZ function title="x(pi)/2+(pi)k, k(in)(bbZ)">!}
The derivative is zero at , however, at these points it does not change sign:
Therefore, title="3/(cos^2(x))>=3">, значит, title="3/(cos^2(x))-3>=0">, то есть производная при всех допустимых значених х неотрицательна, следовательно, функция !} increases and takes the greatest value at the right end of the interval, at .
To make it clear why the derivative does not change sign, we transform the expression for the derivative as follows:
Title="y^(prime)=3/(cos^2(x))-3=(3-3cos^2(x))/(cos^2(x))=(3sin^2 (x))/(cos^2(x))=3tg^2(x)>=0">!}
Answer: 5.
3 . Task B15 (#26708)
Find the smallest value of the function on the interval .
1. ODZ functions: title="x(pi)/2+(pi)k, k(in)(bbZ)">!}
Let's place the roots of this equation on a trigonometric circle.
The interval contains two numbers: and
Let's put up the signs. To do this, we determine the sign of the derivative at the point x=0: 
. When passing through the points and the derivative changes sign.
Let's depict the change of signs of the derivative of the function on the coordinate line:
Obviously, the point is a minimum point (where the derivative changes sign from "-" to "+"), and in order to find the smallest value of the function on the interval, you need to compare the values of the function at the minimum point and at the left end of the segment, .
In this article I will talk about algorithm for finding the largest and smallest value function, minimum and maximum points.
From theory, we will definitely need derivative table And differentiation rules. It's all in this board:
Algorithm for finding the largest and smallest values.
I find it easier to explain specific example. Consider:
Example: Find the largest value of the function y=x^5+20x^3–65x on the segment [–4;0].
Step 1. We take the derivative.
Y" = (x^5+20x^3–65x)" = 5x^4 + 20*3x^2 - 65 = 5x^4 + 60x^2 - 65
Step 2 Finding extremum points.
extremum point we name such points at which the function reaches its maximum or minimum value.
To find the extremum points, it is necessary to equate the derivative of the function to zero (y "= 0)
5x^4 + 60x^2 - 65 = 0
Now we solve this biquadratic equation and the found roots are our extremum points.
I solve such equations by replacing t = x^2, then 5t^2 + 60t - 65 = 0.
Reduce the equation by 5, we get: t^2 + 12t - 13 = 0
D = 12^2 - 4*1*(-13) = 196
T_(1) = (-12 + sqrt(196))/2 = (-12 + 14)/2 = 1
T_(2) = (-12 - sqrt(196))/2 = (-12 - 14)/2 = -13
We make the reverse substitution x^2 = t:
X_(1 and 2) = ±sqrt(1) = ±1
x_(3 and 4) = ±sqrt(-13) (we exclude, there cannot be negative numbers under the root, unless of course we are talking about complex numbers)
Total: x_(1) = 1 and x_(2) = -1 - these are our extremum points.
Step 3 Determine the largest and smallest value.
Substitution method.
In the condition, we were given the segment [b][–4;0]. The point x=1 is not included in this segment. So we don't consider it. But in addition to the point x=-1, we also need to consider the left and right borders of our segment, that is, the points -4 and 0. To do this, we substitute all these three points into the original function. Notice the original one is the one given in the condition (y=x^5+20x^3–65x), some start substituting into the derivative...
Y(-1) = (-1)^5 + 20*(-1)^3 - 65*(-1) = -1 - 20 + 65 = [b]44
y(0) = (0)^5 + 20*(0)^3 - 65*(0) = 0
y(-4) = (-4)^5 + 20*(-4)^3 - 65*(-4) = -1024 - 1280 + 260 = -2044
This means that the maximum value of the function is [b]44 and it is reached at the points [b]-1, which is called the maximum point of the function on the segment [-4; 0].
We decided and got an answer, we are great, you can relax. But stop! Don't you think that counting y(-4) is somehow too complicated? In conditions of limited time, it is better to use another method, I call it like this:
Through intervals of constancy.
These gaps are found for the derivative of the function, that is, for our biquadratic equation.
I do it in the following way. I draw a directional line. I set the points: -4, -1, 0, 1. Despite the fact that 1 is not included in the given segment, it should still be noted in order to correctly determine the intervals of constancy. Let's take some number many times greater than 1, let's say 100, mentally substitute it into our biquadratic equation 5(100)^4 + 60(100)^2 - 65. Even without counting anything, it becomes obvious that at the point 100 the function has plus sign. This means that for intervals from 1 to 100 it has a plus sign. When passing through 1 (we go from right to left), the function will change sign to minus. When passing through the point 0, the function will retain its sign, since this is only the boundary of the segment, and not the root of the equation. When passing through -1, the function will again change sign to plus.
From theory, we know that where the derivative of the function is (and we drew this for it) changes sign from plus to minus (point -1 in our case) function reaches its local maximum (y(-1)=44 as calculated earlier) on this segment (this is logically very clear, the function has ceased to increase, since it reached its maximum and began to decrease).
Accordingly, where the derivative of the function changes sign from minus to plus, achieved local minimum of a function. Yes, yes, we also found the local minimum point, which is 1, and y(1) is the minimum value of the function on the interval, let's say from -1 to +∞. Please note that this is only a LOCAL MINIMUM, that is, a minimum on a certain segment. Since the actual (global) minimum function will reach somewhere there, in -∞.
In my opinion, the first method is simpler theoretically, and the second one is simpler in terms of arithmetic operations, but much more difficult in terms of theory. After all, sometimes there are cases when the function does not change sign when passing through the root of the equation, and indeed you can get confused with these local, global maxima and minima, although you will have to master it well anyway if you plan to enter a technical university (and for what else to give profile exam and solve this problem). But practice and only practice will teach you how to solve such problems once and for all. And you can train on our website. Here .
If you have any questions, or something is not clear, be sure to ask. I will be happy to answer you, and make changes, additions to the article. Remember we are making this site together!
Popular in category:
Causes of bruising under the eyes Eternal bruising under the eyes
read
Causes of the uprisings: Reforms and transformations of Peter I were carried out ...
read
Kazan Higher Military Command School Kazan Higher...
read
The main stages in the history of the Baltic States: the formation of political...
read
Top
on the segment. 
