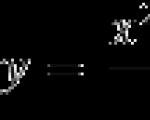Problem B15 je proučavanje funkcije pomoću izvoda. Istraživanje funkcije pomoću izvoda Istraživanje funkcije pomoću izvoda
U zadatku B15 predlaže se istraživanje funkcije zadane formulom za ekstreme. Ovo je standardni problem u računu, a njegova složenost uvelike varira ovisno o funkciji o kojoj je riječ: neki se od njih rješavaju doslovno verbalno, dok drugi zahtijevaju ozbiljno razmišljanje.
Prije učenja metoda rješavanja potrebno je savladati neke pojmove iz područja matematičke analize. Dakle, u zadatku B15 potrebno je pomoću derivacije pronaći sljedeće veličine:
- Točke lokalnog maksimuma (minimuma) - vrijednost varijable pri kojoj funkcija postiže najveću (najmanju) vrijednost. Takve se točke nazivaju i točkama ekstrema.
- Globalni maksimum (minimum) funkcije najveća je (najmanja) vrijednost funkcije pod navedenim ograničenjima. Drugi naziv su globalni ekstremi.
U tom se slučaju globalni ekstremi obično ne traže na cijeloj domeni definicije funkcije, već samo na određenom segmentu. Važno je razumjeti da se globalni ekstrem i vrijednost funkcije u točki ekstrema ne podudaraju uvijek. Objasnimo to na konkretnom primjeru:
Zadatak. Odredite točku minimuma i minimalnu vrijednost funkcije y = 2x 3 − 3x 2 − 12x + 1 na odsječku [−3; 3].
Prvo nalazimo minimalnu točku za koju izračunavamo derivaciju:
y' = (2x 3 - 3x 2 - 12x + 1)' = 6x 2 - 6x - 12.
Nađimo kritične točke rješavanjem jednadžbe y' = 0. Dobivamo standardnu kvadratnu jednadžbu:
y' = 0 ⇒ 6x 2 - 6x - 12 = 0 ⇒ ... ⇒ x 1 = -1, x 2 = 2.
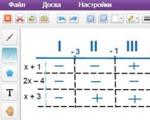
Ove točke označavamo na koordinatnoj liniji, dodamo znakove derivacije i ograničenja - krajeve segmenta:
Mjerilo slike nije važno. Najvažnije je označiti točke pravilnim redoslijedom. Iz školskog tečaja matematike poznato je da u točki minimuma izvod mijenja predznak iz minusa u plus. Očitavanje uvijek ide slijeva na desno – u smjeru pozitivne poluosi. Dakle, postoji samo jedna minimalna točka: x = 2.
Nađimo sada minimalnu vrijednost funkcije na segmentu [−3; 3]. Dostiže se ili na minimalnoj točki (tada postaje globalna minimalna točka), ili na kraju segmenta. Uočimo da je na intervalu (2; 3) derivacija posvuda pozitivna, što znači da je y(3) > y(2), pa se desni kraj intervala može zanemariti. Ostaju samo točke x = −3 (lijevi kraj segmenta) i x = 2 (minimalna točka). Imamo:
y(−3) = 2(−3) 3 − 3(−3) 2 − 12(−3) + 1 = −44;
y(2) = 2*2 3 - 3*2 2 - 12*2 + 1 = -19.
Dakle, najmanju vrijednost funkcija postiže na kraju segmenta i jednaka je −44.
Odgovor: xmin = 2; ymin = −44
Iz gornjeg razmišljanja proizlazi važna činjenica, koju mnogi zaboravljaju. Funkcija uzima najveću (minimalnu) vrijednost, ne nužno u točki ekstrema. Ponekad se takva vrijednost dostigne na kraju segmenta, a tamo derivacija ne mora biti jednaka nuli.
Shema rješavanja problema B15
Ako se u zadatku B15 traži maksimalna ili minimalna vrijednost funkcije f(x) na intervalu, izvodimo sljedeće radnje:
- Riješite jednadžbu f'(x) = 0. Ako nema korijena, preskočite treći korak i idite ravno na četvrti.
- Iz rezultirajućeg skupa korijena izbrišite sve što se nalazi izvan segmenta. Preostale brojeve označit ćemo s x 1 , x 2 , ..., x n - u pravilu će ih biti malo.
- Zamijenite krajeve segmenta i točke x 1 , x 2 , ..., x n u izvornu funkciju. Dobivamo skup brojeva f (a), f (b), f (x 1), f (x 2), ..., f (x n), od kojih biramo najveću ili najmanju vrijednost - to će biti odgovor.
Malo pojašnjenje o brisanju korijena kada se poklapaju s krajevima segmenta. Mogu se i prekrižiti, budući da se u četvrtom koraku krajevi segmenta još uvijek supstituiraju u funkciju - čak i ako jednadžba f’(x) = 0 nije imala rješenja.
Zadatak. Odredi najveću vrijednost funkcije y = x 3 + 3x 2 − 9x − 7 na odsječku [−5; 0].
Prvo, pronađimo izvod: y' = (x 3 + 3x 2 - 9x - 7)' = 3x 2 + 6x - 9.
Zatim rješavamo jednadžbu: y’ = 0 ⇒ 3x 2 + 6x − 9 = 0 ⇒ ... ⇒ x = −3; x = 1.
Precrtaj korijen x = 1 jer ne pripada segmentu [−5; 0].
Ostaje izračunati vrijednost funkcije na krajevima segmenta iu točki x = −3:
y(−5) = (−5) 3 + 4 (−5) 2 − 9 (−5) − 7 = −12;
y(−3) = (−3) 3 + 4 (−3) 2 − 9 (−3) − 7 = 20;
y(0) = 0 3 + 4 0 2 − 9 0 − 7 = −7.
Očito je najveća vrijednost 20 - ona se postiže u točki x = −3.
Sada razmotrite slučaj kada je potrebno pronaći maksimalnu ili minimalnu točku funkcije f(x) na intervalu . Ako segment nije naveden, funkcija se razmatra u svojoj domeni definicije. U svakom slučaju, shema rješenja je sljedeća:
- Odredite izvod funkcije: f'(x).
- Riješite jednadžbu f’(x) = 0. Ako je derivacija razlomačka racionalna funkcija, dodatno saznajemo kada je njen nazivnik nula. Označimo dobivene korijene x 1 , x 2 , ..., x n .
- Na koordinatnoj liniji označite x 1 , x 2 , ..., x n i između tih brojeva postavite predznake koje izvodnica ima. Ako je zadan segment, označite ga i prekrižite sve što se nalazi izvan njega.
- Među preostalim točkama tražimo onu gdje se predznak derivacije mijenja s minusa na plus (to je minimalna točka) ili s plusa na minus (minimalna točka). Treba postojati samo jedna takva točka - ovo će biti odgovor.
Pažljivi čitatelj sigurno će primijetiti da za neke funkcije ovaj algoritam ne radi. Doista, postoji cijela klasa funkcija za koje traženje točaka ekstrema zahtijeva složenije izračune. Međutim, takve funkcije nema na ispitu iz matematike.
Obratite pažnju na raspored znakova između točaka x 1 , x 2 , ..., x n . Zapamtite: kada prolazite kroz korijen parne množine, predznak derivacije se ne mijenja. Kada se traže točke ekstrema, znakovi se uvijek gledaju slijeva na desno, tj. duž numeričke osi.
Zadatak. Pronađite točku maksimuma funkcije
na intervalu [−8; 8].
Nađimo izvod:

Budući da je ovo razlomačka racionalna funkcija, izjednačavamo derivaciju i njen nazivnik s nulom:
y' = 0 ⇒ x 2 − 25 = 0 ⇒ ... ⇒ x = 5; x = −5;
x 2 \u003d 0 ⇒ x \u003d 0 (korijen druge množine).
Označimo na koordinatnoj liniji točke x = −5, x = 0 i x = 5, rasporedimo znakove i granice:
Očito unutar segmenta ostaje samo jedna točka x = −5 u kojoj se predznak derivacije mijenja s plusa na minus. Ovo je maksimalna točka.
Još jednom objasnimo po čemu se točke ekstrema razlikuju od samih ekstrema. Točke ekstrema su vrijednosti varijabli na kojima funkcija poprima najveću ili najmanju vrijednost. Ekstremumi su vrijednosti samih funkcija, maksimalne ili minimalne u nekom njihovom susjedstvu.
Uz obične polinome i frakcijske racionalne funkcije, u zadatku B15 pojavljuju se sljedeće vrste izraza:
- iracionalne funkcije,
- trigonometrijske funkcije,
- eksponencijalne funkcije,
- Logaritamske funkcije.
S iracionalnim funkcijama u pravilu nema problema. Preostale slučajeve vrijedi detaljnije razmotriti.
Trigonometrijske funkcije
Glavna poteškoća trigonometrijskih funkcija je u tome što pri rješavanju jednadžbi nastaje beskonačan broj korijena. Na primjer, jednadžba sin x = 0 ima korijene x = πn, gdje je n ∈ Z. Pa, kako ih označiti na koordinatnoj liniji ako takvih brojeva ima beskonačno mnogo?
Odgovor je jednostavan: trebate zamijeniti određene vrijednosti n. Doista, u zadacima B15 s trigonometrijskim funkcijama uvijek postoji ograničenje - segment. Stoga, za početak, uzimamo n \u003d 0, a zatim povećavamo n dok odgovarajući korijen ne "odleti" izvan segmenta. Slično, smanjenjem n, vrlo brzo ćemo dobiti korijen koji je manji od donje granice.
Lako je pokazati da na intervalu ne postoje drugi korijeni osim onih dobivenih u razmatranom procesu. Razmotrimo sada ovaj proces na konkretnim primjerima.
Zadatak. Nađite točku maksimuma funkcije y = sin x − 5x sin x − 5cos x + 1 koja pripada intervalu [−π/3; π/3].
Izračunajte izvod: y’ = (sin x − 5x sin x − 5cos x + 1)’ = ... = cos x − 5x cos x = (1 − 5x) cos x.
Zatim rješavamo jednadžbu: y’ = 0 ⇒ (1 − 5x) cos x = 0 ⇒ ... ⇒ x = 0,2 ili x = π/2 + πn, n ∈ Z.
S korijenom x = 0,2 sve je jasno, ali formula x = π / 2 + πn zahtijeva dodatnu obradu. Zamijenit ćemo različite vrijednosti n, počevši od n = 0.
n = 0 ⇒ x = π/2. Ali π/2 > π/3, pa korijen x = π/2 nije uključen u izvorni segment. Također, što je veći n, to je veći x, tako da nema smisla razmatrati n > 0.
n = −1 ⇒ x = − π/2. Ali −π/2< −π/3 - этот корень тоже придется отбросить. А вместе с ним - и все корни для n < −1.
Ispada da je na intervalu [−π/3; π/3] leži samo korijen x = 0,2. Označavamo ga zajedno sa znakovima i granicama na koordinatnoj liniji:

Kako bismo bili sigurni da je derivacija desno od x = 0,2 stvarno negativna, dovoljno je zamijeniti vrijednost x = π/4 u y’. Napominjemo samo da u točki x = 0,2 derivacija mijenja predznak iz plusa u minus, pa je to točka maksimuma.
Zadatak. Odredi najveću vrijednost funkcije y = 4tg x − 4x + π − 5 na intervalu [−π/4; π/4].
Izračunajte derivaciju: y’ = (4tg x − 4x + π − 5)’ = 4/cos 2x − 4.
Zatim rješavamo jednadžbu: y’ = 0 ⇒ 4/cos 2x − 4 = 0 ⇒ ... ⇒ x = πn, n ∈ Z.
Izvlačimo korijene iz ove formule zamjenom određenog n, počevši od n = 0:
n = 0 ⇒ x = 0. Ovaj korijen nam odgovara.
n = 1 ⇒ x = π. Ali π > π/4, pa se korijen x = π i vrijednosti n > 1 moraju prekrižiti.
n = −1 ⇒ x = −π. Ali π< −π/4, поэтому x = π и n < −1 тоже вычеркиваем.
Od cjelokupne raznolikosti korijena ostaje samo jedan: x = 0. Stoga računamo vrijednost funkcije za x = 0, x = π/4 i x = −π/4.
y(0) = 4tg 0 − 4 0 + π − 5 = π − 5;
y(π/4) = 4tg (π/4) − 4 π/4 + π − 5 = −1;
y(π/4) = 4tg (−π/4) − 4 (−π/4) + π − 5 = ... = 2π − 9.
Sada primijetite da je π = 3,14...< 4, поэтому π − 5 < 4 − 5 = −1 и 2π − 9 < 8 − 9 = −1. Получается одно положительное число и два отрицательных. Мы ищем наибольшее - очевидно, это y = −1.
Imajte na umu da je u prošlom problemu bilo moguće ne uspoređivati brojeve međusobno. Doista, od brojeva π - 5, 1 i 2π - 9 u listu za odgovore može se upisati samo jedan. Doista, kako napisati u obliku, recimo, broj π? Ali nikako. Ovo je važna značajka prvog dijela ispita iz matematike, koja uvelike pojednostavljuje rješavanje mnogih problema. I ne radi samo u B15.
Ponekad se pri proučavanju funkcije pojavljuju jednadžbe koje nemaju korijena. U ovom slučaju, problem postaje još jednostavniji, jer ostaje uzeti u obzir samo krajeve segmenta.
Zadatak. Odredite najmanju vrijednost funkcije y = 7sin x − 8x + 5 na intervalu [−3π/2; 0].
Prvo nalazimo izvod: y’ = (7sin x − 8x + 5)’ = 7cos x − 8.
Pokušajmo riješiti jednadžbu: y' = 0 ⇒ 7cos x − 8 = 0 ⇒ cos x = 8/7. Ali vrijednosti cos x uvijek leže na intervalu [−1; 1], a 8/7 > 1. Dakle, nema korijena.
Ako nema korijena, onda ništa ne treba prekrižiti. Prelazimo na posljednji korak - izračunavamo vrijednost funkcije:
y(−3π/2) = 7sin (−3π/2) − 8 (−3π/2) + 5 = ... = 12π + 12;
y(0) = 7sin 0 − 8 0 + 5 = 5.
Budući da se broj 12π + 12 ne može napisati na listu za odgovore, ostaje samo y = 5.
eksponencijalne funkcije
Općenito govoreći, eksponencijalna funkcija je izraz oblika y = a x , gdje je a > 0. Ali u zadatku B15 pojavljuju se samo funkcije oblika y = e x i, u ekstremnom slučaju, y = e kx + b. Razlog je što je derivacije ovih funkcija vrlo lako izračunati:
- (e x)" = e x. Ništa se nije promijenilo.
- (e kx + b)" = k e kx + b. Jednostavno se dodaje faktor jednak koeficijentu varijable x. Ovo je poseban slučaj izvoda složene funkcije.
Sve ostalo je apsolutno standardno. Naravno, stvarne funkcije u problemima B15 izgledaju ozbiljnije, ali shema rješenja se od toga ne mijenja. Razmotrimo nekoliko primjera, ističući samo glavne točke rješenja - bez temeljitog obrazloženja i komentara.
Zadatak. Odredite najmanju vrijednost funkcije y = (x 2 − 5x + 5)e x − 3 na intervalu [−1; 5].
Derivacija: y’ = ((x 2 − 5x + 5)e x − 3)’ = ... = (x 2 − 3x)e x − 3 = x(x − 3)e x − 3 .
Nađi korijene: y' = 0 ⇒ x(x − 3)e x − 3 = 0 ⇒ ... ⇒ x = 0; x=3.
Oba korijena leže na intervalu [−1; 5]. Ostaje pronaći vrijednost funkcije u svim točkama:
y(−1) = ((−1) 2 − 5 (−1) + 5)e − 1 − 3 = ... = 11 e −4 ;
y(0) = (0 2 − 5 0 + 5)e 0 − 3 = ... = 5 e −3 ;
y(3) = (3 2 − 5 3 + 5)e 3 − 3 = ... = −1;
y(5) = (5 2 − 5 5 + 5)e 5 − 3 = ... = 5 e 2 .
Od četiri dobivena broja u obrazac se može upisati samo y = −1. Osim toga, ovo je jedini negativni broj - bit će najmanji.
Zadatak. Odredi maksimalnu vrijednost funkcije y = (2x − 7) e 8 − 2x na odsječku .
Derivacija: y’ = ((2x − 7) e 8 − 2x)’ = ... = (16 − 4x) e 8 − 2x = 4(4 − x) e 8 − 2x .
Nalazimo korijene: y' = 0 ⇒ 4(4 − x) e 8 − 2x = 0 ⇒ x = 4.
Korijen x = 4 pripada segmentu . Tražimo vrijednosti funkcije:
y(0) = (2 0 − 7)e 8 − 2 0 = ... = −7 e 8 ;
y(4) = (2 4 − 7)e 8 − 2 4 = ... = 1;
y(6) = (2 6 − 7)e 8 − 2 6 = ... = 5 e −4 .
Očito samo y = 1 može poslužiti kao odgovor.
Logaritamske funkcije
Po analogiji s eksponencijalnim funkcijama, u zadatku B15 pojavljuju se samo prirodni logaritmi, budući da se njihov izvod lako izračunava:
- (lnx)' = 1/x;
- (ln(kx + b))' = k/(kx + b). Konkretno, ako je b = 0, tada je (ln(kx))' = 1/x.
Dakle, derivacija će uvijek biti frakcijska racionalna funkcija. Ostaje samo izjednačiti ovu derivaciju i njen nazivnik s nulom, a zatim riješiti dobivene jednadžbe.
Da biste pronašli maksimalnu ili minimalnu vrijednost logaritamske funkcije, zapamtite da prirodni logaritam postaje "normalan" broj samo u točkama oblika e n . Na primjer, ln 1 \u003d ln e 0 \u003d 0 je logaritamska nula, a najčešće se rješenje svodi na nju. U drugim slučajevima nemoguće je "ukloniti" znak logaritma.
Zadatak. Odredite najmanju vrijednost funkcije y = x 2 − 3x + ln x na odsječku .
Razmatramo izvedenicu:
Nalazimo nulte derivacije i njen nazivnik:
y' = 0 ⇒ 2x 2 − 3x + 1 = 0 ⇒ ... ⇒ x = 0,5; x = 1;
x = 0 - nema se što odlučiti.
Od tri broja x = 0, x = 0,5 i x = 1, samo x = 1 leži unutar segmenta, a broj x = 0,5 je njegov kraj. Imamo:
y(0,5) = 0,5 2 − 3 0,5 + ln 0,5 = ln 0,5 − 1,25;
y(1) = 1 2 − 3 1 + log 1 = −2;
y(5) = 5 2 − 3 5 + ln 5 = 10 + ln 5.
Od tri dobivene vrijednosti, samo y = −2 ne sadrži znak logaritma - to će biti odgovor.
Zadatak. Odredi najveću vrijednost funkcije y = ln(6x) − 6x + 4 na odsječku .
Izračunavamo derivaciju:
Saznajemo kada je izvod ili njegov nazivnik jednak nuli:
y' = 0 ⇒ 1 − 6x = 0 ⇒ x = 1/6;
x = 0 - već odlučeno.
Broj x = 0 precrtavamo jer se nalazi izvan segmenta. Razmatramo vrijednost funkcije na krajevima segmenta iu točki x = 1/6:
y(0,1) = ln(6 0,1) − 6 0,1 + 4 = ln 0,6 + 3,4;
y(1/6) = log(6 1/6) − 6 1/6 + 4 = log 1 + 3 = 3;
y(3) = ln(6 3) − 6 3 + 4 = ln 18 − 14.
Očito, samo y = 3 može djelovati kao odgovor - ostale vrijednosti sadrže znak logaritma i ne mogu se zapisati u listu za odgovore.
Točka se zove maksimalna (minimalna) točka
funkcija , ako postoji takva okolina točke da je za svu tu okolinu nejednakost ![]() (
(![]() ).
).
Točke maksimuma i minimuma funkcije nazivaju se točkama. ekstremno (Sl. 25).
Teorem 3.9 (nužan uvjet za postojanje točaka ekstrema) . U kritičnim točkama 1. vrste derivacija funkcije bilo
 je nula ili ne postoji
je nula ili ne postoji
Kritične točke 1. vrste obično se jednostavno nazivaju kritične točke.
 Kritične točke u kojima je derivacija funkcije jednaka nuli nazivaju se točke stacionarnosti
. Kritične točke u kojima je funkcija kontinuirana, ali nije diferencijabilna nazivaju se kutne točke
. Na primjer, funkcija u točki je kontinuirana, ali nema derivaciju, budući da se u ovoj točki može povući beskonačan broj tangenti na graf funkcije (slika 26). Ovaj se slučaj može smatrati potvrdom da je izjava suprotna teoremu 3.3 netočna.
Kritične točke u kojima je derivacija funkcije jednaka nuli nazivaju se točke stacionarnosti
. Kritične točke u kojima je funkcija kontinuirana, ali nije diferencijabilna nazivaju se kutne točke
. Na primjer, funkcija u točki je kontinuirana, ali nema derivaciju, budući da se u ovoj točki može povući beskonačan broj tangenti na graf funkcije (slika 26). Ovaj se slučaj može smatrati potvrdom da je izjava suprotna teoremu 3.3 netočna.
Funkcija se zove povećavajući se na nekom intervalu, ako na tom intervalu veća vrijednost argumenta odgovara većoj vrijednosti varijable, i opadajući ako manjoj vrijednosti varijable odgovara veća vrijednost argumenta .
Za daljnje istraživanje kritične točke postavljaju se na numeričku os, koju te točke dijele na intervale, nakon čega se provjeravaju sljedeći dovoljni uvjeti.
Teorem 3.10 (dovoljan uvjet za porast i pad funkcije). Ako je funkcija diferencijabilna na nekom intervalu i njezina je derivacija pozitivna (negativna), tada je funkcija rastuća (opadajuća) na tom intervalu
Teorem 3.11 (dovoljan uvjet za postojanje točaka ekstrema funkcije). Ako je funkcija kontinuirana i diferencijabilna u nekoj okolini kritične točke, a pri prolasku kroz nju derivacija mijenja predznak s plusa na minus, tada je točka točka maksimuma; ako je od minusa do plusa, tada je točka minimalna točka funkcije
One kritične točke funkcije za koje nije zadovoljen dovoljan uvjet ostaju jednostavno kritične točke prve vrste.
Kritične točke 1. vrste, na kojima izvodnica ne postoji, dijele se u dvije klase:
su točke u kojima je funkcija kontinuirana (kada je za njih zadovoljen teorem 3.11, funkcija ima "oštar" ekstrem u tim točkama), to su kutak bodovi;
su točke u kojima funkcija trpi diskontinuitet (uvijek prelaze u klasu kritičnih točaka 2. vrste).
No, ovako provedeno istraživanje ne daje odgovor na vrlo važno pitanje: kako se funkcija povećava (smanjuje) - konveksno ili konkavno? Odgovor na ovo pitanje daje daljnje proučavanje funkcije pomoću druge derivacije. Navedimo nekoliko potrebnih definicija.

Funkcija se zove konveksan (konkavan) na nekom intervalu, ako tangenta povučena na graf funkcije u svakoj točki tog intervala leži iznad (ispod) grafa funkcije.
Točke koje odvajaju područja konveksnosti od područja konkavnosti funkcije nazivaju se njezinim točke infleksije (Sl. 27).
Teorem 3.12 (nužan uvjet za postojanje točaka infleksije). U kritičnim točkama 2. vrste druga derivacija funkcije je ili nula ili ne postoji
Za daljnja istraživanja kritične točke 2. vrste postavljaju se na numeričku os koju te točke dijele na intervale, nakon čega se provjeravaju sljedeći dovoljni uvjeti.
Teorem 3.13 (dovoljan uvjet za konveksnost i konkavnost funkcije). Ako je funkcija dva puta diferencijabilna na nekom intervalu, a njena druga derivacija je pozitivna (negativna), tada je funkcija konkavna (konveksna) na tom intervalu
 One kritične točke funkcije za koje nije zadovoljen dovoljan uvjet ostaju jednostavno kritične točke druge vrste.
One kritične točke funkcije za koje nije zadovoljen dovoljan uvjet ostaju jednostavno kritične točke druge vrste.
Kritične točke 2. vrste, u kojima ne postoji druga derivacija, dijele se u dvije klase:
- točke u kojima je funkcija kontinuirana, to su tzv. "oštre" točke infleksije - u takvim točkama može se povući beskonačno mnogo tangenti na graf funkcije (slika 28);
su točke u kojima funkcija trpi diskontinuitet (u točkama diskontinuiteta 2. vrste graf funkcije ima vertikalnu asimptotu).
Za konačno nabrajanje točaka ekstrema i infleksije funkcije, potrebno je pronaći njihove ordinate, a zatim ispisati naznačene točke s dvije koordinate.
Pitanja za samoispitivanje.
1. Koje se točke nazivaju točkama ekstrema (maksimuma i minimuma) funkcije?
2. Koja se funkcija naziva rastućom (opadajućom)?
3. Koji su nužni i dovoljni uvjeti za postojanje točaka ekstrema funkcije?
4. Koji je dovoljan uvjet za porast (padanje) funkcije?
5. Koje se točke nazivaju točkama infleksije funkcije?
6. Koja se funkcija naziva konveksnom (konkavnom)?
7. Koji su nužni i dovoljni uvjeti za postojanje infleksijskih točaka funkcije?
8. Koji je dovoljan uvjet za konveksnost (konkavnost) funkcije?
Svrha lekcije: Naučiti kako provesti studiju funkcija; zacrtati ih.
Oblik: sat razgovora.
Metode: dijalog, vizualna pomagala i slajdovi.
Oprema: ICT, tablice.
Tijekom nastave
I. Provjera domaće zadaće.
Učitelj: - Dečki! Imali ste zadaću "Kritične točke funkcije, maksimumi i minimumi". Definirajte kritičnu točku funkcije.
Učenik: - Kritična točka je unutarnja točka domene definicije u kojoj je derivacija ili jednaka nuli ili ne postoji.
Učitelj: - Kako pronaći kritične točke?
Učenik: - 1
) Naći derivaciju funkcije;
2) Riješite jednadžbu: f "(x) = 0. Korijeni ove jednadžbe su kritične točke.
Učitelj: - Pronađite kritične točke funkcija:
a) f(x)= 4 - 2x + 7x 2
b) f (x) \u003d 4x - x 3/3
a) 1) Nađite derivaciju ove funkcije:
f "(x)= (4 - 2x + 7x 2)" = -2+14x
2) Riješite jednadžbu f "(x) = 0<=>-2+14x=0<=>x=1/7
3) Budući da jednadžba f "(x) \u003d 0 ima jedan korijen, tada ova funkcija ima jednu kritičnu točku x \u003d 1/7.
b) 1) Pronađite izvod ove funkcije: f "(x) \u003d 4 - x 2
2) Riješite jednadžbu: f "(x) = 0<=>4 - x 2 = 0<=>x=2 ili x=-2
3) Budući da jednadžba f "(x) \u003d 0 ima dva korijena, tada ova funkcija ima dvije kritične točke x 1 \u003d 2 i x 2 \u003d -2.
II.usmeni rad.
Učitelj: - Dečki! Ponovimo glavna pitanja koja su potrebna za proučavanje nove teme. Da biste to učinili, razmotrite tablice sa slikama ( Prilog 1).
Navedite točke u kojima se porast funkcije zamjenjuje opadanjem. Kako se zovu ove točke?
Učenik: - Na slici a) - točka K je točka maksimuma, na slici b) - točka M je točka maksimuma.
Učitelj: - Koje su minimalne točke funkcije.
Učenik: - Točka K na slici c) i d) - točka minimuma funkcije.
Učitelj: - Koje točke mogu biti točke ekstrema funkcije?
Učenik: - Kritične točke mogu biti točke ekstrema funkcije.
Učitelj: - Koje su potrebne uvjete znate?
Učenik: - Postoji Fermatov teorem. Neophodan uvjet za ekstrem: Ako je točka x 0 ekstremna točka funkcije f i u ovoj točki postoji derivacija f ", tada je jednaka nuli: f" (x) \u003d 0.
Učitelj: - Pronađite kritične točke za funkciju:
a) f(x) = | x |
b) f(x) = 2x + | x |
Učenik: - Promotrimo funkciju f(x) = | x | ( primjena 2). Ova funkcija nema derivaciju na 0. Dakle, 0 je kritična točka. Očito je da funkcija ima minimum u točki 0.
Učenik: - Promotrimo funkciju f(x) = 2x + | x | ( dodatak 3). Grafikon pokazuje da u točki 0 ova funkcija nema ekstrem. U ovom trenutku ni funkcija nema izvod.
Doista, ako pretpostavimo da funkcija f ima derivaciju u 0, tada f(x) - 2x također ima derivaciju u 0. Ali f(x) - 2x = | x |, a funkcija | x | u točki 0 nije diferencijabilna, tj. došli smo do kontradikcije.
To znači da funkcija f u točki 0 nema derivaciju.
Učitelj: - Iz Fermatovog teorema proizlazi da pri pronalaženju točaka ekstrema treba pronaći kritične točke. Ali iz razmatranih primjera jasno je da je potreban neki dodatni uvjet da bi ta kritična točka bila točka ekstrema.
Koji su dovoljni uvjeti za postojanje ekstrema u točki znate li?
Student: - Znak maksimalne funkcije: Ako je funkcija f kontinuirana u točki x 0, a f "(x)> 0 na intervalu (a; x 0) i f "(x)<0 на интервале (х 0 ; в), то точка х 0 является точкой максимума функции f.
To jest, ako u točki x 0 derivacija promijeni predznak iz plusa u minus, tada je x 0 točka maksimuma.
Student: - Znak minimuma: Ako je funkcija f kontinuirana u točki x 0, a f "(x)<0 на интервале (а;х 0) и f "(x) >0 na intervalu (x 0 ; c), tada je točka x 0 točka minimuma funkcije f.
To jest, ako u točki x 0 derivacija promijeni predznak iz minusa u plus, tada je x 0 minimalna točka.
Učitelj: - A koji algoritam za pronalaženje točaka ekstrema funkcije znate.
Student objašnjava algoritam za proučavanje funkcije f za ekstremum pomoću derivacije ( dodatak 4) i pronalazi točke ekstrema funkcije:
f (x) \u003d x 4 -2x 2
D (f) =IR i f je kontinuirana na cijelom realnom pravcu, kao cijela racionalna funkcija.
2. f "(x) \u003d 4x 3 -4x \u003d 4x (x + 1) (x-1).
3.f"(x)=0<=>x \u003d -1 V x \u003d 0 V x \u003d 1.
Sl.1 (znakovi f ")
Budući da je f kontinuirana u kritičnim točkama, sa slike 1 ( dodatak 5) vidi se da su -1 i 1 točke minimuma, a 0 točka maksimuma funkcije f.
f min = f (-1) = f (1) = -1, f max = f (0) = 0.
Učitelj: - Dečki! Prisjetimo se algoritma za pronalaženje intervala monotonosti funkcije f.
Student se sjeća algoritma za pronalaženje intervala monotonosti funkcije f ( dodatak 6).
Učitelj: - Odredite intervale porasta i opadanja funkcije f zadane formulom
f (x) \u003d x 3 -12x
Riješenje:
1. Kako je f(x) polinom, tada je D (f) =IR.
2. Funkcija f je diferencijabilna na cijeloj realnoj liniji i f "(x) \u003d 3x 2 -12 \u003d 3 (x + 2) (x-2).
3. Samo nule od f "(x) mogu biti kritične točke funkcije f.
f"(x)=0<=>x \u003d -2 V x \u003d 2.
D (f) \ (-2; 2) \u003d (-; -2) U (-2; 2) U (2; +).
Sl.2 (znakovi f ").
Pronađite domene definicije i vrijednosti zadane funkcije f.
Saznajte ima li funkcija značajke koje olakšavaju proučavanje, odnosno ima li funkcija f:
a) par ili nepar;
b) periodički.
3. Izračunajte koordinate sjecišta grafa s koordinatnim osima.
4. Odredite intervale konstantnosti funkcije f.
5. Utvrdite na kojim intervalima funkcija f raste, a na kojim pada.
6. Pronađite točke ekstrema (maksimum ili minimum) i izračunajte vrijednosti f u tim točkama.
7. Istražiti ponašanje funkcije f u okolini karakterističnih točaka koje nisu uključene u domenu definicije.
8. Grafički nacrtajte funkciju.
Ovaj dijagram je ilustrativan.
Uzimajući u obzir sve gore navedeno, ispitujemo funkciju: f (x) \u003d 3x 5 -5x 3 +2 i gradimo njezin graf.
Provedimo istraživanje na sljedeći način:
D (f ") = IR, jer je f (x) polinom.
Funkcija f nije ni parna ni neparna, jer
f (-x)= 3(-x) 5 -5(-x) 3 +2 = -3x 5 +5x 3 +2= -(3x 5 -5x 3 -2) f(x)
Odredite koordinate sjecišta grafa s koordinatnim osima:
a) s osi 0X, za to rješavamo jednadžbu: 3x 5 -5x 3 +2 = 0.
Metodom odabira može se pronaći jedan od korijena (x = 1). Ostali korijeni mogu se pronaći samo približno. Dakle, za ovu funkciju nećemo pronaći preostale točke sjecišta grafa s apscisnom osi i intervale konstantnog predznaka.
b) s osi 0Y: f(0)=2
Točka A (0; 2) - točka presjeka grafa funkcije s osi 0Y.
Napomenuli smo da nećemo pronaći intervale konstantnosti predznaka.
Odredite intervale rasta i opadanja funkcije
a) f "(x) \u003d 15x 4 -15x 2 \u003d 15x 2 (x 2 -1)
D (f ") \u003d IR, stoga nema kritičnih točaka od kojih f "(x) ne postoji.
b) f "(x) \u003d 0 ako je x 2 (x 2 -1) \u003d 0<=>x = -1 V x = 0 V x = 1.
c) Dobivamo tri kritične točke, one dijele koordinatni pravac na četiri intervala. Odredimo predznak derivacije na ovim intervalima:
Sl.3 (znakovi f ")
IV. Popravljanje nove teme. Rješavanje problema.
Učitelj: - Istražite funkciju i izgradite njezin graf: f (x) \u003d x 4 -2x 2 -3.
Učenik: - 1) D (f) =R.
2) f (-x) \u003d (-x) 4 -2 (-x) 2 -3 \u003d x 4 -2x 2 -3; f(-x)= f(x),
dakle funkcija f je parna. Može se proučavati na intervalu u kojem funkcija raste od - do -4, dakle, jednadžba f (x) \u003d 0 nema korijene na ovom intervalu.
b) Na intervalu [-1; 2] jednadžba također nema korijena, jer na tom intervalu funkcija opada od -4 do -31.
c) Na intervalu i opada na [-∞;-1].

Ekstremne točke: x min = -1
Ekstremumi funkcije: y min =y(-1)=1-2= -1
poglavlje III. Istraživanje funkcija.
3.1. Opća shema za proučavanje funkcija.
Kada ispitujete funkciju, morate znati opću shemu istraživanja:
1) D(y) – domena definicije (raspon varijable x)
2) E(y) – područje vrijednosti x (raspon varijable y)
3) Vrsta funkcije: parna, neparna, periodična ili opća funkcija.
4) Točke presjeka grafa funkcije s osi Ohi Oy (ako je moguće).
5) Intervali konstantnosti predznaka:
a) funkcija poprima pozitivnu vrijednost: f(x)>0
b) negativna vrijednost: f(x)<0.
6) Intervali monotonosti funkcije:
a) povećanje;
b) smanjenje;
c) postojanost (f=const).
7) Ekstremne točke (minimalne i maksimalne točke)
8) Ekstremumi funkcije (vrijednost funkcije u minimalnim i maksimalnim točkama)
9) Dodatni bodovi.
Mogu se uzeti kako bi se funkcija točnije iscrtala.
Treba napomenuti da se ekstremi funkcije f ne podudaraju uvijek s maksimalnim i minimalnim vrijednostima funkcije.
3.2. Predznak rastućih i padajućih funkcija.
Ako izgradite graf funkcije pomoću nekih proizvoljno odabranih točaka, povezujući ih glatkom linijom, tada čak i s vrlo velikim brojem nasumično odabranih točaka, može se pokazati da će graf konstruiran na ovaj način biti vrlo različit iz grafa zadane funkcije.
Ako pri proučavanju funkcije koristimo derivaciju i pronađemo takozvane "referentne" točke, tj. prijelomne točke, maksimalne i minimalne točke, intervali monotonosti funkcije, tada ćemo čak i s malim brojem takvih "referentnih" točaka dobiti ispravnu predodžbu o grafu funkcije.
Prije nego prijeđem na primjere, dat ću potrebne definicije i teoreme.
Definicija monotonosti funkcije na intervalu
Funkcija y \u003d f (x) naziva se rastućom na intervalu, ako za bilo koje točke x 1 i x 2 ovog intervala iz uvjeta x 1<х 2
следует, что f(x 1)
Dovoljan kriterij za monotonost funkcije u intervalu. Teorem: ako funkcija ima pozitivnu (negativnu) derivaciju u svakoj točki intervala, tada funkcija raste (opada) na tom intervalu.
Ovaj teorem je prihvaćen u školskim udžbenicima bez dokaza.
Geometrijska interpretacija teorema je vrlo jednostavna, ako se prisjetimo da je f '(x) \u003d tgα, α nagib tangente na graf funkcije u danoj točki x. Ako je npr. f ‘ (x) > 0 u svim točkama određenog intervala, tada tangente na grafu s apscisnom osi čine oštre kutove, što znači da i f (x) raste s x. Ako je f' (x)<0, то касательная с осью абсцисс образуют тупой угол, а значит, с ростом х функция f(x) убывает. Поскольку эти рассуждения основаны лишь на наглядных геометрических представлениях, они не являются доказательством теоремы.
3.3. Kritične točke funkcije, maksimumi i minimumi.
Određivanje točaka ekstrema funkcije . Neka je x 0 unutarnja točka iz domene funkcije f(x). Zatim, ako postoji takva δ - okolina ] x 0 - δ, x 0 + δ [ točke x 0 , da je za sve x iz te okoline zadovoljena nejednakost f(x)≤f(x 0) (nejednakost f (x)≥f (x 0)), točku x 0 nazivamo točkom maksimuma (točkom minimuma) ove funkcije.
Točke maksimuma i minimuma unutarnje su točke domene funkcije.
Nužan kriterij za postojanje ekstrema diferencijabilne funkcije .
Fermatov teorem.
Ako je x 0 točka ekstrema funkcije f (x) iu toj točki postoji derivacija, tada je ona jednaka nuli: f '(x 0) \u003d 0.
Ovaj teorem nije dovoljan uvjet za postojanje ekstrema diferencijabilne funkcije: ako u nekoj točki x 0 derivacija nestane, tada još ne slijedi da u točki x 0 funkcija ima ekstrem.
Definicija kritičnih točaka funkcije . Unutarnje točke područja funkcije, u kojima je njezina derivacija jednaka nuli ili ne postoji, nazivaju se kritičnim točkama funkcije.
Dovoljni uvjeti za postojanje ekstrema .
Teorem 1. Ako je funkcija f (x) kontinuirana u točki x 0, f '(x)> 0 na intervalu i f '(x)<0 на интервале , то х 0 является точкой максимума функции f(x).
Teorem 2. Ako je funkcija f (x) kontinuirana u točki x 0, f '(x)<0 на интервале и f ‘(x)>0 na intervalu, tada je x 0 točka minimuma funkcije f(x).
Za pronalaženje točaka ekstrema funkcije potrebno je pronaći njezine kritične točke i za svaku od njih provjeriti ispunjenje dovoljnih uvjeta ekstrema.
3.4. Najveća i najmanja vrijednost funkcije.
Pravila za pronalaženje najvećih i najmanjih vrijednosti funkcija u intervalu. Da biste pronašli najveću i najmanju vrijednost funkcije koja se može diferencirati u određenom intervalu, morate pronaći sve kritične točke koje leže unutar intervala, izračunati vrijednosti funkcije u tim točkama i na krajevima interval, te od svih tako dobivenih vrijednosti funkcije izabrati najveću i najmanju.
Poglavlje IV. Primjeri primjene izvoda na proučavanje funkcije.
Primjer 11. Istražite funkciju y=x 3 +6x 2 +9x i izgradite graf.
2) Definirajte tip funkcije:
y(-x)=(-x) 3 +6(-x) 2 +9(-x)=-x+6x 2 -9x opća funkcija.
x=0 ili x2 +6x+9=0
D=0, jednadžba ima jedan korijen.
(0;0) i (-3;0) - točke presjeka s x-osi.
y'=(x 3 +6x 2 +9x)'=3x 2 +12x+9
y'=0, tj. 3x 2 +12x+9=0 smanji za 3
D>0, jednadžba ima 2 korijena.
x 1,2 \u003d (-b±√D) / 2a, x 1 \u003d (-4 + 2) / 2, x 2 \u003d (-4-2) / 2
0  -4
-4
x=-4, y’=3*16-48+9=9>0
x=-2, y’=12-24+9=-3<0
x=0, y'=0+0+9=9>0
7) Pronađite x min i x max:
8) Pronađite ekstreme funkcije:
ymin=y(-1)=-1+6-9=-4
ymax=y(-3)=-27+54-27=0
9) Izgradimo graf funkcije:

10) Dodatne točke:
y(-4)=-64+96-36=-4
Primjer 12. Istražite funkciju y=x 2 /(x-2) i izgradite graf
y=x 2 /(x-2)=x+2+4/(x-2)
Nađimo asimptote funkcije:
 x≠ 2, x=2 – vertikalna asimptota
x≠ 2, x=2 – vertikalna asimptota
y=x+2 je kosa asimptota, jer
Nađimo domenu definicije.
2) Definirajmo tip funkcije.
y(-x)=(-x) 2 /(-x-2)=x 2 /(-x-2), opća funkcija.
3) Pronađite točke sjecišta s osi.
Oy: x=0, y=0 (0;0) – točka presjeka s osi y.
x=0 ili x=2 (2;0) – točka presjeka s x-osi
4) Pronađite izvod funkcije:
y'=(2x(x-2)-x 2)/(x-2) 2 =(2x 2 -4x-x 2)/(x-2) 2 =(x(x-4))/(x -2) 2 \u003d (x 2 -4x) / (x-2) 2
5) Definirajte kritične točke:
x 2 -4x=0 x(x-4)=0
y'=0, (x 2 -4x)/(x-2) 2 =0<=> <=>
(x-2) 2 ≠ 0 x≠ 2
x 2 -4x=0, i (x-2) 2 ≠ 0, tj. x≠ 2
6) Na koordinatnoj liniji označimo kritične točke i odredimo predznak funkcije.
 0 8
0 8
x=-1, y’=(1+4)/9=5/9>0
x=1, y’=(1-4)/1=-3<0
x=3, y’=(9-12)/1=-3<0
x=5, y’=(25-20)/9=5/9>0
7) Pronađite točku minimuma i maksimuma funkcije:
8) Pronađite ekstreme funkcije:
ymin=y(4)=16/2=8
9) Izgradimo graf funkcije:

10) Dodatne točke:
y(-3)=9/-5=-1,8 y(3)=9/1=9
y(1)=1/-1=-1 y(6)=36/4=9
Primjer 13 Istražite funkciju y=(6(x-1))/(x 2 +3) i izgradite graf. 1) Pronađite domenu funkcije:
2) Definirajte tip funkcije:
y(-x)=(6(-x-1))/(x 2 +3)=-(6(x+1))/(x 2 -3) je opća funkcija.
3) Pronađite točke sjecišta s osi:
O y: x=0, y=(6(0-1))/(0+3)=-2, (0;-2) – točka presjeka s y-osi.
(6(x-1))/(x 2 +3)=0
O x: y=0,<=>
4) Pronađite izvod funkcije:
y'=(6(x-1)/(x 2 +3))'=6(x 2 +3-2x 2 +2x)/(x 2 +2) 2 =-6(x+1)(x -3)/(x 2 +3) 2
5) Definirajte kritične točke:
y'=0, tj. -6(x+1)(x-3)/(x 2 +3) 2 =0
y’=0, ako je x 1 =-1 ili x 2 =3, onda su x=-1 i x=3, kritične točke.
6) Označimo kritične točke na koordinatnoj liniji i odredimo predznak funkcije:
 -3 2
-3 2
x=-2, y’=-6(-2+1)(-2-3)/(4+3) 2 =-30/49<0
x=0, y'=-6(0+1)(0-3)/(0+3) 2 =2>0
x=4, y’=-6(4+1)(4-3)/(16+3) 2=-30/361<0
7) Pronađite minimalne i maksimalne bodove:
8) Pronađite ekstreme funkcije:
y min =y(-1)=(6(-1-1))/(1+3)=-12/4=-3
y max =y(3)=(6(3-1))/(9+3)=12/12=1
9) Izgradimo graf funkcije:

10) Dodatne točke:
y(-3)=(6(-3-1))/(9+3)=-24/12=-2
y(6)=(6(6-1))/(36+3)=30/39=10/13≈ 0,77
Primjer 14 Istražite funkciju y=xlnx i izgradite njezin grafikon:
1) Pronađite domenu funkcije:
D(y)=R + (samo pozitivne vrijednosti)
2) Definirajte tip funkcije:
y(-x)=-xlnx - opći oblik.
3) Pronađite točke sjecišta s osi:
O y , ali x≠ 0, pa nema točaka sjecišta s y-osi.
Ox: y=0 tj. xlnx=0
x=0 ili lnx=0
(1;0) - točka sjecišta s x-osi
4) Pronađite izvod funkcije:
y'=x' ln x + x(ln x)'=ln x +1
5) Definirajte kritične točke:
y'=0, tj. lnx +1=0
y'=0 , ako je x=1/e , tada je x=1/e kritična točka.
6) Označimo kritične točke na koordinatnoj liniji i odredimo predznak funkcije:
1/e 
x=1/(2e); y'=log(2e) -1 +1=1-ln(2e)=1-ln e=-ln 2<0
x=2e; y'=ln(2e)+1=ln 2+ln e+1=ln 2+2>0
7) 1/e je točka minimuma funkcije.
8) Pronađite ekstreme funkcije:
y min \u003d y (1 / e) \u003d 1 / e ln e -1 \u003d -1 / e (≈ -0,4).
9) Izgradimo graf funkcije:

Zaključak.
Mnogi znanstvenici i filozofi radili su na ovoj temi. Prije mnogo godina pojavili su se ovi pojmovi: funkcija, graf, proučavanje funkcije, te su preživjeli do danas, dobivajući nova obilježja i karakteristike.
Odabrao sam ovu temu jer mi je bilo jako zanimljivo proći ovaj put istraživanja funkcije. Čini mi se da bi mnoge ljude zanimalo saznati više o funkciji, njezinim svojstvima i transformacijama. Nakon što sam napravio ovaj esej, sistematizirao sam svoje vještine i obnovio svoje znanje o ovoj temi.
Želim svima savjetovati da dublje prouče ovu temu.
Bibliografija.
1. Bashmakov, M.I. Algebra i početak analize - M .: Obrazovanje, 1992.
2. Glaser, G.I. Povijest matematike u školi. - M .: Obrazovanje, 1983.
3. Gusev, V.A. Matematika: referentni materijali - M .: Obrazovanje, 1888.
4. Dorofejev, G.V. Matematički priručnik za kandidate za sveučilišta - M .: Nauka, 1974.
5. Zorin, V.V. Matematički priručnik za kandidate za sveučilišta - M .: Viša škola, 1980.
6. Kolmogorov A.N. Algebra i počeci analize.- M.: Prosvjetljenje, 1993.