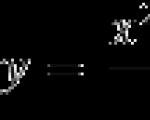Dom › Svjetlo i staklo › Kako ukloniti modul u nejednakosti. Modulo jednadžbe

Kako ukloniti modul u nejednakosti. Modulo jednadžbe

Rješavanje nejednakosti online

Prije rješavanja nejednadžbi potrebno je dobro razumjeti kako se rješavaju jednadžbe.

Nije važno je li nejednakost stroga () ili nije stroga (≤, ≥), prvi korak je riješiti jednadžbu zamjenom znaka nejednakosti s jednakošću (=).

Objasnite što znači riješiti nejednadžbu?

Nakon proučavanja jednadžbi, učenik ima sljedeću sliku u glavi: trebate pronaći takve vrijednosti varijable za koje oba dijela jednadžbe imaju iste vrijednosti. Drugim riječima, pronađite sve točke u kojima vrijedi jednakost. Sve je točno!

Kada se govori o nejednakostima, misli se na pronalaženje intervala (odsječaka) na kojima nejednakost vrijedi. Ako u nejednadžbi postoje dvije varijable, tada rješenje više neće biti intervali, već neka područja na ravnini. Pogodite što će biti rješenje nejednadžbe u tri varijable?

Kako riješiti nejednadžbe?

Metoda intervala (poznata i kao metoda intervala) smatra se univerzalnim načinom rješavanja nejednadžbi, koji se sastoji u određivanju svih intervala unutar kojih će se zadana nejednadžba ispuniti.

Ne ulazeći u vrstu nejednadžbe, u ovom slučaju to nije bit, potrebno je riješiti odgovarajuću jednadžbu i odrediti njezine korijene, a zatim slijedi označavanje tih rješenja na numeričkoj osi.

Kako je ispravno napisati rješenje nejednadžbe?

Kada ste odredili intervale za rješavanje nejednadžbe potrebno je ispravno ispisati samo rješenje. Postoji važna nijansa - jesu li granice intervala uključene u rješenje?

Ovdje je sve jednostavno. Ako rješenje jednadžbe zadovoljava ODZ i nejednadžba nije stroga, tada se granica intervala uključuje u rješenje nejednadžbe. Inače, ne.

S obzirom na svaki interval, rješenje nejednadžbe može biti sam interval, ili poluinterval (kada jedna njegova granica zadovoljava nejednadžbu), ili segment - interval zajedno sa svojim granicama.

Važna točka

Nemojte misliti da samo intervali, poluintervali i segmenti mogu biti rješenje nejednadžbe. Ne, u rješenje se mogu uključiti i pojedinačne točke.

Na primjer, nejednadžba |x|≤0 ima samo jedno rješenje - točku 0.

I nejednakost |x|

Čemu služi kalkulator nejednakosti?

Kalkulator nejednakosti daje točan konačni odgovor. U ovom slučaju, u većini slučajeva, daje se ilustracija numeričke osi ili ravnine. Možete vidjeti jesu li granice intervala uključene u rješenje ili ne - točke se prikazuju ispunjene ili probušene.

Zahvaljujući online kalkulatoru nejednakosti možete provjeriti jeste li točno pronašli korijene jednadžbe, označili ih na brojevnom pravcu i provjerili uvjete nejednakosti na intervalima (i granicama)?

Ako se vaš odgovor razlikuje od odgovora kalkulatora, onda svakako morate još jednom provjeriti svoje rješenje i identificirati pogrešku.

Što više čovjek razumije, to je njegova želja za razumijevanjem jača

Toma Akvinski

Metoda intervala omogućuje vam rješavanje svih jednadžbi koje sadrže modul. Suština ove metode je rastavljanje numeričke osi na nekoliko dionica (intervala), pri čemu je potrebno rastaviti os s nulama izraza u modulima. Zatim, na svakom od rezultirajućih odjeljaka, svaki izraz podmodula je pozitivan ili negativan. Stoga se svaki od modula može proširiti ili znakom minus ili znakom plus. Nakon ovih radnji ostaje samo riješiti svaku od dobivenih jednostavnih jednadžbi na intervalu koji se razmatra i kombinirati dobivene odgovore.

Razmotrimo ovu metodu na konkretnom primjeru.

|x + 1| + |2x – 4| – |x + 3| = 2x - 6.

1) Pronađite nule izraza u modulima. Da bismo to učinili, izjednačimo ih s nulom i riješimo dobivene jednadžbe.

x + 1 = 0 2x – 4 = 0 x + 3 = 0

x = -1 2x = 4 x = -3

2) Rasporedi dobivene točke željenim redoslijedom na koordinatnoj liniji. Oni će razbiti cijelu os u četiri dijela.

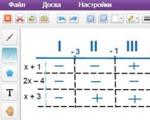
3) Odredimo na svakom od dobivenih odjeljaka predznake izraza u modulima. Da bismo to učinili, zamijenimo ih bilo kojim brojevima iz intervala koji nas zanimaju. Ako je rezultat izračuna pozitivan broj, tada u tablicu stavljamo "+", a ako je broj negativan, tada stavljamo "-". Ovo se može prikazati ovako:

4) Sada ćemo riješiti jednadžbu na svakom od četiri intervala, otvarajući module s predznacima koji se nalaze u tablici. Dakle, razmotrite prvi interval:

I interval (-∞; -3). Na njemu se svi moduli otvaraju znakom "-". Dobivamo sljedeću jednadžbu:

-(x + 1) - (2x - 4) - (-(x + 3)) \u003d 2x - 6. Predstavljamo slične članove, nakon što smo prethodno otvorili zagrade u dobivenoj jednadžbi:

X - 1 - 2x + 4 + x + 3 = 2x - 6

Dobiveni odgovor ne ulazi u razmatrani interval, pa ga nije potrebno upisati u konačni odgovor.

II interval [-3; -1). U ovom intervalu u tablici postoje znakovi "-", "-", "+". Ovako otkrivamo module izvorne jednadžbe:

-(x + 1) - (2x - 4) - (x + 3) = 2x - 6. Pojednostavite širenjem zagrada:

X - 1 - 2x + 4 - x - 3 \u003d 2x - 6. U dobivenoj jednadžbi prikazujemo sljedeće:

x = 6/5. Rezultirajući broj ne pripada intervalu koji se razmatra, stoga nije korijen izvorne jednadžbe.

III interval [-1; 2). Module izvorne jednadžbe otvaramo predznacima koji se nalaze na slici u trećem stupcu. Dobivamo:

(x + 1) - (2x - 4) - (x + 3) = 2x - 6. Riješite se zagrada, pomaknite članove koji sadrže varijablu x na lijevu stranu jednadžbe, a ne sadrže x na desnu stranu. . Imat će:

x + 1 - 2x + 4 - x - 3 = 2x - 6

Broj 2 nije uključen u razmatrani interval.

IV interval

Jednostavno rečeno, modul je "broj bez minusa". I upravo u toj dvojnosti (negdje ne morate ništa raditi s izvornim brojem, ali negdje morate ukloniti neki minus tamo) i leži sva poteškoća za studente početnike.

Postoji i geometrijska definicija. Također ga je korisno znati, ali ćemo se na njega pozivati samo u složenim i nekim posebnim slučajevima, gdje je geometrijski pristup praktičniji od algebarskog (spojler: ne danas).

Definicija. Neka je na realnom pravcu označena točka $a$. Zatim modul $\lijevo| x-a \right|$ je udaljenost od točke $x$ do točke $a$ na ovom pravcu.

Ako nacrtate sliku, dobit ćete nešto poput ovoga:

Definicija grafičkog modula

Na ovaj ili onaj način, njegovo ključno svojstvo neposredno proizlazi iz definicije modula: modul broja uvijek je nenegativna vrijednost. Ta će činjenica biti crvena nit kroz cijelu našu današnju priču.

Rješenje nejednadžbi. Metoda razmaka

Sada se pozabavimo nejednakostima. Ima ih jako puno, ali naš je zadatak sada riješiti barem najjednostavniji od njih. One koje se svode na linearne nejednadžbe, kao i na metodu intervala.

Imam dva velika tutorijala o ovoj temi (usput, vrlo, JAKO korisna - preporučujem proučavanje):

Metoda intervala za nejednakosti (posebno pogledajte video);
Razlomačko-racionalne nejednakosti vrlo je opsežna lekcija, ali nakon nje nećete imati nikakva pitanja.

Ako sve ovo znate, ako fraza “prijeđimo s nejednakosti na jednadžbu” ne budi nejasnu želju da se ubijete u zid, onda ste spremni: dobrodošli u pakao na glavnu temu lekcije. :)

1. Nejednadžbe oblika "Modul manji od funkcije"

Ovo je jedan od zadataka koji se najčešće susreću s modulima. Potrebno je riješiti nejednadžbu oblika:

\[\lijevo| f\desno| \ltg\]

Bilo što može djelovati kao funkcije $f$ i $g$, ali obično su to polinomi. Primjeri takvih nejednakosti:

Svi se rješavaju doslovno u jednom retku prema shemi:

\[\lijevo| f\desno| \lt g\Rightarrow -g \lt f \lt g\quad \left(\Rightarrow \left\( \begin(align) & f \lt g, \\ & f \gt -g \\\end(align) \točno točno)\]

Lako je vidjeti da se rješavamo modula, ali umjesto toga dobivamo dvostruku nejednadžbu (ili, što je isto, sustav dviju nejednadžbi). Ali ovaj prijelaz uzima u obzir apsolutno sve moguće probleme: ako je broj ispod modula pozitivan, metoda radi; ako je negativan, i dalje radi; čak i s najneprikladnijom funkcijom umjesto $f$ ili $g$, metoda će i dalje raditi.

Naravno, postavlja se pitanje: nije li lakše? Nažalost, ne možete. To je cijela poanta modula.

Ali dosta filozofiranja. Riješimo par problema:

Zadatak. Riješite nejednadžbu:

\[\lijevo| 2x+3\desno| \ltx+7\]

Riješenje. Dakle, imamo klasičnu nejednakost oblika "modul je manji od" - čak se nema što transformirati. Radimo prema algoritmu:

\[\begin(align) & \left| f\desno| \lt g\desna strelica -g \lt f \lt g; \\ & \lijevo| 2x+3\desno| \lt x+7\desna strelica -\lijevo(x+7 \desno) \lt 2x+3 \lt x+7 \\\end(align)\]

Nemojte žuriti s otvaranjem zagrada ispred kojih stoji "minus": vrlo je moguće da ćete zbog žurbe napraviti uvredljivu pogrešku.

\[-x-7 \lt 2x+3 \lt x+7\]

\[\lijevo\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(align) \desno.\]

\[\lijevo\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \desno.\]

\[\lijevo\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \desno.\]

Problem je sveden na dvije elementarne nejednakosti. Bilježimo njihova rješenja na paralelnim realnim pravcima:
Sjecište mnogih
Presjek ovih skupova bit će odgovor.

Odgovor: $x\in \lijevo(-\frac(10)(3);4 \desno)$

Zadatak. Riješite nejednadžbu:

\[\lijevo| ((x)^(2))+2x-3 \desno|+3\lijevo(x+1 \desno) \lt 0\]

Riješenje. Ovaj zadatak je malo teži. Za početak, izoliramo modul pomicanjem drugog člana udesno:

\[\lijevo| ((x)^(2))+2x-3 \desno| \lt -3\lijevo(x+1 \desno)\]

Očito opet imamo nejednakost oblika “modul je manji”, pa se rješavamo modula prema već poznatom algoritmu:

\[-\lijevo(-3\lijevo(x+1 \desno) \desno) \lt ((x)^(2))+2x-3 \lt -3\lijevo(x+1 \desno)\]

Sad pozor: netko će reći da sam malo perverznjak sa svim tim zagradama. Ali još jednom vas podsjećam da je naš ključni cilj točno riješiti nejednadžbu i dobiti odgovor. Kasnije, kada savršeno savladate sve što je opisano u ovoj lekciji, možete se pervertirati kako želite: otvarati zagrade, dodavati minuse itd.

I za početak, samo se riješimo dvostrukog minusa s lijeve strane:

\[-\lijevo(-3\lijevo(x+1 \desno) \desno)=\lijevo(-1 \desno)\cdot \lijevo(-3 \desno)\cdot \lijevo(x+1 \desno) =3\lijevo(x+1\desno)\]

Sada otvorimo sve zagrade u dvostrukoj nejednakosti:

Prijeđimo na dvostruku nejednakost. Ovaj put će računice biti ozbiljnije:

\[\lijevo\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(align) \desno.\]

\[\lijevo\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( poravnati)\desno.\]

Obje nejednadžbe su kvadratne i rješavaju se metodom intervala (zato i kažem: ako ne znate što je, bolje da još ne ulazite u module). Prelazimo na jednadžbu u prvoj nejednadžbi:

\[\begin(align) & ((x)^(2))+5x=0; \\ & x\lijevo(x+5 \desno)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\end(align)\]

Kao što vidite, ispostavilo se da je izlaz nepotpuna kvadratna jednadžba, koja se elementarno rješava. Sada se pozabavimo drugom nejednakošću sustava. Tu morate primijeniti Vietin teorem:

\[\begin(align) & ((x)^(2))-x-6=0; \\ & \lijevo(x-3 \desno)\lijevo(x+2 \desno)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\end(align)\]

Dobivene brojeve označavamo na dvije paralelne crte (posebno za prvu nejednadžbu, a posebno za drugu):
Opet, budući da rješavamo sustav nejednadžbi, zanima nas presjek osjenčanih skupova: $x\in \left(-5;-2 \right)$. Ovo je odgovor.
Odgovor: $x\in \lijevo(-5;-2 \desno)$

Mislim da je nakon ovih primjera shema rješenja vrlo jasna:

Izolirajte modul pomicanjem svih ostalih članova na suprotnu stranu nejednakosti. Tako dobivamo nejednakost oblika $\left| f\desno| \ltg$.
Riješite ovu nejednadžbu tako da se riješite modula kako je gore opisano. U jednom trenutku bit će potrebno prijeći s dvostruke nejednadžbe na sustav dva neovisna izraza od kojih se svaki već može zasebno riješiti.
Na kraju, ostaje još samo križati rješenja ova dva nezavisna izraza - i to je to, dobit ćemo konačan odgovor.

Sličan algoritam postoji za nejednakosti sljedećeg tipa, kada je modul veći od funkcije. Međutim, postoji nekoliko ozbiljnih "ali". Sada ćemo govoriti o tim "ali".

2. Nejednadžbe oblika "Modul je veći od funkcije"

Izgledaju ovako:

\[\lijevo| f\desno| \gt g\]

Slično prethodnom? Čini se. Ipak, takvi se zadaci rješavaju na potpuno drugačiji način. Formalno, shema je sljedeća:

\[\lijevo| f\desno| \gt g\Rightarrow \lijevo[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(align) \desno.\]

Drugim riječima, razmatramo dva slučaja:

Prvo, jednostavno zanemarimo modul - rješavamo uobičajenu nejednadžbu;
Tada, zapravo, otvaramo modul s predznakom minus, a zatim oba dijela nejednadžbe množimo s −1, s predznakom.

U ovom slučaju opcije se kombiniraju s uglatom zagradom, tj. Imamo kombinaciju dva zahtjeva.

Obratite pažnju opet: pred nama nije sustav, nego agregat, dakle u odgovoru se skupovi kombiniraju, a ne sijeku. Ovo je temeljna razlika u odnosu na prethodni pasus!

Općenito, mnogi studenti imaju dosta zabune sa sindikatima i raskrižjima, pa pogledajmo ovo pitanje jednom zauvijek:

"∪" je znak ulančavanja. Zapravo, ovo je stilizirano slovo "U", koje nam je došlo iz engleskog jezika i kratica je za "Union", tj. "Udruge".
"∩" je znak raskrižja. Ovo sranje nije došlo niotkuda, nego se samo pojavilo kao opozicija "∪".

Da biste ga još lakše zapamtili, samo dodajte noge ovim znakovima da napravite naočale (samo me nemojte sada optuživati da promičem ovisnost o drogama i alkoholizam: ako ozbiljno učite ovu lekciju, onda ste već narkoman):

Razlika između presjeka i unije skupova

Prevedeno na ruski, to znači sljedeće: unija (zbirka) uključuje elemente iz oba skupa, dakle, ne manje od svakog od njih; ali presjek (sustav) uključuje samo one elemente koji su i u prvom skupu i u drugom. Stoga presjek skupova nikada nije veći od izvornih skupova.

Tako je postalo jasnije? To je odlično. Prijeđimo na praksu.

Zadatak. Riješite nejednadžbu:

\[\lijevo| 3x+1 \desno| \gt 5-4x\]

Riješenje. Djelujemo prema shemi:

\[\lijevo| 3x+1 \desno| \gt 5-4x\desna strelica \lijevo[ \begin(align) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\lijevo(5-4x \desno) \\\end(align) \ pravo.\]

Rješavamo svaku nejednakost stanovništva:

\[\lijevo[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \desno.\]

\[\lijevo[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \desno.\]

\[\lijevo[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(align) \desno.\]

Svaki dobiveni skup označimo na brojevnoj crti, a zatim ih kombiniramo:
Unija skupova
Očito je odgovor $x\in \left(\frac(4)(7);+\infty \right)$

Odgovor: $x\in \lijevo(\frac(4)(7);+\infty \desno)$

Zadatak. Riješite nejednadžbu:

\[\lijevo| ((x)^(2))+2x-3 \desno| \gtx\]

Riješenje. Dobro? Ne, sve je isto. Prelazimo s nejednadžbe s modulom na skup od dvije nejednadžbe:

\[\lijevo| ((x)^(2))+2x-3 \desno| \gt x\desna strelica \lijevo[ \begin(align) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\end(align) \desno.\]

Rješavamo svaku nejednadžbu. Nažalost, korijeni tamo neće biti baš dobri:

\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\ &D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\end(align)\]

U drugoj nejednakosti također ima malo igre:

\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\ &D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\end(align)\]

Sada moramo označiti te brojeve na dvije osi - po jednu os za svaku nejednadžbu. Međutim, trebate označiti točke ispravnim redoslijedom: što je veći broj, to se točka više pomiče udesno.

I ovdje čekamo postavu. Ako je sve jasno s brojevima $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ (članovi u brojniku prvog razlomak manji od članova u brojniku drugog, pa je i zbroj manji), s brojevima $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt (21))(2)$ također neće biti poteškoća (pozitivan broj očito je negativniji), ali s posljednjim parom sve nije tako jednostavno. Što je veće: $\frac(-3+\sqrt(21))(2)$ ili $\frac(-1+\sqrt(13))(2)$? O odgovoru na ovo pitanje ovisi raspored točaka na brojevnim pravcima i, zapravo, odgovor.

Pa usporedimo:

\[\begin(matrix) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matrica)\]

Izolirali smo korijen, dobili nenegativne brojeve na obje strane nejednadžbe, pa imamo pravo kvadrirati obje strane:

\[\begin(matrix) ((\lijevo(2+\sqrt(13) \desno))^(2))\vee ((\lijevo(\sqrt(21) \desno))^(2)) \ \4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(matrix)\]

Mislim da nije pametno da $4\sqrt(13) \gt 3$, dakle $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$, konačno će točke na osi biti raspoređene ovako:
Slučaj ružnih korijena
Podsjetit ću vas da rješavamo skup, pa će odgovor biti unija, a ne presjek osjenčanih skupova.

Odgovor: $x\in \lijevo(-\infty ;\frac(-3+\sqrt(21))(2) \desno)\bigcup \lijevo(\frac(-1+\sqrt(13))(2 );+\infty\desno)$

Kao što vidite, naša shema izvrsno funkcionira i za jednostavne i za vrlo teške zadatke. Jedina "slaba točka" u ovom pristupu je to što morate ispravno usporediti iracionalne brojeve (a vjerujte mi: to nisu samo korijeni). Ali posebna (i vrlo ozbiljna lekcija) bit će posvećena pitanjima usporedbe. I idemo dalje.

3. Nejednadžbe s nenegativnim "repovima"

Pa smo došli do najzanimljivijeg. To su nejednakosti oblika:

\[\lijevo| f\desno| \gt\lijevo| g\desno|\]

Općenito govoreći, algoritam o kojem ćemo sada govoriti vrijedi samo za modul. Radi u svim nejednakostima gdje postoje zajamčeni nenegativni izrazi s lijeve i desne strane:

Što učiniti s tim zadacima? Samo zapamti:

U nejednadžbama s nenegativnim repovima, obje se strane mogu podići na bilo koju prirodnu potenciju. Neće biti dodatnih ograničenja.

Prije svega, zanimat će nas kvadriranje - spaljuje module i korijene:

\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\lijevo(\sqrt(f) \desno))^(2))=f. \\\end(align)\]

Samo nemojte ovo brkati s vađenjem korijena kvadrata:

\[\sqrt(((f)^(2)))=\lijevo| f \desno|\ne f\]

Bezbrojne greške su napravljene kada je student zaboravio instalirati modul! No, ovo je sasvim druga priča (to su, takoreći, iracionalne jednadžbe), pa nećemo sada ulaziti u to. Hajdemo bolje riješiti par problema:

Zadatak. Riješite nejednadžbu:

\[\lijevo| x+2 \desno|\ge \lijevo| 1-2x \desno|\]

Riješenje. Odmah uočavamo dvije stvari:

Ovo je nestriktna nejednakost. Točke na brojevnom pravcu bit će izbušene.

Obje strane nejednakosti su očito nenegativne (ovo je svojstvo modula: $\left| f\left(x \right) \right|\ge 0$).

Stoga možemo kvadrirati obje strane nejednadžbe kako bismo se riješili modula i riješili problem koristeći uobičajenu metodu intervala:

\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\lijevo(x+2 \desno))^(2))\ge ((\lijevo(2x-1 \desno))^(2)). \\\end(align)\]

U zadnjem koraku sam malo varao: promijenio sam redoslijed članova, koristeći parnost modula (zapravo, pomnožio sam izraz $1-2x$ s −1).

\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \lijevo(\lijevo(2x-1 \desno)-\lijevo(x+2 \desno) \desno)\cdot \lijevo(\lijevo(2x-1 \desno)+\lijevo(x+2 \ desno)\desno)\le 0; \\ & \lijevo(2x-1-x-2 \desno)\cdot \lijevo(2x-1+x+2 \desno)\le 0; \\ & \lijevo(x-3 \desno)\cdot \lijevo(3x+1 \desno)\le 0. \\\end(align)\]

Rješavamo metodom intervala. Prijeđimo s nejednakosti na jednadžbu:

\[\begin(align) & \left(x-3 \desno)\lijevo(3x+1 \desno)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\end(align)\]

Pronađene korijene označavamo na brojevnoj crti. Još jednom: sve su točke osjenčane jer izvorna nejednakost nije stroga!
Uklanjanje znaka modula
Podsjetit ću vas za posebno tvrdoglave: uzimamo predznake iz posljednje nejednakosti, koja je zapisana prije nego što smo prešli na jednadžbu. I bojimo površine potrebne u istoj nejednadžbi. U našem slučaju, to je $\lijevo(x-3 \desno)\lijevo(3x+1 \desno)\le 0$.

OK, sada je sve gotovo. Problem riješen.

Odgovor: $x\in \lijevo[ -\frac(1)(3);3 \desno]$.

Zadatak. Riješite nejednadžbu:

\[\lijevo| ((x)^(2))+x+1 \desno|\le \lijevo| ((x)^(2))+3x+4 \desno|\]

Riješenje. Sve radimo isto. Neću komentirati - samo pogledajte slijed radnji.

Kvadriramo to:

\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \right| \right))^(2))\le ((\left(\left | ((x)^(2))+3x+4 \desno| \desno))^(2)); \\ & ((\lijevo(((x)^(2))+x+1 \desno))^(2))\le ((\lijevo(((x)^(2))+3x+4 \desno))^(2)); \\ & ((\lijevo(((x)^(2))+x+1 \desno))^(2))-((\lijevo(((x)^(2))+3x+4 \ desno))^(2))\le 0; \\ & \lijevo(((x)^(2))+x+1-((x)^(2))-3x-4 \desno)\times \\ & \times \lijevo(((x) ^(2))+x+1+((x)^(2))+3x+4 \desno)\le 0; \\ & \lijevo(-2x-3 \desno)\lijevo(2((x)^(2))+4x+5 \desno)\le 0. \\\end(align)\]

Metoda razmaka:

\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ Desna strelica x=-1,5; \\ & 2((x)^(2))+4x+5=0\Desna strelica D=16-40 \lt 0\Desna strelica \varništa . \\\end(align)\]

Postoji samo jedan korijen na brojevnoj pravoj:
Odgovor je cijeli niz
Odgovor: $x\u \lijevo[ -1,5;+\infty \desno)$.

Mala napomena o zadnjem zadatku. Kao što je jedan od mojih učenika točno primijetio, oba submodulna izraza u ovoj nejednakosti su očito pozitivna, tako da se znak modula može izostaviti bez štete po zdravlje.

Ali to je već sasvim druga razina razmišljanja i drugačiji pristup – to se uvjetno može nazvati metodom posljedica. O njemu - u zasebnoj lekciji. A sada prijeđimo na završni dio današnje lekcije i razmotrimo univerzalni algoritam koji uvijek radi. Čak i kada su svi prethodni pristupi bili nemoćni. :)

4. Metoda nabrajanja opcija

Što ako svi ti trikovi ne upali? Ako se nejednakost ne svodi na nenegativne repove, ako je nemoguće izolirati modul, ako uopće bol-tugu-čežnju?

Tada na scenu stupa “teška artiljerija” svake matematike – metoda nabrajanja. Što se tiče nejednakosti s modulom, to izgleda ovako:

Ispišite sve izraze podmodula i izjednačite ih s nulom;
Riješite dobivene jednadžbe i označite pronađene korijene na jednom brojevnom pravcu;
Ravna linija bit će podijeljena u nekoliko dijelova, unutar kojih svaki modul ima fiksni predznak i stoga se nedvosmisleno širi;
Riješite nejednakost na svakom takvom odjeljku (možete odvojeno razmotriti granične korijene dobivene u paragrafu 2 - za pouzdanost). Kombinirajte rezultate - to će biti odgovor. :)

Pa kako? Slab? Lako! Samo na duže vrijeme. Da vidimo u praksi:

Zadatak. Riješite nejednadžbu:

\[\lijevo| x+2 \desno| \lt\lijevo| x-1 \desno|+x-\frac(3)(2)\]

Riješenje. Ovo sranje se ne svodi na nejednakosti poput $\left| f\desno| \lt g$, $\lijevo| f\desno| \gt g$ ili $\lijevo| f\desno| \lt\lijevo| g \right|$, pa idemo naprijed.

Zapisujemo izraze podmodula, izjednačavamo ih s nulom i nalazimo korijene:

\[\begin(align) & x+2=0\Rightarrow x=-2; \\ & x-1=0\desna strelica x=1. \\\end(align)\]

Ukupno imamo dva korijena koji brojevnu liniju dijele na tri dijela, unutar kojih se svaki modul otkriva jedinstveno:
Rastavljanje brojevnog pravca nulama submodularnih funkcija
Razmotrimo svaki odjeljak zasebno.

1. Neka je $x \lt -2$. Tada su oba izraza submodula negativna, a izvorna nejednakost se prepisuje na sljedeći način:

\[\begin(align) & -\left(x+2 \desno) \lt -\lijevo(x-1 \desno)+x-1,5 \\ & -x-2 \lt -x+1+ x-1,5 \\ & x \gt 1,5 \\\end(align)\]

Dobili smo prilično jednostavno ograničenje. Presjecimo to s izvornom pretpostavkom da je $x \lt -2$:

\[\lijevo\( \begin(align) & x \lt -2 \\ & x \gt 1,5 \\\end(align) \right.\Rightarrow x\in \varnothing \]

Očito, varijabla $x$ ne može istovremeno biti manja od −2, ali veća od 1,5. U ovoj oblasti nema rješenja.

1.1. Razmotrimo odvojeno granični slučaj: $x=-2$. Zamijenimo ovaj broj u izvornu nejednakost i provjerimo: vrijedi li?

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=-2) ) \\ & 0 \lt \lijevo| -3 \desno|-2-1,5; \\ & 0 \lt 3-3,5; \\ & 0 \lt -0,5\Strelica desno \varništa . \\\end(align)\]

Očito nas je lanac izračuna doveo do pogrešne nejednakosti. Stoga je izvorna nejednakost također netočna, a $x=-2$ nije uključeno u odgovor.

2. Neka je sada $-2 \lt x \lt 1$. Lijevi modul će se već otvoriti s "plusom", ali desni je još uvijek s "minusom". Imamo:

\[\begin(align) & x+2 \lt -\lijevo(x-1 \desno)+x-1,5 \\ & x+2 \lt -x+1+x-1,5 \\& x \lt - 2.5 \\\end(align)\]

Opet se križamo s izvornim zahtjevom:

\[\lijevo\( \begin(align) & x \lt -2,5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]

I opet, prazan skup rješenja, jer ne postoje brojevi koji su manji od −2,5 i veći od −2.

2.1. I opet poseban slučaj: $x=1$. Zamjenjujemo u izvornu nejednakost:

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=1)) \\ & \lijevo| 3\desno| \lt\lijevo| 0 \desno|+1-1,5; \\ & 3 \lt -0,5; \\ & 3 \lt -0,5\desna strelica \varništa . \\\end(align)\]

Slično prethodnom "posebnom slučaju", broj $x=1$ očito nije uključen u odgovor.

3. Posljednji dio retka: $x \gt 1$. Ovdje su svi moduli prošireni znakom plus:

\[\begin(align) & x+2 \lt x-1+x-1.5 \\ & x+2 \lt x-1+x-1.5 \\ & x \gt 4.5 \\ \end(align)\ ]

I opet siječemo pronađeni skup s originalnim ograničenjem:

\[\lijevo\( \begin(align) & x \gt 4,5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4,5;+\infty \pravo)\]

Konačno! Našli smo interval, koji će biti odgovor.

Odgovor: $x\u \lijevo(4,5;+\infty \desno)$

Za kraj, jedna napomena koja vas može spasiti od glupih pogrešaka pri rješavanju stvarnih problema:

Rješenja nejednadžbi s modulima najčešće su kontinuirani skupovi na brojevnom pravcu - intervali i segmenti. Izolirane točke su puno rjeđe. A još rjeđe se događa da se granice rješenja (kraj segmenta) podudaraju s granicom raspona koji se razmatra.

Stoga, ako granice (oni vrlo “posebni slučajevi”) nisu uključene u odgovor, tada ni područja lijevo-desno od tih granica gotovo sigurno neće biti uključena u odgovor. I obrnuto: granica unesena kao odgovor, što znači da će neka područja oko nje također biti odgovori.

Imajte to na umu kada budete provjeravali svoja rješenja.

rješenje nejednakosti u načinu rada na liniji riješenje gotovo svaka dana nejednakost na liniji. Matematički nejednakosti online riješiti matematiku. Pronađite brzo rješenje nejednakosti u načinu rada na liniji. Stranica www.site omogućuje pronalaženje riješenje gotovo svaki dan algebarski, trigonometrijski ili transcendentna nejednakost online. Kada proučavate gotovo bilo koji odjeljak matematike u različitim fazama, morate odlučiti nejednakosti online. Da biste odmah dobili odgovor, i što je najvažnije točan odgovor, potreban vam je resurs koji vam to omogućuje. Zahvaljujući www.site rješavanje nejednakosti online trajat će nekoliko minuta. Glavna prednost www.site pri rješavanju matematičkih nejednakosti online- je brzina i točnost izdanog odgovora. Stranica je u stanju riješiti bilo koji algebarske nejednakosti online, trigonometrijske nejednakosti online, transcendentalne nejednakosti online, i nejednakosti s nepoznatim parametrima u načinu rada na liniji. nejednakosti služe kao snažan matematički aparat rješenja praktičnih zadataka. Uz pomoć matematičke nejednakosti moguće je izraziti činjenice i odnose koji na prvi pogled mogu djelovati zbunjujuće i složeno. nepoznate količine nejednakosti može se pronaći formuliranjem problema u matematički jezik u obliku nejednakosti I odlučiti primljeni zadatak u načinu rada na liniji na web stranici www.site. Bilo koje algebarska nejednakost, trigonometrijska nejednakost ili nejednakosti koji sadrži transcendentalno značajke vam lako odlučiti online i dobiti pravi odgovor. Proučavajući prirodne znanosti, neizbježno se susreće potreba rješenje nejednakosti. U tom slučaju odgovor mora biti točan i mora se primiti odmah u načinu rada na liniji. Stoga, za rješavati matematičke nejednakosti online preporučamo stranicu www.site koja će postati vaš nezaobilazan kalkulator za rješavanje algebarskih nejednakosti online, trigonometrijske nejednakosti online, i transcendentalne nejednakosti online ili nejednakosti s nepoznatim parametrima. Za praktične probleme pronalaženja intravol rješenja raznih matematičke nejednakosti resurs www.. Rješavanje nejednakosti online sami, korisno je provjeriti primljeni odgovor pomoću online rješavanje nejednakosti na web stranici www.site. Nejednakost je potrebno točno zapisati i odmah dobiti online rješenje, nakon čega ostaje samo usporediti odgovor sa svojim rješenjem nejednadžbe. Provjera odgovora neće trajati više od minute, dovoljno rješavanje nejednakosti online i usporediti odgovore. To će vam pomoći da izbjegnete pogreške u odluka i ispravite odgovor na vrijeme rješavanje nejednakosti online ili algebarski, trigonometrijski, transcendentan ili nejednakost s nepoznatim parametrima.