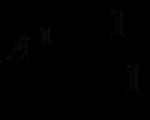Kao rješavanje jednadžbi. Rješavanje linearnih jednadžbi s primjerima

U fazi pripreme za završno testiranje srednjoškolci trebaju unaprijediti svoje znanje o temi "Eksponencijalne jednadžbe". Iskustvo proteklih godina pokazuje da takvi zadaci stvaraju određene poteškoće školarcima. Stoga srednjoškolci, bez obzira na razinu pripremljenosti, moraju pažljivo savladati teoriju, zapamtiti formule i razumjeti princip rješavanja takvih jednadžbi. Nakon što su se naučili nositi s ovom vrstom zadataka, maturanti će moći računati na visoke ocjene pri polaganju ispita iz matematike.

Pripremite se za ispitno testiranje zajedno sa Shkolkovom!

Kod ponavljanja pređenog gradiva mnogi se učenici susreću s problemom pronalaženja formula potrebnih za rješavanje jednadžbi. Školski udžbenik nije uvijek pri ruci, a odabir potrebnih informacija o temi na internetu traje dugo.

Obrazovni portal Shkolkovo poziva studente da koriste našu bazu znanja. Uvodimo potpuno novi način pripreme za završni ispit. Učeći na našim stranicama, moći ćete prepoznati nedostatke u znanju i obratiti pozornost upravo na one zadatke koji uzrokuju najveće poteškoće.

Učitelji "Školkova" prikupili su, sistematizirali i prezentirali sav materijal potreban za uspješno polaganje ispita u najjednostavnijem i najpristupačnijem obliku.

Glavne definicije i formule prikazane su u odjeljku "Teoretska referenca".

Za bolju asimilaciju materijala, preporučujemo da vježbate zadatke. Pažljivo pregledajte primjere eksponencijalnih jednadžbi s rješenjima prikazane na ovoj stranici kako biste razumjeli algoritam izračuna. Nakon toga nastavite sa zadacima u rubrici "Katalozi". Možete početi s najlakšim zadacima ili odmah prijeći na rješavanje složenih eksponencijalnih jednadžbi s nekoliko nepoznanica ili . Baza vježbi na našoj web stranici stalno se nadopunjuje i ažurira.

One primjere s indikatorima koji su vam stvarali poteškoće možete dodati u "Favorite". Tako ih možete brzo pronaći i raspraviti rješenje s učiteljem.

Da biste uspješno položili ispit, učite na portalu Shkolkovo svaki dan!

Dodjela usluge. Matrični kalkulator namijenjen je rješavanju sustava linearnih jednadžbi na matrični način (pogledajte primjer rješavanja sličnih problema).

Uputa. Za online rješenje morate odabrati vrstu jednadžbe i postaviti dimenziju odgovarajućih matrica. gdje su A, B, C zadane matrice, X je željena matrica. Matrične jednadžbe oblika (1), (2) i (3) rješavaju se preko inverzne matrice A -1 . Ako je dan izraz A X - B = C, tada je potrebno prvo zbrojiti matrice C + B i pronaći rješenje za izraz A X = D , gdje je D = C + B . Ako je dan izraz A*X = B 2, tada se matrica B mora prvo kvadrirati.

Također je preporučljivo upoznati se s osnovnim operacijama na matricama.

Primjer #1. Vježbajte. Pronađite rješenje matrične jednadžbe
Riješenje. Označiti:
Tada će matrična jednadžba biti zapisana u obliku: A·X·B = C.
Determinanta matrice A je detA=-1
Kako je A nesingularna matrica, postoji inverzna matrica A -1 . Pomnožite obje strane jednadžbe s lijeve strane s A -1: Pomnožite obje strane ove jednadžbe s lijeve strane s A -1 i s desne s B -1: A -1 A X B B -1 = A -1 C B -1 . Kako je A A -1 = B B -1 = E i E X = X E = X, onda je X = A -1 C B -1

Inverzna matrica A -1:
Nađite inverznu matricu B -1 .
Transponirana matrica B T:
Inverzna matrica B -1:
Matricu X tražimo po formuli: X = A -1 C B -1

Odgovor:

Primjer #2. Vježbajte. Riješite matričnu jednadžbu
Riješenje. Označiti:
Tada će matrična jednadžba biti zapisana u obliku: A X = B.
Determinanta matrice A je detA=0
Budući da je A degenerirana matrica (determinanta je 0), jednadžba nema rješenja.

Primjer #3. Vježbajte. Pronađite rješenje matrične jednadžbe
Riješenje. Označiti:
Tada će matrična jednadžba biti zapisana u obliku: X·A = B.
Determinanta matrice A je detA=-60
Kako je A nesingularna matrica, postoji inverzna matrica A -1 . Pomnožimo s desne obje strane jednadžbe s A -1: X A A -1 = B A -1 , iz čega nalazimo da je X = B A -1
Nađi inverznu matricu A -1 .
Transponirana matrica A T:
Inverzna matrica A -1:
Matricu X tražimo po formuli: X = B A -1


Odgovor: >

riješiti matematiku. Pronađite brzo rješenje matematičke jednadžbe u načinu rada na liniji. Web stranica www.site dopušta riješiti jednadžbu gotovo svaki dan algebarski, trigonometrijski ili transcendentalna jednadžba online. Kada proučavate gotovo bilo koji odjeljak matematike u različitim fazama, morate odlučiti jednadžbe online. Da biste odmah dobili odgovor, i što je najvažnije točan odgovor, potreban vam je resurs koji vam to omogućuje. Zahvaljujući www.site rješavati jednadžbe online trajat će nekoliko minuta. Glavna prednost www.site pri rješavanju matematičkih jednadžbe online- je brzina i točnost izdanog odgovora. Stranica je u stanju riješiti bilo koji algebarske jednadžbe online, trigonometrijske jednadžbe online, transcendentalne jednadžbe online, i jednadžbe s nepoznatim parametrima u načinu rada na liniji. Jednadžbe služe kao snažan matematički aparat rješenja praktičnih zadataka. Uz pomoć matematičke jednadžbe moguće je izraziti činjenice i odnose koji na prvi pogled mogu djelovati zbunjujuće i složeno. nepoznate količine jednadžbe može se pronaći formuliranjem problema u matematički jezik u obliku jednadžbe I odlučiti primljeni zadatak u načinu na liniji na web stranici www.site. Bilo koje algebarska jednadžba, trigonometrijska jednadžba ili jednadžbe koji sadrži transcendentalno značajke vam lako odlučiti online i dobiti pravi odgovor. Proučavajući prirodne znanosti, neizbježno se susreće potreba rješavanje jednadžbi. U tom slučaju odgovor mora biti točan i mora se primiti odmah u načinu rada na liniji. Stoga, za rješavanje matematičkih jednadžbi online preporučamo stranicu www.site koja će postati vaš nezaobilazan kalkulator za rješavanje algebarskih jednadžbi online, trigonometrijske jednadžbe online, i transcendentalne jednadžbe online ili jednadžbe s nepoznatim parametrima. Za praktične probleme pronalaženja korijena raznih matematičke jednadžbe resurs www.. Rješavanje jednadžbe online sami, korisno je provjeriti primljeni odgovor pomoću online rješavanje jednadžbi na web stranici www.site. Potrebno je napisati jednadžbu ispravno i odmah dobiti online rješenje, nakon čega ostaje samo usporediti odgovor sa svojim rješenjem jednadžbe. Provjera odgovora neće trajati više od minute, dovoljno riješite jednadžbu online i usporediti odgovore. To će vam pomoći da izbjegnete pogreške u odluka i ispravite odgovor na vrijeme online rješavanje jednadžbi ili algebarski, trigonometrijski, transcendentan ili jednadžba s nepoznatim parametrima.

U ovom videu ćemo analizirati čitav niz linearnih jednadžbi koje se rješavaju istim algoritmom – zato se i nazivaju najjednostavnijima.

Za početak, definirajmo: što je linearna jednadžba i koju od njih treba nazvati najjednostavnijom?

Linearna jednadžba je ona u kojoj postoji samo jedna varijabla i to samo u prvom stupnju.

Najjednostavnija jednadžba znači konstrukciju:

Sve ostale linearne jednadžbe svode se na najjednostavnije pomoću algoritma:

1. Otvorene zagrade, ako postoje;
2. Pomaknite pojmove koji sadrže varijablu s jedne strane znaka jednakosti, a pojmove bez varijable s druge strane;
3. Donesite slične pojmove lijevo i desno od znaka jednakosti;
4. Dobivenu jednadžbu podijelite s koeficijentom varijable $x$ .

Naravno, ovaj algoritam ne pomaže uvijek. Činjenica je da ponekad, nakon svih tih makinacija, koeficijent varijable $x$ ispadne jednak nuli. U ovom slučaju moguće su dvije opcije:

1. Jednadžba uopće nema rješenja. Na primjer, kada dobijete nešto poput $0\cdot x=8$, tj. na lijevoj strani je nula, a na desnoj je broj različit od nule. U videu u nastavku pogledat ćemo nekoliko razloga zašto je ova situacija moguća.
2. Rješenje su svi brojevi. Jedini slučaj kada je to moguće je kada je jednadžba svedena na konstrukciju $0\cdot x=0$. Sasvim je logično da bez obzira koji $x$ zamijenimo, svejedno će ispasti “nula je jednaka nuli”, tj. ispravna brojčana jednakost.

A sada da vidimo kako sve to funkcionira na primjeru stvarnih problema.

Primjeri rješavanja jednadžbi

Danas se bavimo linearnim jednadžbama, i to samo onim najjednostavnijim. Općenito, linearna jednadžba označava svaku jednakost koja sadrži točno jednu varijablu, a ide samo do prvog stupnja.

Takve konstrukcije rješavaju se približno na isti način:

1. Prije svega, morate otvoriti zagrade, ako postoje (kao u našem zadnjem primjeru);
2. Zatim donesi slično
3. Na kraju, izolirajte varijablu, tj. sve što je povezano s varijablom - termini u kojima je sadržana - prenosi se na jednu stranu, a sve što ostane bez nje prenosi se na drugu stranu.

Zatim, u pravilu, trebate donijeti slično sa svake strane dobivene jednakosti, a nakon toga ostaje samo podijeliti s koeficijentom na "x", i dobit ćemo konačni odgovor.

U teoriji ovo izgleda lijepo i jednostavno, ali u praksi čak i iskusni srednjoškolci mogu napraviti uvredljive pogreške u prilično jednostavnim linearnim jednadžbama. Obično se griješi ili pri otvaranju zagrada, ili pri prebrojavanju "pluseva" i "minusa".

Osim toga, događa se da linearna jednadžba uopće nema rješenja ili da je rješenje cijeli brojevni pravac, tj. bilo koji broj. Analizirat ćemo ove suptilnosti u današnjoj lekciji. Ali počet ćemo, kao što ste već shvatili, s najjednostavnijim zadacima.

Shema za rješavanje jednostavnih linearnih jednadžbi

Za početak, dopustite mi da još jednom napišem cijelu shemu rješavanja najjednostavnijih linearnih jednadžbi:

1. Proširite zagrade, ako postoje.
2. Izdvojite varijable, tj. sve što sadrži "x" prenosi se na jednu stranu, a bez "x" - na drugu.
3. Predstavljamo slične uvjete.
4. Sve dijelimo s koeficijentom kod "x".

Naravno, ova shema ne radi uvijek, ima određene suptilnosti i trikove, a sada ćemo ih upoznati.

Rješavanje stvarnih primjera jednostavnih linearnih jednadžbi

Zadatak #1

U prvom koraku moramo otvoriti zagrade. Ali oni nisu u ovom primjeru, pa preskačemo ovaj korak. U drugom koraku moramo izolirati varijable. Napomena: govorimo samo o pojedinačnim terminima. Idemo pisati:

Slične termine dajemo s lijeve i desne strane, ali to je ovdje već učinjeno. Stoga prelazimo na četvrti korak: dijelimo s faktorom:

\[\frac(6x)(6)=-\frac(72)(6)\]

Ovdje smo dobili odgovor.

Zadatak #2

U ovom zadatku možemo promatrati zagrade, pa ih proširimo:

I s lijeve i s desne strane vidimo približno istu konstrukciju, ali postupajmo prema algoritmu, tj. varijable sekvestra:

Evo nekih poput:

Na kojim korijenima ovo radi? Odgovor: za bilo koji. Stoga možemo napisati da je $x$ bilo koji broj.

Zadatak #3

Treća linearna jednadžba je već zanimljivija:

\[\lijevo(6-x \desno)+\lijevo(12+x \desno)-\lijevo(3-2x \desno)=15\]

Ovdje postoji nekoliko zagrada, ali se ničim ne množe, samo imaju različite znakove ispred sebe. Razdvojimo ih:

Izvodimo drugi korak koji nam je već poznat:

\[-x+x+2x=15-6-12+3\]

Izračunajmo:

Izvodimo posljednji korak - sve dijelimo s koeficijentom na "x":

\[\frac(2x)(x)=\frac(0)(2)\]

Stvari koje treba zapamtiti prilikom rješavanja linearnih jednadžbi

Ako zanemarimo prejednostavne zadatke, onda bih želio reći sljedeće:

• Kao što sam rekao gore, nema svaka linearna jednadžba rješenje - ponekad jednostavno nema korijena;
• Čak i ako postoje korijeni, nula može ući među njih - nema ništa loše u tome.

Nula je isti broj kao i ostali, ne biste je trebali nekako diskriminirati ili pretpostaviti da ste, ako dobijete nulu, učinili nešto pogrešno.

Još jedna značajka povezana je s proširenjem zagrada. Imajte na umu: kada je ispred njih "minus", uklanjamo ga, ali u zagradama mijenjamo znakove u suprotan. A onda ga možemo otvoriti prema standardnim algoritmima: dobit ćemo ono što smo vidjeli u gornjim izračunima.

Razumijevanje ove jednostavne činjenice pomoći će vam da izbjegnete glupe i bolne pogreške u srednjoj školi, kada se takve radnje podrazumijevaju.

Rješavanje složenih linearnih jednadžbi

Prijeđimo na složenije jednadžbe. Sada će konstrukcije postati kompliciranije i pojavit će se kvadratna funkcija pri izvođenju raznih transformacija. Međutim, ne biste se trebali bojati toga, jer ako, prema namjeri autora, riješimo linearnu jednadžbu, tada će se u procesu transformacije svi monomi koji sadrže kvadratnu funkciju nužno reducirati.

Primjer #1

Očito, prvi korak je otvaranje zagrada. Učinimo to vrlo pažljivo:

Pogledajmo sada privatnost:

\[-x+6((x)^(2))-6((x)^(2))+x=-12\]

Evo nekih poput:

Očito ova jednadžba nema rješenja, pa u odgovoru pišemo kako slijedi:

\[\raznolikost \]

ili bez korijena.

Primjer #2

Izvodimo iste korake. Prvi korak:

Pomaknimo sve s varijablom ulijevo, a bez nje - udesno:

Evo nekih poput:

Očito, ova linearna jednadžba nema rješenja, pa je pišemo ovako:

\[\varnothing\],

ili bez korijena.

Nijanse rješenja

Obje jednadžbe su potpuno riješene. Na primjeru ova dva izraza još jednom smo se uvjerili da i u najjednostavnijim linearnim jednadžbama sve može biti i ne tako jednostavno: može biti ili jedan, ili nijedan, ili beskonačno mnogo. U našem slučaju razmatrali smo dvije jednadžbe, u obje jednostavno nema korijena.

Ali želio bih vam skrenuti pozornost na još jednu činjenicu: kako raditi sa zagradama i kako ih proširiti ako je ispred njih znak minus. Razmotrite ovaj izraz:

Prije otvaranja potrebno je sve pomnožiti sa "x". Napomena: umnožite svaki pojedini termin. Unutra se nalaze dva pojma - odnosno dva pojma i umnožava se.

I tek nakon tih naizgled elementarnih, ali vrlo važnih i opasnih transformacija, može se otvoriti zagrada s gledišta da iza nje stoji znak minus. Da, da: tek sada, kada su transformacije gotove, sjetimo se da ispred zagrada stoji znak minus, što znači da sve ispod samo mijenja predznak. U isto vrijeme, sami nosači nestaju i, što je najvažnije, nestaje i prednji "minus".

Isto radimo s drugom jednadžbom:

Nije slučajno što obraćam pozornost na ove male, naizgled beznačajne činjenice. Zato što je rješavanje jednadžbi uvijek slijed elementarnih transformacija, gdje nemogućnost jasnog i kompetentnog izvođenja jednostavnih radnji dovodi do toga da srednjoškolci dolaze kod mene i ponovno uče rješavati tako jednostavne jednadžbe.

Naravno, doći će dan kada ćete te vještine izbrusiti do automatizma. Ne morate više svaki put izvoditi toliko transformacija, sve ćete napisati u jednom retku. No, dok tek učite, svaku akciju trebate napisati zasebno.

Rješavanje još složenijih linearnih jednadžbi

Ovo što ćemo sada riješiti teško se može nazvati najjednostavnijim zadatkom, ali smisao ostaje isti.

Zadatak #1

\[\lijevo(7x+1 \desno)\lijevo(3x-1 \desno)-21((x)^(2))=3\]

Pomnožimo sve elemente u prvom dijelu:

Napravimo povlačenje:

Evo nekih poput:

Napravimo zadnji korak:

\[\frac(-4x)(4)=\frac(4)(-4)\]

Evo našeg konačnog odgovora. I unatoč tome što smo u procesu rješavanja imali koeficijente s kvadratnom funkcijom, oni su se međusobno poništili, što čini jednadžbu točno linearnom, a ne kvadratnom.

Zadatak #2

\[\lijevo(1-4x \desno)\lijevo(1-3x \desno)=6x\lijevo(2x-1 \desno)\]

Pažljivo napravimo prvi korak: pomnožimo svaki element u prvoj zagradi sa svakim elementom u drugoj. Ukupno bi se nakon transformacija trebala dobiti četiri nova člana:

A sada pažljivo izvršite množenje u svakom članu:

Pomaknimo članove s "x" ulijevo, a bez - udesno:

\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]

Evo sličnih pojmova:

Dobili smo konačan odgovor.

Nijanse rješenja

Najvažnija primjedba o ove dvije jednadžbe je sljedeća: čim počnemo množiti zagrade u kojima je više od jednog člana, onda se to radi prema sljedećem pravilu: uzimamo prvi član od prvog i množimo sa svakim elementom iz drugog; zatim uzimamo drugi element iz prvog i slično množimo sa svakim elementom iz drugog. Kao rezultat, dobivamo četiri pojma.

Na algebarskom zbroju

Posljednjim primjerom želio bih podsjetiti učenike što je algebarski zbroj. U klasičnoj matematici, pod $1-7$ mislimo na jednostavnu konstrukciju: sedam oduzimamo od jedan. U algebri pod ovim podrazumijevamo sljedeće: broju "jedan" dodajemo još jedan broj, naime "minus sedam". Ovaj algebarski zbroj razlikuje se od uobičajenog aritmetičkog zbroja.

Čim prilikom izvođenja svih transformacija, svakog zbrajanja i množenja, počnete vidjeti konstrukcije slične gore opisanim, jednostavno nećete imati problema u algebri kada radite s polinomima i jednadžbama.

Zaključno, pogledajmo još nekoliko primjera koji će biti još složeniji od ovih koje smo upravo pogledali, a da bismo ih riješili, morat ćemo malo proširiti naš standardni algoritam.

Rješavanje jednadžbi s razlomkom

Za rješavanje takvih zadataka morat ćemo dodati još jedan korak našem algoritmu. Ali prvo ću podsjetiti na naš algoritam:

1. Otvorene zagrade.
2. Odvojene varijable.
3. Donesite slično.
4. Podijelite s faktorom.

Nažalost, ovaj prekrasan algoritam, usprkos svoj svojoj učinkovitosti, nije sasvim prikladan kada pred sobom imamo razlomke. A u onome što ćemo vidjeti u nastavku, imamo razlomak s lijeve i s desne strane u obje jednadžbe.

Kako raditi u ovom slučaju? Da, vrlo je jednostavno! Da biste to učinili, morate dodati još jedan korak u algoritam, koji se može izvesti i prije prve radnje i nakon nje, naime, da se riješite razlomaka. Dakle, algoritam će biti sljedeći:

1. Riješite se razlomaka.
2. Otvorene zagrade.
3. Odvojene varijable.
4. Donesite slično.
5. Podijelite s faktorom.

Što znači "riješiti se razlomaka"? I zašto je to moguće učiniti i nakon i prije prvog standardnog koraka? Zapravo, u našem slučaju, svi razlomci su numerički u smislu nazivnika, tj. svugdje je nazivnik samo broj. Stoga, ako oba dijela jednadžbe pomnožimo ovim brojem, tada ćemo se riješiti razlomaka.

Primjer #1

\[\frac(\lijevo(2x+1 \desno)\lijevo(2x-3 \desno))(4)=((x)^(2))-1\]

Riješimo se razlomaka u ovoj jednadžbi:

\[\frac(\lijevo(2x+1 \desno)\lijevo(2x-3 \desno)\cdot 4)(4)=\lijevo(((x)^(2))-1 \desno)\cdot 4\]

Imajte na umu: sve se jednom množi s "četiri", tj. samo zato što imate dvije zagrade ne znači da morate svaku od njih množiti s "četiri". Idemo pisati:

\[\lijevo(2x+1 \desno)\lijevo(2x-3 \desno)=\lijevo(((x)^(2))-1 \desno)\cdot 4\]

Sada ga otvorimo:

Izvodimo izdvajanje varijable:

Vršimo smanjenje sličnih termina:

\[-4x=-1\lijevo| :\lijevo(-4 \desno) \desno.\]

\[\frac(-4x)(-4)=\frac(-1)(-4)\]

Dobili smo konačno rješenje, prelazimo na drugu jednadžbu.

Primjer #2

\[\frac(\lijevo(1-x \desno)\lijevo(1+5x \desno))(5)+((x)^(2))=1\]

Ovdje izvodimo sve iste radnje:

\[\frac(\lijevo(1-x \desno)\lijevo(1+5x \desno)\cdot 5)(5)+((x)^(2))\cdot 5=5\]

\[\frac(4x)(4)=\frac(4)(4)\]

Problem riješen.

To je, zapravo, sve što sam danas htio ispričati.

Ključne točke

Ključni nalazi su sljedeći:

• Poznavati algoritam za rješavanje linearnih jednadžbi.
• Mogućnost otvaranja zagrada.
• Ne brinite ako negdje imate kvadratne funkcije, najvjerojatnije će se u procesu daljnjih transformacija smanjiti.
• Korijeni u linearnim jednadžbama, čak i onim najjednostavnijim, su tri vrste: jedan korijen, cijeli brojevni pravac je korijen, korijena uopće nema.

Nadam se da će vam ova lekcija pomoći da savladate jednostavnu, ali vrlo važnu temu za daljnje razumijevanje cijele matematike. Ako nešto nije jasno, idite na stranicu, riješite tamo prikazane primjere. Ostanite s nama, čeka vas još puno zanimljivih stvari!