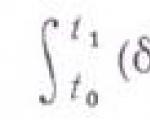Il principio di minima azione. Principio variazionale di Hamilton-Ostrogradsky in configurazioni e spazi delle fasi Formula d'onda piana
PRINCIPIO DI HAMILTON-OSTROGRAD
Principio di azione stazionaria, - integrale generale principio variazionale della meccanica classica, stabilito da W.
Hamilton per sistemi olonomi vincolati da vincoli stazionari ideali e generalizzati da M. V. Ostrogradskii a vincoli non stazionari. Secondo G.-O.
ha un valore stazionario rispetto ai movimenti cinematicamente possibili, per i quali le posizioni iniziale e finale del sistema e il tempo del movimento sono gli stessi del movimento reale. Qui T - cinetico, U- energia potenziale, L-T-U la funzione di Lagrange del sistema. In alcuni casi, vero corrisponde non solo a un punto stazionario del funzionale S, ma gli dà anche il valore più piccolo. Pertanto, G. -O. n. spesso chiamato. il principio di minima azione. Nel caso di forze attive non potenziali F contro condizione di stazionarietà dell'azione d S= 0 è sostituito dalla condizione
Illuminato.: Hamilton W., Rapporto del quarto incontro della British Association for the Advancement of Science, L., 1835, p. 513-18; Ostrogradsku M., "Mem. de 1" Acad. della Sci. de St-Petershourg", 1850, vol. 8, n. 3, p. 33-48.
V. V. Rumyantsev.
Enciclopedia matematica. - M.: Enciclopedia sovietica. I. M. Vinogradov. 1977-1985.
Scopri cos'è il "PRINCIPIO HAMILTON - OSTROGRAD" in altri dizionari:
Il principio di Fisher è un modello evolutivo che spiega perché il rapporto tra i sessi delle specie di organismi viventi, circa 1:1, è predominante in natura; in cui i geni per la produzione di più individui di entrambi i sessi... ...Wikipedia
Hamilton (anche solo principio di Hamilton), più precisamente, il principio di stazionarietà dell'azione è un metodo per ottenere le equazioni del moto di un sistema fisico ricercandone uno stazionario (spesso estremo, solitamente in connessione con la tradizione consolidata... ...Wikipedia
Rifrazione delle onde secondo Huygens... Wikipedia
Nella metodologia della scienza, l'affermazione che qualsiasi nuova teoria scientifica, in presenza di una vecchia teoria ben collaudata, non è in completa contraddizione con essa, ma dà le stesse conseguenze in qualche approssimazione limite (caso speciale). Ad esempio, la legge... ...Wikipedia
Principio del massimo di Pontryagin discreto per processi di controllo tempo-discreti. Per un tale processo, il M. p. potrebbe non essere soddisfatto, anche se per il suo analogo continuo, che si ottiene sostituendo l'operatore alle differenze finite con uno differenziale... ... Enciclopedia matematica
Oppure l'inizio di Hamilton, in meccanica e fisica matematica, serve per ottenere equazioni differenziali del moto. Questo principio si estende a tutti i sistemi materiali, qualunque siano le forze a cui possono essere soggetti; per prima cosa lo esprimeremo in questo... Dizionario Enciclopedico F.A. Brockhaus e I.A. Efron
Postulato quantistico. meccanica, che richiede la coincidenza della sua fisica. conseguenze nel caso limite di grandi numeri quantici con i risultati classici. teorie. In S. p., il fatto che il quanto. gli effetti sono significativi solo se si considerano i microoggetti, quando... ... Enciclopedia fisica
Principio variazionale di Hamilton- Hamiltono variacinis principas statusas T sritis fizika atitikmenys: engl. Principio di variazione di Hamilton vok. Hamiltonsches Variationsprinzip, n rus. Principio variazionale di Hamilton, m pranc. principe variazionenel d'Hamilton, m … Fizikos terminų žodynas
Un postulato della meccanica quantistica (Vedi Meccanica Quantistica) che richiede la coincidenza delle sue conseguenze fisiche nel caso limite di grandi numeri quantici (Vedi Numeri Quantici) con i risultati della teoria classica. Nella S.p. si manifesta il fatto che... ... Grande Enciclopedia Sovietica
- (meccanica delle onde), una teoria che stabilisce il metodo di descrizione e le leggi del movimento delle microparticelle (elem. h c, atomi, molecole, nuclei atomici) e dei loro sistemi (ad esempio cristalli), nonché la relazione delle quantità caratterizzare particelle e sistemi, con fisica dimensioni, ... ... Enciclopedia fisica
Questo termine ha altri significati, vedi Azione (fisica). Dimensione dell'azione L2MT−1 L'azione in fisica è una quantità fisica scalare che è ... Wikipedia
Libri
- Principi di movimento del sistema economico. Monografia, Kusner Yuri Semenovich, Tsarev Igor Gennadievich. Le equazioni fondamentali del movimento di un sistema economico vengono presentate in forma analitica e viene risolto il problema di trovare metodi adeguati per controllarne il movimento. Si usa la matematica...
L'idea che sta alla base di tutti i principi integrali e di alcuni differenziali è la posizione secondo cui il movimento reale di un sistema meccanico conferisce estremalità a una certa quantità fisica. Per la formulazione matematica di questa proposizione è necessario, come prima, prendere in considerazione, insieme al movimento reale, l'insieme dei movimenti concepibili, sottoponendoli a requisiti ben determinati.
La formulazione dei principi integrali viene effettuata nello spazio delle configurazioni. Ricordiamo che per un sistema con gradi di libertà, le coordinate generalizzate 
, che determinano la configurazione del sistema in quel momento 
, vengono trattate come coordinate cartesiane nel corrispondente 
-spazio dimensionale, che è lo spazio delle configurazioni. Nel tempo, lo stato del sistema meccanico cambia e il punto che rappresenta questo sistema descrive una certa curva. È conveniente considerare il moto del sistema come il moto del punto rappresentativo lungo questa curva. Tempo 
sotto questa considerazione c'è un parametro, e ogni punto della traiettoria corrisponderà ad uno o più valori 
.
Se siamo interessati alla posizione del sistema sulla traiettoria di configurazione in ogni momento 
, quindi è necessario aggiungere un altro asse 
.
Otterremo quindi un "grafico multidimensionale" del moto del sistema che stiamo considerando. Si possono anche studiare le proiezioni di un grafico multivariato su determinati piani, ad esempio 
(Fig. 2.7). Sull'immagine A, B sono le proiezioni del punto rappresentativo al momento 
E 
di conseguenza, la linea continua rappresenta il reale, tratteggiato - uno dei movimenti immaginabili.
Il principio integrale è un'affermazione su come il movimento reale del sistema viene eseguito su un intervallo di tempo finito (non infinitamente piccolo!) 
.
Cosa c'era nel sistema prima del momento giusto 
,
non siamo interessati. Ma poiché i momenti iniziali e finali del tempo sono fissi, si ritiene che il sistema meccanico per tutti i movimenti immaginabili in quel momento 
passa per un punto UN, nel momento 
- IN;
questi punti corrispondono alle posizioni iniziale e finale del sistema nel suo moto reale.
La formulazione più generale della posizione sul moto dei sistemi meccanici è contenuta nel cosiddetto principio di minima azione (è chiamato anche principio di Hamilton-Ostrogradsky):
Il movimento reale del sistema meccanico nell'intervallo di tempo da
Prima
è tale che l'integrale, chiamato funzione di azione
e pari
, (60.7)
Dove
-- La lagrangiana del sistema meccanico dato, ha un estremo (minimo). Variabile
non varia.
In altre parole, durante il moto reale, la variazione dell'azione dovrebbe essere pari a zero
(61.7)
a condizione che tutte le traiettorie di configurazione negli istanti di tempo 
E 
passare attraverso i punti di inizio e fine del movimento reale, cioè
Questo principio, in contrasto con il principio differenziale di d'Alembert, è integrale nel senso che contiene un'affermazione sul moto del sistema nel suo insieme in un periodo di tempo finito. 
.
Da esso infatti discendono le equazioni di Lagrange, quindi dal principio di minima azione si può dire che si ottiene l'intera dinamica di un sistema meccanico.
Passiamo alle funzioni 
, descrivere il movimento reale, cioè 
quelle funzioni per le quali 
ha un minimo. Consideriamo l'insieme delle funzioni 
Dove 
- variazioni di funzione 
, che si presume siano piccoli rispetto a 
durante l'intero intervallo di tempo da 
Prima 
. Inoltre, tutto 
soddisfare le relazioni (62.7). Calcoliamo la cosiddetta prima variazione 
, tenendo presente che la funzione di Lagrange può dipendere dalle coordinate generalizzate 
,
velocità generalizzate 
, E tempo 
:
Perché il 
, il secondo termine in 
può essere integrato dalle parti da ottenere
.
A causa delle condizioni (62.7), la somma
svanisce e l'integrale rimanente sarà uguale a zero per valori arbitrari 
solo quando ogni termine della somma dell'integrando svanisce. Otteniamo così le equazioni di Lagrange del 2° tipo
.
(63.7)
È utile ricordare che dalla soluzione del problema per l'estremo di una funzione si ottiene un sistema di equazioni finite, da cui si trova il punto in cui la funzione raggiunge un estremo. In questo caso si tratta di un funzionale, la soluzione di un problema estremo, che è dato da un sistema di equazioni differenziali del 2° ordine. Da queste equazioni si ricava una linea nello spazio delle configurazioni, dato dalle funzioni 
dove il funzionale raggiunge il suo minimo. Questa linea è chiamata estremale.
Poiché il compito di costruire l'uno o l'altro modello meccanico consiste nel compilare le equazioni del movimento, vediamo che, in effetti, la dinamica del sistema è determinata da una funzione: la Lagrangiana, poiché è questa funzione che risolve il problema. Pertanto, la Lagrangiana del sistema è un oggetto fisico interessante, il cui studio è necessario in relazione ai problemi della dinamica. In particolare, si può vedere dal principio di minima azione che la funzione 
è definita solo fino all'aggiunta ad essa della derivata totale di una funzione arbitraria di coordinate e tempo. Ciò va inteso in quanto il sistema definito dalle sue equazioni del moto corrisponde a più di una funzione di Lagrange 
.
Infatti, lasciamo che sia 
Associato a 
rapporto
(64.7)
,
.
Ma da allora 
,
e, di conseguenza, le equazioni di Lagrange ottenute utilizzando le funzioni 
E 
, Stesso. L'ambiguità della definizione della funzione di Lagrange della forma (64.7) non influisce sulle equazioni del moto, e ciascuna 
dalla classe (64.7) risolve il problema di costruire in modo univoco la dinamica del sistema.
Una proprietà importante del sistema di equazioni di Lagrange è la loro covarianza. Ciò significa che le equazioni di Lagrange mantengono la loro forma sotto trasformazioni puntuali di coordinate generalizzate 4
cioè quando si utilizzano coordinate generalizzate 
Le equazioni di Lagrange avranno la stessa forma:
,
come quando si utilizzano le coordinate generalizzate 
:
.
Dimostriamo direttamente che le equazioni di Lagrange sono covarianti rispetto alla trasformazione (65.7). Costruiamo 
:
e derivati
,
1. Cinematica di un punto materiale. Per punto materiale si intende un oggetto fisico, geometricamente equivalente a un punto matematico, ma dotato di massa. La cinematica è una branca della fisica che studia i tipi di movimento dei corpi senza considerare le cause del movimento. La posizione di un punto nello spazio è caratterizzata da un raggio vettore. Il raggiovettore di un punto è un vettore il cui inizio coincide con l'origine del sistema di coordinate e la cui fine coincide con il punto considerato. R = io x+ J sì+ K z. La velocità è la distanza percorsa da un corpo nell'unità di tempo. v(t) = d R/dt. v(t) = io dx/dt+ J dy/dt+ K dz/dt. L'accelerazione è il tasso di variazione della velocità. UN=d v/dt = d2 R/dt2= io d2x/dt2+ J d 2 anni/dt 2 + K d2z/dt2 . UN = UN τ + UN n= τ dv/dt + N v2/R.
D R = v dt; D v = UN dt, quindi v = v 0 + UN T; R = R 2 – R 1 = v 0t+ UN t2/2.
2. Dinamica di un punto materiale. Le leggi di Newton. I concetti base della dinamica sono il concetto di massa e di forza. La forza è la causa del movimento, cioè sotto l'influenza della forza del corpo guadagna velocità. La forza è una grandezza vettoriale. La massa è una misura dell'inerzia di un corpo. Il prodotto della massa per la velocità si chiama quantità di moto. P= m v. Il momento angolare di un punto materiale è il vettore l = R * P. Il momento della forza che agisce su un punto materiale è chiamato vettore M = R * F. Se differenziamo l'espressione del momento angolare, otteniamo: d l/dt=d R/dt* P + R*D P/dt. Considerato che il d R/dt= v E v parallelo P, otteniamo d l/dt= M.Le leggi di Newton. La prima legge di Newton afferma che un corpo mantiene uno stato di quiete o di moto rettilineo uniforme se su di esso non agiscono altre forze o se la loro azione è compensata. La seconda legge di Newton afferma che la variazione della quantità di moto nel tempo è un valore costante ed è uguale alla forza agente d P/dt = d/dt(m v) = md v/dt= F.Questa è la seconda legge di Newton scritta in forma differenziale. La terza legge di Newton dice che nell'interazione di due corpi, ciascuno di essi agisce sull'altro con lo stesso valore, ma in direzione opposta, forza. F 1 = - F 2 .
3. Dinamica del sistema di punti materiali. Leggi di conservazione. Il sistema dei punti materiali è la totalità del loro numero finito. Ogni punto del sistema è influenzato da forze interne (da altri punti) ed esterne. Sia m la massa, r i il raggio vettore. x io, y io, z i - corda. i-esimo punto. L'impulso di un sistema di punti materiali è la somma degli impulsi dei punti materiali che compongono il sistema: P= Σ(i=1,n) P io = [ P 1 + P 2 +…+ P N]. Il momento angolare di un sistema di punti materiali è la somma dei momenti di moto che compongono il sistema di punti materiali: l = Σ [ l io] = Σ [ R io * P io ]. La forza che agisce su un sistema di punti materiali è definita come la somma di tutte le forze che agiscono sui punti del sistema, comprese le forze di interazione tra i punti del sistema: F = Σ [ F Io dove F io = F i' + Σ(j ≠ i) F ji è la forza che agisce sul punto materiale del sistema, indicato con l'indice i. È costituito da una forza esterna F i ’ e la forza interna Σ(i ≠ j) [ F ji], agendo sul punto come risultato dell'interazione con altri punti del sistema. Allora: F = Σ (i=1,n) [ F i ’] + Σ (i=1,n) Σ(j ≠ i) [ F ji]. Secondo la terza legge di Newton Σ (i=1,n) Σ(j ≠ i) [ F ji] = 0, quindi F = Σ [ F io']. Il momento di forza agente su un sistema di punti materiali è la somma dei momenti di forza applicati ai punti del sistema M= Σ (i) [ M io] = Σ(i) [ R io * F io] = Σ(i) [ R io * F io']. Per un sistema di punti materiali, l'equazione del moto ha la forma d P/ dt = Σ = Σ [ F io ].
Il centro di massa di un sistema di punti materiali è un punto immaginario con un raggio vettore R= 1/mΣ. La velocità del suo movimento V=d R/dt. Quindi l'equazione del moto m d V/dt= F. L'equazione dei momenti per il sistema di punti materiali d l/dt= M. Leggi di conservazione. Un sistema isolato è un sistema che non è influenzato da forze esterne. In lei F= 0, quindi d P/dt = 0. Quindi P= cost. In un sistema isolato, il momento delle forze esterne M= 0. Pertanto, d l/dt = 0, il che significa l= cost. La variazione dell'energia cinetica di un punto materiale quando si sposta tra due posizioni è uguale al lavoro compiuto dalla forza. m0 v2 2 /2 – m0 v1 2 /2 = ∫(1,2) F D l oppure m 0 v 2 /2 + E p \u003d const.
4. Moto in un campo centralmente simmetrico. Le leggi di Keplero. Il campo si dice centrale se l'energia potenziale del corpo in esso contenuto dipende solo dalla distanza r da un certo punto fisso. Forza F= - ∂U(r)/ ∂ R= - dU/dr R/r che agisce sulla particella, in valore assoluto dipende anch'esso solo da r ed è diretto in ogni punto lungo il raggio vettore. Quando ci si sposta nel campo centrale si conserva il momento del sistema rispetto al centro del campo. Per un momento particellare M = [R*R]. Poiché i vettori M e r sono reciprocamente perpendicolari, la costanza di M significa che quando la particella si muove, il suo raggio vettore rimane sempre sullo stesso piano, il piano perpendicolare a M. Pertanto, la traiettoria della particella nel campo centrale giace interamente su un piano. Introducendo in esso le coordinate polari r, φ, scriviamo la funzione di Lagrange nella forma L = m/2 (r 2 (∙) + r 2 φ 2 (∙)) - U(r). Questa funzione non contiene esplicitamente la coordinata φ. Per tale coordinata, la quantità di moto generalizzata pi corrispondente ad essa è l'integrale del moto. In questo caso, la quantità di moto generalizzata p φ = mr 2 φ(∙) coincide con il momento M z = M, per cui M = mr 2 φ(∙) (1). Si noti che per il moto piano di una particella in un campo centrale, questa legge ammette una semplice interpretazione geometrica. L'espressione 1/2 r r d φ è l'area del settore formato da due vettori di raggio infinitamente vicini e un elemento arco della traiettoria. Indicandolo come df, scriviamo la quantità di moto della particella nella forma M = 2mf, dove la derivata f è chiamata velocità settoriale. Pertanto, la conservazione della quantità di moto significa la costanza della velocità settoriale: a parità di periodi di tempo, il raggio vettore di un punto in movimento descrive aree uguali ( Seconda legge di Keplero). Esprimendo φ(∙) attraverso M da (1) e sostituendo nell'espressione l'energia, otteniamo: E = m/2 (r 2 (∙) + r 2 φ 2 (∙)) + U(r) = mr 2 (∙ )/2 + M 2 /2mr 2 + U(r). Quindi r(∙) = √(2/m (E – U(r)) - M 2 /m 2 r 2) oppure, separando le variabili e integrando: t = ∫dr/√(2/m (E – U( r)) - M 2 /m 2 r 2) + cost. Inoltre, scrivendo la (1) come dφ = M 2 /mr 2 dt, sostituendo qui dt e integrando, troviamo: φ = ∫dr (M/r 2)/√(2/m (E – U(r)) - M 2 /r 2) + cost. La prima legge di Keplero. Ogni pianeta ruota attorno a un'ellisse con il Sole in uno dei suoi fuochi. Terza legge di Keplero. I quadrati dei periodi siderali dei pianeti si rapportano come cubi dei semiassi maggiori delle loro orbite T 1 2 /T 2 2 = a 1 3 /a 2 3 .
5. La funzione di Lagrange e le equazioni di Lagrange di un sistema di punti materiali. Integrali del moto. Consideriamo un sistema chiuso di punti materiali. La funzione di Lagrange ha la forma L = Σ(a) – U(r 1 , r 2 , …), dove T = Σ (a) è l'energia cinetica e U è l'energia potenziale di interazione delle particelle. Allora le equazioni del moto d/dt (∂L/∂v a) = ∂L/∂r a assumono la forma m a dv a /dt = - ∂U/∂r a . Queste equazioni del moto sono chiamate equazioni di Newton. Vettore F a = - ∂U/∂r a è detta forza. Se per descrivere il movimento non si utilizzano coordinate cartesiane dei punti, ma coordinate generalizzate arbitrarie q i , per ottenere la funzione lagrangiana è necessario eseguire la trasformazione corrispondente: x a = f(q 1 , q 2 , .., q s) , x a (∙) = Σ(k ) [∂f a /∂q k (∙)], ecc. Sostituendo queste espressioni nella funzione L= 1 / 2 Σ(a) – U, otteniamo la funzione di Lagrange desiderata della forma L = 1/2 Σ(i,k) – U(q). Integrali del moto. Esistono funzioni di coordinate generalizzate che mantengono valori costanti durante il movimento, a seconda solo delle condizioni iniziali. Si chiamano integrali del moto. A causa dell'omogeneità del tempo, dL/ dt = Σ(i) [∂L/∂q i q i (∙)] + Σ(i) [∂L/∂q i (∙) q i (∙∙)]. Sostituendo ∂L/∂q i secondo le equazioni di Lagrange con d/dt (∂L/∂q i (∙)), otteniamo dL/dt = Σ(i) oppure d/dt (Σ(i) - L) = 0 Ciò dimostra che la quantità E = Σ(i) – L, chiamata energia, non cambia, cioè integrale del movimento. A causa dell'omogeneità dello spazio con un trasferimento infinitamente piccolo ε, quando tutti i punti del sistema vengono spostati di ε = δr, la variazione nella funzione di Lagrange, pari a δL = ε Σ(a) [∂L/∂r a ], dovrebbe essere uguale a zero, cioè Σ(a) [∂L/∂r a ] = 0. Utilizzando le equazioni di Lagrange, otteniamo Σ(a) = d/dt (Σ(a)[ ∂L/∂v a ]) = 0. Quindi la quantità R= Σ(a)[ ∂L/∂v a ], detto quantità di moto, rimane invariato, cioè integrale del movimento. A causa dell'isotropia dello spazio con una rotazione infinitamente piccola attraverso l'angolo δφ, la variazione della funzione di Lagrange è pari a δL = Σ(a) [∂L/∂r a δ R a + ∂L/∂v aδ v a] deve essere zero. Effettuare la modifica ∂L/∂ v un = P a e ∂L/∂ R un = P a (∙) vista l’arbitrarietà di δφ, otteniamo d/dt Σ(a) [ R UN P a ] = 0. Il valore Ì = Σ(a) [ R UN P a ], detto momento angolare, rimane costante, cioè integrale del movimento.
6. Dinamica di un corpo assolutamente rigido. Tensore d'inerzia. Equazioni di Eulero. Un corpo rigido è un sistema di punti materiali, la cui distanza rimane costante. Per una descrizione completa del moto di un corpo rigido, oltre al moto di uno dei suoi punti, è necessario conoscere il moto del corpo vicino a questo punto come punto di fissaggio. Sia fissato il corpo nel punto O. Indichiamo il raggio vettore del punto mi rispetto a O R io , wè la velocità angolare istantanea del corpo, quindi il momento angolare l= Σ [ R io*io v io] = Σ = wΣ - Σ . Questa uguaglianza vettoriale può essere scritta come tre proiezioni sugli assi coordinati L x = w x Σ - Σ ; L y = w y Σ - Σ ; L z = w z Σ - Σ . Dato che ( w R i) = x i w x + y i w y + z i w z otteniamo L x = J xx w x + J xy w y + J xz w z ; L y = J yx w x + J yy w y + J yz w z ; L x = J zx w x + J zy w y + J zz w z , dove J xx = Σ , J xy = Σ , altri sono simili. I valori J xx , J yy , J zz sono chiamati momenti d'inerzia assiali, e J xy = J yx , J xz = J zx , J yz = J zy sono chiamati momenti d'inerzia centrifughi. L'insieme dei valori J ij è detto tensore d'inerzia. Gli elementi di J ii si dicono diagonali. Se tutti gli elementi fuori diagonale sono uguali a zero, allora dicono che gli assi del corpo che coincidono con gli assi delle coordinate sono gli assi di inerzia principali e le quantità J ii sono chiamate i momenti di inerzia principali. Tale tensore è ridotto alla forma diagonale.
Equazioni di Eulero. L'equazione del moto del centro di massa del corpo ha la forma m d v 0 /dt = md/dt ( w * R 0) = F, Dove R 0 è il raggio vettore del centro di massa del corpo, tracciato dal punto del suo attacco. È conveniente dirigere gli assi del sistema di coordinate associato al corpo lungo gli assi principali di inerzia. In questo caso, il momento angolare assume una forma semplice L 1 = J 1 w 1 , L 2 = J 2 w 2 , L 3 = J 3 w 3 , e w i sono le proiezioni della velocità angolare sugli assi coordinati che si muovono insieme con il corpo. Utilizzando la formula generale d UN/dt = ∂ UN/∂t + w* UN, possiamo rappresentare l'equazione dei momenti come segue: ∂ l/∂t + w * l = M. Tenendo conto che L x = J x w x , L y = J y w y , L z = J z w z , riscriviamo questa equazione in proiezioni sugli assi del sistema di coordinate mobili: J x dw x /dt + (J z - J y )w y w z = M x , J y dw y /dt + (J x – J z)w z w x = M y , J z dw z /dt + (J y – J x)w x w y = M z . Queste equazioni sono chiamate equazioni di Eulero.
7.
Moto relativo a sistemi di riferimento non inerziali.
NISO è un sistema in cui il corpo si muove con accelerazione rispetto al riposo. sistemi di coordinate. Qui i concetti di omogeneità e isotropia dello spazio e del tempo non sono soddisfatti, perché la durata e la lunghezza in NISO variano. Inoltre si perde il contenuto della 3a legge di Newton e delle leggi di conservazione. La ragione di tutto sono le forze di inerzia associate solo al sistema di coordinate, il gatto. influenzare il movimento del corpo. QUELLO. l'accelerazione può essere modificata da una forza esterna o dall'inerzia. F=∑Fi=ma (ISO), F=F(ext.)+Fi=ma′(NISO), dove Fi è la forza di inerzia, a è l'accelerazione. corpi in IFR, a′-accel. lo stesso corpo in NISO. In NISO la prima legge di Newton non è soddisfatta! Fi=-m(a′-a), cioè le forze inerziali non obbediscono alla terza z di Newton, perché sono di breve durata. Durante il passaggio da ISO a NISO le forze d'inerzia scompaiono. Inerzia le forze sono sempre dirette contro le palpebre. forze esterne. Le forze d'inerzia possono essere sommate vettorialmente. Nell'ISO: v=cost, v< dx/dt=Ux=dx′/dt+dv(t)/dt′=U′x+v(t) dUx/dt=d/dt′(U′x+v(t))=dU′x/ dt′+dv(t)/dt′=a x ' + a 0 = a x . I concetti di velocità assoluta, relativa e traslazionale vengono introdotti in NISO: u 0 - velocità assoluta, a 0 - accelerazione relativa. dormiente sistemi di coordinate. u x 0 \u003d v + u x 0 '; a x 0 \u003d a ' + a x; u x ’ a x - velocità e accelerazione relative. movimento sistemi di coordinate. (parente) ; v, a′-velocità. e accelerato. k′ si riferisce. k, cioè velocità e accelerazione portatile Esiste una funzione delle coordinate generalizzate, velocità, tempo. Considerando uno spazio 2S dimensionale, allora la posizione del sistema S = ∫(t 1 , t 2) L(g, g( ), t)dt, L è la funzione di Lagrange; Azione S. La funzione dell'azione è detta itnegrale S=∫ Ldt=0, con il cat. preso lungo la traiettoria reale del moto, il sistema avrà un valore minimo, cioè S=Smin, δS=0. Quelli. il sistema da 1 a 2 si muove lungo una traiettoria tale che la sua azione è minima: principio di minima azione di Hamilton. L = T – U è la differenza tra l'energia cinetica e quella potenziale del sistema. Secondo Hamilton la traiettoria reale corrisponde all'azione minima. Troviamo una traiettoria. La traiettoria effettiva è la traiettoria minima. S-funzionale. Troviamo il suo min. δS = 0 prima variazione. δS = ∫(t 1 ,t 2)(Σ[∂L/∂g i δg i ] + Σ[∂L/∂g i ( ) δg i ( )])dt; ∫(t 1 ,t 2) ∂L/∂g i ( ) δg i ( ) dt = ∫(t 1 ,t 2) ∂L/∂g i ( ) dδg i = ∂L/∂g i ( )δg i (t 1 ,t 2) - ∫(t 1 ,t 2) δg i d/dt (∂L/∂g i ( )) dt; δg non dipendono l'uno dall'altro 9.
Oscillazioni di sistemi ad uno e molti gradi di libertà. Vibrazioni libere e forzate
.
Il caso più semplice è quando il sistema ha un grado di libertà. Un equilibrio stabile corrisponde a tale posizione del sistema, nel cat. il suo potenziale. en. U(q) ha un minimo. La deviazione da questa posizione porta all'emergere di una forza - dU/dq, che tende a riportare indietro il sistema. q 0 - coordinata generalizzata. Espandiamo U(q) - U(q0) in potenze e otteniamo U(q) - U(q0) ≈ k / 2 (q - q 0) 2 dove k \u003d U '' (q 0) è un coefficiente positivo . U(q 0) \u003d 0, denotiamo x \u003d q - q 0 - la deviazione della coordinata dal valore di equilibrio, quindi U (x) \u003d kx 2 / 2 è energia potenziale. 1/2a(q) q' 2 =1/2a(q)x' 2 -energia cinetica a q = q0 e a(q0) = m otteniamo la funzione di Lagrange per un sistema che esegue oscillazioni unidimensionali: L = mx 2 (∙) /2 – kx 2 /2. L'equazione del moto corrispondente a questa funzione sarà: mx(∙∙) + kx = 0 oppure x(∙∙) + w 2 x = 0, dove w = √(k/m) è la frequenza di oscillazione ciclica. La soluzione a questi ur-esimo è x \u003d a cos (wt + α) dove a è l'ampiezza delle oscillazioni, wt + α è la fase delle oscillazioni. Quello. l'energia del sistema oscillante sarà E = mx 2 (∙)/2 + kx 2 /2. Vibrazioni forzate. In questo caso, oltre alla propria energia potenziale ½ kx 2, il sistema possiede anche un'energia potenziale U e (x, m) associata all'azione di un campo esterno. Di conseguenza, la funzione di Lagrange di un tale sistema sarà: L = mx 2 (∙)/2 + kx 2 /2 + x F(t), dove F(t) è una forza esterna. L'equazione del moto corrispondente sarà mx(∙∙) + kx = F(t), oppure x(∙∙) + w 2 x = F(t)/m. Se F(t) è una semplice funzione periodica del tempo con una certa frequenza γ: F(t) = f cos(γt + β) allora la soluzione delle equazioni del moto sarà: X = a cos(wt + α) + f cos(γt + β)/(m(w 2 – γ 2)) a e α sono determinati dalle condizioni iniziali. Quello. sotto l'azione di una forza motrice, il sistema effettua un movimento che rappresenta una combinazione di due oscillazioni - con la frequenza naturale del sistema w e con la frequenza della forza motrice - γ. Oscillazioni di sistemi a molti gradi di libertà
.
Pentola. en. il sistema U(q i) ha un minimo in q i =q i 0 . Introducendo piccoli spostamenti x i = q i - q i 0 ed espandendo U in essi con una precisione in termini del 2° ordine, otteniamo il potenziale. energia: U = 1/2 Σ(i,k) , k ik =k ki . Kinet. en. per un tale sistema sarà 1/2 Σ(i,k) , dove m ik =m ki . L'equazione di Lagrange per un tale sistema sarebbe: L = 1/2 Σ(i,k) . Allora dL = Σ(i,k) . Stiamo cercando x k (t) nella forma x k \u003d A k exp (-iwt), A k è una costante. Sostituendo questo nell'equazione di Lagrange, otteniamo un sistema di equazioni lineari omogenee. Σ(k) [(-w 2 m ik +k ik)A k ] = 0 - equazione caratteristica, ha s radici diverse w 2 α (α=1,2,….,s) w α - frequenze naturali di il sistema. Una soluzione particolare del sistema ha la forma: x k = ∆ kα C α exp(-iw α t). La soluzione generale è la somma di tutte le soluzioni particolari: x k = Σ(α) [∆ kα Q α ], dove Q = Re (C α exp(-iw α t)). 10.
Equazione canonica di Hamilton.
Un certo numero di vantaggi nello studio delle questioni di meccanica è la descrizione con l'aiuto di coordinate e momenti generalizzati, la transizione da un insieme di variabili indipendenti a un altro può essere effettuata mediante la trasformazione di Legendre. In questo caso, la questione è quanto segue. Il differenziale totale delle funzioni di Lagrange in funzione delle coordinate e delle velocità è: dL = Σ(i) [∂L/∂q i ] + Σ(i) [[∂L/∂q i (∙)]. Questa espressione può essere scritta come dL = Σ(i) + Σ(i) . Riscriviamolo nella forma: d(Σ(i) – L) = - Σ(i) + Σ(i) . Il valore sotto il segno del differenziale è l'energia del sistema espressa in termini di coordinate e momenti, e si chiama funzione hamiltoniana: H (p, q, t) = Σ (i) - L. Dal dif. le uguaglianze dH = - Σ(i) + Σ(i) seguono le equazioni: q i (∙) = ∂H/∂p i , p i (∙) = - ∂H/∂q i sono le equazioni hamiltoniane. Per la loro semplicità e simmetria vengono anche chiamati. canonico. Parentesi di Poisson. La derivata temporale di qualsiasi funzione F di coordinate generalizzate, momenti e tempo è dF/dt = ∂F/∂t + Σ(i) [∂F/∂q i dq i /dt] + Σ(i) [∂F/∂ p i dpi /dt]. Usando le equazioni di Hamilton, possiamo riscrivere questa equazione nella seguente forma: dF/dt = ∂F/∂t + , dove = Σ(i) [∂F/∂q i ∂H/∂p i - ∂H/∂q i ∂F /∂ p i ] - chiamato. la parentesi di Poisson. Ovviamente l'equazione di Hamilton può essere scritta utilizzando le parentesi di Poisson. 11.
Equazione di Hamilton-Jacobi
.
Per il principio di minima azione abbiamo S = ∫(t 1 ,t 2)Ldt. Consideriamo l'azione (S) come una quantità che caratterizza il movimento lungo traiettorie vere. Basandosi sull'equazione di Lagrange per cambiare l'azione quando ci si sposta da una traiettoria ad un'altra traiettoria vicina ad essa (con un grado di libertà), otteniamo: δS = pδq o per qualsiasi numero di gradi di libertà: δS = Σ(i) . Ne consegue che le derivate parziali dell'azione rispetto alle coordinate sono pari ai momenti corrispondenti: ∂S/∂q i = p i (1). Per definizione dS/dt = L, invece, considerando S in funzione delle coordinate e del tempo e utilizzando la formula (1), abbiamo: dS/dt = ∂S/∂t + Σ(i) [∂S /∂q io q io (∙)] = ∂S/∂t + Σ(i) . Confrontando le due espressioni si ottiene ∂S/∂t = L - Σ(i) oppure ∂S/∂t = - H(p,q,t) (2). Le formule (1), (2) possono essere scritte insieme come dS = Σ(i) – Hdt. E l'azione stessa (S) sarà S = ∫ (Σ(i) – Hdt). Per H indipendente da t, S(q,t)=S 0 (q) - Et, dove S 0 (q) = Σ(i) [∫p i dq i ] è un'azione abbreviata ed Еt è sostituito da H(p ,q). La funzione S(q,t) soddisfa una certa dif. equazione che otteniamo sostituendo gli impulsi à nella relazione (2) con le derivate ∂S/∂q: ∂S/∂t + H(∂S/∂q 1 ,…, ∂S/∂q s ;q 1 ,… ,q s ,t) = 0 è un'equazione in derivate parziali del 1° ordine chiamata. Equazione di Hamilton-Jacobi. Quindi, per una particella in un campo esterno U(x,y,z,t) ha la forma: ∂S/∂t + 1/(2m)((∂S/∂x) 2 + (∂S/∂ y) 2 + (∂S/∂z) 2) + U(x,y,z,t) = 0. 12.
Deformazioni e tensioni nei solidi. Moduli di Young, taglio. rapporto di Poisson
.
La deformazione è un cambiamento nella forma e nel volume di un corpo sotto l'influenza di forze esterne. Sotto l'azione di una forza esterna, la forma del corpo cambia. Tutte le deformazioni in natura possono essere ridotte a 3 M principali deformazioni: 1) tensione, compressione; 2) taglio; 3) torsione. Distinguere tra deformazioni omogenee e disomogenee. Se tutte le parti sono deformate allo stesso modo, allora questo uniformemente deformato. Se tutte le parti del corpo si deformano diversamente, allora questo deformato in modo disomogeneo. La legge di Hooke è soddisfatta nella regione di sola deformazione elastica. = MI’. F/S = E ∆l/l 0 ; Controllo F = ES∆l/l 0 = kx; k = ES/l 0 ; Controllo F \u003d ESx / l 0. La legge di Hooke definisce la relazione tra e . k è il coefficiente di elasticità, dipende dalle dimensioni geometriche, dal materiale di cui è fatto il corpo. E è il modulo di Young. Il modulo di Young è uguale alla forza che deve essere applicata ad un corpo di sezione unitaria affinché il suo corpo aumenti di 2 volte. Un altro tipo di deformazione è quella a taglio, che si osserva quando la superficie è applicata tangenzialmente; è parallelo alla superficie di deformazione di taglio, osservata sotto l'azione delle forze tangenziali, cioè le forze sono applicate tangenzialmente. Ψ~F t /S (angolo di spostamento). Ψ = nF t /S; n è il fattore di spostamento. F t = nS. (E>N, E~4N). 13.
Meccanica dei liquidi e dei gas.
Per tutti i liquidi e gas, il parametro unificante è: densità ρ, pressione P=F n /S. Nei liquidi e nei gas si verifica il modulo di Young, ma non si verifica il modulo di taglio |σ|=|P|, σ - sollecitazione. Se il liquido (gas) è immobile, abbiamo a che fare con l'idrostatica (aerostatica). Leggi caratteristiche: Legge di Pascal: la sovrappressione creata nei gas e nei liquidi si trasmette equamente in tutte le direzioni. Zn Archimede è valido sia per i liquidi che per i gas. La forza di Archimede agisce sempre contro la forza di gravità. Il motivo dell'emergere della forza di Archimede è la presenza di un corpo di volume V. Zn Archimede: Un corpo in un liquido o in un gas è sempre influenzato da una forza pari al peso del liquido o del gas spostato dalla parte immersa di il corpo e diretto verticalmente verso l'alto. Se F A >F HEAVY il corpo galleggia, viceversa affonda. Se scorre un liquido (gas), a queste equazioni viene aggiunta l'equazione di continuità del getto. Viene chiamata la traiettoria del movimento di una particella in un fluido. linea corrente. Viene chiamata la parte di spazio delimitata da una linea corrente. tubo di corrente. Il fluido nel tubo del flusso può scorrere stazionario o non stazionario. La corrente si chiama stazione se attraverso una determinata sezione del tubo di corrente per unità. nel tempo passa la stessa quantità di liquido (gas), altrimenti il flusso non è statico. Consideriamo un tubo di corrente della forma seguente: Se il flusso del fluido è statico. Allora m 1 =m 2 =…=m n per unità di tempo, se il fluido è incomprimibile, allora ρ 1 V 1 =ρ 2 V 2 =…; =ρ n V n , ρ 1 Δx 1 = ρ 2 Δx 2 =…; \u003d ρ n Δx n, ρ 1 υ 1 ΔtS 1 \u003d ρ 2 υ 2 ΔtS 2 =…= ρ n υ n ΔtS n, poiché il liquido è incomprimibile ρ è costante υ 1 S 1 = υ 2 S 2 =… = υ n S n , υS=cost; υ=cost/S è l'equazione di continuità del getto. p d v/dt = ρ G– grado P – eq. Eulero - 2° ordine. Newton per liquidi e gas. La legge è preservata. Energia nei liquidi e nei gas. Liv. Bernoulli. Id. Naz. Un fluido incomprimibile in cui le forze di attrito viscoso possono essere trascurate. L'energia cinetica non viene spesa per compiere lavoro contro le forze di attrito. Ρυ 2 /2+ρgh + P = cost – eq. Bernoulli, ρυ 2 /2 – pressione dinamica, ρgh – idrostato. Pressione, P - pressione molecolare. Mυ 2 /2 \u003d E K; mυ 2 /2V= E K /V= ρυ 2 /2. Forza di attrito viscoso F A = - ηΔυΔS/ΔZ 6 π r η υ – Forza di Stokes. Η - coefficiente. viscosità, Δυ/ΔZ – grad υ, r – dimensioni del corpo. Questa è la formula di Newton per le forze di attrito viscoso. Se ci sono forze di attrito nel fluido, allora id. Il liquido diventa viscoso. ρ v 1 2 /2 + ρgh 1 + P 1 = ρ v 2 2 /2 + ρgh 2 + P 2 ; (P 1 - P 2) \u003d ρ (υ 2 2 - υ 1 2) / 2. Se ΔP = 0, allora υ 2 2 - υ 1 2 = 0 e non ci sarà flusso di fluido. Dove P è maggiore, c'è veloce. Meno attuale. Se la sezione trasversale S aumenta, allora P aumenta e υ diminuisce. Se il tubo corrente non si trova orizzontalmente, allora υ 2 2 -υ 1 2 \u003d 2g (h 1 -h 2); υ \u003d sqrt (2g (h 1 -h 2)) - Formula di Torricelli. Le traiettorie che descrivono i movimenti dei sistemi meccanici nella configurazione estesa e negli spazi delle fasi hanno una proprietà notevole: sono estremi di alcuni problemi variazionali, forniscono valori stazionari al funzionale dell'azione. Consideriamo la formulazione del problema variazionale nello spazio delle configurazioni estese R"*", i cui punti sono gli insiemi (q, ().
Sia la curva yn = ((q, T): q e Rt e , 5q(/ 0)= 8q(/,) = 0). La variazione 8q(/) è una funzione arbitraria della classe C 1 che si annulla agli estremi del segmento = 0. A La prima variazione del funzionale Si a y = y 0 secondo la definizione è uguale a e dopo l'integrazione per parti assume la forma Il termine non integrale nell'espressione (2.3) svanisce, Perché bq k (t 0) = bq k (t y) = 0, A - 1.....l, e l'espressione in quadrato parentesi sotto il segno integrale è uguale a zero, poiché y 0 è una traiettoria reale che soddisfa le equazioni di Lagrange (2.1). Pertanto la variazione 55(y 0) = 0. ? Vale anche l'affermazione inversa: se la variazione 65(y*) = 0, dove y* appartiene alla classe delle traiettorie rotatorie, allora y* = y 0 è una traiettoria reale. La validità di questa affermazione deriva dall'espressione della prima variazione (2.3) e dal lemma principale del calcolo delle variazioni. In questo caso dall'uguaglianza a zero della prima variazione e l'indipendenza delle variazioni 6 k - 1, ..., la validità delle equazioni di Lagrange del secondo tipo l, segue bene Quando qk = qk *(t), k= 1.....l. Ciò significa che y* è la traiettoria effettiva del sistema meccanico. 3.1. Nel caso di un sistema non conservativo è impossibile indicare un funzionale il cui valore stazionario sia stato raggiunto su una traiettoria reale. Tuttavia, in questo caso le seguenti affermazioni sono equivalenti: dove q(/) è la traiettoria reale. La prima delle affermazioni di cui sopra è il contenuto del principio variazionale di Hamilton-Ostrogradsky per sistemi non conservativi. 3.2. Si può dimostrare che il valore stazionario del funzionale d'azione è minimo se la differenza - / 0 è sufficientemente piccola. Questa circostanza è collegata ad un altro nome del principio discusso: il principio di minima azione di Hamilton-Ostrogradkogo. Il problema variazionale considerato sopra può essere formulato nello spazio delle fasi esteso, il che risulta essere importante quando si considerano questioni di integrabilità delle equazioni canoniche di Hamilton. Indichiamo con à = ((р + 6р. q + 8q, IO): p, q, 6 p. 6q e R",te[r0, /,]. 5q(/ 0)= 8q(/|) = 0) nello spazio delle fasi esteso e sia, per 8p = 8q = 0, la curva à 0 la soluzione del sistema di equazioni canoniche hamiltoniane Tutte le funzioni temporali appartengono alla classe C 1 . Si definisce così una famiglia di traiettorie rotatorie (Г), alla quale appartiene la traiettoria reale à 0 (Fig. 46). Il funzionale dell'azione, tenendo conto della connessione tra le funzioni di Lagrange e Hamilton, assume la forma Qui si usano per brevità le lettere p, q al posto delle lettere p + 8p, q + 8q. Calcolando la variazione del funzionale 5[Γ] sulla traiettoria reale, otteniamo Integrando per parti, tenendo conto delle condizioni al contorno, si trova: Da ciò segue che la variazione 85|Γ 0 1 = 0 se p(/), q(f) soddisfano le canoniche equazioni di Hamilton (2.4), u. invece, dalla condizione di indipendenza delle variazioni 8p(r), 6q(/) seguono le equazioni (2.4) secondo il lemma principale del calcolo delle variazioni. È stata così dimostrata la validità del principio di minima azione nello spazio delle fasi del sistema: l’azione funzionale 5[Г] definita sullo spazio delle traiettorie rotatorie (Г|. assume valore stazionario sulla traiettoria reale, cioè 85 [ƒ 0 1 = 0. Riso. 46 Quando ho appreso per la prima volta di questo principio, ho avuto una sensazione di una sorta di misticismo. Sembra che la natura scelga misteriosamente tutte le possibili modalità di movimento del sistema e scelga la migliore. Oggi voglio parlare un po' di uno dei principi fisici più notevoli: il principio di minima azione. Anche la luce, quando viene riflessa, si muove in modo da arrivare da un punto all'altro nel modo più breve. Nell'immagine, il percorso più breve sarà il percorso verde, in cui l'angolo di incidenza è uguale all'angolo di riflessione. Qualsiasi altro percorso, come quello rosso, sarà più lungo. Nel 1662, Pierre Fermat suggerì che la velocità della luce in una sostanza densa, come il vetro, è inferiore a quella dell'aria. Prima di ciò, la versione generalmente accettata era Cartesio, secondo la quale la velocità della luce nella materia doveva essere maggiore che nell'aria per ottenere la corretta legge di rifrazione. Per Fermat, l’ipotesi che la luce potesse muoversi più velocemente in un mezzo più denso che in uno rarefatto sembrava innaturale. Pertanto, ipotizzò che tutto fosse esattamente il contrario e dimostrò una cosa sorprendente: secondo questo presupposto, la luce viene rifratta in modo da raggiungere la sua destinazione nel minor tempo possibile. Tutti questi fatti suggeriscono che la natura agisce in modo razionale, la luce e i corpi si muovono nel modo più ottimale, consumando il minor sforzo possibile. Ma quali fossero questi sforzi e come calcolarli rimaneva un mistero. Nel 1744 Maupertuis introduce il concetto di "azione" e formula il principio secondo cui la vera traiettoria di una particella differisce da qualsiasi altra in quanto l'azione su di essa è minima. Tuttavia, lo stesso Maupertuis non è riuscito a dare una definizione chiara di cosa significhi questa azione. Una formulazione matematica rigorosa del principio di minima azione fu sviluppata da altri matematici - Eulero, Lagrange, e fu infine data da William Hamilton: Allora come devi guidare per arrivare al punto in tempo e consumare meno carburante possibile? È chiaro che devi andare in linea retta. Con un aumento della distanza percorsa, il carburante non verrà consumato esattamente di meno. E poi puoi scegliere diverse tattiche. Ad esempio, puoi arrivare rapidamente al punto in anticipo e semplicemente sederti, aspettare che arrivi il momento. La velocità di guida, e quindi il consumo di carburante in ogni momento, sarà elevata, ma anche il tempo di guida sarà ridotto. Forse il consumo complessivo di carburante in questo caso non sarà così elevato. Oppure puoi andare in modo uniforme, con la stessa velocità, in modo tale da arrivare, senza fretta, esattamente al momento giusto. Oppure parte del percorso va veloce e parte più lentamente. Qual è il modo migliore per procedere? Si scopre che il modo più ottimale ed economico di guidare è guidare a una velocità costante, in modo da essere esattamente nel punto stabilito all'ora stabilita. Qualsiasi altra opzione utilizzerà più carburante. Puoi verificare tu stesso con alcuni esempi. Il motivo è che il consumo di carburante aumenta con il quadrato della velocità. Pertanto, all'aumentare della velocità, il consumo di carburante aumenta più velocemente di quanto diminuisce il tempo di guida e aumenta anche il consumo complessivo di carburante. Quindi, abbiamo scoperto che se un'auto consuma carburante in un dato momento in proporzione alla sua energia cinetica, allora il modo più economico per spostarsi da un punto all'altro esattamente all'ora stabilita è guidare in modo uniforme e in linea retta, proprio come un corpo si muove in assenza di forze che agiscono su di esso. Qualsiasi altro modo di guidare comporterà un consumo complessivo di carburante più elevato. Il consumo di carburante in ogni momento è uguale all'energia cinetica meno l'energia potenziale dell'auto (meno l'energia potenziale, perché il veicolo installato produce carburante e non consuma). Ora il nostro compito è lo spostamento più economico dell'auto tra i punti e diventa più difficile. Il moto rettilineo uniforme in questo caso non è il più efficace. Si scopre che è più ottimale salire un po ', indugiare lì per un po', avendo sviluppato più carburante, e poi scendere al punto. Con la traiettoria di volo corretta, il consumo totale di carburante dovuto alla salita coprirà i costi aggiuntivi del carburante per aumentare la lunghezza della traiettoria e aumentare la velocità. Se calcolato attentamente, il modo più economico per un'auto sarebbe volare in una parabola, esattamente nella stessa traiettoria e esattamente alla stessa velocità di una pietra che volerebbe nel campo gravitazionale terrestre. Un analogo della quantità totale di carburante consumato per l'intero tempo di movimento, ad es. il valore della lagrangiana accumulato durante l'intero tempo del moto è chiamato "azione". Il principio di minima azione è che il corpo si muove in modo tale che l'azione (che dipende dalla traiettoria del movimento) sia minima. In questo caso, non bisogna dimenticare che sono date le condizioni iniziali e finali, cioè dove si trova il corpo in un momento e in un momento. In questo caso il corpo non deve muoversi in un campo gravitazionale uniforme, come abbiamo considerato per la nostra macchina. Puoi considerare situazioni completamente diverse. Un corpo può oscillare su un elastico, oscillare su un pendolo o volare attorno al Sole, in tutti questi casi si muove in modo tale da minimizzare il “consumo totale di carburante” cioè azione. Se il sistema è costituito da più corpi, la lagrangiana di tale sistema sarà uguale all'energia cinetica totale di tutti i corpi meno l'energia potenziale totale di tutti i corpi. E ancora, tutti i corpi si muoveranno di concerto in modo che l'effetto dell'intero sistema durante tale movimento sia minimo. Ad esempio, prendiamo una palla e posizioniamola in uno spazio vuoto. A una certa distanza da esso mettiamo un muro elastico. Diciamo che vogliamo che la palla finisca nello stesso posto dopo un po' di tempo. In queste condizioni la palla può muoversi in due modi diversi. Per prima cosa, può semplicemente restare lì. In secondo luogo, puoi spingerlo verso il muro. La palla raggiungerà il muro, rimbalzerà e tornerà indietro. È chiaro che puoi spingerlo con tale velocità che ritorni esattamente al momento giusto. Come si può salvare il principio di minima azione affinché sia vero in tali situazioni? Ne parleremo tra.8. Principio variazionale di Hamilton. (principio di minima azione).
;
=0
sulla traiettoria effettiva deve essere soddisfatta la seguente equazione: 
- Equazione di Lagrange (per ogni i= 1,…S).
La relazione quantitativa tra E e N è data tramite il rapporto di Poisson. N = E/(2(1+μ)), dove è il rapporto di Poisson. μ = |∆d/d 0 |/|∆l/l 0 |. Il rapporto di Poisson determina la variazione delle dimensioni trasversali durante la tensione o la compressione. 0,5.
sfondo
Sin dai tempi di Galileo è noto che i corpi su cui non agisce alcuna forza si muovono in linea retta, cioè lungo il percorso più breve. Anche i raggi luminosi viaggiano in linea retta. 
Ciò è facile da dimostrare riflettendo semplicemente i percorsi dei raggi sul lato opposto dello specchio. Sono mostrati con linee tratteggiate nell'immagine. 
Si può vedere che il percorso verde ACB si trasforma in una linea retta ACB'. E il percorso rosso si trasforma in una linea spezzata ADB ', che, ovviamente, è più lunga di quella verde. 
Ancora nella figura, il colore verde indica il percorso che effettivamente percorre il raggio luminoso. Il percorso segnato in rosso è il più breve, ma non il più veloce, perché la luce ha un percorso più lungo da percorrere nel vetro, e in esso la sua velocità è più lenta. Il più veloce è il percorso effettivo del raggio luminoso. 
Nel linguaggio matematico, il principio di minima azione è formulato in modo abbastanza breve, ma non tutti i lettori potrebbero comprendere il significato della notazione utilizzata. Voglio provare a spiegare questo principio in modo più chiaro e in termini più semplici. corpo sciolto
Quindi, immagina di essere seduto in una macchina a un certo punto e in un certo momento ti viene assegnato un compito semplice: a quel punto devi guidare un'auto fino al punto. 
Il carburante per l’auto è costoso e, ovviamente, vuoi spenderlo il meno possibile. La tua auto è realizzata utilizzando le supertecnologie più recenti e può accelerare o decelerare alla velocità che desideri. Tuttavia, è progettato in modo tale che più va veloce, più carburante consuma. Inoltre, il consumo di carburante è proporzionale al quadrato della velocità. Se guidi due volte più veloce, consumi 4 volte più carburante nello stesso lasso di tempo. Oltre alla velocità, il consumo di carburante è ovviamente influenzato dalla massa dell'auto. Più la nostra macchina è pesante, più carburante consuma. Il consumo di carburante della nostra auto in ogni momento è , cioè è esattamente uguale all'energia cinetica dell'auto. Nel campo della gravità
Ora miglioriamo un po' la nostra macchina. Attacciamogli i motori a reazione in modo che possa volare liberamente in qualsiasi direzione. In generale, il design è rimasto lo stesso, quindi il consumo di carburante è rimasto strettamente proporzionale all'energia cinetica dell'auto. Se ora viene assegnato il compito di decollare da un punto al tempo e arrivare a un punto al tempo t, allora il modo più economico, come prima, ovviamente, volerà uniformemente e in linea retta per arrivare esattamente al punto l'ora stabilita t. Ciò corrisponde ancora una volta al libero movimento del corpo nello spazio tridimensionale. 
Tuttavia, nell'ultimo modello dell'auto è stato installato un dispositivo insolito. Questa unità è in grado di produrre carburante letteralmente dal nulla. Ma il design è tale che più l'auto è alta, più carburante produce il dispositivo in un dato momento. La produzione di carburante è direttamente proporzionale all'altezza alla quale si trova attualmente il veicolo. Inoltre, più pesante è l'auto, più potente è il dispositivo installato su di essa e più carburante produce, e la potenza è direttamente proporzionale alla massa dell'auto. L'apparato si è rivelato tale che la produzione di carburante è esattamente uguale a (dov'è l'accelerazione di caduta libera), ad es. energia potenziale dell’auto. 
Qui vale la pena fare una spiegazione. Naturalmente è possibile lanciare una pietra da un punto in molti modi diversi affinché colpisca il punto. Ma devi lanciarlo in modo tale che, volando via da un punto alla volta, colpisca un punto esattamente in quel momento. È questo movimento che sarà il più economico per la nostra auto. La funzione di Lagrange e il principio di minima azione
Ora possiamo trasferire questa analogia ai corpi fisici reali. Un analogo dell'intensità del consumo di carburante per i corpi è chiamato funzione Lagrange o Lagrangiana (in onore di Lagrange) ed è indicato con la lettera . La Lagrangiana mostra quanto "carburante" consuma il corpo in un dato momento. Per un corpo che si muove in un campo potenziale, la lagrangiana è uguale alla sua energia cinetica meno la sua energia potenziale. Non così semplice
In effetti ho barato un po' dicendo che i corpi si muovono sempre in modo da minimizzare l'azione. Sebbene in moltissimi casi ciò sia vero, è possibile pensare a situazioni in cui l'azione evidentemente non è minima. 
Sono possibili entrambe le varianti del movimento della palla, ma l'azione nel secondo caso sarà maggiore, perché per tutto questo tempo la palla si muoverà con energia cinetica diversa da zero.
