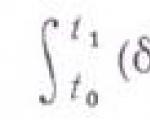Mažiausio veiksmo principas. Hamiltono-Ostrogradskio variacijos principas konfigūracijos ir fazių erdvėse Plokštumos bangos formulė
HAMILTONAS – OSTROGRADSKY PRINCIPAS
Stacionaraus veikimo principas – bendrasis integralas klasikinės mechanikos variacinis principas,įdiegė U.
Hamiltonas holoninėms sistemoms, kurias suvaržo idealūs stacionarūs ryšiai, o M. V. Ostrogradskis apibendrino nestacionarioms jungtims. Pasak G. - O.
turi stacionarią reikšmę, lyginant su panašiais kinematiskai įmanomais judesiais, kurių pradinė ir galutinė sistemos padėtis bei judėjimo laikas yra tokie patys kaip ir faktinio judėjimo. Čia T - kinetinis, U- potencinė energija, L-T-U Sistemos Lagrange funkcija. Kai kuriais atvejais tiesa atitinka ne tik stacionarų funkcinį tašką S, bet ir suteikia jam mažiausiai reikšmės. Todėl G. -O. n. dažnai vadinamas mažiausio veiksmo principas. Esant nepotencialioms aktyvioms jėgoms Fv veiksmo stacionarumo sąlyga d S = 0 pakeičiama sąlyga
Lit.: Hamilton W., Britų mokslo pažangos asociacijos ketvirtojo susirinkimo ataskaita, L., 1835, p. 513-18; Оstrоgradsky M., "Mem. de 1" Akad. des Sci. de St-Petershourg", 1850, t. 8, nr. 3, p. 33-48.
V. V. Rumjantsevas.
Matematinė enciklopedija. - M.: Tarybinė enciklopedija. I. M. Vinogradovas. 1977-1985 m.
Pažiūrėkite, kas yra "HAMILTON - OSTROGRAD PRINCIPAS" kituose žodynuose:
Fišerio principas yra evoliucinis modelis, paaiškinantis, kodėl gamtoje vyraujantis gyvų organizmų rūšių lyčių santykis yra maždaug 1:1; kuriame genai, skirti gaminti daugiau abiejų lyčių individų ... ... Vikipedija
Hamiltonas (taip pat tiesiog Hamiltono principas), tiksliau veiksmo stacionarumo principas, fizinės sistemos judėjimo lygčių gavimo būdas, ieškant stacionarios (dažnai ekstremalios, dažniausiai susijusios su nusistovėjusia tradicija... ... Vikipedija
Bangos refrakcija pagal Huygensą ... Vikipedija
Mokslo metodologijoje teigiama, kad bet kuri nauja mokslinė teorija, esant senai, gerai patikrintai teorijai, jai visiškai neprieštarauja, bet suteikia tokias pačias pasekmes tam tikru kraštutiniu aproksimavimu (ypatingu atveju). Pavyzdžiui, įstatymas... ... Vikipedija
Pontryagin diskretiškas maksimalus principas, skirtas laiko diskretiškiems valdymo procesams. Tokiam procesui baigtinio skirtumo operatorius gali neveikti, nors jo tęstiniam analogui, gautam baigtinio skirtumo operatorių pakeitus diferencialiniu... ... Matematinė enciklopedija
Arba Hamiltono principas mechanikoje ir matematinėje fizikoje padeda gauti diferencialines judesio lygtis. Šis principas galioja visoms materialioms sistemoms, kad ir kokioms jėgoms jos būtų veikiamos; Pirmiausia tai išreikšime tuo... Enciklopedinis žodynas F.A. Brockhausas ir I.A. Efronas
Kvantinis postulatas. mechanika, reikalaujanti jos fizinio sutapimo. pasekmės ribojančiu didelių kvantinių skaičių atveju su klasikinės rezultatais. teorijos. S. p. atskleidžiamas faktas, kad kvantinis. poveikis reikšmingas tik kalbant apie mikroobjektus, kai... ... Fizinė enciklopedija
Hamiltono variacijos principas- Hamiltono variacinis principas statusas T sritis fizika atitikmenys: engl. Hamiltono variacijos principas vok. Hamiltonsches Variationsprinzip, n rus. Hamiltono variacinis principas, m pranc. principe variationnel d’Hamilton, m … Fizikos terminų žodynas
Kvantinės mechanikos postulatas (žr. Kvantinė mechanika), reikalaujantis, kad jo fizinės pasekmės ribiniu didelių kvantinių skaičių atveju (žr. Kvantinius skaičius) sutaptų su klasikinės teorijos rezultatais. S. p. pasireiškia faktas, kad... ... Didžioji sovietinė enciklopedija
- (bangų mechanika), teorija, nustatanti mikrodalelių (elementų, atomų, molekulių, atomų branduolių) ir jų sistemų (pavyzdžiui, kristalų) aprašymo metodą ir judėjimo dėsnius, taip pat santykį tarp dalelių charakterizuojančių dydžių ir sistemos, su fizinėmis dydžiai...... Fizinė enciklopedija
Šis terminas turi kitas reikšmes, žr. Veiksmas (fizika). Veiksmo dimensija L2MT−1 Veiksmas fizikoje yra skaliarinis fizikinis dydis, kuris yra ... Wikipedia
Knygos
- Ekonominės sistemos judėjimo principai. Monografija, Kusneris Jurijus Semenovičius, Tsarevas Igoris Genadjevičius. Analitine forma pateikiamos pagrindinės ekonominės sistemos judėjimo lygtys ir išspręsta adekvačių jos judėjimo valdymo metodų suradimo problema. Matematinis aparatas buvo naudojamas...
Idėja, kuria grindžiami visi integralieji ir kai kurie diferencialiniai principai, yra nuostata, kad tikrasis mechaninės sistemos judėjimas tam tikram fiziniam dydžiui suteikia kraštutinumą. Norint matematiškai suformuluoti šią poziciją, kaip ir anksčiau, kartu su realiu judesiu reikia atsižvelgti į įsivaizduojamų judesių rinkinį, pajungiant juos tiksliai apibrėžtiems reikalavimams.
Integralų principų formulavimas atliekamas konfigūracijos erdvėje. Prisiminkite, kad sistemai su laisvės laipsniais apibendrintos koordinatės 
, apibrėžiantis sistemos konfigūraciją tam tikru momentu 
, yra laikomos Dekarto koordinatėmis atitinkamoje 
-dimensinė erdvė, kuri yra konfigūracijos erdvė. Laikui bėgant mechaninės sistemos būsena kinta ir šią sistemą vaizduojantis taškas apibūdina tam tikrą kreivę. Sistemos judėjimą patogu laikyti reprezentuojančio taško judėjimu šia kreive. Laikas 
su šiuo aspektu yra parametras, ir kiekvienas trajektorijos taškas atitiks vieną ar daugiau reikšmių 
.
Jei mus domina sistemos padėtis konfigūracijos trajektorijoje kiekvieną akimirką 
, tada reikia pridėti kitą ašį 
.
Tada gausime nagrinėjamos sistemos judėjimo „daugiamatį grafiką“. Taip pat galima tirti daugiamačio grafiko projekcijas tam tikrose plokštumose, tarkime 
(2.7 pav.). Ant paveikslėlio A, B yra reprezentuojančio taško projekcijos momentais 
Ir 
Atitinkamai, ištisinė linija vaizduoja tikrąjį, punktyrinė – vieną iš įsivaizduojamų judesių.
Integralinis principas yra teiginys apie tai, kaip realus sistemos judėjimas vyksta per ribotą (ne be galo mažą!) laikotarpį. 
.
Kas buvo su sistema iki to laiko 
,
mums neįdomu. Tačiau kol yra fiksuoti pradiniai ir galutiniai laiko momentai, manoma, kad mechaninė sistema su visais įmanomais judesiais laiko momentu 
eina per tašką A, šiuo metu 
- IN;
šie taškai atitinka pradinę ir galutinę sistemos padėtis jos realiame judėjime.
Bendriausia pozicijos dėl mechaninių sistemų judėjimo formuluotė yra vadinamame mažiausio veiksmo principu (jis taip pat vadinamas Hamiltono-Ostrogradskio principu):
Realus mechaninės sistemos judėjimas laiko intervalu nuo
prieš
taip, kad integralas, vadinamas veiksmo funkcija
ir lygus
, (60.7)
Kur
-- tam tikros mechaninės sistemos Lagrandženas turi ekstremumą (minimumą). Kintamasis
tai nesiskiria.
Kitaip tariant, realaus judėjimo metu veiksmo kitimas turėtų būti lygus nuliui
(61.7)
su sąlyga, kad visos konfigūracijos trajektorijos kartais 
Ir 
pereiti per tikrojo judėjimo pradžios ir pabaigos taškus, t.y.
Šis principas, priešingai nei D'Alemberto diferencialinis principas, yra vientisas ta prasme, kad jame yra teiginys apie visos sistemos judėjimą per ribotą laikotarpį. 
.
Tiesą sakant, iš jo išplaukia Lagranžo lygtys, taigi iš mažiausio veiksmo principo, galima sakyti, gaunama visa mechaninės sistemos dinamika.
Tegul funkcijos 
, apibūdinti tikrą judėjimą, t.y. 
– tas funkcijas, kurioms 
turi minimumą. Panagrinėkime funkcijų rinkinį 
Kur 
- funkcijų variacijos 
, kurios laikomos mažomis, palyginti su 
per visą laiko intervalą nuo 
prieš 
. Be to, viskas 
patenkinti santykius (62,7). Apskaičiuokime vadinamąjį pirmąjį variantą 
, turint omenyje, kad Lagrange funkcija gali priklausyti nuo apibendrintų koordinačių 
,
apibendrintas greitis 
, ir laikas 
:
Nes 
, antra kadencija m 
galima integruoti dalimis ir gauti
.
Dėl sąlygų (62,7), suma
išnyksta, o likęs integralas bus lygus nuliui savavališkoms reikšmėms 
tik tada, kai išnyksta kiekvienas integrando sumos narys. Taigi gauname 2-osios rūšies Lagranžo lygtis
.
(63.7)
Pravartu prisiminti, kad išsprendus funkcijos ekstremumo uždavinį, gaunama baigtinių lygčių sistema, iš kurios randamas taškas, kuriame funkcija pasiekia ekstremaliąją reikšmę. Šiuo atveju mes susiduriame su funkcine, ekstremumo uždavinio sprendimu, kurį pateikia 2 eilės diferencialinių lygčių sistema. Iš šių lygčių konfigūracijos erdvėje randama eilutė, apibrėžta funkcijomis 
, kai funkcionalumas pasiekia minimumą. Ši linija vadinama ekstremalia.
Kadangi konkretaus mechaninio modelio konstravimo uždavinys yra sudaryti judėjimo lygtis, matome, kad iš tikrųjų sistemos dinamiką lemia viena funkcija - Lagranžo, nes būtent ši funkcija išsprendžia problemą. Taigi sistemos Lagranžas yra įdomus fizinis objektas, kurio tyrimas yra būtinas sprendžiant dinamikos problemas. Visų pirma iš mažiausio veiksmo principo aišku, kad funkcija 
apibrėžiamas tik nepridedant visos savavališkos koordinačių ir laiko funkcijos išvestinės. Tai turi būti suprantama taip: sistema, apibrėžta jos judėjimo lygtimis, atitinka daugiau nei vieną Lagrange funkciją 
.
Tikrai, tegul būna 
susiję su 
santykis
(64.7)
,
.
Bet kadangi 
,
ir todėl Lagranžo lygtys, gautos naudojant funkcijas 
Ir 
, tas pats. Formos (64.7) Lagranžo funkcijos apibrėžimo neaiškumas neturi įtakos judėjimo lygtims, ir kiekviena 
iš klasės (64.7) išsprendžia sistemos dinamikos konstravimo unikaliai problemą.
Svarbi Lagranžo lygčių sistemos savybė yra jų kovariacija. Tai reiškia, kad Lagranžo lygtys išlaiko savo formą atliekant apibendrintų koordinačių 4 taškines transformacijas
y. naudojant apibendrintas koordinates 
Lagranžo lygtys bus tokios pačios formos:
,
kaip ir naudojant apibendrintas koordinates 
:
.
Tiesiogiai įrodykime, kad Lagranžo lygtys yra kovariantinės transformuojant (65.7). Pastatykime 
:
ir dariniai
,
1. Materialaus taško kinematika. Materialus taškas yra fizinis objektas, kuris geometriškai prilygsta matematiniam taškui, bet turi masę. Kinematika yra fizikos šaka, kuri tiria kūnų judėjimo tipus, neatsižvelgdama į judėjimo priežastis. Taško padėtis erdvėje apibūdinama spindulio vektoriumi. Taško spindulio vektorius yra vektorius, kurio pradžia sutampa su koordinačių sistemos pradžia, o pabaiga su nagrinėjamu tašku. r = i x+ j y + k z. Greitis yra atstumas, kurį kūnas nuvažiuoja per laiko vienetą v(t) = d r/dt. v(t) = i dx/dt + j dy/dt + k dz/dt. Pagreitis yra greičio kitimo greitis. a=d v/dt = d 2 r/ dt 2 = i d 2 x/dt 2 + j d 2 y/dt 2 + k d 2 z/dt 2 . a = a τ + a n= τ dv/dt + n v 2 /R.
d r = v dt; d v = a dt, todėl v = v 0 + a t; r = r 2 – r 1 = v 0t+ a t 2 /2.
2. Materialaus taško dinamika. Niutono dėsniai. Pagrindinės dinamikos sąvokos yra masės ir jėgos sąvokos. Jėga yra judėjimo priežastis, t.y. veikiami jėgos kūnai įgauna greitį. Jėga yra vektorinis dydis. Masė yra kūno inercijos matas. Masės ir greičio sandauga vadinama impulsu p= m v. Materialaus taško kampinis impulsas yra vektorius L = r * p. Jėgos momentas, veikiantis materialųjį tašką, vadinamas vektoriumi M = r * F. Jei diferencijuosime kampinio momento išraišką, gautume: d L/ dt = d r/dt* p + r*d p/dt. Atsižvelgiant į tai, kad d r/dt= v Ir v lygiagrečiai p, gauname d L/dt= M.Niutono dėsniai. Pirmasis Niutono dėsnis teigia, kad kūnas lieka ramybės būsenoje arba tolygiai juda tiesiškai, nebent jį veiktų kitos jėgos arba nekompensuojamas jų poveikis. Antrasis Niutono dėsnis teigia, kad impulso pokytis laikui bėgant yra pastovus dydis ir lygus efektyviajai jėgai d p/ dt = d / dt (m v) = m d v/dt= F.Tai antrasis Niutono dėsnis, parašytas diferencine forma. Trečiasis Niutono dėsnis teigia, kad dviejų kūnų sąveikoje kiekvienas iš jų veikia kitą vienodos vertės, bet priešingos krypties jėga. F 1 = - F 2 .
3. Materialių taškų sistemos dinamika. Apsaugos įstatymai. Materialių taškų sistema yra baigtinio jų skaičiaus rinkinys. Kiekvieną sistemos tašką veikia vidinės (iš kitų taškų) ir išorinės jėgos. Tegu m yra masė, r i spindulio vektorius. x i, y i, z i – laidas. i-tas taškas. Materialių taškų sistemos impulsas yra sistemą sudarančių materialių taškų impulsų suma: p= Σ (i=1,n) p aš = [ p 1 + p 2 +…+ p n]. Materialių taškų sistemos kampinis impulsas yra kampinio momento, sudarančio materialių taškų sistemą, suma: L = Σ [ L i ] = Σ [ r aš* p aš]. Jėga, veikianti materialių taškų sistemą, apibrėžiama kaip visų jėgų, veikiančių sistemos taškus, suma, įskaitant sistemos taškų sąveikos jėgas: F = Σ [ F aš ], kur F aš = F i ’ + Σ(j ≠ i) F ji – jėga, veikianti materialųjį sistemos tašką, žymima indeksu i. Jį sudaro išorinė jėga F i ’ ir vidinė jėga Σ(i ≠ j) [ F ji ], veikiantis taške dėl sąveikos su kitais sistemos taškais. Tada: F = Σ (i=1,n) [ F i ’] + Σ (i=1,n) Σ(j ≠ i) [ F ji]. Pagal trečiąjį Niutono dėsnį Σ (i=1,n) Σ(j ≠ i) [ F ji ] = 0, taigi F = Σ [ F aš']. Jėgos momentas, veikiantis materialių taškų sistemą, yra jėgų momentų, veikiančių sistemos taškuose, suma M= Σ (i) [ M i ] = Σ (i) [ r aš* F i ] = Σ (i) [ r aš* F aš']. Materialiųjų taškų sistemoje judesio lygtis turi formą d p/ dt = Σ = Σ [ F aš].
Materialių taškų sistemos masės centras yra įsivaizduojamas taškas su spindulio vektoriumi R= 1/m Σ . Jo judėjimo greitis V=d R/dt. Tada judesio lygtis m d V/dt= F. Momentinė lygtis materialių taškų sistemai d L/dt= M. Apsaugos įstatymai. Izoliuota sistema yra ta, kurios neveikia išorinės jėgos. Jame F= 0, taigi d p/dt = 0. Tada p= konst. Izoliuotoje sistemoje išorinių jėgų momentas M= 0. Todėl d L/dt = 0, o tai reiškia L= konst. Materialaus taško kinetinės energijos pokytis jam judant tarp dviejų padėčių yra lygus jėgos atliekamam darbui. m 0 v 2 2/2 – m 0 v 1 2 /2 = ∫(1,2) F d l arba m 0 v 2 /2 + E p = konst.
4. Judėjimas centre simetriškame lauke. Keplerio dėsniai. Laukas vadinamas centriniu, jei jame esančio kūno potencinė energija priklauso tik nuo atstumo r iki tam tikro fiksuoto taško. Jėga F= - ∂U(r)/ ∂ r= - dU/dr r/r, veikiantis dalelę, absoliučia reikšme taip pat priklauso tik nuo r ir yra nukreiptas į kiekvieną tašką išilgai spindulio vektoriaus. Judant centriniame lauke išsaugomas sistemos momentas lauko centro atžvilgiu. Vienai dalelei momentas M = [r*R]. Kadangi vektoriai M ir r yra vienas kitam statmeni, tai M pastovumas reiškia, kad dalelei judant jos spindulio vektorius visada išlieka vienoje plokštumoje – plokštumoje, statmenoje M. Taigi dalelės trajektorija centriniame lauke yra visiškai vienas lėktuvas. Įvedę joje polines koordinates r, φ, Lagranžo funkciją užrašome forma L = m/2 (r 2 (∙) + r 2 φ 2 (∙)) - U(r). Šioje funkcijoje nėra aiškiai φ koordinatės. Tokiai koordinatei atitinkamas apibendrintas impulsas p i yra judėjimo integralas. Šiuo atveju apibendrintas impulsas p φ = mr 2 φ(∙) sutampa su momentu M z = M, taigi M = mr 2 φ(∙) (1). Atkreipkite dėmesį, kad vienos dalelės plokštuminiam judėjimui centriniame lauke šis dėsnis leidžia lengvai interpretuoti geometrinį vaizdą. Išraiška 1/2 r r d φ reiškia sektoriaus plotą, kurį sudaro du be galo artimi spindulio vektoriai ir trajektorijos lanko elementas. Pažymėdami jį kaip df, dalelės momentą užrašome forma M = 2mf, kur f išvestinė vadinama sektoriniu greičiu. Todėl impulso išsaugojimas reiškia sektoriaus greičio pastovumą – vienodais laikotarpiais judančio taško spindulio vektorius apibūdina lygias sritis ( Antrasis Keplerio dėsnis). Išreiškę φ(∙) iki M iš (1) ir pakeitę jį energijos išraiška, gauname: E = m/2 (r 2 (∙) + r 2 φ 2 (∙)) + U(r) = mr 2 (∙ )/2 + M 2 /2mr 2 + U(r). Taigi r(∙) = √(2/m (E – U(r)) – M 2 /m 2 r 2) arba, atskiriant kintamuosius ir integruojant: t = ∫dr/√(2/m (E – U( r)) - M 2 /m 2 r 2) + konst. Toliau, rašydami (1) forma dφ = M 2 /mr 2 dt, čia pakeitę dt ir integruodami, gauname: φ = ∫dr (M/r 2)/√(2/m (E – U(r)) ) - M 2 /r 2) + konst. Pirmasis Keplerio dėsnis. Kiekviena planeta sukasi elipsėje, kurios viename iš židinių yra Saulė. Trečiasis Keplerio dėsnis.Žvaigždžių planetų apsisukimų periodų kvadratai yra susieti kaip jų orbitų pusdidžiųjų ašių kubai T 1 2 /T 2 2 = a 1 3 /a 2 3 .
5. Materialių taškų sistemos Lagranžo funkcija ir Lagranžo lygtys. Judesio integralai. Panagrinėkime uždarą materialių taškų sistemą. Jai skirta Lagranžo funkcija turi formą L = Σ(a) – U(r 1 , r 2 , …), kur T = Σ (a) – kinetinė energija, o U – potenciali dalelių sąveikos energija. Tada judėjimo lygtys d/dt (∂L/∂v a) = ∂L/∂r a įgauna formą m a dv a /dt = - ∂U/∂r a . Šios judėjimo lygtys vadinamos Niutono lygtimis. Vektorius F a = - ∂U/∂r a vadinama jėga. Jei judėjimui apibūdinti naudojamos ne Dekarto taškų koordinatės, o savavališkos apibendrintos koordinatės q i, tai norint gauti Lagranžo funkciją, reikia atlikti atitinkamą transformaciją: x a = f(q 1, q 2, .., q s) , x a (∙) = Σ(k ) [∂f a /∂q k (∙)] ir tt Pakeitę šias išraiškas į funkciją L= 1 / 2 Σ(a) – U, gauname norimos formos Lagranžo funkciją L = 1/2 Σ(i,k) – U(q). Judesio integralai. Yra apibendrintų koordinačių funkcijos, kurios judėjimo metu išlaiko pastovias reikšmes, priklausomai tik nuo pradinių sąlygų. Jie vadinami judesio integralais. Dėl laiko homogeniškumo dL/ dt = Σ(i) [∂L/∂q i q i (∙)] + Σ(i) [∂L/∂q i (∙) q i (∙∙)]. Pakeitę ∂L/∂q i pagal Lagranžo lygtis d/dt (∂L/∂q i (∙)), gauname dL/dt = Σ(i) arba d/dt (Σ(i) - L) = 0 Iš to matome , kad dydis E = Σ(i) – L, vadinamas energija, nekinta, t.y. judesio integralas. Dėl erdvės homogeniškumo su be galo mažu perkėlimu ε, kai visi sistemos taškai yra perkeliami ε = δr, Lagranžo funkcijos pokytis, lygus δL = ε Σ(a) [∂L/∂r a ], turi būti lygus iki nulio, t.y. Σ(a) [∂L/∂r a ] = 0. Naudodami Lagranžo lygtis gauname Σ(a) = d/dt (Σ(a)[ ∂L/∂v a ]) = 0. Tada dydis R= Σ(a)[ ∂L/∂v a ], vadinamas impulsu, lieka nepakitęs, t.y. judesio integralas. Dėl erdvės izotropijos, esant be galo mažam pasukimui kampu δφ, Lagranžo funkcijos pokytis lygus δL = Σ(a) [∂L/∂r a δ r a + ∂L/∂v a δ v a ] turi būti lygus nuliui. Pakeitus ∂L/∂ v a = p a ir ∂L/∂ r a = p a (∙) dėl δφ savavališkumo gauname d/dt Σ(a) [ r a p a ] = 0. Reikšmė M = Σ(a) [ r a p a ], vadinamas kampiniu momentu, išlieka pastovus, t.y. judesio integralas.
6. Absoliučiai standaus kūno dinamika. Inercijos tenzorius. Eulerio lygtys. Kietas kūnas – tai materialių taškų sistema, atstumas tarp kurių išlieka pastovus. Norint visiškai apibūdinti standaus kūno judėjimą, be vieno iš jo taškų judėjimo, būtina žinoti kūno judėjimą aplink šį tašką kaip fiksavimo tašką. Tegu kūnas fiksuotas taške O. Pažymime taško m i spindulio vektorių O atžvilgiu r aš, w yra momentinis kampinis kūno greitis, tada kampinis momentas L= Σ [ r aš * aš v i ] = Σ = wΣ – Σ. Šią vektorių lygybę galima užrašyti trijų projekcijų pavidalu koordinačių ašyse L x = w x Σ - Σ ; L y = w y Σ - Σ ; L z = w z Σ - Σ . Atsižvelgiant į tai ( w r i) = x i w x + y i w y + z i w z gauname L x = J xx w x + J xy w y + J xz w z ; L y = J yx w x + J yy w y + J yz w z ; L x = J zx w x + J zy w y + J zz w z, kur J xx = Σ, J xy = Σ, kiti panašiai. Dydžiai J xx , J yy , J zz vadinami ašiniais inercijos momentais, o J xy = J yx , J xz = J zx , J yz = J zy – išcentriniais inercijos momentais. Dydžių aibė J ij vadinama inercijos tenzoriumi. J ii elementai vadinami įstrižais. Jei visi neįstrižainiai elementai lygūs nuliui, tai jie sako, kad kūno ašys, sutampančios su koordinačių ašimis, yra pagrindinės inercijos ašys, o dydžiai J ii vadinami pagrindiniais inercijos momentais. Toks tenzorius sumažinamas iki įstrižainės.
Eulerio lygtys. Kūno masės centro judėjimo lygtis yra m d v 0 /dt = m d/dt ( w * r 0) = F, Kur r 0 – kūno masės centro spindulio vektorius, nubrėžtas iš jo tvirtinimo taško. Su kūnu susietos koordinačių sistemos ašis patogu nukreipti išilgai pagrindinių inercijos ašių. Šiuo atveju kampinis impulsas įgauna paprastą formą L 1 = J 1 w 1, L 2 = J 2 w 2, L 3 = J 3 w 3, o w i yra kampinio greičio projekcijos į judančias koordinačių ašis. su kūnu. Naudojant bendrąją formulę d A/dt = ∂ A/∂t + w* A, momento lygtį galime pavaizduoti taip ∂ L/∂t + w * L = M. Atsižvelgdami į tai, kad L x = J x w x , L y = J y w y , L z = J z w z , šią lygtį perrašome projekcijose ant judančios koordinačių sistemos ašies: J x dw x /dt + (J z - J y )w y w z = M x , J y dw y /dt + (J x – J z)w z w x = M y , J z dw z /dt + (J y – J x)w x w y = M z . Šios lygtys vadinamos Eilerio lygtimis.
7.
Judėjimas neinercinių atskaitos sistemų atžvilgiu.
NISO yra sistema katėje. kūnas juda su pagreičiu, palyginti su poilsiu. koordinavimo sistemos Čia neišsipildo erdvės ir laiko homogeniškumo ir izotropijos sąvokos, nes trukmė ir apimtis NISO skiriasi. Be to, prarandamas 3-iojo Niutono principo turinys ir konservavimo principai. Visko priežastis – inercijos jėgos, susijusios tik su koordinačių sistema, kat. turi įtakos kūno judėjimui. TAI. pagreitis gali būti keičiamas naudojant išorinę jėgą arba inercijos jėgą. F=∑Fi=ma (ISO), F=F(ext.)+Fi=ma′(NISO), kur Fi – inercinė jėga, a – pagreitis. kūnai ISO, a′-pagreičiu. tas pats kūnas NISO. NISO 1-asis Niutono dėsnis nėra patenkintas! Fi=-m(a′-a), t.y. inercinės jėgos nepaklūsta 3-iajam Niutono dėsniui, nes jie yra trumpalaikiai. Pereinant nuo ISO prie NISO, inercinės jėgos išnyksta. Inercija jėgos visada nukreiptos prieš akių vokus. išorinės jėgos. Inercijos jėgas galima pridėti vektoriškai. ISO: v=const, v< dx/dt=Ux=dx′/dt+dv(t)/dt′=U′x+v(t) dUx/dt=d/dt′(U′x+v(t))=dU′x/ dt′+dv(t)/dt′=a x ' + a 0 = a x . NISO pristato absoliutaus, santykinio ir nešiojamojo greičio sąvokas: u 0 yra absoliutus greitis, o 0 yra santykinis pagreitis. ilsintis koordinavimo sistemos u x 0 = v + u x 0 '; a x 0 = a’ + a x ; u x ’ a x – santykinis greitis ir pagreitis. judėjimas koordinavimo sistemos (gimine) ; v, a′-greitis ir pagreitėjo. į′ nurodo. į, t.y. nešiojamas greitis ir pagreitis Yra apibendrintų koordinačių, greičio, laiko funkcija. Panagrinėkime 2S matmenų erdvę, tada sistemos padėtis S = ∫(t 1 , t 2) L(g, g( ), t)dt, L yra Lagranžo funkcija; S veiksmas. Veiksmo funkcija vadinama itnegraline S=∫ Ldt=0, esant kat. imant tikrąją judėjimo trajektoriją, sistema turės minimalią reikšmę, t.y. S = Smin, δS = 0. Tie. sistema nuo 1 iki 2 juda tokia trajektorija, kad jos veikimas būtų minimalus – Hamiltono mažiausio veiksmo principas. L = T – U yra skirtumas tarp sistemos kinetinės ir potencialinės energijos. Anot Hamiltono, tikroji trajektorija atitinka minimalų veiksmą. Raskime trajektoriją. Tikroji trajektorija yra minimali trajektorija. S-funkcinis. Suraskime min. δS = 0 pirmasis variantas. δS = ∫(t 1 , t 2)(Σ[∂L/∂g i δg i ] + Σ[∂L/∂g i ( ) δg i ( )])dt; ∫(t 1 ,t 2) ∂L/∂g i ( ) δg i ( ) dt = ∫(t 1 ,t 2) ∂L/∂g i ( ) dδg i = ∂L/∂g i ( )δg 1 ,t 2) - ∫(t 1,t 2) δg i d/dt (∂L/∂g i ( )) dt; δg i nepriklauso vienas nuo kito 9.
Sistemų su vienu ir daugybe laisvės laipsnių virpesiai. Laisvos ir priverstinės vibracijos
.
Paprasčiausias atvejis, kai sistema turi vieną laisvės laipsnį. Stabili pusiausvyra atitinka šią sistemos padėtį katėje. jo potencialas lt. U(q) turi minimumą. Nukrypimas nuo šios padėties lemia jėgos – dU/dq atsiradimą, kuri linkusi grąžinti sistemą atgal. q 0 – apibendrinta koordinatė. Išplėskime U(q) - U(q0) laipsniais ir gausime U(q) - U(q0) ≈ k/2 (q - q 0) 2 kur k = U’’(q 0) yra teigiamas koeficientas. U(q 0) = 0, pažymėkime x = q - q 0 - koordinatės nuokrypį nuo pusiausvyros reikšmės, tada U(x) = kx 2 /2 – potencinė energija. 1/2a(q) q' 2 =1/2a(q)x' 2 -kinetinė energija esant q = q0 ir a(q0) = m, gauname Lagranžo funkciją sistemai, atliekančiai vienmačius virpesius: L = mx 2 (∙) /2 – kx 2 /2. Šią funkciją atitinkanti judesio lygtis bus tokia: mx(∙∙) + kx = 0 arba x(∙∙) + w 2 x = 0, kur w = √(k/m) – ciklinių virpesių dažnis. Šių lygčių sprendimas yra x = a cos(wt + α), kur a yra svyravimų amplitudė, wt + α yra svyravimų fazė. Tai. sistemos virpesių energija bus E = mx 2 (∙)/2 + kx 2 /2. Priverstinės vibracijos.Šiuo atveju, kartu su savo potencialia energija ½ kx 2, sistema taip pat turi potencialią energiją U e (x, m), susijusią su išorinio lauko veikimu. Atitinkamai tokios sistemos Lagranžo funkcija bus tokia: L = mx 2 (∙)/2 + kx 2 /2 + x F(t), kur F(t) – išorinė jėga. Atitinkamas judesio lygis bus mx(∙∙) + kx = F(t) arba x(∙∙) + w 2 x = F(t)/m. Jei F(t) yra paprasta periodinė laiko funkcija, kurios dažnis γ: F(t) = f cos(γt + β), tai judėjimo lygčių sprendimas bus toks: X = a cos(wt + α) + f cos(γt + β)/(m(w 2 – γ 2)) a ir α nustatomi iš pradinių sąlygų. Tai. veikiama varomosios jėgos, sistema atlieka judesį, atspindintį dviejų svyravimų derinį - su natūraliu sistemos dažniu w ir su varomosios jėgos dažniu - γ. Sistemų su daugybe laisvės laipsnių virpesiai
.
Galingas. lt. sistema U(q i) turi minimumą ties q i =q i 0 . Įvedę nedidelius poslinkius x i = q i - q i 0 ir išplėtę U jų atžvilgiu iki 2 eilės terminų, gauname potencialą. energija: U = 1/2 Σ(i,k) , k ik =k ki . Kinet. lt. tokiai sistemai bus 1/2 Σ(i,k) , kur m ik =m ki . Tokios sistemos Lagranžo lygtis bus tokia: L = 1/2 Σ(i,k) . Tada dL = Σ(i,k) . Ieškome x k (t) formoje x k = A k exp(-iwt), A k yra konstanta. Pakeitę tai Lagranžo lygtimi, gauname tiesinių vienalyčių lygčių sistemą. Σ(k) [(-w 2 m ik +k ik)A k ] = 0 - charakteristikos lygtis, ji turi s skirtingas šaknis w 2 α (α=1,2,….,s) w α - natūralių dažnių sistema. Konkretus sistemos sprendimas turi tokią formą: x k = ∆ kα C α exp(-iw α t). Bendrasis sprendinys yra visų dalinių sprendinių suma: x k = Σ(α) [∆ kα Q α ], kur Q = Re (C α exp(-iw α t)). 10.
Hamiltono kanoninė lygtis.
Nemažai privalumų studijuojant mechanikos klausimus suteikia aprašymas naudojant apibendrintas koordinates ir impulsus, perėjimas iš vieno nepriklausomų kintamųjų rinkinio į kitą gali būti atliktas naudojant Legendre transformaciją. Šiuo atveju viskas vyksta taip. Bendras Lagranžo funkcijų skirtumas kaip koordinačių ir greičių funkcija yra lygus: dL = Σ(i) [∂L/∂q i ] + Σ(i) [[∂L/∂q i (∙)]. Šią išraišką galima parašyti kaip dL = Σ(i) + Σ(i) . Perrašykime į formą: d(Σ(i) – L) = - Σ(i) + Σ(i) . Dydis po diferencialo ženklu parodo sistemos energiją, išreikštą koordinatėmis ir momentais, ir ji vadinama Hamiltono funkcija: H(p,q,t) = Σ(i) – L. Iš diferencialo. lygybės dH = - Σ(i) + Σ(i) seka lygtis: q i (∙) = ∂H/∂p i, p i (∙) = - ∂H/∂q i – tai Hamiltono lygtys. Dėl savo paprastumo ir simetrijos jie dar vadinami. kanoninis. Poisson skliausteliuose. Bet kurios apibendrintų koordinačių, impulsų ir laiko funkcijos F laiko išvestinė bus dF/dt = ∂F/∂t + Σ(i) [∂F/∂q i dq i /dt] + Σ(i) [∂F/ ∂p i dp i /dt]. Naudodami Hamiltono lygtis, šią lygtį galime perrašyti tokia forma: dF/dt = ∂F/∂t + , kur = Σ(i) [∂F/∂q i ∂H/∂p i - ∂H/∂q i ∂F /∂ p i ] – skambinama Puasono laikiklis. Akivaizdu, kad Hamiltono lygtį galima parašyti naudojant Puasono skliaustus. 11.
Hamiltono-Jacobi lygtis
.
Mažiausio veiksmo principu gauname S = ∫(t 1 ,t 2)Ldt. Veiksmą (S) laikykime dydžiu, apibūdinančiu judėjimą tikromis trajektorijomis. Remdamiesi Lagranžo lygtimi, skirtą keisti veiksmą, kai iš vienos trajektorijos į kitą artimą trajektoriją (vienu laisvės laipsniu), gauname: δS = pδq arba bet kuriam laisvės laipsnių skaičiui: δS = Σ(i) . Iš to seka, kad dalinės veiksmo išvestinės koordinačių atžvilgiu yra lygios atitinkamiems impulsams: ∂S/∂q i = p i (1). Pagal apibrėžimą dS/dt = L, kita vertus, laikant S kaip koordinačių ir laiko funkciją ir naudojant formulę (1), gauname: dS/dt = ∂S/∂t + Σ(i) [∂S/ ∂q i q i (∙)] = ∂S/∂t + Σ(i) . Palyginus abi išraiškas, gauname ∂S/∂t = L - Σ(i) arba ∂S/∂t = - H(p,q,t) (2). Formulės (1), (2) gali būti parašytos kartu kaip dS = Σ(i) – Hdt. O pats veiksmas (S) bus S = ∫ (Σ(i) – Hdt). Kai H nepriklauso nuo t – S(q,t)=S 0 (q) - Et, kur S 0 (q) = Σ(i) [∫p i dq i ] yra sutrumpintas veiksmas, o Et pakeičiamas H( p, q) . Funkcija S(q,t) tenkina tam tikrą diferencialą. lygtis, kurią gauname (2) santykio impulsus P pakeitę išvestinėmis ∂S/∂q: ∂S/∂t + H(∂S/∂q 1 ,…, ∂S/∂q s ;q 1 ,… ,q s ,t) = 0 yra 1 eilės dalinė diferencialinė lygtis, vadinama. Hamiltono-Jacobi lygtis. Taigi, viena dalelė išoriniame lauke U(x,y,z,t) turi tokią formą: ∂S/∂t + 1/(2m)((∂S/∂x) 2 + (∂S/∂) y) 2 + (∂S/∂z) 2) + U(x,y,z,t) = 0. 12.
Kietųjų medžiagų deformacijos ir įtempimai. Youngo moduliai, kirpimas. Puasono koeficientas
.
Deformacija – tai kūno formos ir tūrio pasikeitimas veikiant išorinėms jėgoms. Veikiant išorinei jėgai, keičiasi kūno forma. Visos deformacijos gamtoje gali būti sumažintos iki 3 m pagrindinės deformacijos: 1) tempimas, gniuždymas; 2) pamaina; 3) sukimas. Yra vienalyčių ir nehomogeniškų deformacijų. Jei visos dalys yra deformuotos vienodai, tada tai homogeniškai deformuotas. Jei visos kūno dalys deformuotos nevienodai, tai nevienalyčiai deformuota. Huko dėsnis tenkinamas tik tampriosios deformacijos srityje. = E'. F/S = E ∆l/l 0 ; F kontrolė = ES∆l/l 0 = kx; k = ES/l0; F kontrolė = ESx/l 0 . Huko dėsnis apibrėžia ryšį tarp ir . k yra elastingumo koeficientas, jis priklauso nuo geometrinių matmenų, medžiagos ir nuo ko pagamintas korpusas. E-Youngo modulis. Youngo modulis yra lygus jėgai, kuri turi būti taikoma vienetinio skerspjūvio korpusui, kad jo kūnas padidėtų dvigubai. Kitas deformacijų tipas yra šlyties deformacija, kuri stebima, kai paviršius yra liečiamas; jis yra lygiagretus šlyties deformacijos paviršiui ir stebimas veikiant tangentinėms jėgoms, t.y., jėgos veikia tangentiškai. Ψ~F t /S (poslinkio kampas). Ψ = nF t/S; n yra poslinkio koeficientas. F t = nS. (E>N, E~ 4N). 13.
Skysčių ir dujų mechanika.
Visiems skysčiams ir dujoms vienijantis parametras yra: tankis ρ, slėgis P=F n /S. Skysčiuose ir dujose Youngo modulis vyksta, bet šlyties modulis |σ|=|P| nevyksta, σ yra įtempis. Jei skystis (dujos) yra nejudantis, tai mes turime reikalą su hidrostatika (aerostatika). Būdingi dėsniai: Paskalio dėsnis: perteklinis slėgis, susidaręs dujose ir skysčiuose, vienodai perduodamas visomis kryptimis. Archimedo principas galioja ir skysčiams, ir dujoms. Archimedo jėga visada veikia prieš gravitaciją. Archimedo jėgos atsiradimo priežastis yra tūrio V buvimas kūne Archimedo principas: Kūną, esantį skystyje ar dujose, visada veikia jėga, lygi skysčio ar dujų, išstumto kūno svoriui. panardinta kūno dalis ir nukreipta vertikaliai aukštyn. Jei F A >F GRAVITĖ, tai kūnas plūduriuoja, jei priešingai, tada skęsta. Jei skystis (dujos) teka, tada prie šių lygčių pridedama srovės tęstinumo lygtis. Skysčio dalelės trajektorija vadinama. dabartinė linija. Srovės linijos apribota erdvės dalis vadinama. srovės vamzdis. Skystis srovės vamzdyje gali tekėti stacionariai arba netvirtai. Srovė vadinama statinis jei per tam tikrą vamzdžio atkarpą vienetui tenka srovė. laiko praeina toks pat skysčio (dujų) kiekis, kitaip srautas netolygus. Turėkime tokios formos srovės vamzdį: Jei skysčio srautas yra statinis. Tada m 1 =m 2 =…=m n per laiko vienetą, jei skystis nesuspaudžiamas, tai ρ 1 V 1 =ρ 2 V 2 =…; =ρ n V n , ρ 1 Δx 1 = ρ 2 Δx 2 =…; = ρ n Δx n, ρ 1 υ 1 ΔtS 1 =ρ 2 υ 2 ΔtS 2 =…= ρ n υ n ΔtS n, nes skystis yra nesuspaudžiamas ρ pastovus υ 1 S 1 =… 2 υ2 n S n , υS = const; υ=const/S – srovės tęstinumo lygtis. ρ d v/dt = ρ g– grad P – ekv. Euleris – 2 eilė. Niutonas skysčiams ir dujoms. Įstatymas išsaugotas Energija skysčiuose ir dujose. Lv. Bernulis. ID. vardas Nesuspaudžiamas skystis, kuriame galima nepaisyti klampių trinties jėgų. Kinetinė energija nėra švaistoma dirbant prieš trinties jėgas. Ρυ 2 /2+ρgh + P = const – ekv. Bernoulli, ρυ 2 /2 – dinaminis slėgis, ρgh – hidrostatas. Slėgis, P – molekulinis slėgis. Mυ 2/2 = E K ; mυ 2 /2V= E K /V= ρυ 2 /2. Klampios trinties jėga F A = - ηΔυΔS/ΔZ 6 π r η υ – Stokeso jėga. Η – koeficientas klampumas, Δυ/ΔZ – grad υ, r – korpuso matmenys. Tai Niutono klampių trinties jėgų formulė. Jei skystyje yra trinties jėgų, tai id. Skystis tampa klampus. ρ v 1 2 / 2 + ρgh 1 + P 1 = ρ v 2 2 / 2 + ρgh 2 + P 2 ; (P 1 – P 2) = ρ(υ 2 2 – υ 1 2)/2. Jei ΔP = 0, tai υ 2 2 – υ 1 2 = 0, ir skysčio srauto nebus. Kur P didesnis, ten greitis. Yra mažiau srovės. Jei skerspjūvis S didėja, tai P didėja, o υ mažėja. Jei srovės vamzdis guli ne horizontaliai, tai υ 2 2 -υ 1 2 =2g (h 1 -h 2); υ = sqrt(2g (h 1 -h 2)) – Torricelli formulė. Trajektorijos, apibūdinančios mechaninių sistemų judėjimą išplėstinės konfigūracijos ir fazių erdvėse, turi nepaprastą savybę – jos yra tam tikros variacinės problemos kraštutinumai ir veiksmo funkcinei funkcijai suteikia stacionarias vertes. Panagrinėkime variacinės problemos formulavimą išplėstinėje konfigūracijos erdvėje R"*", kurių taškai yra aibės (q, ().
Tegul kreivė y„ = ((q, t): q e Rt e, 5q(/0)= 8q(/,) = 0). Variantas 8q(/) yra savavališka C1 klasės funkcija, kuri išnyksta atkarpos = 0 galuose. Pirmasis funkcionalumo variantas Sy kai y = y 0 pagal apibrėžimą yra lygus o po integravimo dalimis įgauna formą Išraiškoje (2.3) išnyksta išorinis terminas, nes bq k (t 0) = bq k (t y) = 0, į - 1.....l, o išraiška yra kvadrate skliausteliuose po integralo ženklu yra lygus nuliui, nes 0 yra reali trajektorija, atitinkanti Lagranžo lygtis (2.1). Todėl variacija 55(y 0) = 0. ? Teisingas ir atvirkštinis teiginys: jei variacija 65(y*) = 0, kur y* priklauso žiedinių sankryžų trajektorijų klasei, tai y* = y 0 yra reali trajektorija. Šio teiginio pagrįstumas išplaukia iš pirmosios variacijos (2.3) išraiškos ir pagrindinės variacijų skaičiavimo lemos. Šiuo atveju nuo pirmojo varianto lygybės iki nulio ir variacijų nuo 6 iki - 1 nepriklausomumas, ..., antros rūšies Lagranžo lygčių galiojimas l, iš to išplaukia, kad tai tiesa Kada q k = q k *(t), k= 1.....l. Tai reiškia, kad y* yra tikroji mechaninės sistemos trajektorija. 3.1. Nekonservatyvios sistemos atveju neįmanoma nurodyti funkcinio, kurio stacionari vertė buvo pasiekta faktinėje trajektorijoje. Tačiau šiuo atveju šie teiginiai yra lygiaverčiai: kur q(/) yra tikroji trajektorija. Pirmasis iš aukščiau pateiktų teiginių sudaro Hamiltono-Ostrogradskio variacinio principo turinį nekonservatyvioms sistemoms. 3.2. Galima parodyti, kad stacionari veiksmo funkcionalumo reikšmė yra minimali, jei skirtumas - / 0 yra pakankamai mažas. Ši aplinkybė siejama su kitu aptariamo principo pavadinimu – Hamiltono-Ostrogrado mažiausių veiksmų principu. Aukščiau nagrinėta variacinė problema gali būti suformuluota išplėstinėje fazių erdvėje, kuri pasirodo esanti svarbi svarstant Hamiltono kanoninių lygčių integralumo klausimus. Pažymėkime Г = ((р + 6р. q + 8q, aš): p, q, 6p. 6q e R",te[r 0 , /,]. 5q(/ )= 8q(/|) = 0) kreivė išplėstinėje fazių erdvėje ir tegul esant 8p = 8q = 0 kreivė Г 0 yra kanoninių Hamiltono lygčių sistemos sprendimas Visos laiko funkcijos priklauso C 1 klasei. Taigi buvo apibrėžta žiedinių sankryžų trajektorijų (G) šeima, kuriai priklauso tikroji trajektorija G 0 (46 pav.). Funkcinis veiksmas, atsižvelgiant į ryšį tarp Lagrange ir Hamilton funkcijų, įgauna formą Čia trumpumui naudojamos raidės p, q vietoj raidžių p + 8p, q + 8q. Apskaičiavę funkcinės S[Г] kitimą realioje trajektorijoje, gauname Integruodami dalimis, atsižvelgdami į ribines sąlygas, randame Iš to seka, kad variacija 85|Г 0 1 = 0, jei p(/), q(f) tenkina kanonines Hamiltono lygtis (2.4), ir. priešingai, iš variacijų nepriklausomumo sąlygos 8p(r), pagal pagrindinę variacijų skaičiavimo lemą seka 6q(/) lygtys (2.4). Taigi įrodytas mažiausio veikimo principo pagrįstumas sistemos fazių erdvėje: funkcinis veiksmas 5[Г], duotas žiedinių trajektorijų erdvėje (Г|. faktinėje trajektorijoje įgauna stacionarią reikšmę, t.y. 85[Г 0 1 = 0. Ryžiai. 46 Kai pirmą kartą sužinojau apie šį principą, pajutau kažkokią mistiką. Atrodo, kad gamta paslaptingai eina per visus įmanomus sistemos judėjimo kelius ir pasirenka geriausią. Šiandien noriu šiek tiek pakalbėti apie vieną ryškiausių fizikos principų – mažiausio veiksmo principą. Atsispindėjusi šviesa taip pat juda taip, kad iš vieno taško į kitą patektų per trumpiausią įmanomą kelią. Paveikslėlyje trumpiausias kelias bus žalias kelias, kuriame kritimo kampas yra lygus atspindžio kampui. Bet koks kitas kelias, pavyzdžiui, raudonas, bus ilgesnis. 1662 m. Pierre'as Fermatas pasiūlė, kad šviesos greitis tankioje medžiagoje, pavyzdžiui, stikle, yra mažesnis nei ore. Prieš tai buvo visuotinai priimta Dekarto versija, pagal kurią šviesos greitis medžiagoje turi būti didesnis nei ore, kad būtų gautas teisingas lūžio dėsnis. Fermatui prielaida, kad šviesa gali judėti greičiau tankesnėje terpėje nei retesnėje terpėje, atrodė nenatūrali. Todėl jis manė, kad viskas buvo visiškai priešingai, ir pasirodė nuostabus dalykas – laikantis šios prielaidos, šviesa lūžta taip, kad tikslą pasiektų per trumpiausią laiką. Visi šie faktai leido manyti, kad gamta elgiasi kažkaip racionaliai, šviesa ir kūnai juda optimaliausiu būdu, išeikvodami kuo mažiau pastangų. Tačiau kokios tai pastangos ir kaip jas apskaičiuoti, liko paslaptis. 1744 m. Maupertuisas pristatė „veiksmo“ sąvoką ir suformulavo principą, pagal kurį tikroji dalelės trajektorija skiriasi nuo bet kurios kitos tuo, kad veiksmas jai yra minimalus. Tačiau pats Maupertuisas niekada negalėjo aiškiai apibrėžti, ką reiškia šis veiksmas. Griežtą matematinę mažiausio veiksmo principo formuluotę jau sukūrė kiti matematikai – Euleris, Lagranžas, o galiausiai ją pateikė Williamas Hamiltonas: Taigi, kaip važiuoti, kad pasiektumėte tikslą tiksliai nustatytu laiku ir sunaudotumėte kuo mažiau degalų? Aišku, kad reikia eiti tiesia linija. Didėjant nuvažiuotam atstumui, degalų sunaudos ne mažiau. Ir tada galite pasirinkti skirtingas taktikas. Pavyzdžiui, galite greitai atvykti į tašką iš anksto ir tiesiog sėdėti ir laukti, kol ateis laikas. Važiavimo greitis, taigi ir degalų sąnaudos kiekvienu laiko momentu, bus didelis, tačiau sutrumpės ir važiavimo laikas. Galbūt bendros degalų sąnaudos nebus tokios didelės. Arba galite važiuoti tolygiai, tuo pačiu greičiu, kad neskubėdami atvyktumėte tiksliai tuo momentu. Arba dalį kelio važiuokite greitai, o dalį lėčiau. Koks yra geriausias būdas? Pasirodo, optimaliausias, ekonomiškiausias važiavimo būdas – važiuoti pastoviu greičiu, tokiu, kad į tikslą atvyktumėte tiksliai nustatytu laiku. Bet koks kitas pasirinkimas sunaudos daugiau degalų. Galite tai patikrinti patys naudodami kelis pavyzdžius. Priežastis ta, kad degalų sąnaudos didėja didėjant greičio kvadratui. Todėl, didėjant greičiui, degalų sąnaudos didėja greičiau nei mažėja važiavimo laikas, o bendrosios degalų sąnaudos taip pat didėja. Taigi, išsiaiškinome, kad jei automobilis kiekvienu laiko momentu sunaudoja kuro proporcingai savo kinetinei energijai, tai ekonomiškiausias būdas nuvykti iš taško į tašką tiksliai nustatytu laiku yra važiuoti tolygiai ir tiesia linija, tiksliai. kūno judėjimo būdas nesant jį veikiančių jėgų.jėga Bet koks kitas vairavimo būdas padidins bendras degalų sąnaudas. Kuro sąnaudos kiekvienu laiko momentu yra lygios kinetinei energijai atėmus potencinę automobilio energiją (atėmus potencialią energiją, nes sumontuotas įrenginys gamina degalus ir jo nevartoja). Dabar mūsų užduotis kuo efektyviau perkelti automobilį tarp taškų tampa sunkesnė. Tiesus vienodas judesys šiuo atveju nėra pats efektyviausias. Pasirodo, optimaliau šiek tiek pakilti aukštyje, kurį laiką ten pabūti, sunaudojant daugiau degalų, o tada nusileisti į tašką . Esant teisingai skrydžio trajektorijai, bendra kuro gamyba dėl kilimo padengs papildomas degalų sąnaudas ilginant trasą ir didinant greitį. Jei gerai paskaičiuosite, ekonomiškiausias būdas automobiliui bus skristi parabole, lygiai ta pačia trajektorija ir lygiai tokiu greičiu, kaip akmuo skristų Žemės gravitaciniame lauke. Bendro sunaudoto kuro kiekio analogas per visą judėjimo laikotarpį, t.y. Lagranžo vertė, sukaupta per visą judėjimo laiką, vadinama „veiksmu“. Mažiausio veiksmo principas – kūnas juda taip, kad veiksmas (kuris priklauso nuo judėjimo trajektorijos) būtų minimalus. Kartu reikia nepamiršti, kad nurodomos pradinės ir galutinės sąlygos, t.y. kur kūnas yra laiko momentu ir laiko momentu. Šiuo atveju kėbulas nebūtinai turi judėti vienodame gravitaciniame lauke, ką mes laikėme savo automobiliui. Galima svarstyti visiškai skirtingas situacijas. Kūnas gali svyruoti ant elastinės juostos, siūbuoti ant švytuoklės ar skristi aplink Saulę, visais šiais atvejais jis juda taip, kad sumažintų „bendras kuro sąnaudas“, t.y. veiksmas. Jei sistema susideda iš kelių kūnų, tai tokios sistemos Lagranžas bus lygus bendrai visų kūnų kinetinei energijai atėmus bendrą visų kūnų potencinę energiją. Ir vėl, visi kūnai judės kartu, kad visos sistemos poveikis tokio judėjimo metu būtų minimalus. Pavyzdžiui, paimkime kamuolį ir padėkite jį į tuščią vietą. Tam tikru atstumu nuo jo pastatysime elastingą sieną. Tarkime, norime, kad po kurio laiko kamuolys atsidurtų toje pačioje vietoje. Esant šioms sąlygoms, kamuolys gali judėti dviem skirtingais būdais. Pirma, jis gali tiesiog likti vietoje. Antra, galite stumti jį link sienos. Kamuolys skris į sieną, atsimuš nuo jos ir grįš atgal. Akivaizdu, kad galite jį stumti tokiu greičiu, kad jis grįžtų tiksliai tinkamu laiku. Kaip išsaugoti mažiausio veiksmo principą, kad jis galiotų tokiose situacijose? Apie tai kalbėsime.8. Hamiltono variacinis principas. (mažiausio veiksmo principas).
;
=0
tikrojoje trajektorijoje turi būti įvykdyta ši lygtis: 
- Lagranžo lygtis (bet kuriai i= 1,…S).
Kiekybinis ryšys tarp E ir N nurodomas per Puasono koeficientą. N = E/(2(1+μ)), kur yra Puasono koeficientas. μ = |∆d/d 0 |/|∆l/l 0 |. Puasono santykis lemia skersinių matmenų pokytį tempimo ar suspaudimo metu. 0,5.
Fonas
Nuo Galilėjaus laikų buvo žinoma, kad kūnai, kurių neveikia jokios jėgos, juda tiesiomis linijomis, tai yra trumpiausiu keliu. Šviesos spinduliai taip pat sklinda tiesiomis linijomis. 
Tai lengva įrodyti tiesiog atspindint spindulių kelius priešingoje veidrodžio pusėje. Paveiksle jie pavaizduoti punktyrinėmis linijomis. 
Matyti, kad žalias kelias ACB virsta tiesia ACB'. Ir raudonas kelias virsta laužta linija ADB’, kuri, žinoma, yra ilgesnė už žaliąją. 
Vėlgi, žalia spalva rodo kelią, kuriuo iš tikrųjų keliauja šviesos spindulys. Raudonai pažymėtas kelias yra trumpiausias, bet ne greičiausias, nes šviesa turi ilgesnį kelią per stiklą ir ten yra lėtesnė. Greičiausias kelias yra tikrasis šviesos pluošto kelias. 
Matematinėje kalboje mažiausio veiksmo principas suformuluotas gana trumpai, tačiau ne visi skaitytojai gali suprasti vartojamo žymėjimo reikšmę. Noriu pabandyti paaiškinti šį principą aiškiau ir paprasčiau. Laisvas kūnas
Taigi įsivaizduokite, kad sėdite automobilyje tam tikrame taške ir šiuo metu jums duota paprasta užduotis: iki to momento jums reikia nuvažiuoti mašiną į tašką. 
Degalai automobiliui yra brangūs ir, žinoma, norisi jų išleisti kuo mažiau. Jūsų automobilis pagamintas naudojant naujausias super technologijas ir gali įsibėgėti arba stabdyti taip greitai, kaip jums patinka. Tačiau jis sukurtas taip, kad kuo greičiau važiuoja, tuo daugiau sunaudoja degalų. Be to, degalų sąnaudos yra proporcingos greičio kvadratui. Jei važiuosite dvigubai greičiau, per tą patį laiką sunaudosite 4 kartus daugiau degalų. Be greičio, degalų sąnaudoms, žinoma, įtakos turi ir transporto priemonės svoris. Kuo mūsų automobilis sunkesnis, tuo daugiau jis sunaudoja degalų. Mūsų automobilio degalų sąnaudos kiekvienu laiko momentu yra lygios, t.y. lygiai lygus automobilio kinetinei energijai. Gravitacijos srityje
Dabar šiek tiek patobulinkime savo automobilį. Prie jo pritvirtinkime reaktyvinius variklius, kad jis galėtų laisvai skristi bet kuria kryptimi. Apskritai konstrukcija išliko ta pati, todėl degalų sąnaudos vėl išliko griežtai proporcingos automobilio kinetinei energijai. Jei dabar duota užduotis skristi iš taško tam tikru momentu ir atvykti į tašką tam tikru momentu, tai ekonomiškiausias būdas, kaip ir anksčiau, bus skraidyti tolygiai ir tiesia linija, kad būtų baigta. tiksliu nustatytu laiku. Tai vėlgi atitinka laisvą kūno judėjimą trimatėje erdvėje. 
Tačiau naujausiame automobilio modelyje buvo sumontuotas neįprastas įrenginys. Šis prietaisas gali gaminti degalus tiesiogine prasme iš nieko. Tačiau konstrukcija tokia, kad kuo aukštesnis automobilis, tuo daugiau kuro prietaisas gamina bet kuriuo metu. Degalų gamyba yra tiesiogiai proporcinga aukščiui, kuriame šiuo metu yra automobilis. Taip pat kuo automobilis sunkesnis, tuo galingesnis įrenginys jame sumontuotas ir daugiau degalų pagaminama, o gamyba yra tiesiogiai proporcinga automobilio svoriui. Prietaisas pasirodė toks, kad degalų gamyba lygiai lygi (kur laisvojo kritimo pagreitis), t.y. automobilio potenciali energija. 
Čia verta paaiškinti. Žinoma, jūs galite mesti akmenį iš taško įvairiais būdais, kad jis pataikytų į tašką. Bet reikia mesti taip, kad, pakilęs iš taško momentu, jis pataikytų į tašką būtent tuo momentu. Būtent šis judėjimas bus ekonomiškiausias mūsų automobiliui. Lagranžo funkcija ir mažiausio veiksmo principas
Dabar šią analogiją galime perkelti į tikrus fizinius kūnus. Kėbulų degalų sąnaudų normos analogas vadinamas Lagranžo funkcija arba Lagranžo (Lagranžo garbei) ir žymimas raide . Lagranžas rodo, kiek „kuro“ kūnas sunaudoja tam tikru metu. Potencialiame lauke judančiam kūnui Lagranžo kinetinė energija yra lygi jo kinetinei energijai atėmus potencialią energiją. Ne taip paprasta
Tiesą sakant, aš šiek tiek apgavau sakydamas, kad kūnai visada juda taip, kad būtų kuo mažiau veiksmų. Nors daugeliu atvejų tai tiesa, galima pagalvoti apie situacijas, kuriose veiksmai akivaizdžiai nėra minimalūs. 
Galimi abu kamuoliuko judėjimo variantai, tačiau veiksmas antruoju atveju bus didesnis, nes visą šį laiką kamuolys judės su ne nuline kinetine energija.
