Gauso teorema vakuume. Gauso teoremos taikymas elektriniams laukams apskaičiuoti

Kaip minėta aukščiau, buvo sutarta nubrėžti jėgos linijas tokiu tankiu, kad linijų, perveriančių paviršiaus vienetą, statmeną aikštelės linijoms, skaičius būtų lygus vektoriaus moduliui. Tada iš įtempimo linijų rašto galima spręsti ne tik kryptį, bet ir vektoriaus dydį įvairiuose erdvės taškuose.

Panagrinėkime stacionaraus teigiamo taško krūvio lauko linijas. Tai radialinės linijos, besitęsiančios nuo krūvio ir baigiančios begalybe. Vykdykime N tokios linijos. Tada per atstumą r nuo krūvio – jėgos linijų, kertančių vienetinį spindulio sferos paviršių, skaičius r, bus lygus. Ši vertė yra proporcinga taškinio krūvio lauko stiprumui per atstumą r. Skaičius N visada galite pasirinkti taip, kad būtų lygybė

kur . Kadangi jėgos linijos yra ištisinės, tiek pat jėgos linijų kerta bet kokios formos uždarą paviršių, apimantį krūvį. q. Priklausomai nuo krūvio ženklo, jėgos linijos arba patenka į šį uždarą paviršių, arba išeina į lauką. Jei išeinančių eilučių skaičius laikomas teigiamu, o įeinančių eilučių skaičius yra neigiamas, tada modulio ženklą galime praleisti ir parašyti:

.

(1.4)

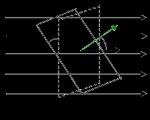
Įtempimo vektoriaus srautas. Padėkime elementarų trinkelę su plotu . Plotas turi būti toks mažas, kad elektrinio lauko stiprumą visuose jo taškuose būtų galima laikyti vienodu. Nubraižykime normalią vietą (1.17 pav.). Šio normalaus kryptis pasirenkama savavališkai. Normalus sudaro kampą su vektoriumi. Elektrinio lauko stiprumo vektoriaus srautas per pasirinktą paviršių yra paviršiaus ploto ir elektrinio lauko stiprumo vektoriaus projekcijos į normaliąją plotą sandauga:

kur yra vektoriaus projekcija į normaliąją vietą.

Kadangi lauko linijų, kertančių vieną sritį, skaičius yra lygus intensyvumo vektoriaus moduliui šalia pasirinktos srities, intensyvumo vektoriaus srautas per paviršių yra proporcingas lauko linijų, kertančių šį paviršių, skaičiui. Todėl bendruoju atveju lauko stiprumo vektoriaus srautas per sritį gali būti vizualiai interpretuojamas kaip reikšmė, lygi lauko linijų, prasiskverbiančių į šią sritį, skaičiui:

.

(1.5)

Atkreipkite dėmesį, kad normalaus krypties pasirinkimas yra sąlyginis, jis gali būti nukreiptas į kitą pusę. Vadinasi, srautas yra algebrinis dydis: srauto ženklas priklauso ne tik nuo lauko konfigūracijos, bet ir nuo normaliojo vektoriaus bei intensyvumo vektoriaus santykinės orientacijos. Jei šie du vektoriai sudaro smailųjį kampą, srautas yra teigiamas; jei jis yra bukas, srautas yra neigiamas. Esant uždaram paviršiui, įprasta paimti normalų už ploto, kurį dengia šis paviršius, tai yra pasirinkti išorinį normalų.

Jei laukas nehomogeniškas, o paviršius savavališkas, srautas apibrėžiamas taip. Visas paviršius turi būti padalintas į mažus elementus, kurių plotas , apskaičiuokite įtempių srautus per kiekvieną iš šių elementų ir tada susumuokite srautus per visus elementus:

Taigi lauko stiprumas apibūdina elektrinį lauką erdvės taške. Intensyvumo srautas priklauso ne nuo lauko stiprumo vertės tam tikrame taške, o nuo lauko pasiskirstymo tam tikros srities paviršiuje.

Elektrinio lauko linijos gali prasidėti tik esant teigiamiems krūviams ir baigtis neigiamais. Jie negali prasidėti ar baigtis erdvėje. Todėl, jei tam tikro uždaro tūrio viduje nėra elektros krūvio, tai bendras eilučių, įeinančių ir išeinančių į šį tūrį, skaičius turi būti lygus nuliui. Jei iš tūrio išeina daugiau eilučių nei į jį patenka, vadinasi, tūrio viduje yra teigiamas krūvis; jei įeina daugiau eilučių nei išeina, tai viduje turi būti neigiamas krūvis. Kai bendras krūvis tūrio viduje lygus nuliui arba kai jame nėra elektros krūvio, pro jį prasiskverbia lauko linijos, o bendras srautas lygus nuliui.

Šie paprasti svarstymai nepriklauso nuo to, kaip elektros krūvis pasiskirsto tūryje. Jis gali būti tūrio centre arba šalia paviršiaus, kuris riboja tūrį. Tūryje gali būti keli teigiami ir neigiami krūviai, bet kokiu būdu paskirstyti tūryje. Tik bendras įkrovimas lemia bendrą įeinančių arba išeinančių įtampos linijų skaičių.

Kaip matyti iš (1.4) ir (1.5), elektrinio lauko stiprumo vektoriaus srautas per savavališką uždarą paviršių, apimantį krūvį q, lygus . Jei paviršiaus viduje yra n krūviai, tada pagal lauko superpozicijos principą bendras srautas bus visų krūvių lauko stiprių srautų suma ir bus lygus , kur šiuo atveju turime galvoje algebrinę visų krūvių, padengtų uždaru paviršius.

Gauso teorema. Gausas pirmasis atrado paprastą faktą, kad elektrinio lauko stiprumo vektoriaus srautas per savavališką uždarą paviršių turi būti susietas su visu krūviu, esančiu šio tūrio viduje:

Gausas Karlas Friedrichas (1777–1855)

Puikus vokiečių matematikas, fizikas ir astronomas, absoliučios fizikos vienetų sistemos kūrėjas. Jis sukūrė elektrostatinio potencialo teoriją ir įrodė svarbiausią elektrostatikos teoremą (Gauso teorema). Sukūrė vaizdų konstravimo sudėtingose ​​optinėse sistemose teoriją. Jis buvo vienas iš pirmųjų, kurie atėjo į idėją apie neeuklido geometrijos egzistavimo galimybę. Be to, Gaussas padarė išskirtinį indėlį į beveik visas matematikos šakas.

Paskutinis ryšys yra Gauso teorema elektriniam laukui: intensyvumo vektoriaus srautas per savavališką uždarą paviršių yra proporcingas šio paviršiaus viduje esančių krūvių algebrinei sumai.Proporcingumo koeficientas priklauso nuo vienetų sistemos pasirinkimo.

Pažymėtina, kad Gauso teorema gaunama kaip Kulono dėsnio ir superpozicijos principo pasekmė. Jei elektrinio lauko stiprumas nepasikeistų atvirkščiai proporcingai atstumo kvadratui, teorema būtų negaliojanti. Todėl Gauso teorema taikytina bet kokiems laukams, kuriuose atvirkštinis kvadrato dėsnis ir superpozicijos principas yra griežtai tenkinami, pavyzdžiui, gravitaciniam laukui. Gravitacinio lauko atveju lauką sukuriančių krūvių vaidmenį atlieka kūnų masės. Gravitacinio lauko linijų srautas per uždarą paviršių yra proporcingas bendrai tame paviršiuje esančiai masei.

Įkrautos plokštumos lauko stipris. Begalinio krūvio plokštumos elektrinio lauko stiprumui nustatyti pritaikykime Gauso teoremą. Jei plokštuma yra begalinė ir tolygiai įkrauta, tai yra, paviršiaus krūvio tankis yra vienodas bet kurioje vietoje, tai elektrinio lauko stiprumo linijos bet kuriame taške yra statmenos šiai plokštumai. Norėdami tai parodyti, įtempimo vektoriui naudosime superpozicijos principą. Plokštumoje parinksime dvi elementarias atkarpas, kurias galima laikyti tašku A, kuriame būtina nustatyti lauko stiprumą. Kaip matyti iš fig. 1.18, gautas įtempimo vektorius bus nukreiptas statmenai plokštumai. Kadangi plokštuma gali būti padalinta į begalę tokių pjūvių porų bet kuriam stebėjimo taškui, akivaizdu, kad įkrautos plokštumos lauko linijos yra statmenos plokštumai, o laukas yra vienodas (1.19 pav.). Jei taip nebūtų, plokštumai judant išilgai savęs, laukas kiekviename erdvės taške pasikeistų, tačiau tai prieštarauja įkrautos sistemos simetrijai (plokštuma yra begalinė). Teigiamo krūvio plokštumos atveju jėgos linijos prasideda plokštumoje ir baigiasi begalybėje, o neigiamo krūvio plokštumos jėgos linijos prasideda begalybėje ir patenka į plokštumą.

Ryžiai. 1.18	Ryžiai. 1.19

Norėdami nustatyti begalinės teigiamai įkrautos plokštumos elektrinio lauko stiprumą, mintyse pasirenkame erdvėje cilindrą, kurio ašis yra statmena įkrautai plokštumai, o pagrindai yra lygiagrečiai jai, o viena iš bazių eina per lauko tašką. mus dominančių (1.19 pav.). Cilindras išpjauna plotą iš įkrautos plokštumos, o cilindro pagrindai, esantys skirtingose ​​plokštumos pusėse, turi tą patį plotą.

Pagal Gauso teoremą elektrinio lauko stiprumo vektoriaus srautas per cilindro paviršių yra susijęs su elektros krūviu cilindro viduje pagal išraišką:

.

Kadangi įtempių linijos kerta tik cilindro pagrindus, srautas per cilindro šoninį paviršių yra lygus nuliui. Todėl įtempimo vektoriaus srautas per cilindrinį paviršių susideda tik iš srautų per cilindro pagrindus, todėl

Palyginę dvi paskutines intensyvumo vektoriaus srauto išraiškas, gauname

Elektrinio lauko stipris tarp priešingai įkrautų plokščių. Jei plokščių matmenys žymiai viršija atstumą tarp jų, tai kiekvienos plokštės elektrinis laukas gali būti laikomas artimu begalinės tolygiai įkrautos plokštumos laukui. Kadangi priešingai įkrautų plokščių elektrinio lauko stiprumo linijos tarp plokščių nukreiptos viena kryptimi (1.20 pav.), lauko stiprumas tarp plokščių lygus

.

Išorinėje erdvėje priešingai įkrautų plokščių elektrinio lauko stiprumo linijos turi priešingas kryptis, todėl už šių plokščių išorėje susidarantis elektrinio lauko stiprumas lygus nuliui. Gauta intensyvumo išraiška galioja didelėms įkrautoms plokštėms, kai intensyvumas nustatomas taške, esančiame toli nuo jų kraštų.

Vienodai įkrautos plonos, begalinio ilgio vielos elektrinio lauko stipris. Raskime tolygiai įkrautos plonos begalinio ilgio vielos elektrinio lauko stiprio priklausomybę nuo atstumo iki vielos ašies, naudodamiesi Gauso teorema. Pasirinkime riboto ilgio vielos atkarpą. Jei tiesinio krūvio tankis ant vielos yra , tai pasirinktos srities krūvis yra lygus .

Panagrinėkime taškinio krūvio $q$ lauką ir raskime intensyvumo vektoriaus ($\overrightarrow(E)$) srautą per uždarą paviršių $S$. Darysime prielaidą, kad įkrova yra paviršiaus viduje. Įtempimo vektoriaus srautas per bet kurį paviršių yra lygus išeinančių įtempimo vektoriaus linijų skaičiui (pradedant nuo įkrovos, jei $q>0$) arba eilučių $\overrightarrow(E)$, įeinančių. , jei $q \[Ф_E=\frac( q)((\varepsilon )_0)\ \left(1\right),\]

kur srauto ženklas sutampa su krūvio ženklu.

Ostrogradskio-Gauso teorema integralia forma

Tarkime, kad paviršiaus S viduje yra N taškinių krūvių, reikšmės $q_1,q_2,\taškai q_N.$ Iš superpozicijos principo žinome, kad gautą visų N krūvių lauko stiprumą galima rasti kaip suma lauko stiprumą, kurį sukuria kiekvienas iš krūvių, tada yra:

Todėl taškinių mokesčių sistemos srautui galime parašyti:

Naudodami (1) formulę gauname, kad:

\[Ф_E=\oint\limits_S(\overrightarrow(E)d\overrightarrow(S))=\frac(1)((\varepsilon )_0)\sum\limits^N_(i=1)(q_i\ )\ kairėn(4\dešinėn).\]

(4) lygtis reiškia, kad elektrinio lauko stiprumo vektoriaus srautas per uždarą paviršių yra lygus šio paviršiaus viduje esančių krūvių algebrinei sumai, padalytai iš elektrinės konstantos. Tai Ostrogradskio-Gausso teorema integralia forma. Ši teorema yra Kulono dėsnio pasekmė. Šios teoremos reikšmė yra ta, kad ji leidžia gana paprastai apskaičiuoti elektrinius laukus įvairiems krūvio pasiskirstymams.

Dėl Ostrogradskio-Gausso teoremos reikia pasakyti, kad intensyvumo vektoriaus ($Ф_E$) srautas per uždarą paviršių tuo atveju, kai krūviai yra už šio paviršiaus, yra lygus nuliui.

Tuo atveju, kai krūvių diskretiškumo galima nepaisyti, naudojama tūrinio krūvio tankio sąvoka ($\rho $), jei krūvis paskirstomas visame tūryje. Jis apibrėžiamas taip:

\[\rho =\frac(dq)(dV)\left(5\right),\]

kur $dq$ yra krūvis, kuris gali būti laikomas taškiniu, $dV$ yra mažas tūris. (Dėl $dV$ reikia padaryti tokią pastabą. Šis tūris yra pakankamai mažas, kad krūvio tankį jame būtų galima laikyti pastoviu, bet pakankamai didelis, kad neatsirastų įkrovos diskretiškumas). Visą ertmėje esantį krūvį galima rasti taip:

\[\sum\limits^N_(i=1)(q_i\ )=\int\limits_V(\rho dV)\left(6\right).\]

Šiuo atveju formulę (4) perrašome į formą:

\[\oint\limits_S(\overrightarrow(E)d\overrightarrow(S))=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV)\left(7\right).\ ]

Ostrogradskio-Gausso teorema diferencine forma

Naudojant Ostrogradsky-Gauss formulę bet kuriam vektoriaus pobūdžio laukui, kurios pagalba atliekamas perėjimas nuo integracijos per uždarą paviršių prie integracijos per tūrį:

\[\oint\limits_S(\overrightarrow(a)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(a)dV\ \left(8\right),\]

kur $\overrightarrow(a)-$lauko vektorius (mūsų atveju tai $\overrightarrow(E)$), $div\overrightarrow(a)=\overrightarrow(\nabla )\overrightarrow(a)=\frac(\ dalinis a_x)(\partial x)+\frac(\partial a_y)(\partial y)+\frac(\partial a_z)(\partial z)$ -- vektoriaus $\overrightarrow(a)$ nukrypimas taškas su koordinatėmis ( x,y,z), kuris atvaizduoja vektorinį lauką į skaliarinį. $\overrightarrow(\nabla )=\frac(\partial )(\partial x)\overrightarrow(i)+\frac(\partial )(\partial y)\overrightarrow(j)+\frac(\partial )(\ dalinis z)\overrightarrow(k)$ – stebimas operatorius. (Mūsų atveju tai bus $div\overrightarrow(E)=\overrightarrow(\nabla )\overrightarrow(E)=\frac(\partial E_x)(\partial x)+\frac(\partial E_y)(\partial y) +\frac(\partial E_z)(\partial z)$) -- įtempimo vektoriaus divergencija. Vadovaudamiesi tuo, kas išdėstyta aukščiau, formulę (6) perrašome taip:

\[\oint\limits_S(\overrightarrow(E)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(E)dV=\frac(1)((\varepsilon )_0)\int\limits_V( \rho dV)\left(9\right).\]

(9) lygties lygybės tenkinamos bet kokiam tūriui, ir tai įmanoma tik tuo atveju, jei integranduose esančios funkcijos yra lygios kiekvienoje erdvės srovėje, tai yra, galime parašyti, kad:

Išraiška (10) yra Ostrogradskio-Gausso teorema diferencine forma. Jo aiškinimas yra toks: krūviai yra elektrinio lauko šaltiniai. Jei $div\overrightarrow(E)>0$, tai šiuose lauko taškuose (mokesčiai yra teigiami) turime lauko šaltinius, jei $div\overrightarrow(E)

Užduotis: Krūvis tolygiai paskirstomas tūryje; šiame tūryje pasirenkamas kubinis paviršius su b puse. Jis įrašytas į sferą. Raskite įtempimo vektoriaus srautų per šiuos paviršius santykį.

Pagal Gauso teoremą intensyvumo vektoriaus $\overrightarrow(E)$ srautas ($Ф_E$) per uždarą paviršių, kurio krūvis tolygiai pasiskirsto tūryje, yra lygus:

\[Ф_E=\frac(1)((\varepsilon )_0)Q=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV=\frac(\rho )((\varepsilon ) _0)\int\limits_V(dV)=\frac(\rho V)((\varepsilon )_0))\left(1.1\right).\]

Todėl turime nustatyti kubo ir rutulio tūrius, jei rutulys aprašytas aplink šį kubą. Pirmiausia kubo tūris ($V_k$), jei jo kraštinė b lygi:

Raskime rutulio tūrį ($V_(sh)$) naudodami formulę:

kur $D$ yra rutulio skersmuo ir (kadangi rutulys yra aplink kubą) pagrindinė kubo įstrižainė. Todėl kubo įstrižainę turime išreikšti jo kraštine. Tai lengva padaryti, jei naudojate Pitagoro teoremą. Norėdami apskaičiuoti, pavyzdžiui, kubo įstrižainę (1,5), pirmiausia turime rasti kvadrato (apatinio kubo pagrindo) įstrižainę (1,6). Įstrižainės ilgis (1,6) yra lygus:

Šiuo atveju įstrižainės ilgis (1,5) yra lygus:

\[(D=D)_(15)=\sqrt(b^2+((\sqrt(b^2+b^2\ \ \ )))^2)=b\sqrt(3)\ \left (1,5\dešinėn).\]

Rastą rutulio skersmenį pakeisdami į (1.3), gauname:

Dabar galime rasti įtempimo vektoriaus srautus per kubo paviršių, jis lygus:

\[Ф_(Ek)=\frac(\rho V_k)((\varepsilon )_0)=\frac(\rho b^3)((\varepsilon )_0)\left(1,7\right),\]

per rutulio paviršių:

\[Ф_(Esh)=\frac(\rho V_(sh))((\varepsilon )_0)=\frac(\rho )((\varepsilon )_0)\frac(\sqrt(3))(2) \pi b^3\ \left(1,8\right).\]

Raskime santykį $\frac(Ф_(Esh))(Ф_(Ek))$:

\[\frac(Ф_(Esh))(Ф_(Ek))=\frac(\frac(с)(\varepsilon_0)\frac(\sqrt(3))(2) \pi b^3)(\frac (сb^3)(\varepsilon_0))=\frac(\pi)(2)\sqrt(3)\ \apytiksliai 2,7\left(1,9\right).\]

Atsakymas: srautas per rutulio paviršių yra 2,7 karto didesnis.

Užduotis: Įrodykite, kad laidininko krūvis yra ant jo paviršiaus.

Tam įrodyti naudojame Gauso teoremą. Parinkime savavališkos formos uždarą paviršių laidininke šalia laidininko paviršiaus (2 pav.).

Tarkime, kad laidininko viduje yra krūviai, parašome Ostrogradskio-Gausso teoremą lauko divergencijai bet kuriame paviršiaus taške S:

kur $\rho yra vidinio krūvio tankis\ $. Tačiau laidininko viduje nėra lauko, ty $\overrightarrow(E)=0$, todėl $div\overrightarrow(E)=0\to \rho =0$. Ostrogradskio-Gausso teorema diferencine forma yra lokali, tai yra, ji parašyta lauko taškui, taško specialiai nepasirinkome, todėl bet kuriame lauko taške laidininko viduje krūvio tankis yra lygus nuliui.

Superpozicijos principas kartu su Kulono dėsniu suteikia pagrindą savavališkos krūvių sistemos elektriniam laukui apskaičiuoti, tačiau tiesioginiam laukų sumavimui naudojant (4.2) formulę paprastai reikia atlikti sudėtingus skaičiavimus. Tačiau, esant vienai ar kitai krūvių sistemos simetrijai, skaičiavimai gerokai supaprastėja, jei įvedame elektrinio lauko srauto sąvoką ir panaudojame Gauso teoremą.

Elektrinio lauko srauto sąvoka buvo įvesta į elektrodinamiką iš hidrodinamikos. Hidrodinamikoje skysčio srautas vamzdžiu, ty skysčio N tūris, praeinantis vamzdžio skerspjūviu per laiko vienetą, yra lygus v ⋅ S, kur v yra skysčio greitis, o S yra vamzdžio skerspjūvio plotas. Jei skysčio greitis skerspjūvyje skiriasi, reikia naudoti integralinę formulę N = ∫ S v → ⋅ d S → . Iš tiesų, greičio lauke paryškinkime nedidelį plotą d S, statmeną greičio vektoriui (pav.).

Ryžiai. 1.4: Skysčio tekėjimas

Per šią sritį tekančio skysčio tūris per laiką d t lygus v d S d t . Jei platforma yra pasvirusi į srautą, tai atitinkamas tūris bus v d S cos θ d t , kur θ yra kampas tarp greičio vektoriaus v → ir normaliosios n → į platformą d S . Skysčio tūris, tekantis per plotą d S per laiko vienetą, gaunamas padalijus šią reikšmę iš d t. Jis lygus v d S cos θ d t, t.y. skaliarinė sandauga v → ⋅ d S → greičio vektorius v → pagal ploto elemento vektorių d S → = n → d S . Vieneto vektorius n → normalus plotui d S gali būti nubrėžtas dviem tiesiai priešingomis kryptimis. vienas iš jų sąlyginai priimamas kaip teigiamas. Šia kryptimi brėžiamas normalusis n →. Svetainės pusė, iš kurios atsiranda normalioji n →, vadinama išorine, o pusė, į kurią įeina normalioji n → – vidine. Ploto elemento vektorius d S → yra nukreiptas išilgai išorinės normaliosios n → į paviršių, o dydis yra lygus elemento d S = ∣ d S → ∣ plotui. Skaičiuojant skysčio, tekančio per baigtinių matmenų plotą S, tūrį, jis turi būti išplėtotas į be galo mažus plotus d S ir tada apskaičiuojamas viso paviršiaus S integralas ∫ S v → ⋅ d S →.

Tokios išraiškos kaip ∫ S v → ⋅ d S → randamos daugelyje fizikos ir matematikos šakų. Jie vadinami vektoriaus v → srautu per paviršių S, nepriklausomai nuo vektoriaus v → pobūdžio. Elektrodinamikoje integralas

N = ∫ S E → ⋅ d S →

(5.1)

vadinamas elektrinio lauko stiprio E → srautu per savavališką paviršių S, nors realus srautas su šia sąvoka nesusijęs.

Tarkime, kad vektorius E → pavaizduotas geometrine suma

E → = ∑ j E → j .

Padauginę šią lygybę skaliariai iš d S → ir integruodami, gauname

N = ∑ j N j .

čia N j – vektoriaus E → j srautas per tą patį paviršių. Taigi iš elektrinio lauko stiprio superpozicijos principo išplaukia, kad srautai per tą patį paviršių sumuojasi algebriškai.

Gauso teorema teigia, kad vektoriaus E → srautas per savavališką uždarą paviršių yra lygus bendram visų dalelių, esančių šio paviršiaus viduje, krūviui Q, padaugintam iš 4 π:

Teoremos įrodymą atliksime trimis etapais.

1. Pradėkime nuo vieno taško krūvio q elektrinio lauko srauto apskaičiavimo (pav.). Paprasčiausiu atveju, kai integracinis paviršius S yra rutulys, o krūvis yra jo centre, Gauso teoremos pagrįstumas yra beveik akivaizdus. Sferos paviršiuje elektrinio lauko stipris yra

E → = q r → ∕ r 3

pastovus dydis ir visur nukreiptas normaliai į paviršių, kad elektrinio lauko srautas būtų tiesiog lygus sandaugai E = q ∕ r 2 ir sferos plotui S = 4 π r 2 . Todėl N = 4 π q. Šis rezultatas nepriklauso nuo krūvį supančio paviršiaus formos. Norėdami tai įrodyti, pasirenkame savavališką pakankamai mažo dydžio paviršiaus plotą su išorinės normalios n → kryptimi. Fig. vienas toks segmentas parodytas perdėtai dideliu (aiškumo dėlei) dydžiu.

Vektoriaus E → srautas per šią sritį yra lygus d N = E → ⋅ d S → = E cos θ d S ,

čia θ yra kampas tarp krypties E → ir išorinės normaliosios n → į plotą d S . Kadangi E = q ∕ r 2 , o d S cos θ ∕ ​​​​r 2 absoliučia verte yra erdvinio kampo d Ω = d S ∣ cos θ ∣ ∕ r 2 elementas, iš kurio matomas plotas d S taškas, kuriame yra užtaisas,

D N = ± q d Ω .

kur pliuso ir minuso ženklai atitinka cos θ ženklą, būtent: turėtumėte paimti pliuso ženklą, jei vektorius E → sudaro smailų kampą su išorinės normaliosios n → kryptimi, o priešingu atveju minuso ženklas.

2. Dabar apsvarstykite baigtinį paviršių S, apimantį tam tikrą pasirinktą tūrį V. Atsižvelgiant į šį tūrį, visada galima nustatyti, kuri iš dviejų priešingų normalios krypčių bet kuriam paviršiaus S elementui turėtų būti laikoma išorine. Išorinis normalus yra nukreiptas iš V tūrio į išorę. Apibendrinant segmentus, iki ženklo gauname N = q Ω, kur Ω yra erdvės kampas, kuriame paviršius S matomas iš taško, kuriame yra krūvis q. Jei paviršius S yra uždaras, tada Ω = 4 π, su sąlyga, kad krūvis q yra S viduje. Kitu atveju Ω = 0. Norėdami paaiškinti paskutinį teiginį, vėl galime remtis Fig. .

Akivaizdu, kad srautai per uždaro paviršiaus segmentus, pagrįstus vienodais erdviniais kampais, bet nukreiptais priešingomis kryptimis, vienas kitą panaikina. Taip pat akivaizdu, kad jei krūvis yra už uždaro paviršiaus, tada bet kuriam segmentui, nukreiptam į išorę, yra atitinkamas segmentas, nukreiptas į vidų.

3. Galiausiai, naudodamiesi superpozicijos principu, pasiekiame galutinę Gauso teoremos formuluotę (). Iš tiesų, krūvių sistemos laukas yra lygus kiekvieno krūvio laukų sumai atskirai, tačiau tik mokesčiai, esantys uždaro paviršiaus viduje, įeina į dešinę teoremos pusę (). Tai užbaigia įrodymą.

Makroskopiniuose kūnuose krūvininkų skaičius yra toks didelis, kad patogu pavaizduoti atskirą dalelių ansamblį nuolatinio pasiskirstymo pavidalu, įvedant krūvio tankio sąvoką. Pagal apibrėžimą, krūvio tankis ρ yra santykis Δ Q ∕ Δ V riboje, kai tūris Δ V linkęs į fiziškai be galo mažą vertę:

kur integravimas dešinėje pusėje atliekamas per tūrį V, uždarytą paviršiumi S.

Gauso teorema pateikia vieną skaliarinę lygtį trims vektoriaus E → komponentams, todėl vien šios teoremos elektriniam laukui apskaičiuoti nepakanka. Būtina žinoti įkrovos tankio pasiskirstymo simetriją, kad problemą būtų galima sumažinti iki vienos skaliarinės lygties. Gauso teorema leidžia rasti lauką tais atvejais, kai integracijos paviršių () galima pasirinkti taip, kad elektrinio lauko stipris E būtų pastovus visame paviršiuje. Pažvelkime į labiausiai pamokančius pavyzdžius.

▸ 5.1 uždavinys

Raskite tolygiai įkrautos tūrio arba sferos lauką paviršiai.

Sprendimas: Taškinio krūvio elektrinis laukas E → = q r → ∕ r 3 linkęs begalybė ties r → 0 . Šis faktas rodo idėjos nenuoseklumą elementariosios dalelės taškiniais krūviais. Jei mokestis q tolygiai pasiskirstę per baigtinio spindulio sferos tūrį a, tada elektrinis laukas neturi singuliarumų.

Iš uždavinio simetrijos aišku, kad elektrinis laukas E → visur nukreipta radialiai, ir jos įtampa E = E(r) priklauso tik nuo atstumo r į kamuoliuko centrą. Tada elektrinis laukas teka spindulio sfera r tiesiog lygus 4 π r 2 E (pav.).

Kita vertus, toje pačioje sferoje esantis krūvis yra lygus bendram krūviui rutulys Q, jei r ≥ a. Prilyginę 4 π r 2 E rutulio krūviui q, padaugintam iš 4 π, gauname: E (r) = q ∕ r 2 .

Taigi išorinėje erdvėje susidaro įkrautas rutulys toks laukas tarsi visas krūvis būtų sutelktas jo centre. Šis rezultatas galioja bet kokiam sferiniam simetriškumui mokesčių paskirstymas.

Laukas rutulio viduje yra E (r) = Q ∕ r 2, kur Q yra krūvis spindulio r sieros viduje. Jei krūvis yra tolygiai paskirstytas visame rutulio tūryje, tada Q = q (r ∕ a) 3 . Tokiu atveju

E (r) = q r ∕ a 3 = (4 π ∕ 3) ρ r ,

kur ρ = q ∕ (4 π a 3 ∕ 3) — krūvio tankis. Rutulio viduje laukas tiesiškai mažėja nuo maksimumo reikšmės rutulio paviršiuje iki nulio jo centre (1 pav.). ).

Funkcija E(r) kartu jis visur baigtinis ir nenutrūkstamas.

Jei krūvis pasiskirsto rutulio paviršiuje, tada Q = 0, taigi ir E = 0. Šis rezultatas taip pat galioja tuo atveju, kai yra sferinės formos viduje nėra krūvio ertmės, o išoriniai krūviai pasiskirsto sferiškai simetriškai. ▸ 5.2 uždavinys

Raskite vienodai įkrautos begalinės gijos lauką; sriegio spindulys a, mokestis už ilgio vienetą ϰ.

▸ 5.3 uždavinys

Raskite begalinės tiesios gijos ir be galo ilgo gijos lauką vienodai įkrautas cilindras.

▸ 5.4 uždavinys

Raskite begalinio krūvio plokštumos lauką ir tolygiai įkrautas begalinis plokščias sluoksnis.

Sprendimas: Dėl uždavinio simetrijos laukas yra nukreiptas normalus sluoksniui ir priklauso tik nuo atstumo x nuo plokštės simetrijos plokštuma. Norėdami apskaičiuoti lauką naudodami Gauso teorema, patogu pasirinkti integravimo paviršių S in gretasienio formos, kaip parodyta Fig. .

Paskutinis rezultatas gaunamas pereinant prie ribos a → 0 tuo pačiu didinant krūvio tankįρ taip, kad reikšmė σ = ρ a liko nepakitęs. Priešingose ​​plokštumos pusėse elektrinio lauko stiprumas yra tokio paties dydžio, bet priešinga kryptimi. Todėl pravažiuojant įkrauta plokštuma, laukas staigiai pasikeičia kiekiu 4 π σ . Atkreipkite dėmesį, kad plokštelė gali būti laikoma begaline, jei atstumas nuo yra nereikšmingas, palyginti su jo dydžiu. Įjungta atstumai labai dideli lyginant su plokštės matmenimis, tai veikia kaip taškinis krūvis, o jo laukas mažėja atgal proporcingas atstumo kvadratui.

Elektrostatinį lauką galima aiškiai pavaizduoti naudojant jėgos linijas (įtempimo linijas). Elektros laidai vadinamos kreivėmis, kurių liestinės kiekviename taške sutampa su įtempimo vektoriumi E.

Jėgos linijos yra įprastinė sąvoka ir iš tikrųjų neegzistuoja. Vieno neigiamo ir vieno teigiamo krūvio lauko linijos parodytos Fig. 5 yra radialinės linijos, kylančios iš teigiamo krūvio arba einančios į neigiamą krūvį.

Jei lauko linijų tankis ir kryptis visame lauko tūryje nesikeičia, toks elektrostatinis laukas laikomas vienalyčiu (linijų skaičius turi būti skaitiniu būdu lygus lauko stiprumui E).

Lauko linijų, pažymėtų ">dS, joms statmenai, skaičius lemia elektrostatinio lauko stiprumo vektoriaus srautas:

formula" src="http://hi-edu.ru/e-books/xbook785/files/17-1.gif" border="0" align="absmiddle" alt="- vektoriaus E projekcija į normaliosios n kryptį į vietą dS (6 pav.).

Atitinkamai, vektoriaus E srautas per savavališką uždarą paviršių S

mark">S gali keistis ne tik srauto dydis, bet ir ženklas:

1) su formule" src="http://hi-edu.ru/e-books/xbook785/files/17-4.gif" border="0" align="absmiddle" alt="

3) renkantis"> Raskime vektoriaus E srautą per sferinį paviršių S, kurio centre yra taškinis krūvis q.

Šiuo atveju ženklas ">E ir n sutampa visuose sferinio paviršiaus taškuose.

Atsižvelgiant į taškinio krūvio lauko stiprumą, formulė" src="http://hi-edu.ru/e-books/xbook785/files/18-2.gif" border="0" align="absmiddle " alt="(! LANG:mes gauname

formula" src="http://hi-edu.ru/e-books/xbook785/files/Fe.gif" border="0" align="absmiddle" alt="- algebrinis dydis, priklausantis nuo krūvio ženklo. Pavyzdžiui, kai q<0 линии Е направлены к заряду и противоположны направлению внешней нормали n ..gif" border="0" align="absmiddle" alt="aplink krūvį q turi savavališką formą. Akivaizdu, kad paviršius pažymėtas ">E, kaip ir paviršius S. Todėl vektoriaus E srautas per savavališką paviršių yra formulė" src="http://hi-edu.ru/e-books/xbook785/ files/Fe.gif" border ="0" align="absmiddle" alt=".

Jei krūvis yra už uždaro paviršiaus, akivaizdu, kiek linijų patenka į uždarą sritį, tiek pat iš jos išeis. Dėl to vektoriaus E srautas bus lygus nuliui.

Jeigu elektrinį lauką sukuria taškinių krūvių sistema formula" src="http://hi-edu.ru/e-books/xbook785/files/18-4.gif" border="0" align="absmiddle" alt="

Ši formulė yra matematinė Gauso teoremos išraiška: elektrinio lauko stiprumo vektoriaus E srautas vakuume per savavališką uždarą paviršių yra lygus jo padengtų krūvių algebrinei sumai, padalytai iš formula" src="http://hi-edu.ru/e-books/xbook785/files/18-6.gif" border="0" align="absmiddle" alt="

Norėdami užbaigti aprašymą, taip pat pateiksime Gauso teoremą lokaliu pavidalu, remdamiesi ne integraliniais santykiais, o lauko parametrais tam tikrame erdvės taške. Norėdami tai padaryti, patogu naudoti diferencialinį operatorių - vektoriaus skirtumą, -

formula" src="http://hi-edu.ru/e-books/xbook785/files/nabla.gif" border="0" align="absmiddle" alt="("nabla") -

formula" src="http://hi-edu.ru/e-books/xbook785/files/19-1.gif" border="0" align="absmiddle" alt="

Matematinės analizės metu žinoma Gauso-Ostrogradskio teorema: vektoriaus srautas per uždarą paviršių yra lygus jo divergencijos per šio paviršiaus ribojamą tūrį integralui -

formula" src="http://hi-edu.ru/e-books/xbook785/files/ro.gif" border="0" align="absmiddle" alt=":

formula" src="http://hi-edu.ru/e-books/xbook785/files/19-4.gif" border="0" align="absmiddle" alt="

Ši išraiška yra Gauso teorema vietine (diferencine) forma.

Gauso teorema (2.2) leidžia nustatyti įvairių elektrostatinių laukų stiprius. Pažvelkime į kelis Gauso teoremos taikymo pavyzdžius.

1. Paskaičiuokime E elektrostatinis laukas, sukurtas tolygiai įkrauto sferinio paviršiaus.

Tarkime, kad R spindulio sferinis paviršius turi tolygiai paskirstytą krūvį q, t.y. Paviršiaus krūvio tankis yra vienodas visur ">r >R nuo sferos centro, mintyse sukonstruojame naują sferinį paviršių S, simetrišką įkrautai sferai. Pagal Gauso teoremą

formula" src="http://hi-edu.ru/e-books/xbook785/files/20-1.gif" border="0" align="absmiddle" alt="

Taškams, esantiems R spindulio įkrautos sferos paviršiuje, pagal analogiją galime parašyti:

atranka">įkrautoje sferoje, savyje nėra elektros krūvių, todėl srauto ženklas">E = 0.

Elektros krūvių sistemos lauko stiprio skaičiavimo, naudojant elektrostatinių laukų superpozicijos principą, užduotį galima labai supaprastinti, jei taikysime vokiečių mokslininko K. Gausso (1777-1855) atrastą teoremą, nustatančią elektros krūvio srautą. elektrinio lauko stiprumo vektorius per savavališką uždarą paviršių.

Pagal intensyvumo vektoriaus srauto per uždarą paviršių apibrėžimą, intensyvumo vektoriaus srautas per spindulio r sferinį paviršių, apimantį taškinį krūvį Q, esantį jo centre (1 pav.), yra lygus

Šis rezultatas galioja savavališkos formos uždaram paviršiui. Iš tiesų, jei jūs uždarysite sferą (1 pav.) į savavališką uždarą paviršių, tada kiekviena įtempimo linija, kuri prasiskverbia į sferą, taip pat praeis per šį paviršių.

Jei bet kokios formos uždaras paviršius apgaubia krūvį (2 pav.), tai bet kuriai įtempimo linijai susikirtus su paviršiumi, ji arba įeina, arba išeina iš jo. Skaičiuojant srautą, nelyginis sankryžų skaičius galiausiai sumažinamas iki vienos sankryžos, nes manoma, kad srautas yra teigiamas, jei įtempimo linijos palieka paviršių, ir neigiamas, jei linijos patenka į paviršių. Jei uždaras paviršius neapima krūvio , tada srautas per jį yra lygus nuliui, taigi, kaip įtempimo linijų, patenkančių į paviršių, skaičius yra lygus įtempimo linijų, išeinančių iš jo, skaičiui.

Tai reiškia, kad bet kokios formos paviršiui, jei jis yra uždaras ir turi taškinį krūvį Q, vektoriaus srautas E bus lygus Q/ε 0, t.y.

Srauto ženklas sutampa su krūvio Q ženklu.

Išnagrinėkime bendrą savavališko paviršiaus, supančio n krūvius, atvejį. Naudojant superpozicijos principą, įtampa E laukas, kurį sukuria visi krūviai, yra lygus intensyvumo sumai E i laukus, kuriuos sukuria kiekvienas mokestis atskirai. Štai kodėl

Pagal (1) kiekvienas integralas, esantis po sumos ženklu, yra lygus Q i /ε 0 . Reiškia,

(2)

(2) formulė išreiškia Gauso teorema elektrostatiniam laukui vakuume: elektrostatinio lauko stiprumo vektoriaus srautas vakuume per savavališką uždarą paviršių yra lygus šio paviršiaus viduje esančių krūvių algebrinei sumai, padalytai iš ε 0. Šią teoremą savavališko pobūdžio vektoriniam laukui matematiškai gavo rusų matematikas M.V.Ostrogradskis (1801-1862), o vėliau nepriklausomai nuo jo elektrostatinio lauko atžvilgiu – K.Gausas.

Bendru atveju elektros krūviai gali būti paskirstomi tam tikru tūrio tankiu ρ=dQ/dV, kuris skirtingose ​​erdvės vietose yra skirtingas. Tada bendras krūvis, esantis uždarame paviršiuje S, kuris apima tam tikrą tūrį V,

(3)

Naudojant (3) formulę, Gauso teoremą (2) galima parašyti taip:

Įtampos vektoriaus cirkuliacija yra darbas, kurį atlieka elektrinės jėgos, judant vieną teigiamą krūvį uždaru keliu L

(13.18)

Kadangi elektrostatinio lauko jėgų darbas išilgai uždaros kilpos yra lygus nuliui (potencialaus lauko jėgų darbas), tai elektrostatinio lauko stiprumo cirkuliacija išilgai uždaros grandinės yra lygi nuliui.

Elektrostatinio lauko potencialas. Konservatyvios jėgos lauką galima apibūdinti ne tik vektorine funkcija, bet lygiavertį šio lauko aprašymą galima gauti apibrėžiant tinkamą skaliarinį dydį kiekviename jo taške. Elektrostatiniam laukui šis dydis yra elektrostatinio lauko potencialas, apibrėžiamas kaip bandomojo krūvio potencialios energijos santykis q iki šio krūvio dydžio,  = W P / q, iš to išplaukia, kad potencialas skaitine prasme yra lygus potencialiai energijai, kurią turi vienetinis teigiamas krūvis tam tikrame lauko taške. Potencialo matavimo vienetas yra voltas (1 V).

Taškinio krūvio lauko potencialas K vienalytėje izotropinėje terpėje, kurios dielektrinė konstanta :

Superpozicijos principas. Potencialas yra skaliarinė funkcija, jai galioja superpozicijos principas. Taigi taškinių krūvių sistemos lauko potencialui K 1, K 2, Qn mes turime

,

Kur r i- atstumas nuo lauko taško su potencialu  iki krūvio Qi. Jei krūvis savavališkai paskirstomas erdvėje, tada

,

Kur r- atstumas nuo elementaraus tūrio d x,d y,d z parodyti ( x, y, z), kur nustatomas potencialas; V- erdvės, kurioje pasiskirsto krūvis, tūris.

Elektrinio lauko jėgų potencialas ir darbas. Remiantis potencialo apibrėžimu, galima parodyti, kad elektrinio lauko atliktas darbas judina taškinį krūvį q nuo vieno lauko taško iki kito yra lygus šio krūvio dydžio ir potencialų skirtumo sandaugai pradiniame ir galutiniame kelio taške, A = q (     
Jei pagal analogiją su potencialine energija darome prielaidą, kad taškuose, kurie yra be galo nutolę nuo elektros krūvių - lauko šaltinių, potencialas yra lygus nuliui, tada elektrinio lauko jėgų darbas judant krūviui q nuo taško 1 iki begalybės galima pavaizduoti kaip A   q  1 .
Taigi potencialas tam tikrame elektrostatinio lauko taške yra fizikinis dydis skaitine prasme lygus darbui, kurį atlieka elektrinio lauko jėgos, perkeliant vienetinį teigiamą taškinį krūvį iš tam tikro lauko taško į be galo tolimą.:  = A  / q.
Kai kuriais atvejais elektrinio lauko potencialas yra aiškiau apibrėžtas kaip fizikinis dydis, skaitiniu požiūriu lygus išorinių jėgų darbui elektrinio lauko jėgų atžvilgiu, kai vienetinis teigiamas taškinis krūvis perkeliamas iš begalybės į tam tikrą tašką. Patogu paskutinį apibrėžimą parašyti taip:

Šiuolaikiniame moksle ir technikoje, ypač aprašant mikrokosmose vykstančius reiškinius, darbo ir energijos vienetas, vadinamas elektronų voltų(eV). Tai darbas, atliekamas perkeliant elektrono krūviui lygų krūvį tarp dviejų taškų, kurių potencialų skirtumas yra 1 V: 1 eV = 1,6010  C1 V = 1,6010  J

Ekvipotencialūs paviršiai- sąvoka, taikoma bet kuriam potencialaus vektoriaus laukui, pavyzdžiui, statiniam elektriniam laukui arba Niutono gravitaciniam laukui. Ekvipotencialus paviršius – tai paviršius, ant kurio tam tikro potencialo lauko skaliarinis potencialas įgauna pastovią reikšmę (potencialų lygmens paviršius). Kitas, lygiavertis, apibrėžimas yra paviršius, kuris bet kuriame taške yra statmenas lauko linijoms.

Laidininko paviršius elektrostatikoje yra ekvipotencialus paviršius. Be to, laidininko pastatymas ant ekvipotencialaus paviršiaus nepakeičia elektrostatinio lauko konfigūracijos. Šis faktas naudojamas vaizdo metodu, kuris leidžia apskaičiuoti elektrostatinį lauką sudėtingoms konfigūracijoms.

(Stacionariame) gravitaciniame lauke nejudančio skysčio lygis nustatomas išilgai ekvipotencialaus paviršiaus. Visų pirma, galima apytiksliai teigti, kad vandenynų lygis eina išilgai Žemės gravitacinio lauko ekvipotencialaus paviršiaus. Vandenynų paviršiaus forma, išsiplėtusi iki Žemės paviršiaus, vadinama geoidu ir atlieka svarbų vaidmenį geodezijoje. Taigi geoidas yra ekvipotencialus gravitacijos paviršius, susidedantis iš gravitacinio ir išcentrinio komponento.