Gauss sin teorem i et vakuum. Anvendelse av Gauss' teorem for å beregne elektriske felt
Som nevnt ovenfor ble det enighet om å tegne kraftlinjene med en slik tetthet at antall linjer som gjennomborer en overflateenhet vinkelrett på linjene til stedet, ville være lik vektorens modul. Så, fra mønsteret av spenningslinjer, kan man bedømme ikke bare retningen, men også størrelsen på vektoren på forskjellige punkter i rommet.
La oss vurdere feltlinjene til en stasjonær positiv punktladning. De er radielle linjer som strekker seg fra ladningen og slutter i det uendelige. La oss gjennomføre N slike linjer. Så på avstand r fra ladningen, antall kraftlinjer som skjærer en enhetsoverflate av en kule med radius r, vil være lik. Denne verdien er proporsjonal med feltstyrken til en punktladning på avstand r. Antall N du kan alltid velge slik at likheten holder
hvor . Siden kraftlinjene er kontinuerlige, skjærer det samme antall kraftlinjer en lukket overflate av hvilken som helst form som omslutter ladningen q. Avhengig av ladningens tegn, går kraftlinjene enten inn i denne lukkede overflaten eller går utenfor. Hvis antall utgående linjer anses som positivt og antall innkommende linjer som negative, kan vi utelate modultegnet og skrive:
| . | (1.4) |
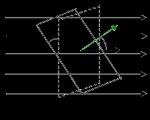
Spenningsvektorflyt. La oss plassere en elementær pute med areal. Arealet må være så lite at den elektriske feltstyrken på alle punktene kan betraktes som den samme. La oss tegne en normal til stedet (fig. 1.17). Retningen til denne normalen er valgt vilkårlig. Normalen lager en vinkel med vektoren. Strømmen av den elektriske feltstyrkevektoren gjennom en valgt overflate er produktet av overflatearealet og projeksjonen av den elektriske feltstyrkevektoren på normalen til området:
 |
hvor er projeksjonen av vektoren på normalen til stedet.
Siden antallet feltlinjer som gjennomborer et enkelt område er lik modulen til intensitetsvektoren i nærheten av det valgte området, er strømmen av intensitetsvektoren gjennom overflaten proporsjonal med antall feltlinjer som krysser denne overflaten. Derfor, i det generelle tilfellet, kan flyten av feltstyrkevektoren gjennom området tolkes visuelt som en verdi lik antall feltlinjer som penetrerer dette området:
| . | (1.5) |
Merk at valget av retningen til det normale er betinget; det kan rettes i den andre retningen. Følgelig er strømmen en algebraisk størrelse: strømmens tegnet avhenger ikke bare av feltets konfigurasjon, men også av den relative orienteringen til normalvektoren og intensitetsvektoren. Hvis disse to vektorene danner en spiss vinkel, er fluksen positiv; hvis den er stump, er fluksen negativ. Ved lukket overflate er det vanlig å ta normalen utenfor området som dekkes av denne overflaten, det vil si å velge den ytre normalen.
Hvis feltet er inhomogent og overflaten er vilkårlig, defineres strømmen som følger. Hele overflaten må deles inn i små elementer med areal , beregn spenningsfluksene gjennom hvert av disse elementene, og summer deretter fluksene gjennom alle elementene:
Dermed karakteriserer feltstyrken det elektriske feltet på et punkt i rommet. Intensitetsstrømmen avhenger ikke av verdien av feltstyrken ved et gitt punkt, men av fordelingen av feltet over overflaten av et bestemt område.
Elektriske feltlinjer kan bare begynne på positive ladninger og slutte på negative. De kan ikke begynne eller slutte i verdensrommet. Derfor, hvis det ikke er noen elektrisk ladning inne i et visst lukket volum, må det totale antallet linjer som kommer inn og ut av dette volumet være null. Hvis flere linjer forlater volumet enn det kommer inn, er det en positiv ladning inne i volumet; hvis det kommer flere linjer inn enn som kommer ut, så må det være en negativ ladning inni. Når den totale ladningen inne i volumet er lik null eller når det ikke er noen elektrisk ladning i det, trenger feltlinjene gjennom det, og den totale fluksen er null.
Disse enkle betraktningene avhenger ikke av hvordan den elektriske ladningen er fordelt innenfor volumet. Den kan være plassert i midten av volumet eller nær overflaten som begrenser volumet. Et volum kan inneholde flere positive og negative ladninger fordelt i volumet på hvilken som helst måte. Bare den totale ladningen bestemmer det totale antallet innkommende eller utgående spenningslinjer.
Som man kan se fra (1.4) og (1.5), strømmen av den elektriske feltstyrkevektoren gjennom en vilkårlig lukket overflate som omslutter ladningen q, lik . Hvis det er inne i overflaten n ladninger, da, i henhold til prinsippet om feltsuperposisjon, vil den totale fluksen være summen av fluksene av feltstyrker for alle ladninger og vil være lik , hvor vi i dette tilfellet mener den algebraiske summen av alle ladninger dekket av den lukkede flate.
Gauss sin teorem. Gauss var den første som oppdaget det enkle faktum at strømmen av den elektriske feltstyrkevektoren gjennom en vilkårlig lukket overflate må være assosiert med den totale ladningen som ligger inne i dette volumet:
 |
Gauss Karl Friedrich (1777–1855)
Stor tysk matematiker, fysiker og astronom, skaperen av det absolutte enhetssystemet i fysikk. Han utviklet teorien om elektrostatisk potensial og beviste det viktigste teoremet for elektrostatikk (Gauss' teorem). Laget en teori for å konstruere bilder i komplekse optiske systemer. Han var en av de første som kom til ideen om muligheten for eksistensen av ikke-euklidisk geometri. I tillegg ga Gauss fremragende bidrag til nesten alle grener av matematikk.
Den siste relasjonen er Gauss sin teorem for det elektriske feltet: fluksen til intensitetsvektoren gjennom en vilkårlig lukket flate er proporsjonal med den algebraiske summen av ladningene som befinner seg inne i denne flaten Proporsjonalitetskoeffisienten avhenger av valget av enhetssystemet.
Det skal bemerkes at Gauss' teorem er oppnådd som en konsekvens av Coulombs lov og superposisjonsprinsippet. Hvis den elektriske feltstyrken ikke endret seg i omvendt proporsjon med kvadratet på avstanden, ville teoremet være ugyldig. Derfor er Gauss' teorem anvendelig for alle felt der den omvendte kvadratloven og superposisjonsprinsippet er strengt oppfylt, for eksempel for gravitasjonsfeltet. Når det gjelder et gravitasjonsfelt, spilles rollen til ladninger som skaper feltet av massene av kropper. Strømmen av gravitasjonsfeltlinjer gjennom en lukket overflate er proporsjonal med den totale massen inne i den overflaten.
Feltstyrken til et ladet fly. La oss bruke Gauss' teorem for å bestemme den elektriske feltstyrken til et uendelig ladet plan. Hvis planet er uendelig og jevnt ladet, det vil si at overflateladningstettheten er den samme hvor som helst, så er de elektriske feltstyrkelinjene på et hvilket som helst punkt vinkelrett på dette planet. For å vise dette skal vi bruke superposisjonsprinsippet for spenningsvektoren. La oss velge to elementære seksjoner på planet, som kan betraktes som punkt for punktet EN, der det er nødvendig å bestemme feltstyrken. Som det fremgår av fig. 1.18, vil den resulterende spenningsvektoren bli rettet vinkelrett på planet. Siden planet kan deles inn i et uendelig antall par av slike seksjoner for ethvert observasjonspunkt, er det åpenbart at feltlinjene til det ladede planet er vinkelrett på planet, og feltet er ensartet (fig. 1.19). Hvis dette ikke var tilfelle, ville feltet ved hvert punkt i rommet endret seg når flyet beveget seg langs seg selv, men dette motsier symmetrien til det ladede systemet (planet er uendelig). Når det gjelder et positivt ladet plan, begynner kraftlinjene i planet og slutter ved uendelig, mens for et negativt ladet plan begynner kraftlinjene ved uendelig og går inn i planet.
 |  |
| Ris. 1.18 | Ris. 1.19 |
For å bestemme den elektriske feltstyrken til et uendelig positivt ladet plan, velger vi mentalt en sylinder i rommet, hvis akse er vinkelrett på det ladede planet, og basene er parallelle med det, og en av basene går gjennom feltpunktet av interesse for oss (fig. 1.19). Sylinderen kutter ut et område fra det ladede planet, og sylinderens base, plassert på forskjellige sider av flyet, har samme område.
I følge Gauss teorem er strømmen av den elektriske feltstyrkevektoren gjennom overflaten av sylinderen relatert til den elektriske ladningen inne i sylinderen ved uttrykket:
![]() .
.
Siden spenningslinjene bare skjærer bunnen av sylinderen, er strømmen gjennom sideflaten til sylinderen null. Derfor vil fluksen av spenningsvektoren gjennom den sylindriske overflaten bare bestå av fluksene gjennom sylinderens base, derfor,
Ved å sammenligne de to siste uttrykkene for intensitetsvektorfluksen får vi
Elektrisk feltstyrke mellom motsatt ladede plater. Hvis dimensjonene til platene betydelig overstiger avstanden mellom dem, kan det elektriske feltet til hver av platene betraktes som nær feltet til et uendelig jevnt ladet plan. Siden de elektriske feltstyrkelinjene til motsatt ladede plater mellom platene er rettet i én retning (fig. 1.20), er feltstyrken mellom platene lik.
![]() .
.
I det ytre rom har de elektriske feltstyrkelinjene til motsatt ladede plater motsatte retninger, derfor, utenfor disse platene, er den resulterende elektriske feltstyrken null. Uttrykket som oppnås for intensiteten er gyldig for store ladede plater, når intensiteten bestemmes på et punkt som ligger langt fra kantene deres.

Elektrisk feltstyrke til en jevnt ladet tynn ledning med uendelig lengde. La oss finne avhengigheten av den elektriske feltstyrken til en jevnt ladet tynn ledning med uendelig lengde på avstanden til ledningsaksen ved å bruke Gauss' teorem. La oss velge en seksjon av tråd med begrenset lengde. Hvis den lineære ladningstettheten på ledningen er , er ladningen til det valgte området lik .
La oss vurdere feltet til en punktladning $q$ og finne flyten til intensitetsvektoren ($\overrightarrow(E)$) gjennom den lukkede overflaten $S$. Vi vil anta at ladningen er plassert inne i overflaten. Strømmen til spenningsvektoren gjennom en hvilken som helst overflate er lik antall linjer i spenningsvektoren som går ut (start ved ladningen, hvis $q>0$) eller antall linjer $\overrightarrow(E)$ som går inn , hvis $q \[Ф_E=\frac( q)((\varepsilon )_0)\ \venstre(1\høyre),\]
der fluksens tegn sammenfaller med ladningens tegn.
Ostrogradsky-Gauss teorem i integralform
La oss anta at inne i overflaten S er det N punktladninger, verdier $q_1,q_2,\dots q_N.$ Fra superposisjonsprinsippet vet vi at den resulterende feltstyrken til alle N ladninger kan finnes som summen av feltstyrkene som skapes av hver av ladningene, så er det:
Derfor, for flyten av et system av punktladninger kan vi skrive:
Ved å bruke formel (1) får vi at:
\[Ф_E=\oint\limits_S(\overrightarrow(E)d\overrightarrow(S))=\frac(1)((\varepsilon )_0)\sum\limits^N_(i=1)(q_i\ )\ venstre(4\høyre).\]
Ligning (4) betyr at strømmen av den elektriske feltstyrkevektoren gjennom en lukket overflate er lik den algebraiske summen av ladningene som er inne i denne overflaten, delt på den elektriske konstanten. Dette er Ostrogradsky-Gauss-teoremet i integralform. Denne teoremet er en konsekvens av Coulombs lov. Betydningen av denne teoremet er at den lar en ganske enkelt beregne elektriske felt for ulike ladningsfordelinger.
Som en konsekvens av Ostrogradsky-Gauss-teoremet må det sies at fluksen til intensitetsvektoren ($Ф_E$) gjennom en lukket overflate i tilfelle ladningene er utenfor denne overflaten er lik null.
I tilfellet hvor diskretiteten til ladninger kan ignoreres, brukes konseptet volumetrisk ladningstetthet ($\rho $) hvis ladningen er fordelt over hele volumet. Det er definert som:
\[\rho =\frac(dq)(dV)\venstre(5\høyre),\]
der $dq$ er en belastning som kan betraktes som punktlignende, er $dV$ et lite volum. (Angående $dV$ må følgende bemerkning gjøres. Dette volumet er lite nok til at ladningstettheten i det kan anses som konstant, men stort nok til at ladningsdiskret ikke begynner å vises). Den totale ladningen som er i hulrommet kan finnes som:
\[\sum\limits^N_(i=1)(q_i\ )=\int\limits_V(\rho dV)\venstre(6\høyre).\]
I dette tilfellet omskriver vi formel (4) i formen:
\[\oint\limits_S(\overrightarrow(E)d\overrightarrow(S))=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV)\left(7\right).\ ]
Ostrogradsky-Gauss teorem i differensialform
Ved å bruke Ostrogradsky-Gauss-formelen for ethvert felt av vektornatur, ved hjelp av hvilken overgangen fra integrasjon over en lukket overflate til integrasjon over et volum utføres:
\[\oint\limits_S(\overrightarrow(a)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(a)dV\ \left(8\right),\]
hvor $\overrightarrow(a)-$feltvektor (i vårt tilfelle er det $\overrightarrow(E)$), $div\overrightarrow(a)=\overrightarrow(\nabla )\overrightarrow(a)=\frac(\ partial a_x)(\partial x)+\frac(\partial a_y)(\partial y)+\frac(\partial a_z)(\partial z)$ -- divergens av vektoren $\overrightarrow(a)$ ved punkt med koordinater ( x,y,z), som tilordner et vektorfelt til et skalarfelt. $\overrightarrow(\nabla )=\frac(\partial )(\partial x)\overrightarrow(i)+\frac(\partial )(\partial y)\overrightarrow(j)+\frac(\partial )(\ partial z)\overrightarrow(k)$ - observerbar operator. (I vårt tilfelle vil det være $div\overrightarrow(E)=\overrightarrow(\nabla )\overrightarrow(E)=\frac(\partial E_x)(\partial x)+\frac(\partial E_y)(\partial y) +\frac(\partial E_z)(\partial z)$) -- divergens av spenningsvektoren. Etter det ovenfor, omskriver vi formel (6) som:
\[\oint\limits_S(\overrightarrow(E)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(E)dV=\frac(1)((\varepsilon )_0)\int\limits_V( \rho dV)\venstre(9\høyre).\]
Likhetene i ligning (9) er oppfylt for et hvilket som helst volum, og dette er bare mulig hvis funksjonene som er i integrandene er like i hver strøm av rom, det vil si at vi kan skrive at:
Uttrykk (10) er Ostrogradsky-Gauss-teoremet i differensialform. Dens tolkning er som følger: ladninger er kilder til et elektrisk felt. Hvis $div\overrightarrow(E)>0$, så har vi på disse punktene i feltet (kostnadene er positive) feltkilder, hvis $div\overrightarrow(E)
Oppgave: Ladningen er jevnt fordelt over volumet, en kubisk flate med side b velges i dette volumet. Det er innskrevet i sfæren. Finn forholdet mellom spenningsvektorfluksene gjennom disse flatene.
I følge Gauss' teorem er fluksen ($Ф_E$) til intensitetsvektoren $\overrightarrow(E)$ gjennom en lukket overflate med en jevn ladningsfordeling over volumet lik:
\[Ф_E=\frac(1)((\varepsilon )_0)Q=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV=\frac(\rho )((\varepsilon ) _0)\int\limits_V(dV)=\frac(\rho V)((\varepsilon )_0))\venstre(1.1\høyre).\]
Derfor må vi bestemme volumene til kuben og ballen hvis ballen er beskrevet rundt denne kuben. Til å begynne med, volumet til en kube ($V_k$) hvis siden b er lik:
La oss finne volumet til ballen ($V_(sh)$) ved å bruke formelen:
der $D$ er diameteren til ballen og (siden ballen er omskrevet rundt kuben), hoveddiagonalen til kuben. Derfor må vi uttrykke diagonalen til en terning i form av siden. Dette er enkelt å gjøre hvis du bruker Pythagoras teorem. For å beregne diagonalen til en terning, for eksempel (1,5), må vi først finne diagonalen til kvadratet (den nedre bunnen av kuben) (1,6). Lengden på diagonalen (1,6) er lik:
I dette tilfellet er lengden på diagonalen (1,5) lik:
\[(D=D)_(15)=\sqrt(b^2+((\sqrt(b^2+b^2\ \ \ )))^2)=b\sqrt(3)\ \venstre (1,5\høyre).\]
Ved å erstatte den funnet diameteren til ballen med (1.3), får vi:
Nå kan vi finne fluksene til spenningsvektoren gjennom overflaten av kuben, den er lik:
\[Ф_(Ek)=\frac(\rho V_k)((\varepsilon )_0)=\frac(\rho b^3)((\varepsilon )_0)\left(1.7\right),\]
gjennom ballens overflate:
\[Ф_(Esh)=\frac(\rho V_(sh))((\varepsilon )_0)=\frac(\rho )((\varepsilon )_0)\frac(\sqrt(3))(2) \pi b^3\ \venstre(1,8\høyre).\]
La oss finne forholdet $\frac(Ф_(Esh))(Ф_(Ek))$:
\[\frac(Ф_(Esh))(Ф_(Ek))=\frac(\frac(с)(\varepsilon_0)\frac(\sqrt(3))(2) \pi b^3)(\frac (сb^3)(\varepsilon_0))=\frac(\pi)(2)\sqrt(3)\ \ca. 2.7\venstre(1.9\høyre).\]
Svar: Fluksen gjennom ballens overflate er 2,7 ganger større.
Oppgave: Bevis at ladningen til en leder er plassert på overflaten.
Vi bruker Gauss sin teorem for å bevise det. La oss velge en lukket overflate av vilkårlig form i lederen nær overflaten av lederen (fig. 2).

La oss anta at det er ladninger inne i lederen, vi skriver Ostrogradsky-Gauss-teoremet for feltdivergens for ethvert punkt på overflaten S:
hvor $\rho er tettheten\ $av den indre ladningen. Imidlertid er det ikke noe felt inne i lederen, det vil si $\overrightarrow(E)=0$, derfor $div\overrightarrow(E)=0\to \rho =0$. Ostrogradsky-Gauss-teoremet i differensialform er lokalt, det vil si at det er skrevet for et feltpunkt, vi valgte ikke punktet på en spesiell måte, derfor er ladningstettheten null på et hvilket som helst punkt i feltet inne i lederen.
Prinsippet om superposisjon i kombinasjon med Coulombs lov gir nøkkelen til å beregne det elektriske feltet til et vilkårlig ladningssystem, men direkte summering av feltene ved hjelp av formel (4.2) krever vanligvis komplekse beregninger. Imidlertid, i nærvær av en eller annen symmetri av ladningssystemet, blir beregningene betydelig forenklet hvis vi introduserer begrepet elektrisk feltstrøm og bruker Gauss teorem.
Konseptet med elektrisk feltstrøm ble introdusert i elektrodynamikk fra hydrodynamikk. I hydrodynamikk er strømmen av væske gjennom et rør, det vil si volumet av væske N som passerer gjennom et tverrsnitt av et rør per tidsenhet, lik v ⋅ S, der v er hastigheten til væsken og S er rørets tverrsnittsareal. Hvis væskehastigheten varierer over tverrsnittet, må du bruke integralformelen N = ∫ S v → ⋅ d S → . La oss faktisk fremheve et lite område d S i hastighetsfeltet, vinkelrett på hastighetsvektoren (fig. ).
|
Volumet av væske som strømmer gjennom dette området i tid d t er lik v d S d t . Hvis plattformen er tilbøyelig til strømmen, vil det tilsvarende volumet være v d S cos θ d t , hvor θ er vinkelen mellom hastighetsvektoren v → og normalen n → til plattformen d S . Volumet av væske som strømmer gjennom området d S per tidsenhet oppnås ved å dele denne verdien med d t. Den er lik v d S cos θ d t , dvs. skalarprodukt v → ⋅ d S → hastighetsvektor v → ved arealelementvektoren d S → = n → d S . Enhetsvektoren n → normal til området d S kan tegnes i to direkte motsatte retninger. en av dem er betinget akseptert som positiv. Normalen n → er tegnet i denne retningen. Siden av stedet der normalen n → kommer ut kalles ekstern, og siden som normalen n → kommer inn i kalles intern. Arealelementvektoren d S → er rettet langs den ytre normalen n → til overflaten, og er i størrelse lik arealet til elementet d S = ∣ d S → ∣ . Når man beregner volumet av væske som strømmer gjennom et område S med endelige dimensjoner, må det utvikles til uendelig små arealer d S , og deretter beregne integralet ∫ S v → ⋅ d S → over hele overflaten S .
Uttrykk som ∫ S v → ⋅ d S → finnes i mange grener av fysikk og matematikk. De kalles flyten av vektoren v → gjennom overflaten S, uavhengig av vektorens v → natur. I elektrodynamikk er integralet
| N = ∫ S E → ⋅ d S → | (5.1) |
La oss anta at vektoren E → er representert av en geometrisk sum
E → = ∑ j E → j .
Ved å multiplisere denne likheten skalært med d S → og integrere, får vi
N = ∑ j N j .
hvor N j er strømmen av vektoren E → j gjennom samme overflate. Av prinsippet om superposisjon av elektrisk feltstyrke følger det at fluksene gjennom den samme overflaten summerer seg algebraisk.
Gauss' teorem sier at fluksen til vektoren E → gjennom en vilkårlig lukket overflate er lik den totale ladningen Q til alle partikler som befinner seg inne på denne overflaten multiplisert med 4 π:
Vi skal gjennomføre beviset for teoremet i tre trinn.
1. La oss starte med å beregne den elektriske feltfluksen til én punktladning q (fig. ). I det enkleste tilfellet, når integrasjonsflaten S er en kule og ladningen er i sentrum, er gyldigheten av Gauss sin teorem nesten åpenbar. På overflaten av sfæren er den elektriske feltstyrken
E → = q r → ∕ r 3
konstant i størrelse og overalt rettet normalt mot overflaten, slik at den elektriske feltfluksen ganske enkelt er lik produktet E = q ∕ r 2 og arealet av kulen S = 4 π r 2 . Derfor er N = 4 π q. Dette resultatet er uavhengig av formen på overflaten som omgir ladningen. For å bevise dette velger vi et vilkårlig område av overflaten med en tilstrekkelig liten størrelse med retningen til den ytre normalen n → satt på den. I fig. ett slikt segment er vist i en overdrevet stor (for klarhetens skyld) størrelse.
Fluksen til vektoren E → gjennom dette området er lik d N = E → ⋅ d S → = E cos θ d S ,
hvor θ er vinkelen mellom retningen E → og den ytre normalen n → til området d S . Siden E = q ∕ r 2 , og d S cos θ ∕ r 2 i absolutt verdi er elementet i romvinkelen d Ω = d S ∣ cos θ ∣ ∕ r 2 , hvorunder området d S er synlig fra punktet hvor ladningen er plassert,
D N = ± q d Ω .
hvor pluss- og minustegnet tilsvarer cos θ-tegnet, nemlig: du skal ta plusstegnet hvis vektoren E → lager en spiss vinkel med retningen til den ytre normalen n →, og minustegnet ellers.
2. Betrakt nå en begrenset overflate S som dekker et valgt volum V. Med hensyn til dette volumet er det alltid mulig å bestemme hvilken av de to motsatte retningene av normalen til ethvert element av overflaten S som skal betraktes som ekstern. Den ytre normalen er rettet fra volum V utover. Oppsummering over segmenter, frem til fortegn har vi N = q Ω, hvor Ω er den helromsvinkelen der overflaten S er synlig fra punktet hvor ladningen q befinner seg. Hvis overflaten S er lukket, er Ω = 4 π, forutsatt at ladningen q er inne i S. Ellers Ω = 0. For å klargjøre den siste uttalelsen kan vi igjen referere til fig. .
Det er åpenbart at strømmene gjennom segmenter av en lukket overflate, basert på like solide vinkler, men vendt i motsatte retninger, opphever hverandre. Det er også åpenbart at hvis ladningen er utenfor den lukkede overflaten, så for ethvert segment som vender utover er det et tilsvarende segment som vender innover.
3. Til slutt, ved å bruke superposisjonsprinsippet, kommer vi frem til den endelige formuleringen av Gauss sin teorem (). Faktisk er feltet til et ladningssystem lik summen av feltene til hver ladning separat, men bare ladninger som befinner seg inne i den lukkede overflaten gir et bidrag som ikke er null til høyre side av teoremet (). Dette fullfører beviset.
I makroskopiske legemer er antallet ladningsbærere så stort at det er praktisk å representere et diskret ensemble av partikler i form av en kontinuerlig fordeling, og introduserer konseptet ladningstetthet. Per definisjon er ladningstettheten ρ forholdet Δ Q ∕ Δ V i grensen når volumet Δ V tenderer til en fysisk uendelig verdi:
hvor integrasjonen på høyre side utføres over volumet V lukket av overflaten S.Gauss sin teorem gir én skalarligning for tre komponenter av vektoren E →, så denne teoremet alene er ikke nok til å beregne det elektriske feltet. En kjent symmetri av ladningstetthetsfordelingen er nødvendig slik at problemet kan reduseres til en enkelt skalarligning. Gauss sin teorem gjør det mulig å finne feltet i tilfeller der integrasjonsflaten i () kan velges slik at den elektriske feltstyrken E er konstant over hele overflaten. La oss se på de mest lærerike eksemplene.
▸ Oppgave 5.1
Finn feltet til en kule jevnt ladet i volum eller overflater.
Løsning: Elektrisk felt for en punktladning E → = q r → ∕ r 3 har en tendens til uendelig kl r → 0. Dette faktum viser inkonsekvensen i ideen elementærpartikler ved punktladninger. Hvis kostnaden q jevnt fordelt over volumet til en kule med begrenset radius a, da det elektriske feltet har ingen singulariteter.
Fra symmetrien til problemet er det klart at det elektriske feltet E → overalt er rettet radialt, og dens spenning E = E(r) avhenger kun av avstanden r til midten av ballen. Deretter strømmer det elektriske feltet gjennom en kule med radius r er ganske enkelt lik 4 π r 2 E (Fig. ).
På den annen side er ladningen inne i samme kule lik den totale ladningen ball Q hvis r ≥ a. Ved å likestille 4 π r 2 E med ladningen q til ballen multiplisert med 4 π, får vi: E (r) = q ∕ r 2 .Således, i det ytre rom, skaper en ladet ball et slikt felt som om all ladningen var konsentrert i midten. Dette resultatet er gyldig for enhver sfærisk symmetrisk ladningsfordeling.
Feltet inne i ballen er E (r) = Q ∕ r 2, der Q er ladningen inne i svovelet med radius r. Hvis ladningen er jevnt fordelt over hele volumet av ballen, da Q = q (r ∕ a) 3 . I dette tilfellet
E (r) = q r ∕ a 3 = (4 π ∕ 3) ρ r ,
hvor ρ = q ∕ (4 π a 3 ∕ 3) — ladningstetthet. Inne i ballen minker feltet lineært fra sitt maksimum verdier på overflaten av ballen til null i midten (fig. ).
Funksjon E(r) samtidig er den endelig og kontinuerlig overalt.Hvis ladningen er fordelt over overflaten av ballen, da Q = 0, og derfor også E = 0. Dette resultatet er også gyldig for tilfellet inne i en sfærisk det er ikke noe ladningshulrom, og ytre ladninger er fordelt sfærisk symmetrisk. ▸ Oppgave 5.2
Finn feltet til en jevnt ladet uendelig tråd; trådradius a, ladning per lengdeenhet ϰ.
▸ Oppgave 5.3
Finn feltet til en uendelig rett tråd og en uendelig lang jevnt ladet sylinder.
▸ Oppgave 5.4
Finn feltet til et uendelig ladet plan og jevnt ladet uendelig flatt lag.
Løsning: På grunn av problemets symmetri er feltet rettet normal til laget og avhenger kun av avstanden x fra symmetriplanet til platen. For å beregne et felt ved hjelp av Gauss teorem, er det praktisk å velge overflaten av integrasjon S inn i form av et parallellepipedum, som vist i fig. .
Det siste resultatet oppnås ved å passere til grensen a → 0 samtidig som ladningstettheten økesρ slik at verdien σ = ρ a forble uendret. På motsatte sider av flyet den elektriske feltstyrken er den samme i størrelsesorden, men motsatt i retning. Derfor, når du passerer gjennom ladet fly, endres feltet brått med mengden 4 π σ . Merk at platen kan betraktes som uendelig hvis avstanden fra er ubetydelig sammenlignet med størrelsen. På avstander veldig store sammenlignet med dimensjonene til platen, det fungerer som en punktladning, og feltet minker tilbake proporsjonal med kvadratet på avstanden.Det elektrostatiske feltet kan tydelig avbildes ved hjelp av kraftlinjer (strekklinjer). Strømledninger kalles kurver hvis tangenter i hvert punkt faller sammen med spenningsvektoren E.
Kraftlinjer er et konvensjonelt konsept og eksisterer egentlig ikke. Feltlinjene til en enkelt negativ og enkel positiv ladning er vist i fig. 5 er radielle rette linjer som kommer fra en positiv ladning eller går til en negativ ladning.
Hvis tettheten og retningen til feltlinjene gjennom hele feltets volum forblir uendret, anses et slikt elektrostatisk felt som homogent (antall linjer må være numerisk lik feltstyrken E).
Antall feltlinjer merket ">dS, vinkelrett på dem, avgjør flyt av den elektrostatiske feltstyrkevektoren:
formula" src="http://hi-edu.ru/e-books/xbook785/files/17-1.gif" border="0" align="absmiddle" alt="- projeksjon av vektoren E på retningen av normalen n til stedet dS (fig. 6).
Følgelig vil strømmen av vektor E gjennom en vilkårlig lukket overflate S
mark">S ikke bare størrelsen, men også tegnet på strømmen kan endres:
1) med formel" src="http://hi-edu.ru/e-books/xbook785/files/17-4.gif" border="0" align="absmiddle" alt="
3) når du velger"> La oss finne strømmen av vektor E gjennom en sfærisk overflate S, i midten av hvilken det er en punktladning q.
I dette tilfellet faller merket ">E og n sammen på alle punkter på den sfæriske overflaten.
Tatt i betraktning feltstyrken til en punktladning, formelen" src="http://hi-edu.ru/e-books/xbook785/files/18-2.gif" border="0" align="absmiddle " alt="(! LANG:vi får
formula" src="http://hi-edu.ru/e-books/xbook785/files/Fe.gif" border="0" align="absmiddle" alt="- en algebraisk mengde avhengig av ladningens tegn. For eksempel, når q<0 линии Е направлены к заряду и противоположны направлению внешней нормали n ..gif" border="0" align="absmiddle" alt="rundt ladningen har q en vilkårlig form. Selvfølgelig er overflaten merket ">E, som er overflaten S. Derfor er flyten av vektor E gjennom en vilkårlig overflate formelen" src="http://hi-edu.ru/e-books/xbook785/ files/Fe.gif" border ="0" align="absmiddle" alt=".
Hvis ladningen er plassert utenfor den lukkede overflaten, vil åpenbart hvor mange linjer som kommer inn i det lukkede området, forlate det samme antallet. Som et resultat vil fluksen til vektor E være lik null.
Hvis det elektriske feltet skapes av et system av punktladninger formula" src="http://hi-edu.ru/e-books/xbook785/files/18-4.gif" border="0" align="absmiddle" alt="
Denne formelen er det matematiske uttrykket for Gauss sin teorem: strømmen av den elektriske feltstyrkevektoren E i et vakuum gjennom en vilkårlig lukket overflate er lik den algebraiske summen av ladningene den dekker, delt på formula" src="http://hi-edu.ru/e-books/xbook785/files/18-6.gif" border="0" align="absmiddle" alt="
For å fullføre beskrivelsen, la oss også presentere Gauss' teorem i en lokal form, ikke basert på integrerte relasjoner, men på feltparametrene på et gitt punkt i rommet. For å gjøre dette er det praktisk å bruke differensialoperatoren - vektordivergens, -
formula" src="http://hi-edu.ru/e-books/xbook785/files/nabla.gif" border="0" align="absmiddle" alt="("nabla") -
formula" src="http://hi-edu.ru/e-books/xbook785/files/19-1.gif" border="0" align="absmiddle" alt="
I matematisk analyse er Gauss-Ostrogradsky-teoremet kjent: strømmen av en vektor gjennom en lukket overflate er lik integralet av dens divergens over volumet begrenset av denne overflaten -
formula" src="http://hi-edu.ru/e-books/xbook785/files/ro.gif" border="0" align="absmiddle" alt=":
formula" src="http://hi-edu.ru/e-books/xbook785/files/19-4.gif" border="0" align="absmiddle" alt="
Dette uttrykket er Gauss sin teorem i lokal (differensial) form.
Gauss sin teorem (2.2) lar oss bestemme styrken til ulike elektrostatiske felt. La oss se på flere eksempler på anvendelsen av Gauss sin teorem.
1. La oss beregne E elektrostatisk felt skapt av en jevnt ladet sfærisk overflate.
La oss anta at en sfærisk overflate med radius R bærer en jevnt fordelt ladning q, dvs. overflateladningstetthet er det samme merket overalt ">r >R fra sfærens sentrum, konstruerer vi mentalt en ny sfærisk overflate S, symmetrisk til den ladede sfæren. I samsvar med Gauss teorem
formula" src="http://hi-edu.ru/e-books/xbook785/files/20-1.gif" border="0" align="absmiddle" alt="
For punkter som ligger på overflaten av en ladet sfære med radius R, kan vi analogt skrive:
select">inne i en ladet sfære, inneholder ikke elektriske ladninger i seg selv, så fluksmerket">E = 0.
Oppgaven med å beregne feltstyrken til et system av elektriske ladninger ved å bruke prinsippet om superposisjon av elektrostatiske felt kan forenkles sterkt hvis vi bruker teoremet oppdaget av den tyske forskeren K. Gauss (1777-1855), som bestemmer strømmen av elektrisk feltstyrkevektor gjennom en vilkårlig lukket overflate.
Fra definisjonen av intensitetsvektorfluksen gjennom en lukket flate, er intensitetsvektorfluksen gjennom en sfærisk overflate med radius r, som dekker en punktladning Q plassert i midten (fig. 1), lik med
Dette resultatet er gyldig for en lukket overflate med vilkårlig form. Faktisk, hvis du omslutter en kule (fig. 1) i en vilkårlig lukket overflate, vil hver spenningslinje som trenger gjennom kulen også passere gjennom denne overflaten.
Hvis en lukket overflate av en hvilken som helst form omslutter en ladning (fig. 2), så når en strekklinje krysser overflaten, går den enten inn eller ut av den. Ved beregning av fluks reduseres til slutt et odde antall skjæringer til et enkelt skjæringspunkt, siden fluksen antas å være positiv hvis spenningslinjer forlater overflaten, og negativ for linjer som kommer inn i overflaten. Hvis en lukket flate ikke omslutter en ladning , da er fluksen gjennom den null, så hvordan antallet spenningslinjer som kommer inn i overflaten er lik antallet spenningslinjer som går ut av den.
Dette betyr at for en overflate med vilkårlig form, hvis den er lukket og inneholder en punktladning Q, flyten av vektoren E vil være lik Q/ε 0, dvs.
Tegnet på fluksen sammenfaller med tegnet på ladningen Q.
La oss studere det generelle tilfellet av en vilkårlig overflate som omgir n ladninger. Ved å bruke prinsippet om superposisjon, spenning E felt, som skapes av alle ladninger, er lik summen av intensitetene E i felt som opprettes av hver belastning separat. Derfor
I følge (1) er hvert av integralene som vises under sumtegnet lik Q i /ε 0 . Midler,
![]() (2)
(2)
Formel (2) uttrykker Gauss sin teorem for det elektrostatiske feltet i vakuum: strømmen av den elektrostatiske feltstyrkevektoren i et vakuum gjennom en vilkårlig lukket overflate er lik den algebraiske summen av ladningene inne i denne overflaten, delt på ε 0. Denne teoremet ble oppnådd matematisk for et vektorfelt av vilkårlig natur av den russiske matematikeren M.V. Ostrogradsky (1801-1862), og deretter uavhengig av ham i forhold til det elektrostatiske feltet - av K. Gauss.
I det generelle tilfellet kan elektriske ladninger fordeles med en viss volumtetthet ρ=dQ/dV, som er forskjellig på forskjellige steder i rommet. Deretter den totale ladningen inne i den lukkede overflaten S, som dekker et visst volum V,
![]() (3)
(3)
Ved å bruke formel (3), kan Gauss teorem (2) skrives som følger:
Sirkulasjon av spenningsvektoren er arbeidet som utføres av elektriske krefter når en enkelt positiv ladning beveges langs en lukket bane L
| | (13.18) |
Siden arbeidet til de elektrostatiske feltkreftene langs en lukket sløyfe er null (arbeidet til de potensielle feltkreftene), er derfor sirkulasjonen av den elektrostatiske feltstyrken langs en lukket sløyfe null.
Elektrostatisk feltpotensial. Feltet til en konservativ kraft kan beskrives ikke bare av en vektorfunksjon, men en ekvivalent beskrivelse av dette feltet kan oppnås ved å definere en passende skalar mengde ved hvert av punktene. For et elektrostatisk felt er denne mengden elektrostatisk feltpotensial, definert som forholdet mellom den potensielle energien til testladningen q til størrelsen på denne ladningen, = W P / q, hvorfra det følger at potensialet er numerisk lik den potensielle energien som en enhets positiv ladning besitter ved et gitt punkt i feltet. Måleenheten for potensial er Volt (1 V).
Punktladningsfeltpotensial Q i et homogent isotropisk medium med dielektrisk konstant :
Superposisjonsprinsipp. Potensialet er en skalarfunksjon; superposisjonsprinsippet er gyldig for det. Så for feltpotensialet til et system av punktladninger Q 1, Q 2, Q n vi har
![]() ,
,
Hvor r jeg- avstand fra feltpunktet med potensial til ladningen Q i. Hvis ladningen er vilkårlig fordelt i rommet, da
![]() ,
,
Hvor r- avstand fra elementærvolumet d x,d y,d zå peke ( x, y, z), hvor potensialet bestemmes; V- volumet av rommet der ladningen er fordelt.
Potensial og arbeid av elektriske feltkrefter. Basert på definisjonen av potensial kan det vises at arbeidet som utføres av det elektriske feltet, styrker når en punktladning flyttes q fra ett punkt i feltet til et annet er lik produktet av størrelsen på denne ladningen og potensialforskjellen ved de innledende og siste punktene på banen, A = q (
Hvis vi analogt med potensiell energi antar at potensialet er null på punkter som er uendelig langt fra elektriske ladninger - feltkilder, så er arbeidet til elektriske feltkrefter når en ladning flyttes q fra punkt 1 til uendelig kan representeres som EN q 1 .
Dermed er potensialet ved et gitt punkt i det elektrostatiske feltet fysisk mengde numerisk lik arbeidet utført av kreftene til det elektriske feltet når en enhets positiv punktladning flyttes fra et gitt punkt i feltet til et uendelig fjernt: = EN / q.
I noen tilfeller er det elektriske feltpotensialet tydeligere definert som en fysisk størrelse numerisk lik arbeidet til eksterne krefter mot kreftene til det elektriske feltet når en enhets positiv punktladning flyttes fra uendelig til et gitt punkt. Det er praktisk å skrive den siste definisjonen som følger:
I moderne vitenskap og teknologi, spesielt når man beskriver fenomener som oppstår i mikrokosmos, kalles en enhet av arbeid og energi elektron-volt(eV). Dette er arbeidet som gjøres når man flytter en ladning lik ladningen til et elektron mellom to punkter med en potensialforskjell på 1 V: 1 eV = 1,6010 C1 V = 1,6010 J
Ekvipotensialflater- et konsept som gjelder for ethvert potensielt vektorfelt, for eksempel et statisk elektrisk felt eller et Newtonsk gravitasjonsfelt. En ekvipotensialflate er en overflate der skalarpotensialet til et gitt potensielt felt får en konstant verdi (potensialnivåflate). En annen ekvivalent definisjon er en overflate som er ortogonal til feltlinjene på et hvilket som helst punkt.
Overflaten til en leder i elektrostatikk er en ekvipotensialflate. I tillegg endrer ikke det å plassere en leder på en ekvipotensialoverflate konfigurasjonen av det elektrostatiske feltet. Dette faktum brukes i bildemetoden, som tillater beregning av det elektrostatiske feltet for komplekse konfigurasjoner.
I et (stasjonært) gravitasjonsfelt etableres nivået av en stasjonær væske langs ekvipotensialoverflaten. Spesielt kan det tilnærmet fastslås at nivået på havene passerer langs ekvipotensialoverflaten til jordens gravitasjonsfelt. Formen på overflaten av havene, utvidet til jordens overflate, kalles geoiden og spiller en viktig rolle i geodesi. Geoiden er altså en ekvipotensialoverflate av tyngdekraften, bestående av en gravitasjons- og en sentrifugalkomponent.