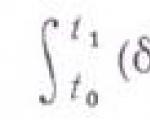O princípio da menor ação. Princípio variacional de Hamilton-Ostrogradsky em configuração e espaços de fase Fórmula de onda plana
PRINCÍPIO DE HAMILTON-OSTROGRADO
Princípio de ação estacionária, - integral geral princípio variacional da mecânica clássica, estabelecida por W.
Hamilton para sistemas holonômicos restringidos por restrições estacionárias ideais e generalizado por M. V. Ostrogradskii para restrições não estacionárias. De acordo com G.-O.
tem um valor estacionário em comparação com movimentos cinematicamente possíveis, para os quais as posições inicial e final do sistema e o tempo de movimento são iguais aos do movimento real. Aqui T - cinético, VOCÊ- energia potencial, LTU a função de Lagrange do sistema. Em alguns casos, verdadeiro corresponde não apenas a um ponto estacionário do funcional S, mas também fornece o menor valor. Portanto, G.-O. N. chamado frequentemente. o princípio da menor ação. No caso de forças ativas não potenciais F v condição de estacionariedade para a ação d S= 0 é substituído pela condição
Aceso.: Hamilton W., Relatório da Quarta Reunião da Associação Britânica para o Avanço da Ciência, L., 1835, p. 513-18; Ostrogradsku M., "Mem. de 1" Acad. des Sci. de St-Petershourg", 1850, vol. 8, no. 3, p. 33-48.
V. V. Rumyantsev.
Enciclopédia matemática. - M.: Enciclopédia Soviética. I. M. Vinogradov. 1977-1985.
Veja o que é o "PRINCÍPIO HAMILTON - OSTROGRAD" em outros dicionários:
O princípio de Fisher é um modelo evolutivo que explica por que a proporção sexual das espécies de organismos vivos, aproximadamente 1:1, é predominante na natureza; em que genes para a produção de mais indivíduos de ambos os sexos ... ... Wikipedia
Hamilton (também apenas o princípio de Hamilton), mais precisamente, o princípio da estacionariedade da ação é um método para obter as equações de movimento de um sistema físico por meio da busca por um estacionário (muitas vezes extremo, geralmente em conexão com a tradição estabelecida...). .. Wikipédia
Refração das ondas de acordo com Huygens ... Wikipedia
Na metodologia da ciência, a afirmação de que qualquer nova teoria científica, na presença de uma teoria antiga e bem testada, não está em completa contradição com ela, mas dá as mesmas consequências em alguma aproximação limitante (caso especial). Por exemplo, a lei ... ... Wikipedia
Princípio do máximo discreto de Pontryagin para processos de controle discreto no tempo. Para tal processo, o M. p. pode não ser satisfeito, embora para o seu análogo contínuo, que é obtido substituindo o operador de diferenças finitas por um diferencial... ... Enciclopédia Matemática
Ou o início de Hamilton, na mecânica e na física matemática, serve para obter equações diferenciais de movimento. Este princípio estende-se a todos os sistemas materiais, quaisquer que sejam as forças a que estejam sujeitos; primeiro vamos expressar isso nisso ... Dicionário Enciclopédico F.A. Brockhaus e I.A. Efron
Postular quântico. mecânica, exigindo a coincidência de seu físico. consequências no caso limite de grandes números quânticos com os resultados do clássico. teorias. Em S. p., o fato de o quantum. os efeitos são significativos apenas quando se consideram micro-objetos, quando ... ... Enciclopédia Física
Princípio variacional de Hamilton- Hamiltono variacinis principas statusas T sritis fizika atitikmenys: engl. Princípio de variação de Hamilton vok. Hamiltonsches Variationsprinzip, n rus. Princípio variacional de Hamilton, m pranc. príncipe variacional d'Hamilton, m … Fizikos terminų žodynas
Um postulado da mecânica quântica (ver Mecânica Quântica) que exige a coincidência de suas consequências físicas no caso limite de grandes números quânticos (ver números quânticos) com os resultados da teoria clássica. Em S. p., manifesta-se o fato de que... ... Grande Enciclopédia Soviética
- (mecânica ondulatória), uma teoria que estabelece o método de descrição e as leis do movimento das micropartículas (elem. h c, átomos, moléculas, núcleos atômicos) e seus sistemas (por exemplo, cristais), bem como a relação de quantidades caracterizando partículas e sistemas, com física tamanhos, ... ... Enciclopédia Física
Este termo tem outros significados, veja Ação (física). Dimensão de Ação L2MT-1 Ação em física é uma quantidade física escalar que é ... Wikipedia
Livros
- Princípios de movimento do sistema econômico. Monografia, Kusner Yuri Semenovich, Tsarev Igor Gennadievich. As equações básicas do movimento de um sistema econômico são apresentadas de forma analítica e o problema de encontrar métodos adequados para controlar seu movimento é resolvido. A matemática é usada...
A ideia subjacente a todos os princípios integrais e alguns princípios diferenciais é a posição de que o movimento real de um sistema mecânico confere extremabilidade a alguma quantidade física. Para a formulação matemática desta proposição é necessário, como antes, levar em consideração, juntamente com o movimento real, a totalidade dos movimentos concebíveis, submetendo-os a requisitos bastante definidos.
A formulação dos princípios integrais é realizada no espaço de configuração. Lembre-se que para um sistema com graus de liberdade, as coordenadas generalizadas 
, que determinam a configuração do sistema no momento 
, são tratados como coordenadas cartesianas no correspondente 
espaço -dimensional, que é o espaço de configuração. Com o tempo, o estado do sistema mecânico muda e o ponto que representa este sistema descreve uma determinada curva. É conveniente considerar o movimento do sistema como o movimento do ponto representativo ao longo desta curva. Tempo 
sob esta consideração é um parâmetro, e cada ponto da trajetória corresponderá a um ou mais valores 
.
Se estivermos interessados na posição do sistema na trajetória de configuração em cada momento 
, então você precisa adicionar outro eixo 
.
Então obteremos um “gráfico multidimensional” do movimento do sistema que estamos considerando. Também se pode estudar as projeções de um gráfico multivariado em certos planos, digamos 
(Fig. 2.7). Na imagem A, B são as projeções do ponto representativo nos momentos 
E 
conseqüentemente, a linha sólida representa o movimento real, tracejado - um dos movimentos concebíveis.
O princípio integral é uma afirmação sobre como o movimento real do sistema é realizado ao longo de um intervalo de tempo finito (não infinitamente pequeno!) 
.
O que havia com o sistema antes do momento 
,
não estamos interessados. Mas como os momentos inicial e final do tempo são fixos, acredita-se que o sistema mecânico para todos os movimentos concebíveis no momento 
passa por um ponto A, no momento 
- EM;
estes pontos correspondem às posições inicial e final do sistema em seu movimento real.
A formulação mais geral da posição sobre o movimento dos sistemas mecânicos está contida no chamado princípio da menor ação (também chamado de princípio de Hamilton-Ostrogradsky):
O movimento real do sistema mecânico no intervalo de tempo de
antes
é tal que a integral, chamada função de ação
e igual
, (60.7)
Onde
-- Lagrangiana do sistema mecânico dado, tem um extremo (mínimo). Variável
isso não varia.
Em outras palavras, durante o movimento real, a variação da ação deve ser igual a zero
(61.7)
desde que todas as trajetórias de configuração nos instantes de tempo 
E 
passe pelos pontos inicial e final do movimento real, ou seja,
Este princípio, em contraste com o princípio diferencial de d'Alembert, é integral no sentido de que contém uma afirmação sobre o movimento do sistema como um todo durante um período finito de tempo. 
.
Na verdade, dela decorrem as equações de Lagrange, assim, a partir do princípio da menor ação, pode-se dizer, obtém-se toda a dinâmica de um sistema mecânico.
Deixe as funções 
, descreva o movimento real, ou seja, 
aquelas funções para as quais 
tem um mínimo. Considere o conjunto de funções 
Onde 
- variações de função 
, que são considerados pequenos em comparação com 
durante todo o intervalo de tempo de 
antes 
. Além disso, todos 
satisfazer relações (62,7). Calculamos a chamada primeira variação 
, tendo em mente que a função de Lagrange pode depender das coordenadas generalizadas 
,
velocidades generalizadas 
, e tempo 
:
Porque o 
, o segundo termo em 
pode ser integrado por partes para obter
.
Devido às condições (62,7), a soma
desaparece, e a integral restante será igual a zero para valores arbitrários 
somente quando cada termo da soma do integrando desaparece. Assim, obtemos as equações de Lagrange de 2º tipo
.
(63.7)
É útil lembrar que a partir da solução do problema para o extremo de uma função, obtém-se um sistema de equações finitas, a partir do qual se encontra o ponto em que a função atinge um extremo. Neste caso, trata-se de um funcional, a solução de um problema extremo, que é dado por um sistema de equações diferenciais de 2ª ordem. A partir dessas equações, encontra-se uma reta no espaço de configuração, dada pelas funções 
onde o funcional atinge seu mínimo. Esta linha é chamada de extremal.
Como a tarefa de construir um ou outro modelo mecânico consiste em compilar as equações de movimento, vemos que, de fato, a dinâmica do sistema é determinada por uma função - a Lagrangiana, pois é esta função que resolve o problema. Assim, o Lagrangiano do sistema é um objeto físico interessante, cujo estudo é necessário em relação aos problemas de dinâmica. Em particular, pode ser visto a partir do princípio da menor ação que a função 
é definido apenas até a adição da derivada total de uma função arbitrária de coordenadas e tempo. Isto deve ser entendido como o sistema definido pelas suas equações de movimento corresponde a mais de uma função de Lagrange 
.
Na verdade, que haja 
associado com 
razão
(64.7)
,
.
Mas desde 
,
e, consequentemente, as equações de Lagrange obtidas através das funções 
E 
, mesmo. A ambigüidade da definição da função de Lagrange da forma (64.7) não afeta as equações de movimento, e cada 
da classe (64.7) resolve o problema de construir a dinâmica do sistema de forma única.
Uma propriedade importante do sistema de equações de Lagrange é a sua covariância. Isso significa que as equações de Lagrange mantêm sua forma sob transformações pontuais de coordenadas generalizadas 4
ou seja, ao usar coordenadas generalizadas 
As equações de Lagrange terão a mesma forma:
,
como ao usar coordenadas generalizadas 
:
.
Provemos diretamente que as equações de Lagrange são covariantes em relação à transformação (65.7). Vamos construir 
:
e derivados
,
1. Cinemática de um ponto material. Um ponto material é entendido como um objeto físico, geometricamente equivalente a um ponto matemático, mas possuindo massa. A cinemática é um ramo da física que estuda os tipos de movimento dos corpos sem considerar as causas do movimento. A posição de um ponto no espaço é caracterizada por um vetor raio. O vetor raio de um ponto é um vetor cujo início coincide com a origem do sistema de coordenadas e cujo final coincide com o ponto considerado. R = eu x + j sim + k z. Velocidade é a distância percorrida por um corpo por unidade de tempo. v(t) = d R/dt. v(t) = eu dx/dt + j tingido/dt + k dz/dt. A aceleração é a taxa de variação da velocidade. a=d v/dt = d2 R/dt2= eu d2x/dt2 + j d 2 anos/dt 2 + k d 2 z/dt 2 . a = a τ + a n= τ dv/dt + n v2/R.
d R = v dt; d v = a dt, portanto v = v 0 + a t; R = R 2 – R 1 = v 0 t + a t2/2.
2. Dinâmica de um ponto material. Leis de Newton. Os conceitos básicos em dinâmica são o conceito de massa e força. A força é a causa do movimento, ou seja, sob a influência da força do corpo ganha velocidade. Força é uma grandeza vetorial. Massa é uma medida da inércia de um corpo. O produto da massa pela velocidade é chamado de momento. p=m v. O momento angular de um ponto material é o vetor eu = R * p. O momento da força que atua em um ponto material é chamado de vetor M = R * F. Se diferenciarmos a expressão para o momento angular, obtemos: d eu/dt=d R/dt* p + R*d p/dt. Considerando que d R/dt= v E v paralelo p, nós temos d eu/dt= M.Leis de Newton. A primeira lei de Newton afirma que um corpo mantém um estado de repouso ou movimento retilíneo uniforme se nenhuma outra força atuar sobre ele ou se sua ação for compensada. A segunda lei de Newton afirma que a mudança no momento ao longo do tempo é um valor constante e é igual à força atuante d p/dt=d/dt(m v) = md v/dt= F.Esta é a segunda lei de Newton escrita em forma diferencial. A terceira lei de Newton diz que na interação de dois corpos, cada um deles atua sobre o outro com o mesmo valor, mas com direção oposta, força. F 1 = - F 2 .
3. Dinâmica do sistema de pontos materiais. Leis de conservação. O sistema de pontos materiais é a totalidade do seu número finito. Cada ponto do sistema é afetado por forças internas (de outros pontos) e externas. Seja m a massa, r i o vetor raio. x eu , y eu , z eu - cordão. i-ésimo ponto. O impulso de um sistema de pontos materiais é a soma dos impulsos dos pontos materiais que compõem o sistema: p= Σ (eu=1,n) p eu = [ p 1 + p 2 +…+ p n]. O momento angular de um sistema de pontos materiais é a soma dos momentos de momento que compõem o sistema de pontos materiais: eu = Σ [ eu eu ] = Σ [ R eu * p eu ]. A força que atua em um sistema de pontos materiais é definida como a soma de todas as forças que atuam nos pontos do sistema, incluindo as forças de interação entre os pontos do sistema: F = Σ [ F eu], onde F eu = F eu' + Σ(j ≠ eu) F ji é a força que atua no ponto material do sistema, denotada pelo índice i. É composto por uma força externa F i ’ e força interna Σ(i ≠ j) [ F ji ], atuando no ponto como resultado da interação com outros pontos do sistema. Então: F = Σ (i=1,n) [ F eu ’] + Σ (eu=1,n) Σ(j ≠ eu) [ F j]. De acordo com a terceira lei de Newton Σ (i=1,n) Σ(j ≠ i) [ F ji ] = 0, então F = Σ [ F eu']. O momento da força que atua sobre um sistema de pontos materiais é a soma dos momentos das forças aplicadas aos pontos do sistema M= Σ (eu) [ M eu ] = Σ (eu) [ R eu * F eu ] = Σ (eu) [ R eu * F eu']. Para um sistema de pontos materiais, a equação de movimento tem a forma d p/dt = Σ = Σ [ F eu ].
O centro de massa de um sistema de pontos materiais é um ponto imaginário com um vetor raio R= 1/mΣ . A velocidade de seu movimento V=d R/dt. Então a equação do movimento m d V/dt= F. A equação de momentos para o sistema de pontos materiais d eu/dt= M. Leis de conservação. Um sistema isolado é aquele que não é afetado por forças externas. Nela F= 0, então d p/dt = 0. Então p= const. Num sistema isolado, o momento das forças externas M= 0. Portanto, d eu/dt = 0, o que significa eu= const. A mudança na energia cinética de um ponto material quando ele se move entre duas posições é igual ao trabalho realizado pela força. m 0 v 2 2/2 – m 0 v 1 2/2 = ∫(1,2) F d eu ou m 0 v 2 /2 + E p \u003d const.
4. Movimento em um campo centralmente simétrico. Leis de Kepler. O campo é denominado central se a energia potencial do corpo nele contido depende apenas da distância r a um determinado ponto fixo. Força F= - ∂U(r)/ ∂ R= -dU/dr R/r atuando sobre a partícula, em valor absoluto também depende apenas de r e é direcionado a cada ponto ao longo do vetor raio. Ao mover-se no campo central, o momento do sistema em relação ao centro do campo é conservado. Por um momento de partícula M = [R*R]. Como os vetores M e r são perpendiculares entre si, a constância de M significa que quando a partícula se move, seu vetor raio sempre permanece no mesmo plano - o plano perpendicular a M. Assim, a trajetória da partícula no campo central fica inteiramente em um avião. Introduzindo nele as coordenadas polares r, φ, escrevemos a função de Lagrange na forma L = m/2 (r 2 (∙) + r 2 φ 2 (∙)) - U(r). Esta função não contém explicitamente a coordenada φ. Para tal coordenada, o momento generalizado pi correspondente a ela é a integral do movimento. Neste caso, o momento generalizado p φ = mr 2 φ(∙) coincide com o momento M z = M, de modo que M = mr 2 φ(∙) (1). Note que para um movimento plano de uma partícula num campo central, esta lei admite uma interpretação geométrica simples. A expressão 1/2 r r d φ é a área do setor formado por dois vetores de raio infinitamente próximos e um elemento de arco da trajetória. Denotando-o como df, escrevemos o momento da partícula na forma M = 2mf, onde a derivada f é chamada de velocidade setorial. Portanto, a conservação do momento significa a constância da velocidade setorial - por períodos iguais de tempo, o vetor raio de um ponto móvel descreve áreas iguais ( Segunda lei de Kepler). Expressando φ(∙) através de M de (1) e substituindo a energia na expressão, obtemos: E = m/2 (r 2 (∙) + r 2 φ 2 (∙)) + U(r) = mr 2 (∙ )/2 + M 2 /2mr 2 + U(r). Portanto r(∙) = √(2/m (E – U(r)) - M 2 /m 2 r 2) ou, separando variáveis e integrando: t = ∫dr/√(2/m (E – U( r)) - M 2 /m 2 r 2) + const. Além disso, escrevendo (1) como dφ = M 2 /mr 2 dt, substituindo dt aqui e integrando, encontramos: φ = ∫dr (M/r 2)/√(2/m (E – U(r)) - M 2 /r 2) + const. A primeira lei de Kepler. Cada planeta gira em uma elipse com o Sol em um de seus focos. Terceira lei de Kepler. Os quadrados dos períodos siderais dos planetas estão relacionados como cubos dos semieixos maiores de suas órbitas T 1 2 /T 2 2 = a 1 3 /a 2 3 .
5. A função de Lagrange e as equações de Lagrange de um sistema de pontos materiais. Integrais de movimento. Considere um sistema fechado de pontos materiais. A função de Lagrange para isso tem a forma L = Σ(a) – U(r 1 , r 2 , …), onde T = Σ (a) é a energia cinética e U é a energia potencial de interação das partículas. Então as equações de movimento d/dt (∂L/∂v a) = ∂L/∂r a assumem a forma m a dv a /dt = - ∂U/∂r a . Essas equações de movimento são chamadas de equações de Newton. Vetor F a = - ∂U/∂r a é chamada de força. Se não forem usadas coordenadas cartesianas de pontos para descrever o movimento, mas coordenadas generalizadas arbitrárias q eu , então para obter a função Lagrangiana, é necessário realizar a transformação correspondente: x a = f(q 1 , q 2 , .., q s) , x a (∙) = Σ(k ) [∂f a /∂q k (∙)], etc. Substituindo essas expressões na função eu= 1/2 Σ(a) – U, obtemos a função de Lagrange desejada na forma eu = 1/2 Σ(i,k) – você(q). Integrais de movimento. Existem funções de coordenadas generalizadas que mantêm valores constantes durante o movimento, dependendo apenas das condições iniciais. Eles são chamados de integrais de movimento. Devido à homogeneidade do tempo, dL/ dt = Σ(i) [∂L/∂q i q i (∙)] + Σ(i) [∂L/∂q i (∙) q i (∙∙)]. Substituindo ∂L/∂q i de acordo com as equações de Lagrange por d/dt (∂L/∂q i (∙)), obtemos dL/dt = Σ(i) ou d/dt (Σ(i) - L) = 0 Isso mostra que a quantidade E = Σ(i) – L, chamada energia, não muda, ou seja, integral de movimento. Devido à homogeneidade do espaço em uma transferência infinitamente pequena ε, quando todos os pontos do sistema são deslocados por ε = δr, a mudança na função de Lagrange, igual a δL = ε Σ(a) [∂L/∂r a ], deve ser igual a zero, ou seja, Σ(a) [∂L/∂r a ] = 0. Usando as equações de Lagrange, obtemos Σ(a) = d/dt (Σ(a)[ ∂L/∂v a ]) = 0. Então a quantidade R= Σ(a)[ ∂L/∂v a ], chamado momento, permanece inalterado, ou seja, integral de movimento. Devido à isotropia do espaço em uma rotação infinitamente pequena através do ângulo δφ, a mudança na função de Lagrange igual a δL = Σ(a) [∂L/∂r a δ R a + ∂L/∂v a δ v a] deve ser zero. Fazendo a alteração ∂L/∂ v uma = p uma e ∂L/∂ R uma = p a (∙) tendo em vista a arbitrariedade de δφ, obtemos d/dt Σ(a) [ R a p a ] = 0. O valor М = Σ(a) [ R a p a], chamado de momento angular, permanece constante, ou seja, integral de movimento.
6. Dinâmica de um corpo absolutamente rígido. Tensor de inércia. Equações de Euler. Um corpo rígido é um sistema de pontos materiais, cuja distância entre eles permanece constante. Para uma descrição completa do movimento de um corpo rígido, além do movimento de um de seus pontos, é necessário conhecer o movimento do corpo próximo a este ponto como ponto de fixação. Seja o corpo fixado no ponto O. Denotamos o vetor raio do ponto m i em relação a O R eu , cé a velocidade angular instantânea do corpo, então o momento angular eu= Σ [ R eu* sou eu v eu ] = Σ = cΣ - Σ . Esta igualdade vetorial pode ser escrita como três projeções nos eixos coordenados L x = w x Σ - Σ ; L y = wy Σ - Σ ; eu z = w z Σ - Σ . Dado que ( c R i) = x i w x + y i w y + z i w z obtemos L x = J xx w x + J xy w y + J xz w z ; L y = J yx w x + J yy w y + J yz w z ; L x = J zx w x + J zy w y + J zz w z , onde J xx = Σ , J xy = Σ , outros são semelhantes. Os valores J xx , J yy , J zz são chamados de momentos axiais de inércia, e J xy = J yx , J xz = J zx , J yz = J zy são chamados de momentos centrífugos de inércia. O conjunto de valores J ij é denominado tensor de inércia. Os elementos de J ii são chamados de diagonais. Se todos os elementos fora da diagonal forem iguais a zero, então dizem que os eixos do corpo que coincidem com os eixos coordenados são os principais eixos de inércia, e as quantidades J ii são chamadas de principais momentos de inércia. Tal tensor é reduzido a uma forma diagonal.
Equações de Euler. A equação do movimento do centro de massa do corpo tem a forma m d v 0 /dt = md/dt ( c * R 0) = F, Onde R 0 é o vetor raio do centro de massa do corpo, traçado a partir do ponto de sua fixação. É conveniente direcionar os eixos do sistema de coordenadas associado ao corpo ao longo dos eixos principais de inércia. Neste caso, o momento angular adquire uma forma simples L 1 = J 1 w 1 , L 2 = J 2 w 2 , L 3 = J 3 w 3 , e w i são as projeções da velocidade angular nos eixos coordenados movendo-se juntos com o corpo. Usando a fórmula geral d A/dt = ∂ A/∂t + c* A, podemos representar a equação dos momentos da seguinte forma: ∂ eu/∂t + c * eu = M. Levando em consideração que L x = J x w x , L y = J y w y , L z = J z w z , reescrevemos esta equação em projeções nos eixos do sistema de coordenadas móvel: J x dw x /dt + (J z - J y )w y w z = M x , J y dw y /dt + (J x – J z)w z w x = M y , J z dw z /dt + (J y – J x)w x w y = M z . Essas equações são chamadas de equações de Euler.
7.
Movimento relativo a referenciais não inerciais.
NISO é um sistema no qual o corpo se move com aceleração em relação ao repouso. Sistemas coordenados. Aqui os conceitos de homogeneidade e isotropia de espaço e tempo não são cumpridos, porque a duração e a duração no NISO variam. Além disso, o conteúdo da 3ª lei de Newton e das leis de conservação foi perdido. A razão de tudo são as forças de inércia associadas apenas ao sistema de coordenadas, o gato. afetar o movimento do corpo. QUE. a aceleração pode ser alterada por uma força externa ou por inércia. F=∑Fi=ma (ISO), F=F(ext.)+Fi=ma′(NISO), onde Fi é a força de inércia, a é a aceleração. corpos em IFR, a′-accel. o mesmo corpo em NISO. No NISO, a 1ª lei de Newton não é cumprida! Fi=-m(a′-a), ou seja, as forças inerciais não obedecem ao terceiro poço z de Newton, porque eles têm vida curta. Durante a transição de ISO para NISO, as forças inerciais desaparecem. Inércia as forças são sempre direcionadas contra as pálpebras. forças externas. As forças de inércia podem ser somadas vetorialmente. Em ISO: v = const, v< dx/dt=Ux=dx′/dt+dv(t)/dt′=U′x+v(t) dUx/dt=d/dt′(U′x+v(t))=dU′x/ dt′+dv(t)/dt′=a x ' + a 0 = a x . Os conceitos de velocidades absolutas, relativas e translacionais são introduzidos no NISO: você 0 - velocidade absoluta, a 0 - aceleração relativa. dormente Sistemas coordenados. você x 0 \u003d v + você x 0 '; a x 0 \u003d a ' + a x; u x ’ a x - velocidade relativa e aceleração. movimento Sistemas coordenados. (relativo) ; v, velocidade a′. e acelerado. k′ refere-se. k, ou seja velocidade e aceleração portátil Existe uma função da coordenada generalizada, velocidade, tempo. Considere um espaço dimensional 2S, então a posição do sistema S = ∫(t 1 , t 2) L(g, g( ), t)dt, L é a função de Lagrange; Ação S. A função da ação é chamada itnegral S=∫ Ldt=0, com o cat. tomado ao longo da verdadeira trajetória do movimento, o sistema terá um valor mínimo, ou seja, S=Smin, δS=0. Aqueles. o sistema de 1 para 2 se move ao longo de uma trajetória tal que sua ação é mínima - o princípio da mínima ação de Hamilton. L = T – U é a diferença entre as energias cinética e potencial do sistema. Segundo Hamilton, a trajetória real corresponde à ação mínima. Vamos encontrar uma trajetória. A trajetória real é a trajetória mínima. S-funcional. Vamos encontrar seu mínimo. δS = 0 primeira variação. δS = ∫(t 1 ,t 2)(Σ[∂L/∂g i δg i ] + Σ[∂L/∂g i ( ) δg i ( )])dt; ∫(t 1 ,t 2) ∂L/∂g i ( ) δg i ( ) dt = ∫(t 1 ,t 2) ∂L/∂g i ( ) dδg i = ∂L/∂g i ( )δg i (t 1 ,t 2) - ∫(t 1 ,t 2) δg i d/dt (∂L/∂g i ( )) dt; δg eu não dependo um do outro 9.
Oscilações de sistemas com um e vários graus de liberdade. Vibrações livres e forçadas
.
O caso mais simples é quando o sistema possui um grau de liberdade. Um equilíbrio estável corresponde a tal posição do sistema, no gato. seu potencial. en. U(q) tem um mínimo. O desvio desta posição leva ao surgimento de uma força - dU/dq, que tende a trazer o sistema de volta. q 0 - coordenada generalizada. Expandimos U(q) - U(q0) em potências e obtemos U(q) - U(q0) ≈ k / 2 (q - q 0) 2 onde k \u003d U '' (q 0) é um coeficiente positivo . U(q 0) \u003d 0, denotamos x \u003d q - q 0 - o desvio da coordenada do valor de equilíbrio, então U (x) \u003d kx 2/2 é energia potencial. 1/2a(q) q' 2 =1/2a(q)x' 2 -energia cinética em q = q0 e a(q0) = m obtemos a função de Lagrange para um sistema realizando oscilações unidimensionais: L = mx 2 (∙) /2 – kx 2 /2. A equação de movimento correspondente a esta função será: mx(∙∙) + kx = 0 ou x(∙∙) + w 2 x = 0, onde w = √(k/m) é a frequência de oscilação cíclica. A solução para estes ur-ésimo é x \u003d a cos (wt + α) onde a é a amplitude das oscilações, wt + α é a fase das oscilações. Que. a energia do sistema oscilante será E = mx 2 (∙)/2 + kx 2 /2. Vibrações forçadas. Neste caso, junto com sua própria energia potencial ½ kx 2, o sistema também possui uma energia potencial U e (x, m) associada à ação de um campo externo. Conseqüentemente, a função de Lagrange de tal sistema será: L = mx 2 (∙)/2 + kx 2 /2 + x F(t), onde F(t) é uma força externa. A equação de movimento correspondente será mx(∙∙) + kx = F(t), ou x(∙∙) + w 2 x = F(t)/m. Se F(t) é uma função periódica simples do tempo com alguma frequência γ: F(t) = f cos(γt + β) então a solução para as equações de movimento será: X = a cos(wt + α) + f cos(γt + β)/(m(w 2 – γ 2)) a e α são determinados a partir das condições iniciais. Que. sob a ação de uma força motriz, o sistema realiza um movimento que representa uma combinação de duas oscilações - com a frequência natural do sistema w e com a frequência da força motriz - γ. Oscilações de sistemas com muitos graus de liberdade
.
Panela. en. o sistema U(q i) tem um mínimo em q i =q i 0 . Introduzindo pequenos deslocamentos x i = q i - q i 0 e expandindo U neles com uma precisão de termos de 2ª ordem, obtemos o potencial. energia: você = 1/2 Σ(i,k) , k ik =k ki . Kinet. en. para tal sistema será 1/2 Σ(i,k) , onde m ik =m ki . A equação de Lagrange para tal sistema seria: L = 1/2 Σ(i,k) . Então dL = Σ(i,k) . Procuramos x k (t) na forma x k \u003d A k exp (-iwt), A k é uma constante. Substituindo isso na equação de Lagrange, obtemos um sistema de equações lineares homogêneas. Σ(k) [(-w 2 m ik +k ik)A k ] = 0 - equação característica, possui s raízes diferentes w 2 α (α=1,2,….,s) w α - frequências naturais de o sistema. Uma solução particular do sistema tem a forma: x k = ∆ kα C α exp(-iw α t). A solução geral é a soma de todas as soluções particulares: x k = Σ(α) [∆ kα Q α ], onde Q = Re (C α exp(-iw α t)). 10.
Equação canônica de Hamilton.
Uma série de vantagens no estudo de questões de mecânica é a descrição com a ajuda de coordenadas generalizadas e momentos, a transição de um conjunto de variáveis independentes para outro pode ser feita pela transformação de Legendre. Neste caso, tudo se resume ao seguinte. O diferencial total das funções de Lagrange em função de coordenadas e velocidades é: dL = Σ(i) [∂L/∂q i ] + Σ(i) [[∂L/∂q i (∙)]. Esta expressão pode ser escrita como dL = Σ(i) + Σ(i) . Vamos reescrevê-lo na forma: d(Σ(i) – L) = - Σ(i) + Σ(i) . O valor sob o sinal do diferencial é a energia do sistema expressa em termos de coordenadas e momentos, e é chamada de função hamiltoniana: H (p, q, t) = Σ (i) - L. De dif. igualdades dH = - Σ(i) + Σ(i) seguem as equações: q i (∙) = ∂H/∂p i , pi (∙) = - ∂H/∂q i são as equações hamiltonianas. Devido à sua simplicidade e simetria, também são chamados. canônico. Colchetes de Poisson. A derivada temporal de qualquer função F de coordenadas generalizadas, momentos e tempo é dF/dt = ∂F/∂t + Σ(i) [∂F/∂q i dq i /dt] + Σ(i) [∂F/∂ pi dpi /dt]. Usando as equações de Hamilton, podemos reescrever esta equação na seguinte forma: dF/dt = ∂F/∂t + , onde = Σ(i) [∂F/∂q i ∂H/∂p i - ∂H/∂q i ∂F /∂ pi ] - chamado. o suporte de Poisson. Obviamente, a equação de Hamilton pode ser escrita usando colchetes de Poisson. 11.
Equação de Hamilton-Jacobi
.
Pelo princípio da menor ação, temos S = ∫(t 1 ,t 2)Ldt. Considere a ação (S) como uma quantidade que caracteriza o movimento ao longo de trajetórias verdadeiras. Com base na equação de Lagrange para mudar a ação ao passar de uma trajetória para outra trajetória próxima a ela (com um grau de liberdade), obtemos: δS = pδq ou para qualquer número de graus de liberdade: δS = Σ(i) . Segue-se que as derivadas parciais da ação em relação às coordenadas são iguais aos momentos correspondentes: ∂S/∂q i = pi (1). Por definição, dS/dt = L, por outro lado, considerando S em função das coordenadas e do tempo e utilizando a fórmula (1), temos: dS/dt = ∂S/∂t + Σ(i) [∂S /∂q i q i (∙)] = ∂S/∂t + Σ(i) . Comparando ambas as expressões, obtemos ∂S/∂t = L - Σ(i) ou ∂S/∂t = - H(p,q,t) (2). As fórmulas (1), (2) podem ser escritas juntas como dS = Σ(i) – Hdt. E a ação (S) em si será S = ∫ (Σ(i) – Hdt). Para H independente de t, S(q,t)=S 0 (q) - Et, onde S 0 (q) = Σ(i) [∫p i dq i ] é uma ação encurtada e Еt é substituído por H(p , q). A função S(q,t) satisfaz uma certa dif. equação que obtemos substituindo os impulsos Р na relação (2) pelas derivadas ∂S/∂q: ∂S/∂t + H(∂S/∂q 1 ,…, ∂S/∂q s ;q 1 ,… ,q s ,t) = 0 é uma equação em derivadas parciais de 1ª ordem chamada. Equação de Hamilton-Jacobi. Então, para uma partícula em um campo externo U(x,y,z,t) tem a forma: ∂S/∂t + 1/(2m)((∂S/∂x) 2 + (∂S/∂ y) 2 + (∂S/∂z) 2) + você(x,y,z,t) = 0. 12.
Deformações e tensões em sólidos. Módulos de Young, cisalhamento. Razão de Poisson
.
A deformação é uma mudança na forma e no volume de um corpo sob a ação de forças externas. Sob a ação de uma força externa, a forma do corpo muda. Todas as deformações na natureza podem ser reduzidas a 3 eu principais deformações: 1) tração, compressão; 2) cisalhamento; 3) torção. Distinguir entre deformações homogêneas e não homogêneas. Se todas as peças forem deformadas da mesma maneira, então este uniformemente deformado. Se todas as partes do corpo se deformarem de maneira diferente, então isso heterogeneamente deformado. A lei de Hooke é satisfeita apenas na região de deformação elástica. = E’. F/S = E ∆l/l 0 ; Controle F = ES∆l/l 0 = kx; k = ES/l 0 ; Controle F \u003d ESx / l 0. A lei de Hooke define a relação entre e . k é o coeficiente de elasticidade, depende das dimensões geométricas, do material de que o corpo é feito. E é o módulo de Young. O módulo de Young é igual à força que deve ser aplicada a um corpo de seção transversal unitária para que seu corpo aumente 2 vezes. Outro tipo de deformação é a deformação por cisalhamento, observada quando a superfície é aplicada tangencialmente; é paralelo à superfície de deformação por cisalhamento, observada sob a ação de forças tangenciais, ou seja, as forças são aplicadas tangencialmente. Ψ~F t /S (ângulo de deslocamento). Ψ = nFt/S; n é o fator de mudança. F t = nS. (E>N, E~4N). 13.
Mecânica de líquidos e gases.
Para todos os líquidos e gases, o parâmetro unificador é: densidade ρ, pressão P=F n /S. Em líquidos e gases, ocorre o módulo de Young, mas o módulo de cisalhamento |σ|=|P|, σ - tensão não ocorre. Se o líquido (gás) estiver imóvel, estamos lidando com hidrostática (aerostática). Leis características: Lei de Pascal: o excesso de pressão criado em gases e líquidos é transmitido igualmente em todas as direções. Zn Arquimedes é válido tanto para líquidos quanto para gases. A força de Arquimedes sempre atua contra a força da gravidade. A razão para o surgimento da força de Arquimedes é a presença de um corpo de volume V. Zn Arquimedes: Um corpo em um líquido ou gás é sempre afetado por uma força igual ao peso do líquido ou gás deslocado pela parte imersa de corpo e direcionado verticalmente para cima. Se F A >F HEAVY, então o corpo flutua, se vice-versa, então ele afunda. Se um líquido (gás) estiver fluindo, a equação de continuidade do jato será adicionada a essas equações. A trajetória do movimento de uma partícula em um fluido é chamada. linha atual. A parte do espaço delimitada por uma linha atual é chamada. tubo atual. O fluido no tubo de fluxo pode fluir estacionário ou não estacionário. A corrente é chamada estação se através de uma determinada seção do tubo atual por unidade. o tempo passa a mesma quantidade de líquido (gás), caso contrário, o fluxo de não-estático. Deixe-nos ter um tubo de corrente com a seguinte forma: Se o fluxo de fluido for estático. Então m 1 =m 2 =…=m n por unidade de tempo, se o fluido for incompressível, então ρ 1 V 1 =ρ 2 V 2 =…; =ρ n V n , ρ 1 Δx 1 = ρ 2 Δx 2 =…; = ρ n Δx n, ρ 1 υ 1 ΔtS 1 = ρ 2 υ 2 ΔtS 2 =…= ρ n υ n ΔtS n, visto que o líquido é incompressível ρ é constante υ 1 S 1 = υ 2 S 2 =… = υ n S n , υS=const; υ=const/S é a equação de continuidade do jato. pd v/dt =ρ g– grau P – eq. Euler – 2ª ordem. Newton para líquidos e gases. A lei está preservada. Energia em líquidos e gases. Nv. Bernoulli. Eu ia. Naz. Um fluido incompressível no qual as forças de atrito viscoso podem ser desprezadas. A energia cinética não é gasta na realização de trabalho contra forças de atrito. Ρυ 2 /2+ρgh + P = const – eq. Bernoulli, ρυ 2 /2 – pressão dinâmica, ρgh – hidrostato. Pressão, P - pressão molecular. Mυ 2 /2 \u003d E K; mυ 2 /2V= E K /V= ρυ 2 /2. Força de atrito viscoso F A = - ηΔυΔS/ΔZ 6 π r η υ – Força de Stokes. Η - coeficiente. viscosidade, Δυ/ΔZ – grad υ, r – dimensões do corpo. Esta é a fórmula de Newton para forças de atrito viscoso. Se houver forças de atrito no fluido, então id. O líquido fica viscoso. ρ v 1 2 /2 + ρgh 1 + P 1 = ρ v 2 2 /2 + ρgh 2 + P 2 ; (P 1 - P 2) \u003d ρ (υ 2 2 - υ 1 2) / 2. Se ΔP = 0, então υ 2 2 - υ 1 2 = 0, e não haverá fluxo de fluido. Onde P é maior, há rápido. Menos atual. Se a seção transversal S aumentar, então P aumenta e υ diminui. Se o tubo de corrente não estiver horizontalmente, então υ 2 2 -υ 1 2 \u003d 2g (h 1 -h 2); υ \u003d sqrt (2g (h 1 -h 2)) - Fórmula de Torricelli. As trajetórias que descrevem os movimentos de sistemas mecânicos na configuração estendida e nos espaços de fase têm uma propriedade notável - são extremos de algum problema variacional, fornecem valores estacionários ao funcional de ação. Considere a formulação do problema variacional no espaço de configuração estendido R"*", cujos pontos são os conjuntos (q, ().
Deixe a curva yn = ((q, t): q e R t e , 5q(/ 0)= 8q(/,) = 0). A variação 8q(/) é uma função arbitrária da classe C 1 que desaparece nas extremidades do segmento = 0. A A primeira variação do funcional Sy em y = y 0 de acordo com a definição é igual a e após a integração por partes assume a forma O termo não integral na expressão (2.3) desaparece, porque bq k (t 0) = bq k (t y) = 0, Para - 1 ..... l, e a expressão em quadrado colchetes sob o sinal de integral é igual a zero, pois y 0 é uma trajetória real que satisfaz as equações de Lagrange (2.1). Portanto, a variação 55(y 0) = 0. ? A afirmação inversa também é verdadeira: se a variação 65(y*) = 0, onde y* pertence à classe de trajetórias rotatórias, então y* = y 0 é uma trajetória real. A validade desta afirmação decorre da expressão da primeira variação (2.3) e do lema principal do cálculo das variações. Neste caso, da igualdade a zero da primeira variação e a independência das variações 6 k - 1, ..., a validade das equações de Lagrange do segundo tipo eu, segue certo Quando q k = q k *(t), k = 1.....l. Isso significa que y* é a trajetória real do sistema mecânico. 3.1. No caso de um sistema não conservativo, é impossível indicar um funcional cujo valor estacionário foi alcançado em uma trajetória real. No entanto, neste caso, as seguintes afirmações são equivalentes: onde q(/) é a trajetória real. A primeira das afirmações acima é o conteúdo do princípio variacional de Hamilton-Ostrogradsky para sistemas não conservativos. 3.2. Pode-se mostrar que o valor estacionário do funcional de ação é mínimo se a diferença -/0 for pequena o suficiente. Esta circunstância está associada a outro nome do princípio em discussão - o princípio da menor ação de Hamilton-Ostrogradkogo. O problema variacional considerado acima pode ser formulado no espaço de fase estendido, o que se revela importante quando se consideram questões de integrabilidade das equações canônicas de Hamilton. Denote por Г = ((р + 6р. q + 8q, EU): p, q, 6p. 6qe R",te[r 0 , /,]. 5q(/ 0)= 8q(/|) = 0) curva no espaço de fase estendido e seja, para 8p = 8q = 0, a curva Г 0 a solução do sistema de equações canônicas hamiltonianas Todas as funções de tempo pertencem à classe C 1 . Assim, é definida uma família de trajetórias rotatórias (Г), à qual pertence a trajetória real Г 0 (Fig. 46). O funcional de ação, levando em consideração a conexão entre as funções de Lagrange e Hamilton, assume a forma Aqui, as letras p, q são usadas para abreviar, em vez das letras p + 8p, q + 8q. Calculando a variação do funcional 5[Γ] na trajetória real, obtemos Integrando por partes, levando em consideração as condições de contorno, encontramos Disto segue-se que a variação 85|Γ 0 1 = 0 se p(/), q(f) satisfazem as equações canônicas de Hamilton (2.4), u. pelo contrário, da condição de independência das variações 8p(r), 6q(/) as equações (2.4) seguem conforme o lema principal do cálculo das variações. Assim, foi comprovada a validade do princípio da menor ação no espaço de fase do sistema: a ação funcional 5[Г] definida no espaço de trajetórias rotatórias (Г|. assume um valor estacionário na trajetória real, ou seja, 85 [Г 0 1 = 0. Arroz. 46 Quando aprendi sobre esse princípio, tive uma sensação de algum tipo de misticismo. Parece que a natureza classifica misteriosamente todas as formas possíveis de movimento do sistema e escolhe a melhor delas. Hoje quero falar um pouco sobre um dos princípios físicos mais notáveis – o princípio da menor ação. Quando refletida, a luz também se move de forma a ir de um ponto a outro no caminho mais curto. Na figura, o caminho mais curto será o caminho verde, no qual o ângulo de incidência é igual ao ângulo de reflexão. Qualquer outro caminho, como o vermelho, será mais longo. Em 1662, Pierre Fermat sugeriu que a velocidade da luz numa substância densa, como o vidro, é menor que no ar. Antes disso, a versão geralmente aceita era Descartes, segundo a qual a velocidade da luz na matéria deve ser maior do que no ar para se obter a lei de refração correta. Para Fermat, a suposição de que a luz poderia se mover mais rapidamente em um meio mais denso do que em um meio rarefeito não parecia natural. Portanto, ele presumiu que tudo era exatamente o oposto e provou algo surpreendente - sob essa suposição, a luz é refratada de forma a chegar ao seu destino no mínimo de tempo. Todos esses fatos sugeriam que a natureza age de alguma forma racional, a luz e os corpos se movem da maneira mais otimizada, despendendo o mínimo de esforço possível. Mas quais foram esses esforços e como calculá-los permaneceu um mistério. Em 1744, Maupertuis introduz o conceito de "ação" e formula o princípio segundo o qual a verdadeira trajetória de uma partícula difere de qualquer outra porque a ação para ela é mínima. No entanto, o próprio Maupertuis não conseguiu dar uma definição clara do que equivale a esta ação. Uma formulação matemática rigorosa do princípio da menor ação foi desenvolvida por outros matemáticos - Euler, Lagrange, e finalmente dada por William Hamilton: Então, como você precisa dirigir para chegar a tempo e usar o mínimo de combustível possível? É claro que você precisa seguir em linha reta. Com o aumento da distância percorrida, o combustível não será consumido menos. E então você pode escolher táticas diferentes. Por exemplo, você pode chegar rapidamente ao ponto com antecedência e apenas sentar e esperar a hora chegar. A velocidade de condução e, portanto, o consumo de combustível em cada momento, serão elevados, mas o tempo de condução também será reduzido. Talvez o consumo geral de combustível neste caso não seja tão grande. Ou você pode ir uniformemente, com a mesma velocidade, de modo que, sem pressa, chegue exatamente na hora certa. Ou parte do caminho deve ser rápido e parte mais lento. Qual é o melhor caminho a seguir? Acontece que a maneira mais ideal e econômica de dirigir é dirigir a uma velocidade constante, de modo a chegar ao ponto exatamente na hora marcada. Qualquer outra opção consumirá mais combustível. Você pode verificar por si mesmo com alguns exemplos. A razão é que o consumo de combustível aumenta com o quadrado da velocidade. Portanto, à medida que a velocidade aumenta, o consumo de combustível aumenta mais rapidamente do que diminui o tempo de condução, e o consumo geral de combustível também aumenta. Então, descobrimos que se um carro consome combustível em um determinado momento em proporção à sua energia cinética, então a maneira mais econômica de ir de um ponto a outro exatamente na hora marcada é dirigir uniformemente e em linha reta, assim como um corpo se move na ausência de forças agindo sobre ele. Qualquer outra forma de condução resultará num consumo global de combustível mais elevado. O consumo de combustível em cada momento é igual à energia cinética menos a energia potencial do carro (menos a energia potencial, porque o veículo instalado produz combustível e não gasta). Agora nossa tarefa é a movimentação mais econômica do carro entre os pontos e fica mais difícil. O movimento retilíneo uniforme, neste caso, não é o mais eficaz. Acontece que é melhor subir um pouco, ficar ali um pouco, tendo desenvolvido mais combustível, e depois descer até o ponto. Com a trajetória de voo correta, o consumo total de combustível devido à subida cobrirá os custos adicionais de combustível para aumentar o comprimento da trajetória e aumentar a velocidade. Se calculado com cuidado, a maneira mais econômica para um carro seria voar em uma parábola, exatamente na mesma trajetória e exatamente na mesma velocidade que uma pedra voaria no campo gravitacional da Terra. Um análogo da quantidade total de combustível consumido durante todo o tempo de movimento, ou seja, o valor do Lagrangiano acumulado ao longo de todo o tempo de movimento é chamado de "ação". O princípio da menor ação é que o corpo se move de tal forma que a ação (que depende da trajetória do movimento) seja mínima. Neste caso, não se deve esquecer que são dadas as condições inicial e final, ou seja, onde o corpo está na hora e na hora . Nesse caso, o corpo não precisa se mover em um campo gravitacional uniforme, que consideramos para o nosso carro. Você pode considerar situações completamente diferentes. Um corpo pode oscilar sobre um elástico, balançar sobre um pêndulo ou voar ao redor do Sol, em todos esses casos ele se move de forma a minimizar o “consumo total de combustível”, ou seja, Ação. Se o sistema consistir em vários corpos, então o Lagrangiano de tal sistema será igual à energia cinética total de todos os corpos menos a energia potencial total de todos os corpos. E, novamente, todos os corpos se moverão em conjunto, de modo que o efeito de todo o sistema durante esse movimento seja mínimo. Por exemplo, vamos pegar uma bola e colocá-la em um espaço vazio. A alguma distância dela colocamos uma parede elástica. Digamos que queremos que a bola fique no mesmo lugar depois de algum tempo. Nestas condições, a bola pode mover-se de duas maneiras diferentes. Primeiro, ele pode simplesmente ficar parado. Em segundo lugar, você pode empurrá-lo contra a parede. A bola atingirá a parede, quicará nela e voltará. É claro que você pode empurrá-lo com tanta velocidade que ele retornará exatamente no momento certo. Como pode o princípio da menor ação ser salvo para que seja válido em tais situações? Falaremos sobre isso em.8. Princípio variacional de Hamilton. (princípio da menor ação).
;
=0
na trajetória real, a seguinte equação deve ser satisfeita: 
- Equação de Lagrange (para qualquer i= 1,…S).
A relação quantitativa entre E e N é dada através do índice de Poisson. N = E/(2(1+μ)), onde é o índice de Poisson. μ = |∆d/d 0 |/|∆l/l 0 |. O índice de Poisson determina a mudança nas dimensões transversais durante a tração ou compressão. 0,5.
fundo
Desde a época de Galileu, sabe-se que os corpos que não sofrem a ação de nenhuma força se movem em linha reta, ou seja, ao longo do caminho mais curto. Os raios de luz também viajam em linha reta. 
Isto é fácil de provar simplesmente refletindo os caminhos dos raios para o lado oposto do espelho. Eles são mostrados em linhas pontilhadas na imagem. 
Pode-se observar que o caminho verde ACB se transforma em uma linha reta ACB'. E o caminho vermelho se transforma em uma linha quebrada ADB ', que, claro, é mais longa que a verde. 
Novamente na figura, a cor verde mostra o caminho que o feixe de luz realmente percorre. O caminho marcado em vermelho é o mais curto, mas não o mais rápido, porque a luz tem um caminho mais longo para percorrer no vidro e sua velocidade é mais lenta nele. O mais rápido é o caminho real do feixe de luz. 
Na linguagem matemática, o princípio da menor ação é formulado de forma bastante breve, mas nem todos os leitores podem compreender o significado da notação utilizada. Quero tentar explicar este princípio de forma mais clara e em termos mais simples. corpo solto
Então, imagine que você está sentado em um carro em um determinado momento e em determinado momento você recebe uma tarefa simples: nesse momento você precisa dirigir um carro até o ponto . 
O combustível do carro é caro e, claro, você quer gastar o mínimo possível. Seu carro é feito com as mais recentes supertecnologias e pode acelerar ou desacelerar tão rápido quanto você quiser. No entanto, ele foi projetado de tal forma que quanto mais rápido vai, mais combustível consome. Além disso, o consumo de combustível é proporcional ao quadrado da velocidade. Se você dirigir duas vezes mais rápido, consumirá 4 vezes mais combustível no mesmo período de tempo. Além da velocidade, o consumo de combustível, é claro, é afetado pela massa do carro. Quanto mais pesado nosso carro, mais combustível ele consome. O consumo de combustível do nosso carro em cada momento é, ou seja, é exatamente igual à energia cinética do carro. No campo da gravidade
Agora vamos melhorar um pouco nosso carro. Vamos anexar motores a jato a ele para que possa voar livremente em qualquer direção. Em geral, o design permaneceu o mesmo, de modo que o consumo de combustível permaneceu novamente estritamente proporcional à energia cinética do carro. Se agora for dada a tarefa de decolar de um ponto no tempo e chegar a um ponto no tempo t, então a maneira mais econômica, como antes, é claro, será voar uniformemente e em linha reta para chegar ao ponto exatamente a hora marcada t. Isto corresponde novamente ao movimento livre do corpo no espaço tridimensional. 
No entanto, um dispositivo incomum foi instalado no modelo mais recente do carro. Esta unidade é capaz de produzir combustível literalmente do nada. Mas o design é tal que quanto mais alto o carro, mais combustível o dispositivo produz a qualquer momento. A produção de combustível é diretamente proporcional à altura em que o veículo está atualmente localizado. Além disso, quanto mais pesado o carro, mais potente é o dispositivo instalado nele e mais combustível ele produz, e a produção é diretamente proporcional à massa do carro. O aparelho revelou-se tal que a produção de combustível é exatamente igual a (onde está a aceleração de queda livre), ou seja, energia potencial do carro. 
Aqui vale a pena fazer uma explicação. Claro, é possível atirar uma pedra de um ponto de muitas maneiras diferentes para que ela atinja o ponto. Mas você precisa lançá-lo de tal forma que, tendo voado para fora de um ponto no tempo, ele atinja um ponto exatamente no tempo. É esse movimento que será mais econômico para o nosso carro. A função de Lagrange e o princípio da menor ação
Agora podemos transferir esta analogia para corpos físicos reais. Um análogo da intensidade do consumo de combustível dos corpos é chamado de função Lagrange ou Lagrangeana (em homenagem a Lagrange) e é denotado pela letra . O Lagrangiano mostra quanto “combustível” o corpo consome em um determinado momento. Para um corpo que se move num campo potencial, o Lagrangiano é igual à sua energia cinética menos a sua energia potencial. Não tão simples
Na verdade, enganei-me um pouco ao dizer que os corpos movem-se sempre de forma a minimizar a acção. Embora em muitos casos isto seja verdade, é possível pensar em situações em que a ação claramente não é mínima. 
Ambas as variantes do movimento da bola são possíveis, mas a ação no segundo caso será maior, pois durante todo esse tempo a bola se moverá com energia cinética diferente de zero.
