Gauss sats i ett vakuum. Tillämpning av Gauss sats för att beräkna elektriska fält
Som nämnts ovan kom man överens om att rita kraftlinjerna med sådan densitet att antalet linjer som genomborrar en ytenhet vinkelrät mot platsens linjer skulle vara lika med vektorns modul. Sedan kan man utifrån mönstret av spänningslinjer bedöma inte bara riktningen utan också storleken på vektorn vid olika punkter i rymden.
Låt oss betrakta fältlinjerna för en stationär positiv punktladdning. De är radiella linjer som sträcker sig från laddningen och slutar i oändligheten. Låt oss genomföra N sådana rader. Sedan på avstånd r från laddningen, antalet kraftlinjer som skär en enhetsyta av en sfär med radie r, kommer att vara lika. Detta värde är proportionellt mot fältstyrkan hos en punktladdning på avstånd r. siffra N du kan alltid välja så att jämställdheten håller
var . Eftersom kraftlinjerna är kontinuerliga, skär samma antal kraftlinjer en sluten yta av vilken form som helst som omsluter laddningen q. Beroende på laddningens tecken går kraftlinjerna antingen in i denna slutna yta eller går ut. Om antalet utgående linjer anses positivt och antalet inkommande linjer negativt, kan vi utelämna modultecknet och skriva:
| . | (1.4) |
Spänning vektor flöde. Låt oss placera en elementär dyna med area. Ytan måste vara så liten att den elektriska fältstyrkan i alla dess punkter kan anses vara densamma. Låt oss rita en normal till platsen (Fig. 1.17). Riktningen för denna normala väljs godtyckligt. Normalen gör en vinkel med vektorn. Flödet av vektorn för elektrisk fältstyrka genom en vald yta är produkten av ytarean och projektionen av vektorn för elektrisk fältstyrka på normalen till området:
 |
var är projektionen av vektorn på normalen till platsen.
Eftersom antalet fältlinjer som genomborrar ett enskilt område är lika med modulen för intensitetsvektorn i närheten av det valda området, är intensitetsvektorns flöde genom ytan proportionell mot antalet fältlinjer som korsar denna yta. Därför, i det allmänna fallet, kan flödet av fältstyrkevektorn genom området visuellt tolkas som ett värde lika med antalet fältlinjer som penetrerar detta område:
| . | (1.5) |
Observera att valet av normalens riktning är villkorat, det kan riktas åt andra hållet. Följaktligen är flödet en algebraisk storhet: flödets tecken beror inte bara på fältets konfiguration utan också på normalvektorns och intensitetsvektorns relativa orientering. Om dessa två vektorer bildar en spetsig vinkel är flödet positivt, om det är trubbigt är flödet negativt. I fallet med en sluten yta är det vanligt att ta normalen utanför det område som täcks av denna yta, det vill säga att välja den yttre normalen.
Om fältet är inhomogent och ytan är godtycklig, definieras flödet enligt följande. Hela ytan måste delas upp i små element med area , beräkna spänningsflödena genom vart och ett av dessa element och summera sedan flödena genom alla element:
Fältstyrkan kännetecknar således det elektriska fältet vid en punkt i rymden. Intensitetsflödet beror inte på fältstyrkans värde vid en given punkt, utan på fördelningen av fältet över ytan av ett visst område.
Elektriska fältlinjer kan bara börja på positiva laddningar och sluta på negativa. De kan inte börja eller sluta i rymden. Därför, om det inte finns någon elektrisk laddning inuti en viss sluten volym, måste det totala antalet linjer som går in och ut från denna volym vara noll. Om fler linjer lämnar volymen än inträder i den, så finns det en positiv laddning inuti volymen; om det kommer in fler linjer än som kommer ut, måste det finnas en negativ laddning inuti. När den totala laddningen inuti volymen är lika med noll eller när det inte finns någon elektrisk laddning i den, penetrerar fältlinjerna genom den, och det totala flödet är noll.
Dessa enkla överväganden beror inte på hur den elektriska laddningen fördelas inom volymen. Den kan placeras i mitten av volymen eller nära ytan som begränsar volymen. En volym kan innehålla flera positiva och negativa laddningar fördelade inom volymen på vilket sätt som helst. Endast den totala laddningen bestämmer det totala antalet inkommande eller utgående spänningsledningar.
Som kan ses från (1.4) och (1.5), flödet av vektorn för elektrisk fältstyrka genom en godtyckligt sluten yta som omsluter laddningen q, lika med . Om det finns inuti ytan n laddningar, då, enligt principen om fältöverlagring, kommer det totala flödet att vara summan av flödena av fältstyrkor för alla laddningar och kommer att vara lika med , där vi i detta fall menar den algebraiska summan av alla laddningar som omfattas av den slutna yta.
Gauss sats. Gauss var den första att upptäcka det enkla faktum att flödet av vektorn för elektrisk fältstyrka genom en godtyckligt sluten yta måste vara associerad med den totala laddningen som finns inuti denna volym:
 |
Gauss Karl Friedrich (1777–1855)
Stor tysk matematiker, fysiker och astronom, skapare av det absoluta systemet av enheter i fysiken. Han utvecklade teorin om elektrostatisk potential och bevisade elektrostatikens viktigaste sats (Gauss teorem). Skapat en teori för att konstruera bilder i komplexa optiska system. Han var en av de första som kom till idén om möjligheten av förekomsten av icke-euklidisk geometri. Dessutom gjorde Gauss enastående bidrag till nästan varje gren av matematiken.
Den sista relationen är Gauss sats för det elektriska fältet: intensitetsvektorns flöde genom en godtyckligt sluten yta är proportionell mot den algebraiska summan av laddningarna som finns inuti denna yta.Proportionalitetskoefficienten beror på valet av enhetssystemet.
Det bör noteras att Gauss teorem erhålls som en konsekvens av Coulombs lag och superpositionsprincipen. Om den elektriska fältstyrkan inte ändrades i omvänd proportion till kvadraten på avståndet, skulle satsen vara ogiltig. Därför är Gauss teorem tillämpbar på alla fält där den omvända kvadratlagen och superpositionsprincipen strikt är uppfyllda, till exempel på gravitationsfältet. I fallet med ett gravitationsfält, spelas rollen av laddningar som skapar fältet av massorna av kroppar. Flödet av gravitationsfältlinjer genom en stängd yta är proportionell mot den totala massan som finns inom den ytan.
Fältstyrka för ett laddat plan. Låt oss tillämpa Gauss teorem för att bestämma den elektriska fältstyrkan för ett oändligt laddat plan. Om planet är oändligt och likformigt laddat, det vill säga ytladdningstätheten är densamma på vilken plats som helst, så är de elektriska fältstyrkelinjerna vid vilken punkt som helst vinkelräta mot detta plan. För att visa detta kommer vi att använda superpositionsprincipen för spänningsvektorn. Låt oss välja två elementära sektioner på planet, som kan betraktas som punkt för punkten A, där det är nödvändigt att bestämma fältstyrkan. Som framgår av fig. 1.18 kommer den resulterande spänningsvektorn att riktas vinkelrätt mot planet. Eftersom planet kan delas upp i ett oändligt antal par av sådana sektioner för vilken observationspunkt som helst, är det uppenbart att det laddade planets fältlinjer är vinkelräta mot planet, och fältet är enhetligt (fig. 1.19). Om detta inte vore så, då när planet rörde sig längs sig självt, skulle fältet vid varje punkt i rymden förändras, men detta motsäger det laddade systemets symmetri (planet är oändligt). I fallet med ett positivt laddat plan börjar kraftlinjerna i planet och slutar i oändligheten, medan för ett negativt laddat plan börjar kraftlinjerna i oändligheten och går in i planet.
 |  |
| Ris. 1.18 | Ris. 1.19 |
För att bestämma den elektriska fältstyrkan för ett oändligt positivt laddat plan väljer vi mentalt en cylinder i rymden, vars axel är vinkelrät mot det laddade planet, och baserna är parallella med det, och en av baserna passerar genom fältpunkten av intresse för oss (bild 1.19). Cylindern skär ut ett område från det laddade planet, och cylinderns baser, som ligger på olika sidor av planet, har samma area.
Enligt Gauss teorem är flödet av vektorn för elektrisk fältstyrka genom cylinderns yta relaterat till den elektriska laddningen inuti cylindern genom uttrycket:
![]() .
.
Eftersom spänningslinjerna endast skär cylinderns baser, är flödet genom cylinderns sidoyta noll. Därför kommer spänningsvektorns flöde genom den cylindriska ytan endast att bestå av flödena genom cylinderns baser, därför,
Genom att jämföra de två sista uttrycken för intensitetsvektorflödet får vi
Elektrisk fältstyrka mellan motsatt laddade plattor. Om plattornas dimensioner avsevärt överstiger avståndet mellan dem, kan det elektriska fältet för var och en av plattorna anses vara nära fältet för ett oändligt likformigt laddat plan. Eftersom de elektriska fältstyrkelinjerna för motsatt laddade plattor mellan plattorna är riktade i en riktning (Fig. 1.20), är fältstyrkan mellan plattorna lika med
![]() .
.
I det yttre rymden har de elektriska fältstyrkelinjerna för motsatt laddade plattor motsatta riktningar, därför är den resulterande elektriska fältstyrkan noll utanför dessa plattor. Uttrycket som erhålls för intensiteten är giltigt för stora laddade plattor, när intensiteten bestäms vid en punkt belägen långt från deras kanter.

Elektrisk fältstyrka hos en likformigt laddad tunn tråd av oändlig längd. Låt oss ta reda på beroendet av den elektriska fältstyrkan hos en likformigt laddad tunn tråd av oändlig längd på avståndet till trådaxeln med hjälp av Gauss teorem. Låt oss välja en sektion av tråd med ändlig längd. Om den linjära laddningstätheten på tråden är , då är laddningen för det valda området lika med .
Låt oss betrakta fältet för en punktladdning $q$ och hitta flödet av intensitetsvektorn ($\overrightarrow(E)$) genom den slutna ytan $S$. Vi kommer att anta att laddningen är placerad inuti ytan. Spänningsvektorns flöde genom valfri yta är lika med antalet linjer i spänningsvektorn som går ut (börja vid laddningen, om $q>0$) eller antalet linjer $\overrightarrow(E)$ som går in , om $q \[Ф_E=\frac( q)((\varepsilon )_0)\ \left(1\right),\]
där flödets tecken sammanfaller med laddningens tecken.
Ostrogradsky-Gauss sats i integralform
Låt oss anta att det inuti ytan S finns N punktladdningar, värden $q_1,q_2,\dots q_N.$ Från superpositionsprincipen vet vi att den resulterande fältstyrkan för alla N laddningar kan hittas som summan av fältstyrkorna som skapas av var och en av laddningarna, då finns det:
Därför kan vi skriva för flödet av ett system av punktladdningar:
Med formel (1) får vi att:
\[Ф_E=\oint\limits_S(\överhögerpil(E)d\överhögerpil(S))=\frac(1)((\varepsilon )_0)\summa\gränser^N_(i=1)(q_i\ )\ vänster(4\höger).\]
Ekvation (4) betyder att flödet av den elektriska fältstyrkevektorn genom en sluten yta är lika med den algebraiska summan av laddningarna som finns inuti denna yta, dividerat med den elektriska konstanten. Detta är Ostrogradsky-Gauss sats i integralform. Denna sats är en konsekvens av Coulombs lag. Betydelsen av denna sats är att den låter en helt enkelt beräkna elektriska fält för olika laddningsfördelningar.
Som en konsekvens av Ostrogradsky-Gauss-satsen måste man säga att flödet av intensitetsvektorn ($Ф_E$) genom en sluten yta i det fall då laddningarna är utanför denna yta är lika med noll.
I det fall där diskretiteten hos laddningar kan ignoreras, används begreppet volymetrisk laddningstäthet ($\rho $) om laddningen är fördelad över hela volymen. Det definieras som:
\[\rho =\frac(dq)(dV)\vänster(5\höger),\]
där $dq$ är en avgift som kan anses vara punktliknande, är $dV$ en liten volym. (Beträffande $dV$ måste följande anmärkning göras. Denna volym är tillräckligt liten för att laddningstätheten i den kan anses vara konstant, men tillräckligt stor för att laddningsdiskret inte ska börja uppträda). Den totala laddningen som finns i kaviteten kan hittas som:
\[\summa\limits^N_(i=1)(q_i\ )=\int\limits_V(\rho dV)\left(6\right).\]
I det här fallet skriver vi om formel (4) i formen:
\[\oint\limits_S(\overrightarrow(E)d\overrightarrow(S))=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV)\left(7\right).\ ]
Ostrogradsky-Gauss sats i differentialform
Med hjälp av Ostrogradsky-Gauss-formeln för alla områden av vektornatur, med hjälp av vilken övergången från integration över en sluten yta till integration över en volym utförs:
\[\oint\limits_S(\overrightarrow(a)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(a)dV\ \left(8\right),\]
där $\overrightarrow(a)-$fältvektor (i vårt fall är det $\overrightarrow(E)$), $div\overrightarrow(a)=\overrightarrow(\nabla )\overrightarrow(a)=\frac(\ partiell a_x)(\partial x)+\frac(\partial a_y)(\partial y)+\frac(\partial a_z)(\partial z)$ -- divergens av vektorn $\overrightarrow(a)$ vid punkt med koordinater ( x,y,z), som mappar ett vektorfält till ett skalärt. $\overrightarrow(\nabla )=\frac(\partial )(\partial x)\overrightarrow(i)+\frac(\partial )(\partial y)\overrightarrow(j)+\frac(\partial )(\ partiell z)\överhögerpil(k)$ - observerbar operator. (I vårt fall kommer det att vara $div\overrightarrow(E)=\overrightarrow(\nabla )\overrightarrow(E)=\frac(\partial E_x)(\partial x)+\frac(\partial E_y)(\partial y) +\frac(\partial E_z)(\partial z)$) -- divergens av spänningsvektorn. Efter ovanstående skriver vi om formel (6) som:
\[\oint\limits_S(\overrightarrow(E)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(E)dV=\frac(1)((\varepsilon )_0)\int\limits_V( \rho dV)\left(9\right).\]
Likheterna i ekvation (9) är uppfyllda för vilken volym som helst, och detta är endast möjligt om funktionerna som finns i integranderna är lika i varje rymdström, det vill säga vi kan skriva att:
Uttryck (10) är Ostrogradsky-Gauss sats i differentialform. Dess tolkning är följande: laddningar är källor till ett elektriskt fält. Om $div\overrightarrow(E)>0$, så har vi vid dessa punkter i fältet (avgifterna är positiva) fältkällor, om $div\overrightarrow(E)
Uppgift: Laddningen är jämnt fördelad över volymen, en kubisk yta med sidan b väljs i denna volym. Det är inskrivet i sfären. Hitta förhållandet mellan spänningsvektorns flöden genom dessa ytor.
Enligt Gauss teorem är flödet ($Ф_E$) för intensitetsvektorn $\overrightarrow(E)$ genom en sluten yta med en enhetlig laddningsfördelning över volymen lika med:
\[Ф_E=\frac(1)((\varepsilon )_0)Q=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV=\frac(\rho )((\varepsilon ) _0)\int\limits_V(dV)=\frac(\rho V)((\varepsilon )_0))\left(1.1\right).\]
Därför måste vi bestämma volymerna av kuben och bollen om bollen beskrivs runt denna kub. Till att börja med, volymen av en kub ($V_k$) om dess sida b är lika med:
Låt oss hitta bollens volym ($V_(sh)$) med hjälp av formeln:
där $D$ är bollens diameter och (eftersom bollen är omskriven runt kuben), kubens huvuddiagonal. Därför måste vi uttrycka diagonalen för en kub i form av dess sida. Detta är lätt att göra om du använder Pythagoras sats. För att beräkna diagonalen för en kub, till exempel (1,5), måste vi först hitta diagonalen för kvadraten (kubens nedre bas) (1,6). Längden på diagonalen (1,6) är lika med:
I detta fall är längden på diagonalen (1,5) lika med:
\[(D=D)_(15)=\sqrt(b^2+((\sqrt(b^2+b^2\ \ \ )))^2)=b\sqrt(3)\ \vänster (1,5\höger).\]
Genom att ersätta kulans hittade diameter med (1.3) får vi:
Nu kan vi hitta spänningsvektorns flöden genom kubens yta, det är lika med:
\[Ф_(Ek)=\frac(\rho V_k)((\varepsilon )_0)=\frac(\rho b^3)((\varepsilon )_0)\left(1.7\right),\]
genom bollens yta:
\[Ф_(Esh)=\frac(\rho V_(sh))((\varepsilon )_0)=\frac(\rho )((\varepsilon )_0)\frac(\sqrt(3))(2) \pi b^3\ \left(1,8\höger).\]
Låt oss hitta förhållandet $\frac(Ф_(Esh))(Ф_(Ek))$:
\[\frac(Ф_(Esh))(Ф_(Ek))=\frac(\frac(с)(\varepsilon_0)\frac(\sqrt(3))(2) \pi b^3)(\frac (сb^3)(\varepsilon_0))=\frac(\pi)(2)\sqrt(3)\ \ca 2,7\vänster(1,9\höger).\]
Svar: Fluxet genom bollens yta är 2,7 gånger större.
Uppgift: Bevisa att laddningen av en ledare ligger på dess yta.
Vi använder Gauss teorem för att bevisa det. Låt oss välja en sluten yta av godtycklig form i ledaren nära ledarens yta (fig. 2).

Låt oss anta att det finns laddningar inuti ledaren, vi skriver Ostrogradsky-Gauss sats för fältdivergens för någon punkt på ytan S:
där $\rho är densiteten\ $för den inre laddningen. Det finns dock inget fält inuti ledaren, det vill säga $\overrightarrow(E)=0$, därför $div\overrightarrow(E)=0\to \rho =0$. Ostrogradsky-Gauss-satsen i differentialform är lokal, det vill säga den är skriven för en fältpunkt, vi valde inte punkten på ett speciellt sätt, därför är laddningstätheten noll vid någon punkt i fältet inuti ledaren.
Superpositionsprincipen i kombination med Coulombs lag ger nyckeln till att beräkna det elektriska fältet för ett godtyckligt system av laddningar, men direkt summering av fälten med formeln (4.2) kräver vanligtvis komplexa beräkningar. Men i närvaro av en eller annan symmetri av laddningssystemet förenklas beräkningarna avsevärt om vi introducerar begreppet elektriskt fältflöde och använder Gauss sats.
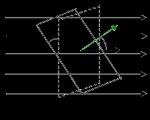
Begreppet elektriskt fältflöde introducerades i elektrodynamiken från hydrodynamiken. Inom hydrodynamik är flödet av vätska genom ett rör, det vill säga volymen av vätska N som passerar genom ett tvärsnitt av ett rör per tidsenhet, lika med v ⋅ S, där v är vätskans hastighet och S är rörets tvärsnittsarea. Om vätskehastigheten varierar över tvärsnittet måste du använda integralformeln N = ∫ S v → ⋅ d S → . Låt oss faktiskt markera ett litet område d S i hastighetsfältet, vinkelrätt mot hastighetsvektorn (Fig. ).
|
Volymen vätska som strömmar genom detta område i tiden d t är lika med v d S d t . Om plattformen lutar mot flödet kommer motsvarande volym att vara v d S cos θ d t , där θ är vinkeln mellan hastighetsvektorn v → och normalen n → till plattformen d S . Volymen vätska som strömmar genom området d S per tidsenhet erhålls genom att dividera detta värde med d t. Det är lika med v d S cos θ d t , dvs. skalär produkt v → ⋅ d S → hastighetsvektor v → av arealementvektorn d S → = n → d S . Enhetsvektorn n → vinkelrät mot arean d S kan ritas i två rakt motsatta riktningar. en av dem accepteras villkorligt som positiv. Det normala n → ritas i denna riktning. Den sida av platsen från vilken det normala n → kommer fram kallas extern, och sidan som det normala n → går in i kallas intern. Arealementvektorn d S → är riktad längs den yttre normalen n → till ytan, och är i storlek lika med arean av elementet d S = ∣ d S → ∣ . När man beräknar volymen av vätska som strömmar genom en area S med ändliga dimensioner, måste den utvecklas till oändliga ytor d S , och sedan beräkna integralen ∫ S v → ⋅ d S → över hela ytan S .
Uttryck som ∫ S v → ⋅ d S → finns i många grenar av fysik och matematik. De kallas flödet av vektorn v → genom ytan S, oavsett karaktären av vektorn v →. Inom elektrodynamiken integralen
| N = ∫ S E → ⋅ d S → | (5.1) |
Låt oss anta att vektorn E → representeras av en geometrisk summa
E → = ∑ j E → j .
Genom att multiplicera denna jämlikhet skalärt med d S → och integrera, får vi
N = ∑jNj.
där N j är flödet av vektorn E → j genom samma yta. Av principen om överlagring av elektrisk fältstyrka följer alltså att flödena genom samma yta adderas algebraiskt.
Gauss teorem säger att flödet av vektorn E → genom en godtyckligt sluten yta är lika med den totala laddningen Q för alla partiklar som finns inuti denna yta multiplicerat med 4 π:
Vi kommer att utföra bevisningen av satsen i tre steg.
1. Låt oss börja med att beräkna det elektriska fältflödet för en punktladdning q (Fig. ). I det enklaste fallet, när integrationsytan S är en sfär och laddningen är i dess centrum, är giltigheten av Gauss sats nästan uppenbar. På sfärens yta är den elektriska fältstyrkan
E → = q r → ∕ r 3
konstant i storlek och överallt riktad vinkelrätt mot ytan, så att det elektriska fältflödet helt enkelt är lika med produkten E = q ∕ r 2 och arean av sfären S = 4 π r 2 . Därför är N = 4 π q. Detta resultat är oberoende av formen på ytan som omger laddningen. För att bevisa detta väljer vi ett godtyckligt område av ytan med en tillräckligt liten storlek med riktningen för den yttre normala n → inställd på den. I fig. ett sådant segment visas i en överdrivet stor (för tydlighetens skull) storlek.
Fluxet för vektorn E → genom detta område är lika med d N = E → ⋅ d S → = E cos θ d S ,
där θ är vinkeln mellan riktningen E → och den yttre normalen n → till området d S . Eftersom E = q ∕ r 2 , och d S cos θ ∕ r 2 i absolut värde är elementet i rymdvinkeln d Ω = d S ∣ cos θ ∣ ∕ r 2 , under vilken arean d S är synlig från punkten där laddningen finns,
D N = ± qd Ω.
där plus- och minustecknet motsvarar tecknet cos θ, nämligen: du ska ta plustecknet om vektorn E → gör en spetsig vinkel med riktningen för den yttre normalen n →, och minustecknet annars.
2. Betrakta nu en ändlig yta S, som täcker en viss vald volym V. Med avseende på denna volym är det alltid möjligt att bestämma vilken av de två motsatta riktningarna av normalen till något element på ytan S som ska anses vara extern. Den yttre normalen är riktad från volym V utåt. Sammanfattningsvis över segment, fram till tecken har vi N = q Ω, där Ω är den rymdvinkel vid vilken ytan S är synlig från den punkt där laddningen q är belägen. Om ytan S är stängd är Ω = 4 π, förutsatt att laddningen q är inuti S. Annars Ω = 0. För att förtydliga det sista påståendet kan vi återigen hänvisa till fig. .
Det är uppenbart att flödena genom segment av en sluten yta, baserade på lika rymda vinklar, men vända i motsatta riktningar, upphäver varandra. Det är också uppenbart att om laddningen är utanför den slutna ytan, så finns det för varje segment som är vänt utåt ett motsvarande segment som är vänt inåt.
3. Slutligen, med hjälp av superpositionsprincipen, kommer vi fram till den slutliga formuleringen av Gauss sats (). Faktum är att fältet för ett laddningssystem är lika med summan av fälten för varje laddning separat, men endast laddningar som finns inuti den slutna ytan ger ett bidrag som inte är noll till den högra sidan av satsen (). Detta fullbordar beviset.
I makroskopiska kroppar är antalet laddningsbärare så stort att det är lämpligt att representera en diskret ensemble av partiklar i form av en kontinuerlig fördelning, vilket introducerar begreppet laddningstäthet. Per definition är laddningstätheten ρ förhållandet Δ Q ∕ Δ V i gränsen när volymen Δ V tenderar till ett fysiskt infinitesimalt värde:
där integrationen på höger sida utförs över volymen V som stängs av ytan S.Gauss sats ger en skalär ekvation för tre komponenter i vektorn E →, så denna sats ensam räcker inte för att beräkna det elektriska fältet. En känd symmetri av laddningstäthetsfördelningen är nödvändig så att problemet kan reduceras till en enda skalär ekvation. Gauss teorem gör det möjligt att hitta fältet i de fall då integrationsytan i () kan väljas så att den elektriska fältstyrkan E är konstant över hela ytan. Låt oss titta på de mest lärorika exemplen.
▸ Problem 5.1
Hitta fältet för en sfär som är jämnt laddad i volym eller ytor.
Lösning: Elektriskt fält för en punktladdning E → = q r → ∕ r 3 tenderar att oändlighet kl r → 0 . Detta faktum visar inkonsekvensen i idén elementarpartiklar genom punktladdningar. Om avgiften q likformigt fördelat över volymen av en sfär med ändlig radie a, då det elektriska fältet har inga singulariteter.
Från symmetri av problemet är det tydligt att det elektriska fältet E → överallt riktas radiellt, och dess spänning E = E(r) beror endast på avståndet r till mitten av bollen. Sedan flödar det elektriska fältet genom en sfär med radie r är helt enkelt lika med 4 π r 2 E (Fig. ).
Å andra sidan är laddningen inuti samma sfär lika med den totala laddningen kula Q om r ≥ a. Genom att likställa 4 π r 2 E med kulans laddning q multiplicerat med 4 π får vi: E (r) = q ∕ r 2 .Sålunda, i yttre rymden, skapar en laddad boll ett sådant fält som om all laddning var koncentrerad till dess centrum. Detta resultat är giltigt för alla sfäriskt symmetriska avgiftsfördelning.
Fältet inuti bollen är E (r) = Q ∕ r 2, där Q är laddningen inuti svavlet med radien r. Om laddningen är jämnt fördelad över bollens volym, då Q = q (r ∕ a) 3 . I detta fall
E (r) = q r ∕ a 3 = (4 π ∕ 3) ρ r ,
där ρ = q ∕ (4 π a 3 ∕ 3) — laddningstäthet. Inuti bollen minskar fältet linjärt från sitt maximum värden på bollens yta till noll i dess mitt (fig. ).
Funktion E(r) samtidigt är den ändlig och kontinuerlig överallt.Om laddningen är fördelad över bollens yta, då Q = 0, och därför även E = 0. Detta resultat är också giltigt för fallet inuti en sfärisk det finns ingen laddningskavitet, och externa laddningar är fördelade sfäriskt symmetriskt. ▸ Problem 5.2
Hitta fältet för en jämnt laddad oändlig tråd; gängradie a, laddning per längdenhet ϰ.
▸ Problem 5.3
Hitta fältet för en oändlig rak tråd och en oändligt lång likformigt laddad cylinder.
▸ Problem 5.4
Hitta fältet för ett oändligt laddat plan och likformigt laddat oändligt platt lager.
Lösning: På grund av problemets symmetri är fältet riktat normal till lagret och beror endast på avståndet x från plattans symmetriplan. För att beräkna ett fält med hjälp av Gauss sats är det bekvämt att välja integrationsytan S in i form av en parallellpiped, som visas i fig. .
Det sista resultatet erhålls genom att passera till gränsen a → 0 samtidigt som laddningstätheten ökarρ så att värdet σ = ρ a förblev oförändrad. På motsatta sidor av planet den elektriska fältstyrkan är densamma i storlek, men motsatt riktning. Därför när man passerar laddat plan ändras fältet abrupt med mängden 4 π σ . Observera att plattan kan betraktas som oändlig om avståndet från är försumbart jämfört med dess storlek. På avstånd mycket stora jämfört med måtten på plattan, det fungerar som en punktladdning, och dess fält minskar tillbaka proportionell mot kvadraten på avståndet.Det elektrostatiska fältet kan tydligt avbildas med hjälp av kraftlinjer (spänningslinjer). Kraftledningar kallas kurvor vars tangenter i varje punkt sammanfaller med spänningsvektorn E.
Kraftlinjer är ett konventionellt begrepp och existerar inte riktigt. Fältlinjerna för en enda negativ och enkel positiv laddning visas i fig. 5 är radiella räta linjer som kommer från en positiv laddning eller går till en negativ laddning.
Om tätheten och riktningen för fältlinjerna över hela fältets volym förblir oförändrade anses ett sådant elektrostatiskt fält vara homogent (antalet linjer måste vara numeriskt lika med fältstyrkan E).
Antalet fältlinjer markerade ">dS, vinkelräta mot dem, avgör flödet av den elektrostatiska fältstyrkevektorn:
formula" src="http://hi-edu.ru/e-books/xbook785/files/17-1.gif" border="0" align="absmiddle" alt="- projektion av vektorn E i riktningen av det normala n till stället dS (fig. 6).
Följaktligen flödet av vektor E genom en godtyckligt sluten yta S
mark">S inte bara storleken, utan också tecknet på flödet kan ändras:
1) med formel" src="http://hi-edu.ru/e-books/xbook785/files/17-4.gif" border="0" align="absmiddle" alt="
3) när vi väljer"> Låt oss hitta flödet av vektor E genom en sfärisk yta S, i vars centrum det finns en punktladdning q.
I detta fall sammanfaller märket ">E och n på alla punkter på den sfäriska ytan.
Med hänsyn till fältstyrkan för en punktladdning, formeln" src="http://hi-edu.ru/e-books/xbook785/files/18-2.gif" border="0" align="absmiddle " alt="(! LANG:vi får
formula" src="http://hi-edu.ru/e-books/xbook785/files/Fe.gif" border="0" align="absmiddle" alt="- en algebraisk mängd beroende på laddningens tecken. Till exempel, när q<0 линии Е направлены к заряду и противоположны направлению внешней нормали n ..gif" border="0" align="absmiddle" alt="runt laddningen har q en godtycklig form. Uppenbarligen är ytan märkt ">E, liksom ytan S. Därför är flödet av vektor E genom en godtycklig yta formeln" src="http://hi-edu.ru/e-books/xbook785/ files/Fe.gif" border ="0" align="absmiddle" alt=".
Om laddningen är placerad utanför den stängda ytan, så kommer uppenbarligen hur många rader som kommer in i det stängda området att lämna det. Som ett resultat kommer flödet av vektor E att vara lika med noll.
Om det elektriska fältet skapas av ett system av punktladdningar formula" src="http://hi-edu.ru/e-books/xbook785/files/18-4.gif" border="0" align="absmiddle" alt="
Denna formel är det matematiska uttrycket för Gauss teorem: flödet av den elektriska fältstyrkevektorn E i ett vakuum genom en godtyckligt sluten yta är lika med den algebraiska summan av laddningarna som den täcker, dividerat med formula" src="http://hi-edu.ru/e-books/xbook785/files/18-6.gif" border="0" align="absmiddle" alt="
För att slutföra beskrivningen, låt oss också presentera Gauss sats i en lokal form, inte beroende på integrala relationer, utan på fältparametrarna vid en given punkt i rymden. För att göra detta är det bekvämt att använda differentialoperatorn - vektordivergens, -
formula" src="http://hi-edu.ru/e-books/xbook785/files/nabla.gif" border="0" align="absmiddle" alt="("nabla") -
formula" src="http://hi-edu.ru/e-books/xbook785/files/19-1.gif" border="0" align="absmiddle" alt="
I matematisk analys är Gauss-Ostrogradsky-satsen känd: flödet av en vektor genom en sluten yta är lika med integralen av dess divergens över volymen som begränsas av denna yta -
formula" src="http://hi-edu.ru/e-books/xbook785/files/ro.gif" border="0" align="absmiddle" alt=":
formula" src="http://hi-edu.ru/e-books/xbook785/files/19-4.gif" border="0" align="absmiddle" alt="
Detta uttryck är Gauss sats i lokal (differentiell) form.
Gauss teorem (2.2) låter oss bestämma styrkorna hos olika elektrostatiska fält. Låt oss titta på flera exempel på tillämpningen av Gauss teorem.
1. Låt oss räkna E elektrostatiskt fält skapat av en likformigt laddad sfärisk yta.
Låt oss anta att en sfärisk yta med radien R bär en likformigt fördelad laddning q, dvs. ytladdningstätheten är samma märke överallt ">r >R från sfärens centrum, bygger vi mentalt en ny sfärisk yta S, symmetrisk med den laddade sfären. I enlighet med Gauss sats
formula" src="http://hi-edu.ru/e-books/xbook785/files/20-1.gif" border="0" align="absmiddle" alt="
För punkter som ligger på ytan av en laddad sfär med radien R kan vi analogt skriva:
select">inuti en laddad sfär, innehåller inte elektriska laddningar i sig själv, så flödesmärket">E = 0.
Uppgiften att beräkna fältstyrkan för ett system av elektriska laddningar med hjälp av principen om överlagring av elektrostatiska fält kan avsevärt förenklas om vi tillämpar teoremet som upptäcktes av den tyske forskaren K. Gauss (1777-1855), som bestämmer flödet av elektrisk fältstyrkevektor genom en godtyckligt sluten yta.
Från definitionen av intensitetsvektorflödet genom en sluten yta är intensitetsvektorflödet genom en sfärisk yta med radien r, som täcker en punktladdning Q belägen i dess centrum (fig. 1), lika med
Detta resultat gäller för en stängd yta med godtycklig form. Faktum är att om du innesluter en sfär (fig. 1) i en godtyckligt sluten yta, kommer varje spänningslinje som penetrerar sfären också att passera genom denna yta.
Om en stängd yta av någon form omsluter en laddning (Fig. 2), så kommer den antingen in i eller ut ur den när någon spänningslinje skär ytan. Vid beräkning av flöde reduceras i slutändan ett udda antal skärningar till en enda skärning, eftersom flödet antas vara positivt om spänningslinjer lämnar ytan och negativt för linjer som kommer in i ytan. Om en sluten yta inte omsluter en laddning , då är flödet genom det noll, så hur antalet spänningslinjer som kommer in i ytan är lika med antalet spänningslinjer som lämnar den.
Detta betyder att för en yta med godtycklig form, om den är stängd och innehåller en punktladdning Q, flödet av vektorn E kommer att vara lika med Q/ε 0, dvs.
Tecknet för flödet sammanfaller med tecknet för laddningen Q.
Låt oss studera det allmänna fallet med en godtycklig yta som omger n laddningar. Med hjälp av principen om superposition, spänning E fält, som skapas av alla laddningar, är lika med summan av intensiteterna E i fält som skapas av varje laddning separat. Det är därför
Enligt (1) är var och en av integralerna som visas under summatecknet lika med Q i /ε 0 . Betyder att,
![]() (2)
(2)
Formel (2) uttrycker Gauss teorem för det elektrostatiska fältet i vakuum: flödet av den elektrostatiska fältstyrkevektorn i ett vakuum genom en godtyckligt sluten yta är lika med den algebraiska summan av laddningarna inuti denna yta, dividerat med ε 0. Detta teorem erhölls matematiskt för ett vektorfält av godtycklig natur av den ryske matematikern M.V. Ostrogradsky (1801-1862), och sedan oberoende av honom i förhållande till det elektrostatiska fältet - av K. Gauss.
I det allmänna fallet kan elektriska laddningar fördelas med en viss volymdensitet ρ=dQ/dV, som är olika på olika platser i rymden. Sedan den totala laddningen inuti den slutna ytan S, som täcker en viss volym V,
![]() (3)
(3)
Med formel (3) kan Gauss sats (2) skrivas på följande sätt:
Cirkulation av spänningsvektorn är det arbete som utförs av elektriska krafter när en enda positiv laddning flyttas längs en sluten bana L
| | (13.18) |
Eftersom arbetet med de elektrostatiska fältkrafterna längs en sluten slinga är noll (arbetet av de potentiella fältkrafterna), är därför cirkulationen av den elektrostatiska fältstyrkan längs en sluten slinga noll.
Elektrostatisk fältpotential. Fältet för en konservativ kraft kan beskrivas inte bara av en vektorfunktion, utan en ekvivalent beskrivning av detta fält kan erhållas genom att definiera en lämplig skalär kvantitet vid var och en av dess punkter. För ett elektrostatiskt fält är denna mängd elektrostatisk fältpotential, definierad som förhållandet mellan den potentiella energin hos testladdningen q till storleken på denna laddning, = W P / q, av vilket det följer att potentialen är numeriskt lika med den potentiella energin som en enhets positiv laddning besitter vid en given punkt i fältet. Måttenheten för potential är Volt (1 V).
Punktladdningsfältpotential F i ett homogent isotropiskt medium med dielektricitetskonstant :
Superpositionsprincipen. Potentialen är en skalär funktion, principen om superposition är giltig för den. Så för fältpotentialen för ett system av punktladdningar F 1, F 2, Qn vi har
![]() ,
,
Var r jag- avstånd från fältpunkten med potential till laddningen Qi. Om laddningen är godtyckligt fördelad i rymden, då
![]() ,
,
Var r- avstånd från den elementära volymen d x,d y,d z att peka ( x, y, z), där potentialen bestäms; V- volymen utrymme där laddningen är fördelad.
Potential och arbete av elektriska fältkrafter. Baserat på definitionen av potential kan det visas att det arbete som utförs av det elektriska fältet tvingar när en punktladdning förflyttas q från en punkt i fältet till en annan är lika med produkten av storleken på denna laddning och potentialskillnaden vid banans initiala och sista punkt, A = q (
Om vi, i analogi med potentiell energi, antar att potentialen är noll i punkter som är oändligt långt borta från elektriska laddningar - fältkällor, så krafter det elektriska fältets arbete när en laddning förflyttas q från punkt 1 till oändlighet kan representeras som A q 1 .
Således är potentialen vid en given punkt av det elektrostatiska fältet fysisk kvantitet numeriskt lika med det arbete som utförs av krafterna i det elektriska fältet när en enhets positiv punktladdning flyttas från en given punkt i fältet till en oändligt avlägsen punkt: = A / q.
I vissa fall är den elektriska fältpotentialen tydligare definierad som en fysisk storhet numeriskt lika med externa krafters arbete mot krafterna i det elektriska fältet när en enhets positiv punktladdning flyttas från oändligheten till en given punkt. Det är bekvämt att skriva den sista definitionen så här:
Inom modern vetenskap och teknik, särskilt när man beskriver fenomen som inträffar i mikrokosmos, en enhet av arbete och energi som kallas elektron-volt(eV). Detta är det arbete som utförs när man flyttar en laddning lika med laddningen av en elektron mellan två punkter med en potentialskillnad på 1 V: 1 eV = 1,6010 C1 V = 1,6010 J
Ekvipotentiella ytor- ett koncept som är tillämpligt på alla potentiella vektorfält, till exempel ett statiskt elektriskt fält eller ett Newtonskt gravitationsfält. En ekvipotentialyta är en yta på vilken skalärpotentialen för ett givet potentialfält får ett konstant värde (potentialnivåyta). En annan, ekvivalent definition är en yta som är ortogonal mot fältlinjerna vid vilken punkt som helst.
Ytan på en ledare i elektrostatik är en ekvipotentialyta. Dessutom ändrar inte konfigurationen av det elektrostatiska fältet att placera en ledare på en ekvipotentialyta. Detta faktum används i bildmetoden, som möjliggör beräkning av det elektrostatiska fältet för komplexa konfigurationer.
I ett (stationärt) gravitationsfält etableras nivån av en stationär vätska längs ekvipotentialytan. Speciellt kan man ungefärligt konstatera att havets nivå passerar längs den ekvipotentiella ytan av jordens gravitationsfält. Formen på havens yta, utsträckt till jordens yta, kallas geoiden och spelar en viktig roll i geodesin. Geoiden är alltså en ekvipotentiell yta av gravitation, bestående av en gravitations- och en centrifugalkomponent.