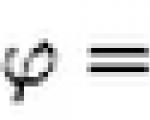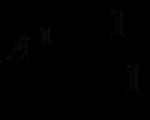Wie schreibt man die Gleichung harmonischer Schwingungen? Harmonische Schwingungen und ihre Eigenschaften

Die einfachste Art von Vibrationen sind harmonische Schwingungen- Schwankungen, bei denen sich die Verschiebung des Schwingpunktes aus der Gleichgewichtslage im Laufe der Zeit nach dem Sinus- oder Kosinusgesetz ändert.

Bei einer gleichmäßigen Drehung der Kugel um den Umfang führt ihre Projektion (Schatten in parallelen Lichtstrahlen) eine harmonische Schwingungsbewegung auf einem vertikalen Bildschirm aus (Abb. 1).

Die Verschiebung aus der Gleichgewichtslage bei harmonischen Schwingungen wird durch eine Gleichung (diese wird als kinematisches Gesetz der harmonischen Bewegung bezeichnet) der Form beschrieben:

wobei x – Verschiebung – ein Wert ist, der die Position des oszillierenden Punktes zum Zeitpunkt t relativ zur Gleichgewichtsposition charakterisiert und anhand des Abstands von der Gleichgewichtsposition zur Position des Punktes zu einem bestimmten Zeitpunkt gemessen wird; A – Schwingungsamplitude – die maximale Verschiebung des Körpers aus der Gleichgewichtslage; T – Schwingungsperiode – die Zeit einer vollständigen Schwingung; diese. der kleinste Zeitraum, nach dem sich die Werte der die Schwingung charakterisierenden physikalischen Größen wiederholen; - Anfangsphase;

Die Phase der Schwingung zum Zeitpunkt t. Die Schwingungsphase ist ein Argument einer periodischen Funktion, die bei gegebener Schwingungsamplitude den Zustand des Schwingungssystems (Auslenkung, Geschwindigkeit, Beschleunigung) des Körpers zu jedem Zeitpunkt bestimmt.

Wenn im Anfangszeitpunkt der oszillierende Punkt maximal aus der Gleichgewichtsposition verschoben ist, dann ändert sich die Verschiebung des Punktes aus der Gleichgewichtsposition gemäß dem Gesetz

Befindet sich der oszillierende Punkt in einer stabilen Gleichgewichtslage, ändert sich gesetzesgemäß die Verschiebung des Punktes aus der Gleichgewichtslage

Der Wert V, der Kehrwert der Periode und gleich der Anzahl der in 1 s durchgeführten vollständigen Schwingungen, wird Schwingungsfrequenz genannt:

Wenn der Körper in der Zeit t N vollständige Schwingungen ausführt, dann

der Wert , die angibt, wie viele Schwingungen der Körper in s ausführt, heißt zyklische (zirkuläre) Frequenz.

Das kinematische Gesetz der harmonischen Bewegung kann wie folgt geschrieben werden:

Grafisch wird die Abhängigkeit der Verschiebung eines oszillierenden Punktes von der Zeit durch einen Kosinus (oder Sinus) dargestellt.

Abbildung 2, a zeigt die Zeitabhängigkeit der Verschiebung des Schwingpunkts aus der Gleichgewichtslage für den Fall .

Lassen Sie uns herausfinden, wie sich die Geschwindigkeit eines oszillierenden Punktes mit der Zeit ändert. Dazu ermitteln wir die zeitliche Ableitung dieses Ausdrucks:

Dabei ist die Amplitude der Geschwindigkeitsprojektion auf der x-Achse.

Diese Formel zeigt, dass sich bei harmonischen Schwingungen auch die Projektion der Körpergeschwindigkeit auf die x-Achse nach dem harmonischen Gesetz mit gleicher Frequenz, unterschiedlicher Amplitude ändert und der Mischphase um (Abb. 2, b) voraus ist. .

Um die Abhängigkeit der Beschleunigung herauszufinden, ermitteln wir die Zeitableitung der Geschwindigkeitsprojektion:

Dabei ist die Amplitude der Beschleunigungsprojektion auf der x-Achse.

Bei harmonischen Schwingungen liegt die Beschleunigungsprojektion um k vor der Phasenverschiebung (Abb. 2, c).

Ebenso können Sie Abhängigkeitsdiagramme erstellen

Harmonische Wellengleichung

Die harmonische Schwingungsgleichung legt die Abhängigkeit der Körperkoordinate von der Zeit fest

Der Kosinusgraph hat im Anfangsmoment einen Maximalwert und der Sinusgraph hat im Anfangsmoment einen Nullwert. Wenn wir beginnen, die Schwingung aus der Gleichgewichtslage zu untersuchen, wird die Schwingung die Sinuskurve wiederholen. Wenn wir beginnen, die Schwingung von der Stelle der maximalen Abweichung aus zu betrachten, dann wird die Schwingung den Kosinus beschreiben. Oder man kann eine solche Schwingung durch die Sinusformel mit der Anfangsphase beschreiben.

Geschwindigkeits- und Beschleunigungsänderung bei harmonischer Schwingung

Nicht nur die Koordinate des Körpers ändert sich mit der Zeit nach dem Sinus- oder Kosinusgesetz. Aber auch Größen wie Kraft, Geschwindigkeit und Beschleunigung verändern sich in ähnlicher Weise. Kraft und Beschleunigung sind maximal, wenn sich der oszillierende Körper in den Extrempositionen befindet, in denen die Verschiebung maximal ist, und sind gleich Null, wenn der Körper die Gleichgewichtsposition durchläuft. Die Geschwindigkeit hingegen ist in den Extrempositionen gleich Null, und wenn der Körper die Gleichgewichtsposition überschreitet, erreicht sie ihren Maximalwert.

Wenn die Schwingung nach dem Kosinusgesetz beschrieben wird

Wenn die Schwingung nach dem Sinusgesetz beschrieben wird

Maximale Geschwindigkeits- und Beschleunigungswerte

Nach der Analyse der Abhängigkeitsgleichungen v(t) und a(t) kann man vermuten, dass die Maximalwerte von Geschwindigkeit und Beschleunigung angenommen werden, wenn der trigonometrische Faktor gleich 1 oder -1 ist. Bestimmt durch die Formel

Mechanische Vibrationen. Schwingungsparameter. Harmonische Schwingungen.

Zögern Als Vorgang bezeichnet man einen Vorgang, der sich in bestimmten Zeitabständen genau oder annähernd wiederholt.

Ein Merkmal von Schwingungen ist das obligatorische Vorhandensein einer stabilen Gleichgewichtslage auf der Flugbahn, in der die Summe aller auf den Körper einwirkenden Kräfte gleich Null ist, was als Gleichgewichtslage bezeichnet wird.

Ein mathematisches Pendel ist ein materieller Punkt, der an einem dünnen, schwerelosen und nicht dehnbaren Faden hängt.

Parameter der oszillierenden Bewegung.

1. Offset oder Koordinate (X) - Abweichung von der Gleichgewichtslage in einem gegebenen Zustand

Moment der Zeit.	[X ]=M

2. Amplitude ( xm) ist die maximale Abweichung von der Gleichgewichtslage.

[ X M ]=M

3. Schwingungsperiode ( T) ist die Zeit, die für eine vollständige Schwingung benötigt wird.

[T ]=C.

0 "style="margin-left:31.0pt;border-collapse:collapse">

Mathematische Pendel

Federpendel

M

https://pandia.ru/text/79/117/images/image006_26.gif" width="134" height="57 src="> Frequenz (linear) ( N ) – die Anzahl der vollständigen Schwingungen in 1 s.

[n]= Hz

5. Zyklische Häufigkeit ( w ) – die Anzahl der vollständigen Schwingungen in 2p Sekunden, also etwa 6,28 s.

w = 2pn ; [w]=0" style="margin-left:116.0pt;border-collapse:collapse">

https://pandia.ru/text/79/117/images/image012_9.jpg" width="90" height="103">

Der Schatten auf dem Bildschirm schwankt.

Gleichung und Diagramm harmonischer Schwingungen.

Harmonische Schwingungen - das sind Schwingungen, bei denen sich die Koordinate im Laufe der Zeit nach dem Sinus- oder Kosinusgesetz ändert.

https://pandia.ru/text/79/117/images/image014_7.jpg" width="254" height="430 src="> X=XMSünde(w T+j 0 )

X=XMcos(w T+j 0 )

x - Koordinate,

Xm ist die Schwingungsamplitude,

w ist die zyklische Frequenz,

wt+j 0 = j ist die Schwingungsphase,

J 0 ist die Anfangsphase der Schwingungen.

https://pandia.ru/text/79/117/images/image016_4.jpg" width="247" height="335 src=">

Diagramme sind unterschiedlich nur Amplitude

Diagramme unterscheiden sich nur in der Periode (Häufigkeit)

https://pandia.ru/text/79/117/images/image018_3.jpg" width="204" height="90 src=">

Ändert sich die Amplitude der Schwingungen im Laufe der Zeit nicht, spricht man von Schwingungen ungedämpft.

Natürliche Schwingungen berücksichtigen keine Reibung, die gesamte mechanische Energie des Systems bleibt konstant: E bis + E n = E Fell = const.

Eigenschwingungen sind ungedämpft.

Bei erzwungenen Schwingungen gleicht die kontinuierlich oder periodisch von außen zugeführte Energie die durch die Arbeit der Reibungskraft entstehenden Verluste aus und die Schwingungen können ungedämpft sein.

Die kinetische und potentielle Energie des Körpers gehen bei Schwingungen ineinander über. Wenn die Abweichung des Systems von der Gleichgewichtslage maximal ist, ist die potentielle Energie maximal und die kinetische Energie Null. Beim Durchlaufen der Gleichgewichtslage verhält es sich umgekehrt.

Die Frequenz freier Schwingungen wird durch die Parameter des Schwingungssystems bestimmt.

Die Frequenz erzwungener Schwingungen wird durch die Frequenz der äußeren Kraft bestimmt. Die Amplitude erzwungener Schwingungen hängt auch von der äußeren Kraft ab.

Resonanz C

Resonanz bezeichnet einen starken Anstieg der Amplitude erzwungener Schwingungen, wenn die Frequenz der Einwirkung einer äußeren Kraft mit der Frequenz der Eigenschwingungen des Systems übereinstimmt.

Wenn die Frequenz w der Kraftänderung mit der Eigenfrequenz w0 der Schwingungen des Systems übereinstimmt, leistet die Kraft über den gesamten Zeitraum positive Arbeit und erhöht die Amplitude der Schwingungen des Körpers. Bei jeder anderen Frequenz verrichtet die Kraft während eines Teils der Periode positive Arbeit und während des anderen Teils der Periode negative Arbeit.

Bei Resonanz kann eine Erhöhung der Schwingungsamplitude zur Zerstörung des Systems führen.

Im Jahr 1905 stürzte unter den Hufen eines Kavalleriegeschwaders der Garde die ägyptische Brücke über den Fluss Fontanka in St. Petersburg ein.

Selbstschwingungen.

Als Eigenschwingungen werden ungedämpfte Schwingungen im System bezeichnet, die durch interne Energiequellen unterstützt werden, sofern keine äußere Kraftänderung vorliegt.

Im Gegensatz zu erzwungenen Schwingungen werden Frequenz und Amplitude von Eigenschwingungen durch die Eigenschaften des Schwingungssystems selbst bestimmt.

Selbstschwingungen unterscheiden sich von freien Schwingungen durch die Unabhängigkeit der Amplitude von der Zeit und von der anfänglichen kurzfristigen Wirkung, die den Schwingungsprozess anregt. Ein selbstschwingendes System lässt sich üblicherweise in drei Elemente unterteilen:

1) Schwingsystem;

2) Energiequelle;

3) ein Rückkopplungsgerät, das den Energiefluss von einer Quelle in ein oszillierendes System reguliert.

Die über einen Zeitraum von der Quelle kommende Energie ist gleich der Energie, die im gleichen Zeitraum im Schwingungssystem verloren geht.

Wir haben mehrere physikalisch völlig unterschiedliche Systeme betrachtet und darauf geachtet, dass die Bewegungsgleichungen auf die gleiche Form reduziert werden

Unterschiede zwischen physikalischen Systemen äußern sich lediglich in unterschiedlichen Definitionen der Größe und in einem anderen physikalischen Sinne der Variablen X: Es kann sich um eine Koordinate, einen Winkel, eine Ladung, einen Strom usw. handeln. Beachten Sie, dass in diesem Fall, wie sich aus der Struktur der Gleichung (1.18) ergibt, die Größe immer die Dimension der umgekehrten Zeit hat.

Gleichung (1.18) beschreibt die sogenannte harmonische Schwingungen.

Die Gleichung harmonischer Schwingungen (1.18) ist eine lineare Differentialgleichung zweiter Ordnung (da sie die zweite Ableitung der Variablen enthält). X). Das bedeutet die Linearität der Gleichung

wenn überhaupt funktion x(t) eine Lösung dieser Gleichung ist, dann ist die Funktion Cx(t) wird auch seine Lösung sein ( C ist eine beliebige Konstante);

wenn funktioniert x 1 (t) Und x 2 (t) sind Lösungen dieser Gleichung, dann ihre Summe x 1 (t) + x 2 (t) wird auch eine Lösung für dieselbe Gleichung sein.

Außerdem wird ein mathematischer Satz bewiesen, nach dem eine Gleichung zweiter Ordnung zwei unabhängige Lösungen hat. Alle anderen Lösungen können entsprechend den Eigenschaften der Linearität als ihre Linearkombinationen erhalten werden. Durch direkte Differenzierung lässt sich leicht überprüfen, ob die unabhängigen Funktionen Gleichung (1.18) erfüllen. Die allgemeine Lösung dieser Gleichung lautet also:

Wo C1,C2 sind beliebige Konstanten. Diese Lösung kann auch in anderer Form dargestellt werden. Wir geben die Menge ein

und definieren Sie den Winkel als:

Dann wird die allgemeine Lösung (1.19) geschrieben als

Gemäß den Trigonometrieformeln lautet der Ausdruck in Klammern

Endlich kommen wir an allgemeine Lösung der Gleichung harmonischer Schwingungen als:

Nicht negativer Wert A angerufen Schwingungsamplitude, - die Anfangsphase der Schwingung. Das gesamte Kosinusargument – ​​die Kombination – wird aufgerufen Schwingungsphase.

Die Ausdrücke (1.19) und (1.23) sind vollkommen äquivalent, sodass wir der Einfachheit halber beide verwenden können. Beide Lösungen sind periodische Funktionen der Zeit. Tatsächlich sind Sinus und Cosinus periodisch mit einer Periode . Daher wiederholen sich verschiedene Zustände eines Systems, das harmonische Schwingungen ausführt, nach einer gewissen Zeit T*, wobei die Schwingungsphase ein Inkrement erhält, das ein Vielfaches von ist :

Daraus folgt daraus

Die geringste dieser Zeiten

angerufen Schwingungsdauer (Abb. 1.8), a - sein kreisförmig (zyklisch) Frequenz.

Reis. 1.8.

Sie verwenden auch Frequenz Zögern

Dementsprechend ist die Kreisfrequenz gleich der Anzahl der Schwingungen pro Sekunden.

Also, wenn das System zur Zeit T gekennzeichnet durch den Wert der Variablen x(t), dann wird die Variable nach einer gewissen Zeit denselben Wert haben (Abb. 1.9), d. h

Der gleiche Wert wird sich natürlich nach einer Weile wiederholen. 2T, ZT usw.

Reis. 1.9. Schwingungsperiode

Die allgemeine Lösung umfasst zwei beliebige Konstanten ( C 1 , C 2 oder A, A), deren Werte durch zwei bestimmt werden sollten Anfangsbedingungen. Normalerweise (wenn auch nicht unbedingt) spielen die Anfangswerte der Variablen ihre Rolle x(0) und seine Ableitung.

Nehmen wir ein Beispiel. Die Lösung (1.19) der Gleichung harmonischer Schwingungen beschreibe die Bewegung eines Federpendels. Die Werte beliebiger Konstanten hängen davon ab, wie wir das Pendel aus dem Gleichgewicht gebracht haben. Wir haben zum Beispiel die Feder auf Abstand gezogen und ließ den Ball ohne Anfangsgeschwindigkeit los. In diesem Fall

Ersetzen t = 0 in (1.19) finden wir den Wert der Konstante Ab 2

Die Lösung sieht also so aus:

Die Geschwindigkeit der Last wird durch Differenzierung nach der Zeit ermittelt

Hier ersetzen T = 0, finde die Konstante Ab 1:

Endlich

Beim Vergleich mit (1.23) finden wir das ist die Schwingungsamplitude und ihre Anfangsphase ist gleich Null: .

Wir bringen das Pendel nun auf andere Weise aus dem Gleichgewicht. Schlagen wir die Ladung so an, dass sie eine Anfangsgeschwindigkeit erhält, sich aber beim Aufprall praktisch nicht bewegt. Wir haben dann andere Anfangsbedingungen:

Unsere Lösung sieht so aus

Die Geschwindigkeit der Last ändert sich gemäß dem Gesetz:

Platzieren wir es hier:

Themen des USE-Kodifikators: harmonische Schwingungen; Amplitude, Periode, Frequenz, Phase der Schwingungen; freie Schwingungen, erzwungene Schwingungen, Resonanz.

Schwankungen sind Veränderungen im Zustand des Systems, die sich im Laufe der Zeit wiederholen. Der Begriff der Schwingungen umfasst ein sehr breites Spektrum an Phänomenen.

Schwingungen mechanischer Systeme, bzw mechanische Schwingungen- Dies ist eine mechanische Bewegung eines Körpers oder eines Körpersystems, die zeitlich wiederholbar ist und in der Nähe der Gleichgewichtslage auftritt. Gleichgewichtslage Dies ist der Zustand des Systems, in dem es beliebig lange verweilen kann, ohne dass es äußere Einflüsse erfährt.

Wird beispielsweise das Pendel ausgelenkt und losgelassen, kommt es zu Schwingungen. Die Gleichgewichtslage ist die Lage des Pendels ohne Auslenkung. In dieser Position kann das Pendel, wenn es unberührt bleibt, auf unbestimmte Zeit verbleiben. Wenn das Pendel schwingt, durchläuft es die Gleichgewichtslage viele Male.

Unmittelbar nachdem das ausgelenkte Pendel losgelassen wurde, begann es sich zu bewegen, passierte die Gleichgewichtsposition, erreichte die entgegengesetzte Extremposition, blieb dort für einen Moment stehen, bewegte sich in die entgegengesetzte Richtung, passierte die Gleichgewichtsposition erneut und kehrte zurück. Eines ist passiert Voller Schwung. Dieser Vorgang wird dann regelmäßig wiederholt.

Amplitude der Körperschwingungen ist der Betrag seiner größten Abweichung von der Gleichgewichtslage.

Schwingungsperiode ist die Zeit für eine vollständige Schwingung. Wir können sagen, dass der Körper für den Zeitraum einen Weg mit vier Amplituden zurücklegt.

Schwingungsfrequenz ist der Kehrwert der Periode: . Die Frequenz wird in Hertz (Hz) gemessen und gibt an, wie viele vollständige Schwingungen in einer Sekunde auftreten.

Harmonische Schwingungen.

Wir gehen davon aus, dass die Position des Schwingkörpers durch eine einzige Koordinate bestimmt wird. Der Wert entspricht der Gleichgewichtslage. Die Hauptaufgabe der Mechanik besteht in diesem Fall darin, eine Funktion zu finden, die jederzeit die Koordinaten des Körpers angibt.

Für die mathematische Beschreibung von Schwingungen ist es naheliegend, periodische Funktionen zu verwenden. Es gibt viele solcher Funktionen, aber zwei davon – Sinus und Cosinus – sind die wichtigsten. Sie haben viele gute Eigenschaften und stehen in engem Zusammenhang mit einer Vielzahl physikalischer Phänomene.

Da sich die Sinus- und Kosinusfunktionen durch Verschiebung des Arguments um voneinander ergeben, können wir uns auf nur eine davon beschränken. Der Bestimmtheit halber verwenden wir den Kosinus.

Harmonische Schwingungen sind Schwingungen, bei denen die Koordinate nach dem harmonischen Gesetz von der Zeit abhängt:

(1)

Lassen Sie uns die Bedeutung der in dieser Formel enthaltenen Größen herausfinden.

Ein positiver Wert ist der größte Koordinatenwert im Absolutwert (da der Maximalwert des Kosinusmoduls gleich eins ist), also die größte Abweichung von der Gleichgewichtslage. Daher - die Amplitude der Schwingungen.

Das Kosinusargument heißt Phase Schwankungen. Der Wert, der dem Wert der Phase at entspricht, wird als Anfangsphase bezeichnet. Die Anfangsphase entspricht der Anfangskoordinate des Körpers: .

Der Wert wird aufgerufen zyklische Frequenz. Lassen Sie uns den Zusammenhang mit der Schwingungsdauer und -frequenz finden. Eine vollständige Schwingung entspricht einem Phaseninkrement gleich dem Bogenmaß: , daher

(2)

(3)

Die zyklische Frequenz wird in rad/s (Radiant pro Sekunde) gemessen.

Gemäß den Ausdrücken (2) und (3) erhalten wir zwei weitere Formen der Aufzeichnung des harmonischen Gesetzes (1) :

Der Graph der Funktion (1), der die Abhängigkeit der Koordinate von der Zeit bei harmonischen Schwingungen ausdrückt, ist in Abb. dargestellt. 1 .

Das harmonische Gesetz der Form (1) ist allgemeinster Natur. Es beantwortet beispielsweise die Situation, in der zwei anfängliche Aktionen gleichzeitig mit dem Pendel ausgeführt wurden: Sie lenkten es um einen Betrag ab und gaben ihm eine gewisse Anfangsgeschwindigkeit. Es gibt zwei wichtige Sonderfälle, in denen eine dieser Aktionen nicht ausgeführt wurde.

Lassen Sie das Pendel zurückweisen, aber die Anfangsgeschwindigkeit wurde nicht gemeldet (sie wurden ohne die Anfangsgeschwindigkeit losgelassen). Es ist klar, dass wir es in diesem Fall so sagen können. Wir erhalten den Kosinussatz:

Der Graph der harmonischen Schwingungen in diesem Fall ist in Abb. dargestellt. 2.

Reis. 2. Kosinusgesetz

Nehmen wir nun an, dass das Pendel nicht ausgelenkt wurde, sondern dass ihm durch einen Schlag die Anfangsgeschwindigkeit aus der Gleichgewichtslage verliehen wurde. In diesem Fall können Sie also sagen. Wir erhalten das Sinusgesetz:

Der Schwankungsplan ist auf Abb. dargestellt. 3 .

Reis. 3. Sinusgesetz

Die Gleichung harmonischer Schwingungen.

Kehren wir zum allgemeinen harmonischen Gesetz (1) zurück. Lassen Sie uns diese Gleichung differenzieren:

. (4)

Nun differenzieren wir die resultierende Gleichheit (4):

. (5)

Vergleichen wir Ausdruck (1) für die Koordinate und Ausdruck (5) für die Beschleunigungsprojektion. Wir sehen, dass sich die Beschleunigungsprojektion von der Koordinate nur um den Faktor unterscheidet:

. (6)

Dieses Verhältnis heißt Gleichung harmonischer Schwingungen. Es kann auch in dieser Form umgeschrieben werden:

. (7)

Aus mathematischer Sicht gilt Gleichung (7). Differentialgleichung. Die Lösungen von Differentialgleichungen sind Funktionen (und keine Zahlen wie in der gewöhnlichen Algebra).
Wir können also Folgendes beweisen:

Die Lösung der Gleichung (7) ist eine beliebige Funktion der Form (1) mit beliebigem ;

Keine andere Funktion ist eine Lösung dieser Gleichung.

Mit anderen Worten, die Beziehungen (6), (7) beschreiben harmonische Schwingungen mit zyklischer Frequenz und nur diese. Aus den Anfangsbedingungen werden zwei Konstanten bestimmt – durch die Anfangswerte der Koordinate und der Geschwindigkeit.

Federpendel.

Federpendel ist eine auf einer Feder befestigte Last, die in horizontaler oder vertikaler Richtung schwingen kann.

Finden wir die Periode kleiner horizontaler Schwingungen des Federpendels (Abb. 4). Die Schwingungen sind gering, wenn das Ausmaß der Verformung der Feder viel geringer ist als ihre Abmessungen. Für kleine Verformungen können wir das Hookesche Gesetz verwenden. Dadurch werden die Schwingungen harmonisch.

Wir vernachlässigen die Reibung. Die Masse hat eine Masse und die Federkonstante ist.

Die Koordinate entspricht der Gleichgewichtslage, in der die Feder nicht verformt ist. Daher ist die Größe der Federverformung gleich dem Modul der Lastkoordinate.

Reis. 4. Federpendel

In horizontaler Richtung wirkt nur die elastische Kraft der Feder auf die Last. Das zweite Newtonsche Gesetz für die Last in der Projektion auf die Achse lautet:

. (8)

Wenn (die Last wird wie in der Abbildung nach rechts verschoben), dann ist die elastische Kraft in die entgegengesetzte Richtung gerichtet und . Umgekehrt gilt: wenn, dann. Die Vorzeichen und sind immer entgegengesetzt, daher kann das Hookesche Gesetz wie folgt geschrieben werden:

Dann nimmt die Beziehung (8) die Form an:

Wir haben eine Gleichung harmonischer Schwingungen der Form (6) erhalten, in der

Die zyklische Schwingungsfrequenz eines Federpendels ist somit gleich:

. (9)

Daraus und aus dem Verhältnis ermitteln wir die Periode der horizontalen Schwingungen des Federpendels:

. (10)

Wenn man ein Gewicht an eine Feder hängt, erhält man ein Federpendel, das in vertikaler Richtung schwingt. Es lässt sich zeigen, dass in diesem Fall die Formel (10) auch für die Schwingungsdauer gilt.

Mathematische Pendel.

Mathematische Pendel - Dies ist ein kleiner Körper, der an einem schwerelosen, nicht dehnbaren Faden hängt (Abb. 5). Ein mathematisches Pendel kann im Bereich der Schwerkraft in einer vertikalen Ebene schwingen.

Reis. 5. Mathematische Pendel

Finden wir die Periode kleiner Schwingungen des mathematischen Pendels. Die Gewindelänge beträgt . Der Luftwiderstand wird vernachlässigt.

Schreiben wir Newtons zweites Gesetz für das Pendel auf:

und projiziere es auf die Achse:

Wenn das Pendel eine Position wie in der Abbildung einnimmt (d. h.), dann:

Befindet sich das Pendel auf der anderen Seite der Gleichgewichtsposition (d. h.), dann gilt:

Für jede Position des Pendels gilt also:

. (11)

Wenn das Pendel in der Gleichgewichtslage ruht, ist die Gleichheit erfüllt. Bei kleinen Schwingungen, wenn die Abweichungen des Pendels von der Gleichgewichtslage klein sind (im Vergleich zur Länge des Fadens), ist die ungefähre Gleichheit erfüllt. Verwenden wir es in Formel (11):

Dies ist eine Gleichung harmonischer Schwingungen der Form (6), in der

Daher ist die zyklische Schwingungsfrequenz eines mathematischen Pendels gleich:

. (12)

Daher die Schwingungsdauer des mathematischen Pendels:

. (13)

Bitte beachten Sie, dass Formel (13) die Masse der Ladung nicht berücksichtigt. Im Gegensatz zu einem Federpendel hängt die Schwingungsdauer eines mathematischen Pendels nicht von seiner Masse ab.

Freie und erzwungene Vibrationen.

Das System soll freie Schwingungen, wenn es einmal aus der Gleichgewichtslage genommen und anschließend sich selbst überlassen wird. Keine periodischen externen
Gleichzeitig erfährt das System keine Stöße und es gibt keine internen Energiequellen, die Schwingungen im System unterstützen.

Die oben betrachteten Schwingungen des Federpendels und des mathematischen Pendels sind Beispiele für freie Schwingungen.

Die Frequenz, bei der freie Schwingungen auftreten, heißt Eigenfrequenz Schwingsystem. Die Formeln (9) und (12) geben also die natürlichen (zyklischen) Schwingungsfrequenzen von Feder- und mathematischen Pendeln an.

In einer idealisierten Situation ohne Reibung sind freie Schwingungen ungedämpft, d. h. sie haben eine konstante Amplitude und dauern unbegrenzt an. In realen Schwingsystemen ist immer Reibung vorhanden, sodass freie Schwingungen allmählich gedämpft werden (Abb. 6).

Erzwungene Vibrationen- Hierbei handelt es sich um Schwingungen, die das System unter dem Einfluss einer äußeren Kraft erzeugt, die sich im Laufe der Zeit periodisch ändert (die sogenannte treibende Kraft).

Nehmen wir an, dass die Eigenschwingungsfrequenz des Systems beträgt und die treibende Kraft gemäß dem harmonischen Gesetz von der Zeit abhängt:

Seit einiger Zeit stellen sich erzwungene Schwingungen ein: Das System führt eine komplexe Bewegung aus, die eine Überlagerung von erzwungenen und freien Schwingungen darstellt. Freie Schwingungen schwächen sich allmählich ab und im eingeschwungenen Zustand führt das System erzwungene Schwingungen aus, die ebenfalls harmonisch ausfallen. Die Frequenz der stetigen erzwungenen Schwingungen stimmt mit der Frequenz überein
treibende Kraft (eine äußere Kraft zwingt dem System sozusagen ihre Frequenz auf).

Die Amplitude stationärer erzwungener Schwingungen hängt von der Frequenz der Antriebskraft ab. Der Graph dieser Abhängigkeit ist in Abb. dargestellt. 7.

Reis. 7. Resonanz

Wir sehen, dass in der Nähe der Frequenz Resonanz auftritt – das Phänomen einer Zunahme der Amplitude erzwungener Schwingungen. Die Resonanzfrequenz ist ungefähr gleich der natürlichen Schwingungsfrequenz des Systems: , und diese Gleichheit ist umso genauer, je geringer die Reibung im System ist. Ohne Reibung stimmt die Resonanzfrequenz mit der natürlichen Schwingungsfrequenz überein und die Schwingungsamplitude steigt bei an.