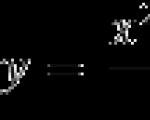समस्या बी15 एक व्युत्पन्न का उपयोग करके एक फ़ंक्शन का अध्ययन है। व्युत्पन्न का उपयोग करके किसी फ़ंक्शन की जांच व्युत्पन्न का उपयोग करके किसी फ़ंक्शन की जांच करना

समस्या बी15 में, चरम सीमा के सूत्र द्वारा दिए गए फ़ंक्शन की जांच करना प्रस्तावित है। यह कैलकुलस में एक मानक समस्या है, और इसकी जटिलता संबंधित कार्य के आधार पर बहुत भिन्न होती है: उनमें से कुछ को शाब्दिक रूप से मौखिक रूप से हल किया जाता है, जबकि अन्य को गंभीर विचार की आवश्यकता होती है।

समाधान के तरीकों को सीखने से पहले, गणितीय विश्लेषण के क्षेत्र से कुछ शब्दों में महारत हासिल करना आवश्यक है। इसलिए, समस्या B15 में, व्युत्पन्न का उपयोग करके निम्नलिखित मात्राएँ ज्ञात करना आवश्यक है:

1. स्थानीय अधिकतम (न्यूनतम) के बिंदु - चर का मान जिस पर फ़ंक्शन अपने अधिकतम (सबसे छोटे) मान तक पहुंचता है। ऐसे बिंदुओं को चरम बिंदु भी कहा जाता है।
2. फ़ंक्शन का वैश्विक अधिकतम (न्यूनतम) निर्दिष्ट प्रतिबंधों के तहत फ़ंक्शन का अधिकतम (सबसे छोटा) मान है। दूसरा नाम वैश्विक चरम सीमा है।

इस मामले में, वैश्विक एक्स्ट्रेमा आमतौर पर फ़ंक्शन परिभाषा के पूरे डोमेन पर नहीं, बल्कि केवल एक निश्चित खंड पर मांगी जाती है। यह समझना महत्वपूर्ण है कि वैश्विक चरम और चरम बिंदु पर फ़ंक्शन का मूल्य हमेशा मेल नहीं खाता है। आइए इसे एक विशिष्ट उदाहरण से समझाएं:

काम। खंड [−3;' पर फ़ंक्शन y = 2x 3 - 3x 2 - 12x + 1 का न्यूनतम बिंदु और न्यूनतम मान ज्ञात करें; 3].

सबसे पहले, हम न्यूनतम बिंदु पाते हैं, जिसके लिए हम व्युत्पन्न की गणना करते हैं:
y' = (2x 3 - 3x 2 - 12x + 1)' = 6x 2 - 6x - 12.

आइए समीकरण y' = 0 को हल करके महत्वपूर्ण बिंदु खोजें। हमें मानक द्विघात समीकरण मिलता है:
y' = 0 ⇒ 6x 2 - 6x - 12 = 0 ⇒ ... ⇒ x 1 = -1, x 2 = 2.

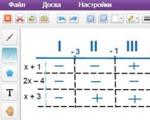
हम इन बिंदुओं को समन्वय रेखा पर चिह्नित करते हैं, व्युत्पन्न और प्रतिबंधों के संकेत जोड़ते हैं - खंड के अंत:

चित्र का पैमाना कोई मायने नहीं रखता. सबसे महत्वपूर्ण बात है बिंदुओं को सही क्रम में अंकित करना। स्कूली गणित पाठ्यक्रम से यह ज्ञात होता है कि न्यूनतम बिंदु पर, व्युत्पन्न चिह्न ऋण से धन में बदल जाता है। रीडिंग हमेशा बाएं से दाएं जाती है - सकारात्मक अर्ध-अक्ष की दिशा में। इसलिए, केवल एक न्यूनतम बिंदु है: x = 2.

आइए अब खंड [−3;'' पर फ़ंक्शन का न्यूनतम मान ज्ञात करें। 3]. यह या तो न्यूनतम बिंदु पर पहुंच जाता है (तब यह वैश्विक न्यूनतम बिंदु बन जाता है), या खंड के अंत में। ध्यान दें कि अंतराल (2; 3) पर व्युत्पन्न हर जगह सकारात्मक है, जिसका अर्थ है कि y(3) > y(2), इसलिए अंतराल के दाहिने छोर को नजरअंदाज किया जा सकता है। केवल बिंदु x = −3 (खंड का बायां छोर) और x = 2 (न्यूनतम बिंदु) ही बचे हैं। हमारे पास है:
y(−3) = 2(−3) 3 − 3(−3) 2 − 12(−3) + 1 = −44;
y(2) = 2*2 3 - 3*2 2 - 12*2 + 1 = -19.

तो, फ़ंक्शन का सबसे छोटा मान खंड के अंत में पहुंच जाता है और -44 के बराबर होता है।

उत्तर: एक्समिन = 2; यमिन = −44

उपरोक्त तर्क से एक महत्वपूर्ण तथ्य निकलता है, जिसे बहुत से लोग भूल जाते हैं। फ़ंक्शन अधिकतम (न्यूनतम) मान लेता है, जरूरी नहीं कि चरम बिंदु पर हो। कभी-कभी ऐसा मान खंड के अंत में पहुंच जाता है, और वहां व्युत्पन्न का शून्य के बराबर होना जरूरी नहीं है।

समस्या समाधान योजना बी15

यदि समस्या B15 में अंतराल पर फ़ंक्शन f(x) का अधिकतम या न्यूनतम मान ज्ञात करना आवश्यक है, तो हम निम्नलिखित क्रियाएं करते हैं:

1. समीकरण f'(x) = 0 को हल करें। यदि कोई मूल नहीं है, तो तीसरा चरण छोड़ें और सीधे चौथे चरण पर जाएँ।
2. जड़ों के परिणामी सेट से, खंड के बाहर मौजूद सभी चीज़ों को हटा दें। शेष संख्याओं को x 1 , x 2 , ..., x n द्वारा निरूपित किया जाएगा - एक नियम के रूप में, उनमें से कुछ ही होंगे।
3. मूल फ़ंक्शन में खंड के सिरों और बिंदुओं x 1 , x 2 , ..., x n को प्रतिस्थापित करें। हमें संख्याओं का एक सेट f (a), f (b), f (x 1), f (x 2), ..., f (x n) मिलता है, जिसमें से हम सबसे बड़ा या सबसे छोटा मान चुनते हैं - यह होगा उत्तर।

जब जड़ें खंड के सिरों से मेल खाती हैं तो उनके विलोपन के बारे में थोड़ा स्पष्टीकरण। उन्हें काटा भी जा सकता है, क्योंकि चौथे चरण में खंड के सिरों को अभी भी फ़ंक्शन में प्रतिस्थापित किया जाता है - भले ही समीकरण f'(x) = 0 का कोई समाधान न हो।

काम। खंड [−5; पर फ़ंक्शन y = x 3 + 3x 2 − 9x − 7 का सबसे बड़ा मान ज्ञात करें; 0].

सबसे पहले, आइए व्युत्पन्न खोजें: y' = (x 3 + 3x 2 - 9x - 7)' = 3x 2 + 6x - 9।

फिर हम समीकरण हल करते हैं: y' = 0 ⇒ 3x 2 + 6x − 9 = 0 ⇒ ... ⇒ x = −3; एक्स = 1.

मूल x = 1 को काट दें क्योंकि यह खंड [−5; 0].

यह खंड के अंत में और बिंदु x = −3 पर फ़ंक्शन के मूल्य की गणना करने के लिए बनी हुई है:
y(−5) = (−5) 3 + 4 (−5) 2 − 9 (−5) − 7 = −12;
y(−3) = (−3) 3 + 4 (−3) 2 − 9 (−3) − 7 = 20;
y(0) = 0 3 + 4 0 2 − 9 0 − 7 = −7.

जाहिर है, सबसे बड़ा मान 20 है - यह बिंदु x = −3 पर पहुंच जाता है।

अब उस मामले पर विचार करें जब अंतराल पर फ़ंक्शन f(x) का अधिकतम या न्यूनतम बिंदु ढूंढना आवश्यक हो। यदि खंड निर्दिष्ट नहीं है, तो फ़ंक्शन को उसकी परिभाषा के डोमेन पर माना जाता है। किसी भी स्थिति में, समाधान योजना इस प्रकार है:

1. फ़ंक्शन का व्युत्पन्न खोजें: f'(x)।
2. समीकरण f'(x) = 0 को हल करें। यदि व्युत्पन्न एक भिन्नात्मक परिमेय फलन है, तो हम अतिरिक्त रूप से यह पता लगाते हैं कि इसका हर कब शून्य है। आइए प्राप्त मूलों को निरूपित करें x 1 , x 2 , ..., x n .
3. निर्देशांक रेखा पर x 1 , x 2 , ..., x n अंकित करें और उन चिह्नों को रखें जो अवकलज इन संख्याओं के बीच लेता है। यदि कोई खंड दिया गया है, तो उसे चिह्नित करें और उसके बाहर मौजूद सभी चीज़ों को काट दें।
4. शेष बिंदुओं में से, हम उस बिंदु की तलाश कर रहे हैं जहां व्युत्पन्न का चिह्न माइनस से प्लस (यह न्यूनतम बिंदु है) या प्लस से माइनस (न्यूनतम बिंदु) में बदल जाता है। ऐसा एक ही बिंदु होना चाहिए - यही उत्तर होगा.

एक विचारशील पाठक निश्चित रूप से नोटिस करेगा कि कुछ कार्यों के लिए यह एल्गोरिदम काम नहीं करता है। वास्तव में, कार्यों का एक पूरा वर्ग है जिसके चरम बिंदुओं को खोजने के लिए अधिक जटिल गणनाओं की आवश्यकता होती है। हालाँकि, गणित की परीक्षा में ऐसे फ़ंक्शन नहीं मिलते हैं।

बिंदुओं x 1 , x 2 , ..., x n के बीच चिह्नों के स्थान पर ध्यान दें। याद रखें: सम बहुलता की जड़ से गुजरने पर, व्युत्पन्न का चिह्न नहीं बदलता है। चरम बिंदुओं की तलाश करते समय, संकेत हमेशा बाएं से दाएं देखे जाते हैं, यानी। संख्यात्मक अक्ष के अनुदिश.

काम। किसी फ़ंक्शन का अधिकतम बिंदु ज्ञात करें

अंतराल पर [−8; 8].

आइए व्युत्पन्न खोजें:

चूँकि यह एक भिन्नात्मक परिमेय फलन है, हम अवकलज और उसके हर को शून्य के बराबर करते हैं:
y' = 0 ⇒ x 2 − 25 = 0 ⇒ ... ⇒ x = 5; एक्स = −5;
x 2 = 0 ⇒ x = 0 (दूसरी बहुलता का मूल)।

आइए निर्देशांक रेखा पर बिंदु x = −5, x = 0 और x = 5 चिह्नित करें, चिह्नों और सीमाओं को व्यवस्थित करें:

जाहिर है, खंड के अंदर केवल एक बिंदु x = −5 रहता है, जिस पर व्युत्पन्न का चिह्न प्लस से माइनस में बदल जाता है। यह अधिकतम बिंदु है.

एक बार फिर, आइए हम बताएं कि चरम बिंदु स्वयं चरम बिंदु से कैसे भिन्न हैं। चरम बिंदु वेरिएबल्स के मान हैं जिन पर फ़ंक्शन सबसे बड़ा या सबसे छोटा मान लेता है। चरम सीमाएँ स्वयं कार्यों के मूल्य हैं, उनके कुछ पड़ोस में अधिकतम या न्यूनतम।

सामान्य बहुपदों और भिन्नात्मक परिमेय फलनों के अलावा, समस्या B15 में निम्नलिखित प्रकार के व्यंजक होते हैं:

1. तर्कहीन कार्य,
2. त्रिकोणमितीय कार्य,
3. घातीय कार्य,
4. लघुगणकीय कार्य.

एक नियम के रूप में, अतार्किक कार्यों में कोई समस्या नहीं होती है। शेष मामले अधिक विस्तार से विचार करने योग्य हैं।

त्रिकोणमितीय कार्य

त्रिकोणमितीय फलनों की मुख्य कठिनाई यह है कि समीकरणों को हल करते समय अनंत संख्या में मूल उत्पन्न होते हैं। उदाहरण के लिए, समीकरण पाप x = 0 के मूल x = πn हैं, जहां n ∈ Z. खैर, यदि ऐसी अनंत संख्याएं हैं तो उन्हें समन्वय रेखा पर कैसे चिह्नित किया जाए?

उत्तर सरल है: आपको n के विशिष्ट मानों को प्रतिस्थापित करने की आवश्यकता है। दरअसल, त्रिकोणमितीय कार्यों के साथ समस्या B15 में हमेशा एक प्रतिबंध होता है - एक खंड। इसलिए, आरंभ करने के लिए, हम n \u003d 0 लेते हैं, और तब तक n बढ़ाते हैं जब तक कि संबंधित रूट खंड से परे "उड़ न जाए"। इसी प्रकार, n घटाने पर, बहुत जल्द हमें एक ऐसा मूल मिलेगा जो निचली सीमा से कम है।

यह दिखाना आसान है कि विचाराधीन प्रक्रिया में प्राप्त जड़ों के अलावा कोई भी जड़ खंड पर मौजूद नहीं है। आइए अब इस प्रक्रिया पर ठोस उदाहरणों के साथ विचार करें।

काम। अंतराल [−π/3; π/3].

व्युत्पन्न की गणना करें: y' = (sin x - 5x syn x - 5cos x + 1)' = ... = cos x - 5x cos x = (1 - 5x) cos x।

फिर हम समीकरण हल करते हैं: y' = 0 ⇒ (1 − 5x) cos x = 0 ⇒ ... ⇒ x = 0.2 या x = π/2 + πn, n ∈ Z.

मूल x = 0.2 के साथ, सब कुछ स्पष्ट है, लेकिन सूत्र x = π / 2 + πn को अतिरिक्त प्रसंस्करण की आवश्यकता है। हम n = 0 से शुरू करके n के विभिन्न मानों को प्रतिस्थापित करेंगे।

n = 0 ⇒ x = π/2. लेकिन π/2 > π/3, इसलिए मूल x = π/2 मूल खंड में शामिल नहीं है। साथ ही, जितना बड़ा n, उतना बड़ा x, इसलिए n > 0 पर विचार करने का कोई मतलब नहीं है।

n = −1 ⇒ x = − π/2. लेकिन −π/2< −π/3 - этот корень тоже придется отбросить. А вместе с ним - и все корни для n < −1.

यह पता चला है कि अंतराल पर [−π/3; π/3] केवल मूल x = 0.2 है। हम इसे समन्वय रेखा पर चिह्नों और सीमाओं के साथ चिह्नित करते हैं:

यह सुनिश्चित करने के लिए कि x = 0.2 के दाईं ओर का व्युत्पन्न वास्तव में नकारात्मक है, यह मान x = π/4 को y' में प्रतिस्थापित करने के लिए पर्याप्त है। हम बस यह नोट करते हैं कि बिंदु x = 0.2 पर, व्युत्पन्न चिह्न प्लस से माइनस में बदल जाता है, और इसलिए यह अधिकतम बिंदु है।

काम। अंतराल [−π/4; पर फ़ंक्शन y = 4tg x - 4x + π - 5 का सबसे बड़ा मान ज्ञात करें; π/4].

व्युत्पन्न की गणना करें: y' = (4tg x - 4x + π - 5)' = 4/cos 2x - 4।

फिर हम समीकरण हल करते हैं: y' = 0 ⇒ 4/cos 2x - 4 = 0 ⇒ ... ⇒ x = πn, n ∈ Z.

हम n = 0 से शुरू करते हुए, विशिष्ट n को प्रतिस्थापित करके इस सूत्र से जड़ें निकालते हैं:
n = 0 ⇒ x = 0. यह मूल हमारे लिए उपयुक्त है।
एन = 1 ⇒ एक्स = π. लेकिन π > π/4, इसलिए मूल x = π और मान n > 1 को काटा जाना चाहिए।
n = −1 ⇒ x = −π. लेकिन π< −π/4, поэтому x = π и n < −1 тоже вычеркиваем.

जड़ों की पूरी विविधता में से केवल एक ही बचता है: x = 0. इसलिए, हम x = 0, x = π/4 और x = −π/4 के लिए फ़ंक्शन के मान की गणना करते हैं।
y(0) = 4tg 0 - 4 0 + π - 5 = π - 5;
y(π/4) = 4tg (π/4) - 4 π/4 + π - 5 = -1;
y(π/4) = 4tg (−π/4) - 4 (−π/4) + π - 5 = ... = 2π - 9.

अब ध्यान दें कि π = 3.14...< 4, поэтому π − 5 < 4 − 5 = −1 и 2π − 9 < 8 − 9 = −1. Получается одно положительное число и два отрицательных. Мы ищем наибольшее - очевидно, это y = −1.

ध्यान दें कि पिछली समस्या में संख्याओं की एक दूसरे से तुलना नहीं करना संभव था। दरअसल, संख्या π - 5, 1 और 2π - 9 में से केवल एक ही उत्तर पुस्तिका में लिखा जा सकता है। दरअसल, संख्या π को फॉर्म में कैसे लिखें? लेकिन कोई रास्ता नहीं. यह गणित में परीक्षा के पहले भाग की एक महत्वपूर्ण विशेषता है, जो कई समस्याओं के समाधान को बहुत सरल बनाती है। और यह सिर्फ B15 में ही काम नहीं करता.

कभी-कभी किसी फलन का अध्ययन करते समय ऐसे समीकरण उत्पन्न होते हैं जिनका कोई मूल नहीं होता। इस मामले में, समस्या और भी सरल हो जाती है, क्योंकि यह केवल खंड के सिरों पर विचार करने के लिए बनी हुई है।

काम। अंतराल पर फ़ंक्शन y = 7sin x - 8x + 5 का सबसे छोटा मान ज्ञात करें [−3π/2; 0].

सबसे पहले हम व्युत्पन्न पाते हैं: y' = (7sin x - 8x + 5)' = 7cos x - 8।

आइए समीकरण को हल करने का प्रयास करें: y' = 0 ⇒ 7cos x - 8 = 0 ⇒ cos x = 8/7। लेकिन cos x का मान हमेशा अंतराल [−1; 1], और 8/7 > 1. इसलिए, कोई जड़ें नहीं हैं।

यदि जड़ें नहीं हैं तो कुछ भी काटने की जरूरत नहीं है। हम अंतिम चरण पर जाते हैं - हम फ़ंक्शन के मान की गणना करते हैं:
y(−3π/2) = 7sin (−3π/2) − 8 (−3π/2) + 5 = ... = 12π + 12;
y(0) = 7sin 0 - 8 0 + 5 = 5.

चूंकि उत्तर पुस्तिका पर संख्या 12π + 12 नहीं लिखी जा सकती, इसलिए केवल y = 5 ही बचता है।

घातीय कार्य

सामान्यतया, एक घातांकीय फलन y = a x के रूप की अभिव्यक्ति है, जहां a > 0. लेकिन समस्या B15 में, केवल y = e x के रूप के फलन होते हैं और चरम स्थिति में, y = e kx + b होते हैं। कारण यह है कि इन कार्यों के व्युत्पन्न की गणना करना बहुत आसान है:

1. (ई एक्स)" = ई एक्स। कुछ भी नहीं बदला है।
2. (ई केएक्स + बी)" = के ई केएक्स + बी। चर एक्स के गुणांक के बराबर एक कारक बस जोड़ा जाता है। यह एक जटिल फ़ंक्शन के व्युत्पन्न का एक विशेष मामला है।

बाकी सब कुछ बिल्कुल मानक है. बेशक, समस्या B15 में वास्तविक कार्य अधिक गंभीर दिखते हैं, लेकिन समाधान योजना इससे नहीं बदलती है। आइए कुछ उदाहरणों पर विचार करें, जिनमें केवल समाधान के मुख्य बिंदुओं पर प्रकाश डाला गया है - बिना गहन तर्क और टिप्पणियों के।

काम। अंतराल [−1; पर फ़ंक्शन y = (x 2 − 5x + 5)e x − 3 का सबसे छोटा मान ज्ञात करें; 5].

व्युत्पन्न: y' = ((x 2 - 5x + 5)e x - 3)' = ... = (x 2 - 3x)e x - 3 = x(x - 3)e x - 3।

हम मूल पाते हैं: y' = 0 ⇒ x(x − 3)e x − 3 = 0 ⇒ ... ⇒ x = 0; एक्स=3.

दोनों जड़ें अंतराल पर स्थित हैं [−1; 5]. सभी बिंदुओं पर फ़ंक्शन का मान ज्ञात करना बाकी है:
y(−1) = ((−1) 2 − 5 (−1) + 5)e − 1 − 3 = ... = 11 e −4 ;
y(0) = (0 2 − 5 0 + 5)e 0 − 3 = ... = 5 e −3 ;
y(3) = (3 2 − 5 3 + 5)ई 3 − 3 = ... = −1;
y(5) = (5 2 − 5 5 + 5)ई 5 − 3 = ... = 5 ई 2।

प्राप्त चार संख्याओं में से केवल y = −1 को ही रूप में लिखा जा सकता है। इसके अलावा, यह एकमात्र ऋणात्मक संख्या है - यह सबसे छोटी होगी।

काम। खंड पर फ़ंक्शन y = (2x - 7) e 8 - 2x का अधिकतम मान ज्ञात करें।

व्युत्पन्न: y' = ((2x - 7) e 8 - 2x)' = ... = (16 - 4x) e 8 - 2x = 4(4 - x) e 8 - 2x।

हम मूल पाते हैं: y' = 0 ⇒ 4(4 − x) e 8 − 2x = 0 ⇒ x = 4.

मूल x = 4 खंड से संबंधित है। हम फ़ंक्शन मान ढूंढ रहे हैं:
y(0) = (2 0 − 7)e 8 − 2 0 = ... = −7 e 8 ;
y(4) = (2 4 − 7)e 8 − 2 4 = ... = 1;
y(6) = (2 6 − 7)e 8 − 2 6 = ... = 5 e −4 .

जाहिर है, केवल y = 1 ही उत्तर के रूप में काम कर सकता है।

लघुगणकीय कार्य

घातीय कार्यों के अनुरूप, समस्या B15 में केवल प्राकृतिक लघुगणक होते हैं, क्योंकि उनके व्युत्पन्न की गणना आसानी से की जाती है:

1. (एलएनएक्स)' = 1/एक्स;
2. (एलएन(केएक्स + बी))' = के/(केएक्स + बी)। विशेष रूप से, यदि b = 0, तो (ln(kx))' = 1/x.

इस प्रकार, व्युत्पन्न हमेशा एक भिन्नात्मक तर्कसंगत कार्य होगा। यह केवल इस व्युत्पन्न और इसके हर को शून्य के बराबर करने और फिर परिणामी समीकरणों को हल करने के लिए ही रह गया है।

किसी लघुगणक फ़ंक्शन का अधिकतम या न्यूनतम मान ज्ञात करने के लिए, याद रखें कि प्राकृतिक लघुगणक केवल e n रूप के बिंदुओं पर एक "सामान्य" संख्या बन जाता है। उदाहरण के लिए, ln 1 = ln e 0 = 0 एक लघुगणकीय शून्य है, और अक्सर समाधान को इसमें घटा दिया जाता है। अन्य मामलों में, लघुगणक के चिह्न को "हटाना" असंभव है।

काम। खंड पर फ़ंक्शन y = x 2 - 3x + ln x का सबसे छोटा मान ज्ञात करें।

हम व्युत्पन्न पर विचार करते हैं:

हम अवकलज और उसके हर के शून्य पाते हैं:
y' = 0 ⇒ 2x 2 - 3x + 1 = 0 ⇒ ... ⇒ x = 0.5; एक्स = 1;
x = 0 - निर्णय लेने के लिए कुछ भी नहीं है।

तीन संख्याओं x = 0, x = 0.5 और x = 1 में से केवल x = 1 खंड के अंदर स्थित है, और संख्या x = 0.5 इसका अंत है। हमारे पास है:
y(0.5) = 0.5 2 − 3 0.5 + एलएन 0.5 = एलएन 0.5 − 1.25;
y(1) = 1 2 − 3 1 + लघुगणक 1 = −2;
y(5) = 5 2 − 3 5 + एलएन 5 = 10 + एलएन 5।

प्राप्त तीन मानों में से केवल y = −2 में लघुगणक का चिह्न नहीं है - यही उत्तर होगा।

काम। खंड पर फ़ंक्शन y = ln(6x) - 6x + 4 का सबसे बड़ा मान ज्ञात करें।

हम व्युत्पन्न की गणना करते हैं:

हम तब पता लगाते हैं जब अवकलज या उसका हर शून्य के बराबर होता है:
y' = 0 ⇒ 1 − 6x = 0 ⇒ x = 1/6;
x = 0 - पहले ही तय हो चुका है।

हम संख्या x = 0 को काट देते हैं, क्योंकि यह खंड के बाहर स्थित है। हम खंड के सिरों पर और बिंदु x = 1/6 पर फ़ंक्शन के मान पर विचार करते हैं:
y(0.1) = ln(6 0.1) − 6 0.1 + 4 = ln 0.6 + 3.4;
y(1/6) = लॉग(6 1/6) − 6 1/6 + 4 = लॉग 1 + 3 = 3;
y(3) = ln(6 3) − 6 3 + 4 = ln 18 − 14.

जाहिर है, केवल y = 3 ही उत्तर के रूप में कार्य कर सकता है - शेष मानों में लघुगणक का चिह्न होता है और उन्हें उत्तर पुस्तिका में नहीं लिखा जा सकता है।

बिंदु कहा जाता है अधिकतम (न्यूनतम) बिंदु फ़ंक्शन, यदि बिंदु का ऐसा पड़ोस है कि इस पूरे पड़ोस के लिए असमानता है ().

किसी फ़ंक्शन के अधिकतम और न्यूनतम बिंदुओं को बिंदु कहा जाता है। चरम (चित्र 25)।

प्रमेय 3.9 (चरम बिंदुओं के अस्तित्व के लिए आवश्यक शर्त) . पहली तरह के महत्वपूर्ण बिंदुओं पर, फ़ंक्शन का व्युत्पन्न या तो

शून्य है या अस्तित्व में नहीं है

पहली तरह के महत्वपूर्ण बिंदुओं को आमतौर पर केवल महत्वपूर्ण बिंदु कहा जाता है।

महत्वपूर्ण बिंदु जिन पर किसी फ़ंक्शन का व्युत्पन्न शून्य के बराबर होता है, कहलाते हैं स्थिरता बिंदु . महत्वपूर्ण बिंदु जिन पर कोई फलन सतत है लेकिन अवकलनीय नहीं है, कहलाते हैं कोने के बिंदु . उदाहरण के लिए, एक बिंदु पर एक फ़ंक्शन निरंतर है, लेकिन इसका कोई व्युत्पन्न नहीं है, क्योंकि इस बिंदु पर फ़ंक्शन के ग्राफ़ पर अनंत संख्या में स्पर्शरेखाएं खींची जा सकती हैं (चित्र 26)। इस मामले को इस बात की पुष्टि के रूप में माना जा सकता है कि प्रमेय 3.3 का विपरीत कथन गलत है।

फ़ंक्शन को कॉल किया जाता है की बढ़ती किसी अंतराल पर, यदि इस अंतराल पर तर्क का बड़ा मान चर के बड़े मान से मेल खाता है, और घट यदि तर्क का बड़ा मान चर के छोटे मान से मेल खाता है।

आगे के शोध के लिए, महत्वपूर्ण बिंदुओं को एक संख्यात्मक अक्ष पर रखा जाता है, जिसे इन बिंदुओं द्वारा अंतरालों में विभाजित किया जाता है, जिसके बाद निम्नलिखित पर्याप्त स्थितियों को सत्यापित किया जाता है।

प्रमेय 3.10 (किसी फ़ंक्शन के बढ़ने और घटने के लिए पर्याप्त स्थिति)।यदि कोई फ़ंक्शन किसी अंतराल पर अवकलनीय है और उसका व्युत्पन्न सकारात्मक (नकारात्मक) है, तो इस अंतराल पर फ़ंक्शन बढ़ रहा है (घट रहा है)

प्रमेय 3.11 (किसी फ़ंक्शन के चरम बिंदुओं के अस्तित्व के लिए पर्याप्त शर्त)।यदि फ़ंक्शन महत्वपूर्ण बिंदु के कुछ पड़ोस में निरंतर और भिन्न है, और इससे गुजरते समय, व्युत्पन्न प्लस से माइनस में संकेत बदलता है, तो बिंदु एक अधिकतम बिंदु है; यदि माइनस से प्लस तक, तो बिंदु फ़ंक्शन का न्यूनतम बिंदु है

फ़ंक्शन के वे महत्वपूर्ण बिंदु जिनके लिए पर्याप्त शर्त पूरी नहीं होती है वे केवल पहले प्रकार के महत्वपूर्ण बिंदु बने रहते हैं।

पहली तरह के महत्वपूर्ण बिंदु, जिन पर व्युत्पन्न मौजूद नहीं है, दो वर्गों में विभाजित हैं:

वे बिंदु हैं जिन पर फ़ंक्शन निरंतर है (जब प्रमेय 3.11 उनके लिए संतुष्ट होता है, तो इन बिंदुओं पर फ़ंक्शन का "तीव्र" चरम होता है), ये हैं कोना अंक;

वे बिंदु हैं जिन पर फ़ंक्शन में असंततता आती है (वे हमेशा दूसरे प्रकार के महत्वपूर्ण बिंदुओं की श्रेणी में चले जाते हैं)।

लेकिन इस तरह से किया गया अध्ययन एक बहुत ही महत्वपूर्ण प्रश्न का उत्तर नहीं देता है: फ़ंक्शन कैसे बढ़ता (घटता) है - उत्तल या अवतल? इस प्रश्न का उत्तर दूसरे व्युत्पन्न का उपयोग करके फ़ंक्शन के आगे के अध्ययन द्वारा दिया गया है। आइए हम कई आवश्यक परिभाषाएँ दें।

फ़ंक्शन को कॉल किया जाता है उत्तल (नतोदर) किसी अंतराल पर, यदि इस अंतराल के प्रत्येक बिंदु पर फ़ंक्शन के ग्राफ़ पर खींची गई स्पर्शरेखा फ़ंक्शन के ग्राफ़ के ऊपर (नीचे) होती है।

किसी फ़ंक्शन के उत्तलता के क्षेत्रों को अवतलता के क्षेत्रों से अलग करने वाले बिंदु इसके कहलाते हैं विभक्ति बिंदु (चित्र 27)।

प्रमेय 3.12 (विभक्ति बिंदुओं के अस्तित्व के लिए आवश्यक शर्त). दूसरे प्रकार के महत्वपूर्ण बिंदुओं पर, फ़ंक्शन का दूसरा व्युत्पन्न या तो शून्य है या मौजूद नहीं है

आगे के शोध के लिए, दूसरे प्रकार के महत्वपूर्ण बिंदुओं को एक संख्यात्मक अक्ष पर रखा जाता है, जिसे इन बिंदुओं द्वारा अंतराल में विभाजित किया जाता है, जिसके बाद निम्नलिखित पर्याप्त स्थितियों का सत्यापन किया जाता है।

प्रमेय 3.13 (किसी फ़ंक्शन की उत्तलता और अवतलता के लिए पर्याप्त स्थिति)।यदि कोई फ़ंक्शन किसी अंतराल पर दो बार अवकलनीय है और इसका दूसरा व्युत्पन्न सकारात्मक (नकारात्मक) है, तो फ़ंक्शन इस अंतराल पर अवतल (उत्तल) है

फ़ंक्शन के वे महत्वपूर्ण बिंदु जिनके लिए पर्याप्त शर्त पूरी नहीं होती है, वे दूसरे प्रकार के महत्वपूर्ण बिंदु मात्र रह जाते हैं।

दूसरे प्रकार के महत्वपूर्ण बिंदु, जिन पर दूसरा व्युत्पन्न मौजूद नहीं है, दो वर्गों में विभाजित हैं:

- जिन बिंदुओं पर फ़ंक्शन निरंतर है, ये तथाकथित "तीव्र" विभक्ति बिंदु हैं - ऐसे बिंदुओं पर, फ़ंक्शन के ग्राफ़ पर अनंत संख्या में स्पर्शरेखाएं खींची जा सकती हैं (चित्र 28);

वे बिंदु हैं जिन पर फ़ंक्शन एक असंततता से ग्रस्त है (दूसरे प्रकार के असंततता बिंदुओं पर, फ़ंक्शन के ग्राफ़ में एक लंबवत अनंतस्पर्शी होता है)।

फ़ंक्शन के चरम और विभक्ति बिंदुओं की अंतिम गणना के लिए, उनके निर्देशांक ढूंढना आवश्यक है, और फिर दो निर्देशांक के साथ संकेतित बिंदुओं को लिखें।

आत्मनिरीक्षण के लिए प्रश्न.

1. किन बिंदुओं को किसी फ़ंक्शन का चरम बिंदु (अधिकतम और न्यूनतम) कहा जाता है?

2. किस क्रिया को बढ़ना (घटना) कहते हैं?

3. किसी फ़ंक्शन के चरम बिंदुओं के अस्तित्व के लिए आवश्यक और पर्याप्त शर्तें क्या हैं?

4. किसी फलन की वृद्धि (कमी) के लिए पर्याप्त शर्त क्या है?

5. किन बिंदुओं को किसी फ़ंक्शन का विभक्ति बिंदु कहा जाता है?

6. किस फलन को उत्तल (अवतल) कहा जाता है?

7. किसी फ़ंक्शन के विभक्ति बिंदुओं के अस्तित्व के लिए आवश्यक और पर्याप्त शर्तें क्या हैं?

8. किसी फलन की उत्तलता (अवतलता) के लिए पर्याप्त शर्त क्या है?

पाठ का उद्देश्य:कार्यों का अध्ययन कैसे करें यह सिखाने के लिए; उन्हें साजिश रचें.

रूप:वार्तालाप पाठ.

तरीके:संवाद, दृश्य सामग्री और स्लाइड।

उपकरण:आईसीटी, टेबल।

कक्षाओं के दौरान

I. होमवर्क की जाँच करना।

टीचर:- दोस्तों! आपका होमवर्क था "फ़ंक्शन के महत्वपूर्ण बिंदु, मैक्सिमा और मिनिमा"। किसी फ़ंक्शन के महत्वपूर्ण बिंदु को परिभाषित करें।

छात्र:- एक महत्वपूर्ण बिंदु परिभाषा के क्षेत्र का एक आंतरिक बिंदु है, जिसमें व्युत्पन्न या तो शून्य के बराबर है या मौजूद नहीं है।

शिक्षक:-महत्वपूर्ण बिंदु कैसे खोजें?

विद्यार्थी:- 1

) फ़ंक्शन का व्युत्पन्न खोजें;

2) समीकरण को हल करें: f "(x) = 0. इस समीकरण की जड़ें महत्वपूर्ण बिंदु हैं।

शिक्षक:- कार्यों के महत्वपूर्ण बिंदु खोजें:

ए) एफ(एक्स)= 4 - 2x + 7x 2

बी) एफ (एक्स) = 4एक्स - एक्स 3/3

ए) 1) इस फ़ंक्शन का व्युत्पन्न खोजें:

f "(x)= (4 - 2x + 7x 2)" = -2+14x

2) समीकरण f'(x) = 0 को हल करें<=>-2+14x=0<=>एक्स=1/7

3) चूँकि समीकरण f "(x) = 0 का एक मूल है, तो इस फ़ंक्शन का एक महत्वपूर्ण बिंदु x = 1/7 है।

बी) 1) इस फ़ंक्शन का व्युत्पन्न खोजें: f "(x) = 4 - x 2

2) समीकरण हल करें: f "(x) = 0<=>4 - x 2 = 0<=>x=2 या x=-2

3) चूँकि समीकरण f "(x) = 0 के दो मूल हैं, तो इस फ़ंक्शन के दो महत्वपूर्ण बिंदु x 1 = 2 और x 2 = -2 हैं।

द्वितीय.मौखिक कार्य.

टीचर:- दोस्तों! आइए उन मुख्य प्रश्नों को दोहराएं जो किसी नए विषय का अध्ययन करने के लिए आवश्यक हैं। ऐसा करने के लिए, आंकड़ों वाली तालिकाओं पर विचार करें ( परिशिष्ट 1).

उन बिंदुओं को निर्दिष्ट करें जिन पर फ़ंक्शन की वृद्धि को कमी से प्रतिस्थापित किया जाता है। इन बिंदुओं को क्या कहा जाता है?

विद्यार्थी: - आकृति a में) - बिंदु K अधिकतम बिंदु है, आकृति b में) - बिंदु M अधिकतम बिंदु है।

टीचर:- फ़ंक्शन के न्यूनतम बिंदु क्या हैं?

छात्र: - चित्र c) और d) में बिंदु K - फ़ंक्शन का न्यूनतम बिंदु।

शिक्षक:- कौन से बिंदु फलन के चरम बिंदु हो सकते हैं?

विद्यार्थी:- महत्वपूर्ण बिंदु किसी फ़ंक्शन के चरम बिंदु हो सकते हैं।

टीचर:- आवश्यक शर्तें क्या हैं आप जानते हैं?

विद्यार्थी:- फ़र्मेट का प्रमेय है। चरम सीमा के लिए आवश्यक शर्त:यदि बिंदु x 0 फ़ंक्शन f का चरम बिंदु है और इस बिंदु पर एक व्युत्पन्न f "है, तो यह शून्य के बराबर है: f" (x) \u003d 0।

शिक्षक:- फ़ंक्शन के लिए महत्वपूर्ण बिंदु खोजें:

ए) एफ(एक्स) = | एक्स |

बी) एफ(एक्स) = 2एक्स + | एक्स |

विद्यार्थी:- फलन f(x) = | पर विचार करें एक्स | ( आवेदन 2). इस फ़ंक्शन का 0 पर कोई व्युत्पन्न नहीं है। इसलिए, 0 एक महत्वपूर्ण बिंदु है। जाहिर है, फ़ंक्शन का बिंदु 0 पर न्यूनतम है।

विद्यार्थी:- फलन f(x) = 2x + | पर विचार करें एक्स | ( परिशिष्ट 3). ग्राफ़ दिखाता है कि बिंदु 0 पर इस फ़ंक्शन का कोई चरम नहीं है। इस बिंदु पर, फ़ंक्शन का कोई व्युत्पन्न भी नहीं है।

वास्तव में, यदि हम मानते हैं कि फलन f का 0 पर अवकलज है, तो f(x) - 2x का भी 0 पर अवकलज है। लेकिन f(x) - 2x = | x |, और फ़ंक्शन | एक्स | बिंदु 0 पर अवकलनीय नहीं है, अर्थात, हम एक विरोधाभास पर आ गये हैं।

इसका मतलब यह है कि बिंदु 0 पर फ़ंक्शन f का कोई व्युत्पन्न नहीं है।

शिक्षक:- फ़र्मेट के प्रमेय से यह निष्कर्ष निकलता है कि चरम बिंदु ढूँढ़ते समय, आपको महत्वपूर्ण बिंदु ढूँढ़ने की आवश्यकता होती है। लेकिन सुविचारित उदाहरणों से यह स्पष्ट है कि इस महत्वपूर्ण बिंदु को चरम बिंदु बनाने के लिए कुछ अतिरिक्त शर्त की आवश्यकता है।

क्या आप जानते हैं कि किसी बिंदु पर चरम के अस्तित्व के लिए पर्याप्त स्थितियाँ क्या हैं?

विद्यार्थी: - अधिकतम कार्य का चिह्न: यदि फ़ंक्शन f बिंदु x 0 पर निरंतर है, और f "(x)> 0 अंतराल (a; x 0) और f "(x) पर है<0 на интервале (х 0 ; в), то точка х 0 является точкой максимума функции f.

अर्थात्, यदि बिंदु x 0 पर व्युत्पन्न चिह्न प्लस से माइनस में बदलता है, तो x 0 अधिकतम बिंदु है।

विद्यार्थी: - न्यूनतम का चिह्न: यदि फ़ंक्शन f बिंदु x 0 पर निरंतर है, और f "(x)<0 на интервале (а;х 0) и f "(x) >अंतराल (x 0 ; c) पर 0, तो बिंदु x 0 फ़ंक्शन f का न्यूनतम बिंदु है।

अर्थात्, यदि बिंदु x 0 पर व्युत्पन्न चिह्न ऋण से धन में बदलता है, तो x 0 न्यूनतम बिंदु है।

शिक्षक:- और आप किसी फ़ंक्शन के चरम बिंदुओं को खोजने के लिए कौन सा एल्गोरिदम जानते हैं।

छात्र व्युत्पन्न ( परिशिष्ट 4) और फ़ंक्शन के चरम बिंदु ढूंढता है:

एफ (एक्स) \u003d x 4 -2x 2

D (f) =IR और f संपूर्ण तर्कसंगत फलन के रूप में संपूर्ण वास्तविक रेखा पर निरंतर है।

2. f "(x) = 4x 3 -4x = 4x (x + 1) (x-1)।

3.f"(x)=0<=>x \u003d -1 V x \u003d 0 V x \u003d 1.

चित्र.1 (संकेत f")

चूँकि f क्रांतिक बिंदुओं पर सतत है, चित्र 1 से ( परिशिष्ट 5) यह देखा जा सकता है कि -1 और 1 न्यूनतम बिंदु हैं, और 0 फ़ंक्शन f का अधिकतम बिंदु है।

एफ न्यूनतम = एफ (-1) = एफ (1) = -1, एफ अधिकतम = एफ (0) = 0।

टीचर:- दोस्तों! आइए फ़ंक्शन f की एकरसता के अंतराल खोजने के लिए एल्गोरिदम को याद करें।

छात्र को फ़ंक्शन f की एकरसता के अंतराल खोजने के लिए एल्गोरिदम याद है ( परिशिष्ट 6).

शिक्षक:- सूत्र द्वारा दिए गए फ़ंक्शन f के वृद्धि और कमी के अंतराल ज्ञात करें

एफ (एक्स) \u003d x 3 -12x

समाधान:

1. चूँकि f(x) एक बहुपद है, तो D (f) =IR.

2. फलन f संपूर्ण वास्तविक रेखा और f "(x) = 3x 2 -12 = 3 (x + 2) (x-2) पर अवकलनीय है।

3. केवल f'(x) के शून्य ही फलन f के क्रांतिक बिंदु हो सकते हैं।

f"(x)=0<=>एक्स \u003d -2 वी एक्स \u003d 2.

डी (एफ) \ (-2; 2) = (-; -2) यू (-2; 2) यू (2; +)।

चित्र 2 (संकेत f")।

दिए गए फ़ंक्शन f की परिभाषा और मान के डोमेन खोजें।

पता लगाएं कि क्या फ़ंक्शन में ऐसी विशेषताएं हैं जो अध्ययन करना आसान बनाती हैं, यानी फ़ंक्शन f है:

क) सम या विषम;

बी) आवधिक।

3. निर्देशांक अक्षों के साथ ग्राफ़ के प्रतिच्छेदन बिंदुओं के निर्देशांक की गणना करें।

4. फलन f की स्थिरता के अंतराल ज्ञात कीजिए।

5. पता लगाएँ कि फलन f किस अंतराल पर बढ़ता है और किस अंतराल पर घटता है।

6. चरम बिंदु (अधिकतम या न्यूनतम) खोजें और इन बिंदुओं पर f के मान की गणना करें।

7. परिभाषा के क्षेत्र में शामिल नहीं किए गए विशेषता बिंदुओं के पड़ोस में फ़ंक्शन एफ के व्यवहार की जांच करें।

8. फ़ंक्शन का ग्राफ़ बनाएं.

यह चित्र उदाहरणात्मक है.

उपरोक्त सभी को ध्यान में रखते हुए, हम फ़ंक्शन की जांच करते हैं: f (x) \u003d 3x 5 -5x 3 +2 और इसका ग्राफ बनाते हैं।

आइए शोध इस प्रकार करें:

डी (एफ ") =आईआर, चूंकि एफ (एक्स) एक बहुपद है।

फलन f न तो सम है और न ही विषम है, क्योंकि

f (-x)= 3(-x) 5 -5(-x) 3 +2 = -3x 5 +5x 3 +2= -(3x 5 -5x 3 -2) f(x)

निर्देशांक अक्षों के साथ ग्राफ़ के प्रतिच्छेदन बिंदुओं के निर्देशांक ज्ञात करें:

a) 0X अक्ष के साथ, इसके लिए हम समीकरण हल करते हैं: 3x 5 -5x 3 +2 = 0.

चयन विधि से किसी एक मूल (x = 1) का पता लगाया जा सकता है। अन्य जड़ें लगभग ही पाई जा सकती हैं। इसलिए, इस फ़ंक्शन के लिए, हमें भुज अक्ष और स्थिर चिह्न के अंतराल के साथ ग्राफ़ के प्रतिच्छेदन के शेष बिंदु नहीं मिलेंगे।

बी) 0Y अक्ष के साथ: f(0)=2

बिंदु A (0; 2) - 0Y अक्ष के साथ फ़ंक्शन ग्राफ़ का प्रतिच्छेदन बिंदु।

हमने नोट किया कि हमें संकेत स्थिरता के अंतराल नहीं मिलेंगे।

फलन के बढ़ने और घटने के अंतराल ज्ञात कीजिए

ए) एफ "(एक्स) \u003d 15x 4 -15x 2 \u003d 15x 2 (x 2 -1)

डी (एफ ") \u003d आईआर, इसलिए ऐसे कोई महत्वपूर्ण बिंदु नहीं हैं जिनमें एफ "(एक्स) मौजूद नहीं है।

बी) एफ "(एक्स) \u003d 0 यदि एक्स 2 (एक्स 2 -1) \u003d 0<=>एक्स = -1 वी एक्स = 0 वी एक्स = 1.

ग) हमें तीन महत्वपूर्ण बिंदु मिलते हैं, वे समन्वय रेखा को चार अंतरालों में विभाजित करते हैं। आइए हम इन अंतरालों पर अवकलज का चिह्न निर्धारित करें:

चित्र 3 (संकेत f")

चतुर्थ. एक नया विषय तय करना. समस्या को सुलझाना.

शिक्षक: - फ़ंक्शन का अन्वेषण करें और उसका ग्राफ़ बनाएं: f (x) = x 4 -2x 2 -3।

छात्र:- 1) डी (एफ) =आर.

2) एफ (-x) = (-x) 4 -2 (-x) 2 -3 = x 4 -2x 2 -3; एफ(-एक्स)= एफ(एक्स),

इसलिए फलन f सम है। इसका अध्ययन उस अंतराल पर किया जा सकता है जिसमें फ़ंक्शन - से -4 तक बढ़ता है, इसलिए, इस अंतराल पर समीकरण f (x) \u003d 0 की कोई जड़ें नहीं हैं।

बी) अंतराल पर [-1; 2] समीकरण का कोई मूल नहीं है, क्योंकि इस अंतराल पर फलन -4 से घटकर -31 हो जाता है।

ग) अंतराल पर और [-∞;-1] पर घटता है।

चरम बिंदु: x मिनट = -1

फ़ंक्शन एक्स्ट्रेमा: y मिनट =y(-1)=1-2= -1

अध्याय III. कार्य अनुसंधान.

3.1. कार्यों के अध्ययन के लिए सामान्य योजना।

किसी फ़ंक्शन की जांच करते समय, आपको सामान्य शोध योजना जानने की आवश्यकता है:

1) डी(वाई) – परिभाषा का क्षेत्र (चर एक्स की सीमा)

2) E(y) – x मान का क्षेत्रफल (वेरिएबल y की सीमा)

3) फ़ंक्शन का प्रकार: सम, विषम, आवधिक या सामान्य फ़ंक्शन।

4) ओही ओय अक्षों के साथ फ़ंक्शन के ग्राफ़ के प्रतिच्छेदन बिंदु (यदि संभव हो)।

5) संकेत स्थिरता का अंतराल:

a) फ़ंक्शन एक सकारात्मक मान लेता है: f(x)>0

बी) नकारात्मक मान: एफ(एक्स)<0.

6) फ़ंक्शन एकरसता के अंतराल:

क) वृद्धि;

बी) कमी;

सी) स्थिरता (एफ = स्थिरांक)।

7) चरम अंक (न्यूनतम और अधिकतम अंक)

8) फ़ंक्शन एक्स्ट्रेमा (न्यूनतम और अधिकतम बिंदुओं पर फ़ंक्शन मान)

9) अतिरिक्त अंक.

फ़ंक्शन को अधिक सटीक रूप से प्लॉट करने के लिए उन्हें लिया जा सकता है।

यह ध्यान दिया जाना चाहिए कि फ़ंक्शन f का चरम हमेशा फ़ंक्शन के अधिकतम और न्यूनतम मानों से मेल नहीं खाता है।

3.2. कार्यों के बढ़ने और घटने का संकेत.

यदि आप किसी फ़ंक्शन के कुछ मनमाने ढंग से चुने गए बिंदुओं का उपयोग करके एक ग्राफ़ बनाते हैं, उन्हें एक चिकनी रेखा से जोड़ते हैं, तो बहुत बड़ी संख्या में यादृच्छिक रूप से चयनित बिंदुओं के साथ भी, यह पता चल सकता है कि इस तरह से बनाया गया ग्राफ़ बहुत अलग होगा किसी दिए गए फ़ंक्शन के ग्राफ़ से।

यदि, किसी फ़ंक्शन का अध्ययन करते समय, हम व्युत्पन्न का उपयोग करते हैं और तथाकथित "संदर्भ" बिंदु पाते हैं, अर्थात। विराम बिंदु, अधिकतम और न्यूनतम बिंदु, फ़ंक्शन एकरसता के अंतराल, फिर ऐसे "संदर्भ" बिंदुओं की एक छोटी संख्या के साथ भी, हमें फ़ंक्शन ग्राफ़ का सही विचार मिलेगा।

उदाहरणों पर जाने से पहले, मैं आवश्यक परिभाषाएँ और प्रमेय दूंगा।

किसी अंतराल पर किसी फ़ंक्शन की एकरसता की परिभाषा फ़ंक्शन y \u003d f (x) को अंतराल पर बढ़ना कहा जाता है, यदि इस अंतराल के किसी भी बिंदु x 1 और x 2 के लिए शर्त x 1 से<х 2 следует, что f(x 1)f(x 2), तो फ़ंक्शन को इस अंतराल पर घटता हुआ कहा जाता है।

किसी अंतराल में किसी फ़ंक्शन की एकरसता के लिए पर्याप्त मानदंड। प्रमेय: यदि किसी फ़ंक्शन में अंतराल के प्रत्येक बिंदु पर एक सकारात्मक (नकारात्मक) व्युत्पन्न होता है, तो इस अंतराल पर फ़ंक्शन बढ़ता (घटता) है।

यह प्रमेय स्कूली पाठ्यपुस्तकों में बिना प्रमाण के स्वीकार किया जाता है।

प्रमेय की ज्यामितीय व्याख्या बहुत सरल है, अगर हम याद रखें कि f '(x) \u003d tgα, α किसी दिए गए बिंदु x पर फ़ंक्शन के ग्राफ के स्पर्शरेखा का ढलान है। यदि, उदाहरण के लिए, एक निश्चित अंतराल के सभी बिंदुओं पर f ' (x)> 0 है, तो भुज अक्ष के साथ ग्राफ की स्पर्शरेखा तीव्र कोण बनाती है, जिसका अर्थ है कि x के साथ f (x) भी बढ़ता है। यदि एफ' (एक्स)<0, то касательная с осью абсцисс образуют тупой угол, а значит, с ростом х функция f(x) убывает. Поскольку эти рассуждения основаны лишь на наглядных геометрических представлениях, они не являются доказательством теоремы.

3.3. फ़ंक्शन के महत्वपूर्ण बिंदु, मैक्सिमा और मिनिमा।

किसी फ़ंक्शन के चरम बिंदुओं का निर्धारण . मान लीजिए x 0 फ़ंक्शन f(x) के डोमेन से एक आंतरिक बिंदु है। फिर, यदि ऐसा कोई δ - पड़ोस ] x 0 - δ, x 0 + δ [अंक x 0 है, तो इस पड़ोस से सभी x के लिए असमानता f(x)≤f(x 0) संतुष्ट है (असमानता f (x)≥f (x 0)), बिंदु x 0 को इस फ़ंक्शन का अधिकतम बिंदु (न्यूनतम बिंदु) कहा जाता है।

अधिकतम-न्यूनतम बिंदु फ़ंक्शन के डोमेन के आंतरिक बिंदु हैं।

एक अवकलनीय फलन के चरम के अस्तित्व के लिए एक आवश्यक मानदंड .

फ़र्मेट का प्रमेय.

यदि x 0 फ़ंक्शन f (x) का एक चरम बिंदु है और इस बिंदु पर व्युत्पन्न मौजूद है, तो यह शून्य के बराबर है: f '(x 0) \u003d 0।

यह प्रमेय एक भिन्न फ़ंक्शन के चरम के अस्तित्व के लिए पर्याप्त शर्त नहीं है: यदि किसी बिंदु x 0 पर व्युत्पन्न गायब हो जाता है, तो यह अभी तक इसका पालन नहीं करता है कि बिंदु x 0 पर फ़ंक्शन का एक चरम है।

किसी फ़ंक्शन के महत्वपूर्ण बिंदुओं की परिभाषा . किसी फ़ंक्शन के डोमेन के आंतरिक बिंदु, जिस पर इसका व्युत्पन्न शून्य के बराबर है या मौजूद नहीं है, फ़ंक्शन के महत्वपूर्ण बिंदु कहलाते हैं।

एक चरम के अस्तित्व के लिए पर्याप्त परिस्थितियाँ .

प्रमेय 1. यदि फ़ंक्शन f (x) बिंदु x 0 पर निरंतर है, तो अंतराल पर f '(x)> 0 और f '(x)<0 на интервале , то х 0 является точкой максимума функции f(x).

प्रमेय 2. यदि फ़ंक्शन f (x) बिंदु x 0 पर निरंतर है, तो f '(x)<0 на интервале и f ‘(x)>अंतराल पर 0 है, तो x 0 फ़ंक्शन f(x) का न्यूनतम बिंदु है।

किसी फ़ंक्शन के चरम बिंदुओं को खोजने के लिए, इसके महत्वपूर्ण बिंदुओं को ढूंढना आवश्यक है और उनमें से प्रत्येक के लिए पर्याप्त चरम स्थितियों की पूर्ति की जांच करना आवश्यक है।

3.4. फ़ंक्शन का सबसे बड़ा और सबसे छोटा मान।

अंतराल में फ़ंक्शन का सबसे बड़ा और सबसे छोटा मान खोजने के नियम। किसी फ़ंक्शन के सबसे बड़े और सबसे छोटे मानों को खोजने के लिए जो एक निश्चित अंतराल में भिन्न होते हैं, आपको अंतराल के अंदर मौजूद सभी महत्वपूर्ण बिंदुओं को ढूंढना होगा, इन बिंदुओं पर और अंत में फ़ंक्शन के मानों की गणना करें अंतराल, और इस प्रकार प्राप्त फ़ंक्शन के सभी मानों में से सबसे बड़ा और सबसे छोटा चुनें।

अध्याय IV. किसी फ़ंक्शन के अध्ययन में व्युत्पन्न को लागू करने के उदाहरण।

उदाहरण 11. फ़ंक्शन y=x 3 +6x 2 +9x का अन्वेषण करें और एक ग्राफ बनाएं।

2) फ़ंक्शन के प्रकार को परिभाषित करें:

y(-x)=(-x) 3 +6(-x) 2 +9(-x)=-x+6x 2 -9x सामान्य फलन।

x=0 या x2 +6x+9=0

D=0, समीकरण का एक मूल है।

(0;0) और (-3;0) - एक्स-अक्ष के साथ प्रतिच्छेदन बिंदु।

y'=(x 3 +6x 2 +9x)'=3x 2 +12x+9

y'=0, यानी 3x 2 +12x+9=0 को 3 से कम करें

D>0, समीकरण के 2 मूल हैं।

x 1,2 = (-b±√D) / 2a, x 1 = (-4 + 2) / 2, x 2 = (-4-2) / 2

0
-4

x=-4, y'=3*16-48+9=9>0

x=-2, y'=12-24+9=-3<0

x=0, y'=0+0+9=9>0

7) x मिनट और x अधिकतम ज्ञात करें:

8) फ़ंक्शन का चरम ज्ञात करें:

ymin=y(-1)=-1+6-9=-4

ymax=y(-3)=-27+54-27=0

9) आइए फ़ंक्शन का एक ग्राफ़ बनाएं:

10) अतिरिक्त बिंदु:

y(-4)=-64+96-36=-4

उदाहरण 12. फ़ंक्शन y=x 2 /(x-2) का अन्वेषण करें और एक ग्राफ बनाएं

y=x 2 /(x-2)=x+2+4/(x-2)

आइए फ़ंक्शन के स्पर्शोन्मुख खोजें:

x≠ 2, x=2 – ऊर्ध्वाधर अनंतस्पर्शी

y=x+2 तिरछा अनंतस्पर्शी है, क्योंकि

आइए परिभाषा का क्षेत्र खोजें।

2) आइए फ़ंक्शन के प्रकार को परिभाषित करें।

y(-x)=(-x) 2 /(-x-2)=x 2 /(-x-2), सामान्य कार्य।

3) अक्षों के साथ प्रतिच्छेदन बिंदु ज्ञात कीजिए।

ओए: x=0, y=0 (0;0) - y-अक्ष के साथ प्रतिच्छेदन बिंदु।

x=0 या x=2 (2;0) - x-अक्ष के साथ प्रतिच्छेदन बिंदु

4) फ़ंक्शन का व्युत्पन्न खोजें:

y'=(2x(x-2)-x 2)/(x-2) 2 =(2x 2 -4x-x 2)/(x-2) 2 =(x(x-4))/(x -2) 2 = (x 2 -4x) / (x-2) 2

5) महत्वपूर्ण बिंदुओं को परिभाषित करें:

x 2 -4x=0 x(x-4)=0

y'=0, (x 2 -4x)/(x-2) 2 =0<=> <=>

(x-2) 2 ≠ 0 x≠ 2

x 2 -4x=0, और (x-2) 2 ≠ 0, यानी। एक्स≠ 2

6) हम समन्वय रेखा पर महत्वपूर्ण बिंदुओं को दर्शाते हैं और फ़ंक्शन का चिह्न निर्धारित करते हैं।

0 8

x=-1, y'=(1+4)/9=5/9>0

x=1, y'=(1-4)/1=-3<0

x=3, y'=(9-12)/1=-3<0

x=5, y'=(25-20)/9=5/9>0

7) फ़ंक्शन के न्यूनतम और अधिकतम बिंदु खोजें:

8) फ़ंक्शन का चरम ज्ञात करें:

ymin=y(4)=16/2=8

9) आइए फ़ंक्शन का एक ग्राफ़ बनाएं:

10) अतिरिक्त बिंदु:

y(-3)=9/-5=-1.8 y(3)=9/1=9

y(1)=1/-1=-1 y(6)=36/4=9

उदाहरण 13 फ़ंक्शन y=(6(x-1))/(x 2 +3) का अन्वेषण करें और एक ग्राफ बनाएं। 1) फ़ंक्शन का डोमेन खोजें:

2) फ़ंक्शन के प्रकार को परिभाषित करें:

y(-x)=(6(-x-1))/(x 2 +3)=-(6(x+1))/(x 2 -3) एक सामान्य फलन है।

3) अक्षों के साथ प्रतिच्छेदन बिंदु ज्ञात करें:

O y: x=0, y=(6(0-1))/(0+3)=-2, (0;-2) - y-अक्ष के साथ प्रतिच्छेदन बिंदु।

(6(x-1))/(x 2 +3)=0

हे एक्स: y=0,<=>

4) फ़ंक्शन का व्युत्पन्न खोजें:

y'=(6(x-1)/(x 2 +3))'=6(x 2 +3-2x 2 +2x)/(x 2 +2) 2 =-6(x+1)(x -3)/(x 2 +3) 2

5) महत्वपूर्ण बिंदुओं को परिभाषित करें:

y'=0, यानी -6(x+1)(x-3)/(x 2 +3) 2 =0

y'=0, यदि x 1 =-1 या x 2 =3, तो x=-1 और x=3, महत्वपूर्ण बिंदु।

6) हम समन्वय रेखा पर महत्वपूर्ण बिंदुओं को दर्शाते हैं और फ़ंक्शन का चिह्न निर्धारित करते हैं:

-3 2

x=-2, y'=-6(-2+1)(-2-3)/(4+3) 2 =-30/49<0

x=0, y'=-6(0+1)(0-3)/(0+3) 2 =2>0

x=4, y'=-6(4+1)(4-3)/(16+3) 2=-30/361<0

7) न्यूनतम और अधिकतम अंक ज्ञात करें:

8) फ़ंक्शन का चरम ज्ञात करें:

y मिनट =y(-1)=(6(-1-1))/(1+3)=-12/4=-3

y अधिकतम =y(3)=(6(3-1))/(9+3)=12/12=1

9) आइए फ़ंक्शन का एक ग्राफ़ बनाएं:

10) अतिरिक्त बिंदु:

y(-3)=(6(-3-1))/(9+3)=-24/12=-2

y(6)=(6(6-1))/(36+3)=30/39=10/13≈ 0.77

उदाहरण 14 फ़ंक्शन y=xlnx का अन्वेषण करें और उसका ग्राफ़ बनाएं:

1) फ़ंक्शन का डोमेन खोजें:

D(y)=R + (केवल सकारात्मक मान)

2) फ़ंक्शन के प्रकार को परिभाषित करें:

y(-x)=-xlnx - सामान्य रूप।

3) अक्षों के साथ प्रतिच्छेदन बिंदु ज्ञात करें:

O y , लेकिन x≠ 0, इसलिए y-अक्ष के साथ कोई प्रतिच्छेदन बिंदु नहीं है।

बैल: y=0 यानी xlnx=0

x=0 या lnx=0

(1;0) - एक्स-अक्ष के साथ प्रतिच्छेदन बिंदु

4) फ़ंक्शन का व्युत्पन्न खोजें:

y'=x' ln x + x(ln x)'=ln x +1

5) महत्वपूर्ण बिंदुओं को परिभाषित करें:

y'=0, यानी lnx +1=0

y'=0 , यदि x=1/e , तो x=1/e एक महत्वपूर्ण बिंदु है।

6) हम समन्वय रेखा पर महत्वपूर्ण बिंदुओं को दर्शाते हैं और फ़ंक्शन का चिह्न निर्धारित करते हैं:

1/इ

x=1/(2e); y'=log(2e) -1 +1=1-ln(2e)=1-ln e=-ln 2<0

x=2e; y'=ln(2e)+1=ln 2+ln e+1=ln 2+2>0

7) 1/e फ़ंक्शन का न्यूनतम बिंदु है।

8) फ़ंक्शन का चरम ज्ञात करें:

y मिनट = y (1 / e) = 1 / e ln e -1 = -1 / e (≈ -0.4)।

9) आइए फ़ंक्शन का एक ग्राफ़ बनाएं:

निष्कर्ष।

इस विषय पर कई वैज्ञानिकों और दार्शनिकों ने काम किया है। कई साल पहले, ये शब्द सामने आए थे: फ़ंक्शन, ग्राफ़, फ़ंक्शन का अध्ययन, और वे नई सुविधाओं और विशेषताओं को प्राप्त करते हुए आज तक जीवित हैं।

मैंने यह विषय इसलिए चुना क्योंकि फ़ंक्शन पर शोध के इस रास्ते से गुजरना मेरे लिए बहुत दिलचस्प था। मुझे ऐसा लगता है कि कई लोगों को फ़ंक्शन, उसके गुणों और परिवर्तनों के बारे में अधिक जानने में रुचि होगी। इस निबंध को बनाने के बाद, मैंने अपने कौशल को व्यवस्थित किया और इस विषय के बारे में अपने ज्ञान के भंडार को फिर से भर दिया।

मैं सभी को इस विषय का अधिक गहराई से अध्ययन करने की सलाह देना चाहता हूं।

ग्रंथ सूची.

1. बश्माकोव, एम.आई. बीजगणित और विश्लेषण की शुरुआत। - एम।: शिक्षा, 1992।

2. ग्लेसर, जी.आई. स्कूल में गणित का इतिहास। - एम.: शिक्षा, 1983।

3. गुसेव, वी.ए. गणित: संदर्भ सामग्री। - एम.: शिक्षा, 1888।

4. डोरोफीव, जी.वी. विश्वविद्यालयों के आवेदकों के लिए गणित मैनुअल। - एम.: नौका, 1974।

5. ज़ोरिन, वी.वी. विश्वविद्यालयों के आवेदकों के लिए गणित मैनुअल। - एम.: हायर स्कूल, 1980।

6. कोलमोगोरोव ए.एन. बीजगणित और विश्लेषण की शुरुआत।- एम.: ज्ञानोदय, 1993।