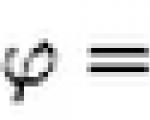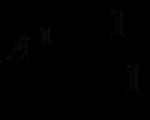जैसे समीकरण हल करना. उदाहरण सहित रैखिक समीकरणों को हल करना

अंतिम परीक्षण की तैयारी के चरण में, हाई स्कूल के छात्रों को "घातीय समीकरण" विषय पर अपने ज्ञान में सुधार करने की आवश्यकता है। पिछले वर्षों का अनुभव बताता है कि ऐसे कार्य स्कूली बच्चों के लिए कुछ कठिनाइयाँ पैदा करते हैं। इसलिए, हाई स्कूल के छात्रों को, उनकी तैयारी के स्तर की परवाह किए बिना, सिद्धांत में सावधानीपूर्वक महारत हासिल करने, सूत्रों को याद रखने और ऐसे समीकरणों को हल करने के सिद्धांत को समझने की आवश्यकता है। इस प्रकार के कार्यों से निपटना सीख लेने के बाद, स्नातक गणित में परीक्षा उत्तीर्ण करते समय उच्च अंकों पर भरोसा करने में सक्षम होंगे।

शकोल्कोवो के साथ मिलकर परीक्षा परीक्षण के लिए तैयार हो जाइए!

कवर की गई सामग्रियों को दोहराते समय, कई छात्रों को समीकरणों को हल करने के लिए आवश्यक सूत्र खोजने की समस्या का सामना करना पड़ता है। एक स्कूल की पाठ्यपुस्तक हमेशा हाथ में नहीं होती है, और इंटरनेट पर किसी विषय पर आवश्यक जानकारी के चयन में काफी समय लगता है।

शकोल्कोवो शैक्षिक पोर्टल छात्रों को हमारे ज्ञान आधार का उपयोग करने के लिए आमंत्रित करता है। हम अंतिम परीक्षा की तैयारी का एक बिल्कुल नया तरीका लागू कर रहे हैं। हमारी साइट पर अध्ययन करते हुए, आप ज्ञान में अंतराल की पहचान करने और उन कार्यों पर ध्यान देने में सक्षम होंगे जो सबसे बड़ी कठिनाइयों का कारण बनते हैं।

"श्कोल्कोवो" के शिक्षकों ने परीक्षा में सफल उत्तीर्ण होने के लिए आवश्यक सभी सामग्री को सबसे सरल और सबसे सुलभ रूप में एकत्र, व्यवस्थित और प्रस्तुत किया।

मुख्य परिभाषाएँ और सूत्र "सैद्धांतिक संदर्भ" खंड में प्रस्तुत किए गए हैं।

सामग्री को बेहतर ढंग से आत्मसात करने के लिए, हम अनुशंसा करते हैं कि आप असाइनमेंट का अभ्यास करें। गणना एल्गोरिथ्म को समझने के लिए इस पृष्ठ पर प्रस्तुत समाधानों के साथ घातीय समीकरणों के उदाहरणों की सावधानीपूर्वक समीक्षा करें। उसके बाद, "कैटलॉग" अनुभाग में कार्यों के साथ आगे बढ़ें। आप सबसे आसान कार्यों से शुरुआत कर सकते हैं या कई अज्ञात या के साथ जटिल घातीय समीकरणों को हल करने के लिए सीधे जा सकते हैं। हमारी वेबसाइट पर अभ्यासों का डेटाबेस लगातार पूरक और अद्यतन किया जाता है।

संकेतकों वाले वे उदाहरण जिनके कारण आपको कठिनाई हुई, उन्हें "पसंदीदा" में जोड़ा जा सकता है। तो आप उन्हें तुरंत ढूंढ सकते हैं और शिक्षक के साथ समाधान पर चर्चा कर सकते हैं।

परीक्षा को सफलतापूर्वक उत्तीर्ण करने के लिए, प्रतिदिन शकोल्कोवो पोर्टल पर अध्ययन करें!

सेवा असाइनमेंट. मैट्रिक्स कैलकुलेटर को रैखिक समीकरणों की प्रणालियों को मैट्रिक्स तरीके से हल करने के लिए डिज़ाइन किया गया है (समान समस्याओं को हल करने का एक उदाहरण देखें)।

अनुदेश. ऑनलाइन समाधान के लिए, आपको समीकरण के प्रकार का चयन करना होगा और संबंधित आव्यूहों का आयाम निर्धारित करना होगा। जहां ए, बी, सी को मैट्रिक्स दिया गया है, एक्स वांछित मैट्रिक्स है। फॉर्म (1), (2) और (3) के मैट्रिक्स समीकरणों को व्युत्क्रम मैट्रिक्स ए -1 के माध्यम से हल किया जाता है। यदि व्यंजक A यदि अभिव्यक्ति A*X = B 2 दी गई है, तो मैट्रिक्स B को पहले वर्गित किया जाना चाहिए।

मैट्रिसेस पर बुनियादी संचालन से खुद को परिचित करने की भी सिफारिश की जाती है।

उदाहरण 1। व्यायाम. मैट्रिक्स समीकरण का हल खोजें
समाधान. निरूपित करें:
फिर मैट्रिक्स समीकरण इस रूप में लिखा जाएगा: A·X·B = C.
मैट्रिक्स A का निर्धारक detA=-1 है
चूँकि A एक गैर-एकवचन मैट्रिक्स है, इसलिए एक व्युत्क्रम मैट्रिक्स A -1 है। बायीं ओर के समीकरण के दोनों पक्षों को A -1 से गुणा करें: इस समीकरण के बायीं ओर के दोनों पक्षों को A -1 से और दायीं ओर के दोनों पक्षों को B -1 से गुणा करें: A -1 A X B B -1 = A -1 C B -1। चूँकि A A -1 = B B -1 = E और E X = X E = X, तो X = A -1 C B -1

उलटा मैट्रिक्स ए -1:
व्युत्क्रम मैट्रिक्स B -1 ज्ञात कीजिए।
ट्रांसपोज़ मैट्रिक्स बी टी:
उलटा मैट्रिक्स बी -1:
हम सूत्र द्वारा मैट्रिक्स एक्स की तलाश कर रहे हैं: एक्स = ए -1 सी बी -1

उत्तर:

उदाहरण #2. व्यायाम।मैट्रिक्स समीकरण हल करें
समाधान. निरूपित करें:
फिर मैट्रिक्स समीकरण इस रूप में लिखा जाएगा: A X = B.
मैट्रिक्स A का निर्धारक detA=0 है
चूँकि A एक पतित मैट्रिक्स है (निर्धारक 0 है), इसलिए, समीकरण का कोई हल नहीं है।

उदाहरण #3. व्यायाम। मैट्रिक्स समीकरण का हल खोजें
समाधान. निरूपित करें:
फिर मैट्रिक्स समीकरण इस रूप में लिखा जाएगा: X·A = B.
मैट्रिक्स A का निर्धारक detA=-60 है
चूँकि A एक गैर-एकवचन मैट्रिक्स है, इसलिए एक व्युत्क्रम मैट्रिक्स A -1 है। समीकरण के दाहिनी ओर दोनों पक्षों को A -1 से गुणा करें: X A A -1 = B A -1, जिससे हमें पता चलता है कि X = B A -1
व्युत्क्रम मैट्रिक्स A -1 खोजें।
ट्रांसपोज़्ड मैट्रिक्स ए टी:
उलटा मैट्रिक्स ए -1:
हम सूत्र द्वारा मैट्रिक्स एक्स की तलाश कर रहे हैं: एक्स = बी ए -1


उत्तर: >

गणित हल करने के लिए. जल्दी ढूंढो गणित समीकरण समाधानमोड में ऑनलाइन. वेबसाइट www.site अनुमति देती है प्रश्न हल करेंलगभग कोई भी दिया गया बीजगणितीय, त्रिकोणमितीयया ट्रान्सेंडैंटल समीकरण ऑनलाइन. गणित के लगभग किसी भी अनुभाग का विभिन्न चरणों में अध्ययन करते समय, व्यक्ति को निर्णय लेना होता है समीकरण ऑनलाइन. तुरंत उत्तर पाने के लिए, और सबसे महत्वपूर्ण रूप से सटीक उत्तर पाने के लिए, आपको एक ऐसे संसाधन की आवश्यकता है जो आपको ऐसा करने की अनुमति दे। www.site को धन्यवाद समीकरणों को ऑनलाइन हल करेंकुछ मिनट लगेंगे. गणितीय हल करते समय www.site का मुख्य लाभ समीकरण ऑनलाइन- जारी प्रतिक्रिया की गति और सटीकता है. साइट किसी का भी समाधान करने में सक्षम है बीजगणितीय समीकरण ऑनलाइन, त्रिकोणमितीय समीकरण ऑनलाइन, ट्रान्सेंडैंटल समीकरण ऑनलाइन, और समीकरणमोड में अज्ञात पैरामीटर के साथ ऑनलाइन. समीकरणएक शक्तिशाली गणितीय उपकरण के रूप में कार्य करें समाधानव्यावहारिक कार्य. मदद से गणितीय समीकरणउन तथ्यों और संबंधों को व्यक्त करना संभव है जो पहली नज़र में भ्रमित करने वाले और जटिल लग सकते हैं। अज्ञात मात्राएँ समीकरणसमस्या को सूत्रबद्ध करके पाया जा सकता है गणितीयरूप में भाषा समीकरणऔर तय करनामोड में प्राप्त कार्य ऑनलाइनवेबसाइट www.site पर। कोई बीजगणितीय समीकरण, त्रिकोणमितीय समीकरणया समीकरणयुक्त ट्रान्सेंडैंटलआपको आसानी से सुविधाएँ देता है तय करनाऑनलाइन और सही उत्तर प्राप्त करें। प्राकृतिक विज्ञान का अध्ययन करते समय व्यक्ति को अनिवार्य रूप से आवश्यकता का सामना करना पड़ता है समीकरण हल करना. इस मामले में, उत्तर सटीक होना चाहिए और इसे तुरंत मोड में प्राप्त किया जाना चाहिए ऑनलाइन. इसलिए, के लिए गणित के समीकरण ऑनलाइन हल करेंहम साइट www.site की अनुशंसा करते हैं, जो आपके लिए अपरिहार्य कैलकुलेटर बन जाएगी बीजगणितीय समीकरणों को ऑनलाइन हल करें, त्रिकोणमितीय समीकरण ऑनलाइन, और ट्रान्सेंडैंटल समीकरण ऑनलाइनया समीकरणअज्ञात मापदंडों के साथ. विभिन्न की जड़ों को खोजने की व्यावहारिक समस्याओं के लिए गणितीय समीकरणसंसाधन www.. समाधान समीकरण ऑनलाइनस्वयं, प्राप्त उत्तर की जाँच करना उपयोगी है समीकरणों का ऑनलाइन समाधानवेबसाइट www.site पर। समीकरण को सही ढंग से लिखना और तुरंत प्राप्त करना आवश्यक है ऑनलाइन समाधान, जिसके बाद यह केवल समीकरण के आपके समाधान के साथ उत्तर की तुलना करने के लिए रह जाता है। उत्तर जांचने में एक मिनट से ज्यादा नहीं लगेगा, काफी है समीकरण को ऑनलाइन हल करेंऔर उत्तरों की तुलना करें. इससे आपको गलतियों से बचने में मदद मिलेगी फ़ैसलाऔर समय रहते उत्तर सही करें समीकरणों को ऑनलाइन हल करनादोनों में से एक बीजगणितीय, त्रिकोणमितीय, उत्कृष्टया समीकरणअज्ञात मापदंडों के साथ.

इस वीडियो में, हम रैखिक समीकरणों के एक पूरे सेट का विश्लेषण करेंगे जिन्हें एक ही एल्गोरिदम का उपयोग करके हल किया जाता है - यही कारण है कि उन्हें सबसे सरल कहा जाता है।

आरंभ करने के लिए, आइए परिभाषित करें: एक रैखिक समीकरण क्या है और उनमें से किसे सबसे सरल कहा जाना चाहिए?

एक रैखिक समीकरण वह होता है जिसमें केवल एक चर होता है, और केवल पहली डिग्री में।

सबसे सरल समीकरण का अर्थ है निर्माण:

एल्गोरिथम का उपयोग करके अन्य सभी रैखिक समीकरणों को सरलतम समीकरणों में बदल दिया गया है:

1. खुले कोष्ठक, यदि कोई हों;
2. एक चर वाले पदों को समान चिह्न के एक ओर ले जाएँ, और बिना चर वाले पदों को दूसरी ओर ले जाएँ;
3. समान पदों को समान चिन्ह के बायीं और दायीं ओर लाएँ;
4. परिणामी समीकरण को चर $x$ के गुणांक से विभाजित करें।

बेशक, यह एल्गोरिथम हमेशा मदद नहीं करता है। तथ्य यह है कि कभी-कभी, इन सभी साजिशों के बाद, चर $x$ का गुणांक शून्य के बराबर हो जाता है। इस मामले में, दो विकल्प संभव हैं:

1. समीकरण का कोई समाधान नहीं है। उदाहरण के लिए, जब आपको $0\cdot x=8$ जैसा कुछ मिलता है, यानी। बाईं ओर शून्य है, और दाईं ओर एक गैर-शून्य संख्या है। नीचे दिए गए वीडियो में, हम कई कारणों पर गौर करेंगे कि यह स्थिति क्यों संभव है।
2. समाधान सभी संख्याएँ हैं। यह एकमात्र मामला है जब यह संभव है जब समीकरण को $0\cdot x=0$ की संरचना में घटा दिया गया हो। यह काफी तर्कसंगत है कि चाहे हम $x$ को किसी भी स्थान पर रखें, फिर भी यह "शून्य, शून्य के बराबर है" ही निकलेगा, यानी। सही संख्यात्मक समानता.

और अब आइए देखें कि वास्तविक समस्याओं के उदाहरण पर यह सब कैसे काम करता है।

समीकरणों को हल करने के उदाहरण

आज हम रैखिक समीकरणों से निपटते हैं, और केवल सबसे सरल समीकरणों से। सामान्य तौर पर, एक रैखिक समीकरण का मतलब किसी भी समानता से होता है जिसमें बिल्कुल एक चर होता है, और यह केवल पहली डिग्री तक जाता है।

ऐसे निर्माण लगभग उसी तरह हल किए जाते हैं:

1. सबसे पहले, आपको कोष्ठक खोलने होंगे, यदि कोई हो (जैसा कि हमारे पिछले उदाहरण में है);
2. फिर समान ले आओ
3. अंत में, वेरिएबल को अलग करें, यानी वह सब कुछ जो चर के साथ जुड़ा हुआ है - वे शब्द जिनमें यह निहित है - एक तरफ स्थानांतरित हो जाता है, और जो कुछ इसके बिना रहता है वह दूसरी तरफ स्थानांतरित हो जाता है।

फिर, एक नियम के रूप में, आपको परिणामी समानता के प्रत्येक पक्ष पर समान लाने की आवश्यकता है, और उसके बाद यह केवल "x" पर गुणांक द्वारा विभाजित करने के लिए बनी हुई है, और हमें अंतिम उत्तर मिलेगा।

सिद्धांत रूप में, यह अच्छा और सरल दिखता है, लेकिन व्यवहार में, अनुभवी हाई स्कूल के छात्र भी काफी सरल रैखिक समीकरणों में आक्रामक गलतियाँ कर सकते हैं। आमतौर पर, गलतियाँ या तो कोष्ठक खोलते समय, या "प्लस" और "माइनस" गिनते समय की जाती हैं।

इसके अलावा, ऐसा होता है कि एक रैखिक समीकरण का कोई समाधान नहीं होता है, या ऐसा होता है कि समाधान पूरी संख्या रेखा होती है, यानी। कोई संख्या। आज के पाठ में हम इन सूक्ष्मताओं का विश्लेषण करेंगे। लेकिन जैसा कि आप पहले ही समझ चुके हैं, हम सबसे सरल कार्यों से शुरुआत करेंगे।

सरल रैखिक समीकरणों को हल करने की योजना

आरंभ करने के लिए, मैं एक बार फिर सबसे सरल रैखिक समीकरणों को हल करने की पूरी योजना लिखूंगा:

1. कोष्ठक, यदि कोई हो, विस्तृत करें।
2. वैरिएबल को अलग करें, यानी वह सब कुछ जिसमें "x" होता है उसे एक तरफ स्थानांतरित कर दिया जाता है, और "x" के बिना - दूसरी तरफ।
3. हम समान शर्तें प्रस्तुत करते हैं।
4. हम हर चीज़ को "x" के गुणांक से विभाजित करते हैं।

बेशक, यह योजना हमेशा काम नहीं करती है, इसमें कुछ सूक्ष्मताएं और तरकीबें हैं, और अब हम उन्हें जानेंगे।

सरल रैखिक समीकरणों के वास्तविक उदाहरणों को हल करना

कार्य 1

पहले चरण में, हमें कोष्ठक खोलने होंगे। लेकिन वे इस उदाहरण में नहीं हैं, इसलिए हम इस चरण को छोड़ देते हैं। दूसरे चरण में, हमें वेरिएबल्स को अलग करने की आवश्यकता है। कृपया ध्यान दें: हम केवल व्यक्तिगत शब्दों के बारे में बात कर रहे हैं। चलो लिखते है:

हम बायीं और दायीं ओर समान शब्द देते हैं, लेकिन यह यहां पहले ही किया जा चुका है। इसलिए, हम चौथे चरण पर आगे बढ़ते हैं: एक कारक से विभाजित करें:

\[\frac(6x)(6)=-\frac(72)(6)\]

यहां हमें जवाब मिल गया.

कार्य #2

इस कार्य में, हम कोष्ठकों का अवलोकन कर सकते हैं, तो आइए उनका विस्तार करें:

बाईं ओर और दाईं ओर, हम लगभग एक ही निर्माण देखते हैं, लेकिन आइए एल्गोरिथम के अनुसार कार्य करें, अर्थात। अनुक्रमिक चर:

यहाँ कुछ इस प्रकार हैं:

यह किन जड़ों पर काम करता है? उत्तर: किसी के लिए. इसलिए, हम लिख सकते हैं कि $x$ कोई भी संख्या है।

कार्य #3

तीसरा रैखिक समीकरण पहले से ही अधिक दिलचस्प है:

\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]

यहां कई कोष्ठक हैं, लेकिन उन्हें किसी भी चीज़ से गुणा नहीं किया जाता है, बस उनके सामने अलग-अलग चिह्न होते हैं। आइए उन्हें तोड़ें:

हम दूसरा चरण करते हैं जो हमें पहले से ही ज्ञात है:

\[-x+x+2x=15-6-12+3\]

आइए गणना करें:

हम अंतिम चरण करते हैं - हम हर चीज़ को "x" के गुणांक से विभाजित करते हैं:

\[\frac(2x)(x)=\frac(0)(2)\]

रैखिक समीकरणों को हल करते समय याद रखने योग्य बातें

यदि हम बहुत सरल कार्यों को नज़रअंदाज कर दें, तो मैं निम्नलिखित कहना चाहूँगा:

• जैसा कि मैंने ऊपर कहा, प्रत्येक रैखिक समीकरण का कोई हल नहीं होता - कभी-कभी कोई मूल ही नहीं होता;
• यदि जड़ें हैं भी, तो शून्य उनके बीच में आ सकता है - इसमें कुछ भी गलत नहीं है।

शून्य बाकी संख्याओं के समान ही है, आपको इसमें किसी तरह का भेदभाव नहीं करना चाहिए या यह नहीं मान लेना चाहिए कि यदि आपको शून्य मिलता है, तो आपने कुछ गलत किया है।

एक अन्य विशेषता कोष्ठक के विस्तार से संबंधित है। कृपया ध्यान दें: जब उनके सामने "माइनस" होता है, तो हम उसे हटा देते हैं, लेकिन कोष्ठक में हम संकेतों को बदल देते हैं विलोम. और फिर हम इसे मानक एल्गोरिदम के अनुसार खोल सकते हैं: हमें वही मिलेगा जो हमने ऊपर की गणना में देखा था।

इस सरल तथ्य को समझने से आपको हाई स्कूल में मूर्खतापूर्ण और हानिकारक गलतियाँ करने से बचने में मदद मिलेगी, जब ऐसे कार्यों को हल्के में लिया जाता है।

जटिल रैखिक समीकरणों को हल करना

आइए अधिक जटिल समीकरणों की ओर बढ़ते हैं। अब निर्माण अधिक जटिल हो जाएंगे और विभिन्न परिवर्तन करते समय एक द्विघात फ़ंक्शन दिखाई देगा। हालाँकि, आपको इससे डरना नहीं चाहिए, क्योंकि यदि, लेखक की मंशा के अनुसार, हम एक रैखिक समीकरण को हल करते हैं, तो परिवर्तन की प्रक्रिया में द्विघात फलन वाले सभी एकपदी आवश्यक रूप से कम हो जाएंगे।

उदाहरण 1

जाहिर है, पहला कदम कोष्ठक खोलना है। आइए इसे बहुत सावधानी से करें:

आइए अब गोपनीयता की बात करें:

\[-x+6((x)^(2))-6((x)^(2))+x=-12\]

यहाँ कुछ इस प्रकार हैं:

जाहिर है, इस समीकरण का कोई समाधान नहीं है, इसलिए उत्तर में हम इस प्रकार लिखते हैं:

\[\विविधता \]

या कोई जड़ नहीं.

उदाहरण #2

हम वही चरण निष्पादित करते हैं. पहला कदम:

आइए एक वेरिएबल के साथ सब कुछ बाईं ओर ले जाएं, और इसके बिना - दाईं ओर:

यहाँ कुछ इस प्रकार हैं:

जाहिर है, इस रैखिक समीकरण का कोई हल नहीं है, इसलिए हम इसे इस तरह लिखते हैं:

\[\कुछ नहीं\],

या कोई जड़ नहीं.

समाधान की बारीकियां

दोनों समीकरण पूर्णतः हल हो गये हैं। इन दो अभिव्यक्तियों के उदाहरण पर, हमने एक बार फिर यह सुनिश्चित किया कि सबसे सरल रैखिक समीकरणों में भी, सब कुछ इतना सरल नहीं हो सकता है: या तो एक हो सकता है, या कोई नहीं, या अनंत रूप से कई हो सकते हैं। हमारे मामले में, हमने दो समीकरणों पर विचार किया, दोनों में कोई जड़ें नहीं हैं।

लेकिन मैं आपका ध्यान एक अन्य तथ्य की ओर आकर्षित करना चाहूंगा: कोष्ठक के साथ कैसे काम किया जाए और यदि उनके सामने ऋण चिह्न हो तो उनका विस्तार कैसे किया जाए। इस अभिव्यक्ति पर विचार करें:

खोलने से पहले, आपको हर चीज़ को "x" से गुणा करना होगा। कृपया ध्यान दें: गुणा करें प्रत्येक व्यक्तिगत पद. अंदर दो पद हैं - क्रमशः, दो पद और गुणा किया गया है।

और इन प्रतीत होने वाले प्राथमिक, लेकिन बहुत महत्वपूर्ण और खतरनाक परिवर्तनों के पूरा होने के बाद ही, ब्रैकेट को इस दृष्टिकोण से खोला जा सकता है कि इसके बाद एक ऋण चिह्न है। हाँ, हाँ: केवल अब, जब परिवर्तन किए जाते हैं, तो हमें याद आता है कि कोष्ठक के सामने एक ऋण चिह्न है, जिसका अर्थ है कि नीचे सब कुछ केवल चिह्न बदलता है। उसी समय, कोष्ठक स्वयं गायब हो जाते हैं और, सबसे महत्वपूर्ण बात, सामने वाला "माइनस" भी गायब हो जाता है।

हम दूसरे समीकरण के साथ भी ऐसा ही करते हैं:

यह कोई संयोग नहीं है कि मैं इन छोटे, प्रतीत होने वाले महत्वहीन तथ्यों पर ध्यान देता हूं। क्योंकि समीकरणों को हल करना हमेशा प्रारंभिक परिवर्तनों का एक क्रम होता है, जहां स्पष्ट रूप से और सक्षम रूप से सरल कार्यों को करने में असमर्थता इस तथ्य की ओर ले जाती है कि हाई स्कूल के छात्र मेरे पास आते हैं और ऐसे सरल समीकरणों को फिर से हल करना सीखते हैं।

निःसंदेह, वह दिन आएगा जब आप इन कौशलों को स्वचालितता तक निखार लेंगे। अब आपको हर बार इतने सारे परिवर्तन करने की ज़रूरत नहीं है, आप सब कुछ एक पंक्ति में लिखेंगे। लेकिन जब आप अभी सीख रहे हैं, तो आपको प्रत्येक क्रिया को अलग से लिखना होगा।

और भी अधिक जटिल रैखिक समीकरणों को हल करना

अब हम जो हल करने जा रहे हैं उसे शायद ही सबसे सरल कार्य कहा जा सकता है, लेकिन अर्थ वही रहता है।

कार्य 1

\[\left(7x+1 \right)\left(3x-1 \right)-21((x)^(2))=3\]

आइए पहले भाग के सभी तत्वों को गुणा करें:

आइए एक रिट्रीट करें:

यहाँ कुछ इस प्रकार हैं:

आइए अंतिम चरण करें:

\[\frac(-4x)(4)=\frac(4)(-4)\]

यहाँ हमारा अंतिम उत्तर है. और, इस तथ्य के बावजूद कि हल करने की प्रक्रिया में हमारे पास द्विघात फलन वाले गुणांक थे, तथापि, उन्होंने पारस्परिक रूप से रद्द कर दिया, जिससे समीकरण बिल्कुल रैखिक हो जाता है, वर्गाकार नहीं।

कार्य #2

\[\left(1-4x \right)\left(1-3x \right)=6x\left(2x-1 \right)\]

आइए पहला चरण सावधानी से करें: पहले ब्रैकेट के प्रत्येक तत्व को दूसरे ब्रैकेट के प्रत्येक तत्व से गुणा करें। कुल मिलाकर, परिवर्तनों के बाद चार नए शब्द प्राप्त होने चाहिए:

और अब प्रत्येक पद में सावधानीपूर्वक गुणन करें:

आइए "x" वाले शब्दों को बाईं ओर और बिना - दाईं ओर ले जाएँ:

\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]

यहाँ समान शब्द हैं:

हमें एक निश्चित उत्तर प्राप्त हुआ है।

समाधान की बारीकियां

इन दो समीकरणों के बारे में सबसे महत्वपूर्ण टिप्पणी यह ​​है: जैसे ही हम उन कोष्ठकों को गुणा करना शुरू करते हैं जिनमें एक से अधिक पद हैं, तो यह निम्नलिखित नियम के अनुसार किया जाता है: हम पहले से पहला पद लेते हैं और प्रत्येक तत्व से गुणा करते हैं दूसरे से; फिर हम पहले से दूसरा तत्व लेते हैं और इसी तरह दूसरे तत्व से प्रत्येक तत्व को गुणा करते हैं। परिणामस्वरूप, हमें चार पद प्राप्त होते हैं।

बीजगणितीय योग पर

अंतिम उदाहरण के साथ, मैं छात्रों को याद दिलाना चाहूंगा कि बीजगणितीय योग क्या है। शास्त्रीय गणित में, $1-7$ से हमारा तात्पर्य एक साधारण निर्माण से है: हम एक में से सात घटाते हैं। बीजगणित में, इससे हमारा तात्पर्य निम्नलिखित है: संख्या "एक" में हम एक और संख्या जोड़ते हैं, जिसका नाम है "शून्य से सात।" यह बीजगणितीय योग सामान्य अंकगणितीय योग से भिन्न होता है।

जैसे ही सभी परिवर्तन, प्रत्येक जोड़ और गुणा करते समय, आपको ऊपर वर्णित संरचनाओं के समान संरचनाएं दिखाई देने लगती हैं, बहुपद और समीकरणों के साथ काम करते समय आपको बीजगणित में कोई समस्या नहीं होगी।

अंत में, आइए कुछ और उदाहरण देखें जो हमारे द्वारा अभी देखे गए उदाहरणों से भी अधिक जटिल होंगे, और उन्हें हल करने के लिए, हमें अपने मानक एल्गोरिदम को थोड़ा विस्तारित करना होगा।

भिन्न के साथ समीकरण हल करना

ऐसे कार्यों को हल करने के लिए हमारे एल्गोरिदम में एक और कदम जोड़ना होगा। लेकिन सबसे पहले, मैं हमारे एल्गोरिदम को याद दिलाऊंगा:

1. कोष्ठक खोलें.
2. अलग चर.
3. समान लाओ.
4. एक कारक से विभाजित करें.

अफसोस, यह अद्भुत एल्गोरिदम, अपनी सभी दक्षता के बावजूद, पूरी तरह उपयुक्त नहीं है जब हमारे सामने भिन्न हों। और जो हम नीचे देखेंगे, उसमें दोनों समीकरणों में बायीं और दायीं ओर एक भिन्न है।

इस मामले में कैसे काम करें? हाँ, यह बहुत आसान है! ऐसा करने के लिए, आपको एल्गोरिदम में एक और चरण जोड़ने की आवश्यकता है, जिसे पहली क्रिया से पहले और उसके बाद, अर्थात् भिन्नों से छुटकारा पाने के लिए किया जा सकता है। इस प्रकार, एल्गोरिथ्म इस प्रकार होगा:

1. भिन्नों से छुटकारा पाएं.
2. कोष्ठक खोलें.
3. अलग चर.
4. समान लाओ.
5. एक कारक से विभाजित करें.

"भिन्नों से छुटकारा पाने" का क्या मतलब है? और पहले मानक चरण के बाद और पहले दोनों समय ऐसा करना क्यों संभव है? वास्तव में, हमारे मामले में, सभी भिन्न हर के संदर्भ में संख्यात्मक हैं, अर्थात। हर जगह हर सिर्फ एक संख्या है। इसलिए, यदि हम समीकरण के दोनों भागों को इस संख्या से गुणा करें, तो हमें भिन्नों से छुटकारा मिल जाएगा।

उदाहरण 1

\[\frac(\left(2x+1 \right)\left(2x-3 \right))(4)=((x)^(2))-1\]

आइए इस समीकरण में भिन्नों से छुटकारा पाएं:

\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \right)\cdot 4\]

कृपया ध्यान दें: प्रत्येक चीज़ को एक बार "चार" से गुणा किया जाता है, अर्थात। सिर्फ इसलिए कि आपके पास दो कोष्ठक हैं इसका मतलब यह नहीं है कि आपको उनमें से प्रत्येक को "चार" से गुणा करना होगा। चलो लिखते है:

\[\left(2x+1 \right)\left(2x-3 \right)=\left(((x)^(2))-1 \right)\cdot 4\]

अब इसे खोलें:

हम एक चर का पृथक्करण करते हैं:

हम समान शर्तों की कमी करते हैं:

\[-4x=-1\बाएँ| :\left(-4 \right) \right.\]

\[\frac(-4x)(-4)=\frac(-1)(-4)\]

हमें अंतिम समाधान प्राप्त हो गया है, हम दूसरे समीकरण पर चलते हैं।

उदाहरण #2

\[\frac(\left(1-x \right)\left(1+5x \right))(5)+((x)^(2))=1\]

यहां हम वही सभी क्रियाएं करते हैं:

\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]

\[\frac(4x)(4)=\frac(4)(4)\]

समस्या हल हो गई।

वास्तव में, मैं आज बस यही बताना चाहता था।

प्रमुख बिंदु

मुख्य निष्कर्ष इस प्रकार हैं:

• रैखिक समीकरणों को हल करने के लिए एल्गोरिदम को जानें।
• कोष्ठक खोलने की क्षमता.
• यदि आपके पास कहीं द्विघात कार्य हैं तो चिंता न करें, सबसे अधिक संभावना है, आगे के परिवर्तनों की प्रक्रिया में, वे कम हो जाएंगे।
• रैखिक समीकरणों में जड़ें, यहां तक ​​कि सबसे सरल भी, तीन प्रकार की होती हैं: एक एकल जड़, पूरी संख्या रेखा एक जड़ होती है, कोई जड़ नहीं होती है।

मुझे आशा है कि यह पाठ आपको संपूर्ण गणित को और अधिक समझने के लिए एक सरल, लेकिन बहुत महत्वपूर्ण विषय पर महारत हासिल करने में मदद करेगा। यदि कुछ स्पष्ट नहीं है तो साइट पर जाएं, वहां प्रस्तुत उदाहरणों को हल करें। देखते रहिए, कई और दिलचस्प चीज़ें आपका इंतज़ार कर रही हैं!