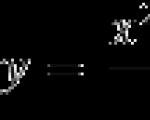असमानता में एक मॉड्यूल को कैसे हटाएं। मॉड्यूलो समीकरण

असमानताओं को ऑनलाइन हल करना

असमानताओं को हल करने से पहले यह अच्छी तरह से समझना आवश्यक है कि समीकरणों को कैसे हल किया जाता है।

इससे कोई फर्क नहीं पड़ता कि असमानता सख्त () है या गैर-सख्त (≤, ≥) है, पहला कदम असमानता चिह्न को समानता (=) से बदलकर समीकरण को हल करना है।

बताएं कि असमानता को हल करने का क्या मतलब है?

समीकरणों का अध्ययन करने के बाद, छात्र के दिमाग में निम्नलिखित तस्वीर होती है: आपको चर के ऐसे मान खोजने की आवश्यकता है जिसके लिए समीकरण के दोनों भाग समान मान लेते हैं। दूसरे शब्दों में, वे सभी बिंदु खोजें जहां समानता है। सब कुछ सही है!

जब असमानताओं के बारे में बात की जाती है, तो उनका मतलब उन अंतरालों (खंडों) को ढूंढना होता है जिन पर असमानता टिकी होती है। यदि असमानता में दो चर हैं, तो समाधान अब अंतराल नहीं होगा, बल्कि समतल पर कुछ क्षेत्र होंगे। अंदाजा लगाइए कि तीन चरों में असमानता का समाधान क्या होगा?

असमानताओं को कैसे हल करें?

अंतराल की विधि (उर्फ अंतराल की विधि) को असमानताओं को हल करने का एक सार्वभौमिक तरीका माना जाता है, जिसमें उन सभी अंतरालों को निर्धारित करना शामिल है जिनके भीतर दी गई असमानता पूरी हो जाएगी।

असमानता के प्रकार में जाने के बिना, इस मामले में यह सार नहीं है, संबंधित समीकरण को हल करना और इसकी जड़ों को निर्धारित करना आवश्यक है, इसके बाद संख्यात्मक अक्ष पर इन समाधानों का पदनाम किया जाता है।

किसी असमानता का समाधान लिखने का सही तरीका क्या है?

जब आपने असमानता को हल करने के लिए अंतराल निर्धारित कर लिया है, तो आपको समाधान को सही ढंग से लिखना होगा। एक महत्वपूर्ण बारीकियां है - क्या समाधान में अंतराल की सीमाएं शामिल हैं?

यहां सब कुछ सरल है. यदि समीकरण का समाधान ODZ को संतुष्ट करता है और असमानता सख्त नहीं है, तो अंतराल की सीमा असमानता के समाधान में शामिल है। अन्यथा, नहीं.

प्रत्येक अंतराल को ध्यान में रखते हुए, असमानता का समाधान अंतराल ही हो सकता है, या आधा-अंतराल (जब इसकी सीमाओं में से एक असमानता को संतुष्ट करता है), या एक खंड - इसकी सीमाओं के साथ एक अंतराल।

महत्वपूर्ण बिंदु

यह मत सोचिए कि केवल अंतराल, अर्ध-अंतराल और खंड ही किसी असमानता का समाधान हो सकते हैं। नहीं, समाधान में व्यक्तिगत बिंदुओं को भी शामिल किया जा सकता है।

उदाहरण के लिए, असमानता |x|≤0 का केवल एक ही समाधान है - बिंदु 0।

और असमानता |x|

असमानता कैलकुलेटर किसके लिए है?

असमानता कैलकुलेटर सही अंतिम उत्तर देता है। अधिकांश मामलों में, संख्यात्मक अक्ष या तल का चित्रण दिया जाता है। आप देख सकते हैं कि अंतराल की सीमाएँ समाधान में शामिल हैं या नहीं - बिंदु भरे हुए या छेदे हुए प्रदर्शित होते हैं।

ऑनलाइन असमानता कैलकुलेटर के लिए धन्यवाद, आप जांच सकते हैं कि क्या आपने समीकरण की जड़ों को सही ढंग से पाया है, उन्हें संख्या रेखा पर चिह्नित किया है और अंतराल (और सीमाओं) पर असमानता की स्थिति की जांच की है?

यदि आपका उत्तर कैलकुलेटर के उत्तर से भिन्न है, तो आपको निश्चित रूप से अपने समाधान की दोबारा जांच करने और की गई गलती की पहचान करने की आवश्यकता है।

व्यक्ति जितना अधिक समझता है, उसकी समझने की इच्छा उतनी ही प्रबल होती है

थॉमस एक्विनास

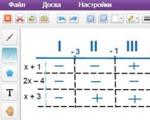
अंतराल विधि आपको मापांक वाले किसी भी समीकरण को हल करने की अनुमति देती है। इस पद्धति का सार संख्यात्मक अक्ष को कई खंडों (अंतराल) में विभाजित करना है, और मॉड्यूल में अभिव्यक्तियों के शून्य के साथ अक्ष को विभाजित करना आवश्यक है। फिर, प्रत्येक परिणामी अनुभाग पर, कोई भी सबमॉड्यूल अभिव्यक्ति या तो सकारात्मक या नकारात्मक होती है। इसलिए, प्रत्येक मॉड्यूल को ऋण चिह्न या प्लस चिह्न के साथ विस्तारित किया जा सकता है। इन क्रियाओं के बाद, विचाराधीन अंतराल पर प्रत्येक प्राप्त सरल समीकरण को हल करना और प्राप्त उत्तरों को संयोजित करना ही शेष रह जाता है।

आइए एक विशिष्ट उदाहरण पर इस पद्धति पर विचार करें।

|एक्स + 1| + |2x – 4| – |एक्स + 3| = 2x - 6.

1) मॉड्यूल में भावों के शून्य ज्ञात कीजिए। ऐसा करने के लिए, हम उन्हें शून्य के बराबर करते हैं, और परिणामी समीकरणों को हल करते हैं।

x + 1 = 0 2x – 4 = 0 x + 3 = 0

एक्स = -1 2एक्स = 4 एक्स = -3

2) परिणामी बिंदुओं को निर्देशांक रेखा पर वांछित क्रम में व्यवस्थित करें। वे पूरी धुरी को चार खंडों में तोड़ देंगे।

3) आइए प्रत्येक परिणामी अनुभाग पर मॉड्यूल में अभिव्यक्तियों के संकेत निर्धारित करें। ऐसा करने के लिए, हम उनमें हमारी रुचि के अंतरालों में से कोई भी संख्या प्रतिस्थापित करते हैं। यदि गणना का परिणाम एक सकारात्मक संख्या है, तो हम तालिका में "+" डालते हैं, और यदि संख्या नकारात्मक है, तो हम "-" डालते हैं। इसे इस तरह चित्रित किया जा सकता है:

4) अब हम तालिका में मौजूद संकेतों के साथ मॉड्यूल खोलकर, चार अंतरालों में से प्रत्येक पर समीकरण को हल करेंगे। तो, पहले अंतराल पर विचार करें:

मैं अंतराल (-∞; -3). इस पर सभी मॉड्यूल "-" चिह्न के साथ खोले जाते हैं। हमें निम्नलिखित समीकरण मिलता है:

-(x + 1) - (2x - 4) - (-(x + 3)) = 2x - 6। परिणामी समीकरण में पहले कोष्ठक खोलकर हम समान पद प्रस्तुत करते हैं:

एक्स - 1 - 2x + 4 + x + 3 = 2x - 6

प्राप्त उत्तर विचारित अंतराल में शामिल नहीं है, इसलिए इसे अंतिम उत्तर में लिखना आवश्यक नहीं है।

द्वितीय अंतराल [-3; -1). तालिका में इस अंतराल पर "-", "-", "+" चिह्न हैं। इस प्रकार हम मूल समीकरण के मॉड्यूल को प्रकट करते हैं:

-(x + 1) - (2x - 4) - (x + 3) = 2x - 6. कोष्ठक का विस्तार करके सरल करें:

X - 1 - 2x + 4 - x - 3 \u003d 2x - 6. हम परिणामी समीकरण में निम्नलिखित प्रस्तुत करते हैं:

एक्स = 6/5. परिणामी संख्या विचाराधीन अंतराल से संबंधित नहीं है, इसलिए यह मूल समीकरण की जड़ नहीं है।

तृतीय अंतराल [-1; 2). हम मूल समीकरण के मॉड्यूल को उन चिह्नों के साथ खोलते हैं जो तीसरे कॉलम में चित्र में हैं। हम पाते हैं:

(x + 1) - (2x - 4) - (x + 3) = 2x - 6. कोष्ठक से छुटकारा पाएं, चर x वाले पदों को समीकरण के बाईं ओर ले जाएं, और x नहीं वाले पदों को दाईं ओर ले जाएं . होगा:

x + 1 - 2x + 4 - x - 3 = 2x - 6

संख्या 2 विचारित अंतराल में शामिल नहीं है।

चतुर्थ अंतराल

सरल शब्दों में, मापांक "बिना ऋण के एक संख्या" है। और यह इस द्वंद्व में है (कहीं आपको मूल संख्या के साथ कुछ भी करने की ज़रूरत नहीं है, लेकिन कहीं आपको वहां कुछ माइनस हटाना है) और नौसिखिए छात्रों के लिए सारी कठिनाई निहित है।

एक ज्यामितीय परिभाषा भी है. इसे जानना भी उपयोगी है, लेकिन हम इसका उल्लेख केवल जटिल और कुछ विशेष मामलों में करेंगे, जहां ज्यामितीय दृष्टिकोण बीजगणितीय दृष्टिकोण की तुलना में अधिक सुविधाजनक है (स्पॉइलर: आज नहीं)।

परिभाषा। मान लीजिए कि बिंदु $a$ को वास्तविक रेखा पर अंकित किया गया है। फिर मॉड्यूल $\left| x-a \right|$ इस रेखा पर बिंदु $x$ से बिंदु $a$ तक की दूरी है।

यदि आप कोई चित्र बनाते हैं, तो आपको कुछ इस प्रकार मिलता है:

ग्राफ़िकल मॉड्यूल परिभाषा

एक तरह से या किसी अन्य, इसकी मुख्य संपत्ति तुरंत मॉड्यूल की परिभाषा से मिलती है: किसी संख्या का मापांक सदैव एक गैर-ऋणात्मक मान होता है. यह तथ्य आज हमारी पूरी कहानी में एक लाल धागे की तरह रहेगा।

असमानताओं का समाधान. रिक्ति विधि

अब आइए असमानताओं से निपटें। उनमें से बहुत सारे हैं, लेकिन अब हमारा काम उनमें से कम से कम सबसे सरल को हल करने में सक्षम होना है। वे जो रैखिक असमानताओं के साथ-साथ अंतराल की विधि से भी कम हो जाते हैं।

मेरे पास इस विषय पर दो बड़े ट्यूटोरियल हैं (वैसे, बहुत, बहुत उपयोगी - मैं अध्ययन करने की सलाह देता हूं):

1. असमानताओं के लिए अंतराल विधि (विशेषकर वीडियो देखें);
2. भिन्नात्मक-तर्कसंगत असमानताएँ एक बहुत बड़ा पाठ है, लेकिन इसके बाद आपके पास कोई प्रश्न नहीं होगा।

यदि आप यह सब जानते हैं, यदि वाक्यांश "आइए असमानता से समीकरण की ओर चलें" आपको दीवार के खिलाफ खुद को मारने के लिए प्रेरित नहीं करता है, तो आप तैयार हैं: पाठ के मुख्य विषय में नरक में आपका स्वागत है। :)

1. "फ़ंक्शन से कम मॉड्यूल" फॉर्म की असमानताएं

यह मॉड्यूल के साथ सबसे अधिक बार सामने आने वाले कार्यों में से एक है। फॉर्म की असमानता को हल करना आवश्यक है:

\[\बाएं| f\दाएं| \ltg\]

कुछ भी फ़ंक्शन $f$ और $g$ के रूप में कार्य कर सकता है, लेकिन आमतौर पर वे बहुपद होते हैं। ऐसी असमानताओं के उदाहरण:

\[\शुरू(संरेखित करें) और \बाएं| 2x+3\दाएं| \ltx+7; \\ & \बाएं| ((x)^(2))+2x-3 \दाएं|+3\बाएं(x+1 \दाएं) \lt 0; \\ & \बाएं| ((x)^(2))-2\left| x \दाएं|-3 \दाएं| \lt 2. \\\end(संरेखित करें)\]

उन सभी को योजना के अनुसार वस्तुतः एक पंक्ति में हल किया जाता है:

\[\बाएं| f\दाएं| \lt g\राइटएरो -g \lt f \lt g\quad \left(\राइटएरो \left\( \begin(संरेखित) & f \lt g, \\ & f \gt -g \\\end(संरेखित) \सही सही)\]

यह देखना आसान है कि हमें मॉड्यूल से छुटकारा मिल जाता है, लेकिन इसके बजाय हमें दोहरी असमानता मिलती है (या, जो एक ही बात है, दो असमानताओं की एक प्रणाली)। लेकिन यह परिवर्तन बिल्कुल सभी संभावित समस्याओं को ध्यान में रखता है: यदि मॉड्यूल के अंतर्गत संख्या सकारात्मक है, तो विधि काम करती है; यदि नकारात्मक है, तो यह अभी भी काम करता है; और $f$ या $g$ के स्थान पर सबसे अपर्याप्त फ़ंक्शन के साथ भी, विधि अभी भी काम करेगी।

स्वाभाविक रूप से, सवाल उठता है: क्या यह आसान नहीं है? दुर्भाग्य से, आप नहीं कर सकते. यह मॉड्यूल का संपूर्ण बिंदु है.

लेकिन दार्शनिकता बहुत हो गई। आइए कुछ समस्याओं का समाधान करें:

काम। असमानता का समाधान करें:

\[\बाएं| 2x+3\दाएं| \ltx+7\]

समाधान। तो, हमारे पास "मॉड्यूल से कम है" के रूप में एक शास्त्रीय असमानता है - यहां तक ​​कि बदलने के लिए कुछ भी नहीं है। हम एल्गोरिथम के अनुसार काम करते हैं:

\[\शुरू(संरेखित करें) और \बाएं| f\दाएं| \lt g\राइटएरो -g \lt f \lt g; \\ & \बाएं| 2x+3\दाएं| \lt x+7\दायां तीर -\बाएं(x+7 \दाएं) \lt 2x+3 \lt x+7 \\\end(संरेखित)\]

उन कोष्ठकों को खोलने में जल्दबाजी न करें जिनके पहले "माइनस" लिखा है: यह बहुत संभव है कि जल्दबाजी के कारण आप कोई आपत्तिजनक गलती कर देंगे।

\[-x-7 \lt 2x+3 \lt x+7\]

\[\बाएं\( \begin(संरेखित) और -x-7 \lt 2x+3 \\ और 2x+3 \lt x+7 \\ \end(संरेखित) \दाएं।\]

\[\बाएँ\( \begin(संरेखित) और -3x \lt 10 \\ और x \lt 4 \\ \end(संरेखित) \दाएँ।\]

\[\left\( \begin(संरेखित) और x \gt -\frac(10)(3) \\ और x \lt 4 \\ \end(संरेखित) \दाएं।\]

समस्या को दो प्राथमिक असमानताओं तक सीमित कर दिया गया है। हम उनके समाधानों को समानांतर वास्तविक रेखाओं पर नोट करते हैं:

अनेकों का अंतर्विच्छेद

इन सेटों का प्रतिच्छेदन उत्तर होगा।

उत्तर: $x\in \left(-\frac(10)(3);4 \right)$

काम। असमानता का समाधान करें:

\[\बाएं| ((x)^(2))+2x-3 \दाएं|+3\बाएं(x+1 \दाएं) \lt 0\]

समाधान। यह कार्य थोड़ा अधिक कठिन है. आरंभ करने के लिए, हम दूसरे पद को दाईं ओर ले जाकर मॉड्यूल को अलग करते हैं:

\[\बाएं| ((x)^(2))+2x-3 \right| \lt -3\left(x+1 \right)\]

जाहिर है, हमारे पास फिर से "मॉड्यूल कम है" फॉर्म की असमानता है, इसलिए हम पहले से ज्ञात एल्गोरिदम के अनुसार मॉड्यूल से छुटकारा पाते हैं:

\[-\left(-3\left(x+1 \right) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \right)\]

अब ध्यान दें: कोई कहेगा कि मैं इन सभी कोष्ठकों के साथ थोड़ा विकृत हूं। लेकिन एक बार फिर मैं आपको याद दिलाता हूं कि हमारा मुख्य लक्ष्य है असमानता को सही ढंग से हल करें और उत्तर प्राप्त करें. बाद में, जब आपने इस पाठ में वर्णित हर चीज में पूरी तरह से महारत हासिल कर ली है, तो आप अपने आप को अपनी इच्छानुसार विकृत कर सकते हैं: कोष्ठक खोलें, माइनस जोड़ें, आदि।

और शुरुआत के लिए, हम बाईं ओर के दोहरे माइनस से छुटकारा पा लेते हैं:

\[-\left(-3\left(x+1 \right) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\बाएं(x+1\दाएं)\]

आइए अब दोहरी असमानता में सभी कोष्ठक खोलें:

आइए दोहरी असमानता की ओर आगे बढ़ें। इस बार गणना अधिक गंभीर होगी:

\[\left\( \begin(संरेखित) और ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(संरेखित करें) \दाएं।\]

\[\left\( \begin(संरेखित) और ((x)^(2))+5x \lt 0 \\ और ((x)^(2))-x-6 \gt 0 \\ \end( सही संरेखित।\]

दोनों असमानताएँ वर्गाकार हैं और अंतराल विधि द्वारा हल की जाती हैं (इसीलिए मैं कहता हूँ: यदि आप नहीं जानते कि यह क्या है, तो मॉड्यूल को अभी तक न लेना ही बेहतर है)। हम पहली असमानता में समीकरण को पास करते हैं:

\[\begin(संरेखित) और ((x)^(2))+5x=0; \\ & x\left(x+5 \right)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\end(संरेखित करें)\]

जैसा कि आप देख सकते हैं, आउटपुट एक अपूर्ण द्विघात समीकरण निकला, जिसे प्राथमिक रूप से हल किया गया है। अब आइए व्यवस्था की दूसरी असमानता से निपटें। वहां आपको विएटा का प्रमेय लागू करना होगा:

\[\begin(संरेखित) और ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\end(संरेखित करें)\]

हम प्राप्त संख्याओं को दो समानांतर रेखाओं पर अंकित करते हैं (पहली असमानता के लिए अलग और दूसरी के लिए अलग):

फिर, चूँकि हम असमानताओं की एक प्रणाली को हल कर रहे हैं, हम छायांकित सेटों के प्रतिच्छेदन में रुचि रखते हैं: $x\in \left(-5;-2 \right)$। यह उत्तर है.

उत्तर: $x\in \left(-5;-2 \right)$

मुझे लगता है कि इन उदाहरणों के बाद समाधान योजना बहुत स्पष्ट है:

1. अन्य सभी पदों को असमानता के विपरीत दिशा में ले जाकर मॉड्यूल को अलग करें। इस प्रकार हमें $\left| के रूप की एक असमानता प्राप्त होती है f\दाएं| \ltg$.
2. ऊपर वर्णित अनुसार मॉड्यूल से छुटकारा पाकर इस असमानता को हल करें। कुछ बिंदु पर, दोहरी असमानता से दो स्वतंत्र अभिव्यक्तियों की प्रणाली में जाना आवश्यक होगा, जिनमें से प्रत्येक को पहले से ही अलग से हल किया जा सकता है।
3. अंत में, यह केवल इन दो स्वतंत्र अभिव्यक्तियों के समाधानों को पार करने के लिए ही रह गया है - और बस इतना ही, हमें अंतिम उत्तर मिलेगा।

एक समान एल्गोरिथ्म निम्नलिखित प्रकार की असमानताओं के लिए मौजूद है, जब मापांक फ़ंक्शन से बड़ा होता है। हालाँकि, कुछ गंभीर "लेकिन" भी हैं। अब हम इन "लेकिन" के बारे में बात करेंगे।

2. "मॉड्यूल फ़ंक्शन से बड़ा है" फॉर्म की असमानताएं

वे इस तरह दिखते हैं:

\[\बाएं| f\दाएं| \gt जी\]

पिछले वाले के समान? जान पड़ता है। फिर भी, ऐसे कार्यों को बिल्कुल अलग तरीके से हल किया जाता है। औपचारिक रूप से, योजना इस प्रकार है:

\[\बाएं| f\दाएं| \gt g\दायां तीर \बाएं[ \begin(संरेखित) और f \gt g, \\ और f \lt -g \\\end(संरेखित) \दाएं।\]

दूसरे शब्दों में, हम दो मामलों पर विचार करते हैं:

1. सबसे पहले, हम केवल मॉड्यूल को अनदेखा करते हैं - हम सामान्य असमानता को हल करते हैं;
2. फिर, वास्तव में, हम मॉड्यूल को ऋण चिह्न के साथ खोलते हैं, और फिर हम असमानता के दोनों हिस्सों को एक चिह्न के साथ -1 से गुणा करते हैं।

इस मामले में, विकल्पों को एक वर्गाकार ब्रैकेट के साथ जोड़ा जाता है, अर्थात। हमारी दो आवश्यकताओं का संयोजन है।

फिर से ध्यान दें: हमारे सामने एक प्रणाली नहीं है, बल्कि एक समुच्चय है उत्तर में, समुच्चय संयुक्त हैं, प्रतिच्छेदित नहीं. यह पिछले पैराग्राफ से एक मूलभूत अंतर है!

सामान्य तौर पर, कई छात्रों को यूनियनों और अंतर्विरोधों को लेकर बहुत भ्रम होता है, तो आइए इस मुद्दे पर एक बार और सभी के लिए गौर करें:

• "∪" एक सम्मिलन चिह्न है। वास्तव में, यह एक शैलीबद्ध अक्षर "यू" है, जो अंग्रेजी भाषा से हमारे पास आया है और यह "यूनियन" का संक्षिप्त रूप है, अर्थात। "संघ"।
• "∩" प्रतिच्छेदन चिन्ह है। यह बकवास कहीं से नहीं आई, बल्कि "∪" के विरोध के रूप में सामने आई।

इसे याद रखना और भी आसान बनाने के लिए, बस इन संकेतों के साथ पैरों को जोड़कर चश्मा बना लें (अभी मुझ पर नशीली दवाओं की लत और शराब को बढ़ावा देने का आरोप न लगाएं: यदि आप गंभीरता से इस पाठ का अध्ययन कर रहे हैं, तो आप पहले से ही नशे के आदी हैं):

समुच्चयों के प्रतिच्छेदन और मिलन के बीच अंतर

रूसी में अनुवादित, इसका मतलब निम्नलिखित है: संघ (संग्रह) में दोनों सेटों के तत्व शामिल हैं, इसलिए, उनमें से प्रत्येक से कम नहीं; लेकिन प्रतिच्छेदन (सिस्टम) में केवल वे तत्व शामिल हैं जो पहले सेट और दूसरे सेट दोनों में हैं। इसलिए, सेटों का प्रतिच्छेदन कभी भी स्रोत सेट से अधिक नहीं होता है।

तो यह स्पष्ट हो गया? यह बहुत बढ़िया बात है। आइए अभ्यास की ओर आगे बढ़ें।

काम। असमानता का समाधान करें:

\[\बाएं| 3x+1 \दाएं| \gt 5-4x\]

समाधान। हम योजना के अनुसार कार्य करते हैं:

\[\बाएं| 3x+1 \दाएं| \gt 5-4x\दायां तीर \बाएं[ \शुरू(संरेखित) और 3x+1 \gt 5-4x \\ और 3x+1 \lt -\बाएं(5-4x \दाएं) \\\अंत(संरेखित) \ सही।\]

हम प्रत्येक जनसंख्या असमानता का समाधान करते हैं:

\[\बाएँ[ \begin(संरेखित) और 3x+4x \gt 5-1 \\ और 3x-4x \lt -5-1 \\ \end(संरेखित) \दाएँ।\]

\[\बाएं[ \शुरू(संरेखित) और 7x \gt 4 \\ और -x \lt -6 \\ \अंत(संरेखित) \दाएं।\]

\[\बाएं[ \begin(संरेखित) और x \gt 4/7\ \\ और x \gt 6 \\ \end(संरेखित) \दाएं।\]

हम प्रत्येक परिणामी सेट को संख्या रेखा पर चिह्नित करते हैं, और फिर उन्हें जोड़ते हैं:

समुच्चयों का संघ

स्पष्ट रूप से उत्तर $x\in \left(\frac(4)(7);+\infty \right)$ है

उत्तर: $x\in \left(\frac(4)(7);+\infty \right)$

काम। असमानता का समाधान करें:

\[\बाएं| ((x)^(2))+2x-3 \right| \gtx\]

समाधान। कुंआ? नहीं, यह सब वैसा ही है. हम मापांक वाली असमानता से दो असमानताओं के समुच्चय की ओर बढ़ते हैं:

\[\बाएं| ((x)^(2))+2x-3 \right| \gt x\दायां तीर \बाएं[ \begin(संरेखित करें) और ((x)^(2))+2x-3 \gt x \\ और ((x)^(2))+2x-3 \lt -x \\\end(संरेखित करें) \दाएं।\]

हम प्रत्येक असमानता का समाधान करते हैं। दुर्भाग्य से, वहाँ जड़ें बहुत अच्छी नहीं होंगी:

\[\begin(संरेखित) और ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\ &D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\end(संरेखित करें)\]

दूसरी असमानता में भी थोड़ा सा खेल है:

\[\begin(संरेखित) और ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\ &D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\end(संरेखित करें)\]

अब हमें इन संख्याओं को दो अक्षों पर अंकित करने की आवश्यकता है - प्रत्येक असमानता के लिए एक अक्ष। हालाँकि, आपको बिंदुओं को सही क्रम में चिह्नित करने की आवश्यकता है: संख्या जितनी बड़ी होगी, बिंदु उतना ही दाईं ओर शिफ्ट होगा।

और यहां हम एक सेटअप की प्रतीक्षा कर रहे हैं। यदि संख्याओं के साथ सब कुछ स्पष्ट है $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ (पहले के अंश में पद भिन्न दूसरे के अंश में पदों से कम है, इसलिए योग भी छोटा है), संख्याओं के साथ $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt (21))(2)$ कोई कठिनाई नहीं होगी (एक सकारात्मक संख्या स्पष्ट रूप से नकारात्मक से अधिक है), लेकिन अंतिम जोड़े के साथ, सब कुछ इतना सरल नहीं है। कौन सा बड़ा है: $\frac(-3+\sqrt(21))(2)$ या $\frac(-1+\sqrt(13))(2)$? संख्या रेखाओं पर बिंदुओं की व्यवस्था और वास्तव में उत्तर इस प्रश्न के उत्तर पर निर्भर करेगा।

तो आइए तुलना करें:

\[\begin(matrix) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matrix)\]

हमने मूल को अलग कर दिया, असमानता के दोनों पक्षों पर गैर-ऋणात्मक संख्याएँ प्राप्त कीं, इसलिए हमें दोनों पक्षों का वर्ग करने का अधिकार है:

\[\begin(matrix) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(matrix)\]

मुझे लगता है कि यह कोई दिमाग लगाने वाली बात नहीं है कि $4\sqrt(13) \gt 3$, इसलिए $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$, अंत में अक्षों पर बिंदुओं को इस प्रकार व्यवस्थित किया जाएगा:

बदसूरत जड़ों का मामला

मैं आपको याद दिला दूं कि हम एक सेट को हल कर रहे हैं, इसलिए उत्तर संघ होगा, न कि छायांकित सेट का प्रतिच्छेदन।

उत्तर: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty\right)$

जैसा कि आप देख सकते हैं, हमारी योजना सरल कार्यों और बहुत कठिन कार्यों दोनों के लिए बढ़िया काम करती है। इस दृष्टिकोण में एकमात्र "कमजोर स्थान" यह है कि आपको अपरिमेय संख्याओं की सही ढंग से तुलना करने की आवश्यकता है (और मेरा विश्वास करें: ये केवल जड़ें नहीं हैं)। लेकिन एक अलग (और बहुत गंभीर पाठ) तुलना के प्रश्नों के लिए समर्पित होगा। और हम आगे बढ़ते हैं.

3. गैर-नकारात्मक "पूंछ" के साथ असमानताएं

तो हम सबसे दिलचस्प तक पहुंचे। ये प्रपत्र की असमानताएँ हैं:

\[\बाएं| f\दाएं| \gt\बाएं| जी\दाएं|\]

सामान्यतया, जिस एल्गोरिदम के बारे में हम अभी बात करने जा रहे हैं वह केवल मॉड्यूल के लिए सत्य है। यह उन सभी असमानताओं में काम करता है जहां बाएं और दाएं तरफ गैर-नकारात्मक अभिव्यक्ति की गारंटी होती है:

इन कार्यों का क्या करें? बस याद रखना:

गैर-नकारात्मक पूँछ वाली असमानताओं में, दोनों पक्षों को किसी भी प्राकृतिक शक्ति तक बढ़ाया जा सकता है। कोई अतिरिक्त प्रतिबंध नहीं होगा.

सबसे पहले, हमें चुकता करने में रुचि होगी - यह मॉड्यूल और जड़ों को जलाता है:

\[\begin(संरेखित करें) और ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f. \\\end(संरेखित करें)\]

बस इसे वर्ग का मूल लेने के साथ भ्रमित न करें:

\[\sqrt(((f)^(2)))=\left| f \दाएं|\ne f\]

जब कोई छात्र मॉड्यूल स्थापित करना भूल गया तो अनगिनत गलतियाँ हुईं! लेकिन यह एक पूरी तरह से अलग कहानी है (ये, जैसे कि यह थे, अतार्किक समीकरण हैं), इसलिए हम अभी इसमें नहीं जाएंगे। आइए कुछ समस्याओं का बेहतर समाधान करें:

काम। असमानता का समाधान करें:

\[\बाएं| x+2 \दाएं|\ge \बाएं| 1-2x \दाएं|\]

समाधान। हम तुरंत दो बातें नोटिस करते हैं:

1. यह एक गैर-सख्त असमानता है. संख्या रेखा पर बिन्दुओं को छिद्रित कर दिया जाएगा।
2. असमानता के दोनों पक्ष स्पष्ट रूप से गैर-नकारात्मक हैं (यह मॉड्यूल की एक संपत्ति है: $\left| f\left(x \right) \right|\ge 0$)।

इसलिए, हम मापांक से छुटकारा पाने के लिए असमानता के दोनों पक्षों का वर्ग कर सकते हैं और सामान्य अंतराल विधि का उपयोग करके समस्या को हल कर सकते हैं:

\[\begin(संरेखित) और ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\left(x+2 \right))^(2))\ge ((\left(2x-1 \right))^(2)). \\\end(संरेखित करें)\]

अंतिम चरण में, मैंने थोड़ा धोखा दिया: मैंने मापांक की समता का उपयोग करते हुए, शब्दों के अनुक्रम को बदल दिया (वास्तव में, मैंने अभिव्यक्ति $1-2x$ को −1 से गुणा कर दिया)।

\[\begin(संरेखित करें) और ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ दाएँ)\दाएँ)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(संरेखित)\]

हम अंतराल विधि से हल करते हैं। आइए असमानता से समीकरण की ओर चलें:

\[\begin(संरेखित करें) और \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\end(संरेखित करें)\]

हम पाए गए मूलों को संख्या रेखा पर अंकित करते हैं। एक बार फिर: सभी बिंदु छायांकित हैं क्योंकि मूल असमानता सख्त नहीं है!

मॉड्यूल चिह्न से छुटकारा

विशेष रूप से जिद्दी लोगों के लिए मैं आपको याद दिला दूं: हम अंतिम असमानता से संकेत लेते हैं, जो समीकरण पर आगे बढ़ने से पहले लिखा गया था। और हम उसी असमानता में आवश्यक क्षेत्रों पर चित्रित करते हैं। हमारे मामले में, यह $\left(x-3 \right)\left(3x+1 \right)\le 0$ है।

ठीक है अब सब ख़त्म हो गया। समस्या हल हो गई।

उत्तर: $x\in \left[ -\frac(1)(3);3 \right]$.

काम। असमानता का समाधान करें:

\[\बाएं| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \दाएं|\]

समाधान। हम सब कुछ वैसे ही करते हैं. मैं कोई टिप्पणी नहीं करूंगा - बस कार्यों के क्रम को देखें।

आइए इसे वर्गित करें:

\[\begin(संरेखित करें) और ((\left(\left| ((x)^(2))+x+1 \right| \right))^(2))\le ((\left(\left) | ((x)^(2))+3x+4 \दाएं| \दाएं))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))\le ((\left(((x)^(2))+3x+4 \दाएं))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))-((\left(((x)^(2))+3x+4 \ दाएँ))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x) ^(2))+x+1+((x)^(2))+3x+4 \दाएं)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(संरेखित)\]

रिक्ति विधि:

\[\begin(संरेखित करें) और \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ दायां तीर x=-1.5; \\ & 2((x)^(2))+4x+5=0\राइटएरो D=16-40 \lt 0\राइटएरो \varnothing। \\\end(संरेखित करें)\]

संख्या रेखा पर केवल एक मूल होता है:

उत्तर एक पूरी श्रृंखला है

उत्तर: $x\in \left[ -1.5;+\infty \right)$.

पिछले कार्य के बारे में एक छोटा सा नोट. जैसा कि मेरे एक छात्र ने सटीक रूप से नोट किया है, इस असमानता में दोनों सबमॉड्यूल अभिव्यक्ति स्पष्ट रूप से सकारात्मक हैं, इसलिए स्वास्थ्य को नुकसान पहुंचाए बिना मापांक चिह्न को छोड़ा जा सकता है।

लेकिन यह पहले से ही सोच का एक बिल्कुल अलग स्तर और एक अलग दृष्टिकोण है - इसे सशर्त रूप से परिणामों की विधि कहा जा सकता है। उसके बारे में - एक अलग पाठ में। और अब आइए आज के पाठ के अंतिम भाग पर आगे बढ़ें और एक सार्वभौमिक एल्गोरिदम पर विचार करें जो हमेशा काम करता है। तब भी जब पिछले सभी दृष्टिकोण शक्तिहीन थे। :)

4. विकल्पों की गणना की विधि

यदि ये सभी तरकीबें काम न करें तो क्या होगा? यदि असमानता गैर-नकारात्मक पूंछों तक कम नहीं होती है, यदि मॉड्यूल को अलग करना असंभव है, यदि दर्द-दुःख-लालसा बिल्कुल भी है?

फिर सभी गणित का "भारी तोपखाना" दृश्य में प्रवेश करता है - गणना पद्धति। मापांक के साथ असमानताओं के संबंध में, यह इस तरह दिखता है:

1. सभी सबमॉड्यूल अभिव्यक्तियाँ लिखें और उन्हें शून्य के बराबर करें;
2. परिणामी समीकरणों को हल करें और पाए गए मूलों को एक संख्या रेखा पर चिह्नित करें;
3. सीधी रेखा को कई खंडों में विभाजित किया जाएगा, जिसके भीतर प्रत्येक मॉड्यूल का एक निश्चित चिह्न होता है और इसलिए स्पष्ट रूप से विस्तार होता है;
4. ऐसे प्रत्येक अनुभाग पर असमानता को हल करें (आप विश्वसनीयता के लिए पैराग्राफ 2 में प्राप्त सीमा जड़ों पर अलग से विचार कर सकते हैं)। परिणामों को संयोजित करें - यही उत्तर होगा। :)

कितनी अच्छी तरह से? कमज़ोर? आसानी से! केवल लंबे समय के लिए. आइए व्यवहार में देखें:

काम। असमानता का समाधान करें:

\[\बाएं| x+2 \दाएं| \lt\बाएं| x-1 \right|+x-\frac(3)(2)\]

समाधान। यह बकवास $\left| जैसी असमानताओं तक सीमित नहीं है f\दाएं| \lt g$, $\बाएं| f\दाएं| \gt g$ या $\left| f\दाएं| \lt\बाएं| g \right|$, तो चलिए आगे बढ़ते हैं।

हम सबमॉड्यूल अभिव्यक्तियाँ लिखते हैं, उन्हें शून्य के बराबर करते हैं और मूल ढूंढते हैं:

\[\begin(संरेखित) और x+2=0\दायां तीर x=-2; \\ & x-1=0\दायां तीर x=1. \\\end(संरेखित करें)\]

कुल मिलाकर, हमारे पास दो जड़ें हैं जो संख्या रेखा को तीन खंडों में विभाजित करती हैं, जिसके अंदर प्रत्येक मॉड्यूल विशिष्ट रूप से प्रकट होता है:

सबमॉड्यूलर फ़ंक्शंस के शून्य द्वारा संख्या रेखा को विभाजित करना

आइए प्रत्येक अनुभाग पर अलग से विचार करें।

1. मान लीजिए $x \lt -2$। फिर दोनों सबमॉड्यूल अभिव्यक्तियाँ नकारात्मक हैं, और मूल असमानता को निम्नानुसार फिर से लिखा गया है:

\[\begin(संरेखित) और -\left(x+2 \right) \lt -\left(x-1 \right)+x-1,5 \\ & -x-2 \lt -x+1+ x-1.5 \\ & x \gt 1.5 \\\end(संरेखित)\]

हमें एक काफी सरल बाधा मिली। आइए इसे मूल धारणा के साथ प्रतिच्छेद करें कि $x \lt -2$:

\[\बाएं\( \begin(संरेखित) और x \lt -2 \\ और x \gt 1,5 \\\end(संरेखित) \दाएं।\दायां तीर x\in \varnothing \]

जाहिर है, वेरिएबल $x$ एक साथ −2 से कम लेकिन 1.5 से अधिक नहीं हो सकता है। इस क्षेत्र में कोई समाधान नहीं हैं.

1.1. आइए सीमा मामले पर अलग से विचार करें: $x=-2$। आइए बस इस संख्या को मूल असमानता में प्रतिस्थापित करें और जांचें: क्या यह कायम है?

\[\begin(संरेखित करें) और ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=-2) ) \\ & 0 \lt \left| -3 \दाएं|-2-1.5; \\ & 0 \lt 3-3.5; \\ & 0 \lt -0,5\राइटएरो \varnothing . \\\end(संरेखित करें)\]

जाहिर है, गणनाओं की श्रृंखला हमें गलत असमानता की ओर ले गई है। इसलिए, मूल असमानता भी झूठी है, और $x=-2$ उत्तर में शामिल नहीं है।

2. अब $-2 \lt x \lt 1$ मान लीजिए। बायां मॉड्यूल पहले से ही "प्लस" के साथ खुलेगा, लेकिन दायां मॉड्यूल अभी भी "माइनस" के साथ खुलेगा। हमारे पास है:

\[\begin(संरेखित) और x+2 \lt -\left(x-1 \right)+x-1.5 \\ & x+2 \lt -x+1+x-1.5 \\& x \lt - 2.5 \\\end(संरेखित करें)\]

फिर से हम मूल आवश्यकता के साथ प्रतिच्छेद करते हैं:

\[\बाएँ\( \begin(संरेखित) और x \lt -2,5 \\ और -2 \lt x \lt 1 \\\end(संरेखित) \दाएँ।\दायाँ तीर x\in \varnothing \]

और फिर, समाधानों का खाली सेट, क्योंकि ऐसी कोई संख्या नहीं है जो −2.5 से कम और −2 से अधिक हो।

2.1. और फिर से एक विशेष मामला: $x=1$। हम मूल असमानता में स्थानापन्न करते हैं:

\[\begin(संरेखित करें) और ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=1)) \\ & \बाएं| 3\दाएं| \lt\बाएं| 0 \दाएं|+1-1.5; \\ & 3 \lt -0.5; \\ & 3 \lt -0,5\राइटएरो \varnothing . \\\end(संरेखित करें)\]

पिछले "विशेष मामले" के समान, संख्या $x=1$ स्पष्ट रूप से उत्तर में शामिल नहीं है।

3. पंक्ति का अंतिम भाग: $x \gt 1$. यहां सभी मॉड्यूल को प्लस चिह्न के साथ विस्तारित किया गया है:

\[\begin(संरेखित) और x+2 \lt x-1+x-1.5 \\ और x+2 \lt x-1+x-1.5 \\ और x \gt 4.5 \\ \end(संरेखित)\ ]

और फिर से हम पाए गए सेट को मूल बाधा के साथ जोड़ते हैं:

/ \सही)\]

अंत में! हमें अंतराल मिल गया है, जो उत्तर होगा।

उत्तर: $x\in \left(4,5;+\infty \right)$

अंत में, एक नोट जो आपको वास्तविक समस्याओं को हल करते समय मूर्खतापूर्ण गलतियों से बचा सकता है:

मॉड्यूल के साथ असमानताओं के समाधान आमतौर पर संख्या रेखा पर निरंतर सेट होते हैं - अंतराल और खंड। पृथक बिंदु बहुत दुर्लभ हैं। और इससे भी अधिक दुर्लभ रूप से, ऐसा होता है कि समाधान की सीमाएं (खंड का अंत) विचाराधीन सीमा की सीमा के साथ मेल खाती हैं।

इसलिए, यदि सीमाएँ (वे बहुत "विशेष मामले") उत्तर में शामिल नहीं हैं, तो इन सीमाओं के बाएँ-दाएँ क्षेत्र भी लगभग निश्चित रूप से उत्तर में शामिल नहीं होंगे। और इसके विपरीत: सीमा प्रतिक्रिया में प्रवेश करती है, जिसका अर्थ है कि इसके आसपास के कुछ क्षेत्रों में भी प्रतिक्रिया होगी।

जब आप अपने समाधानों की जाँच करें तो इसे ध्यान में रखें।

असमानता समाधानमोड में ऑनलाइन समाधानलगभग किसी भी असमानता ऑनलाइन. गणितीय असमानताएँ ऑनलाइनगणित हल करने के लिए. जल्दी ढूंढो असमानता समाधानमोड में ऑनलाइन. साइट www.site आपको खोजने की अनुमति देती है समाधानलगभग कोई भी दिया गया बीजगणितीय, त्रिकोणमितीयया उत्कृष्ट असमानता ऑनलाइन. गणित के लगभग किसी भी अनुभाग का विभिन्न चरणों में अध्ययन करते समय, व्यक्ति को निर्णय लेना होता है असमानताएँ ऑनलाइन. तुरंत उत्तर पाने के लिए, और सबसे महत्वपूर्ण रूप से सटीक उत्तर पाने के लिए, आपको एक ऐसे संसाधन की आवश्यकता है जो आपको ऐसा करने की अनुमति दे। www.site को धन्यवाद असमानता को ऑनलाइन हल करेंकुछ मिनट लगेंगे. गणितीय हल करते समय www.site का मुख्य लाभ असमानताएँ ऑनलाइन- जारी प्रतिक्रिया की गति और सटीकता है. साइट किसी का भी समाधान करने में सक्षम है बीजगणितीय असमानताएँ ऑनलाइन, त्रिकोणमितीय असमानताएँ ऑनलाइन, पारलौकिक असमानताएँ ऑनलाइन, और असमानतामोड में अज्ञात पैरामीटर के साथ ऑनलाइन. असमानताएक शक्तिशाली गणितीय उपकरण के रूप में कार्य करें समाधानव्यावहारिक कार्य. मदद से गणितीय असमानताएँउन तथ्यों और संबंधों को व्यक्त करना संभव है जो पहली नज़र में भ्रमित करने वाले और जटिल लग सकते हैं। अज्ञात मात्राएँ असमानतासमस्या को सूत्रबद्ध करके पाया जा सकता है गणितीयरूप में भाषा असमानताऔर तय करनामोड में प्राप्त कार्य ऑनलाइनवेबसाइट www.site पर। कोई बीजगणितीय असमानता, त्रिकोणमितीय असमानताया असमानतायुक्त ट्रान्सेंडैंटलआपको आसानी से सुविधाएँ देता है तय करनाऑनलाइन और सही उत्तर प्राप्त करें। प्राकृतिक विज्ञान का अध्ययन करते समय व्यक्ति को अनिवार्य रूप से आवश्यकता का सामना करना पड़ता है असमानताओं का समाधान. इस मामले में, उत्तर सटीक होना चाहिए और इसे तुरंत मोड में प्राप्त किया जाना चाहिए ऑनलाइन. इसलिए, के लिए गणितीय असमानताओं को ऑनलाइन हल करेंहम साइट www.site की अनुशंसा करते हैं, जो आपके लिए अपरिहार्य कैलकुलेटर बन जाएगी बीजगणितीय असमानताओं को ऑनलाइन हल करें, त्रिकोणमितीय असमानताएँ ऑनलाइन, और पारलौकिक असमानताएँ ऑनलाइनया असमानताअज्ञात मापदंडों के साथ. विभिन्न के इंट्रावोल समाधान खोजने की व्यावहारिक समस्याओं के लिए गणितीय असमानताएँसंसाधन www.. समाधान असमानताएँ ऑनलाइनस्वयं, प्राप्त उत्तर की जाँच करना उपयोगी है असमानताओं का ऑनलाइन समाधानवेबसाइट www.site पर। असमानता को सही ढंग से लिखना और तुरंत प्राप्त करना आवश्यक है ऑनलाइन समाधान, जिसके बाद यह केवल असमानता के आपके समाधान के साथ उत्तर की तुलना करने के लिए रह जाता है। उत्तर जांचने में एक मिनट से ज्यादा नहीं लगेगा, काफी है असमानता को ऑनलाइन हल करेंऔर उत्तरों की तुलना करें. इससे आपको गलतियों से बचने में मदद मिलेगी फ़ैसलाऔर समय रहते उत्तर सही करें असमानताओं को ऑनलाइन हल करनादोनों में से एक बीजगणितीय, त्रिकोणमितीय, उत्कृष्टया असमानताअज्ञात मापदंडों के साथ.