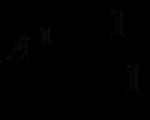हार्मोनिक दोलनों का समीकरण कैसे लिखें। हार्मोनिक दोलन और उनकी विशेषताएं

कंपन का सबसे सरल प्रकार है हार्मोनिक कंपन- उतार-चढ़ाव जिसमें संतुलन स्थिति से दोलन बिंदु का विस्थापन साइन या कोसाइन कानून के अनुसार समय के साथ बदलता है।

तो, परिधि के चारों ओर गेंद के एक समान घूर्णन के साथ, इसका प्रक्षेपण (प्रकाश की समानांतर किरणों में छाया) एक ऊर्ध्वाधर स्क्रीन पर एक हार्मोनिक दोलन गति करता है (चित्र 1)।

हार्मोनिक कंपन के दौरान संतुलन स्थिति से विस्थापन को एक समीकरण (इसे हार्मोनिक गति का गतिज नियम कहा जाता है) द्वारा वर्णित किया गया है:

जहां x - विस्थापन - संतुलन स्थिति के सापेक्ष समय t पर दोलन बिंदु की स्थिति को दर्शाने वाला मान और एक निश्चित समय पर संतुलन स्थिति से बिंदु की स्थिति तक की दूरी से मापा जाता है; ए - दोलन आयाम - संतुलन स्थिति से शरीर का अधिकतम विस्थापन; टी - दोलन अवधि - एक पूर्ण दोलन का समय; वे। समय की सबसे छोटी अवधि जिसके बाद दोलन को चिह्नित करने वाली भौतिक मात्राओं के मान दोहराए जाते हैं; - पहला भाग;

समय t पर दोलन का चरण। दोलन चरण एक आवधिक कार्य का एक तर्क है, जो किसी दिए गए दोलन आयाम के लिए, किसी भी समय शरीर की दोलन प्रणाली (विस्थापन, गति, त्वरण) की स्थिति निर्धारित करता है।

यदि समय के प्रारंभिक क्षण में दोलन बिंदु संतुलन स्थिति से अधिकतम विस्थापित हो जाता है, तो, और संतुलन स्थिति से बिंदु का विस्थापन कानून के अनुसार बदल जाता है

यदि दोलन बिंदु स्थिर संतुलन की स्थिति में है, तो संतुलन स्थिति से बिंदु का विस्थापन कानून के अनुसार बदलता है

मान V, अवधि का व्युत्क्रम और 1 s में किए गए पूर्ण दोलनों की संख्या के बराबर, दोलन आवृत्ति कहलाता है:

यदि समय t में शरीर N पूर्ण दोलन करता है, तो

मूल्य , यह दर्शाता है कि शरीर एस में कितने दोलन करता है, कहलाता है चक्रीय (परिपत्र) आवृत्ति.

हार्मोनिक गति का गतिक नियम इस प्रकार लिखा जा सकता है:

ग्राफ़िक रूप से, समय पर एक दोलन बिंदु के विस्थापन की निर्भरता को कोसाइन (या साइनसॉइड) द्वारा दर्शाया जाता है।

चित्र 2, ए मामले के लिए संतुलन स्थिति से दोलन बिंदु के विस्थापन की समय निर्भरता को दर्शाता है।

आइए जानें कि समय के साथ एक दोलन बिंदु की गति कैसे बदलती है। ऐसा करने के लिए, हम इस अभिव्यक्ति का समय व्युत्पन्न पाते हैं:

x-अक्ष पर वेग प्रक्षेपण का आयाम कहां है।

यह सूत्र दर्शाता है कि हार्मोनिक दोलनों के दौरान, एक्स अक्ष पर शरीर के वेग का प्रक्षेपण भी हार्मोनिक कानून के अनुसार एक ही आवृत्ति के साथ, एक अलग आयाम के साथ बदलता है, और मिश्रण चरण से आगे होता है (चित्र 2, बी) .

त्वरण की निर्भरता का पता लगाने के लिए, हम वेग प्रक्षेपण का समय व्युत्पन्न पाते हैं:

एक्स-अक्ष पर त्वरण प्रक्षेपण का आयाम कहां है।

हार्मोनिक दोलनों के लिए, त्वरण प्रक्षेपण k (छवि 2, सी) द्वारा चरण बदलाव की ओर जाता है।

इसी तरह, आप निर्भरता ग्राफ़ बना सकते हैं

हार्मोनिक तरंग समीकरण

हार्मोनिक दोलन समीकरण समय पर शरीर के समन्वय की निर्भरता स्थापित करता है

प्रारंभिक क्षण में कोसाइन ग्राफ का अधिकतम मान होता है, और प्रारंभिक क्षण में साइन ग्राफ का शून्य मान होता है। यदि हम संतुलन स्थिति से दोलन की जांच शुरू करते हैं, तो दोलन साइनसॉइड को दोहराएगा। यदि हम अधिकतम विचलन की स्थिति से दोलन पर विचार करना शुरू करें, तो दोलन कोसाइन का वर्णन करेगा। या ऐसे दोलन को प्रारंभिक चरण के साथ साइन सूत्र द्वारा वर्णित किया जा सकता है।

हार्मोनिक दोलन के दौरान गति और त्वरण में परिवर्तन

न केवल शरीर का समन्वय साइन या कोसाइन के नियम के अनुसार समय के साथ बदलता है। लेकिन बल, गति और त्वरण जैसी मात्राएँ भी इसी तरह बदलती हैं। बल और त्वरण तब अधिकतम होते हैं जब दोलन करने वाला शरीर चरम स्थिति में होता है जहां विस्थापन अधिकतम होता है, और जब शरीर संतुलन स्थिति से गुजरता है तो शून्य के बराबर होता है। इसके विपरीत, चरम स्थिति में गति शून्य के बराबर होती है, और जब शरीर संतुलन की स्थिति से गुजरता है, तो यह अपने अधिकतम मूल्य तक पहुंच जाता है।

यदि दोलन का वर्णन कोज्या के नियम के अनुसार किया जाए

यदि दोलन का वर्णन साइन नियम के अनुसार किया जाता है

अधिकतम गति और त्वरण मान

निर्भरता v(t) और a(t) के समीकरणों का विश्लेषण करने के बाद, कोई अनुमान लगा सकता है कि गति और त्वरण के अधिकतम मान तब लिए जाते हैं जब त्रिकोणमितीय कारक 1 या -1 के बराबर होता है। सूत्र द्वारा निर्धारित किया गया है

यांत्रिक कंपन. दोलन पैरामीटर. हार्मोनिक कंपन.

संकोच किसी प्रक्रिया को निश्चित अंतराल पर बिल्कुल या लगभग दोहराई जाने वाली प्रक्रिया कहा जाता है।

दोलनों की एक विशेषता प्रक्षेप पथ पर एक स्थिर संतुलन स्थिति की अनिवार्य उपस्थिति है, जिसमें शरीर पर कार्य करने वाले सभी बलों का योग शून्य के बराबर होता है, संतुलन स्थिति कहलाती है।

गणितीय लोलक एक पतले, भारहीन और अवितानीय धागे पर लटका हुआ एक भौतिक बिंदु है।

दोलन गति के पैरामीटर.

1. ऑफसेट या समन्वय (एक्स) - किसी दिए गए संतुलन स्थिति से विचलन

समय का क्षण.	[एक्स ]=एम

2. आयाम ( एक्सएम) संतुलन स्थिति से अधिकतम विचलन है।

[ एक्स एम ]=एम

3. दोलन अवधि ( टी) वह समय है जो एक पूर्ण दोलन में लगता है।

[टी ]=सी।

0 "style='margin-left:31.0pt;border-collapse:collapse'>

गणितीय पेंडुलम

स्प्रिंग पेंडुलम

एम

https://pandia.ru/text/79/117/images/image006_26.gif" width=”134” ऊंचाई=”57 src=”> आवृत्ति (रैखिक) (एन ) – 1 एस में पूर्ण दोलनों की संख्या।

[एन]= हर्ट्ज

5. चक्रीय आवृत्ति (डब्ल्यू ) – 2p सेकंड में पूर्ण दोलनों की संख्या, यानी लगभग 6.28 s।

डब्ल्यू = 2pn ; [w]=0" style="margin-left:116.0pt;border-collapse:collapse">

https://pandia.ru/text/79/117/images/image012_9.jpg" width=”90” ऊंचाई=”103”>

स्क्रीन पर छाया में उतार-चढ़ाव होता है।

हार्मोनिक दोलनों का समीकरण और ग्राफ।

हार्मोनिक कंपन - ये ऐसे दोलन हैं जिनमें समन्वय समय के साथ साइन या कोसाइन के नियम के अनुसार बदलता है।

https://pandia.ru/text/79/117/images/image014_7.jpg" width=”254” ऊंचाई=”430 src=”> एक्स=एक्सएमपाप(डब्ल्यू टी+ जे 0 )

एक्स=एक्सएमओल(डब्ल्यू टी+ जे 0 )

एक्स - समन्वय,

एक्सएम दोलन आयाम है,

w चक्रीय आवृत्ति है,

wt+j 0 = j दोलन चरण है,

जे 0 दोलनों का प्रारंभिक चरण है।

https://pandia.ru/text/79/117/images/image016_4.jpg" width=”247” ऊंचाई=”335 src=”>

ग्राफ़ अलग हैं केवलआयाम

ग्राफ़ केवल अवधि (आवृत्ति) में भिन्न होते हैं

https://pandia.ru/text/79/117/images/image018_3.jpg" width=”204” ऊंचाई=”90 src=”>

यदि दोलनों का आयाम समय के साथ नहीं बदलता है, तो दोलन कहलाते हैं अन्देंप्त.

प्राकृतिक कंपन घर्षण को ध्यान में नहीं रखते हैं, सिस्टम की कुल यांत्रिक ऊर्जा स्थिर रहती है: इसे + तक इएन = इफर = स्थिरांक.

प्राकृतिक दोलन अबाधित हैं।

मजबूर दोलनों के साथ, बाहरी स्रोत से लगातार या समय-समय पर आपूर्ति की जाने वाली ऊर्जा घर्षण बल के काम के कारण होने वाले नुकसान की भरपाई करती है, और दोलनों को कम नहीं किया जा सकता है।

कंपन के दौरान शरीर की गतिज और स्थितिज ऊर्जा एक दूसरे में प्रवाहित होती हैं। जब संतुलन स्थिति से सिस्टम का विचलन अधिकतम होता है, तो संभावित ऊर्जा अधिकतम होती है, और गतिज ऊर्जा शून्य होती है। संतुलन की स्थिति से गुजरते समय, इसके विपरीत।

मुक्त दोलनों की आवृत्ति दोलन प्रणाली के मापदंडों द्वारा निर्धारित की जाती है।

मजबूर दोलनों की आवृत्ति बाहरी बल की आवृत्ति से निर्धारित होती है। मजबूर दोलनों का आयाम बाहरी बल पर भी निर्भर करता है।

अनुनाद सी

गूंज जब किसी बाहरी बल की क्रिया की आवृत्ति प्रणाली के प्राकृतिक दोलनों की आवृत्ति के साथ मेल खाती है तो इसे मजबूर दोलनों के आयाम में तेज वृद्धि कहा जाता है।

जब बल में परिवर्तन की आवृत्ति w प्रणाली के दोलनों की प्राकृतिक आवृत्ति w0 के साथ मेल खाती है, तो बल पूरी अवधि के दौरान सकारात्मक कार्य करता है, जिससे शरीर के दोलनों का आयाम बढ़ जाता है। किसी अन्य आवृत्ति पर, अवधि के एक भाग के दौरान, बल सकारात्मक कार्य करता है, और अवधि के दूसरे भाग के दौरान, यह नकारात्मक कार्य करता है।

अनुनाद पर, दोलन आयाम में वृद्धि से प्रणाली का विनाश हो सकता है।

1905 में, गार्ड घुड़सवार सेना के एक स्क्वाड्रन के खुरों के नीचे, सेंट पीटर्सबर्ग में फोंटंका नदी पर मिस्र का पुल ढह गया।

स्व-दोलन.

बाहरी बल परिवर्तन की अनुपस्थिति में आंतरिक ऊर्जा स्रोतों द्वारा समर्थित, सिस्टम में स्व-दोलनों को अविभाजित दोलन कहा जाता है।

मजबूर दोलनों के विपरीत, स्व-दोलनों की आवृत्ति और आयाम दोलन प्रणाली के गुणों द्वारा ही निर्धारित होते हैं।

स्व-दोलन समय से आयाम की स्वतंत्रता और प्रारंभिक अल्पकालिक प्रभाव से मुक्त दोलनों से भिन्न होते हैं जो दोलनों की प्रक्रिया को उत्तेजित करते हैं। एक स्व-दोलन प्रणाली को आमतौर पर तीन तत्वों में विभाजित किया जा सकता है:

1) दोलन प्रणाली;

2) ऊर्जा स्रोत;

3) एक फीडबैक उपकरण जो एक स्रोत से एक दोलन प्रणाली में ऊर्जा के प्रवाह को नियंत्रित करता है।

किसी अवधि में स्रोत से आने वाली ऊर्जा उसी समय के दौरान दोलन प्रणाली में खोई गई ऊर्जा के बराबर होती है।

हमने कई शारीरिक रूप से पूरी तरह से अलग प्रणालियों पर विचार किया, और यह सुनिश्चित किया कि गति के समीकरण एक ही रूप में कम हो जाएं

भौतिक प्रणालियों के बीच अंतर केवल मात्रा की विभिन्न परिभाषाओं में ही प्रकट होते हैं और चर के एक अलग भौतिक अर्थ में एक्स: यह एक निर्देशांक, कोण, आवेश, धारा आदि हो सकता है। ध्यान दें कि इस मामले में, समीकरण (1.18) की संरचना के अनुसार, मात्रा में हमेशा व्युत्क्रम समय का आयाम होता है।

समीकरण (1.18) तथाकथित का वर्णन करता है हार्मोनिक कंपन.

हार्मोनिक दोलनों का समीकरण (1.18) एक दूसरे क्रम का रैखिक अंतर समीकरण है (क्योंकि इसमें चर का दूसरा व्युत्पन्न शामिल है) एक्स). समीकरण की रैखिकता का अर्थ है कि

यदि कोई फ़ंक्शन है एक्स(टी)इस समीकरण का एक समाधान है, फिर फ़ंक्शन सीएक्स(टी)उसका समाधान भी होगा ( सीएक मनमाना स्थिरांक है);

यदि कार्य करता है एक्स 1 (टी)और एक्स 2 (टी)इस समीकरण के समाधान हैं, तो उनका योग एक्स 1 (टी) + एक्स 2 (टी)भी उसी समीकरण का हल होगा.

एक गणितीय प्रमेय भी सिद्ध होता है, जिसके अनुसार दूसरे क्रम के समीकरण के दो स्वतंत्र समाधान होते हैं। अन्य सभी समाधान, रैखिकता के गुणों के अनुसार, उनके रैखिक संयोजन के रूप में प्राप्त किए जा सकते हैं। प्रत्यक्ष विभेदन द्वारा यह जांचना आसान है कि स्वतंत्र कार्य करता है और समीकरण (1.18) को संतुष्ट करता है। तो इस समीकरण का सामान्य समाधान है:

कहाँ सी1,सी2मनमाना स्थिरांक हैं. इस समाधान को दूसरे रूप में भी प्रस्तुत किया जा सकता है. हम मात्रा का परिचय देते हैं

और कोण को इस प्रकार परिभाषित करें:

फिर सामान्य समाधान (1.19) इस प्रकार लिखा जाता है

त्रिकोणमिति सूत्रों के अनुसार कोष्ठक में व्यंजक है

हम अंततः पहुँच गए हार्मोनिक दोलनों के समीकरण का सामान्य समाधानजैसा:

गैर-नकारात्मक मान एबुलाया दोलन आयाम, - दोलन का प्रारंभिक चरण. संपूर्ण कोसाइन तर्क - संयोजन - कहा जाता है दोलन चरण.

व्यंजक (1.19) और (1.23) बिल्कुल समतुल्य हैं, इसलिए हम सरलता के कारण उनमें से किसी एक का उपयोग कर सकते हैं। दोनों समाधान समय के आवधिक कार्य हैं। दरअसल, साइन और कोसाइन एक आवर्त के साथ आवर्ती होते हैं . इसलिए, एक प्रणाली की विभिन्न अवस्थाएँ जो हार्मोनिक दोलन करती हैं, एक समय अवधि के बाद दोहराई जाती हैं टी*, जिसके लिए दोलन चरण को एक वृद्धि प्राप्त होती है जो कि एक गुणक है :

अत: यह उसका अनुसरण करता है

इनमें से सबसे कम बार

बुलाया दोलन की अवधि (चित्र 1.8), ए - उसका गोलाकार (चक्रीय) आवृत्ति.

चावल। 1.8.

वे भी प्रयोग करते हैं आवृत्ति संकोच

तदनुसार, वृत्ताकार आवृत्ति प्रति दोलनों की संख्या के बराबर है सेकंड.

तो, अगर सिस्टम समय पर टीचर के मूल्य द्वारा विशेषता एक्स(टी),फिर, समय की अवधि के बाद चर का वही मान होगा (चित्र 1.9), अर्थात

निस्संदेह, वही मान कुछ समय बाद दोहराया जाएगा। 2टी, ZTवगैरह।

चावल। 1.9. दोलन काल

सामान्य समाधान में दो मनमाने स्थिरांक शामिल हैं ( सी 1 , सी 2या ए, ए), जिसका मान दो द्वारा निर्धारित किया जाना चाहिए आरंभिक स्थितियां. आमतौर पर (हालांकि जरूरी नहीं) उनकी भूमिका चर के प्रारंभिक मूल्यों द्वारा निभाई जाती है एक्स(0)और इसका व्युत्पन्न.

चलिए एक उदाहरण लेते हैं. मान लीजिए कि हार्मोनिक दोलनों के समीकरण का समाधान (1.19) एक स्प्रिंग पेंडुलम की गति का वर्णन करता है। मनमाना स्थिरांक का मान इस बात पर निर्भर करता है कि हमने लोलक को किस प्रकार संतुलन से बाहर लाया। उदाहरण के लिए, हमने स्प्रिंग को कुछ दूरी तक खींच लिया और बिना प्रारंभिक वेग के गेंद को छोड़ दिया। इस मामले में

स्थानापन्न टी = 0(1.19) में, हम स्थिरांक का मान पाते हैं 2 से

समाधान इस प्रकार दिखता है:

भार की गति समय के सापेक्ष विभेदन द्वारा ज्ञात की जाती है

यहाँ प्रतिस्थापित कर रहा हूँ टी = 0, अचर ज्ञात कीजिए 1 से:

अंत में

(1.23) से तुलना करने पर हम पाते हैं कि दोलन आयाम है, और इसका प्रारंभिक चरण शून्य के बराबर है:।

अब हम पेंडुलम को दूसरे तरीके से संतुलन से बाहर लाते हैं। आइए भार पर प्रहार करें, ताकि वह प्रारंभिक गति प्राप्त कर ले, लेकिन प्रभाव के दौरान व्यावहारिक रूप से हिलता नहीं है। फिर हमारे पास अन्य प्रारंभिक शर्तें हैं:

हमारा समाधान दिखता है

भार की गति नियम के अनुसार बदलेगी:

आइए इसे यहां रखें:

USE कोडिफायर के विषय: हार्मोनिक दोलन; आयाम, अवधि, आवृत्ति, दोलनों का चरण; मुक्त कंपन, मजबूर कंपन, अनुनाद।

उतार चढ़ाव सिस्टम की स्थिति में परिवर्तन होते हैं जो समय के साथ दोहराए जाते हैं। दोलनों की अवधारणा घटनाओं की एक बहुत विस्तृत श्रृंखला को कवर करती है।

यांत्रिक प्रणालियों के कंपन, या यांत्रिक कंपन- यह किसी पिंड या पिंडों की प्रणाली की एक यांत्रिक गति है, जिसकी समय में पुनरावृत्ति होती है और संतुलन स्थिति के आसपास होती है। संतुलन स्थितियह सिस्टम की वह स्थिति है जिसमें वह बाहरी प्रभावों का अनुभव किए बिना मनमाने ढंग से लंबे समय तक रह सकता है।

उदाहरण के लिए, यदि पेंडुलम को विक्षेपित और छोड़ दिया जाता है, तो दोलन शुरू हो जाएगा। संतुलन की स्थिति विक्षेप की अनुपस्थिति में पेंडुलम की स्थिति है। इस स्थिति में, यदि पेंडुलम को अछूता छोड़ दिया जाए, तो वह अनिश्चित काल तक रह सकता है। जब पेंडुलम दोलन करता है, तो यह कई बार संतुलन की स्थिति से गुजरता है।

विक्षेपित पेंडुलम को छोड़े जाने के तुरंत बाद, उसने चलना शुरू कर दिया, संतुलन की स्थिति को पार कर लिया, विपरीत चरम स्थिति पर पहुंच गया, एक पल के लिए इसमें रुक गया, विपरीत दिशा में चला गया, फिर से संतुलन की स्थिति को पार कर गया और वापस लौट आया। एक बात हुई पूरे जोरों पर. फिर यह प्रक्रिया समय-समय पर दोहराई जाएगी।

शरीर के दोलनों का आयाम संतुलन स्थिति से इसके सबसे बड़े विचलन का परिमाण है।

दोलन काल एक पूर्ण दोलन का समय है। हम कह सकते हैं कि उस अवधि के लिए शरीर चार आयामों का मार्ग तय करता है।

दोलन आवृत्ति अवधि का व्युत्क्रम है: . आवृत्ति को हर्ट्ज़ (हर्ट्ज) में मापा जाता है और यह इंगित करता है कि एक सेकंड में कितने पूर्ण दोलन होते हैं।

हार्मोनिक कंपन.

हम मान लेंगे कि दोलनशील पिंड की स्थिति एकल निर्देशांक द्वारा निर्धारित होती है। मान संतुलन स्थिति से मेल खाता है। इस मामले में यांत्रिकी का मुख्य कार्य एक फ़ंक्शन ढूंढना है जो किसी भी समय शरीर का समन्वय देता है।

दोलनों के गणितीय विवरण के लिए, आवधिक कार्यों का उपयोग करना स्वाभाविक है। ऐसे कई कार्य हैं, लेकिन उनमें से दो - साइन और कोसाइन - सबसे महत्वपूर्ण हैं। उनके पास कई अच्छे गुण हैं और वे भौतिक घटनाओं की एक विस्तृत श्रृंखला से निकटता से संबंधित हैं।

चूँकि तर्क को स्थानांतरित करके ज्या और कोज्या फलन एक दूसरे से प्राप्त किए जाते हैं, हम खुद को उनमें से केवल एक तक ही सीमित कर सकते हैं। निश्चितता के लिए हम कोज्या का प्रयोग करेंगे।

हार्मोनिक कंपनवे दोलन हैं जिनमें समन्वय हार्मोनिक नियम के अनुसार समय पर निर्भर करता है:

(1)

आइए इस सूत्र में शामिल मात्राओं का अर्थ जानें।

एक सकारात्मक मान निरपेक्ष मान में सबसे बड़ा समन्वय मान है (चूंकि कोसाइन मापांक का अधिकतम मान एक के बराबर है), यानी, संतुलन स्थिति से सबसे बड़ा विचलन। इसलिए - दोलनों का आयाम.

कोसाइन तर्क कहा जाता है चरणउतार-चढ़ाव. चरण के मान के बराबर मान को प्रारंभिक चरण कहा जाता है। प्रारंभिक चरण शरीर के प्रारंभिक समन्वय से मेल खाता है:।

मान कहा जाता है चक्रीय आवृत्ति. आइए दोलन अवधि और आवृत्ति के साथ इसका संबंध खोजें। एक पूर्ण दोलन रेडियन के बराबर चरण वृद्धि से मेल खाता है: , कहाँ से

(2)

(3)

चक्रीय आवृत्ति को रेड/एस (रेडियन प्रति सेकंड) में मापा जाता है।

अभिव्यक्ति (2) और (3) के अनुसार, हमें हार्मोनिक कानून की रिकॉर्डिंग के दो और रूप मिलते हैं (1) :

फ़ंक्शन का ग्राफ़ (1), जो हार्मोनिक दोलनों के दौरान समय पर निर्देशांक की निर्भरता को व्यक्त करता है, चित्र में दिखाया गया है। 1 .

फॉर्म (1) का हार्मोनिक नियम सबसे सामान्य प्रकृति का है। उदाहरण के लिए, यह उस स्थिति का उत्तर देता है जब पेंडुलम के साथ दो प्रारंभिक क्रियाएं एक साथ की गईं: उन्होंने इसे एक मात्रा से विक्षेपित किया और इसे कुछ प्रारंभिक गति दी। ऐसे दो महत्वपूर्ण विशेष मामले हैं जहां इनमें से एक भी कार्रवाई नहीं की गई थी।

बता दें कि पेंडुलम को खारिज कर दिया गया था, लेकिन प्रारंभिक गति की सूचना नहीं दी गई थी (उन्हें प्रारंभिक गति के बिना जारी किया गया था)। यह स्पष्ट है कि इस मामले में, तो हम डाल सकते हैं। हमें कोसाइन का नियम मिलता है:

इस मामले में हार्मोनिक दोलनों का ग्राफ चित्र में दिखाया गया है। 2.

चावल। 2. कोज्या का नियम

आइए अब मान लें कि पेंडुलम विक्षेपित नहीं हुआ था, बल्कि एक झटके से उसे संतुलन स्थिति से प्रारंभिक वेग प्रदान किया गया था। इस मामले में, तो आप डाल सकते हैं. हमें साइन नियम मिलता है:

उतार-चढ़ाव का शेड्यूल अंजीर में प्रस्तुत किया गया है। 3 .

चावल। 3. ज्या का नियम

हार्मोनिक दोलनों का समीकरण.

आइए सामान्य हार्मोनिक नियम (1) पर वापस लौटें। आइए इस समीकरण को अलग करें:

. (4)

अब हम परिणामी समानता (4) को अलग करते हैं:

. (5)

आइए समन्वय के लिए अभिव्यक्ति (1) और त्वरण प्रक्षेपण के लिए अभिव्यक्ति (5) की तुलना करें। हम देखते हैं कि त्वरण प्रक्षेपण केवल कारक द्वारा निर्देशांक से भिन्न होता है:

. (6)

इस अनुपात को कहा जाता है हार्मोनिक दोलनों का समीकरण. इसे इस रूप में भी पुनः लिखा जा सकता है:

. (7)

गणितीय दृष्टि से समीकरण (7) है अंतर समीकरण. अवकल समीकरणों के समाधान फलन हैं (और संख्याएँ नहीं, जैसा कि सामान्य बीजगणित में होता है)।
तो, हम यह साबित कर सकते हैं:

समीकरण (7) का हल मनमाने ढंग से फॉर्म (1) का कोई भी कार्य है;

कोई अन्य फलन इस समीकरण का हल नहीं है।

दूसरे शब्दों में, संबंध (6) , (7) चक्रीय आवृत्ति के साथ हार्मोनिक दोलनों का वर्णन करते हैं और केवल उन्हें। दो स्थिरांक प्रारंभिक स्थितियों से निर्धारित होते हैं - समन्वय और वेग के प्रारंभिक मूल्यों द्वारा।

स्प्रिंग पेंडुलम.

स्प्रिंग पेंडुलम एक स्प्रिंग पर लगा हुआ भार है, जो क्षैतिज या ऊर्ध्वाधर दिशा में दोलन करने में सक्षम है।

आइए स्प्रिंग पेंडुलम के छोटे क्षैतिज दोलनों की अवधि ज्ञात करें (चित्र 4)। यदि स्प्रिंग के विरूपण का परिमाण उसके आयामों से बहुत कम है तो दोलन छोटे होंगे। छोटी विकृतियों के लिए, हम हुक के नियम का उपयोग कर सकते हैं। इससे दोलन हार्मोनिक हो जाएंगे।

हम घर्षण की उपेक्षा करते हैं। द्रव्यमान में एक द्रव्यमान होता है और स्प्रिंग स्थिरांक होता है।

निर्देशांक संतुलन स्थिति से मेल खाता है जिसमें स्प्रिंग विकृत नहीं होता है। इसलिए, स्प्रिंग विरूपण का परिमाण भार समन्वय के मापांक के बराबर है।

चावल। 4. स्प्रिंग पेंडुलम

क्षैतिज दिशा में, स्प्रिंग से केवल लोचदार बल भार पर कार्य करता है। अक्ष पर प्रक्षेपण में भार के लिए न्यूटन का दूसरा नियम है:

. (8)

यदि (भार को दाईं ओर स्थानांतरित किया जाता है, जैसा कि चित्र में है), तो लोचदार बल विपरीत दिशा में निर्देशित होता है, और। इसके विपरीत, यदि , तो . संकेत और हर समय विपरीत होते हैं, इसलिए हुक का नियम इस प्रकार लिखा जा सकता है:

तब संबंध (8) रूप लेता है:

हमने फॉर्म (6) के हार्मोनिक दोलनों का एक समीकरण प्राप्त किया है, जिसमें

स्प्रिंग पेंडुलम के दोलन की चक्रीय आवृत्ति इस प्रकार बराबर है:

. (9)

यहां से और अनुपात से हम स्प्रिंग पेंडुलम के क्षैतिज दोलनों की अवधि पाते हैं:

. (10)

यदि आप स्प्रिंग पर कोई भार लटकाते हैं, तो आपको एक स्प्रिंग पेंडुलम मिलता है जो ऊर्ध्वाधर दिशा में दोलन करता है। यह दिखाया जा सकता है कि इस मामले में सूत्र (10) दोलन अवधि के लिए भी मान्य है।

गणितीय पेंडुलम.

गणितीय पेंडुलम - यह एक भारहीन अवितानीय धागे पर लटका हुआ एक छोटा पिंड है (चित्र 5)। एक गणितीय लोलक गुरुत्वाकर्षण के क्षेत्र में ऊर्ध्वाधर तल में दोलन कर सकता है।

चावल। 5. गणितीय लोलक

आइए गणितीय लोलक के छोटे दोलनों की अवधि ज्ञात करें। धागे की लंबाई है. वायु प्रतिरोध की उपेक्षा की जाती है।

आइए पेंडुलम के लिए न्यूटन का दूसरा नियम लिखें:

और इसे अक्ष पर प्रक्षेपित करें:

यदि पेंडुलम चित्र (अर्थात्) के अनुसार स्थिति रखता है, तो:

यदि पेंडुलम संतुलन स्थिति के दूसरी तरफ है (यानी), तो:

तो, पेंडुलम की किसी भी स्थिति के लिए हमारे पास:

. (11)

जब पेंडुलम संतुलन की स्थिति में आराम पर होता है, तो समानता पूरी हो जाती है। छोटे दोलनों के लिए, जब संतुलन स्थिति से पेंडुलम का विचलन छोटा होता है (धागे की लंबाई की तुलना में), तो अनुमानित समानता पूरी हो जाती है। आइए इसे सूत्र (11) में उपयोग करें:

यह फॉर्म (6) के हार्मोनिक दोलनों का एक समीकरण है

इसलिए, गणितीय पेंडुलम के दोलन की चक्रीय आवृत्ति बराबर है:

. (12)

इसलिए गणितीय पेंडुलम के दोलन की अवधि:

. (13)

कृपया ध्यान दें कि सूत्र (13) में भार का द्रव्यमान शामिल नहीं है। स्प्रिंग पेंडुलम के विपरीत, गणितीय पेंडुलम के दोलन की अवधि उसके द्रव्यमान पर निर्भर नहीं करती है।

मुक्त और मजबूर कंपन.

सिस्टम को कहा जाता है मुक्त कंपन, यदि इसे एक बार संतुलन की स्थिति से बाहर निकाल लिया जाए और बाद में अपने आप पर छोड़ दिया जाए। कोई आवधिक बाह्य नहीं
साथ ही, सिस्टम पर कोई प्रभाव नहीं पड़ता है, और सिस्टम में दोलनों का समर्थन करने वाले ऊर्जा के कोई आंतरिक स्रोत नहीं हैं।

ऊपर माने गए स्प्रिंग और गणितीय पेंडुलम के दोलन मुक्त दोलन के उदाहरण हैं।

वह आवृत्ति जिस पर मुक्त कंपन होता है, कहलाती है प्राकृतिक आवृत्तिदोलन प्रणाली. तो, सूत्र (9) और (12) स्प्रिंग और गणितीय पेंडुलम की प्राकृतिक (चक्रीय) दोलन आवृत्तियाँ देते हैं।

घर्षण की अनुपस्थिति में एक आदर्श स्थिति में, मुक्त दोलन अवमंदित होते हैं, अर्थात, उनका एक स्थिर आयाम होता है और अनिश्चित काल तक रहता है। वास्तविक दोलन प्रणालियों में, घर्षण हमेशा मौजूद रहता है, इसलिए मुक्त दोलन धीरे-धीरे समाप्त हो जाते हैं (चित्र 6)।

जबरदस्ती कंपन- ये बाहरी बल के प्रभाव में सिस्टम द्वारा किए गए दोलन हैं, जो समय-समय पर समय के साथ बदलते रहते हैं (तथाकथित ड्राइविंग बल)।

आइए मान लें कि सिस्टम की प्राकृतिक दोलन आवृत्ति है, और ड्राइविंग बल हार्मोनिक कानून के अनुसार समय पर निर्भर करता है:

कुछ समय के लिए, मजबूर दोलन स्थापित होते हैं: सिस्टम एक जटिल आंदोलन करता है, जो मजबूर और मुक्त दोलनों का एक सुपरपोजिशन है। मुक्त दोलन धीरे-धीरे ख़त्म हो जाते हैं, और स्थिर अवस्था में सिस्टम मजबूर दोलन करता है, जो हार्मोनिक भी हो जाता है। स्थिर मजबूर दोलनों की आवृत्ति आवृत्ति के साथ मेल खाती है
प्रेरक शक्ति (एक बाहरी शक्ति, जैसे वह थी, सिस्टम पर अपनी आवृत्ति लगाती है)।

स्थिर-अवस्था मजबूर दोलनों का आयाम ड्राइविंग बल की आवृत्ति पर निर्भर करता है। इस निर्भरता का ग्राफ चित्र में दिखाया गया है। 7.

चावल। 7. अनुनाद

हम देखते हैं कि अनुनाद आवृत्ति के निकट होता है - मजबूर दोलनों के आयाम में वृद्धि की घटना। गुंजयमान आवृत्ति प्रणाली की प्राकृतिक दोलन आवृत्ति के लगभग बराबर है: और यह समानता जितनी अधिक सटीक होगी, प्रणाली में घर्षण उतना ही कम होगा। घर्षण की अनुपस्थिति में, गुंजयमान आवृत्ति प्राकृतिक दोलन आवृत्ति के साथ मेल खाती है, और दोलन आयाम अनंत तक बढ़ जाता है।