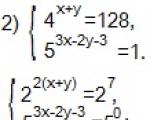Homogeninių eksponentinių nelygybių sprendimas. Eksponentinių lygčių ir nelygybių sprendimas
Tai yra privalomas sprendžiant eksponentinių lygčių sistemą? tikrai, transformacijašią sistemą į paprastų lygčių sistemą.
Pavyzdžiai.
Išspręskite lygčių sistemas:
Išreikškime adresu per X iš (2) sistemos lygties ir šią reikšmę pakeiskite (1) sistemos lygtimi.
Išsprendžiame (2) gautos sistemos lygtį:
2 x +2 x +2 =10, taikykite formulę: a x + y=a x∙ a y.
2 x +2 x ∙2 2 =10, išimkime bendrą koeficientą 2 x iš skliaustų:
2 x (1+2 2) = 10 arba 2 x ∙5 = 10, taigi 2 x =2.
2 x = 2 1, iš čia x=1. Grįžkime prie lygčių sistemos.

Atsakymas: (1; 2).
Sprendimas.
Kairę ir dešinę (1) lygties puses pavaizduojame galių su baze forma 2 , o dešinioji (2) lygties pusė yra nulinė skaičiaus galia 5 .
Jei dvi laipsniai su vienodomis bazėmis yra lygūs, tai šių laipsnių laipsniai yra lygūs – laipsnius prilyginame bazėms 2 ir eksponentus su bazėmis 5 .
Gautą tiesinių lygčių sistemą su dviem kintamaisiais sprendžiame pridėjimo metodu.
Mes randame x=2 ir vietoj to pakeičiame šią vertę Xį antrąją sistemos lygtį.
Mes randame adresu.
Atsakymas: (2; 1,5).

Sprendimas.
Jei ankstesniuose dviejuose pavyzdžiuose perėjome prie paprastesnės sistemos, dviejų laipsnių rodiklius sulygindami su tomis pačiomis bazėmis, tai 3 pavyzdyje ši operacija neįmanoma. Tokias sistemas patogu spręsti įvedant naujus kintamuosius. Supažindinsime su kintamaisiais u Ir v, ir tada išreikškite kintamąjį u per v ir gauname kintamojo lygtį v.
Išsprendžiame (2) sistemos lygtį.
v 2 +63v-64=0. Pasirinkime šaknis naudodami Vietos teoremą, žinodami, kad: v 1 +v 2 = -63; v 1 ∙v 2 =-64.
Gauname: v 1 =-64, v 2 =1. Grįžtame į sistemą ir randame jus.

Kadangi eksponentinės funkcijos reikšmės visada yra teigiamos, lygtys 4 x = -1 ir 4 m = -64 neturi sprendimų.
Lygčių sistemų sprendimo metodai
Pirmiausia trumpai prisiminkime, kokie metodai paprastai egzistuoja sprendžiant lygčių sistemas.
Egzistuoti keturi pagrindiniai būdai lygčių sistemų sprendimai:
Pakeitimo būdas: paimkite bet kurią iš pateiktų lygčių ir išreikškite $y$ kaip $x$, tada $y$ pakeičiama į sistemos lygtį, iš kurios randamas kintamasis $x.$. Po to galime lengvai apskaičiuoti kintamasis $y.$
Sudėjimo metodas: taikant šį metodą, vieną arba abi lygtis reikia padauginti iš tokių skaičių, kad sudėjus abi kartu vienas iš kintamųjų „dingtų“.
Grafinis metodas: abi sistemos lygtys pavaizduojamos koordinačių plokštumoje ir randamas jų susikirtimo taškas.
Naujų kintamųjų įvedimo metodas: šiuo metodu pakeičiame kai kurias išraiškas, kad supaprastintume sistemą, ir tada naudojame vieną iš aukščiau pateiktų metodų.
Eksponentinių lygčių sistemos
1 apibrėžimas
Lygčių sistemos, susidedančios iš eksponentinių lygčių, vadinamos eksponentinių lygčių sistemomis.
Apsvarstysime, kaip spręsti eksponentinių lygčių sistemas naudojant pavyzdžius.
1 pavyzdys
Išspręskite lygčių sistemą
1 paveikslas.
Sprendimas.
Šiai sistemai išspręsti naudosime pirmąjį metodą. Pirmiausia išreikškime $y$ pirmoje lygtyje $x$.

2 pav.
Pakeiskime $y$ į antrąją lygtį:
\ \ \[-2-x=2\] \ \
Atsakymas: $(-4,6)$.
2 pavyzdys
Išspręskite lygčių sistemą

3 pav.
Sprendimas.
Ši sistema yra lygiavertė sistemai

4 pav.
Taikykime ketvirtąjį lygčių sprendimo būdą. Tegu $2^x=u\ (u >0)$ ir $3^y=v\ (v >0)$, gauname:

5 pav.
Išspręskime gautą sistemą naudodami pridėjimo metodą. Sudėkime lygtis:
\ \
Tada iš antrosios lygties tai gauname
Grįžtant prie pakeitimo, gavau naują eksponentinių lygčių sistemą:
6 pav.
Mes gauname:
7 pav.
Atsakymas: $(0,1)$.
Eksponentinių nelygybių sistemos
2 apibrėžimas
Nelygybių sistemos, susidedančios iš eksponentinių lygčių, vadinamos eksponentinių nelygybių sistemomis.
Apsvarstysime, kaip spręsti eksponentinių nelygybių sistemas naudojant pavyzdžius.
3 pavyzdys
Išspręskite nelygybių sistemą

8 pav.
Sprendimas:
Ši nelygybių sistema yra lygiavertė sistemai

9 pav.
Norėdami išspręsti pirmąją nelygybę, prisiminkite šią teoremą apie eksponentinių nelygybių ekvivalentiškumą:
1 teorema. Nelygybė $a^(f(x)) >a^(\varphi (x)) $, kur $a >0,a\ne 1$ yra lygiavertė dviejų sistemų rinkiniui
\}