व्हॅक्यूममध्ये गॉसचे प्रमेय. इलेक्ट्रिक फील्डची गणना करण्यासाठी गॉसच्या प्रमेयाचा वापर

वर नमूद केल्याप्रमाणे, अशा घनतेने बलाच्या रेषा काढण्याचे मान्य केले गेले की साइटच्या रेषांना लंब असलेल्या पृष्ठभागाच्या एककाला छेदणाऱ्या रेषांची संख्या व्हेक्टरच्या मॉड्यूलसच्या बरोबरीची असेल. मग, तणाव रेषांच्या नमुन्यावरून, केवळ दिशाच नाही तर अंतराळातील विविध बिंदूंवरील वेक्टरची विशालता देखील ठरवता येते.

स्थिर धनात्मक बिंदू शुल्काच्या फील्ड रेषांचा विचार करूया. त्या चार्जपासून विस्तारलेल्या आणि अनंतापर्यंत संपणाऱ्या रेडियल रेषा आहेत. चला पार पाडूया एनअशा ओळी. मग काही अंतरावर आरचार्जमधून, त्रिज्येच्या गोलाच्या एकक पृष्ठभागाला छेदणाऱ्या बलाच्या रेषांची संख्या आर, समान असेल. हे मूल्य अंतरावरील पॉइंट चार्जच्या फील्ड ताकदीच्या प्रमाणात आहे आरक्रमांक एनतुम्ही नेहमी अशी निवड करू शकता की समानता असेल

कुठे बलाच्या रेषा सतत असल्यामुळे, समान संख्येच्या बलाच्या रेषा कोणत्याही आकाराच्या बंद पृष्ठभागास चार्ज करतात qचार्जच्या चिन्हावर अवलंबून, शक्तीच्या रेषा एकतर या बंद पृष्ठभागामध्ये प्रवेश करतात किंवा बाहेर जातात. जर आउटगोइंग रेषांची संख्या सकारात्मक मानली गेली आणि येणार्‍या ओळींची संख्या नकारात्मक मानली गेली, तर आपण मॉड्यूलस चिन्ह वगळू शकतो आणि लिहू शकतो:

.

(1.4)

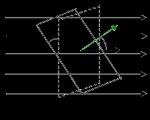
तणाव वेक्टर प्रवाह.क्षेत्रफळ असलेले एक प्राथमिक पॅड ठेवूया. क्षेत्रफळ इतके लहान असले पाहिजे की त्याच्या सर्व बिंदूंवरील विद्युत क्षेत्राची ताकद समान मानली जाऊ शकते. साइटवर एक सामान्य काढूया (चित्र 1.17). या सामान्यची दिशा अनियंत्रितपणे निवडली जाते. सामान्य वेक्टरसह एक कोन बनवतो. निवडलेल्या पृष्ठभागाद्वारे विद्युतीय क्षेत्र शक्ती वेक्टरचा प्रवाह हा पृष्ठभागाच्या क्षेत्राचे उत्पादन आणि विद्युत क्षेत्राच्या सामर्थ्य वेक्टरचे सामान्य क्षेत्रावरील प्रक्षेपण आहे:

साइटवर सामान्य वर वेक्टरचे प्रक्षेपण कुठे आहे.

एका क्षेत्राला छेदणाऱ्या फील्ड रेषांची संख्या निवडलेल्या क्षेत्राच्या परिसरातील तीव्रता वेक्टरच्या मापांकाइतकी असल्याने, तीव्रतेच्या वेक्टरचा पृष्ठभागावरून होणारा प्रवाह हा पृष्ठभाग ओलांडणाऱ्या फील्ड रेषांच्या संख्येच्या प्रमाणात आहे. म्हणून, सर्वसाधारण बाबतीत, क्षेत्राद्वारे फील्ड स्ट्रेंथ वेक्टरचा प्रवाह या क्षेत्रामध्ये प्रवेश करणार्‍या फील्ड रेषांच्या संख्येच्या समान मूल्य म्हणून दृष्यदृष्ट्या अर्थ लावला जाऊ शकतो:

.

(1.5)

लक्षात घ्या की सामान्यच्या दिशेची निवड सशर्त आहे; ती इतर दिशेने निर्देशित केली जाऊ शकते. परिणामी, प्रवाह हे बीजगणितीय प्रमाण आहे: प्रवाहाचे चिन्ह केवळ फील्डच्या कॉन्फिगरेशनवर अवलंबून नाही तर सामान्य वेक्टर आणि तीव्रता वेक्टरच्या सापेक्ष अभिमुखतेवर देखील अवलंबून असते. जर हे दोन वेक्टर एक तीव्र कोन बनवतात, तर प्रवाह धनात्मक असतो; जर तो स्थूल असेल तर प्रवाह ऋणात्मक असतो. बंद पृष्ठभागाच्या बाबतीत, या पृष्ठभागाने व्यापलेल्या क्षेत्राच्या बाहेर नॉर्मल घेण्याची प्रथा आहे, म्हणजेच बाह्य सामान्य निवडणे.

जर क्षेत्र एकसंध असेल आणि पृष्ठभाग अनियंत्रित असेल तर प्रवाह खालीलप्रमाणे परिभाषित केला जातो. संपूर्ण पृष्ठभागाचे क्षेत्रफळ असलेल्या लहान घटकांमध्ये विभागले जाणे आवश्यक आहे, या प्रत्येक घटकाद्वारे ताण प्रवाहांची गणना करा आणि नंतर सर्व घटकांमधील प्रवाहांची बेरीज करा:

अशा प्रकारे, फील्ड स्ट्रेंथ स्पेसमधील एका बिंदूवर विद्युत क्षेत्राचे वैशिष्ट्य दर्शवते. तीव्रतेचा प्रवाह एखाद्या दिलेल्या बिंदूवर फील्ड ताकदीच्या मूल्यावर अवलंबून नाही, परंतु विशिष्ट क्षेत्राच्या पृष्ठभागावर फील्डच्या वितरणावर अवलंबून असतो.

इलेक्ट्रिक फील्ड लाईन्स फक्त सकारात्मक चार्जेसवर सुरू होऊ शकतात आणि ऋणावर संपू शकतात. ते अंतराळात सुरू किंवा समाप्त करू शकत नाहीत. म्हणून, एका विशिष्ट बंद खंडामध्ये विद्युत शुल्क नसल्यास, या खंडामध्ये प्रवेश करणार्या आणि बाहेर जाणाऱ्या ओळींची एकूण संख्या शून्य असणे आवश्यक आहे. जर जास्त ओळींनी आवाज सोडला तर आवाजाच्या आत एक सकारात्मक चार्ज असतो; जर बाहेर येण्यापेक्षा जास्त ओळी येत असतील तर आतमध्ये ऋण शुल्क असणे आवश्यक आहे. जेव्हा व्हॉल्यूमच्या आत एकूण चार्ज शून्य असतो किंवा जेव्हा त्यात कोणतेही विद्युत शुल्क नसते तेव्हा फील्ड रेषा त्यातून आत प्रवेश करतात आणि एकूण प्रवाह शून्य असतो.

हे साधे विचार व्हॉल्यूममध्ये इलेक्ट्रिक चार्ज कसे वितरित केले जातात यावर अवलंबून नाहीत. हे व्हॉल्यूमच्या मध्यभागी किंवा व्हॉल्यूमला सीमा असलेल्या पृष्ठभागाजवळ स्थित असू शकते. व्हॉल्यूममध्ये कोणत्याही प्रकारे व्हॉल्यूममध्ये वितरित केलेले अनेक सकारात्मक आणि नकारात्मक शुल्क असू शकतात. केवळ एकूण शुल्क इनकमिंग किंवा आउटगोइंग व्होल्टेज लाईन्सची एकूण संख्या निर्धारित करते.

(1.4) आणि (1.5) मधून पाहिल्याप्रमाणे, विद्युत क्षेत्र शक्ती वेक्टरचा प्रवाह एका अनियंत्रित बंद पृष्ठभागाद्वारे चार्जला जोडून q,च्या समान जर पृष्ठभागाच्या आत असेल तर nशुल्क, नंतर, फील्ड सुपरपोझिशनच्या तत्त्वानुसार, एकूण प्रवाह सर्व शुल्कांच्या फील्ड सामर्थ्याच्या प्रवाहांची बेरीज असेल आणि बरोबर असेल, जेथे या प्रकरणात आपला अर्थ क्लोज्डद्वारे समाविष्ट असलेल्या सर्व शुल्कांची बीजगणितीय बेरीज आहे. पृष्ठभाग

गॉसचे प्रमेय. गॉसएका अनियंत्रित बंद पृष्ठभागाद्वारे विद्युत क्षेत्र शक्ती वेक्टरचा प्रवाह या व्हॉल्यूमच्या आत असलेल्या एकूण चार्जशी संबंधित असणे आवश्यक आहे हे साधे तथ्य शोधणारे पहिले होते:

गॉस कार्ल फ्रेडरिक (१७७७-१८५५)

महान जर्मन गणितज्ञ, भौतिकशास्त्रज्ञ आणि खगोलशास्त्रज्ञ, भौतिकशास्त्रातील एककांच्या परिपूर्ण प्रणालीचे निर्माता. त्याने इलेक्ट्रोस्टॅटिक क्षमतेचा सिद्धांत विकसित केला आणि इलेक्ट्रोस्टॅटिक्सचे सर्वात महत्वाचे प्रमेय (गॉसचे प्रमेय) सिद्ध केले. जटिल ऑप्टिकल प्रणालींमध्ये प्रतिमा तयार करण्यासाठी एक सिद्धांत तयार केला. नॉन-युक्लिडियन भूमितीच्या अस्तित्वाच्या शक्यतेची कल्पना येणार्‍या पहिल्या लोकांपैकी तो एक होता. याव्यतिरिक्त, गॉसने गणिताच्या जवळजवळ प्रत्येक शाखेत उत्कृष्ट योगदान दिले.

विद्युत क्षेत्रासाठी शेवटचा संबंध गॉसचा प्रमेय आहे: अनियंत्रित बंद पृष्ठभागाद्वारे तीव्रतेच्या वेक्टरचा प्रवाह या पृष्ठभागाच्या आत असलेल्या शुल्काच्या बीजगणितीय बेरीजच्या प्रमाणात आहे. समानुपातिकता गुणांक युनिट्सच्या प्रणालीच्या निवडीवर अवलंबून असतो.

हे लक्षात घेतले पाहिजे की गॉसचे प्रमेय कूलॉम्बच्या नियमाचा आणि सुपरपोझिशन तत्त्वाचा परिणाम म्हणून प्राप्त झाले आहे. जर विद्युत क्षेत्राची ताकद अंतराच्या वर्गाच्या व्यस्त प्रमाणात बदलली नाही, तर प्रमेय अवैध असेल. म्हणून, गॉसचे प्रमेय अशा कोणत्याही क्षेत्रासाठी लागू आहे ज्यामध्ये व्यस्त वर्ग नियम आणि सुपरपोझिशनचे तत्त्व काटेकोरपणे समाधानी आहे, उदाहरणार्थ, गुरुत्वाकर्षण क्षेत्रासाठी. गुरुत्वाकर्षण क्षेत्राच्या बाबतीत, फील्ड तयार करणार्‍या शुल्काची भूमिका शरीराच्या वस्तुमानाद्वारे खेळली जाते. बंद पृष्ठभागाद्वारे गुरुत्वाकर्षण क्षेत्र रेषांचा प्रवाह त्या पृष्ठभागामध्ये असलेल्या एकूण वस्तुमानाच्या प्रमाणात असतो.

चार्ज केलेल्या विमानाची फील्ड ताकद.अनंत चार्ज केलेल्या विमानाची विद्युत क्षेत्राची ताकद निश्चित करण्यासाठी गॉसचे प्रमेय लागू करूया. जर विमान अनंत आणि एकसमान चार्ज केलेले असेल, म्हणजेच पृष्ठभागावरील चार्ज घनता कोणत्याही ठिकाणी सारखीच असेल, तर कोणत्याही बिंदूवरील विद्युत क्षेत्राच्या मजबुती रेषा या समतलाला लंब असतात. हे दाखवण्यासाठी, आम्ही टेंशन वेक्टरसाठी सुपरपोझिशन तत्त्व वापरू. आपण समतल भागावर दोन प्राथमिक विभाग निवडू या, जे बिंदूसाठी बिंदू मानले जाऊ शकतात ए, ज्यामध्ये फील्ड ताकद निश्चित करणे आवश्यक आहे. अंजीर पासून पाहिले जाऊ शकते. 1.18, परिणामी तणाव वेक्टर विमानाला लंब दिशेने निर्देशित केले जाईल. कोणत्याही निरीक्षण बिंदूसाठी विमानाला अशा विभागांच्या अनंत जोड्यांमध्ये विभागले जाऊ शकते, हे स्पष्ट आहे की चार्ज केलेल्या विमानाच्या फील्ड रेषा विमानाला लंब आहेत आणि फील्ड एकसमान आहे (चित्र 1.19). जर असे नसते, तर जेव्हा विमान स्वतःच्या बाजूने फिरते तेव्हा अंतराळातील प्रत्येक बिंदूवरील फील्ड बदलेल, परंतु हे चार्ज केलेल्या प्रणालीच्या सममितीला विरोध करते (विमान अनंत आहे). सकारात्मक चार्ज केलेल्या विमानाच्या बाबतीत, बलाच्या रेषा विमानापासून सुरू होतात आणि अनंतावर संपतात, तर नकारात्मक चार्ज केलेल्या विमानासाठी, बलाच्या रेषा अनंतापासून सुरू होतात आणि विमानात प्रवेश करतात.

तांदूळ. 1.18	तांदूळ. १.१९

अनंत सकारात्मक चार्ज केलेल्या विमानाची विद्युत क्षेत्राची ताकद निश्चित करण्यासाठी, आम्ही अंतराळातील एक सिलेंडर मानसिकरित्या निवडतो, ज्याचा अक्ष चार्ज केलेल्या विमानाला लंब असतो आणि तळ त्याच्या समांतर असतात, आणि पायांपैकी एक फील्ड पॉईंटमधून जातो. आम्हाला स्वारस्य आहे (चित्र 1.19). सिलेंडर चार्ज केलेल्या विमानातून क्षेत्रफळ कापतो आणि विमानाच्या वेगवेगळ्या बाजूंना असलेल्या सिलेंडरच्या पायाचे क्षेत्र समान असते.

गॉसच्या प्रमेयानुसार, सिलिंडरच्या पृष्ठभागावरून विद्युत क्षेत्र शक्ती वेक्टरचा प्रवाह अभिव्यक्तीद्वारे सिलेंडरच्या आत असलेल्या विद्युत शुल्काशी संबंधित आहे:

.

तणाव रेषा केवळ सिलेंडरच्या पायाला छेदत असल्याने, सिलेंडरच्या बाजूच्या पृष्ठभागावरून प्रवाह शून्य आहे. म्हणून, बेलनाकार पृष्ठभागाद्वारे तणाव वेक्टरचा प्रवाह केवळ सिलेंडरच्या पायथ्यांद्वारे प्रवाहांचा समावेश असेल, म्हणून,

तीव्रता वेक्टर फ्लक्ससाठी शेवटच्या दोन अभिव्यक्तींची तुलना केल्यास, आम्ही प्राप्त करतो

विरुद्ध चार्ज केलेल्या प्लेट्समधील विद्युत क्षेत्राची ताकद.जर प्लेट्सचे परिमाण त्यांच्यामधील अंतर लक्षणीयरीत्या ओलांडत असतील, तर प्रत्येक प्लेटचे इलेक्ट्रिक फील्ड अनंत एकसमान चार्ज केलेल्या प्लेनच्या फील्डच्या जवळ मानले जाऊ शकते. प्लेट्समधील विरुद्ध चार्ज केलेल्या प्लेट्सच्या इलेक्ट्रिक फील्ड स्ट्रेंथ लाईन्स एका दिशेने निर्देशित केल्या जात असल्याने (चित्र 1.20), प्लेट्समधील फील्ड स्ट्रेंथ समान आहे

.

बाह्य जागेत, विरुद्ध चार्ज केलेल्या प्लेट्सच्या इलेक्ट्रिक फील्ड स्ट्रेंथच्या विरुद्ध दिशा असतात, म्हणून, या प्लेट्सच्या बाहेर, परिणामी इलेक्ट्रिक फील्ड ताकद शून्य असते. तीव्रतेसाठी प्राप्त केलेली अभिव्यक्ती मोठ्या चार्ज केलेल्या प्लेट्ससाठी वैध आहे, जेव्हा तीव्रता त्यांच्या कडापासून दूर असलेल्या बिंदूवर निर्धारित केली जाते.

अनंत लांबीच्या एकसमान चार्ज केलेल्या पातळ वायरची इलेक्ट्रिक फील्ड ताकद.गॉसचे प्रमेय वापरून वायर अक्षाच्या अंतरावर असीम लांबीच्या एकसमान चार्ज केलेल्या पातळ वायरच्या विद्युत क्षेत्राच्या ताकदीचे अवलंबित्व शोधू. मर्यादित लांबीच्या वायरचा एक विभाग निवडू या. जर वायरवरील रेखीय चार्ज घनता असेल, तर निवडलेल्या क्षेत्राचा चार्ज समान असेल.

बिंदू शुल्क $q$ च्या फील्डचा विचार करू आणि बंद पृष्ठभाग $S$ मधून तीव्रता वेक्टर ($\overrightarrow(E)$) चा प्रवाह शोधू. आम्ही असे गृहीत धरू की चार्ज पृष्ठभागाच्या आत स्थित आहे. कोणत्याही पृष्ठभागावरून टेंशन वेक्टरचा प्रवाह बाहेर जाणार्‍या टेंशन वेक्टरच्या ओळींच्या संख्येइतका असतो (चार्ज पासून सुरू होतो, जर $q>0$) किंवा $\overrightarrow(E)$ आत जात असेल तर , जर $q \[Ф_E=\frac( q)((\varepsilon )_0)\ \left(1\उजवे),\]

जेथे फ्लक्सचे चिन्ह चार्जच्या चिन्हाशी जुळते.

अविभाज्य स्वरूपात ऑस्ट्रोग्राडस्की-गॉस प्रमेय

आपण असे गृहीत धरू की पृष्ठभाग S च्या आत N बिंदू शुल्क आहेत, मूल्ये आहेत $q_1,q_2,\dots q_N.$ सुपरपोझिशनच्या तत्त्वावरून आपल्याला माहित आहे की सर्व N शुल्कांची परिणामी फील्ड ताकद ही बेरीज म्हणून आढळू शकते. फील्ड सामर्थ्य जे प्रत्येक शुल्काद्वारे तयार केले जाते, त्यानंतर आहे:

म्हणून, बिंदू शुल्क प्रणालीच्या प्रवाहासाठी आम्ही लिहू शकतो:

सूत्र (1) वापरून, आम्ही ते प्राप्त करतो:

\[Ф_E=\oint\limits_S(\overrightarrow(E)d\overrightarrow(S))=\frac(1)((\varepsilon )_0)\sum\limits^N_(i=1)(q_i\ )\ डावीकडे(4\उजवीकडे).\]

समीकरण (4) याचा अर्थ असा आहे की बंद पृष्ठभागाद्वारे विद्युत क्षेत्राच्या ताकदीच्या वेक्टरचा प्रवाह या पृष्ठभागाच्या आत असलेल्या शुल्काच्या बीजगणितीय बेरजेइतका असतो, ज्याला विद्युत स्थिरांकाने भागले जाते. हे अविभाज्य स्वरूपात ऑस्ट्रोग्राडस्की-गॉस प्रमेय आहे. हे प्रमेय कूलॉम्बच्या नियमाचा परिणाम आहे. या प्रमेयाचे महत्त्व असे आहे की ते विविध चार्ज वितरणासाठी इलेक्ट्रिक फील्डची अगदी सहजपणे गणना करू देते.

ऑस्ट्रोग्राडस्की-गॉस प्रमेयाचा परिणाम म्हणून, असे म्हटले पाहिजे की या पृष्ठभागाच्या बाहेर चार्जेस असलेल्या स्थितीत बंद पृष्ठभागाद्वारे तीव्रता वेक्टरचा प्रवाह ($Ф_E$) शून्य असतो.

शुल्काच्या विवेचकतेकडे दुर्लक्ष केले जाऊ शकते अशा बाबतीत, शुल्क संपूर्ण व्हॉल्यूममध्ये वितरीत केले असल्यास व्हॉल्यूमेट्रिक चार्ज घनता ($\rho $) ची संकल्पना वापरली जाते. हे असे परिभाषित केले आहे:

\[\rho =\frac(dq)(dV)\left(5\उजवे),\]

जेथे $dq$ हे शुल्क आहे जे पॉइंट-समान मानले जाऊ शकते, $dV$ हे लहान व्हॉल्यूम आहे. ($dV$ बद्दल, खालील टिप्पणी करणे आवश्यक आहे. हा खंड इतका लहान आहे की त्यातील चार्ज घनता स्थिर मानली जाऊ शकते, परंतु इतकी मोठी आहे की चार्ज वेगळेपणा दिसू नये). पोकळीतील एकूण चार्ज खालीलप्रमाणे आढळू शकतो:

\[\sum\limits^N_(i=1)(q_i\ )=\int\limits_V(\rho dV)\left(6\right).\]

या प्रकरणात, आम्ही फॉर्म्युला (4) फॉर्ममध्ये पुन्हा लिहितो:

\[\oint\limits_S(\overrightarrow(E)d\overrightarrow(S))=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV)\left(7\right).\ ]

विभेदक स्वरूपात ऑस्ट्रोग्राडस्की-गॉस प्रमेय

वेक्टर निसर्गाच्या कोणत्याही क्षेत्रासाठी ऑस्ट्रोग्राडस्की-गॉस फॉर्म्युला वापरणे, ज्याच्या मदतीने बंद पृष्ठभागावरील एकात्मिकतेपासून एका खंडावरील एकत्रीकरणापर्यंत संक्रमण केले जाते:

\[\oint\limits_S(\overrightarrow(a)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(a)dV\ \left(8\right),\]

जेथे $\overrightarrow(a)-$फील्ड वेक्टर (आमच्या बाबतीत ते $\overrightarrow(E)$ आहे), $div\overrightarrow(a)=\overrightarrow(\nabla )\overrightarrow(a)=\frac(\ partial a_x)(\partial x)+\frac(\partial a_y)(\partial y)+\frac(\partial a_z)(\partial z)$ -- व्हेक्टर $\overrightarrow(a)$ चे विचलन निर्देशांक (x,y,z) सह बिंदू, जे वेक्टर फील्डला स्केलरमध्ये मॅप करते. $\overrightarrow(\nabla )=\frac(\partial )(\partial x)\overrightarrow(i)+\frac(\partial )(\partial y)\overrightarrow(j)+\frac(\partial )(\ partial z)\overrightarrow(k)$ - निरीक्षण करण्यायोग्य ऑपरेटर. (आमच्या बाबतीत ते $div\overrightarrow(E)=\overrightarrow(\nabla )\overrightarrow(E)=\frac(\partial E_x)(\partial x)+\frac(\partial E_y)(\partial असेल y) +\frac(\partial E_z)(\partial z)$) -- टेंशन वेक्टरचे विचलन. वरील प्रमाणे, आम्ही सूत्र (6) पुन्हा लिहितो:

\[\oint\limits_S(\overrightarrow(E)\overrightarrow(dS)=\int\nolimits_V(div))\overrightarrow(E)dV=\frac(1)((\varepsilon )_0)\int\limits_V( \rho dV)\left(9\उजवीकडे).\]

समीकरण (9) मधील समानता कोणत्याही व्हॉल्यूमसाठी समाधानी आहेत आणि हे केवळ तेव्हाच शक्य आहे जेव्हा इंटिग्रँड्समधील कार्ये स्पेसच्या प्रत्येक प्रवाहामध्ये समान असतील, म्हणजेच आपण असे लिहू शकतो:

अभिव्यक्ती (10) हे विभेदक स्वरूपात ऑस्ट्रोग्राडस्की-गॉस प्रमेय आहे. त्याची व्याख्या खालीलप्रमाणे आहे: शुल्क हे विद्युत क्षेत्राचे स्त्रोत आहेत. जर $div\overrightarrow(E)>0$, तर फील्डच्या या बिंदूंवर (शुल्क सकारात्मक आहेत) आमच्याकडे फील्ड स्रोत आहेत, जर $div\overrightarrow(E)

असाइनमेंट: चार्ज व्हॉल्यूमवर समान रीतीने वितरीत केला जातो; या व्हॉल्यूममध्ये बाजू b असलेली घन पृष्ठभाग निवडली जाते. हे गोलामध्ये कोरलेले आहे. या पृष्ठभागांद्वारे टेंशन वेक्टर फ्लक्सचे गुणोत्तर शोधा.

गॉसच्या प्रमेयानुसार, घनफळावर एकसमान चार्ज वितरणासह बंद पृष्ठभागाद्वारे तीव्रता वेक्टर $\overrightarrow(E)$ चा प्रवाह ($Ф_E$) समान आहे:

\[Ф_E=\frac(1)((\varepsilon )_0)Q=\frac(1)((\varepsilon )_0)\int\limits_V(\rho dV=\frac(\rho )((\varepsilon ) _0)\int\limits_V(dV)=\frac(\rho V)((\varepsilon )_0))\left(1.1\right).\]

म्हणून, जर या घनभोवती बॉलचे वर्णन केले असेल तर आपल्याला क्यूब आणि बॉलची मात्रा निश्चित करणे आवश्यक आहे. सुरुवातीला, घनाचा आकारमान ($V_k$) जर त्याची बाजू b समान असेल:

चला सूत्र वापरून चेंडूचा आवाज ($V_(sh)$) शोधू:

जेथे $D$ हा चेंडूचा व्यास आहे आणि (चेंडू क्यूबभोवती परिक्रमा करत असल्याने), क्यूबचा मुख्य कर्ण आहे. म्हणून, आपल्याला घनाचा कर्ण त्याच्या बाजूच्या संदर्भात व्यक्त करणे आवश्यक आहे. आपण पायथागोरियन प्रमेय वापरल्यास हे करणे सोपे आहे. घनाच्या कर्णाची गणना करण्यासाठी, उदाहरणार्थ, (1.5), आपल्याला प्रथम चौकोनाचा कर्ण (घनाचा खालचा पाया) (1.6) शोधणे आवश्यक आहे. कर्णाची लांबी (1.6) समान आहे:

या प्रकरणात, कर्णाची लांबी (1.5) समान आहे:

\[(D=D)_(15)=\sqrt(b^2+((\sqrt(b^2+b^2\ \ )))^2)=b\sqrt(3)\ \left (1.5\उजवे).\]

बॉलचा आढळलेला व्यास (1.3) मध्ये बदलून, आम्हाला मिळते:

आता आपण क्यूबच्या पृष्ठभागावरून टेंशन वेक्टरचे फ्लक्स शोधू शकतो, ते समान आहे:

\[Ф_(एक)=\frac(\rho V_k)((\varepsilon )_0)=\frac(\rho b^3)((\varepsilon )_0)\left(1.7\right),\]

चेंडूच्या पृष्ठभागाद्वारे:

\[Ф_(Esh)=\frac(\rho V_(sh))((\varepsilon )_0)=\frac(\rho )((\varepsilon )_0)\frac(\sqrt(3))(2) \pi b^3\ \left(1.8\उजवे).\]

चला $\frac(Ф_(Esh))(Ф_(Ek))$ हे प्रमाण शोधू.

\[\frac(Ф_(Esh))(Ф_(Ek))=\frac(\frac(с)(\varepsilon_0)\frac(\sqrt(3))(2) \pi b^3)(\frac (сb^3)(\varepsilon_0))=\frac(\pi)(2)\sqrt(3)\ सुमारे 2.7\left(1.9\उजवे).\]

उत्तर: बॉलच्या पृष्ठभागावरून प्रवाह 2.7 पट जास्त आहे.

कार्य: कंडक्टरचा चार्ज त्याच्या पृष्ठभागावर स्थित आहे हे सिद्ध करा.

ते सिद्ध करण्यासाठी आम्ही गॉसचे प्रमेय वापरतो. कंडक्टरच्या पृष्ठभागाजवळील कंडक्टरमध्ये अनियंत्रित आकाराचा बंद पृष्ठभाग निवडू या (चित्र 2).

कंडक्टरच्या आत चार्जेस आहेत असे गृहीत धरू या, आम्ही पृष्ठभाग S वरील कोणत्याही बिंदूसाठी फील्ड विचलनासाठी ऑस्ट्रोग्राडस्की-गॉस प्रमेय लिहू:

जेथे $\rho ही अंतर्गत शुल्काची घनता\$ आहे. तथापि, कंडक्टरमध्ये कोणतेही फील्ड नाही, म्हणजे $\overrightarrow(E)=0$, म्हणून, $div\overrightarrow(E)=0\to \rho =0$. विभेदक स्वरूपात ऑस्ट्रोग्राडस्की-गॉस प्रमेय स्थानिक आहे, म्हणजेच ते फील्ड पॉइंटसाठी लिहिलेले आहे, आम्ही बिंदू विशेष प्रकारे निवडला नाही, म्हणून, कंडक्टरच्या आत फील्डच्या कोणत्याही बिंदूवर चार्ज घनता शून्य आहे.

कूलॉम्बच्या कायद्याच्या संयोजनात सुपरपोझिशनचे तत्त्व एका अनियंत्रित शुल्क प्रणालीच्या इलेक्ट्रिक फील्डची गणना करण्याची गुरुकिल्ली प्रदान करते, परंतु सूत्र (4.2) वापरून फील्डच्या थेट बेरीजसाठी सहसा जटिल गणना आवश्यक असते. तथापि, शुल्क प्रणालीच्या एक किंवा दुसर्या सममितीच्या उपस्थितीत, जर आपण विद्युत क्षेत्राच्या प्रवाहाची संकल्पना मांडली आणि गॉसचे प्रमेय वापरला तर गणना लक्षणीयरीत्या सरलीकृत केली जाते.

विद्युत क्षेत्राच्या प्रवाहाची संकल्पना हायड्रोडायनॅमिक्समधून इलेक्ट्रोडायनामिक्समध्ये आणली गेली. हायड्रोडायनॅमिक्समध्ये, पाईपमधून द्रवपदार्थाचा प्रवाह, म्हणजेच प्रति युनिट वेळेत पाईपच्या क्रॉस-सेक्शनमधून जाणाऱ्या द्रव N चे प्रमाण v ⋅ S च्या बरोबरीचे असते, जेथे v हा द्रवाचा वेग असतो आणि S असतो. पाईपचे क्रॉस-सेक्शनल क्षेत्र. जर द्रवपदार्थाचा वेग क्रॉस विभागात बदलत असेल, तर तुम्हाला अविभाज्य सूत्र N = ∫ S v → ⋅ d S → वापरावे लागेल. खरंच, वेग वेक्टर (चित्र ) ला लंब असलेल्या वेग फील्डमधील d S हे लहान क्षेत्र हायलाइट करूया.

तांदूळ. १.४: द्रव प्रवाह

या भागातून dt वेळेत वाहणार्‍या द्रवाचे प्रमाण v d S d t च्या बरोबरीचे असते. जर प्लॅटफॉर्म प्रवाहाकडे झुकलेला असेल, तर संबंधित खंड v d S cos θ d t असेल, जेथे θ हा वेग वेक्टर v → आणि प्लॅटफॉर्म d S मधील सामान्य n → मधील कोन आहे. या मूल्याला d t ने भागून d S प्रति युनिट वेळेत क्षेत्रफळातून वाहणाऱ्या द्रवाचे प्रमाण मिळते. ते v d S cos θ d t , म्हणजे स्केलर उत्पादन v → ⋅ d S → वेग वेक्टर v → क्षेत्रीय घटक सदिश d S → = n → d S द्वारे. एकक सदिश n → सामान्य ते क्षेत्रफळ d S दोन थेट विरुद्ध दिशेने काढता येतो. त्यापैकी एक सशर्त सकारात्मक म्हणून स्वीकारला जातो. सामान्य n → या दिशेने काढले आहे. ज्या बाजूने सामान्य n → बाहेर पडते त्या बाजूस बाह्य म्हणतात आणि ज्या बाजूमध्ये सामान्य n → प्रवेश करते त्या बाजूस अंतर्गत म्हणतात. क्षेत्रीय घटक d S → बाह्य सामान्य n → बाजूने पृष्ठभागावर निर्देशित केले जाते आणि परिमाण d S = ∣ d S → ∣ घटकाच्या क्षेत्रफळाच्या समान असते. मर्यादित परिमाणांच्या क्षेत्र S मधून वाहणार्‍या द्रवाचे प्रमाण मोजताना, ते असीम क्षेत्र d S मध्ये विकसित केले जाणे आवश्यक आहे आणि नंतर संपूर्ण पृष्ठभाग S वरील अविभाज्य ∫ S v → ⋅ d S → ची गणना करा.

∫ S v → ⋅ d S → सारख्या अभिव्यक्ती भौतिकशास्त्र आणि गणिताच्या अनेक शाखांमध्ये आढळतात. वेक्टर v → च्या स्वरूपाकडे दुर्लक्ष करून, पृष्ठभाग S मधून व्हेक्टर v → चा प्रवाह त्यांना म्हणतात. इलेक्ट्रोडायनामिक्समध्ये इंटिग्रल

N = ∫ S E → ⋅ d S →

(5.1)

याला या संकल्पनेशी कोणताही वास्तविक प्रवाह संबद्ध नसला तरी, अनियंत्रित पृष्ठभाग S द्वारे विद्युत क्षेत्र शक्ती E → चा प्रवाह म्हणतात.

सदिश E → हे भौमितिक बेरीज द्वारे दर्शविले जाते असे गृहीत धरू

E → = ∑ j E → j .

या समानतेला d S → ने स्केलरली गुणाकार केल्याने आणि एकत्रित केल्याने आपल्याला मिळते

N = ∑ j N j .

जेथे N j हा सदिश E → j चा प्रवाह आहे त्याच पृष्ठभागावरून. अशाप्रकारे, विद्युत क्षेत्राच्या सामर्थ्याच्या सुपरपोझिशनच्या तत्त्वावरून असे दिसून येते की समान पृष्ठभागावरील प्रवाह बीजगणितानुसार जोडले जातात.

गॉसचे प्रमेय असे सांगते की एका अनियंत्रित बंद पृष्ठभागाद्वारे वेक्टर E → चा प्रवाह 4 π ने गुणाकार केलेल्या या पृष्ठभागाच्या आत असलेल्या सर्व कणांच्या एकूण चार्ज Q च्या समान आहे:

प्रमेयाचा पुरावा आपण तीन टप्प्यांत पार पाडू.

1. एक पॉइंट चार्ज q (Fig.) च्या इलेक्ट्रिक फील्ड फ्लक्सची गणना करून प्रारंभ करूया. सर्वात सोप्या बाबतीत, जेव्हा एकीकरण पृष्ठभाग S हा एक गोल असतो आणि चार्ज त्याच्या केंद्रस्थानी असतो, तेव्हा गॉसच्या प्रमेयची वैधता जवळजवळ स्पष्ट असते. गोलाच्या पृष्ठभागावर, विद्युत क्षेत्राची ताकद आहे

E → = q r → ∕ r 3

परिमाणात स्थिर आणि सर्वत्र पृष्ठभागावर सामान्य दिशेने निर्देशित केले जाते, जेणेकरून विद्युत क्षेत्र प्रवाह फक्त उत्पादन E = q ∕ r 2 आणि गोलाचे क्षेत्रफळ S = 4 π r 2 या समान असेल. म्हणून, N = 4 π q. हा परिणाम चार्जच्या सभोवतालच्या पृष्ठभागाच्या आकारापेक्षा स्वतंत्र आहे. हे सिद्ध करण्यासाठी, आम्ही बाह्य सामान्य n → सेट केलेल्या दिशेसह पुरेसे लहान आकाराच्या पृष्ठभागाचे अनियंत्रित क्षेत्र निवडतो. अंजीर मध्ये. असा एक विभाग अतिशयोक्तीने मोठ्या (स्पष्टतेसाठी) आकारात दर्शविला आहे.

या क्षेत्रातून E → सदिशाचा प्रवाह d N = E → ⋅ d S → = E cos θ d S , बरोबर आहे.

जेथे θ हा दिशा E → आणि बाह्य सामान्य n → ते क्षेत्र d S मधील कोन आहे. E = q ∕ r 2 , आणि d S cos θ ∕ ​​r 2 निरपेक्ष मूल्यात d Ω = d S ∣ cos θ ∣ ∕ r 2 या घन कोनाचा घटक आहे, ज्याखाली d S क्षेत्रफळ दिसत आहे. बिंदू जेथे चार्ज स्थित आहे,

D N = ± q d Ω .

जेथे अधिक आणि वजा चिन्हे cos θ चिन्हाशी सुसंगत आहेत, म्हणजे: जर सदिश E → बाह्य सामान्य n → च्या दिशेने तीव्र कोन बनवत असेल आणि अन्यथा वजा चिन्ह घ्या.

2. आता काही निवडलेल्या व्हॉल्यूम V व्यापून मर्यादित पृष्ठभाग S चा विचार करा. या व्हॉल्यूमच्या संदर्भात, पृष्ठभागाच्या कोणत्याही घटकाच्या सामान्यच्या दोन विरुद्ध दिशांपैकी कोणती दिशा बाह्य मानली पाहिजे हे निर्धारित करणे नेहमीच शक्य आहे. बाह्य सामान्य व्हॉल्यूम V मधून बाहेरच्या दिशेने निर्देशित केले जाते. सेगमेंट्सचा सारांश, साइन अप करण्यासाठी आपल्याकडे N = q Ω आहे, जेथे Ω हा घन कोन आहे ज्यावर चार्ज q स्थित आहे त्या बिंदूपासून पृष्ठभाग S दृश्यमान आहे. जर पृष्ठभाग S बंद असेल, तर Ω = 4 π, जर चार्ज q S च्या आत असेल तर. अन्यथा Ω = 0. शेवटचे विधान स्पष्ट करण्यासाठी, आम्ही पुन्हा चित्राचा संदर्भ घेऊ शकतो. .

हे स्पष्ट आहे की बंद पृष्ठभागाच्या विभागांमधून प्रवाह समान घन कोनांवर आधारित, परंतु विरुद्ध दिशेने तोंड करून एकमेकांना रद्द करतात. हे देखील स्पष्ट आहे की जर चार्ज बंद पृष्ठभागाच्या बाहेर असेल, तर बाहेरील बाजूस असलेल्या कोणत्याही विभागासाठी आतील बाजूस एक संबंधित विभाग आहे.

3. शेवटी, सुपरपोझिशनच्या तत्त्वाचा वापर करून, आपण गॉसच्या प्रमेय () च्या अंतिम सूत्रीकरणावर पोहोचतो. खरंच, शुल्क प्रणालीचे क्षेत्र स्वतंत्रपणे प्रत्येक शुल्काच्या फील्डच्या बेरजेइतके असते, परंतु केवळ बंद पृष्ठभागाच्या आत असलेले शुल्क प्रमेय () च्या उजव्या बाजूला शून्य नसलेले योगदान देतात. हे पुरावे पूर्ण करते.

मॅक्रोस्कोपिक बॉडीजमध्ये, चार्ज वाहकांची संख्या इतकी मोठी असते की चार्ज घनतेची संकल्पना सादर करून, सतत वितरणाच्या स्वरूपात कणांच्या वेगळ्या जोडणीचे प्रतिनिधित्व करणे सोयीचे असते. व्याख्येनुसार, चार्ज घनता ρ हे प्रमाण Δ Q ∕ Δ V मर्यादेतील असते जेव्हा Δ V भौतिकदृष्ट्या असीम मूल्याकडे झुकते:

जेथे उजव्या बाजूचे एकत्रीकरण पृष्ठभाग S द्वारे बंद केलेल्या व्हॉल्यूम V वर केले जाते.

गॉसचे प्रमेय E → व्हेक्टरच्या तीन घटकांसाठी एक स्केलर समीकरण देते, त्यामुळे केवळ हे प्रमेय विद्युत क्षेत्राची गणना करण्यासाठी पुरेसे नाही. चार्ज घनता वितरणाची ज्ञात सममिती आवश्यक आहे जेणेकरून समस्या एका स्केलर समीकरणात कमी केली जाऊ शकते. गॉसच्या प्रमेयामुळे () मध्ये समाकलनाची पृष्ठभाग निवडली जाऊ शकते अशा प्रकरणांमध्ये फील्ड शोधणे शक्य करते जेणेकरून विद्युत क्षेत्राची ताकद E संपूर्ण पृष्ठभागावर स्थिर असेल. चला सर्वात बोधप्रद उदाहरणे पाहू.

▸ समस्या 5.1

व्हॉल्यूममध्ये समान चार्ज केलेल्या गोलाचे क्षेत्र शोधा किंवापृष्ठभाग

उपाय: पॉइंट चार्जचे इलेक्ट्रिक फील्ड E → = q r → ∕ r 3 कडे झुकते येथे अनंत r → 0 . ही वस्तुस्थिती कल्पनेतील विसंगती दर्शवते बिंदू शुल्कानुसार प्राथमिक कण. चार्ज तर q मर्यादित त्रिज्येच्या गोलाच्या व्हॉल्यूमवर एकसमान वितरीत केले जाते a, नंतर इलेक्ट्रिक फील्डमध्ये एकलता नाही.

समस्येच्या सममितीवरून हे स्पष्ट आहे की विद्युत क्षेत्रई → सर्वत्र त्रिज्या निर्देशित केले जाते, आणि त्याचा ताण E = E(r) फक्त r अंतरावर अवलंबून आहे चेंडूच्या मध्यभागी. मग विद्युत क्षेत्र त्रिज्येच्या गोलातून वाहते r फक्त 4 π r 2 E (Fig. ) च्या समान आहे.

दुसरीकडे, त्याच गोलाच्या आत चार्ज एकूण चार्ज समान आहेचेंडू Q जर r ≥ a. 4 π r 2 E ला बॉलच्या चार्ज q ला 4 π ने गुणाकार केल्याने आपल्याला मिळते: E (r) = q ∕ r 2 .

अशा प्रकारे, बाह्य जागेत, चार्ज केलेला चेंडू तयार होतो असे क्षेत्र जसे की सर्व शुल्क त्याच्या केंद्रस्थानी केंद्रित आहे. हा परिणाम कोणत्याही गोलाकार सममितीसाठी वैध आहे शुल्क वितरण.

चेंडूच्या आत फील्ड आहे E (r) = Q ∕ r 2, जेथे Q हा r त्रिज्या सल्फरच्या आत चार्ज आहे. जर चार्ज बॉलच्या संपूर्ण व्हॉल्यूममध्ये समान रीतीने वितरीत केला असेल तर Q = q (r ∕ a) 3 . या प्रकरणात

E (r) = q r ∕ a 3 = (4 π ∕ 3) ρ r ,

जिथे ρ = q ∕ (4 π a 3 ∕ 3) — चार्ज घनता. चेंडूच्या आत, फील्ड त्याच्या कमाल वरून रेषीयपणे कमी होते चेंडूच्या पृष्ठभागावरील मूल्ये त्याच्या केंद्रस्थानी शून्य (चित्र. ).

कार्य E(r) त्याच वेळी, ते सर्वत्र मर्यादित आणि निरंतर आहे.

जर चार्ज चेंडूच्या पृष्ठभागावर वितरीत केला असेल तर Q = 0, आणि म्हणून E = 0 देखील. हा परिणाम गोलाकाराच्या आत असताना केससाठी देखील वैध आहे कोणतीही चार्ज पोकळी नाही आणि बाह्य शुल्क गोलाकाररित्या वितरीत केले जातातसममितीने ▸ समस्या 5.2

एकसमान चार्ज केलेल्या अनंत थ्रेडचे फील्ड शोधा; थ्रेड त्रिज्या a, प्रति युनिट लांबी शुल्क ϰ.

▸ समस्या 5.3

अनंत सरळ धाग्याचे क्षेत्र शोधा आणि अनंत लांब एकसमान चार्ज केलेला सिलेंडर.

▸ समस्या 5.4

अनंत चार्ज केलेल्या विमानाचे फील्ड आणि एकसारखे शोधा चार्ज केलेला अनंत सपाट थर.

उपाय: समस्येच्या सममितीमुळे, फील्ड निर्देशित केले जाते लेयरसाठी सामान्य आणि फक्त अंतरावर अवलंबून असते x पासून प्लेटच्या सममितीचे विमान. वापरून फील्ड मोजण्यासाठी गॉसचे प्रमेय, एकत्रीकरणाची पृष्ठभाग निवडणे सोयीचे आहेमध्ये एस अंजीर मध्ये दर्शविल्याप्रमाणे समांतर लिपिड स्वरूपात. .

अंतिम निकाल मर्यादेपर्यंत उत्तीर्ण करून प्राप्त केला जातो a → 0 एकाच वेळी चार्ज घनता वाढवतानाρ जेणेकरून मूल्य σ = ρ a अपरिवर्तित राहिले. विमानाच्या विरुद्ध बाजूंनी विद्युत क्षेत्राची ताकद परिमाणात समान आहे, परंतु विरुद्ध दिशेने. त्यामुळे जात असताना चार्ज केलेले विमान, फील्ड रकमेनुसार अचानक बदलते४ π σ . लक्षात ठेवा की प्लेटला अनंत मानले जाऊ शकते जर पासूनचे अंतर त्याच्या आकाराच्या तुलनेत नगण्य आहे. चालू प्लेटच्या परिमाणांच्या तुलनेत अंतर खूप मोठे आहे पॉइंट चार्ज सारखे कार्य करते आणि त्याचे फील्ड परत कमी होते अंतराच्या वर्गाच्या प्रमाणात.

इलेक्ट्रोस्टॅटिक फील्ड बलाच्या रेषा (तणाव रेषा) वापरून स्पष्टपणे चित्रित केले जाऊ शकते. पॉवर लाईन्सवक्र म्हणतात ज्यांच्या स्पर्शिका प्रत्येक बिंदूवर ताण वेक्टर E शी जुळतात.

शक्तीच्या रेषा ही एक परंपरागत संकल्पना आहे आणि ती प्रत्यक्षात अस्तित्वात नाही. एकल ऋण आणि एकल सकारात्मक शुल्काच्या फील्ड रेषा अंजीर मध्ये दर्शविल्या आहेत. 5 या धनभारातून येणार्‍या किंवा ऋण शुल्काकडे जाणार्‍या रेडियल सरळ रेषा आहेत.

फील्डच्या संपूर्ण व्हॉल्यूममध्ये फील्ड लाईन्सची घनता आणि दिशा अपरिवर्तित राहिल्यास, असे इलेक्ट्रोस्टॅटिक फील्ड एकसंध मानले जाते (रेषांची संख्या संख्यात्मकदृष्ट्या फील्ड ताकद E च्या समान असणे आवश्यक आहे).

">dS चिन्हांकित केलेल्या फील्ड रेषांची संख्या, त्यांना लंब, निर्धारित करते इलेक्ट्रोस्टॅटिक फील्ड स्ट्रेंथ वेक्टरचा प्रवाह:

सूत्र" src="http://hi-edu.ru/e-books/xbook785/files/17-1.gif" border="0" align="absmiddle" alt="- वेक्टर E चे प्रक्षेपण सामान्य n च्या दिशेने साइट dS (Fig. 6) वर.

त्यानुसार, वेक्टर E चा प्रवाह अनियंत्रित बंद पृष्ठभाग S द्वारे होतो

मार्क">एस केवळ परिमाणच नाही तर प्रवाहाचे चिन्ह देखील बदलू शकते:

1) सूत्रासह" src="http://hi-edu.ru/e-books/xbook785/files/17-4.gif" border="0" align="absmiddle" alt="

3) निवडताना"> गोलाकार पृष्ठभाग S मधून व्हेक्टर E चा प्रवाह शोधू, ज्याच्या मध्यभागी बिंदू शुल्क q आहे.

या प्रकरणात, गोलाकार पृष्ठभागाच्या सर्व बिंदूंवर ">E आणि n हे चिन्ह एकरूप होतात.

पॉइंट चार्जची फील्ड ताकद लक्षात घेऊन, सूत्र" src="http://hi-edu.ru/e-books/xbook785/files/18-2.gif" border="0" align="absmiddle " alt="(! LANG:आम्हाला मिळते

सूत्र" src="http://hi-edu.ru/e-books/xbook785/files/Fe.gif" border="0" align="absmiddle" alt="- शुल्काच्या चिन्हावर अवलंबून बीजगणितीय प्रमाण. उदाहरणार्थ, जेव्हा q<0 линии Е направлены к заряду и противоположны направлению внешней нормали n ..gif" border="0" align="absmiddle" alt="चार्ज q च्या आसपास एक अनियंत्रित आकार आहे. साहजिकच, पृष्ठभागावर ">E असे चिन्हांकित केले आहे, जसे पृष्ठभाग S आहे. त्यामुळे, अनियंत्रित पृष्ठभागाद्वारे वेक्टर E चा प्रवाह हे सूत्र आहे" src="http://hi-edu.ru/e-books/xbook785/ files/Fe.gif" सीमा ="0" align="absmiddle" alt=".

जर चार्ज बंद पृष्ठभागाच्या बाहेर स्थित असेल तर, उघडपणे, किती ओळी बंद क्षेत्रात प्रवेश करतात, समान संख्या त्यास सोडेल. परिणामी, वेक्टर E चा प्रवाह शून्याच्या बरोबरीचा असेल.

पॉइंट चार्जेसच्या प्रणालीद्वारे विद्युत क्षेत्र तयार केले असल्याससूत्र" src="http://hi-edu.ru/e-books/xbook785/files/18-4.gif" border="0" align="absmiddle" alt="

हे सूत्र गॉसच्या प्रमेयाची गणितीय अभिव्यक्ती आहे: एका अनियंत्रित बंद पृष्ठभागाद्वारे व्हॅक्यूममध्ये विद्युतीय क्षेत्र शक्ती वेक्टर E चा प्रवाह तो व्यापलेल्या शुल्काच्या बीजगणितीय बेरजेएवढा असतो, ज्याला भागिले जातेसूत्र" src="http://hi-edu.ru/e-books/xbook785/files/18-6.gif" border="0" align="absmiddle" alt="

वर्णन पूर्ण करण्यासाठी, आपण अविभाज्य संबंधांवर अवलंबून न राहता, अवकाशातील दिलेल्या बिंदूवर फील्ड पॅरामीटर्सवर अवलंबून राहून गॉसचे प्रमेय स्थानिक स्वरूपात सादर करूया. हे करण्यासाठी, विभेदक ऑपरेटर वापरणे सोयीचे आहे - वेक्टर डायव्हर्जन, -

सूत्र" src="http://hi-edu.ru/e-books/xbook785/files/nabla.gif" border="0" align="absmiddle" alt="("नबला") -

सूत्र" src="http://hi-edu.ru/e-books/xbook785/files/19-1.gif" border="0" align="absmiddle" alt="

गणितीय विश्लेषणामध्ये, गॉस-ऑस्ट्रोग्राडस्की प्रमेय ज्ञात आहे: बंद पृष्ठभागाद्वारे वेक्टरचा प्रवाह या पृष्ठभागाद्वारे मर्यादित असलेल्या व्हॉल्यूमवर त्याच्या विचलनाच्या अविभाज्य भागाच्या समान असतो -

सूत्र" src="http://hi-edu.ru/e-books/xbook785/files/ro.gif" border="0" align="absmiddle" alt=":

सूत्र" src="http://hi-edu.ru/e-books/xbook785/files/19-4.gif" border="0" align="absmiddle" alt="

ही अभिव्यक्ती गॉसचे स्थानिक (विभेदक) स्वरूपातील प्रमेय आहे.

गॉसचे प्रमेय (2.2) आपल्याला विविध इलेक्ट्रोस्टॅटिक क्षेत्रांची ताकद निश्चित करण्यास अनुमती देते. गॉसच्या प्रमेयाच्या उपयोगाची अनेक उदाहरणे पाहू.

1. चला गणना करूया E इलेक्ट्रोस्टॅटिक फील्ड एकसमान चार्ज केलेल्या गोलाकार पृष्ठभागाद्वारे तयार केले जाते.

आपण असे गृहीत धरू की त्रिज्या R च्या गोलाकार पृष्ठभागावर एकसमान वितरित शुल्क q आहे, म्हणजे. पृष्ठभाग चार्ज घनता सर्वत्र समान चिन्ह आहे ">r >R गोलाच्या मध्यभागी, आम्ही मानसिकदृष्ट्या नवीन गोलाकार पृष्ठभाग S तयार करतो, जो चार्ज केलेल्या गोलाशी सममित आहे. गॉसच्या प्रमेयानुसार

सूत्र" src="http://hi-edu.ru/e-books/xbook785/files/20-1.gif" border="0" align="absmiddle" alt="

त्रिज्या R च्या चार्ज केलेल्या गोलाच्या पृष्ठभागावर असलेल्या बिंदूंसाठी, सादृश्यतेने आपण लिहू शकतो:

Selection">चार्ज केलेल्या गोलाच्या आत, स्वतःमध्ये विद्युत शुल्क नसतात, त्यामुळे फ्लक्स मार्क">E = 0.

जर्मन शास्त्रज्ञ के. गॉस (१७७७-१८५५) याने शोधलेले प्रमेय लागू केल्यास इलेक्ट्रोस्टॅटिक फील्डच्या सुपरपोझिशनच्या तत्त्वाचा वापर करून इलेक्ट्रिक चार्जेसच्या सिस्टीमची फील्ड ताकद मोजण्याचे काम बरेच सोपे केले जाऊ शकते, जे विद्युत प्रवाह निश्चित करते. अनियंत्रित बंद पृष्ठभागाद्वारे विद्युत क्षेत्र शक्ती वेक्टर.

बंद पृष्ठभागाद्वारे तीव्रता वेक्टर फ्लक्सच्या व्याख्येवरून, त्रिज्या r च्या गोलाकार पृष्ठभागाद्वारे तीव्रता वेक्टर फ्लक्स, जे त्याच्या केंद्रस्थानी स्थित बिंदू शुल्क Q कव्हर करते (चित्र 1)

हा परिणाम अनियंत्रित आकाराच्या बंद पृष्ठभागासाठी वैध आहे. खरंच, जर तुम्ही एक गोलाकार (Fig. 1) अनियंत्रित बंद पृष्ठभागामध्ये बंद केला तर, गोलामध्ये प्रवेश करणारी प्रत्येक ताणाची ओळ देखील या पृष्ठभागावरून जाईल.

जर कोणत्याही आकाराच्या बंद पृष्ठभागावर शुल्क (चित्र 2) जोडलेले असेल, तर जेव्हा कोणतीही ताण रेषा पृष्ठभागाला छेदते तेव्हा ती एकतर त्यात प्रवेश करते किंवा सोडते. फ्लक्सची गणना करताना, छेदनबिंदूंची विषम संख्या शेवटी एका छेदनबिंदूवर कमी होते, कारण ताणाच्या रेषा पृष्ठभाग सोडल्यास प्रवाह सकारात्मक आणि पृष्ठभागावर प्रवेश करणार्‍या रेषांसाठी ऋण गृहित धरले जाते. जर बंद पृष्ठभागावर शुल्क आकारले जात नाही. , तर त्यातून प्रवाह शून्य आहे, त्यामुळे पृष्ठभागावर प्रवेश करणार्‍या तणाव रेषांची संख्या त्यातून बाहेर पडणार्‍या तणाव रेषांच्या संख्येइतकी कशी आहे.

याचा अर्थ असा की अनियंत्रित आकाराच्या पृष्ठभागासाठी, जर ते बंद असेल आणि त्यात पॉइंट चार्ज Q असेल तर, वेक्टरचा प्रवाह इ Q/ε 0 बरोबर असेल, म्हणजे

फ्लक्सचे चिन्ह चार्ज Q च्या चिन्हाशी जुळते.

n चार्जेसच्या आसपासच्या अनियंत्रित पृष्ठभागाच्या सामान्य प्रकरणाचा अभ्यास करूया. सुपरपोझिशन, टेंशन या तत्त्वाचा वापर करून इफील्ड, जे सर्व शुल्कांद्वारे तयार केले जाते, तीव्रतेच्या बेरजेइतके असते इ iफील्ड जे प्रत्येक शुल्काद्वारे स्वतंत्रपणे तयार केले जातात. म्हणून

(1) नुसार, बेरीज चिन्हाखाली दिसणारे प्रत्येक अविभाज्य Q i /ε 0 च्या बरोबरीचे आहे. म्हणजे,

(2)

सूत्र (2) व्यक्त करतो व्हॅक्यूममधील इलेक्ट्रोस्टॅटिक क्षेत्रासाठी गॉसचे प्रमेय: एका अनियंत्रित बंद पृष्ठभागाद्वारे व्हॅक्यूममधील इलेक्ट्रोस्टॅटिक फील्ड ताकद वेक्टरचा प्रवाह या पृष्ठभागाच्या आत असलेल्या शुल्काच्या बीजगणितीय बेरीजच्या बरोबर असतो, ज्याला ε 0 ने भागले जाते. हे प्रमेय रशियन गणितज्ञ एम.व्ही. ऑस्ट्रोग्राडस्की (1801-1862) यांनी अनियंत्रित स्वरूपाच्या वेक्टर क्षेत्रासाठी गणितीयदृष्ट्या प्राप्त केले होते, आणि नंतर इलेक्ट्रोस्टॅटिक क्षेत्राच्या संबंधात स्वतंत्रपणे - के. गॉस यांनी.

सामान्य स्थितीत, विद्युत शुल्क विशिष्ट घनता घनता ρ=dQ/dV सह वितरित केले जाऊ शकते, जे अंतराळातील वेगवेगळ्या ठिकाणी भिन्न असते. नंतर बंद पृष्ठभाग S मध्ये समाविष्ट असलेले एकूण शुल्क, जे विशिष्ट व्हॉल्यूम V व्यापते,

(3)

सूत्र (3) वापरून, गॉसचे प्रमेय (2) खालीलप्रमाणे लिहिता येईल:

व्होल्टेज व्हेक्टरचे अभिसरण म्हणजे विद्युत शक्तींद्वारे एकच सकारात्मक चार्ज बंद मार्गावर हलवताना एल.

(13.18)

बंद लूपच्या बाजूने इलेक्ट्रोस्टॅटिक फील्ड फोर्सचे कार्य शून्य (संभाव्य फील्ड फोर्सचे कार्य) असल्याने, बंद लूपसह इलेक्ट्रोस्टॅटिक फील्ड शक्तीचे अभिसरण शून्य आहे.

इलेक्ट्रोस्टॅटिक फील्ड संभाव्यता.कंझर्व्हेटिव्ह फोर्सच्या फील्डचे वर्णन केवळ वेक्टर फंक्शनद्वारे केले जाऊ शकत नाही, परंतु या फील्डचे समतुल्य वर्णन त्याच्या प्रत्येक बिंदूवर योग्य स्केलर प्रमाण परिभाषित करून मिळवता येते. इलेक्ट्रोस्टॅटिक फील्डसाठी, हे प्रमाण आहे इलेक्ट्रोस्टॅटिक फील्ड संभाव्यता, चाचणी शुल्काच्या संभाव्य उर्जेचे गुणोत्तर म्हणून परिभाषित केले आहे qया शुल्काच्या परिमाणापर्यंत,  = पपी / q, ज्यावरून असे दिसून येते की संभाव्यता संख्यात्मकदृष्ट्या फील्डमधील दिलेल्या बिंदूवर युनिट पॉझिटिव्ह चार्ज असलेल्या संभाव्य उर्जेच्या समान असते. संभाव्यतेसाठी मोजण्याचे एकक व्होल्ट (1 V) आहे.

पॉइंट चार्ज फील्ड संभाव्य प्रडायलेक्ट्रिक स्थिरांकासह एकसंध समस्थानिक माध्यमात :

सुपरपोझिशन तत्त्व.संभाव्य हे एक स्केलर फंक्शन आहे; सुपरपोझिशनचे तत्त्व त्यासाठी वैध आहे. तर पॉइंट चार्जेसच्या प्रणालीच्या फील्ड संभाव्यतेसाठी प्र 1, प्र 2, प्र nआमच्याकडे आहे

,

कुठे r i- फील्ड पॉईंटपासून संभाव्य  चार्जपर्यंतचे अंतर Qi. जर प्रभार जागेवर अनियंत्रितपणे वितरित केला जात असेल तर

,

कुठे आर- प्राथमिक खंडापासून अंतर d x,d y,d zनिर्देश करणे ( x, y, z), जेथे संभाव्यता निर्धारित केली जाते; व्ही- ज्या जागेत शुल्क वितरीत केले जाते.

विद्युत क्षेत्राच्या शक्तींचे संभाव्य आणि कार्य.संभाव्यतेच्या व्याख्येवर आधारित, हे दर्शविले जाऊ शकते की पॉइंट चार्ज हलवताना विद्युत क्षेत्र शक्तींनी केलेले कार्य qफील्डच्या एका बिंदूपासून दुस-या बिंदूपर्यंत या चार्जच्या परिमाण आणि मार्गाच्या प्रारंभिक आणि अंतिम बिंदूंवरील संभाव्य फरकाच्या गुणाकाराच्या समान आहे, A = q (     
जर, संभाव्य उर्जेशी साधर्म्य करून, आम्ही असे गृहीत धरतो की विद्युत शुल्कापासून असीम दूर असलेल्या बिंदूंवर - फील्ड स्त्रोत, संभाव्यता शून्य आहे, तर चार्ज हलवताना विद्युत क्षेत्र शक्तींचे कार्य qबिंदू 1 ते अनंत असे दर्शविले जाऊ शकते ए   q  1 .
अशा प्रकारे, इलेक्ट्रोस्टॅटिक फील्डच्या दिलेल्या बिंदूवर संभाव्यता आहे एकक पॉझिटिव्ह पॉइंट चार्ज फील्डमधील दिलेल्या बिंदूपासून असीम दूरच्या बिंदूवर हलवताना विद्युत क्षेत्राच्या शक्तींनी केलेल्या कार्याच्या संख्येच्या समान भौतिक प्रमाण:  = ए  / q.
काही प्रकरणांमध्ये, विद्युत क्षेत्र क्षमता अधिक स्पष्टपणे परिभाषित केली जाते एका युनिट पॉझिटिव्ह पॉइंट चार्जला अनंतापासून दिलेल्या बिंदूकडे हलवताना विद्युत क्षेत्राच्या शक्तींविरुद्ध बाह्य शक्तींच्या कार्याप्रमाणे संख्यात्मकदृष्ट्या समान भौतिक प्रमाण. शेवटची व्याख्या खालीलप्रमाणे लिहिणे सोयीचे आहे:

आधुनिक विज्ञान आणि तंत्रज्ञानामध्ये, विशेषत: सूक्ष्म जगामध्ये घडणाऱ्या घटनांचे वर्णन करताना, कार्य आणि उर्जेचे एकक म्हणतात. इलेक्ट्रॉन-व्होल्ट(eV). 1 V: 1 eV = 1.6010  C1 V = 1.6010  J च्या संभाव्य फरकासह दोन बिंदूंमधील इलेक्ट्रॉनच्या चार्जाइतके चार्ज हलवताना हे केले जाणारे कार्य आहे.

समतुल्य पृष्ठभाग- कोणत्याही संभाव्य सदिश क्षेत्राला लागू होणारी संकल्पना, उदाहरणार्थ, स्थिर विद्युत क्षेत्र किंवा न्यूटोनियन गुरुत्वीय क्षेत्र. इक्विपोटेंशियल पृष्ठभाग अशी पृष्ठभाग असते ज्यावर दिलेल्या संभाव्य क्षेत्राची स्केलर संभाव्यता स्थिर मूल्य (संभाव्य पातळी पृष्ठभाग) घेते. दुसरी, समतुल्य, व्याख्या अशी पृष्ठभाग आहे जी कोणत्याही बिंदूवर फील्ड रेषांना ऑर्थोगोनल असते.

इलेक्ट्रोस्टॅटिक्समधील कंडक्टरची पृष्ठभाग एक समतुल्य पृष्ठभाग आहे. याव्यतिरिक्त, समतुल्य पृष्ठभागावर कंडक्टर ठेवल्याने इलेक्ट्रोस्टॅटिक फील्डचे कॉन्फिगरेशन बदलत नाही. ही वस्तुस्थिती प्रतिमा पद्धतीमध्ये वापरली जाते, जी जटिल कॉन्फिगरेशनसाठी इलेक्ट्रोस्टॅटिक फील्डची गणना करण्यास अनुमती देते.

(स्थिर) गुरुत्वाकर्षण क्षेत्रामध्ये, स्थिर द्रवपदार्थाची पातळी समतुल्य पृष्ठभागावर स्थापित केली जाते. विशेषतः, असे अंदाजे म्हटले जाऊ शकते की महासागरांची पातळी पृथ्वीच्या गुरुत्वाकर्षण क्षेत्राच्या समतुल्य पृष्ठभागाच्या बाजूने जाते. पृथ्वीच्या पृष्ठभागापर्यंत विस्तारलेल्या महासागरांच्या पृष्ठभागाच्या आकाराला जिओड म्हणतात आणि भूगर्भशास्त्रात महत्त्वाची भूमिका बजावते. अशाप्रकारे जिओइड हा गुरुत्वाकर्षणाचा समतुल्य पृष्ठभाग आहे, ज्यामध्ये गुरुत्वाकर्षण आणि केंद्रापसारक घटक असतात.