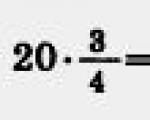Hvordan multiplisere enkle brøker. Regler for å multiplisere og dele brøker med et heltall
Multiplikasjon og deling av brøker.
Merk følgende!
Det er flere
materiale i spesialseksjon 555.
For de som sterkt "ikke veldig..."
Og for de som "veldig mye...")
Denne operasjonen er mye bedre enn addisjon-subtraksjon! Fordi det er lettere. Jeg minner deg om: for å multiplisere en brøk med en brøk, må du multiplisere tellerne (dette vil være telleren for resultatet) og nevnerne (dette vil være nevneren). Det er:
For eksempel:

Alt er ekstremt enkelt. Og vær så snill, ikke se etter en fellesnevner! Trenger det ikke her...
For å dele en brøk på en brøk, må du snu sekund(dette er viktig!) brøk og gang dem, dvs.:

For eksempel:

Hvis multiplikasjon eller divisjon med heltall og brøker fanges opp, er det greit. Som med addisjon lager vi en brøk fra et helt tall med en enhet i nevneren - og går! For eksempel:

På videregående må du ofte forholde deg til tre-etasjers (eller til og med fire-etasjers!) brøker. For eksempel:
Hvordan bringe denne brøken til en anstendig form? Ja, veldig enkelt! Bruk divisjon gjennom to punkter:

Men ikke glem delingsrekkefølgen! I motsetning til multiplikasjon er dette veldig viktig her! Selvfølgelig skal vi ikke forveksle 4:2 eller 2:4. Men i en tre-etasjers brøk er det lett å gjøre feil. Vær for eksempel oppmerksom på:
I det første tilfellet (uttrykket til venstre):

I det andre (uttrykket til høyre):

Føl forskjellen? 4 og 1/9!
Hva er rekkefølgen på delingen? Eller parentes, eller (som her) lengden på horisontale streker. Utvikle et øye. Og hvis det ikke er noen parenteser eller bindestreker, som:
deretter dividere-multipliser i rekkefølge, venstre til høyre!
Og et annet veldig enkelt og viktig triks. I aksjoner med grader vil det komme godt med for deg! La oss dele enheten med en hvilken som helst brøk, for eksempel med 13/15:

Skuddet har snudd! Og det skjer alltid. Når du deler 1 med en hvilken som helst brøk, er resultatet den samme brøken, bare invertert.
Det er alle handlingene med brøker. Saken er ganske enkel, men gir mer enn nok feil. Merk praktiske råd, og de (feil) vil være færre!
Praktiske tips:
1. Det viktigste når du jobber med brøkuttrykk er nøyaktighet og oppmerksomhet! Dette er ikke vanlige ord, ikke gode ønsker! Dette er et alvorlig behov! Gjør alle beregningene på eksamen som en fullverdig oppgave, med konsentrasjon og klarhet. Det er bedre å skrive to ekstra linjer i et utkast enn å rote til når du regner i hodet.
2. I eksemplene med forskjellige typer brøker - gå til vanlige brøker.
3. Vi reduserer alle brøker til stopp.
4. Vi reduserer brøkuttrykk på flere nivåer til vanlige ved å bruke divisjon gjennom to punkter (vi følger divisjonsrekkefølgen!).
5. Vi deler enheten inn i en brøk i tankene våre, ganske enkelt ved å snu brøken.
Her er oppgavene du må fullføre. Svar gis etter alle oppgaver. Bruk materialene til dette emnet og praktiske råd. Anslå hvor mange eksempler du kan løse riktig. Den første gangen! Uten kalkulator! Og trekke de riktige konklusjonene...
Husk riktig svar hentet fra andre (spesielt tredje) gang - teller ikke! Slik er det harde livet.
Så, løse i eksamensmodus ! Dette er forresten forberedelse til eksamen. Vi løser et eksempel, vi sjekker, vi løser følgende. Vi bestemte alt - vi sjekket igjen fra første til siste. Men bare Deretter se på svarene.
Regne ut:


Bestemte du deg?
Ser etter svar som matcher ditt. Jeg skrev dem spesifikt ned i et rot, vekk fra fristelsen, for å si det sånn... Her er de, svarene, skrevet ned med semikolon.
0; 17/22; 3/4; 2/5; 1; 25.
Og nå trekker vi konklusjoner. Hvis alt ordnet seg - glad i deg! Elementære beregninger med brøker er ikke ditt problem! Du kan gjøre mer alvorlige ting. Hvis ikke...
Så du har ett av to problemer. Eller begge deler på en gang.) Mangel på kunnskap og (eller) uoppmerksomhet. Men dette løselig Problemer.
Hvis du liker denne siden...
Forresten, jeg har et par flere interessante nettsteder for deg.)
Du kan trene på å løse eksempler og finne ut nivået ditt. Testing med umiddelbar verifisering. Læring - med interesse!)
du kan bli kjent med funksjoner og deriverte.
Multiplikasjon vanlige brøker
Tenk på et eksempel.
La det være $\frac(1)(3)$ del av et eple på tallerkenen. Vi må finne $\frac(1)(2)$-delen av den. Den nødvendige delen er resultatet av å multiplisere brøkene $\frac(1)(3)$ og $\frac(1)(2)$. Resultatet av å multiplisere to vanlige brøker er en vanlig brøk.
Multiplisere to vanlige brøker
Regel for å multiplisere vanlige brøker:
Resultatet av å multiplisere en brøk med en brøk er en brøk hvis teller er lik produktet av tellerne til de multipliserte brøkene, og nevneren er lik produktet av nevnerne:
Eksempel 1
Multipliser vanlige brøker $\frac(3)(7)$ og $\frac(5)(11)$.
Løsning.
La oss bruke regelen for multiplikasjon av vanlige brøker:
\[\frac(3)(7)\cdot \frac(5)(11)=\frac(3\cdot 5)(7\cdot 11)=\frac(15)(77)\]
Svar:$\frac(15)(77)$
Hvis det oppnås en kansellerbar eller upassende brøk som et resultat av å multiplisere fraksjoner, er det nødvendig å forenkle det.
Eksempel 2
Multipliser brøkene $\frac(3)(8)$ og $\frac(1)(9)$.
Løsning.
Vi bruker regelen for å multiplisere vanlige brøker:
\[\frac(3)(8)\cdot \frac(1)(9)=\frac(3\cdot 1)(8\cdot 9)=\frac(3)(72)\]
Som et resultat fikk vi en reduserbar brøk (på grunnlag av divisjon med $3$. Del telleren og nevneren av brøken med $3$, får vi:
\[\frac(3)(72)=\frac(3:3)(72:3)=\frac(1)(24)\]
Kort løsning:
\[\frac(3)(8)\cdot \frac(1)(9)=\frac(3\cdot 1)(8\cdot 9)=\frac(3)(72)=\frac(1)(24)\]
Svar:$\frac(1)(24).$
Når du multipliserer brøker, kan du redusere tellerne og nevnerne for å finne produktet deres. I dette tilfellet blir telleren og nevneren for brøken dekomponert i enkle faktorer, hvoretter de repeterende faktorene reduseres og resultatet blir funnet.
Eksempel 3
Regn ut produktet av brøkene $\frac(6)(75)$ og $\frac(15)(24)$.
Løsning.
La oss bruke formelen for å multiplisere vanlige brøker:
\[\frac(6)(75)\cdot \frac(15)(24)=\frac(6\cdot 15)(75\cdot 24)\]
Telleren og nevneren inneholder tydeligvis tall som kan reduseres i par med tallene $2$, $3$ og $5$. Vi dekomponerer telleren og nevneren i enkle faktorer og gjør reduksjonen:
\[\frac(6\cdot 15)(75\cdot 24)=\frac(2\cdot 3\cdot 3\cdot 5)(3\cdot 5\cdot 5\cdot 2\cdot 2\cdot 2\cdot 3) =\fracdot(1)=\fracdot(1) )\]
Svar:$\frac(1)(20).$
Når du multipliserer brøker, kan den kommutative loven brukes:
Multiplisere en brøk med et naturlig tall
Regelen for å multiplisere en vanlig brøk med et naturlig tall:
Resultatet av å multiplisere en brøk med et naturlig tall er en brøk der telleren er lik produktet av telleren til den multipliserte brøken med det naturlige tallet, og nevneren er lik nevneren til den multipliserte brøken:
der $\frac(a)(b)$ er en vanlig brøk, er $n$ et naturlig tall.
Eksempel 4
Multipliser brøken $\frac(3)(17)$ med $4$.
Løsning.
La oss bruke regelen for å multiplisere en vanlig brøk med et naturlig tall:
\[\frac(3)(17)\cdot 4=\frac(3\cdot 4)(17)=\frac(12)(17)\]
Svar:$\frac(12)(17).$
Ikke glem å sjekke resultatet av multiplikasjon for sammentrekbarheten til en brøk eller for en uekte brøk.
Eksempel 5
Multipliser brøken $\frac(7)(15)$ med $3$.
Løsning.
La oss bruke formelen for å multiplisere en brøk med et naturlig tall:
\[\frac(7)(15)\cdot 3=\frac(7\cdot 3)(15)=\frac(21)(15)\]
Ved kriteriet om divisjon med tallet $3$), kan det bestemmes at den resulterende brøken kan reduseres:
\[\frac(21)(15)=\frac(21:3)(15:3)=\frac(7)(5)\]
Resultatet er en upassende brøkdel. La oss ta hele delen:
\[\frac(7)(5)=1\frac(2)(5)\]
Kort løsning:
\[\frac(7)(15)\cdot 3=\frac(7\cdot 3)(15)=\frac(21)(15)=\frac(7)(5)=1\frac(2)(5)\]
Det var også mulig å redusere brøker ved å erstatte tallene i telleren og nevneren med deres utvidelser til primfaktorer. I dette tilfellet kan løsningen skrives som følger:
\[\frac(7)(15)\cdot 3=\frac(7\cdot 3)(15)=\frac(7\cdot 3)(3\cdot 5)=\frac(7)(5)=1\frac(2)(5)\]
Svar:$1\frac(2)(5).$
Når du multipliserer en brøk med et naturlig tall, kan du bruke den kommutative loven:
Deling av vanlige brøker
Divisjonsoperasjonen er inversen av multiplikasjon og resultatet er en brøk, som du må multiplisere en kjent brøk med for å få kjent verk to brøker.
Deling av to vanlige brøker
Regelen for å dele vanlige brøker: Tydeligvis kan telleren og nevneren til den resulterende brøken dekomponeres i enkle faktorer og redusere:
\[\frac(8\cdot 35)(15\cdot 12)=\frac(2\cdot 2\cdot 2\cdot 5\cdot 7)(3\cdot 5\cdot 2\cdot 2\cdot 3)=\frac(2\cdot 7)(3)\cdot 7)
Som et resultat fikk vi en uekte brøk, som vi velger heltallsdelen fra:
\[\frac(14)(9)=1\frac(5)(9)\]
Svar:$1\frac(5)(9).$
§ 87. Addisjon av brøker.
Å legge til brøker har mange likheter med å legge til heltall. Addisjon av brøk er en handling som består i at flere gitte tall (ledd) slås sammen til ett tall (sum), som inneholder alle enheter og brøker av leddenheter.
Vi vil vurdere tre saker etter tur:
1. Addisjon av brøker med samme nevnere.
2. Addisjon av brøker med ulike nevnere.
3. Addisjon av blandede tall.
1. Addisjon av brøker med samme nevnere.
Tenk på et eksempel: 1 / 5 + 2 / 5 .
Ta segmentet AB (fig. 17), ta det som en enhet og del det i 5 like deler, så vil delen AC av dette segmentet være lik 1/5 av segmentet AB, og delen av samme segment CD vil være lik 2/5 AB.
Det kan sees fra tegningen at hvis vi tar segmentet AD, så vil det være lik 3/5 AB; men segment AD er nøyaktig summen av segmentene AC og CD. Så vi kan skrive:
1 / 5 + 2 / 5 = 3 / 5
Tatt i betraktning disse begrepene og det resulterende beløpet, ser vi at telleren av summen ble oppnådd ved å legge til tellerne til begrepene, og nevneren forble uendret.
Fra dette får vi følgende regel: For å legge til brøker med de samme nevnerne, må du legge til deres tellere og la den samme nevneren være igjen.
Tenk på et eksempel:
2. Addisjon av brøker med ulike nevnere.
La oss legge til brøker: 3/4 + 3/8 Først må de reduseres til laveste fellesnevner:
Mellomlenken 6/8 + 3/8 kunne ikke vært skrevet; vi har skrevet det her for større klarhet.
For å legge til brøker med forskjellige nevner, må du derfor først bringe dem til laveste fellesnevner, legge til tellerne og signere fellesnevneren.
Tenk på et eksempel (vi vil skrive tilleggsfaktorer over de tilsvarende brøkene):
3. Addisjon av blandede tall.
La oss legge til tallene: 2 3 / 8 + 3 5 / 6.
La oss først bringe brøkdelene av tallene våre til en fellesnevner og skrive dem om igjen:
![]()
Legg nå til heltalls- og brøkdelene i rekkefølge:
§ 88. Subtraksjon av brøker.
Subtraksjon av brøker er definert på samme måte som subtraksjon av hele tall. Dette er en handling som, gitt summen av to ledd og ett av dem, finner et annet ledd. La oss vurdere tre tilfeller etter tur:
1. Subtraksjon av brøker med samme nevnere.
2. Subtraksjon av brøker med ulike nevnere.
3. Subtraksjon av blandede tall.
1. Subtraksjon av brøker med samme nevnere.
Tenk på et eksempel:
13 / 15 - 4 / 15
La oss ta segmentet AB (fig. 18), ta det som en enhet og dele det i 15 like deler; da vil AC-delen av dette segmentet være 1/15 av AB, og AD-delen av samme segment vil tilsvare 13/15 AB. La oss sette til side et annet segment ED, lik 4/15 AB.
Vi må trekke 4/15 fra 13/15. På tegningen betyr dette at segmentet ED må trekkes fra segmentet AD. Som et resultat vil segment AE forbli, som er 9/15 av segment AB. Så vi kan skrive:

Eksemplet vi laget viser at telleren av forskjellen ble oppnådd ved å trekke fra tellerne, og nevneren forble den samme.
Derfor, for å trekke fra brøker med de samme nevnerne, må du trekke fra telleren til subtrahenden fra telleren til minuenden og la den samme nevneren være igjen.
2. Subtraksjon av brøker med ulike nevnere.
Eksempel. 3/4 - 5/8
Først, la oss redusere disse brøkene til den minste fellesnevneren:

Mellomlenken 6 / 8 - 5 / 8 er skrevet her for klarhet, men den kan hoppes over i fremtiden.
For å trekke en brøk fra en brøk, må du derfor først bringe dem til den minste fellesnevneren, deretter trekke fra telleren til subtrahenden fra telleren til minuenden og signere fellesnevneren under deres forskjell.
Tenk på et eksempel:
![]()
3. Subtraksjon av blandede tall.
Eksempel. 10 3/4 - 7 2/3.
La oss bringe brøkdelene av minuenden og subtrahenden til laveste fellesnevner:
Vi trakk en helhet fra en helhet og en brøk fra en brøk. Men det er tilfeller der brøkdelen av subtrahenden er større enn brøkdelen av minuenden. I slike tilfeller må du ta en enhet fra heltallsdelen av den reduserte, dele den inn i de delene der brøkdelen er uttrykt, og legge til brøkdelen av den reduserte. Og så vil subtraksjonen utføres på samme måte som i forrige eksempel:
§ 89. Multiplikasjon av brøker.
Når vi studerer multiplikasjonen av brøker, vil vi vurdere følgende spørsmål:
1. Multiplisere en brøk med et heltall.
2. Finne en brøkdel av et gitt tall.
3. Multiplikasjon av et helt tall med en brøk.
4. Multiplisere en brøk med en brøk.
5. Multiplikasjon av blandede tall.
6. Rentebegrepet.
7. Finne prosenter av et gitt tall. La oss vurdere dem sekvensielt.
1. Multiplisere en brøk med et heltall.
Å multiplisere en brøk med et heltall har samme betydning som å multiplisere et heltall med et heltall. Å multiplisere en brøk (multiplikand) med et heltall (multiplikator) betyr å komponere summen av identiske ledd, der hvert ledd er lik multiplikanten, og antall ledd er lik multiplikatoren.
Så hvis du trenger å multiplisere 1/9 med 7, kan dette gjøres slik:
Vi fikk lett resultatet, siden handlingen ble redusert til å legge til brøker med samme nevnere. Derfor,
Betraktning av denne handlingen viser at å multiplisere en brøk med et heltall tilsvarer å øke denne brøken så mange ganger som det er enheter i heltallet. Og siden økningen i brøken oppnås enten ved å øke telleren
![]() eller ved å redusere nevneren
eller ved å redusere nevneren ![]() , så kan vi enten multiplisere telleren med heltallet, eller dele nevneren på det, hvis en slik divisjon er mulig.
, så kan vi enten multiplisere telleren med heltallet, eller dele nevneren på det, hvis en slik divisjon er mulig.
Herfra får vi regelen:
For å multiplisere en brøk med et heltall, må du multiplisere telleren med dette heltall og la nevneren være den samme, eller om mulig dele nevneren på dette tallet, slik at telleren forblir uendret.
Når du multipliserer, er forkortelser mulig, for eksempel:
2. Finne en brøkdel av et gitt tall. Det er mange problemer der du må finne, eller beregne, en del av et gitt tall. Forskjellen mellom disse oppgavene og andre er at de gir antall objekter eller måleenheter, og du må finne en del av dette tallet, som også er angitt her med en viss brøkdel. For å lette forståelsen vil vi først gi eksempler på slike problemer, og deretter introdusere metoden for å løse dem.
Oppgave 1. Jeg hadde 60 rubler; 1/3 av disse pengene brukte jeg på kjøp av bøker. Hvor mye kostet bøkene?
Oppgave 2. Toget skal dekke avstanden mellom byer A og B, lik 300 km. Han har allerede tilbakelagt 2/3 av den distansen. Hvor mange kilometer er dette?
Oppgave 3. Det er 400 hus i landsbyen, 3/4 av dem er murstein, resten er av tre. Hvor mange murhus er det?
Her er noen av de mange problemene vi må forholde oss til for å finne en brøkdel av et gitt tall. De kalles vanligvis problemer for å finne en brøkdel av et gitt tall.
Løsning av oppgave 1. Fra 60 rubler. Jeg brukte 1/3 på bøker; Så for å finne kostnadene for bøker, må du dele tallet 60 med 3:
Oppgave 2 løsning. Meningen med problemet er at du må finne 2/3 av 300 km. Beregn første 1/3 av 300; dette oppnås ved å dele 300 km med 3:
300: 3 = 100 (det er 1/3 av 300).
For å finne to tredjedeler av 300, må du doble den resulterende kvotienten, det vil si multiplisere med 2:
100 x 2 = 200 (det er 2/3 av 300).
Løsning av oppgave 3. Her må du bestemme antall murhus, som er 3/4 av 400. La oss først finne 1/4 av 400,
400: 4 = 100 (det er 1/4 av 400).
For å beregne tre fjerdedeler av 400, må den resulterende kvotienten tredobles, det vil si multiplisert med 3:
100 x 3 = 300 (det er 3/4 av 400).
Basert på løsningen av disse problemene kan vi utlede følgende regel:
For å finne verdien av en brøkdel av et gitt tall, må du dele dette tallet med nevneren til brøken og multiplisere den resulterende kvotienten med telleren.
3. Multiplikasjon av et helt tall med en brøk.
Tidligere (§ 26) ble det fastslått at multiplikasjonen av heltall skulle forstås som tillegg av identiske termer (5 x 4 \u003d 5 + 5 + 5 + 5 \u003d 20). I dette avsnittet (avsnitt 1) ble det fastslått at å multiplisere en brøk med et heltall betyr å finne summen av identiske ledd lik denne brøken.
I begge tilfeller besto multiplikasjonen i å finne summen av identiske ledd.
Nå går vi videre til å multiplisere et helt tall med en brøk. Her møter vi for eksempel multiplikasjon: 9 2 / 3. Det er ganske åpenbart at den tidligere definisjonen av multiplikasjon ikke gjelder for dette tilfellet. Dette fremgår av det faktum at vi ikke kan erstatte en slik multiplikasjon ved å legge til like tall.
På grunn av dette må vi gi en ny definisjon av multiplikasjon, det vil si, med andre ord, for å svare på spørsmålet om hva som skal forstås ved multiplikasjon med en brøk, hvordan denne handlingen skal forstås.
Betydningen av å multiplisere et heltall med en brøk er tydelig fra følgende definisjon: å multiplisere et heltall (multiplikator) med en brøk (multiplikator) betyr å finne denne brøken av multiplikatoren.
Å multiplisere 9 med 2/3 betyr nemlig å finne 2/3 av ni enheter. I forrige avsnitt ble slike problemer løst; så det er lett å finne ut at vi ender opp med 6.
Men nå oppstår et interessant og viktig spørsmål: hvorfor slikt ved første øyekast ulike aktiviteter, som å finne summen av like tall og finne brøkdelen av et tall, i aritmetikk kalles det samme ordet "multiplikasjon"?
Dette skjer fordi den forrige handlingen (gjenta tallet med termer flere ganger) og den nye handlingen (finne brøkdelen av et tall) gir svar på homogene spørsmål. Det betyr at vi her går ut fra betraktningene om at homogene spørsmål eller oppgaver løses ved en og samme handling.
For å forstå dette, vurder følgende problem: "1 m tøy koster 50 rubler. Hvor mye vil 4 m slikt tøy koste?
Dette problemet løses ved å multiplisere antall rubler (50) med antall meter (4), dvs. 50 x 4 = 200 (rubler).
La oss ta det samme problemet, men i det vil mengden tøy bli uttrykt som et brøktall: "1 m tøy koster 50 rubler. Hvor mye vil 3/4 m av en slik klut koste?
Dette problemet må også løses ved å multiplisere antall rubler (50) med antall meter (3/4).
Du kan også endre tallene i den flere ganger uten å endre betydningen av problemet, for eksempel ta 9/10 m eller 2 3/10 m, etc.
Siden disse problemene har samme innhold og bare er forskjellige i tall, kaller vi handlingene som brukes for å løse dem det samme ordet - multiplikasjon.
Hvordan multipliseres et helt tall med en brøk?
La oss ta tallene som ble funnet i den siste oppgaven:
I følge definisjonen skal vi finne 3/4 av 50. Først finner vi 1/4 av 50, og deretter 3/4.
1/4 av 50 er 50/4;
3/4 av 50 er .
Derfor.
Tenk på et annet eksempel: 12 5 / 8 = ?
1/8 av 12 er 12/8,
5/8 av tallet 12 er .
Derfor,
Herfra får vi regelen:
For å multiplisere et heltall med en brøk, må du multiplisere heltallet med telleren til brøken og gjøre dette produktet til telleren, og signere nevneren til den gitte brøken som nevner.
Vi skriver denne regelen med bokstaver:
For å gjøre denne regelen helt klar, bør det huskes at en brøk kan betraktes som en kvotient. Derfor er det nyttig å sammenligne den funnet regelen med regelen for å multiplisere et tall med en kvotient, som ble angitt i § 38
Det må huskes at før du utfører multiplikasjon, bør du gjøre (hvis mulig) kutt, For eksempel:
4. Multiplisere en brøk med en brøk.Å multiplisere en brøk med en brøk har samme betydning som å multiplisere et heltall med en brøk, det vil si at når du multipliserer en brøk med en brøk, må du finne brøken i multiplikatoren fra den første brøken (multiplikatoren).
Å multiplisere 3/4 med 1/2 (halvparten) betyr nemlig å finne halvparten av 3/4.
Hvordan multipliserer du en brøk med en brøk?
La oss ta et eksempel: 3/4 ganger 5/7. Dette betyr at du må finne 5/7 fra 3/4. Finn først 1/7 av 3/4 og deretter 5/7
1/7 av 3/4 vil bli uttrykt slik:
5/7 tall 3/4 vil bli uttrykt som følger:
Dermed,
![]()
Et annet eksempel: 5/8 ganger 4/9.
1/9 av 5/8 er ,
4/9 tall 5/8 er .
Dermed, ![]()
Fra disse eksemplene kan følgende regel utledes:
For å multiplisere en brøk med en brøk, må du multiplisere telleren med telleren, og nevneren med nevneren og gjøre det første produktet til telleren og det andre produktet til produktets nevner.
Dette er regelen i generelt syn kan skrives slik:
![]()
Ved multiplikasjon er det nødvendig å foreta (om mulig) reduksjoner. Tenk på eksempler:

5. Multiplikasjon av blandede tall. Siden blandede tall lett kan erstattes med uekte brøker, brukes denne omstendigheten vanligvis når man multipliserer blandede tall. Dette betyr at i de tilfellene hvor multiplikatoren, eller multiplikatoren, eller begge faktorene er uttrykt som blandede tall, så erstattes de med uekte brøker. Multipliser, for eksempel, blandede tall: 2 1/2 og 3 1/5. Vi gjør hver av dem til en uekte brøk, og deretter multipliserer vi de resulterende brøkene i henhold til regelen om å multiplisere en brøk med en brøk:
Regel. For å multiplisere blandede tall, må du først konvertere dem til uekte brøker og deretter multiplisere i henhold til regelen om å multiplisere en brøk med en brøk.
Merk. Hvis en av faktorene er et heltall, kan multiplikasjonen utføres basert på fordelingsloven som følger:
6. Rentebegrepet. Ved oppgaveløsning og ved ulike praktiske beregninger bruker vi alle slags brøker. Men man må huske på at mange mengder ikke tillater noen, men naturlige underinndelinger for dem. For eksempel kan du ta en hundredel (1/100) av en rubel, det vil være en krone, to hundredeler er 2 kopek, tre hundredeler er 3 kopek. Du kan ta 1/10 av en rubel, det vil være "10 kopek, eller en krone. Du kan ta en fjerdedel av en rubel, det vil si 25 kopek, en halv rubel, det vil si 50 kopek (femti kopek). Men de tar praktisk talt ikke for eksempel 2/7 rubler fordi rubelen ikke er delt inn i sjuende.
Måleenheten for vekt, det vil si kilogram, tillater først og fremst desimalinndelinger, for eksempel 1/10 kg, eller 100 g. Og slike brøkdeler av et kilo som 1/6, 1/11, 1/13 er uvanlige.
Generelt er våre (metriske) mål desimaler og tillater desimalinndelinger.
Det skal imidlertid bemerkes at det er ekstremt nyttig og praktisk i en lang rekke tilfeller å bruke den samme (uniforme) metoden for å dele opp mengder. Mange års erfaring har vist at en så godt begrunnet inndeling er «hundredeler». La oss se på noen få eksempler relatert til de mest forskjellige områdene av menneskelig praksis.
1. Prisen på bøker har gått ned med 12/100 av forrige pris.
Eksempel. Den forrige prisen på boken er 10 rubler. Hun gikk ned med 1 rubel. 20 kop.
2. Sparebanker utbetaler i løpet av året til innskytere 2/100 av beløpet som settes inn på sparing.
Eksempel. 500 rubler settes inn i kassen, inntekten fra dette beløpet for året er 10 rubler.
3. Antall nyutdannede ved en skole var 5/100 av det totale antallet elever.
EKSEMPEL Bare 1200 elever studerte ved skolen, 60 av dem ble uteksaminert fra skolen.
Hundredelen av et tall kalles en prosentandel..
Ordet "prosent" er lånt fra det latinske språket og roten "cent" betyr hundre. Sammen med preposisjonen (pro centum) betyr dette ordet "for hundre." Betydningen av dette uttrykket følger av det faktum at først i antikkens Roma renter var pengene som skyldneren betalte til utlåneren «for hvert hundre». Ordet "cent" høres i slike kjente ord: centner (hundre kilo), centimeter (de sier centimeter).
For eksempel, i stedet for å si at anlegget produserte 1/100 av alle produktene som ble produsert i løpet av den siste måneden, vil vi si dette: anlegget produserte én prosent av avslagene i løpet av den siste måneden. I stedet for å si: anlegget produserte 4/100 flere produkter enn den fastsatte planen, vil vi si: anlegget overskred planen med 4 prosent.
Eksemplene ovenfor kan uttrykkes annerledes:
1. Prisen på bøker har gått ned med 12 prosent av forrige pris.
2. Sparebanker betaler innskytere 2 prosent per år av beløpet som settes inn på sparing.
3. Antall nyutdannede ved én skole var 5 prosent av antallet av alle elever i skolen.
For å forkorte bokstaven er det vanlig å skrive %-tegnet i stedet for ordet "prosent".
Det må imidlertid huskes at %-tegnet vanligvis ikke skrives i beregninger, det kan skrives i problemstillingen og i sluttresultatet. Når du utfører beregninger, må du skrive en brøk med en nevner på 100 i stedet for et heltall med dette ikonet.
Du må kunne erstatte et heltall med det angitte ikonet med en brøkdel med en nevner på 100:
Omvendt må du venne deg til å skrive et heltall med det angitte ikonet i stedet for en brøk med en nevner på 100:
7. Finne prosenter av et gitt tall.
Oppgave 1. Skolen fikk 200 kubikkmeter. m ved, med bjørkeved som utgjør 30 %. Hvor mye bjørkeved var det?
Meningen med denne oppgaven er at bjørkeved bare var en del av veden som ble levert til skolen, og denne delen er uttrykt som en brøkdel av 30/100. Så vi står overfor oppgaven med å finne en brøkdel av et tall. For å løse det må vi multiplisere 200 med 30 / 100 (oppgaver for å finne brøken av et tall løses ved å multiplisere et tall med en brøk.).
Så 30 % av 200 tilsvarer 60.
Fraksjonen 30 / 100 som oppstår i dette problemet kan reduseres med 10. Det ville være mulig å utføre denne reduksjonen helt fra begynnelsen; løsningen på problemet ville ikke endre seg.
Oppgave 2. Det var 300 barn i ulike aldre i leiren. Barn på 11 år var 21 %, barn på 12 år var 61 % og til slutt 13 åringer var 18 %. Hvor mange barn i hver alder var i leiren?
I denne oppgaven må du utføre tre beregninger, det vil si suksessivt finne antall barn 11 år gamle, deretter 12 år gamle og til slutt 13 år gamle.
Så her vil det være nødvendig å finne en brøkdel av et tall tre ganger. La oss gjøre det:
1) Hvor mange barn var 11 år?
2) Hvor mange barn var 12 år?
3) Hvor mange barn var 13 år?
Etter å ha løst problemet, er det nyttig å legge til tallene som er funnet; summen deres skal være 300:
63 + 183 + 54 = 300
Du bør også være oppmerksom på det faktum at summen av prosentene gitt i tilstanden til problemet er 100:
21% + 61% + 18% = 100%
Dette tyder på det totalt antall barn som var i leiren ble tatt som 100 %.
3 a da cha 3. Arbeideren mottok 1200 rubler per måned. Av disse brukte han 65 % på mat, 6 % på leilighet og oppvarming, 4 % på gass, strøm og radio, 10 % på kulturelle behov og 15 % sparte han. Hvor mye penger ble brukt på behovene angitt i oppgaven?
For å løse dette problemet må du finne en brøkdel av tallet 1200 5 ganger. La oss gjøre det.
1) Hvor mye penger brukes på mat? Oppgaven sier at denne utgiften er 65 % av all inntekt, dvs. 65/100 av tallet 1200. La oss regne ut:
![]()
2) Hvor mye penger ble betalt for en leilighet med oppvarming? Ved å argumentere som den forrige, kommer vi til følgende beregning:
3) Hvor mye betalte du for gass, strøm og radio?
4) Hvor mye penger brukes på kulturelle behov?
5) Hvor mye penger sparte arbeideren?
For verifisering er det nyttig å legge til tallene i disse 5 spørsmålene. Beløpet skal være 1200 rubler. All inntjening tas som 100 %, noe som er enkelt å sjekke ved å legge sammen prosentene gitt i problemstillingen.
Vi har løst tre problemer. Til tross for at disse oppgavene handlet om forskjellige ting (leveranse av ved til skolen, antall barn i ulike aldre, utgiftene til arbeideren), ble de løst på samme måte. Dette skjedde fordi det i alle oppgaver var nødvendig å finne noen prosent av de oppgitte tallene.
§ 90. Brøkdeling.
Når vi studerer delingen av brøker, vil vi vurdere følgende spørsmål:
1. Del et heltall med et heltall.
2. Divisjon av en brøk med et heltall
3. Divisjon av et heltall med en brøk.
4. Divisjon av en brøk med en brøk.
5. Deling av blandede tall.
6. Finne et tall gitt brøken.
7. Finne et tall etter prosentandelen.
La oss vurdere dem sekvensielt.
1. Del et heltall med et heltall.
Som det ble indikert i delen av heltall, er divisjon handlingen som består i det faktum at gitt produktet av to faktorer (utbyttet) og en av disse faktorene (deleren), finnes en annen faktor.
Delingen av et heltall med et heltall vurderte vi i avdelingen for heltall. Vi møtte der to tilfeller av deling: divisjon uten en rest, eller "helt" (150: 10 = 15), og divisjon med en rest (100: 9 = 11 og 1 i resten). Vi kan derfor si at i hele talls rike er nøyaktig deling ikke alltid mulig, fordi utbyttet ikke alltid er produktet av divisor og heltall. Etter introduksjonen av multiplikasjon med en brøk, kan vi vurdere ethvert tilfelle av divisjon av heltall som mulig (bare divisjon med null er ekskludert).
For eksempel betyr å dele 7 med 12 å finne et tall hvis produkt ganger 12 ville være 7. Dette tallet er brøken 7/12 fordi 7/12 12 = 7. Et annet eksempel: 14: 25 = 14/25 fordi 14/25 25 = 14.
For å dele et heltall med et heltall, må du derfor lage en brøk, hvis teller er lik utbyttet, og nevneren er divisor.
2. Divisjon av en brøk med et heltall.
Del brøken 6 / 7 med 3. I henhold til definisjonen av divisjon gitt ovenfor, har vi her produktet (6 / 7) og en av faktorene (3); det kreves å finne en slik andre faktor, som fra multiplikasjon med 3 ville gitt denne jobben 6/7. Det skal selvsagt være tre ganger mindre enn dette produktet. Dette betyr at oppgaven som ble satt foran oss var å redusere brøkdelen 6/7 med 3 ganger.
Vi vet allerede at reduksjonen av en brøk kan gjøres enten ved å redusere telleren eller øke nevneren. Derfor kan du skrive:
![]()
I denne saken teller 6 er delelig med 3, så telleren bør reduseres med 3 ganger.
La oss ta et annet eksempel: 5 / 8 delt på 2. Her er ikke telleren 5 delelig med 2, noe som betyr at nevneren må multipliseres med dette tallet:
![]()
Basert på dette kan vi angi regelen: For å dele en brøk med et heltall, må du dele telleren til brøken på det hele tallet(hvis mulig), forlater den samme nevneren, eller multipliser nevneren til brøken med dette tallet, og forlater den samme telleren.
3. Divisjon av et heltall med en brøk.
La det kreves å dele 5 med 1/2, dvs. finne et tall som etter å ha multiplisert med 1/2 vil gi produktet 5. Dette tallet må selvsagt være større enn 5, siden 1/2 er en egenbrøk, og når man multipliserer et tall med en egenbrøk, må produktet være mindre enn multiplikanet. For å gjøre det klarere, la oss skrive handlingene våre som følger: 5: 1 / 2 = X , altså x 1/2 \u003d 5.
Vi må finne et slikt tall X , som, når multiplisert med 1/2, ville gi 5. Siden å multiplisere et bestemt tall med 1/2 betyr å finne 1/2 av dette tallet, så derfor 1/2 av det ukjente tallet X er 5, og hele tallet X dobbelt så mye, dvs. 5 2 \u003d 10.
Så 5: 1 / 2 = 5 2 = 10
La oss sjekke: ![]()
La oss ta et eksempel til. La det være nødvendig å dele 6 med 2/3. La oss først prøve å finne ønsket resultat ved hjelp av tegningen (fig. 19).
Fig.19
Tegn et segment AB, lik 6 av noen enheter, og del hver enhet i 3 like deler. I hver enhet er tre tredjedeler (3 / 3) i hele segmentet AB 6 ganger større, dvs. e. 18/3. Vi kobler til ved hjelp av små parenteser 18 oppnådde segmenter av 2; Det vil bare være 9 segmenter. Dette betyr at brøken 2/3 er inneholdt i b-enheter 9 ganger, eller med andre ord, brøken 2/3 er 9 ganger mindre enn 6 heltallsenheter. Derfor,
Hvordan få dette resultatet uten en tegning kun ved å bruke beregninger? Vi vil argumentere som følger: det er nødvendig å dele 6 med 2 / 3, det vil si at det er nødvendig å svare på spørsmålet, hvor mange ganger 2 / 3 er inneholdt i 6. La oss først finne ut: hvor mange ganger er 1 / 3 inneholdt i 6? I en hel enhet - 3 tredjedeler, og i 6 enheter - 6 ganger mer, det vil si 18 tredjedeler; for å finne dette tallet må vi multiplisere 6 med 3. Derfor er 1/3 inneholdt i b enheter 18 ganger, og 2/3 er inneholdt i b enheter ikke 18 ganger, men halvparten så mange ganger, dvs. 18: 2 = 9. Derfor, når vi delte 6 med 2/3, utførte vi følgende handlinger:
![]()
Herfra får vi regelen for å dele et heltall med en brøk. For å dele et heltall med en brøk, må du multiplisere dette heltall med nevneren til den gitte brøken, og for å gjøre dette produktet til telleren, dele det med telleren til den gitte brøken.
Vi skriver regelen med bokstaver:
For å gjøre denne regelen helt klar, bør det huskes at en brøk kan betraktes som en kvotient. Derfor er det nyttig å sammenligne den funnet regelen med regelen for å dele et tall med en kvotient, som ble angitt i § 38. Merk at den samme formelen ble oppnådd der.
Ved deling er forkortelser mulige, for eksempel:
4. Divisjon av en brøk med en brøk.
La det kreves å dele 3/4 med 3/8. Hva vil betegne tallet som vil bli oppnådd som et resultat av divisjon? Det vil svare på spørsmålet hvor mange ganger brøken 3/8 er inneholdt i brøken 3/4. For å forstå dette problemet, la oss lage en tegning (fig. 20).

Ta segmentet AB, ta det som en enhet, del det i 4 like deler og merk 3 slike deler. Segment AC vil være lik 3/4 av segment AB. La oss nå dele hvert av de fire innledende segmentene i to, så vil segmentet AB bli delt inn i 8 like deler og hver slik del vil være lik 1/8 av segmentet AB. Vi kobler 3 slike segmenter med buer, så vil hvert av segmentene AD og DC være lik 3/8 av segmentet AB. Tegningen viser at segmentet lik 3/8 er inneholdt i segmentet lik 3/4 nøyaktig 2 ganger; Så resultatet av delingen kan skrives slik:
3 / 4: 3 / 8 = 2
La oss ta et eksempel til. La det være nødvendig å dele 15/16 med 3/32:
Vi kan resonnere slik: vi må finne et tall som, etter å ha blitt multiplisert med 3 / 32, vil gi et produkt lik 15 / 16. La oss skrive beregningene slik:
15 / 16: 3 / 32 = X
3 / 32 X = 15 / 16
3/32 ukjent nummer X gjøre opp 15/16
1/32 ukjent nummer X er ,
32 / 32 tall X sminke .
Derfor,
![]()
For å dele en brøk med en brøk, må du multiplisere telleren til den første brøken med nevneren til den andre, og multiplisere nevneren til den første brøken med telleren til den andre og gjøre det første produktet til telleren og det andre til nevneren.
La oss skrive regelen med bokstaver:
Ved deling er forkortelser mulige, for eksempel:
5. Deling av blandede tall.
Når du deler blandede tall, må de først konverteres til uekte brøker, og deretter skal de resulterende brøkene deles i henhold til reglene for deling av brøktall. Tenk på et eksempel:
Konverter blandede tall til uekte brøker:
![]()
La oss nå dele opp:
Derfor, for å dele blandede tall, må du konvertere dem til uekte brøker og deretter dele i henhold til regelen for å dele brøker.
6. Finne et tall gitt brøken.
Blant de forskjellige oppgavene på brøker er det noen ganger de der verdien av en brøkdel av et ukjent tall er gitt, og det kreves å finne dette tallet. Denne typen problemer vil være omvendt til problemet med å finne en brøkdel av et gitt tall; der ble det gitt et tall og det var nødvendig å finne en brøkdel av dette tallet, her er det gitt en brøkdel av et tall og det kreves for å finne dette tallet selv. Denne ideen vil bli enda tydeligere hvis vi vender oss til løsningen av denne typen problemer.
Oppgave 1. Den første dagen glaserte glassmestre 50 vinduer, som er 1/3 av alle vinduer i det bygde huset. Hvor mange vinduer er det i dette huset?
Løsning. Problemstillingen sier at 50 glassvinduer utgjør 1/3 av alle vinduene i huset, noe som betyr at det er 3 ganger flere vinduer totalt, d.v.s.
Huset hadde 150 vinduer.
Oppgave 2. Butikken solgte 1500 kg mel, som er 3/8 av det totale lageret av mel i butikken. Hva var butikkens opprinnelige tilførsel av mel?
Løsning. Av problemets tilstand kan man se at de solgte 1500 kg mel utgjør 3/8 av det totale lageret; dette betyr at 1/8 av denne beholdningen vil være 3 ganger mindre, dvs. for å beregne den, må du redusere 1500 med 3 ganger:
1.500:3 = 500 (dette er 1/8 av beholdningen).
Helt klart vil hele beholdningen være 8 ganger større. Derfor,
500 8 \u003d 4000 (kg).
Den opprinnelige tilførselen av mel i butikken var 4000 kg.
Fra vurderingen av dette problemet kan følgende regel utledes.
For å finne et tall med en gitt verdi av brøken, er det nok å dele denne verdien med telleren til brøken og multiplisere resultatet med brøkens nevner.
Vi løste to problemer ved å finne et tall gitt brøken. Slike problemer, som det er spesielt godt sett fra den siste, løses ved to handlinger: divisjon (når en del er funnet) og multiplikasjon (når hele tallet er funnet).
Men etter at vi har studert delingen av brøker, kan problemene ovenfor løses i én handling, nemlig: divisjon med en brøk.
For eksempel kan den siste oppgaven løses i en handling som dette:
I fremtiden vil vi løse problemet med å finne et tall ved brøken i en handling - divisjon.
7. Finne et tall etter prosentandelen.
I disse oppgavene må du finne et tall, og vite noen få prosent av dette tallet.
Oppgave 1. I begynnelsen av dette året mottok jeg 60 rubler fra sparebanken. inntekt fra beløpet jeg la inn i sparing for ett år siden. Hvor mye penger la jeg i sparebanken? (Kassekontorer gir innskytere 2 % av inntekten per år.)
Meningen med problemet er at en viss sum penger ble lagt av meg i en sparebank og ligget der i ett år. Etter et år mottok jeg 60 rubler fra henne. inntekt, som er 2/100 av pengene jeg legger inn. Hvor mye penger satte jeg inn?
Derfor, når vi kjenner delen av disse pengene, uttrykt på to måter (i rubler og i brøker), må vi finne hele, foreløpig ukjente, beløp. Dette er et vanlig problem med å finne et tall gitt brøken. Følgende oppgaver løses ved divisjon:
Så 3000 rubler ble satt inn i sparebanken.
Oppgave 2. På to uker oppfylte fiskerne månedsplanen med 64 %, etter å ha forberedt 512 tonn fisk. Hva var planen deres?
Fra tilstanden til problemet er det kjent at fiskerne fullførte en del av planen. Denne delen er lik 512 tonn, som er 64 % av planen. Hvor mange tonn fisk som skal slaktes etter planen, vet vi ikke. Løsningen av problemet vil bestå i å finne dette tallet.
Slike oppgaver løses ved å dele:
Så, i henhold til planen, må du forberede 800 tonn fisk.
Oppgave 3. Toget gikk fra Riga til Moskva. Da han passerte den 276. kilometeren spurte en av passasjerene den forbipasserende konduktøren hvor mye av reisen de allerede hadde tilbakelagt. Til dette svarte konduktøren: "Vi har allerede dekket 30 % av hele reisen." Hva er avstanden fra Moskva til Riga?
Det kan sees fra tilstanden til problemet at 30 % av reisen fra Riga til Moskva er 276 km. Vi må finne hele avstanden mellom disse byene, dvs. for denne delen, finne helheten:
§ 91. Gjensidige tall. Erstatte divisjon med multiplikasjon.
Ta brøken 2/3 og omorganiser telleren til stedet for nevneren, vi får 3/2. Vi har en brøkdel, den gjensidige av denne.
For å få en brøkdel som er gjensidig av en gitt, må du sette telleren i stedet for nevneren, og nevneren i stedet for telleren. På denne måten kan vi få en brøk som er den gjensidige av en hvilken som helst brøk. For eksempel:
3/4, omvendt 4/3; 5/6, omvendt 6/5
To brøker som har egenskapen at telleren til den første er nevneren til den andre og nevneren til den første er telleren til den andre kalles gjensidig omvendt.
La oss nå tenke på hvilken brøk som vil være den gjensidige av 1/2. Åpenbart vil det være 2/1, eller bare 2. På jakt etter det gjensidige av dette, fikk vi et heltall. Og denne saken er ikke isolert; tvert imot, for alle brøker med en teller på 1 (en), vil de gjensidige være heltall, for eksempel:
1/3, invers 3; 1/5, omvendt 5
Siden når vi fant resiproke, møtte vi også heltall, i fremtiden vil vi ikke snakke om resiproke, men om resiproke.
La oss finne ut hvordan du skriver den gjensidige av et helt tall. For brøker løses dette enkelt: du må sette nevneren i stedet for telleren. På samme måte kan du få det resiproke av et heltall, siden ethvert heltall kan ha en nevner på 1. Derfor vil den resiproke av 7 være 1 / 7, fordi 7 \u003d 7 / 1; for tallet 10 er det motsatte 1 / 10 siden 10 = 10 / 1
Denne ideen kan uttrykkes på en annen måte: gjensidigheten til et gitt tall oppnås ved å dele en med gitt nummer . Denne uttalelsen gjelder ikke bare for heltall, men også for brøker. Faktisk, hvis du vil skrive et tall som er det gjensidige av brøken 5/9, kan vi ta 1 og dele det med 5/9, dvs.

La oss nå peke ut en eiendom gjensidig gjensidige tall, som vil være nyttige for oss: produktet av gjensidige tall er lik en. Faktisk:
Ved å bruke denne egenskapen kan vi finne gjensidige på følgende måte. La oss finne den gjensidige av 8.
La oss betegne det med bokstaven X , deretter 8 X = 1, derfor X = 1/8. La oss finne et annet tall, inversen av 7/12, angi det med en bokstav X , deretter 7/12 X = 1, derfor X = 1:7 / 12 eller X = 12 / 7 .
Vi introduserte her begrepet gjensidige tall for å supplere informasjonen om brøkdelingen litt.
Når vi deler tallet 6 med 3/5, gjør vi følgende:
![]()
Vær spesielt oppmerksom på uttrykket og sammenlign det med det gitte: .
Hvis vi tar uttrykket separat, uten sammenheng med det forrige, er det umulig å løse spørsmålet om hvor det kom fra: fra å dele 6 med 3/5 eller fra å multiplisere 6 med 5/3. I begge tilfeller er resultatet det samme. Så vi kan si at å dele ett tall med et annet kan erstattes ved å multiplisere utbyttet med den gjensidige av divisoren.
Eksemplene som vi gir nedenfor bekrefter denne konklusjonen fullt ut.
For å riktig gange en brøk med en brøk eller en brøk med et tall, må du kjenne til enkle regler. Vi vil nå analysere disse reglene i detalj.
Å multiplisere en brøk med en brøk.
For å multiplisere en brøk med en brøk, må du beregne produktet av tellerne og produktet av nevnerne til disse brøkene.
\(\bf \frac(a)(b) \times \frac(c)(d) = \frac(a \times c)(b \times d)\\\)
Tenk på et eksempel:
Vi multipliserer telleren til den første brøken med telleren til den andre brøken, og vi multipliserer også nevneren til den første brøken med nevneren til den andre brøken.
\(\frac(6)(7) \times \frac(2)(3) = \frac(6 \times 2)(7 \times 3) = \frac(12)(21) = \frac(4 \times 3)(7 \times 3) = \frac(4)(7)\\\)
Brøken \(\frac(12)(21) = \frac(4 \times 3)(7 \times 3) = \frac(4)(7)\\\) er redusert med 3.
Multiplisere en brøk med et tall.
La oss starte med regelen ethvert tall kan representeres som en brøk \(\bf n = \frac(n)(1)\) .
La oss bruke denne regelen for multiplikasjon.
\(5 \times \frac(4)(7) = \frac(5)(1) \times \frac(4)(7) = \frac(5 \times 4)(1 \times 7) = \frac(20)(7) = 2\frac(6)(7)\\\)
Uekte brøken \(\frac(20)(7) = \frac(14 + 6)(7) = \frac(14)(7) + \frac(6)(7) = 2 + \frac(6)(7)= 2\frac(6)(7)\\\) ble konvertert til en blandet brøk.
Med andre ord, Når du multipliserer et tall med en brøk, multipliserer du tallet med telleren og lar nevneren stå uendret. Eksempel:
\(\frac(2)(5) \times 3 = \frac(2 \times 3)(5) = \frac(6)(5) = 1\frac(1)(5)\\\\\) \(\bf \frac(a)(b) \times c = \frac(a \times c)(b)\\\)
Multiplikasjon av blandede brøker.
For å multiplisere blandede brøker, må du først representere hver blandede brøk som en uekte brøk, og deretter bruke multiplikasjonsregelen. Telleren multipliseres med telleren, nevneren multipliseres med nevneren.
Eksempel:
\ (2 \ frac (1) (4) \ ganger 3 \ frac (5) (6) = \ frac (9) (4) \ ganger \ frac (23) (6) = \ frac (9 \ ganger 23) (3) (3) (3) (3) (3) (3) (3) (3) (3 \ times \ Times \ Times \ Times \ Times \ Times \ Times \ Times \ Times \ Color (Røde) (3 \ ganger (3 \ tider \ Times \ Times \ Times \ Times \ Times \ Times \ Fell) (3 \ ganger. (8) = 8 \ frac (5) (8) \\\)
Multiplikasjon av gjensidige brøker og tall.
Brøken \(\bf \frac(a)(b)\) er den inverse av brøken \(\bf \frac(b)(a)\), forutsatt a≠0,b≠0.
Brøkene \(\bf \frac(a)(b)\) og \(\bf \frac(b)(a)\) kalles resiproke. Produktet av gjensidige fraksjoner er 1.
\(\bf \frac(a)(b) \ ganger \frac(b)(a) = 1 \\\)
Eksempel:
\(\frac(5)(9) \ ganger \frac(9)(5) = \frac(45)(45) = 1\\\)
Relaterte spørsmål:
Hvordan multiplisere en brøk med en brøk?
Svar: produktet av vanlige brøker er multiplikasjonen av telleren med telleren, nevneren med nevneren. For å få produktet av blandede brøker, må du konvertere dem til en uekte brøk og multiplisere i henhold til reglene.
Hvordan multiplisere brøker med forskjellige nevnere?
Svar: det spiller ingen rolle om de er like eller ulike nevnere for brøker skjer multiplikasjon i henhold til regelen om å finne produktet av telleren med telleren, nevneren med nevneren.
Hvordan multiplisere blandede brøker?
Svar: Først av alt må du konvertere den blandede brøken til en uekte brøk og deretter finne produktet i henhold til reglene for multiplikasjon.
Hvordan multiplisere et tall med en brøk?
Svar: Vi multipliserer tallet med telleren, og lar nevneren være den samme.
Eksempel #1:
Beregn produktet: a) \(\frac(8)(9) \times \frac(7)(11)\) b) \(\frac(2)(15) \times \frac(10)(13)\)
Løsning:
a) \(\frac(8)(9) \times \frac(7)(11) = \frac(8 \times 7)(9 \times 11) = \frac(56)(99)\\\\\)
b) \(\frac(2)(15) \times \frac(10)(13) = \frac(2 \times 10)(15 \times 13) = \frac(2 \times 2 \times \color(red) (5))(3 \times \color(red) (5) \times 13)\(3)
Eksempel #2:
Regn ut produktet av et tall og en brøk: a) \(3 \ ganger \frac(17)(23)\) b) \(\frac(2)(3) \times 11\)
Løsning:
a) \(3 \times \frac(17)(23) = \frac(3)(1) \times \frac(17)(23) = \frac(3 \times 17)(1 \times 23) = \frac(51)(23) = 2\frac(5)(23)\\\\\)
b) \(\frac(2)(3) \times 11 = \frac(2)(3) \times \frac(11)(1) = \frac(2 \times 11)(3 \times 1) = \frac(22)(3) = 7\frac(1)(3)\)
Eksempel #3:
Skriv den gjensidige av \(\frac(1)(3)\)?
Svar: \(\frac(3)(1) = 3\)
Eksempel #4:
Regn ut produktet av to gjensidige brøker: a) \(\frac(104)(215) \times \frac(215)(104)\)
Løsning:
a) \(\frac(104)(215) \ ganger \frac(215)(104) = 1\)
Eksempel #5:
Kan gjensidig inverse brøker være:
a) begge egenbrøkene;
b) samtidig uekte fraksjoner;
c) naturlige tall samtidig?
Løsning:
a) La oss bruke et eksempel for å svare på det første spørsmålet. Brøken \(\frac(2)(3)\) er riktig, dens gjensidige vil være lik \(\frac(3)(2)\) - en uekte brøk. Svar: nei.
b) i nesten alle oppregninger av brøker er ikke denne betingelsen oppfylt, men det er noen tall som oppfyller betingelsen om å være en uekte brøk samtidig. For eksempel er uekte brøk \(\frac(3)(3)\), dens gjensidige er \(\frac(3)(3)\). Vi får to uekte brøker. Svar: ikke alltid under visse forhold, når teller og nevner er like.
c) naturlige tall er tallene vi bruker når vi teller for eksempel 1, 2, 3, .... Hvis vi tar tallet \(3 = \frac(3)(1)\), vil dets gjensidige være \(\frac(1)(3)\). Brøken \(\frac(1)(3)\) er ikke et naturlig tall. Hvis vi går gjennom alle tallene, er det resiproke alltid en brøk, bortsett fra 1. Hvis vi tar tallet 1, vil dets gjensidige være \(\frac(1)(1) = \frac(1)(1) = 1\). Tallet 1 er et naturlig tall. Svar: de kan være naturlige tall samtidig bare i ett tilfelle, hvis dette tallet er 1.
Eksempel #6:
Utfør produktet av blandede fraksjoner: a) \(4 \ ganger 2\frac(4)(5)\) b) \(1\frac(1)(4) \ ganger 3\frac(2)(7)\)
Løsning:
a) \(4 \times 2\frac(4)(5) = \frac(4)(1) \times \frac(14)(5) = \frac(56)(5) = 11\frac(1)(5)\\\\ \)
b) \(1\frac(1)(4) \times 3\frac(2)(7) = \frac(5)(4) \times \frac(23)(7) = \frac(115)(28) = 4\frac(3)(7)\)
Eksempel #7:
Kan to gjensidige tall være samtidig blandede tall?
La oss se på et eksempel. La oss ta en blandet brøk \(1\frac(1)(2)\), finne dens gjensidige, for å gjøre dette oversetter vi den til en uekte brøk \(1\frac(1)(2) = \frac(3)(2)\) . Dens gjensidighet vil være lik \(\frac(2)(3)\) . Brøken \(\frac(2)(3)\) er en egenbrøk. Svar: To gjensidig inverse brøker kan ikke være blandede tall samtidig.
I det femte århundre f.Kr. formulerte den antikke greske filosofen Zeno av Elea sine berømte aporier, den mest kjente av disse er aporien "Akilles og skilpadden". Slik høres det ut:La oss si at Akilles løper ti ganger raskere enn skilpadden og er tusen skritt bak den. I løpet av tiden Akilles løper denne distansen, kryper skilpadden hundre skritt i samme retning. Når Akilles har løpt hundre skritt, vil skilpadden krype ytterligere ti skritt, og så videre. Prosessen vil fortsette i det uendelige, Akilles vil aldri ta igjen skilpadden.
Dette resonnementet ble et logisk sjokk for alle påfølgende generasjoner. Aristoteles, Diogenes, Kant, Hegel, Gilbert... Alle av dem betraktet på en eller annen måte Zenons aporier. Sjokket var så sterkt at " ... diskusjoner fortsetter på det nåværende tidspunkt, det vitenskapelige samfunnet har ennå ikke klart å komme til en felles mening om essensen av paradokser ... matematisk analyse, settteori, nye fysiske og filosofiske tilnærminger var involvert i studiet av problemet; ingen av dem ble en universelt akseptert løsning på problemet ..."[Wikipedia," Zenos Aporias "]. Alle forstår at de blir lurt, men ingen forstår hva bedraget er.
Fra et matematisk synspunkt demonstrerte Zeno i sin aporia tydelig overgangen fra verdien til. Denne overgangen innebærer å bruke i stedet for konstanter. Så vidt jeg forstår, det matematiske applikasjonsapparatet variable enheter målingen er enten ikke utviklet ennå, eller så har den ikke blitt brukt på Zenos aporia. Anvendelsen av vår vanlige logikk fører oss inn i en felle. Vi, ved tenkingens treghet, bruker konstante tidsenheter på det gjensidige. Fra et fysisk synspunkt ser det ut som om tiden går langsommere til å stoppe helt i det øyeblikket Akilles tar igjen skilpadden. Hvis tiden stopper, kan ikke Akilles lenger innhente skilpadden.
Om vi snur logikken vi er vant til, faller alt på plass. Akilles løper med konstant hastighet. Hvert påfølgende segment av banen er ti ganger kortere enn den forrige. Følgelig er tiden brukt på å overvinne den ti ganger mindre enn den forrige. Hvis vi bruker begrepet "uendelighet" i denne situasjonen, så ville det være riktig å si "Akilles vil uendelig raskt overta skilpadden."
Hvordan unngå denne logiske fellen? Forbli i konstante tidsenheter og ikke bytt til gjensidige verdier. På Zenos språk ser det slik ut:
På tiden det tar Akilles å løpe tusen skritt, kryper skilpadden hundre skritt i samme retning. I løpet av neste tidsintervall, lik det første, vil Akilles løpe ytterligere tusen skritt, og skilpadden vil krype hundre skritt. Nå er Achilles åtte hundre skritt foran skilpadden.
Denne tilnærmingen beskriver virkeligheten tilstrekkelig uten noen logiske paradokser. Men dette er ikke en fullstendig løsning på problemet. Einsteins utsagn om lyshastighetens uoverkommelighet er veldig lik Zenos aporia «Akilles og skilpadden». Vi har ennå ikke studert, revurdert og løst dette problemet. Og løsningen må søkes ikke i uendelig store antall, men i måleenheter.
En annen interessant aporia av Zeno forteller om en flygende pil:
En flygende pil er ubevegelig, siden den i hvert øyeblikk er i ro, og siden den er i ro i hvert øyeblikk av tiden, er den alltid i ro.
I denne aporiaen logisk paradoks det overvinnes veldig enkelt - det er nok til å klargjøre at i hvert øyeblikk hviler den flygende pilen på forskjellige punkter i rommet, som faktisk er bevegelse. Det er et annet poeng å merke seg her. Fra ett fotografi av en bil på veien er det umulig å fastslå verken bevegelsen eller avstanden til den. For å fastslå bevegelsen til bilen er det nødvendig med to bilder tatt fra samme punkt på forskjellige tidspunkter, men de kan ikke brukes til å bestemme avstanden. For å bestemme avstanden til bilen trenger du to bilder tatt fra forskjellige punkter plass på et tidspunkt, men det er umulig å bestemme bevegelsen fra dem (naturligvis er det fortsatt behov for ytterligere data for beregninger, trigonometri vil hjelpe deg). Det jeg spesielt vil påpeke er at to punkter i tid og to punkter i rom er to forskjellige ting som ikke bør forveksles da de gir ulike muligheter for utforskning.
onsdag 4. juli 2018
Veldig bra er forskjellene mellom sett og multisett beskrevet i Wikipedia. Vi ser.
Som du ser kan "settet ikke ha to identiske elementer", men hvis det er identiske elementer i settet, kalles et slikt sett et "multiset". Fornuftige vesener vil aldri forstå en slik absurditetslogikk. Dette er nivået av snakkende papegøyer og trente aper, der sinnet er fraværende fra ordet "helt." Matematikere fungerer som vanlige trenere og forkynner sine absurde ideer for oss.
En gang i tiden var ingeniørene som bygde brua i en båt under brua under testene av brua. Hvis broen kollapset, døde den middelmådige ingeniøren under ruinene av sin skapelse. Hvis broen tålte belastningen, bygde den dyktige ingeniøren andre broer.
Uansett hvordan matematikere gjemmer seg bak frasen «pass på, jeg er i huset», eller rettere sagt «matematikk studerer abstrakte begreper», er det én navlestreng som uløselig forbinder dem med virkeligheten. Denne navlestrengen er penger. La oss anvende matematisk settteori på matematikere selv.
Vi studerte matematikk veldig bra, og nå sitter vi ved kassen og betaler lønn. Her kommer en matematiker til oss for pengene sine. Vi teller hele beløpet til ham og legger det ut på bordet vårt i forskjellige hauger, der vi legger sedler av samme valør. Så tar vi en regning fra hver bunke og gir matematikeren hans "matematiske lønnssett". Vi forklarer matematikken at han vil motta resten av regningene først når han beviser at mengden uten identiske elementer ikke er lik settet med identiske elementer. Det er her moroa begynner.
Først av alt vil varamedlemmenes logikk fungere: "du kan bruke det på andre, men ikke på meg!" Videre vil vi begynne å forsikre oss om at det er sedler med samme valør forskjellige tall regninger, noe som betyr at de ikke kan anses som identiske elementer. Vel, vi teller lønnen i mynter - det er ingen tall på myntene. Her vil matematikeren febrilsk huske fysikk: forskjellige mynter har forskjellige mengder skitt, krystallstrukturen og arrangementet av atomer for hver mynt er unik ...
Og nå har jeg mest interesse Spør: hvor går grensen utenfor hvilke elementer i et multisett som blir til elementer i et sett og omvendt? En slik linje eksisterer ikke - alt bestemmes av sjamaner, vitenskapen her er ikke engang i nærheten.
Se her. Vi velger fotballstadioner med samme feltareal. Arealet av feltene er det samme, noe som betyr at vi har et multisett. Men hvis vi vurderer navnene på de samme stadionene, får vi mye, fordi navnene er forskjellige. Som du kan se, er det samme settet med elementer både et sett og et multisett på samme tid. Hvor riktig? Og her tar matematikeren-sjaman-shulleren frem et trumf-ess fra ermet og begynner å fortelle oss om enten et sett eller et multisett. Uansett vil han overbevise oss om at han har rett.
For å forstå hvordan moderne sjamaner opererer med settteori og knytter den til virkeligheten, er det nok å svare på ett spørsmål: hvordan skiller elementene i ett sett fra elementene i et annet sett? Jeg vil vise deg, uten noen "tenkelig som ikke en enkelt helhet" eller "ikke tenkelig som en enkelt helhet."
Søndag 18. mars 2018
Summen av sifrene til et tall er en dans av sjamaner med en tamburin, som ikke har noe med matematikk å gjøre. Ja, i matematikktimene blir vi lært opp til å finne summen av sifrene til et tall og bruke det, men de er sjamaner for det, for å lære etterkommerne deres ferdigheter og visdom, ellers vil sjamanene ganske enkelt dø ut.
Trenger du bevis? Åpne Wikipedia og prøv å finne siden "Sum av siffer av et tall". Hun finnes ikke. Det er ingen formel i matematikk som du kan finne summen av sifrene til et hvilket som helst tall. Tross alt er tall grafiske symboler som vi skriver tall med, og på matematikkspråket høres oppgaven slik ut: «Finn summen av grafiske symboler som representerer et hvilket som helst tall». Matematikere kan ikke løse dette problemet, men sjamaner kan gjøre det elementært.
La oss finne ut hva og hvordan vi gjør for å finne summen av sifrene til et gitt tall. Og så, la oss si at vi har tallet 12345. Hva må gjøres for å finne summen av sifrene til dette tallet? La oss vurdere alle trinnene i rekkefølge.
1. Skriv ned tallet på et stykke papir. Hva har vi gjort? Vi har konvertert tallet til et tallgrafisk symbol. Dette er ikke en matematisk operasjon.
2. Vi kuttet ett mottatt bilde i flere bilder som inneholder separate tall. Å kutte et bilde er ikke en matematisk operasjon.
3. Konverter individuelle grafiske tegn til tall. Dette er ikke en matematisk operasjon.
4. Legg sammen de resulterende tallene. Nå er det matematikk.
Summen av sifrene til tallet 12345 er 15. Dette er "skjære- og sykursene" fra sjamaner brukt av matematikere. Men det er ikke alt.
Fra et matematisk synspunkt spiller det ingen rolle i hvilket tallsystem vi skriver tallet. Så inn ulike systemer utregning vil summen av sifrene i samme tall være forskjellig. I matematikk er tallsystemet angitt som et abonnent til høyre for tallet. Med et stort antall på 12345, vil jeg ikke lure hodet mitt, tenk på tallet 26 fra artikkelen om. La oss skrive dette tallet i binære, oktale, desimale og heksadesimale tallsystemer. Vi vil ikke vurdere hvert trinn under et mikroskop, det har vi allerede gjort. La oss se på resultatet.
Som du kan se, i forskjellige tallsystemer er summen av sifrene til samme tall forskjellig. Dette resultatet har ingenting med matematikk å gjøre. Det er som å finne arealet til et rektangel i meter og centimeter vil gi deg helt andre resultater.
Null i alle tallsystemer ser likt ut og har ingen tallsum. Dette er et annet argument for det faktum at . Et spørsmål til matematikere: hvordan betegnes det i matematikk som ikke er et tall? Hva, for matematikere, finnes det ikke annet enn tall? For sjamaner kan jeg tillate dette, men for forskere, nei. Virkeligheten handler ikke bare om tall.
Resultatet som oppnås bør betraktes som bevis på at tallsystemer er måleenheter for tall. Vi kan tross alt ikke sammenligne tall med ulike måleenheter. Hvis de samme handlingene med forskjellige måleenheter av samme mengde fører til forskjellige resultater etter å ha sammenlignet dem, så har det ingenting med matematikk å gjøre.
Hva er ekte matematikk? Dette er når resultatet av en matematisk handling ikke er avhengig av verdien av tallet, måleenheten som brukes, og hvem som utfører denne handlingen.
Åh! Er ikke dette dametoalettet?
- Ung kvinne! Dette er et laboratorium for å studere sjelenes ubestemte hellighet ved oppstigning til himmelen! Nimbus på toppen og pil opp. Hvilket annet toalett?
Kvinne... En glorie på toppen og en pil ned er hann.
Hvis du har et slikt designverk som blinker foran øynene dine flere ganger om dagen,
Da er det ikke overraskende at du plutselig finner et merkelig ikon i bilen din:
Personlig anstrenger jeg meg for å se minus fire grader hos en som bæser (ett bilde) (sammensetning av flere bilder: minustegn, nummer fire, gradersbetegnelse). Og jeg anser ikke denne jenta som en tosk som ikke kan fysikk. Hun har bare en bue stereotyp oppfatning av grafiske bilder. Og matematikere lærer oss dette hele tiden. Her er et eksempel.
1A er ikke "minus fire grader" eller "en a". Dette er "bajsende mann" eller tallet "tjueseks" i det heksadesimale tallsystemet. De menneskene som hele tiden jobber i dette tallsystemet, oppfatter automatisk tallet og bokstaven som ett grafisk symbol.