lar › Corpo › O projeto Diofanto e suas descobertas. Resumo: Diofanto

O projeto Diofanto e suas descobertas. Resumo: Diofanto

Coeficientes cujas soluções devem ser encontradas entre inteiros.

Diofanto de Alexandria
Διόφαντος ὁ Ἀλεξανδρεύς

Data de nascimento	nem antes nem depois ou
Local de nascimento	Alexandria, Egito
Data da morte	nem antes nem depois
Um país	Roma antiga
Campo científico	Teoria dos Números
Conhecido como	"pai da álgebra"
Diofanto de Alexandria no Wikimedia Commons

Biografia

Quase nada se sabe sobre os detalhes de sua vida. Por um lado, Diofanto cita Hípsicles (século II a.C.); por outro lado, Teão de Alexandria (cerca de 350 d.C.) escreve sobre Diofanto, do qual podemos concluir que a sua vida decorreu dentro dos limites deste período. Um possível esclarecimento sobre o tempo de vida de Diofanto baseia-se no fato de ele Aritmética dedicado ao “venerável Dionísio”. Acredita-se que este Dionísio não seja outro senão o bispo Dionísio de Alexandria, que viveu em meados do século III. n. e.

É equivalente a resolver a seguinte equação:

x = x 6 + x 12 + x 7 + 5 + x 2 + 4 (\displaystyle x=(\frac (x)(6))+(\frac (x)(12))+(\frac (x) (7))+5+(\frac(x)(2))+4)

Esta equação dá x = 84 (\estilo de exibição x=84), ou seja, a idade de Diofanto é igual a 84 anos. No entanto, a veracidade das informações não pode ser confirmada.

Aritmética Diofanta

A principal obra de Diofanto - Aritmética em 13 livros. Infelizmente, apenas 6 (ou 10, veja abaixo) dos primeiros 13 livros sobreviveram.

O primeiro livro é precedido por uma extensa introdução, que descreve a notação utilizada por Diofante. Diofanto chama o desconhecido de “número” ( ἀριθμός ) e é denotado pela letra ς , quadrado desconhecido - símbolo Δ Υ (abreviatura de δύναμις - “grau”), o cubo do desconhecido - símbolo Κ Υ (abreviatura de κύβος - “cubo”). Sinais especiais são fornecidos para os seguintes graus da incógnita, até o sexto, chamados cubo-cubo, e para seus graus opostos, até menos o sexto.

Diofanto não tem sinal de adição: ele simplesmente escreve termos positivos próximos uns dos outros em ordem decrescente de grau, e em cada termo é escrito primeiro o grau da incógnita e depois o coeficiente numérico. Os termos subtraídos também são escritos lado a lado, e um sinal especial na forma de uma letra Ψ invertida é colocado na frente de todo o grupo. O sinal de igual é representado por duas letras ἴσ (abreviatura de ἴσος - “igual”).

Foram formuladas uma regra para trazer termos semelhantes e uma regra para adicionar ou subtrair o mesmo número ou expressão a ambos os lados de uma equação: o que al-Khorezmi mais tarde começou a chamar de “álgebra e almukabala”. Foi introduzida a regra dos sinais: “menos por mais dá menos”, “menos por menos dá mais”; Esta regra é usada ao multiplicar duas expressões com termos subtraídos. Tudo isso é formulado em termos gerais, sem referência a interpretações geométricas.

A maior parte da obra é uma coleção de problemas com soluções (há um total de 189 nos seis livros sobreviventes, junto com os quatro da parte árabe - 290), habilmente selecionados para ilustrar métodos gerais. Questões principais Aritmética- encontrar soluções racionais positivas para equações incertas. Os números racionais são tratados por Diofanto da mesma forma que os números naturais, o que não é típico dos matemáticos antigos.

Primeiro, Diofanto examina sistemas de equações de segunda ordem em duas incógnitas; especifica um método para encontrar outras soluções, caso uma já seja conhecida. Em seguida, ele aplica métodos semelhantes a equações de graus superiores. O Livro VI examina problemas relacionados a triângulos retângulos com lados racionais.

Influência Aritmética para o desenvolvimento da matemática

No século 10 Aritmética foi traduzido para o árabe (ver Kusta ibn Luka), após o que matemáticos de países islâmicos (Abu Kamil e outros) continuaram algumas das pesquisas de Diofanto. Na Europa, o interesse em Aritmética aumentou depois que Raphael Bombelli traduziu e publicou esta obra para o latim, e publicou 143 problemas dela em seu Álgebra(1572). Em 1621, apareceu uma tradução latina clássica e minuciosamente comentada Aritmética, executado por Bachet de Meziriac.

Os métodos de Diofanto influenciaram muito François Viète e Pierre Fermat; entretanto, nos tempos modernos, as equações indefinidas são geralmente resolvidas em números inteiros, e não em números racionais, como fez Diofanto. Quando Pierre Fermat leu a Aritmética de Diofante, editada por Bachet de Mezyriac, chegou à conclusão de que uma das equações semelhantes às consideradas por Diofante não tinha soluções em números inteiros, e anotou na margem que havia encontrado "uma prova verdadeiramente maravilhosa de este teorema... no entanto, as margens do livro são estreitas demais para incluí-lo.” Esta afirmação é agora conhecida como Último Teorema de Fermat.

No século 20, o texto árabe de mais quatro livros foi descoberto sob o nome de Diofanto. Aritmética. I. G. Bashmakova e E. I. Slavutin, tendo analisado este texto, levantaram a hipótese de que seu autor não era Diofante, mas um comentarista bem versado nos métodos de Diofante, muito provavelmente Hipátia. No entanto, a lacuna significativa na metodologia de resolução de problemas nos três primeiros e nos três últimos livros é bem preenchida por quatro livros de tradução para o árabe. Isso nos obriga a reconsiderar os resultados de estudos anteriores. . [ ]

Outras obras de Diofanto

Tratado de Diofanto Sobre números poligonais (Περὶ πολυγώνων ἀριθμῶν ) não completamente preservado; na parte preservada, vários teoremas auxiliares são derivados usando métodos de álgebra geométrica.

Das obras de Diofanto Sobre medir superfícies (ἐπιπεδομετρικά ) E Sobre multiplicação (Περὶ πολλαπλασιασμοῦ ) também apenas fragmentos sobreviveram.

Livro de Diofanto Porismos conhecido apenas por alguns teoremas usados em Aritmética.

Veja também

Coleção Budé" (2 volumes publicados: Livros 4 - 7).

Pesquisar:

Bashmakova I.G., Slavutin E.I., Rosenfeld B.A. Versão árabe de “Aritmética” de Diofante // Estudos históricos e matemáticos. - M., 1978. - Edição. XXIII. - P. 192-225.
Bashmakova I.G. Aritmética das curvas algébricas: (De Diofanto a Poincaré) // Estudos históricos e matemáticos. - 1975. - Edição. 20. - páginas 104 - 124.
Bashmakova I.G. Equações de Diofanto e Diofantina. - M.: Nauka, 1972 (Reimpressão: M.: LKI, 2007). Por. Nele. linguagem: Diofante e diofantische Gleichungen. - Basileia; Estugarda: Birkhauser, 1974. Trad. Em inglês. linguagem: Equações de Diofanto e Diofantina/ Trad. por A. Shenitzer com a assistência editorial de H. Grant e atualizado por J. Silverman // The Dolciani Mathematical Expositions. - Nº 20. - Washington, DC: Mathematical Association of America, 1997.
Bashmakova I.G. Diofanto e Fermat: (Sobre a história do método das tangentes e extremos) // Estudos históricos e matemáticos. - M., 1967. - Edição. VII. - P. 185 - 204.
Bashmakova I. G., Slavutin E. I. História da análise diofantina de Diofanto a Fermat. - M.: Nauka, 1984.
História da matemática desde a antiguidade até o início do século XIX. - T.I: Dos mais antigos. vezes antes do início da Nova Era. tempo /Ed. AP Yushkevich. -M., Nauka, 1970.
Slavutin E.I. A álgebra de Diofante e suas origens // Estudos históricos e matemáticos. - M., 1975. - Edição. 20. - pp. 63 - 103.
Shchetnikov A. I. O livro “Sobre Números Poligonais” de Diofanto de Alexandria pode ser chamado de puramente algébrico? // Pesquisa histórica e matemática. - M., 2003. - Edição. 8 (43). - páginas 267-277.
Heath Th. EU. Diofanto de Alexandria, Um Estudo na História da Álgebra Grega. - Cambridge, 1910 (Repr.: NY, 1964).
Knorr W.R. Arithmktikê stoicheiôsis: Sobre Diofanto e o Herói de Alexandria // Historia Mathematica. - 20. - 1993. - P. 180 - 192.
Christianidis J. O caminho de Diofante: Alguns esclarecimentos sobre o método de solução de Diofante // Historia Mathematica. - 34. - 2007. - S. 289 - 305.
Rashed R., Houzel C. Les Arithmétiques de Diofante. Palestra histórica e matemática . -De Gruyter, 2013.

Instituição de ensino municipal

"Liceu No. 10" Permanente

Diofanto. Equações diofantinas

Feito o trabalho

Ilyina Yana,

aluno do 11º ano

Supervisor

Zolotukhina L.V.

professor de matemática

Permanente, 2010

Introdução………………………………………………………………………….3

1. Diofanto………………………………………………………………………………..…4

2. Números e símbolos……………………………………………………6

3. Equação diofantina…………………………………………..…8

4. Soluções………………………………………………………..12

Conclusão………………………………………………………………………………15

Referências………………………………………………………16

Introdução

Os alunos de hoje resolvem várias equações. Na Parte C das tarefas do Exame de Estado Unificado há uma equação interessante chamada equação Diofantina. Em suas obras, Diofanto não apenas apresentou o problema de resolver equações indefinidas em números racionais, mas também forneceu alguns métodos gerais para resolvê-las. Esses métodos serão muito úteis para os alunos do décimo primeiro ano que estão prestes a fazer o exame de matemática.

Diofanto deu uma contribuição tão grande para o desenvolvimento da matemática quanto Arquimedes. Foi o que fez Arquimedes, por exemplo: ao determinar as áreas de uma elipse, um segmento de parábola, a superfície de uma esfera, os volumes de uma esfera e outros corpos, utilizou o método das somas integrais e o método da passagem até o limite, mas em nenhum lugar ele deu uma descrição geral abstrata desses métodos. Os cientistas dos séculos 16 e 17 tiveram que estudar cuidadosamente e reorganizar suas obras de uma nova maneira, a fim de isolar daí os métodos de Arquimedes. A situação é semelhante com Diofanto. Seus métodos foram compreendidos e aplicados a novos problemas por Viethe e Fermat, ou seja, ao mesmo tempo em que Arquimedes foi resolvido.

1. Diofanto

Diofanto apresenta um dos mistérios mais difíceis da história da ciência. Não sabemos a época em que viveu, nem seus antecessores que teriam atuado na mesma área. Suas obras são como um fogo cintilante em meio a uma escuridão completamente impenetrável. O período de tempo em que Diofanto poderia ter vivido é de meio milênio! O limite inferior deste intervalo é determinado sem dificuldade: em seu livro sobre números poligonais, Diofante menciona repetidamente o matemático Hipscles de Alexandria, que viveu em meados do século II aC. e. Por outro lado, nos comentários de Téon de Alexandria ao “Almagesto” do famoso astrônomo Ptolomeu, é colocado um trecho da obra de Diofante. Theon viveu em meados do século 4 DC. e. Isso determina o limite superior deste intervalo. Então, 500 anos!

Mas o local de residência de Diofanto é bem conhecido - esta é a famosa Alexandria, o centro do pensamento científico do mundo helenístico.

Para esgotar tudo o que se sabe sobre a personalidade de Diofante, apresentamos um poema enigma que chegou até nós:

As cinzas de Diofanto repousam na tumba; maravilhe-se com ela - e com a pedra
A idade do falecido falará através de sua sábia arte.
Pela vontade dos deuses, ele viveu um sexto de sua vida quando criança.
E me encontrei às cinco e meia com penugem nas bochechas.
Foi apenas no sétimo dia que ele ficou noivo da namorada.
Depois de passar cinco anos com ela, o sábio esperou pelo filho;
O amado filho de seu pai viveu apenas metade de sua vida.
Ele foi tirado de seu pai por seu túmulo precoce.
Duas vezes, dois anos, o pai lamentou uma grande dor,
Aqui eu vi o limite da minha triste vida.

A partir daqui é fácil calcular que Diofanto viveu 84 anos. Porém, para isso você não precisa dominar a arte de Diofante! Basta poder resolver uma equação de 1º grau com uma incógnita, e os escribas egípcios conseguiram fazer isso há 2 mil anos aC. e.

Mas o mais misterioso é o trabalho de Diofanto. Chegaram até nós seis livros de 13, que foram combinados em “Aritmética”. O estilo e o conteúdo desses livros diferem nitidamente dos trabalhos clássicos antigos sobre teoria dos números e álgebra, exemplos dos quais conhecemos nos Elementos de Euclides, em seus Dados e nos lemas das obras de Arquimedes e Apolônio. A "Aritmética" foi sem dúvida o resultado de numerosos estudos que nos permaneceram completamente desconhecidos. Só nos resta adivinhar as suas raízes e maravilhar-nos com a riqueza e a beleza dos seus métodos e resultados.

“Aritmética” de Diofanto é uma coleção de problemas (são 189 no total), cada um dos quais equipado com uma solução (ou vários métodos de solução) e as explicações necessárias. Portanto, à primeira vista parece que não se trata de um trabalho teórico. No entanto, uma leitura atenta mostra que os problemas são cuidadosamente selecionados e servem para ilustrar métodos muito específicos e rigorosamente pensados. Como era habitual nos tempos antigos, os métodos não são formulados de forma geral, mas são repetidos para resolver problemas semelhantes.

2. Números e símbolos

Diofanto começa com definições básicas e uma descrição dos símbolos das letras que usará.

Na matemática grega clássica, que encontrou sua conclusão nos Elementos de Euclides, sob o número άριJμός - “ arritmia" ou " aritmos"; daí o nome “aritmética” para a ciência dos números) era entendido como um conjunto de unidades, ou seja, inteiro. Nem frações nem irracionalidade eram chamadas de números. A rigor, não existem frações nos Principia. A unidade é considerada indivisível e em vez de frações de uma unidade, são consideradas proporções de inteiros; as irracionalidades aparecem como razões de segmentos incomensuráveis, por exemplo, o número que agora denotamos √2 era para os gregos clássicos a razão entre a diagonal de um quadrado e o seu lado. Não se falava em números negativos. Não havia sequer equivalentes para eles. Encontramos uma imagem completamente diferente em Diofanto.

Diofanto dá a definição tradicional de número como um conjunto de unidades, mas depois procura para seus problemas racional positivo soluções, e chama cada solução de um número (άριJμός - “ arritmia »).

Mas o assunto não para por aí. Diofanto introduz números negativos: ele os chama de termo especial λει̃ψις - “ leipsis" - derivado do verbo λει̃πω - " leipo”, que significa faltar, faltar, de modo que o próprio termo poderia ser traduzido pela palavra “falta”. A propósito, é isso que faz o famoso historiador da ciência russo I. Timchenko. Diofanto chama um número positivo de palavra ΰπαρξις - “ iparxis”, que significa existência, ser, e no plural esta palavra pode significar propriedade ou propriedade. Assim, a terminologia de Diofanto para números relativos é próxima daquela usada na Idade Média no Oriente e na Europa. Muito provavelmente, foi simplesmente uma tradução do grego para o árabe, sânscrito, latim e depois para várias línguas da Europa.

Observe que o termo λει̃ψις é “ leipsis" - não pode ser traduzido como "subtraído", como fazem muitos tradutores de Diofanto, porque para a operação de subtração Diofante usa termos completamente diferentes, nomeadamente άφελει̃ν - " afelein"ou άφαιρει̃ν -" chuva de fogo", que são derivados do verbo άφαιρεω - " afireo"- remover. Ao transformar equações, o próprio Diofanto costuma usar a expressão padrão “adicione λει̃ψις a ambos os lados”.

Detivemo-nos detalhadamente na análise filológica do texto de Diofante para convencer o leitor de que não nos desviaremos da verdade se traduzirmos os termos de Diofante como “positivos” e “negativos”.

Diofanto formula a regra dos sinais para números relativos:

“um negativo multiplicado por um negativo dá um positivo, enquanto um negativo multiplicado por um positivo dá um negativo, e o sinal distintivo de um negativo é um ψ invertido e abreviado.”

“Depois que expliquei a multiplicação para vocês, a divisão dos termos propostos também fica clara; Agora será bom começar a praticar a adição, subtração e multiplicação desses termos. Adicione termos positivos e negativos com coeficientes diferentes a outros termos que sejam positivos ou igualmente positivos e negativos, e de termos positivos e outros termos negativos subtraia outros termos positivos e igualmente positivos e negativos.

Observe que embora Diofanto busque apenas soluções racionais positivas, em cálculos intermediários ele usa voluntariamente números negativos.

Podemos assim notar que Diofanto expandiu o campo numérico para um campo de números racionais no qual todas as quatro operações aritméticas podem ser realizadas sem obstáculos.

3. Equação diofantina

Definição - equações algébricas ou sistemas de equações algébricas com coeficientes inteiros, tendo um número de incógnitas superior ao número de equações, e para os quais se procuram soluções inteiras ou racionais.

machado + por = 1

Onde A E b- inteiros coprimos

Números coprimos vários inteiros tais que os divisores comuns para todos esses números sejam apenas + 1 e - 1. O menor múltiplo de um par de números primos é igual ao seu produto.

tem infinitas soluções:

Se x0 E y0- uma solução, depois os números

X = x0 + bilhões

no = y0 -um

(n- qualquer número inteiro) também serão soluções.

Outro exemplo de D. você.

x2 + y2 = z2

Soluções inteiras positivas para esta equação representam os comprimentos das pernas X , no e hipotenusa z triângulos retângulos com comprimentos laterais inteiros são chamados de números pitagóricos.

triplos de números naturais tais que um triângulo cujos comprimentos laterais são proporcionais (ou iguais) a esses números seja retangular.

Todos os trigêmeos de números pitagóricos coprimos podem ser obtidos usando as fórmulas

X = m2 - n2

no = 2homem

z = m2 + n2

Onde eu E n- números inteiros ( eu > n > 0).

Esta equação define no plano R 2 algébrico curvaΓ. Chamaremos a solução racional (2) ponto racional curva Γ. A seguir, recorreremos frequentemente à linguagem da geometria, embora o próprio Diofanto não a utilize em lugar nenhum. No entanto, a linguagem geométrica tornou-se agora uma parte tão integrante do pensamento matemático que muitos factos serão mais fáceis de compreender e explicar com a sua ajuda.

Em primeiro lugar, é necessário dar alguma classificação às equações (2) ou, o que dá no mesmo, às curvas algébricas. O mais natural e mais precoce a surgir é a sua classificação por ordem.

Lembremos que em ordem curva (2) é a ordem máxima dos termos do polinômio f (x , sim), onde a ordem de um termo é entendida como a soma dos poderes em x E sim. O significado geométrico deste conceito é que uma linha reta cruza uma curva de ordem n exatamente em n pontos. Ao contar pontos, é claro que deve-se levar em consideração a multiplicidade de pontos de intersecção, bem como pontos complexos e “infinitamente distantes”. Então, por exemplo, um círculo x 2 + sim 2 = 1 e direto x + sim= 2 se cruzam em dois pontos complexos, e a hipérbole x 2 – sim 2 = 1 e direto sim =x- em dois pontos no infinito, a mesma hipérbole com uma linha reta x=1 tem um ponto comum de multiplicidade 2.

Contudo, para efeitos análise diofantina(este nome foi dado ao campo da matemática que surgiu dos problemas de resolução de equações indeterminadas; no entanto, agora é mais frequentemente chamado de geometria diofantina) a classificação por ordem revelou-se muito grosseira.

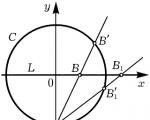
Arroz. 1.

Vamos explicar isso com um exemplo. Deixe um círculo ser dado C : x 2 + sim 2 = 1 e qualquer linha reta com coeficientes racionais, por exemplo, eu : sim=0. Vamos mostrar que os pontos racionais deste círculo e da reta podem ser colocados em uma correspondência biunívoca. Isso pode ser feito, por exemplo, assim: fixe o ponto A(0,–1) círculos e atribua cada ponto racional B direto eu apontar B" círculo C, deitado no cruzamento C e liso AB(Figura 1). Que as coordenadas do ponto B" será racional, deixaremos que o leitor prove por si mesmo ou leia uma prova semelhante de Diofanto (será apresentada no próximo parágrafo). Obviamente, a mesma correspondência pode ser estabelecida entre os pontos racionais de qualquer seção cônica, se nela repousar pelo menos um ponto racional, e uma reta racional. Vemos que do ponto de vista da análise diofantina o círculo C e liso eu são indistinguíveis: seus conjuntos de soluções racionais são equivalentes. E isto apesar de as ordens de ambas as curvas serem diferentes.

Mais sutil é a classificação das curvas algébricas por gênero, introduzida apenas no século XIX por Abel e Riemann. Esta classificação leva em consideração o número de pontos singulares da curva Γ.

Assumimos que na equação (2) da curva Γ o polinômio f (x , sim) é irredutível no corpo dos números racionais, ou seja, não se expande para um produto de polinômios com coeficientes racionais. Como se sabe, a equação da tangente à curva Γ no ponto P (x 0 , sim 0) vai

sim – sim 0 = k (x – x 0),

k = –

efeitos especiais" (x 0 , sim 0)

fy" (x 0 , sim 0)

Se no ponto P derivado efeitos especiais" ou fy"é diferente de zero, então a inclinação k tangente tem um significado muito definido (se fy" (x 0 , sim 0) = 0, uma efeitos especiais" (x 0 , sim 0) ≠ 0, então k=∞ e tangente em P será vertical).

Se no ponto P ambas as derivadas parciais desaparecem,

efeitos especiais" (x 0 , sim 0) = 0 e fy" (x 0 , sim 0) = 0,

então aponte P chamado especial .

Por exemplo, na curva sim 2 = x 2 + x 3 pontos (0, 0) serão especiais, pois nele efeitos especiais" = –2x – 3x 2 e fy" = 2sim vá para zero.

Arroz. 2.

Os pontos singulares mais simples são os duplos, nos quais pelo menos uma das derivadas fxx "" , f xy "" E aaa ""é diferente de zero. Na Fig. A Figura 2 mostra um ponto duplo onde a curva possui duas tangentes diferentes. Outros pontos singulares mais complexos são mostrados na Fig. 3.

Arroz. 3.

4. Soluções

Regra 1. Se c não é divisível por d, então a equação ax + vy = c não tem soluções em números inteiros. NOD(a,b) = d.

Regra 2. Para encontrar uma solução para a equação ax + vy = c com coprime a e b, você deve primeiro encontrar uma solução (X o; y o) para a equação ax + y = 1; os números CX o, Su o formam uma solução para a equação ax + vy = c.

Resolva a equação em números inteiros (x,y)

5x - 8y = 19... (1)

Primeira maneira. Encontrar uma solução particular usando o método de seleção e registrar a solução geral.

Sabemos que se N.O.D.(a;b) =1, ou seja, aeb são números primos, então equação (1)

tem uma solução em inteiros x e y. NOD(5;8) =1. Usando o método de seleção encontramos uma solução particular: X o = 7; eo =2.

Portanto, o par de números (7;2) é uma solução particular da equação (1).

Isso significa que a igualdade é válida: 5 x 7 – 8 x 2 = 19… (2)

Pergunta: Como, dada uma solução, anotar todas as outras soluções?

Vamos subtrair a igualdade (2) da equação (1) e obter: 5(x -7) – 8(y - 2) =0.

Portanto x – 7 = . Da igualdade resultante fica claro que o número (x – 7) será um número inteiro se e somente se (y – 2) for divisível por 5, ou seja, y – 2 = 5n, onde n é algum número inteiro. Então, y = 2 + 5n, x = 7 + 8n, onde n Z.

Assim, todas as soluções inteiras da equação original podem ser escritas da seguinte forma:

Segunda via . Resolvendo uma equação para uma incógnita.

Resolvemos esta equação em relação à incógnita que possui o menor coeficiente (módulo). 5x - 8y = 19 x = .

Restos quando dividido por 5: 0,1,2,3,4. Vamos substituir esses números por y.

Se y = 0, então x = =.

Se y = 1, então x = =.

Se y = 2, então x = = = 7 Z.

Se y = 3, então x = =.

Se y = 4 então x = =.) Conclusão

Enquanto isso, a maioria dos historiadores da ciência, ao contrário dos matemáticos, até agora subestimou as obras de Diofanto. Muitos deles acreditavam que Diofanto se limitava a encontrar apenas uma solução e utilizava para isso técnicas artificiais, diferentes para problemas diferentes. Mas, na verdade, na maioria das equações diofantinas observamos algoritmos de solução semelhantes.

Hoje, como vemos, existem várias soluções diferentes, cujos algoritmos são fáceis de lembrar. Conforme mencionado anteriormente, esta equação geralmente é encontrada na tarefa C6 do Exame Estadual Unificado. O estudo de algoritmos para resolução de equações diofantinas pode ajudar na resolução desta tarefa, que vale um número significativo de pontos.

Bibliografia

1. Diofanto de Alexandria. Aritmética e um livro sobre números poligonais (tradução do grego antigo por I. N. Veselovsky; edição e comentários de I. G. Bashmakova). M., “Ciência”, 1974.

2. BL Van der Waerden, Awakening Science (tradução de I. N. Veselovsky). M., Fizmatgiz, 1959.

3. G. G. Tseyten, História da matemática na antiguidade e na Idade Média (tradução de P. Yushkevich). M.–L., Gostekhizdat, 1932

4. A. V. Vasiliev, inteiro. Petersburgo, 1919

5. I. V. Yashchenko, S. A. Shestakov, P. I. Zakharov, Matemática, Exame de Estado Unificado, MTsNMO, 2010

Diofanto de Alexandria(grego antigo Διόφαντος ὁ Ἀλεξανδρεύς ; lat. Diofanto) é um matemático grego antigo que provavelmente viveu no século III dC. e. Muitas vezes referido como o "pai da álgebra". Autor de "Aritmética" - um livro dedicado a encontrar soluções racionais positivas para equações indeterminadas. Hoje em dia, “equações diofantinas” geralmente significam equações com coeficientes inteiros, cujas soluções devem ser encontradas entre números inteiros.

Biografia [ | ]

Tradução latina Aritmética (1621)

É equivalente a resolver a seguinte equação:

x = x 6 + x 12 + x 7 + 5 + x 2 + 4 (\displaystyle x=(\frac (x)(6))+(\frac (x)(12))+(\frac (x) (7))+5+(\frac(x)(2))+4)

Esta equação dá x = 84 (\estilo de exibição x=84), ou seja, a idade de Diofanto é igual a 84 anos. No entanto, a veracidade das informações não pode ser confirmada.

Aritmética Diofanta[ | ]

A principal obra de Diofanto - Aritmética em 13 livros. Infelizmente, apenas 6 (ou 10, veja abaixo) dos primeiros 13 livros sobreviveram.

Influência Aritmética para o desenvolvimento da matemática[ | ]

No século 10 Aritmética foi traduzido para o árabe, após o que matemáticos de países islâmicos (Abu Kamil e outros) continuaram algumas das pesquisas de Diofanto. Na Europa, o interesse em Aritmética aumentou depois que Raphael Bombelli traduziu e publicou esta obra para o latim, e publicou 143 problemas dela em seu Álgebra(1572). Em 1621, apareceu uma tradução latina clássica e minuciosamente comentada Aritmética, executado por Bachet de Meziriac.

Outras obras de Diofanto[ | ]

Das obras de Diofanto Sobre medir superfícies (ἐπιπεδομετρικά ) E Sobre multiplicação (Περὶ πολλαπλασιασμοῦ ) também apenas fragmentos sobreviveram.

Livro de Diofanto Porismos conhecido apenas por alguns teoremas usados em Aritmética.

Na seção sobre a questão de onde morava Diofanto, feita pelo autor Lera... a melhor resposta é Diofanto - (final do século III dC) - famoso matemático grego antigo.
Quase não há informações sobre sua vida; mesmo as datas de seu nascimento e morte não são totalmente confiáveis.
Viveu na cidade egípcia de Alexandria.
A atividade de Diofanto coincidiu com o declínio da Grécia, conquistada – como se sabe – por Roma.
Os cientistas gregos encontraram refúgio no Egito, principalmente em Alexandria, que naquela época já havia se tornado o centro da cultura mundial.
Uma magnífica biblioteca foi criada em Alexandria, que na época de Diofante havia se tornado o centro da cultura mundial e das humanidades; a chamada biblioteca surgiu em Alexandria. Museion (templo ou santuário das musas), onde se concentravam as atividades dos mais destacados representantes das ciências naturais e matemáticas.
Entre esses cientistas estava Diofanto, um matemático que, graças ao seu conhecimento de matemáticos sírios e indianos, transferiu as conquistas dos babilônios no campo da álgebra para a ciência grega.

Resposta de Alexandre[guru]
todos os matemáticos da Grécia

Resposta de contribuir[novato]
A julgar pelo fato de ser Diofanto de Alexandria, ele viveu em Alexandria (no território do Egito moderno) no século III dC. Presumivelmente, as datas de sua vida: nascido - 325, falecido - 409 DC

Resposta de Furar[novato]
Diofanto de Alexandria?
Matemático romano antigo
Um antigo matemático grego que supostamente viveu no século III DC. e. Muitas vezes referido como o "pai da álgebra". Autor de "Aritmética" - um livro dedicado a encontrar soluções racionais positivas para equações indeterminadas. Hoje em dia, “equações diofantinas” geralmente significam equações com coeficientes inteiros, cujas soluções devem ser encontradas entre números inteiros.

Os polvos têm 8 patas, as estrelas do mar têm 5.

Quantos animais marinhos existem no aquário se houver 39 membros no total?

Diofanto de Alexandria é um antigo matemático grego que provavelmente viveu no século III DC.

Quase nada se sabe sobre os detalhes de sua vida. Por um lado, Diofanto cita Hípsicles (século II a.C.); por outro lado, Teão de Alexandria (cerca de 350 d.C.) escreve sobre Diofanto, do qual podemos concluir que a sua vida decorreu dentro dos limites deste período. Um possível esclarecimento sobre a época da vida de Diofanto baseia-se no fato de sua “Aritmética” ser dedicada ao “venerável Dionísio”. Acredita-se que este Dionísio não seja outro senão o bispo Dionísio de Alexandria, que viveu em meados do século III. n. e.

A Antologia Palatina contém uma tarefa de epigrama da qual podemos concluir que Diofanto viveu 84 anos:

As cinzas de Diofanto repousam na tumba; maravilhe-se com ela e a pedra

A idade do falecido falará através de sua sábia arte.

Pela vontade dos deuses, ele viveu um sexto de sua vida quando criança.

E me encontrei às cinco e meia com penugem nas bochechas.

Pouco depois do sétimo dia, ele ficou noivo da namorada.

Depois de passar cinco anos com ela, o sábio teve um filho;

O amado filho de seu pai viveu apenas metade de sua vida.

Ele foi tirado de seu pai por seu túmulo precoce.

Duas vezes, dois anos, o pai lamentou uma grande dor,

Aqui eu vi o limite da minha triste vida.

Usando métodos modernos de resolução de equações, é possível calcular quantos anos Diofante viveu. Vamos criar e resolver a equação:

A solução para esta equação é o número 84. Assim, Diofanto viveu 84 anos.

A principal obra de Diofanto é “Aritmética” em 13 livros. Infelizmente, apenas os primeiros 6 livros de 13 sobreviveram.

O primeiro livro é precedido por uma extensa introdução, que descreve a notação utilizada por Diofante. Diofanto chama o desconhecido de “número” (?ριθμ?ς) e o denota com a letra ς, o quadrado do desconhecido com um símbolo (abreviação de δ?ναμις - “grau”). Sinais especiais são fornecidos para os seguintes graus da incógnita, até o sexto, chamados de cubo-cubo, e para os graus opostos a eles. Diofanto não tem sinal de adição: ele simplesmente escreve termos positivos próximos uns dos outros, e em cada termo é escrito primeiro o grau da incógnita e depois o coeficiente numérico. Os termos subtraídos também são escritos lado a lado, e um sinal especial na forma de uma letra Ψ invertida é colocado na frente de todo o grupo. O sinal de igual é denotado por duas letras ?σ (abreviação de ?σος - “igual”). Foram formuladas a regra para trazer termos semelhantes e a regra para adicionar ou subtrair o mesmo número ou expressão a ambos os lados da equação: o que al-Khwarizmi mais tarde veio a chamar de “al-jabr e al-muqabala”. Foi introduzida uma regra de sinal: menos vezes menos dá mais; Esta regra é usada ao multiplicar duas expressões com termos subtraídos. Tudo isso é formulado em termos gerais, sem referência a interpretações geométricas.

A maior parte da obra é uma coleção de problemas com soluções (há um total de 189 nos seis livros sobreviventes), habilmente selecionados para ilustrar métodos gerais. O principal problema da "Aritmética" é encontrar soluções racionais positivas para equações indeterminadas. Os números racionais são interpretados por Diofanto da mesma forma que os números naturais, o que não é típico dos matemáticos antigos.

Primeiro, Diofanto examina sistemas de equações de 2ª ordem em 2 incógnitas; especifica um método para encontrar outras soluções, caso uma já seja conhecida. Em seguida, ele aplica métodos semelhantes a equações de graus superiores.

No século X, “Aritmética” foi traduzida para o árabe, após o que matemáticos de países islâmicos (Abu Kamil e outros) continuaram algumas das pesquisas de Diofanto. Na Europa, o interesse pela Aritmética aumentou depois que Raphael Bombelli descobriu esta obra na Biblioteca do Vaticano e publicou 143 problemas dela em sua Álgebra (1572). Em 1621, apareceu uma tradução latina clássica e minuciosamente comentada de “Aritmética”, realizada por Bachet de Meziriak. Os métodos de Diofanto tiveram uma enorme influência em François Viète e Pierre Fermat; serviu de ponto de partida para os estudos de Gauss e Euler. Porém, nos tempos modernos, as equações indefinidas costumam ser resolvidas em números inteiros, e não em números racionais, como fez Diofanto.

No século XX, sob o nome de Diofanto, foi descoberto o texto árabe de mais 4 livros de Aritmética. Alguns historiadores da matemática, após analisarem este texto, levantaram a hipótese de que o seu autor não foi Diofanto, mas sim um comentador versado nos métodos de Diofante, muito provavelmente Hipátia.

O tratado de Diofanto “Sobre Números Poligonais” (Περ? πολυγ?νων ?ριθμ?ν) não foi completamente preservado; na parte preservada, vários teoremas auxiliares são derivados usando métodos de álgebra geométrica.

Das obras de Diofanto “Sobre a medição de superfícies” (?πιπεδομετρικ?) e “Sobre a multiplicação” (Περ? πολλαπλασιασμο?) apenas fragmentos também foram preservados.

O livro "Porismos" de Diofanto é conhecido apenas por alguns teoremas usados em aritmética.

Hoje a equação é da forma

Onde P- uma função inteira (por exemplo, um polinômio com coeficientes inteiros), e as variáveis assumem valores inteiros, chamados em homenagem ao antigo matemático grego - Diofantino.

Provavelmente a equação diofantina mais famosa é

Suas soluções são trigêmeos pitagóricos: (3; 4; 5), (6; 8; 10), (5; 12; 13), (12; 35; 37)…

Prova da insolubilidade em números inteiros da equação Diofantina

no (Último Teorema de Fermat) foi concluído pelo matemático inglês Andrew Wiles em 1994.

Outro exemplo de equação diofantina é a equação de Pell

onde está o parâmetro n não é um quadrado exato.

O décimo problema de Hilbert é um dos 23 problemas que David Hilbert propôs em 8 de agosto de 1900 no Segundo Congresso Internacional de Matemáticos. No relatório de Hilbert, a formulação do décimo problema é a mais curta de todas:

Seja dada uma equação diofantina com incógnitas arbitrárias e coeficientes numéricos racionais inteiros. Indique um método pelo qual seja possível, após um número finito de operações, determinar se esta equação é solucionável em números inteiros racionais.

A prova da insolubilidade algorítmica deste problema levou cerca de vinte anos e foi concluída por Yuri Matiyasevich em 1970.

Em grande parte graças às atividades de Pappus de Alexandria (século III), informações sobre cientistas antigos e seus trabalhos chegaram até nós. Depois de Apolônio (a partir do século II aC), começou um declínio na ciência antiga. Nenhuma nova ideia profunda aparece. Em 146 AC. e. Roma captura a Grécia e em 31 AC. e. - Alexandria. Contra o pano de fundo de estagnação e declínio geral, a figura gigantesca de Diofanto de Alexandria, o último dos grandes matemáticos antigos, o “pai da álgebra”, destaca-se nitidamente.

Os seguintes objetos matemáticos têm o nome de Diofanto: