Hem › Motor › Konstruktion av sektioner av polyedrar. Forskningsarbete på ämnet "Metoder för att konstruera sektioner av polyedrar"

Konstruktion av sektioner av polyedrar. Forskningsarbete på ämnet "Metoder för att konstruera sektioner av polyedrar"

Själva uppgiften brukar se ut så här: "skapa en naturlig bild av sektionsfiguren". Naturligtvis bestämde vi oss för att inte lämna denna fråga åt sidan och försöka, om möjligt, förklara hur den sneda sektionen är uppbyggd.

För att förklara hur en sned sektion är uppbyggd ska jag ge några exempel. Naturligtvis kommer jag att börja med det elementära, gradvis öka komplexiteten i exemplen. Jag hoppas att du efter att ha analyserat dessa exempel på sektionsritningar kommer att förstå hur detta går till och att du själv kan slutföra din inlärningsuppgift.

Tänk på en "tegelsten" med dimensioner 40x60x80 mm med ett godtyckligt lutande plan. Skärplanet skär den längs punkterna 1-2-3-4. Jag tror att allt är klart här.

Låt oss gå vidare till konstruktionen av en naturlig form av tvärsnittsfiguren.
1. Låt oss först och främst rita sektionens axel. Axeln ska dras parallellt med sektionsplanet - parallellt med linjen som planet projiceras i på huvudvyn - vanligtvis är det på huvudvyn som uppgiften är inställd på konstruktion av en sned sektion(Längre fram kommer jag alltid att nämna huvudvyn, med tanke på att detta nästan alltid är fallet i träningsritningar).
2. På axeln avsätter vi längden på sektionen. På min ritning är den betecknad som L. Storleken L bestäms i huvudvyn och är lika med avståndet från den punkt där sektionen går in i delen till den punkt där den går ut.
3. Från de resulterande två punkterna på axeln vinkelrät mot den avsätter vi sektionsbredderna vid dessa punkter. Bredden på sektionen vid ingångspunkten i delen och vid utgångspunkten från delen kan bestämmas i ovanifrån. I det här fallet båda segmenten 1-4 och 2-3 är lika med 60 mm. Som du kan se från bilden ovan är kanterna på sektionen raka, så vi kopplar helt enkelt ihop våra två resulterande segment och får en rektangel 1-2-3-4. Detta är - den naturliga vyn av figuren av delen av vår tegelsten med ett lutande plan.

Låt oss nu komplicera vår detalj. Låt oss sätta en tegelsten på basen 120x80x20 mm och lägga till förstyvningar till figuren. Låt oss rita ett skärplan så att det passerar genom alla fyra elementen i figuren (genom basen, tegelstenen och två förstyvningar). På bilden nedan kan du se tre vyer och en realistisk bild av denna del.

Låt oss försöka bygga en naturlig bild av denna lutande sektion. Låt oss börja om med sektionsaxeln: rita den parallellt med sektionsplanet som anges på huvudvyn. På den avsätter vi längden på sektionen lika med A-E. Punkt A är ingångspunkten för sektionen i delen, och i ett särskilt fall, ingångspunkten för sektionen till basen. Utgångspunkten från basen är punkt B. Låt oss markera punkt B på sektionens axel. På samma sätt markerar vi ingångs-utgångspunkterna till kanten, till "tegelstenen" och till den andra kanten. Från punkterna A och B vinkelräta mot axeln avsätter vi segment lika med basens bredd (på varje sida av axeln, 40, endast 80 mm). Ansluta extrema punkter- vi får en rektangel, som är en naturlig bild av delen av delens bas.

Nu är det dags att bygga en sektion, som är en sektion av delens kant. Från punkterna B och C lägger vi åt sidan vinkelräta 5 mm i varje riktning - vi får segment på 10 mm. Anslut de yttersta punkterna och få tvärsnittet av revbenet.

Från punkterna C och D avsätter vi vinkelräta segment som är lika med bredden på "tegelstenen" - helt liknande det första exemplet på denna lektion.

Efter att ha avsatt vinkelrätorna från punkterna D och E lika med bredden på den andra kanten och anslutit de extrema punkterna, får vi en naturlig bild av dess sektion.

Det återstår att radera byglarna mellan de enskilda elementen i den resulterande sektionen och tillämpa kläckning. Du borde få något sånt här:

Om vi delar upp figuren enligt ett givet avsnitt, kommer vi att se följande vy:

Jag hoppas att du inte blir skrämd av de tråkiga styckena i beskrivningen av algoritmen. Om du har läst allt ovan och fortfarande inte helt förstår, hur man ritar ett tvärsnitt, jag rekommenderar starkt att du tar ett papper och en penna i dina händer och försöker upprepa alla steg efter mig - detta kommer nästan 100% att hjälpa dig att lära dig materialet.

En gång lovade jag fortsättning på denna artikel. Slutligen är jag redo att presentera dig med en steg-för-steg-konstruktion av en sned del av en del, närmare läxornas nivå. Dessutom är den sneda sektionen definierad i den tredje vyn (den sneda sektionen definieras i den vänstra vyn)

eller skriv ner vårt telefonnummer och berätta för dina vänner om oss - någon letar förmodligen efter ett sätt att göra ritningar

eller skapa en anteckning om våra lektioner på din sida eller blogg - så kommer någon annan att kunna bemästra teckningen.

Ja, allt är bra, men jag skulle vilja se hur man gör samma sak på en mer komplex del, till exempel med avfasningar och ett konformat hål.

Tack. Men kläcks inte förstyvningarna på skären?
Exakt. Det är de som inte kläcks. För att de är generella regler gör nedskärningar. Men de kläcks vanligtvis när man gör snitt i axonometriska projektioner - isometri, dimetri, etc. När du utför lutande sektioner är området som är relaterat till förstyvningen också skuggat.

Tack, mycket lättillgängligt. Kan du berätta för mig om den sneda sektionen kan göras i toppvyn, eller i vyn till vänster? I så fall skulle jag vilja se det enklaste exemplet. Snälla.

Det är möjligt att göra sådana nedskärningar. Men jag har tyvärr inget exempel till hands just nu. Och det finns en till intressant punkt: å ena sidan är det inget nytt där, men å andra sidan är det i praktiken verkligen svårare att rita sådana sektioner. Av någon anledning börjar allt bli förvirrat i huvudet och de flesta elever har det svårt. Men ge inte upp!

Ja, allt är bra, men jag skulle vilja se hur samma sak görs, men med hål (genom och icke-genom), annars förvandlas de aldrig till en ellips i mitt huvud

hjälpa mig med ett komplext problem

Det är synd att du skrev här. Vi skulle skriva på posten – vi kanske skulle hinna diskutera allt.

Du förklarar bra. Vad händer om en av sidorna av delen är halvcirkelformig? Dessutom finns det hål i delen.

Ilya, använd lektionen från avsnittet om beskrivande geometri "Sektion av en cylinder med ett lutande plan". Med den kan du ta reda på vad du ska göra med hål (de är faktiskt också cylindrar) och med en halvcirkelformad sida.

Jag tackar författaren för artikeln!Kort och begriplig. För cirka 20 år sedan gnagde jag själv på vetenskapens granit, nu hjälper jag min son. Jag glömde mycket, men din artikel gav en grundläggande förståelse av ämnet. Jag ska ta itu med den lutande delen av cylindern.

Lägg till din kommentar.

Planimetrins axiom:

I olika läroböcker kan egenskaperna hos linjer och plan presenteras på olika sätt, i form av ett axiom, en konsekvens av det, en sats, ett lemma, etc. Tänk på läroboken Pogorelov A.V.

Den räta linjen delar planet i två halvplan.

Från vilken halvlinje som helst till ett givet halvplan kan man ta bort en vinkel med en given gradsmått, mindre än 180 0 , och bara en.

Oavsett triangel finns det en lika stor triangel på en given plats med avseende på den givna halvlinjen.

Genom en punkt som inte ligger på en given linje kan högst en linje dras i planet parallellt med den givna linjen.

Stereometrins axiom:

Oavsett plan finns det punkter som tillhör detta plan, och punkter som inte tillhör detta plan, och punkter som inte tillhör det.

Om två olika plan har en gemensam punkt, så skär de sig längs en rät linje som går genom denna punkt.

Om två olika linjer har en gemensam punkt, kan ett plan dras genom dem, och dessutom bara en.

Oavsett linje finns det punkter som hör till denna linje och punkter som inte hör till den.

Genom två valfria punkter kan du dra en linje, och bara en.

Av de tre punkterna på en linje ligger en och bara en mellan de andra två.

Varje segment har en viss längd som är större än noll. Längden på ett segment är lika med summan av längderna på de delar som det delas i med någon av dess punkter.

En rät linje som hör till ett plan delar detta plan i två halvplan.

Varje vinkel har ett visst mått som är större än noll. Den raka vinkeln är 180 0 . Gradmåttet för en vinkel är lika med summan av gradmåtten för de vinklar som den är uppdelad i av en stråle som passerar mellan dess sidor.

På vilken halvlinje som helst från dess startpunkt kan du skjuta bort ett segment med en given längd, och bara ett.

Från en halvlinje på planet som innehåller den kan en vinkel med ett givet gradmått mindre än 180 ritas in i ett givet halvplan 0 , och bara en.

Oavsett triangel finns det en lika stor triangel i det givna planet på en given plats i förhållande till den givna halvlinjen i det planet.

I ett plan, genom en given punkt som inte ligger på en given linje, kan högst en linje parallell med den givna linjen dras.

tvärsnitt

I rymden kan två figurer, för vårt fall, ett plan och en polyeder ha följande inbördes arrangemang: skärs inte, skär varandra i en punkt, skär i en rät linje och planet skär polyedern längs dess inre (fig. 1) , och bildar samtidigt följande figurer:

a) en tom figur (korsas inte)

b) punkt

c) skär

d) polygon

Om det finns en polygon i skärningspunkten mellan en polyeder och ett plan, då denna polygonkallas en sektion av en polyeder med ett plan .

figur 1

Definition. tvärsnitt en rumslig kropp (till exempel en polyeder) är en figur som erhålls vid skärningen av en kropp med ett plan.

skärplan polyeder Låt oss kalla vilket plan som helst, på vars båda sidor det finns punkter för en given polyeder.

Vi kommer endast att överväga fallet när planet skär polyhedronen längs dess inre. I det här fallet kommer skärningen av detta plan med varje yta av polyedern att vara ett visst segment.

Om planen skär varandra i en rät linje, så kallas den räta linjenfrån ett av dessa plan till ett annat.

I det allmänna fallet skär en polyeders sekantplan planet för var och en av dess ytor (liksom alla andra sekantplan för denna polyeder). Den skär också var och en av linjerna på vilka kanterna på polyedern ligger.

Linjen längs vilken sekantplanet skär planet för vilken yta av polyedern som helst kallasefter skärplanet på denna ytas plan, och punkten där sekantplanet skär linjen som innehåller någon kant på polyedern kallasefter skärplanet pådenna raka linje. Denna punkt är också spåret av en rak linje på skärplanet. Om skärplanet direkt skär polyederns yta, kan vi prata om spåret av skärplanet på ytan, och på liknande sätt omspår av ett skärplan på en kant av en polyeder, det vill säga spåret av en kant på ett skärplan.

Eftersom en rät linje bestäms unikt av två punkter, räcker det att konstruera två gemensamma punkter för planen för att hitta spåret av ett sekantplan på vilket annat plan som helst och i synnerhet på planet för vilken yta av en polyeder som helst.

För att konstruera ett spår av ett sekantplan, såväl som för att konstruera en sektion av en polyeder med detta plan, måste inte bara polyedern, utan även sekantplanet specificeras. Och konstruktionen av sektionsplanet sker beroende på tilldelningen av detta plan. De huvudsakliga sätten att definiera ett plan, och i synnerhet ett sekantplan, är följande:

tre punkter som inte ligger på en rak linje;

en rak linje och en punkt som inte ligger på den;

två parallella linjer;

två korsande linjer;

en punkt och två skärande linjer;

Det finns andra sätt att definiera skärplanet.

Därför kan alla metoder för att konstruera sektioner av polyedrar delas in i metoder.

Metoder för att konstruera sektioner av polyedrar

Metoden för sektioner av polyedrar i stereometri används i konstruktionsproblem. Det är baserat på förmågan att bygga en sektion av en polyeder och bestämma typen av sektion.

Det finns tre huvudmetoder för att konstruera sektioner av polyedrar:

Axiomatisk metod:

spårningsmetod.

Kombinerad metod.

koordinatmetod.

Notera att metoden för spår och metoden för hjälpsektioner är varieteterAxiomatisk metod för att konstruera sektioner.

Vi kan också särskilja följande metoder för att konstruera sektioner av polyedrar:

konstruktion av en sektion av en polyeder av ett plan som passerar genom en given punkt parallell med ett givet plan;

konstruktion av en sektion som går genom en given linje parallell med en annan given linje;

konstruktion av en sektion som går genom en given punkt parallellt med två givna snedställda linjer;

konstruktion av en sektion av en polyeder med ett plan som går genom en given linje vinkelrät mot ett givet plan;

konstruktion av en sektion av en polyeder med ett plan som går genom en given punkt vinkelrät mot en given rät linje.

De viktigaste åtgärderna som utgör metoderna för att konstruera sektioner är att hitta skärningspunkten för en rät linje med ett plan, konstruera en skärningslinje för två plan, konstruera en rät linje parallell med ett plan vinkelrätt mot planet. För att konstruera en rät skärningslinje mellan två plan hittas vanligtvis två av dess punkter och en rät linje dras genom dem. För att konstruera skärningspunkten för en linje och ett plan, hitta en linje i planet som skär det givna planet. Därefter erhålls den önskade punkten vid skärningspunkten mellan den hittade linjen och den givna.

Överväg separat listad av ossmetoder för att konstruera sektioner av polyedrar:

spårningsmetod.

spårningsmetod baseras (manövreras) på stereometrins axiom, är essensen av metoden att konstruera en hjälplinje, som är bilden av skärningslinjen för skärplanet med planet för vilken yta av figuren som helst. Det är mest praktiskt att bygga en bild av skärningslinjen för skärplanet med planet för den nedre basen. Den här radenkallas huvudspåret av skärplanet . Med hjälp av spåret är det lätt att konstruera bilder av skärplanets punkter som ligger på sidokanterna eller ytorna på figuren. Genom att konsekvent ansluta bilderna av dessa punkter får vi bilden av den önskade sektionen.

Notera att när man konstruerar huvudspåret för sekantplanet används följande påstående.

Om punkterna tillhör sekantplanet och inte ligger på en rät linje, och deras projektion (central eller parallell) på det plan som valts som huvudplan är respektive punkterna då skärningspunkterna för motsvarande linjer, det vill säga punkterna och ligger på samma linje (fig. 1, a, b).

fig.1.a fig.1.b

Denna linje är huvudspåret av skärplanet. Eftersom punkterna ligger på huvudspåret räcker det att hitta två av dessa tre punkter för att konstruera det.

Metod för hjälpsektioner.

Denna metod för att konstruera sektioner av polyedrar är tillräckligt universell. I de fall där det önskade spåret (eller spåren) av skärplanet ligger utanför ritningen, har denna metod till och med vissa fördelar. Samtidigt bör man komma ihåg att de konstruktioner som utförs med denna metod ofta visar sig vara "fulla". I vissa fall visar sig metoden med hjälpsektioner vara den mest rationella.

Kombinerad metod

Kärnan i den kombinerade metoden för att konstruera sektioner av polyedrar är tillämpningen av satser om parallelliteten mellan linjer och plan i rymden i kombination med den axiomatiska metoden.

Koordinatmetod för att konstruera sektioner.

Kärnan i koordinatmetoden är att beräkna koordinaterna för skärningspunkterna för kanter eller en polyeder med ett sekantplan, vilket ges av planets ekvation. Sektionsplanets ekvation beräknas utifrån problemets förhållanden.

Notera att denna metod för att konstruera en sektion av en polyeder är acceptabel för en dator, eftersom den är förknippad med en stor mängd beräkningar och därför är det tillrådligt att implementera denna metod med hjälp av en dator.

Vår huvuduppgift blir att konstruera en sektion av en polyeder med ett plan, d.v.s. vid konstruktionen av skärningspunkten mellan dessa två uppsättningar.

Konstruktion av sektioner av polyedrar

Först och främst noterar vi att sektionen av en konvex polyeder är en konvex platt polygon, vars hörn i det allmänna fallet är skärningspunkterna för sekantplanet med polyederns kanter och sidorna med dess ytor.

Exempel på att skapa avsnitt:

Det finns många olika sätt att definiera ett avsnitt. Den vanligaste av dessa är metoden att specificera ett skärplan med tre punkter som inte ligger på en rät linje.

Exempel 1 För box ABCDA 1 B 1 C 1 D 1 . Konstruera ett snitt som går genom punkterna M, N, L.

Lösning:

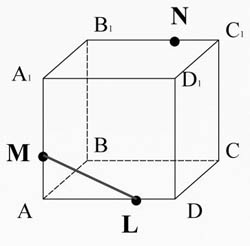
Anslut punkterna M och L som ligger i planet AA 1 D 1 D.

Skär linjen ML (tillhör sektionen) med kanten A 1 D 1 1 D 1 D. Få punkt X 1 .

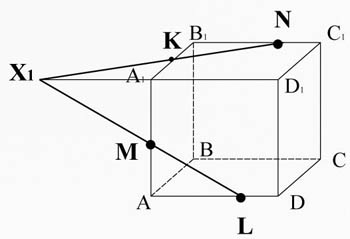
Punkten X1 ligger på kanten A 1 D 1 , och därav planen A 1 B 1 C 1 D 1 , anslut den med en punkt N som ligger i samma plan.

X 1 N skär kant A 1 B 1 vid punkt K.

Anslut punkterna K och M som ligger i samma plan AA 1 B 1 b.

Hitta skärningslinjen för snittplanet med planet DD 1 C 1 C:

Skär linjen ML (tillhör sektionen) med kanten DD 1 , de ligger i samma plan AA 1 D 1 D, få punkt X 2 .

Låt oss skära linjen KN (tillhör sektionen) med kanten D 1 C 1 , de ligger i samma plan A 1 B 1 C 1 D 1 , vi får punkten X3;

Punkterna X2 och X3 ligger i planet DD 1 C 1 C. Rita en linje X 2 X 3 , som skär kanten C 1 C i punkten T, och kanten DC i punkten P. Och låt oss koppla ihop punkterna L och P, som ligger i planet ABCD.

Således anses problemet vara löst om alla segment längs vilka planet skär polyederns ytor hittas, vilket vi gjorde. MKNTPL - önskat avsnitt.

Notera. Samma uppgift för att konstruera en sektion kan lösas med hjälp av egenskapen parallella plan.

Av ovanstående kan vi komponera en algoritm (regel) för att lösa problem av denna typ.

Regler för att konstruera sektioner av polyedrar:

Exempel 2 DL, M

Vi löser med den axiomatiska metoden:

Rita ett hjälpplanDKM, som skär kanterna AB och BC i punkterna E ochF(lösningens förlopp är i fig. 2.). Låt oss bygga ett "spår" av CM för sektionsplanet på detta hjälpplan, hitta skärningspunkten för CM och EF- punkt P. Punkt P, samtL, ligger i planet ABC, och det är möjligt att dra en rät linje längs vilken sektionsplanet skär planet ABC ("spår" av snittet i planet ABC).

Exempel 3 På kanterna AB och AD på pyramiden MABCD sätter vi punkterna P respektive Q, mittpunkterna på dessa kanter, och på kanten MC sätter vi punkten R. Låt oss konstruera en sektion av pyramiden genom att ett plan passerar genom punkterna P, Q och R.

Lösningen kommer att utföras med en kombinerad metod:

1). Det är tydligt att huvudspåret för planet PQR är linjen PQ.

2). Hitta punkten K där MAC-planet skär linjen PQ. Punkterna K och R tillhör både PQR-planet och MAC-planet. Därför, genom att dra den räta linjen KR, får vi skärningslinjen för dessa plan.

3). Låt oss hitta punkten N=AC BD, dra linjen MN och hitta punkten F=KR MN.

4). Punkt F är gemensam punkt planen PQR och MDB, det vill säga dessa plan skär längs en rät linje som går genom punkten F. Samtidigt, eftersom PQ är mittlinjen i triangeln ABD, så är PQ parallell med BD, det vill säga linjen PQ är också parallellt med planet MDB. Sedan skär planet PQR som passerar genom linjen PQ planet MDB längs linjen parallell med linjen PQ, det vill säga parallellt med linjen BD. Därför drar vi i planet MDB genom punkten F en linje parallell med linjen BD.

5). Ytterligare konstruktioner framgår tydligt av figuren. Som ett resultat får vi polygonen PQD"RB" - den nödvändiga sektionen

Tänk på sektionerna av prismat För enkelhetens skull, det vill säga bekvämligheten med logiskt tänkande, överväg sektionerna av kuben (Fig. 3.a):

Ris. 3.a

Sektioner av prismat med plan parallella med sidokanterna är parallellogram. I synnerhet är diagonala sektioner parallellogram (fig. 4).

Def. diagonal sektion ett prisma är ett snitt av ett plan som går genom två sidokanter som inte hör till samma yta.

Polygonen som härrör från en diagonal sektion av ett prisma är ett parallellogram. Fråga om antalet diagonala sektionern-vinkelprisma är svårare än frågan om antalet diagonaler. Det kommer att finnas lika många sektioner som det finns diagonaler vid basen. Vi vet att ett konvext prisma har konvexa polygoner vid sina baser, medan ett konvext prisman-gon av diagonaler. Och så kan vi säga att det finns hälften så många diagonala sektioner som det finns diagonaler.

Notera: När man konstruerar sektioner av en parallellepiped i figuren bör man ta hänsyn till det faktum att om skärplanet skär två motsatta ytor längs vissa segment, så är dessa segment parallella "med egenskapen hos parallellepipeden, dvs. Motsatta ytor av en parallellepiped är parallella och lika.

Vi ger svar på vanliga frågor:

Vilka polygoner erhålls i sektionen av en kub av ett plan?

"triangel, fyrhörning, femhörning, hexagon".

Kan ett plan tvärsnitt av en kub producera en heptagon? Och oktagonen?

"kan inte".

3) Frågan uppstår, vilket är det största antalet sidor av en polygon som erhålls av en sektion av en polyeder med ett plan?

Största antalet sidorna av polygonen som erhålls i sektionen av polyedern av planet är lika med antalet ytor på polyhedronen .

Exempel 3 Konstruera en sektion av prisma A 1 B 1 C 1 D 1 ABCD av ett plan som passerar genom tre punkter M, N, K.

Betrakta fallet med placeringen av punkterna M, N, K på ytan av ett prisma (Fig. 5).

Tänk på fallet: I det här fallet är det uppenbart att M1 = B1.

Byggnad:

Exempel 4 Konstruera en sektion av parallellepiped ABCDA 1 B 1 C 1 D 1 ett plan som går genom punkterna M, N, P (punkterna anges på ritningen (fig. 6)).

Lösning:

Ris. 6

Punkterna N och P ligger i sektionens plan och i planet för den nedre basen av parallellepipeden. Låt oss konstruera en linje som går genom dessa punkter. Denna linje är spåret av sekantplanet på planet för basen av parallellepipeden.

Låt oss fortsätta den linje på vilken sidan AB av parallellepipeden ligger. Linjerna AB och NP skär varandra vid någon punkt S. Denna punkt tillhör snittplanet.

Eftersom även punkten M tillhör sektionsplanet och skär linjen AA 1 någon gång x.

Punkterna X och N ligger i samma plan av ytan AA 1 D 1 D, anslut dem och få linjen XN.

Eftersom planen på parallellepipedens ytor är parallella är det möjligt att dra en rät linje genom punkten M i ytan A 1 B 1 C 1 D 1 parallellt med linjen NP. Denna linje kommer att skära sida B 1 MED 1 vid punkt Y.

På samma sätt ritar vi linjen YZ, parallell med linjen XN. Vi kopplar samman Z med P och får önskad sektion - MYZPNX.

Delar av pyramiden av plan som passerar genom dess topp är trianglar. I synnerhet diagonala sektioner är trianglar. Dessa är sektioner av plan som passerar genom två icke intilliggande sidokanter av pyramiden.

Exempel 4 Konstruera ett avsnitt av pyramiden ABCDett plan som passerar genom punkterna K,L, M.

Lösning:

Låt oss lösa samma exempel annorlunda. .

Låt oss anta att för punkterna K,L, och М avsnittetKLNM(Fig. 7). Beteckna medFskärningspunkten för fyrhörningens diagonalerKLNM. Låt oss rita en rak linjeD.F.och beteckna medF 1 dess skärningspunkt med ansikte ABC. PunktF 1 sammanfaller med skärningspunkten mellan linjerna AM och SK (F 1 tillhör samtidigt planen AMDOchDSC). punktF 1 lätt att bygga. Därefter bygger vi en punktFsom en skärningspunktD.F. 1 OchLM. Därefter hittar vi poängenN.

Metoden som övervägs kallasintern designmetod . (För vårt fall vi pratar om central design. fyrsidigKISA är projektionen av en fyrhörningKMNLfrån en punktD. I detta fall skärningspunkten för diagonalernaKMNL- prickF- går till skärningspunkten för fyrhörningens diagonalerKISA - prickF 1 .

Sektionsarea av en polyeder.

Problemet med att beräkna tvärsnittsarean för en polyeder löses vanligtvis i flera steg. Om problemet säger att sektionen är byggd (eller att skärplanet är ritat, etc.), så upptäcks i det första steget av lösningen formen på figuren som erhålls i sektionen.

Detta måste göras för att välja lämplig formel för beräkning av tvärsnittsarean. Efter att formen på figuren som erhålls i avsnittet har förtydligats och formeln för att beräkna arean av denna figur har valts, fortsätter de direkt till beräkningsarbetet.

I vissa fall kan det visa sig vara lättare om vi, utan att ta reda på formen på figuren som erhålls i avsnittet, omedelbart fortsätter med att beräkna dess area med hjälp av formeln som följer av satsen.

Satsen om arean av den ortogonala projektionen av en polygon: arean av den ortogonala projektionen av en polygon på ett plan är lika med produkten av dess area och cosinus för vinkeln mellan polygonens plan och projektionsplanet: .

En giltig formel för att beräkna tvärsnittsarean är: var är arean för den ortogonala projektionen av figuren som erhålls i sektionen, och är vinkeln mellan sekantplanet och planet på vilket figuren projiceras. Med en sådan lösning är det nödvändigt att konstruera en ortogonal projektion av figuren som erhålls i sektionen och beräkna

Om tillståndet för problemet säger att sektionen måste byggas och området för den erhållna sektionen ska hittas, är det i det första skedet rimligt att bygga den givna sektionen och sedan naturligtvis bestämma formen på den i avsnittet erhållna siffran m.m.

Vi noterar följande faktum: eftersom sektioner av konvexa polyedrar är konstruerade, kommer sektionspolygonen också att vara konvex, så dess area kan hittas genom att dela upp den i trianglar, det vill säga sektionsarean är lika med summan av arean av trianglar som den är sammansatt av.

Uppgift 1.

– korrekt triangulär pyramid med en bassida lika med och lika med en höjd Konstruera en sektion av pyramiden med ett plan som går genom punkterna, där är sidans mittpunkt, och hitta dess area (fig. 8).

Lösning.

Pyramidens tvärsnitt är en triangel. Låt oss hitta dess område.

Eftersom basen av pyramiden är en liksidig triangel och punkten är mittpunkten på sidan, då är det höjden och sedan, .

Arean av en triangel kan hittas:

Uppgift 2.

Sido revben av ett vanligt prisma är lika med sidan av basen. Konstruera sektioner av ett prisma av plan som passerar genom en punktA, vinkelrätt mot linjen Om du hittar arean av den resulterande sektionen av prismat.

Lösning.

Låt oss konstruera det givna avsnittet. Låt oss göra detta utifrån rent geometriska överväganden, till exempel enligt följande.

I ett plan som går genom en given linje och en given punkt, drar vi en linje genom denna punkt vinkelrätt mot linjen (fig. 9). Låt oss använda för detta ändamål det faktum att i triangeln det vill säga dess median är också höjden på denna triangel. Alltså en rak linje.

Genom punkten ritar vi en annan linje vinkelrätt mot linjen. Låt oss rita det till exempel i ett plan som går genom en rät linje. Det är tydligt att denna linje är en linje

Så två skärande linjer, vinkelräta mot linjen, konstrueras. Dessa linjer definierar ett plan som går genom en punkt vinkelrät mot linjen, det vill säga ett sekantplan ges.

Vi konstruerar en sektion av prismat vid detta plan. Observera att eftersom linjen är parallell med planet. Sedan skär planet som passerar genom linjen planet längs en linje parallell med linjen, det vill säga linjen. Rita en rak linje genom punkten och anslut den resulterande punkten med en prick.

Fyrhörning given sektion. Låt oss bestämma dess område.

Det är tydligt att en fyrhörning är en rektangel, det vill säga dess area

ris. 9

KONSTRUKTION AV SEKTIONER OCH SEKTIONER PÅ RITNINGAR

Ritningen av delen bildas genom att sekventiellt lägga till nödvändiga utsprång, snitt och sektioner. Inledningsvis skapas en anpassad vy med en användarspecificerad modell, och modellorienteringen ställs in så att den passar huvudvyn bäst. Vidare skapas nödvändiga snitt och sektioner för denna och följande typer.

Huvudvyn (framifrån) är vald på ett sådant sätt att den ger den mest kompletta uppfattningen om delens former och dimensioner.

Sektioner i ritningar

Beroende på skärplanets position särskiljs följande typer av skärningar:

A) horisontellt, om skärplanet är parallellt med det horisontella projektionsplanet;

B) vertikalt, om skärplanet är vinkelrätt mot det horisontella projektionsplanet;

C) lutande - skärplanet lutar mot projektionsplanen.

Vertikala sektioner är indelade i:

· frontal - skärplanet är parallellt med frontprojektionsplanet;

· profil - skärplanet är parallellt med profilprojektionsplanet.
Beroende på antalet skärplan är skärningarna:

· enkel - med ett skärplan (Fig. 107);

· komplex - med två eller flera skärplan (Fig. 108)
Standarden tillhandahåller följande typer av komplexa snitt:

· stegvis, när sekantplanen är parallella (fig. 108 a) och streckade linjer - skär sekantplanen (fig. 108 b)

Fig.107 Enkelt snitt

A) b)

Fig.108 Komplexa snitt

Beteckning på snitt

I det fall då sekantplanet i en enkel sektion sammanfaller med objektets symmetriplan, indikeras inte sektionen (fig. 107). I alla andra fall indikeras sektionerna med stora bokstäver i det ryska alfabetet, som börjar med bokstaven A, till exempel A-A.

Läget för skärplanet på ritningen indikeras av snittlinjen - en förtjockad öppen linje. Med ett komplext snitt utförs också slag vid sektionslinjens böjningar. Pilar som anger synriktningen ska placeras på de första och sista slagen, pilarna ska vara på ett avstånd av 2-3 mm från de yttre ändarna av slagen. På utsidan av varje pil som anger siktriktningen, är samma stor bokstav applicerad.

Samma knapp används för att markera snitt och sektioner i KOMPAS-systemet Sektionslinje finns på sidan för teckenförklaring (fig.109).

Fig.109 Sektionslinjeknapp

Ansluter halvvy till halvsektion

Om vyn och sektionen är symmetriska figurer (bild 110) kan du koppla ihop hälften av vyn och hälften av sektionen, separera dem med en streckprickad tunn linje, som är symmetriaxeln. En del av sektionen är vanligtvis placerad till höger om symmetriaxeln som skiljer den del av vyn från delen av sektionen, eller under symmetriaxeln. Dolda konturlinjer på de sammankopplade delarna av vyn och snittet visas vanligtvis inte. Om den axiella linjen som skiljer vyn och sektionen sammanfaller med projiceringen av någon linje, till exempel kanten på en facetterad figur, är vyn och sektionen åtskilda av en heldragen våglinje som dras till vänster om symmetriaxeln om kanten ligger på den inre ytan, eller till höger om kanten är yttre .

Ris. 110 Koppla samman del av en vy och en sektion

Byggnadsnedskärningar

Vi kommer att studera konstruktionen av sektioner i KOMPAS-systemet med hjälp av exemplet att konstruera en ritning av ett prisma, vars uppgift visas i Fig. 111.

Ritningssekvensen är som följer:

1. Av givna dimensioner låt oss bygga en solid modell av ett prisma (bild 109 b). Låt oss spara modellen i datorns minne i en fil som heter "Prism".

Fig.112 Linjer panel

3. Att bygga en profilsektion (bild 113) dra ett streck sektion A-A på huvudvyn med knappen Snittlinje.

Fig.113 Konstruktion av en profilsektion

Synriktningen och beteckningens text kan väljas på kontrollpanelen med kommandot längst ner på skärmen (bild 114). Konstruktionen av sektionslinjen slutförs genom att trycka på knappen Skapa objekt.

Fig.114 Kontrollpanel för kommandot för att konstruera snitt och sektioner

4. På panelen Associativa vyer (Fig. 115), välj knappen Klipp linje och ange sedan skärlinjen med fällan som visas på skärmen. Om allt är gjort korrekt (klipplinjen måste ritas i den aktiva vyn), så blir skärlinjen röd. Efter att ha specificerat skärlinjen A-A kommer en bildfantom att dyka upp på skärmen i form av en övergripande rektangel.

Fig.115 Associativa vyer panel

Med hjälp av knappen Klipp/snitt på egenskapsfältet väljs bildtyp - Klipp ut (Fig. 116) och skalan för det visade snittet.

Fig.116 Kontrollpanel för kommandot för att konstruera snitt och sektioner

Profilsektionen kommer att byggas automatiskt i projektionsanslutningen och med standardnotation. Vid behov kan projektionsanslutningen stängas av med strömbrytaren Projektionsanslutning (Fig. 116). För att ställa in kläckningsparametrar som kommer att användas i den skapade sektionen (sektionen), använd kontrollerna på fliken Kläckning.

Fig.117 Konstruktion av en horisontell sektion B-B och sektion C-C

Om det valda skärplanet vid konstruktion av snittet sammanfaller med delens symmetriplan, är ett sådant snitt inte indikerat i enlighet med standarden. Men om du helt enkelt raderar sektionsbeteckningen, kommer hela sektionen att raderas på grund av att vyn och sektionen i datorns minne är sammankopplade. Därför, för att ta bort beteckningen, måste du först förstöra kopplingen mellan vyn och sektionen. För att göra detta klickar du på vänster musknapp för att välja avsnittet och klickar sedan på höger musknapp för att öppna den sammanhangsberoende menyn, från vilken objektet Destroy view är valt (fig. 97). Sektionssymbolen kan nu raderas.

5. För att konstruera en horisontell sektion, låt oss rita en B-B-sektionslinje genom det nedre planet av hålet i frontvyn. Framsidan måste först göras aktuell genom två klick på vänster musknapp. Därefter byggs en horisontell sektion (bild 117).

6. Vid konstruktion av en frontal sektion är en del av vyn och en del av sektionen kompatibla, eftersom de är symmetriska figurer. Prismats ytterkant projiceras på linjen som skiljer vyn och skärningen, så vi avgränsar vy och snitt av en heldragen tunn vågig linje ritad till höger om symmetriaxeln, eftersom yttre revben. Knappen används för att rita en vågig linje. Bezier-kurva placerad på Geometry-panelen ritad med stilen For clipping line (Fig. 118). Ange sekventiellt de punkter genom vilka Bezier-kurvan ska passera. För att avsluta kommandokörningen, klicka på knappen Skapa objekt.

Fig.118 Välja en linjestil för en brytning

Sektionering

En sektion är en bild av ett föremål som erhålls genom att mentalt dissekera ett föremål med ett plan. Avsnittet visar endast vad som finns i skärplanet.

Läget för skärplanet, med vilket sektionen är bildad, anges på ritningen med snittlinjen, precis som för sektioner.

Sektioner, beroende på deras placering i ritningarna, är uppdelade i utökade och överlagrade. De borttagna sektionerna är oftast placerade på ritningens fria fält och är skisserade av huvudlinjen. De överlagrade sektionerna placeras direkt på bilden av objektet och är konturerade med tunna linjer (Fig. 119).

Fig.119 Konstruktion av sektioner

Tänk på sekvensen för att konstruera en ritning av ett prisma med en förlängd snedställning avsnitt B-B(Fig. 117).

1. Aktivera frontvyn genom att dubbelklicka på vänster musknapp på vyn och rita en snittlinje med knappen skärlinje . Låt oss välja texten till inskriptionen В-В.

2. Använd knappen Klipp linje som finns på panelen Associativa vyer (Fig. 115), som visas som en fälla, ange sekantlinjen plan B-B. Använd knappen Klipp/sektion på egenskapsfältet, välj bildtyp - Sektion (Fig. 116), skalan för den visade sektionen väljs från Skala-fönstret.

Den konstruerade sektionen är placerad i ett projektionsförhållande, vilket begränsar dess rörelse i ritningen, men projektionsförhållandet kan stängas av med knappen projektionsanslutning.

Rita på den färdiga ritningen mittlinjer, vid behov, ange måtten.

Uppgifterna för att konstruera sektioner av polyedrar tar betydelsefull plats som skolgeometrikurs för gymnasiet, och vid prov på olika nivåer. Lösningen av denna typ av problem bidrar till assimileringen av stereometrins axiom, systematisering av kunskap och färdigheter, utveckling rumslig representation och konstruktiva färdigheter. Svårigheter som uppstår med att lösa problem vid konstruktion av sektioner är välkända.

Från tidig barndom vi står inför nedskärningar. Vi skär bröd, korv och andra produkter, skär en pinne eller penna med en kniv. Sekantplanet i alla dessa fall är knivens plan. Sektioner (sektioner av bitar) är olika.

Sektionen av en konvex polyeder är en konvex polygon, vars hörn, i det allmänna fallet, är skärningspunkterna för skärplanet med polygonens kanter, och sidorna är skärningslinjerna för skärplanet med ansiktena.

För att konstruera en skärningslinje mellan två plan räcker det att hitta två gemensamma punkter för dessa plan och dra en linje genom dem. Detta är baserat på följande påståenden:

1. om två punkter på en rät linje tillhör ett plan, så tillhör hela linjen detta plan;

2. om två olika plan har en gemensam punkt, så skär de sig längs en rät linje som går genom denna punkt.

Som jag redan har sagt kan konstruktionen av sektioner av polyedrar utföras på basis av stereometrins axiom och satser om parallelliteten mellan linjer och plan. Samtidigt finns det vissa metoder för att konstruera plana sektioner av polyedrar. Följande tre metoder är mest effektiva:

spårningsmetod

Intern designmetod

Kombinerad metod.

I studien av geometri och i synnerhet de delar av den där bilder beaktas geometriska former, bilder av geometriska former hjälper användningen av datorpresentationer. Med hjälp av en dator blir många geometrilektioner mer visuella och dynamiska. Axiom, satser, bevis, problem för konstruktion, problem för att konstruera sektioner kan åtföljas av successiva konstruktioner på bildskärmen. Datorgenererade ritningar kan sparas och klistras in i andra dokument.

Jag vill visa några bilder om ämnet: "Konstruktion av sektioner i geometriska kroppar»

För att konstruera skärningspunkten för en linje och ett plan, hitta en linje i planet som skär den givna linjen. Då är den önskade punkten skärningspunkten för den hittade linjen med den givna. Låt oss se det på nästa bilder.

Uppgift 1.

Två punkter M och N är markerade på kanterna av tetraederns DABC; M GAD, Nb DC. Välj skärningspunkten mellan linjen MN och basens plan.

Lösning: för att hitta skärningspunkten för linjen MN med planet

bas vi kommer att fortsätta AC och segmentera MN. Låt oss markera skärningspunkten för dessa linjer genom X. Punkten X tillhör linjen MN och ytan AC, och AC ligger i basens plan, vilket betyder att punkten X också ligger i basens plan . Därför är punkten X skärningspunkten för linjen MN med basens plan.

Låt oss överväga det andra problemet. Låt oss komplicera det lite.

Uppgift 2.

Givet en tetraeder DABC av punkterna M och N, där M € DA, N C (DBC). Hitta skärningspunkten för linjen MN med planet ABC .

Lösning: Skärningspunkten för linjen MN med planet ABC måste ligga i planet som innehåller linjen MN och i basens plan. Vi fortsätter segmentet DN till skärningspunkten med kanten DC. Vi markerar skärningspunkten genom E. Vi fortsätter linjen AE och MN till skärningspunkten. Notera X. Punkten X tillhör MN, så den ligger på planet som innehåller linjen MN och X tillhör AE, och AE ligger på planet ABC. Så X ligger också i planet ABC. Därför är X skärningspunkten för linjen MN och planet ABC.

Låt oss komplicera uppgiften. Betrakta ett avsnitt av geometriska figurer med plan som passerar genom tre givna punkter.

Uppgift 3

Punkterna M, N och P är markerade på kanterna AC, AD och DB på tetraedern DABC Konstruera en sektion av tetraedern med planet MNP.

Lösning: konstruera en rät linje längs vilken planet MNP. Skär ansiktsplan ABC. Punkt M är en gemensam punkt för dessa plan. För att bygga ytterligare en gemensam punkt fortsätter vi segmentet AB och NP. Vi markerar skärningspunkten genom X, som kommer att vara den andra gemensamma punkten för planet MNP och ABC. Så dessa plan skär längs den raka linjen MX. MX skär kanten BC vid någon punkt E. Eftersom E ligger på MX och MX är en linje som tillhör planet MNP, följer att PE tillhör MNP. Den fyrsidiga MNPE är den obligatoriska sektionen.

Uppgift 4

Vi konstruerar en sektion av ett rakt prisma ABCA1B1C1 av ett plan som går genom punkterna P , F,R, där R tillhör ( AA 1C 1C), R tillhör I 1C1,

Q tillhör AB

Lösning: Alla tre punkterna P,Q,R ligger i olika ytor, så vi kan ännu inte konstruera en skärningslinje för sekantplanet med någon yta av prismat. Låt oss hitta skärningspunkten mellan PR och ABC. Låt oss hitta projektionerna av punkterna P och R på basplanet PP1 vinkelrätt mot BC och RR1 vinkelrätt mot AC. Linje P1R1 skär linjen PR i punkt X. X är skärningspunkten mellan linjen PR och planet ABC. Den ligger i det önskade planet K och i basens plan, liksom punkten Q. XQ är en rät linje som skär K med basens plan. XQ skär AC i punkt K. Därför är KQ segmentet av skärningspunkten mellan planet X och ytan ABC. K och R ligger i X-planet och i AA1C1C-ytans plan. Rita en linje KR och markera skärningspunkten med A1Q E. KE är skärningslinjen för planet X med denna yta. Hitta skärningslinjen för X-planet med planet för ytorna BB1A1A. KE skär A1A i punkt Y. Linjen QY är skärningslinjen mellan sekantplanet och planet AA1B1B. FPEKQ - önskat avsnitt.

Uppgifter för att konstruera delar av en kub vid ett plan är som regel enklare än till exempel uppgifter för delar av en pyramid.

Vi kan dra en linje genom två punkter om de ligger i samma plan. När man konstruerar sektioner av en kub är ytterligare ett alternativ för att konstruera ett spår av ett skärplan möjligt. Eftersom det tredje planet skär två parallella plan längs parallella räta linjer, så om en rät linje redan har byggts i en av ytorna, och det finns en punkt i den andra genom vilken sektionen passerar, så kan vi dra en rät linje genom denna punkt parallell med den givna.

Tänk på konkreta exempel hur man konstruerar delar av en kub vid ett plan.

1) Konstruera en sektion av kuben med ett plan som går genom punkterna A, C och M.

Problem av denna typ är det enklaste av alla problem för att konstruera sektioner av en kub. Eftersom punkterna A och C ligger i samma plan (ABC) kan vi dra en linje genom dem. Dess spår är segment AC. Det är osynligt, så vi avbildar AC med ett slag. På liknande sätt kopplar vi ihop punkterna M och C, som ligger i samma plan (CDD1), och punkterna A och M, som ligger i samma plan (ADD1). Triangel ACM är den obligatoriska sektionen.

2) Konstruera en sektion av kuben med ett plan som går genom punkterna M, N, P.

Här ligger bara punkterna M och N i samma plan (ADD1), så vi drar en rak linje genom dem och får spåret MN (osynligt). Eftersom de motsatta ytorna av kuben ligger i parallella plan, skär skärplanet de parallella planen (ADD1) och (BCC1) längs parallella linjer. Vi har redan byggt en av de parallella linjerna - det här är MN.

Genom punkten P drar vi en linje parallell med MN. Den skär kanten BB1 i punkten S. PS är spåret av sekantplanet i ytan (BCC1).

Vi drar en rät linje genom punkterna M och S, som ligger i samma plan (ABB1). Fick MS-spåret (synligt).

Planen (ABB1) och (CDD1) är parallella. Det finns redan en linje MS i planet (ABB1), så genom punkten N i planet (CDD1) drar vi en linje parallellt med MS. Denna linje skär kanten D1C1 vid punkt L. Dess spår är NL (osynligt). Punkterna P och L ligger i samma plan (A1B1C1), så vi ritar en linje genom dem.

Pentagon MNLPS är den obligatoriska sektionen.

3) Konstruera en sektion av kuben med ett plan som går genom punkterna M, N, P.

Punkterna M och N ligger i samma plan (BCC1), så en rät linje kan dras genom dem. Vi får spåret MN (synligt). Planet (BCC1) är parallellt med planet (ADD1), så genom punkten P som ligger i (ADD1) drar vi en linje parallellt med MN. Den skär kanten AD vid punkt E. Vi fick spåret PE (osynligt).

Det finns inga fler punkter som ligger i samma plan, eller en linje och en punkt i parallella plan. Därför måste en av de redan befintliga linjerna fortsätta för att få ytterligare en poäng.

Om vi fortsätter linjen MN, då den ligger i planet (BCC1), måste vi leta efter skärningspunkten för MN med en av linjerna i detta plan. Det finns redan skärningspunkter med CC1 och B1C1 - dessa är M och N. Linjerna BC och BB1 finns kvar. Vi fortsätter BC och MN till skärningspunkten i punkt K. Punkten K ligger på linjen BC, vilket betyder att den tillhör planet (ABC), så vi kan dra en linje genom det och punkten E som ligger i detta plan. Den skär kanten CD vid punkt H. EH är dess spår (osynligt). Eftersom H och N ligger i samma plan (CDD1) kan en rät linje dras genom dem. Vi får spåret HN (osynligt).

Planen (ABC) och (A1B1C1) är parallella. En av dem innehåller linjen EH, den andra innehåller punkten M. Vi kan dra en linje genom M parallellt med EH. Vi får spåret MF (synligt). Vi ritar en rak linje genom punkterna M och F.

Hexagon MNHEPF är den obligatoriska sektionen.

Om vi fortsatte linjen MN till skärningen med en annan linje i planet (BCC1), med BB1, så skulle vi få en punkt G som hör till planet (ABB1). Det betyder att genom G och P är det möjligt att dra en linje vars spår är PF. Vidare ritar vi raka linjer genom punkter som ligger i parallella plan, och vi kommer fram till samma resultat.

Arbete med rät linje PE ger samma tvärsnitt MNHEPF.

4) Konstruera en sektion av kuben med ett plan som går genom punkten M, N, P.

Här kan vi dra en rät linje genom punkterna M och N som ligger i samma plan (A1B1C1). Hennes fotavtryck är MN (synligt). Det finns inga fler punkter som ligger i samma plan eller i parallella plan.

Vi fortsätter linjen MN. Den ligger i planet (A1B1C1), så den kan bara skära en av linjerna i detta plan. Det finns redan skärningspunkter med A1D1 och C1D1 - N och M. Ytterligare två linjer i detta plan är A1B1 och B1C1. Skärningspunkten för A1B1 och MN är S. Eftersom den ligger på linjen A1B1 tillhör den planet (ABB1), vilket innebär att en linje kan dras genom det och punkten P, som ligger i samma plan. Linjen PS skär kanten AA1 i punkten E. PE är dess spår (synlig). Genom punkterna N och E, som ligger i samma plan (ADD1), är det möjligt att rita en rak linje, vars spår är NE (osynlig). Det finns en linje NE i planet (ADD1), och en punkt P i planet parallellt med det (BCC1) Genom punkten P kan vi dra en linje PL parallellt med NE. Den skär kanten CC1 vid punkt L. PL är spåret av denna linje (synlig). Punkterna M och L ligger i samma plan (CDD1), vilket innebär att en rät linje kan dras genom dem. Hennes fotavtryck är ML (osynligt). Pentagon MLPEN är den obligatoriska sektionen.

Det var möjligt att fortsätta linjen NM i båda riktningarna och leta efter dess skärningspunkter inte bara med linjen A1B1, utan även med linjen B1C1, som också ligger i planet (A1B1C1). I det här fallet ritar vi två räta linjer genom punkten P samtidigt: en i planet (ABB1) genom punkterna P och S, och den andra i planet (BCC1), genom punkterna P och R. Efter det , det återstår att ansluta punkterna som ligger i samma plan: M c L, E - med N.