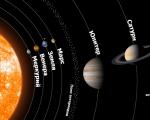
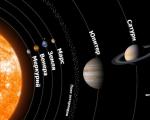
ജ്യാമിതീയ പുരോഗതി ഉദാഹരണങ്ങൾ. എപ്പോഴും മാനസികാവസ്ഥയിലായിരിക്കുക

ഗണിതശാസ്ത്രത്തോടൊപ്പം ജ്യാമിതീയ പുരോഗതിയും 9-ാം ഗ്രേഡിലെ സ്കൂൾ ബീജഗണിത കോഴ്സിൽ പഠിക്കുന്ന ഒരു പ്രധാന സംഖ്യ പരമ്പരയാണ്. ഈ ലേഖനത്തിൽ, ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ ഡിനോമിനേറ്ററും അതിന്റെ മൂല്യം അതിന്റെ ഗുണങ്ങളെ എങ്ങനെ ബാധിക്കുന്നുവെന്നും ഞങ്ങൾ പരിഗണിക്കും.

ജ്യാമിതീയ പുരോഗതിയുടെ നിർവ്വചനം

ആരംഭിക്കുന്നതിന്, ഈ സംഖ്യ ശ്രേണിയുടെ നിർവചനം ഞങ്ങൾ നൽകുന്നു. ഒരു ജ്യാമിതീയ പുരോഗതി എന്നത് അതിന്റെ ആദ്യ മൂലകത്തെ ഡിനോമിനേറ്റർ എന്ന് വിളിക്കുന്ന സ്ഥിരമായ ഒരു സംഖ്യ കൊണ്ട് തുടർച്ചയായി ഗുണിച്ചാൽ രൂപപ്പെടുന്ന യുക്തിസഹ സംഖ്യകളുടെ ഒരു പരമ്പരയാണ്.

ഉദാഹരണത്തിന്, 3, 6, 12, 24, ... ശ്രേണിയിലെ സംഖ്യകൾ ഒരു ജ്യാമിതീയ പുരോഗതിയാണ്, കാരണം നമ്മൾ 3 (ആദ്യ മൂലകം) 2 കൊണ്ട് ഗുണിച്ചാൽ നമുക്ക് 6 ലഭിക്കും. 6 നെ 2 കൊണ്ട് ഗുണിച്ചാൽ നമുക്ക് ലഭിക്കും. 12, തുടങ്ങിയവ.

പരിഗണനയിലുള്ള ശ്രേണിയിലെ അംഗങ്ങളെ സാധാരണയായി AI എന്ന ചിഹ്നത്താൽ സൂചിപ്പിക്കുന്നു, ഇവിടെ i എന്നത് ശ്രേണിയിലെ മൂലകത്തിന്റെ സംഖ്യയെ സൂചിപ്പിക്കുന്ന ഒരു പൂർണ്ണസംഖ്യയാണ്.

ഒരു പുരോഗതിയുടെ മുകളിലുള്ള നിർവചനം ഗണിതശാസ്ത്രത്തിന്റെ ഭാഷയിൽ ഇനിപ്പറയുന്ന രീതിയിൽ എഴുതാം: an = bn-1 * a1, ഇവിടെ b എന്നത് ഡിനോമിനേറ്ററാണ്. ഈ ഫോർമുല പരിശോധിക്കുന്നത് എളുപ്പമാണ്: n = 1 എങ്കിൽ, b1-1 = 1, നമുക്ക് a1 = a1 ലഭിക്കും. n = 2 ആണെങ്കിൽ, an = b * a1, ഞങ്ങൾ വീണ്ടും പരിഗണനയിലുള്ള സംഖ്യകളുടെ ശ്രേണിയുടെ നിർവചനത്തിലേക്ക് വരുന്നു. സമാനമായ ന്യായവാദം തുടരാം വലിയ മൂല്യങ്ങൾഎൻ.

ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ ഡിനോമിനേറ്റർ

മുഴുവൻ സംഖ്യാ ശ്രേണിക്കും ഏത് പ്രതീകമാണ് ഉണ്ടായിരിക്കേണ്ടതെന്ന് സംഖ്യ b പൂർണ്ണമായും നിർണ്ണയിക്കുന്നു. ഡിനോമിനേറ്റർ b പോസിറ്റീവ്, നെഗറ്റീവ് അല്ലെങ്കിൽ ഒന്നിൽ കൂടുതലോ കുറവോ ആകാം. മുകളിലുള്ള എല്ലാ ഓപ്ഷനുകളും വ്യത്യസ്ത ശ്രേണികളിലേക്ക് നയിക്കുന്നു:

• b > 1. റേഷണൽ സംഖ്യകളുടെ വർദ്ധിച്ചുവരുന്ന ഒരു പരമ്പരയുണ്ട്. ഉദാഹരണത്തിന്, 1, 2, 4, 8, ... മൂലകം a1 നെഗറ്റീവ് ആണെങ്കിൽ, മുഴുവൻ ശ്രേണിയും മൊഡ്യൂളിൽ മാത്രം വർദ്ധിക്കും, പക്ഷേ സംഖ്യകളുടെ അടയാളം കണക്കിലെടുത്ത് കുറയുന്നു.
• b = 1. പലപ്പോഴും അത്തരം ഒരു കേസ് ഒരു പുരോഗതി എന്ന് വിളിക്കപ്പെടുന്നില്ല, കാരണം സമാനമായ യുക്തിസഹ സംഖ്യകളുടെ ഒരു സാധാരണ ശ്രേണി ഉണ്ട്. ഉദാഹരണത്തിന്, -4, -4, -4.

തുകയ്ക്കുള്ള ഫോർമുല

പരിഗണനയിലുള്ള പുരോഗതിയുടെ തരം ഡിനോമിനേറ്റർ ഉപയോഗിച്ച് നിർദ്ദിഷ്ട പ്രശ്നങ്ങളുടെ പരിഗണനയിലേക്ക് പോകുന്നതിന് മുമ്പ്, അതിന്റെ ആദ്യ n ഘടകങ്ങളുടെ ആകെത്തുകയ്ക്ക് ഒരു പ്രധാന ഫോർമുല നൽകണം. ഫോർമുല ഇതാണ്: Sn = (bn - 1) * a1 / (b - 1).

പുരോഗതിയിലെ അംഗങ്ങളുടെ ഒരു ആവർത്തന ക്രമം നിങ്ങൾ പരിഗണിക്കുകയാണെങ്കിൽ ഈ പദപ്രയോഗം നിങ്ങൾക്ക് സ്വയം ലഭിക്കും. മേൽപ്പറഞ്ഞ ഫോർമുലയിൽ, ഏകപക്ഷീയമായ പദങ്ങളുടെ ആകെത്തുക കണ്ടെത്താൻ ആദ്യത്തെ ഘടകവും ഡിനോമിനേറ്ററും മാത്രം അറിഞ്ഞാൽ മതിയെന്നതും ശ്രദ്ധിക്കുക.

അനന്തമായി കുറയുന്ന ക്രമം

അതെന്താണെന്നതിന്റെ വിശദീകരണമായിരുന്നു മുകളിൽ. ഇപ്പോൾ, Sn എന്നതിന്റെ സൂത്രവാക്യം അറിഞ്ഞുകൊണ്ട്, നമുക്ക് ഈ സംഖ്യ ശ്രേണിയിൽ പ്രയോഗിക്കാം. മോഡുലസ് 1 കവിയാത്ത ഏതൊരു സംഖ്യയും വലിയ ശക്തികളിലേക്ക് ഉയർത്തുമ്പോൾ പൂജ്യമായി മാറുന്നതിനാൽ, b∞ => 0 ആണെങ്കിൽ -1

ഡിനോമിനേറ്ററിന്റെ മൂല്യം പരിഗണിക്കാതെ തന്നെ, വ്യത്യാസം (1 - b) എല്ലായ്പ്പോഴും പോസിറ്റീവ് ആയിരിക്കുമെന്നതിനാൽ, അനന്തമായി കുറയുന്ന ജ്യാമിതീയ പുരോഗതി S∞ ന്റെ ആകെത്തുകയുടെ അടയാളം അതിന്റെ ആദ്യ ഘടകമായ a1 ന്റെ ചിഹ്നത്താൽ അദ്വിതീയമായി നിർണ്ണയിക്കപ്പെടുന്നു.

ഇപ്പോൾ ഞങ്ങൾ നിരവധി പ്രശ്നങ്ങൾ പരിഗണിക്കും, അവിടെ നേടിയ അറിവ് നിർദ്ദിഷ്ട നമ്പറുകളിലേക്ക് എങ്ങനെ പ്രയോഗിക്കാമെന്ന് ഞങ്ങൾ കാണിക്കും.

ടാസ്ക് നമ്പർ 1. പുരോഗതിയുടെയും തുകയുടെയും അജ്ഞാത ഘടകങ്ങളുടെ കണക്കുകൂട്ടൽ

ഒരു ജ്യാമിതീയ പുരോഗതി നൽകിയാൽ, പുരോഗതിയുടെ ഡിനോമിനേറ്റർ 2 ആണ്, അതിന്റെ ആദ്യ ഘടകം 3 ആണ്. അതിന്റെ 7-ഉം 10-ഉം പദങ്ങൾ എന്തായിരിക്കും, അതിന്റെ ഏഴ് പ്രാരംഭ മൂലകങ്ങളുടെ ആകെത്തുക എന്താണ്?

പ്രശ്നത്തിന്റെ അവസ്ഥ വളരെ ലളിതവും മുകളിൽ പറഞ്ഞ സൂത്രവാക്യങ്ങളുടെ നേരിട്ടുള്ള ഉപയോഗവും ഉൾപ്പെടുന്നു. അതിനാൽ, n എന്ന സംഖ്യയുള്ള മൂലകം കണക്കാക്കാൻ, ഞങ്ങൾ an = bn-1 * a1 എന്ന പദപ്രയോഗം ഉപയോഗിക്കുന്നു. 7-ാമത്തെ ഘടകത്തിന് നമുക്ക് ഉണ്ട്: a7 = b6 * a1, അറിയപ്പെടുന്ന ഡാറ്റയ്ക്ക് പകരമായി, നമുക്ക് ലഭിക്കുന്നത്: a7 = 26 * 3 = 192. 10-ാമത്തെ അംഗത്തിനും ഞങ്ങൾ ഇത് ചെയ്യുന്നു: a10 = 29 * 3 = 1536.

ഞങ്ങൾ ആകെ അറിയപ്പെടുന്ന ഫോർമുല ഉപയോഗിക്കുകയും പരമ്പരയിലെ ആദ്യ 7 ഘടകങ്ങൾക്ക് ഈ മൂല്യം നിർണ്ണയിക്കുകയും ചെയ്യുന്നു. ഞങ്ങൾക്ക് ഉണ്ട്: S7 = (27 - 1) * 3 / (2 - 1) = 381.

ടാസ്ക് നമ്പർ 2. പുരോഗതിയുടെ ഏകപക്ഷീയ ഘടകങ്ങളുടെ ആകെത്തുക നിർണ്ണയിക്കുന്നു

എക്‌സ്‌പോണൻഷ്യൽ പ്രോഗ്രഷൻ bn-1 * 4 ന്റെ ഡിനോമിനേറ്റർ -2 ആയിരിക്കട്ടെ, ഇവിടെ n ഒരു പൂർണ്ണസംഖ്യയാണ്. ഈ ശ്രേണിയുടെ 5 മുതൽ 10 വരെയുള്ള മൂലകങ്ങൾ ഉൾപ്പെടെയുള്ള തുക നിർണ്ണയിക്കേണ്ടത് ആവശ്യമാണ്.

അറിയപ്പെടുന്ന സൂത്രവാക്യങ്ങൾ ഉപയോഗിച്ച് നേരിട്ട പ്രശ്നം പരിഹരിക്കാൻ കഴിയില്ല. ഇത് 2 വ്യത്യസ്ത രീതികളിൽ പരിഹരിക്കാൻ കഴിയും. സമ്പൂർണ്ണതയ്ക്കായി, ഞങ്ങൾ രണ്ടും അവതരിപ്പിക്കുന്നു.

രീതി 1. അതിന്റെ ആശയം ലളിതമാണ്: ആദ്യ നിബന്ധനകളുടെ രണ്ട് അനുബന്ധ തുകകൾ നിങ്ങൾ കണക്കാക്കേണ്ടതുണ്ട്, തുടർന്ന് മറ്റൊന്നിൽ നിന്ന് മറ്റൊന്ന് കുറയ്ക്കുക. ചെറിയ തുക കണക്കാക്കുക: S10 = ((-2)10 - 1) * 4 / (-2 - 1) = -1364. ഇപ്പോൾ ഞങ്ങൾ കണക്കാക്കുന്നു ഒരു വലിയ തുക: S4 = ((-2)4 - 1) * 4 / (-2 - 1) = -20. അവസാന പദപ്രയോഗത്തിൽ, 4 നിബന്ധനകൾ മാത്രമേ സംഗ്രഹിച്ചിട്ടുള്ളൂ എന്നത് ശ്രദ്ധിക്കുക, കാരണം പ്രശ്നത്തിന്റെ അവസ്ഥയനുസരിച്ച് കണക്കാക്കേണ്ട തുകയിൽ 5-ാമത്തേത് ഇതിനകം ഉൾപ്പെടുത്തിയിട്ടുണ്ട്. അവസാനമായി, ഞങ്ങൾ വ്യത്യാസം എടുക്കുന്നു: S510 = S10 - S4 = -1364 - (-20) = -1344.

രീതി 2. സംഖ്യകൾ മാറ്റി എണ്ണുന്നതിന് മുമ്പ്, ചോദ്യം ചെയ്യപ്പെടുന്ന ശ്രേണിയിലെ m, n എന്നീ പദങ്ങൾക്കിടയിലുള്ള തുകയുടെ ഒരു ഫോർമുല നിങ്ങൾക്ക് ലഭിക്കും. ഞങ്ങൾ രീതി 1-ലെ അതേ രീതിയിൽ തന്നെ പ്രവർത്തിക്കുന്നു, തുകയുടെ പ്രതീകാത്മക പ്രതിനിധാനം ഉപയോഗിച്ച് മാത്രമേ ഞങ്ങൾ ആദ്യം പ്രവർത്തിക്കൂ. നമുക്കുള്ളത്: Snm = (bn - 1) * a1 / (b - 1) - (bm-1 - 1) * a1 / (b - 1) = a1 * (bn - bm-1) / (b - 1) . ഫലമായുണ്ടാകുന്ന എക്‌സ്‌പ്രഷനിലേക്ക് നിങ്ങൾക്ക് അറിയപ്പെടുന്ന സംഖ്യകൾ മാറ്റിസ്ഥാപിച്ച് അന്തിമ ഫലം കണക്കാക്കാം: S105 = 4 * ((-2)10 - (-2)4) / (-2 - 1) = -1344.

ടാസ്ക് നമ്പർ 3. ഡിനോമിനേറ്റർ എന്താണ്?

a1 = 2, ജ്യാമിതീയ പുരോഗതിയുടെ ഡിനോമിനേറ്റർ കണ്ടെത്തട്ടെ, അതിന്റെ അനന്തമായ തുക 3 ആണെങ്കിൽ, ഇത് സംഖ്യകളുടെ കുറയുന്ന ശ്രേണിയാണെന്ന് അറിയാം.

പ്രശ്നത്തിന്റെ അവസ്ഥ അനുസരിച്ച്, അത് പരിഹരിക്കാൻ ഏത് ഫോർമുല ഉപയോഗിക്കണമെന്ന് ഊഹിക്കാൻ പ്രയാസമില്ല. തീർച്ചയായും, അനന്തമായി കുറയുന്ന പുരോഗതിയുടെ ആകെത്തുക. ഞങ്ങൾക്ക് ഉണ്ട്: S∞ = a1 / (1 - b). ഞങ്ങൾ ഡിനോമിനേറ്റർ പ്രകടിപ്പിക്കുന്നിടത്ത് നിന്ന്: b = 1 - a1 / S∞. അറിയപ്പെടുന്ന മൂല്യങ്ങൾ മാറ്റി ആവശ്യമായ നമ്പർ നേടുന്നതിന് ഇത് ശേഷിക്കുന്നു: b \u003d 1 - 2 / 3 \u003d -1 / 3 അല്ലെങ്കിൽ -0.333 (3). ഇത്തരത്തിലുള്ള സീക്വൻസിനായി, മോഡുലസ് b 1-നപ്പുറം പോകരുതെന്ന് ഓർമ്മിച്ചാൽ, നമുക്ക് ഈ ഫലം ഗുണപരമായി പരിശോധിക്കാം. നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, |-1 / 3|

ടാസ്ക് നമ്പർ 4. സംഖ്യകളുടെ ഒരു പരമ്പര പുനഃസ്ഥാപിക്കുന്നു

ഒരു സംഖ്യാ ശ്രേണിയുടെ 2 ഘടകങ്ങൾ നൽകട്ടെ, ഉദാഹരണത്തിന്, 5-ആമത്തേത് 30-നും 10-ആമത്തേത് 60-നും തുല്യമാണ്. ഈ ഡാറ്റയിൽ നിന്ന് മുഴുവൻ ശ്രേണിയും പുനഃസ്ഥാപിക്കേണ്ടത് ആവശ്യമാണ്, ഇത് ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ ഗുണങ്ങളെ തൃപ്തിപ്പെടുത്തുന്നു.

പ്രശ്നം പരിഹരിക്കുന്നതിന്, നിങ്ങൾ ആദ്യം അറിയപ്പെടുന്ന ഓരോ അംഗത്തിനും അനുയോജ്യമായ പദപ്രയോഗം എഴുതണം. ഞങ്ങൾക്ക് ഉണ്ട്: a5 = b4 * a1, a10 = b9 * a1. ഇപ്പോൾ നമ്മൾ രണ്ടാമത്തെ പദപ്രയോഗത്തെ ആദ്യത്തേത് കൊണ്ട് ഹരിക്കുന്നു, നമുക്ക് ലഭിക്കുന്നു: a10 / a5 = b9 * a1 / (b4 * a1) = b5. ഇവിടെ നിന്ന്, പ്രശ്നത്തിന്റെ അവസ്ഥയിൽ നിന്ന് അറിയപ്പെടുന്ന അംഗങ്ങളുടെ അനുപാതത്തിന്റെ അഞ്ചാം ഡിഗ്രി റൂട്ട് എടുത്ത് ഞങ്ങൾ ഡിനോമിനേറ്റർ നിർണ്ണയിക്കുന്നു, b = 1.148698. ഫലമായുണ്ടാകുന്ന സംഖ്യയെ അറിയപ്പെടുന്ന ഒരു ഘടകത്തിനായുള്ള എക്സ്പ്രഷനുകളിലൊന്നിലേക്ക് ഞങ്ങൾ മാറ്റിസ്ഥാപിക്കുന്നു, നമുക്ക് ലഭിക്കുന്നു: a1 = a5 / b4 = 30 / (1.148698)4 = 17.2304966.

അങ്ങനെ, പുരോഗതി bn-ന്റെ ഡിനോമിനേറ്റർ എന്താണെന്നും ജ്യാമിതീയ പുരോഗതി bn-1 * 17.2304966 = an, ഇവിടെ b = 1.148698 ആണെന്നും ഞങ്ങൾ കണ്ടെത്തി.

ജ്യാമിതീയ പുരോഗതികൾ എവിടെയാണ് ഉപയോഗിക്കുന്നത്?

പ്രായോഗികമായി ഈ സംഖ്യാ ശ്രേണിയുടെ പ്രയോഗം ഇല്ലായിരുന്നുവെങ്കിൽ, അതിന്റെ പഠനം തികച്ചും സൈദ്ധാന്തിക താൽപ്പര്യമായി ചുരുങ്ങും. എന്നാൽ അത്തരമൊരു അപേക്ഷയുണ്ട്.

ഏറ്റവും പ്രശസ്തമായ 3 ഉദാഹരണങ്ങൾ ചുവടെ പട്ടികപ്പെടുത്തിയിരിക്കുന്നു:

• ചടുലനായ അക്കില്ലസിന് വേഗത കുറഞ്ഞ ആമയെ പിടിക്കാൻ കഴിയാത്ത സീനോയുടെ വിരോധാഭാസം, സംഖ്യകളുടെ അനന്തമായി കുറയുന്ന ക്രമം എന്ന ആശയം ഉപയോഗിച്ച് പരിഹരിക്കപ്പെടുന്നു.
• ചെസ്സ് ബോർഡിന്റെ ഓരോ സെല്ലിലും ഗോതമ്പ് ധാന്യങ്ങൾ വെച്ചാൽ, 1-ാം സെല്ലിൽ 1 ധാന്യം, 2-ൽ 2, 3- 3 എന്നിങ്ങനെ, എല്ലാ സെല്ലുകളും നിറയ്ക്കാൻ 18446744073709551615 ധാന്യങ്ങൾ ആവശ്യമാണ്. പലക!
• "ടവർ ഓഫ് ഹനോയി" എന്ന ഗെയിമിൽ, ഒരു വടിയിൽ നിന്ന് മറ്റൊന്നിലേക്ക് ഡിസ്കുകൾ പുനഃക്രമീകരിക്കുന്നതിന്, 2n - 1 പ്രവർത്തനങ്ങൾ നടത്തേണ്ടത് ആവശ്യമാണ്, അതായത്, ഉപയോഗിച്ച ഡിസ്കുകളുടെ എണ്ണത്തിൽ നിന്ന് അവയുടെ എണ്ണം ഗണ്യമായി വർദ്ധിക്കുന്നു.

ജ്യാമിതീയ പുരോഗതിഗണിതശാസ്ത്രത്തിൽ ഗണിതത്തെക്കാൾ പ്രാധാന്യം കുറവല്ല. ഒരു ജ്യാമിതീയ പുരോഗതിയാണ് ബി1, ബി2,..., ബി[n] സംഖ്യകളുടെ ഒരു ശ്രേണി, അതിൽ ഓരോ അടുത്ത അംഗവും മുമ്പത്തേതിനെ ഒരു സ്ഥിര സംഖ്യ കൊണ്ട് ഗുണിച്ചാൽ ലഭിക്കും. വളർച്ചയുടെ തോത് അല്ലെങ്കിൽ പുരോഗതിയുടെ കുറവിന്റെ സ്വഭാവവും ഈ സംഖ്യയെ വിളിക്കുന്നു ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ ഡിനോമിനേറ്റർസൂചിപ്പിക്കുന്നു

വേണ്ടി പൂർണ്ണമായ ചുമതലജ്യാമിതീയ പുരോഗതി, ഡിനോമിനേറ്ററിന് പുറമേ, അതിന്റെ ആദ്യ പദം അറിയുകയോ നിർണ്ണയിക്കുകയോ ചെയ്യേണ്ടത് ആവശ്യമാണ്. ഡിനോമിനേറ്ററിന്റെ പോസിറ്റീവ് മൂല്യത്തിന്, പുരോഗതി ഒരു മോണോടോൺ സീക്വൻസാണ്, കൂടാതെ ഈ സംഖ്യകളുടെ ക്രമം ഏകതാനമായി കുറയുകയും ഏകതാനമായി വർദ്ധിക്കുകയും ചെയ്യുന്നുവെങ്കിൽ. ഡിനോമിനേറ്റർ ഒന്നിന് തുല്യമാകുമ്പോൾ കേസ് പ്രായോഗികമായി പരിഗണിക്കില്ല, കാരണം ഞങ്ങൾക്ക് സമാനമായ സംഖ്യകളുടെ ഒരു ശ്രേണിയുണ്ട്, മാത്രമല്ല അവയുടെ സംഗ്രഹം പ്രായോഗിക താൽപ്പര്യമില്ലാത്തതുമാണ്.

ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ പൊതുവായ പദംഫോർമുല അനുസരിച്ച് കണക്കാക്കുന്നു

ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ ആദ്യ n പദങ്ങളുടെ ആകെത്തുകഫോർമുല നിർണ്ണയിച്ചിരിക്കുന്നു

ക്ലാസിക്കൽ ജ്യാമിതീയ പുരോഗതി പ്രശ്നങ്ങൾക്കുള്ള പരിഹാരങ്ങൾ നമുക്ക് പരിഗണിക്കാം. ഏറ്റവും ലളിതമായി മനസ്സിലാക്കാൻ തുടങ്ങാം.

ഉദാഹരണം 1. ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ ആദ്യ പദം 27 ആണ്, അതിന്റെ ഡിനോമിനേറ്റർ 1/3 ആണ്. ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ ആദ്യ ആറ് നിബന്ധനകൾ കണ്ടെത്തുക.

പരിഹാരം: പ്രശ്നത്തിന്റെ അവസ്ഥ ഞങ്ങൾ ഫോമിൽ എഴുതുന്നു

കണക്കുകൂട്ടലുകൾക്കായി, ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ n-ആം അംഗത്തിനായുള്ള ഫോർമുല ഞങ്ങൾ ഉപയോഗിക്കുന്നു

അതിന്റെ അടിസ്ഥാനത്തിൽ, പുരോഗതിയുടെ അജ്ഞാതരായ അംഗങ്ങളെ ഞങ്ങൾ കണ്ടെത്തുന്നു

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ നിബന്ധനകൾ കണക്കാക്കുന്നത് ബുദ്ധിമുട്ടുള്ള കാര്യമല്ല. പുരോഗതി തന്നെ ഇതുപോലെ കാണപ്പെടും

ഉദാഹരണം 2. ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ ആദ്യ മൂന്ന് അംഗങ്ങൾ നൽകിയിരിക്കുന്നു: 6; -12; 24. ഡിനോമിനേറ്ററും ഏഴാമത്തെ പദവും കണ്ടെത്തുക.

പരിഹാരം: ജ്യാമിതീയ പുരോഗതിയുടെ ഡിനോമിനേറ്റർ അതിന്റെ നിർവചനത്തെ അടിസ്ഥാനമാക്കി ഞങ്ങൾ കണക്കാക്കുന്നു

ഞങ്ങൾക്ക് ഒരു ഇതര ജ്യാമിതീയ പുരോഗതി ലഭിച്ചു, അതിന്റെ ഡിനോമിനേറ്റർ -2 ആണ്. ഏഴാമത്തെ പദത്തെ ഫോർമുല ഉപയോഗിച്ച് കണക്കാക്കുന്നു

ഈ ടാസ്ക് പരിഹരിച്ചു.

ഉദാഹരണം 3. ഒരു ജ്യാമിതീയ പുരോഗതി അതിലെ രണ്ട് അംഗങ്ങൾ നൽകുന്നു . പുരോഗതിയുടെ പത്താം പദം കണ്ടെത്തുക.

പരിഹാരം:

നൽകിയിരിക്കുന്ന മൂല്യങ്ങൾ ഫോർമുലകളിലൂടെ എഴുതാം

നിയമങ്ങൾ അനുസരിച്ച്, ഡിനോമിനേറ്റർ കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്, തുടർന്ന് ആവശ്യമുള്ള മൂല്യത്തിനായി നോക്കുക, പക്ഷേ പത്താം ടേമിനായി ഞങ്ങൾക്ക് ഉണ്ട്

ഇൻപുട്ട് ഡാറ്റ ഉപയോഗിച്ച് ലളിതമായ കൃത്രിമത്വങ്ങളുടെ അടിസ്ഥാനത്തിൽ സമാന ഫോർമുല ലഭിക്കും. പരമ്പരയുടെ ആറാമത്തെ ടേം ഞങ്ങൾ മറ്റൊന്നായി വിഭജിക്കുന്നു, അതിന്റെ ഫലമായി നമുക്ക് ലഭിക്കും

തത്ഫലമായുണ്ടാകുന്ന മൂല്യം ആറാമത്തെ പദത്താൽ ഗുണിച്ചാൽ, നമുക്ക് പത്താമത്തെ ലഭിക്കും

അങ്ങനെ, അത്തരം പ്രശ്നങ്ങൾക്ക്, ലളിതമായ പരിവർത്തനങ്ങളുടെ സഹായത്തോടെ വേഗത്തിലുള്ള വഴിനിങ്ങൾക്ക് ശരിയായ പരിഹാരം കണ്ടെത്താൻ കഴിയും.

ഉദാഹരണം 4. ആവർത്തിച്ചുള്ള സൂത്രവാക്യങ്ങളാൽ ജ്യാമിതീയ പുരോഗതി നൽകുന്നു

ജ്യാമിതീയ പുരോഗതിയുടെ ഡിനോമിനേറ്ററും ആദ്യത്തെ ആറ് പദങ്ങളുടെ ആകെത്തുകയും കണ്ടെത്തുക.

പരിഹാരം:

നൽകിയിരിക്കുന്ന ഡാറ്റ ഞങ്ങൾ സമവാക്യങ്ങളുടെ ഒരു സിസ്റ്റത്തിന്റെ രൂപത്തിൽ എഴുതുന്നു

രണ്ടാമത്തെ സമവാക്യത്തെ ആദ്യത്തേത് കൊണ്ട് ഹരിച്ചുകൊണ്ട് ഡിനോമിനേറ്റർ പ്രകടിപ്പിക്കുക

ആദ്യ സമവാക്യത്തിൽ നിന്ന് പുരോഗതിയുടെ ആദ്യ പദം കണ്ടെത്തുക

ജ്യാമിതീയ പുരോഗതിയുടെ ആകെത്തുക കണ്ടെത്താൻ ഇനിപ്പറയുന്ന അഞ്ച് പദങ്ങൾ കണക്കാക്കുക

ഓരോ സ്വാഭാവിക സംഖ്യയും ആണെങ്കിൽ എൻ ഒരു യഥാർത്ഥ സംഖ്യയുമായി പൊരുത്തപ്പെടുത്തുക ഒരു എൻ , അപ്പോൾ അവർ പറഞ്ഞു കൊടുത്തു എന്ന് സംഖ്യാ ക്രമം :

എ 1 , എ 2 , എ 3 , . . . , ഒരു എൻ , . . . .

അതിനാൽ, ഒരു സംഖ്യാ ക്രമം ഒരു സ്വാഭാവിക വാദത്തിന്റെ പ്രവർത്തനമാണ്.

നമ്പർ എ 1 വിളിച്ചു ശ്രേണിയിലെ ആദ്യ അംഗം , നമ്പർ എ 2 — ക്രമത്തിലെ രണ്ടാമത്തെ അംഗം , നമ്പർ എ 3 — മൂന്നാമത്തേത് ഇത്യാദി. നമ്പർ ഒരു എൻ വിളിച്ചു nth അംഗംക്രമങ്ങൾ , കൂടാതെ സ്വാഭാവിക സംഖ്യയും എൻ — അവന്റെ നമ്പർ .

രണ്ട് അയൽക്കാരിൽ നിന്ന് ഒരു എൻ ഒപ്പം ഒരു എൻ +1 അംഗ ക്രമങ്ങൾ ഒരു എൻ +1 വിളിച്ചു തുടർന്നുള്ള (നേരെ ഒരു എൻ ), എ ഒരു എൻ — മുമ്പത്തെ (നേരെ ഒരു എൻ +1 ).

ഒരു സീക്വൻസ് വ്യക്തമാക്കുന്നതിന്, ഏത് നമ്പറിലും ഒരു സീക്വൻസ് അംഗത്തെ കണ്ടെത്താൻ നിങ്ങളെ അനുവദിക്കുന്ന ഒരു രീതി നിങ്ങൾ വ്യക്തമാക്കണം.

കൂടെയാണ് പലപ്പോഴും ക്രമം നൽകിയിരിക്കുന്നത് nth term ഫോർമുലകൾ , അതായത്, ഒരു സീക്വൻസ് അംഗത്തെ അതിന്റെ നമ്പർ അനുസരിച്ച് നിർണ്ണയിക്കാൻ നിങ്ങളെ അനുവദിക്കുന്ന ഒരു ഫോർമുല.

ഉദാഹരണത്തിന്,

പോസിറ്റീവ് ഒറ്റ സംഖ്യകളുടെ ക്രമം ഫോർമുല വഴി നൽകാം

ഒരു എൻ= 2n- 1,

ആൾട്ടർനേറ്റ് ചെയ്യുന്നതിന്റെ ക്രമവും 1 ഒപ്പം -1 - ഫോർമുല

ബിഎൻ = (-1)എൻ +1 . ◄

ക്രമം നിർണ്ണയിക്കാൻ കഴിയും ആവർത്തിച്ചുള്ള ഫോർമുല, അതായത്, ചിലതിൽ തുടങ്ങി, മുമ്പത്തെ (ഒന്നോ അതിലധികമോ) അംഗങ്ങളിലൂടെ, ക്രമത്തിലെ ഏതെങ്കിലും അംഗത്തെ പ്രകടിപ്പിക്കുന്ന ഒരു സൂത്രവാക്യം.

ഉദാഹരണത്തിന്,

എങ്കിൽ എ 1 = 1 , എ ഒരു എൻ +1 = ഒരു എൻ + 5

എ 1 = 1,

എ 2 = എ 1 + 5 = 1 + 5 = 6,

എ 3 = എ 2 + 5 = 6 + 5 = 11,

എ 4 = എ 3 + 5 = 11 + 5 = 16,

എ 5 = എ 4 + 5 = 16 + 5 = 21.

എങ്കിൽ a 1= 1, ഒരു 2 = 1, ഒരു എൻ +2 = ഒരു എൻ + ഒരു എൻ +1 , സംഖ്യാ ശ്രേണിയിലെ ആദ്യത്തെ ഏഴ് അംഗങ്ങളെ ഇനിപ്പറയുന്ന രീതിയിൽ സജ്ജീകരിച്ചിരിക്കുന്നു:

a 1 = 1,

ഒരു 2 = 1,

ഒരു 3 = a 1 + ഒരു 2 = 1 + 1 = 2,

ഒരു 4 = ഒരു 2 + ഒരു 3 = 1 + 2 = 3,

ഒരു 5 = ഒരു 3 + ഒരു 4 = 2 + 3 = 5,

എ 6 = എ 4 + എ 5 = 3 + 5 = 8,

എ 7 = എ 5 + എ 6 = 5 + 8 = 13. ◄

സീക്വൻസുകൾ ആകാം ഫൈനൽ ഒപ്പം അനന്തമായ .

ക്രമം വിളിക്കുന്നു ആത്യന്തികമായ അതിന് പരിമിതമായ അംഗങ്ങൾ ഉണ്ടെങ്കിൽ. ക്രമം വിളിക്കുന്നു അനന്തമായ അതിന് അനന്തമായ അംഗങ്ങൾ ഉണ്ടെങ്കിൽ.

ഉദാഹരണത്തിന്,

രണ്ട് അക്ക സ്വാഭാവിക സംഖ്യകളുടെ ക്രമം:

10, 11, 12, 13, . . . , 98, 99

ഫൈനൽ.

പ്രൈം നമ്പർ സീക്വൻസ്:

2, 3, 5, 7, 11, 13, . . .

അനന്തമായ. ◄

ക്രമം വിളിക്കുന്നു വർദ്ധിച്ചുവരുന്ന , അതിന്റെ ഓരോ അംഗവും, രണ്ടാമത്തേതിൽ നിന്ന് ആരംഭിക്കുന്നത്, മുമ്പത്തേതിനേക്കാൾ വലുതാണെങ്കിൽ.

ക്രമം വിളിക്കുന്നു ക്ഷയിക്കുന്നു , അതിന്റെ ഓരോ അംഗവും, രണ്ടാമത്തേതിൽ നിന്ന് ആരംഭിക്കുന്നത്, മുമ്പത്തേതിനേക്കാൾ കുറവാണെങ്കിൽ.

ഉദാഹരണത്തിന്,

2, 4, 6, 8, . . . , 2എൻ, . . . ഒരു ആരോഹണ ക്രമമാണ്;

1, 1 / 2 , 1 / 3 , 1 / 4 , . . . , 1 /എൻ, . . . ഒരു അവരോഹണ ക്രമമാണ്. ◄

സംഖ്യ കൂടുന്നതിനനുസരിച്ച് മൂലകങ്ങൾ കുറയാത്തതോ അല്ലെങ്കിൽ, വർദ്ധിക്കാത്തതോ ആയ ഒരു ശ്രേണിയെ വിളിക്കുന്നു ഏകതാനമായ ക്രമം .

മോണോടോണിക് സീക്വൻസുകൾ, പ്രത്യേകിച്ച്, സീക്വൻസുകൾ വർദ്ധിപ്പിക്കുകയും സീക്വൻസുകൾ കുറയുകയും ചെയ്യുന്നു.

ഗണിത പുരോഗതി

ഗണിത പുരോഗതി ഒരു ശ്രേണിയെ വിളിക്കുന്നു, ഓരോ അംഗവും, രണ്ടാമത്തേതിൽ നിന്ന് ആരംഭിച്ച്, മുമ്പത്തേതിന് തുല്യമാണ്, അതേ സംഖ്യ ചേർത്തിരിക്കുന്നു.

എ 1 , എ 2 , എ 3 , . . . , ഒരു എൻ, . . .

ഏതെങ്കിലും സ്വാഭാവിക സംഖ്യയാണെങ്കിൽ ഒരു ഗണിത പുരോഗതിയാണ് എൻ വ്യവസ്ഥ പാലിക്കുന്നു:

ഒരു എൻ +1 = ഒരു എൻ + ഡി,

എവിടെ ഡി - കുറച്ച് നമ്പർ.

അങ്ങനെ, നൽകിയിരിക്കുന്നതിന്റെ അടുത്തതും മുമ്പത്തെ അംഗങ്ങളും തമ്മിലുള്ള വ്യത്യാസം ഗണിത പുരോഗതിഎപ്പോഴും സ്ഥിരം:

ഒരു 2 - എ 1 = ഒരു 3 - എ 2 = . . . = ഒരു എൻ +1 - ഒരു എൻ = ഡി.

നമ്പർ ഡി വിളിച്ചു ഒരു ഗണിത പുരോഗതിയുടെ വ്യത്യാസം.

ഒരു ഗണിത പുരോഗതി സജ്ജീകരിക്കുന്നതിന്, അതിന്റെ ആദ്യ പദവും വ്യത്യാസവും വ്യക്തമാക്കിയാൽ മതിയാകും.

ഉദാഹരണത്തിന്,

എങ്കിൽ എ 1 = 3, ഡി = 4 , തുടർന്ന് ക്രമത്തിന്റെ ആദ്യ അഞ്ച് നിബന്ധനകൾ ഇനിപ്പറയുന്ന രീതിയിൽ കാണാം:

a 1 =3,

ഒരു 2 = a 1 + ഡി = 3 + 4 = 7,

ഒരു 3 = ഒരു 2 + ഡി= 7 + 4 = 11,

ഒരു 4 = ഒരു 3 + ഡി= 11 + 4 = 15,

എ 5 = എ 4 + ഡി= 15 + 4 = 19. ◄

ആദ്യ ടേമിനൊപ്പം ഒരു ഗണിത പുരോഗതിക്കായി എ 1 വ്യത്യാസവും ഡി അവളുടെ എൻ

ഒരു എൻ = a 1 + (എൻ- 1)ഡി.

ഉദാഹരണത്തിന്,

ഒരു ഗണിത പുരോഗതിയുടെ മുപ്പതാം പദം കണ്ടെത്തുക

1, 4, 7, 10, . . .

a 1 =1, ഡി = 3,

ഒരു 30 = a 1 + (30 - 1)d= 1 + 29· 3 = 88. ◄

ഒരു n-1 = a 1 + (എൻ- 2)d,

ഒരു എൻ= a 1 + (എൻ- 1)d,

ഒരു എൻ +1 = എ 1 + nd,

അപ്പോൾ വ്യക്തമായി

രണ്ടാമത്തേതിൽ നിന്ന് ആരംഭിക്കുന്ന ഗണിത പുരോഗതിയിലെ ഓരോ അംഗവും മുമ്പത്തേതും തുടർന്നുള്ളതുമായ അംഗങ്ങളുടെ ഗണിത ശരാശരിക്ക് തുല്യമാണ്.

എ, ബി, സി എന്നീ സംഖ്യകൾ ചില ഗണിത പുരോഗതിയുടെ തുടർച്ചയായ അംഗങ്ങളാണ്, അവയിലൊന്ന് മറ്റ് രണ്ടിന്റെയും ഗണിത ശരാശരിക്ക് തുല്യമാണെങ്കിൽ മാത്രം.

ഉദാഹരണത്തിന്,

ഒരു എൻ = 2എൻ- 7 , ഒരു ഗണിത പുരോഗതിയാണ്.

മുകളിലുള്ള പ്രസ്താവന നമുക്ക് ഉപയോഗിക്കാം. നമുക്ക് ഉണ്ട്:

ഒരു എൻ = 2എൻ- 7,

ഒരു n-1 = 2(n- 1) - 7 = 2എൻ- 9,

ഒരു n+1 = 2(n+ 1) - 7 = 2എൻ- 5.

അതിനാൽ,

◄

അതല്ല എൻ ഒരു ഗണിത പുരോഗതിയുടെ അംഗത്തെ മാത്രമല്ല കണ്ടെത്താനാകും എ 1 , മാത്രമല്ല മുമ്പത്തെ ഏതെങ്കിലും ഒരു കെ

ഒരു എൻ = ഒരു കെ + (എൻ- കെ)ഡി.

ഉദാഹരണത്തിന്,

വേണ്ടി എ 5 എഴുതാം

ഒരു 5 = a 1 + 4ഡി,

ഒരു 5 = ഒരു 2 + 3ഡി,

ഒരു 5 = ഒരു 3 + 2ഡി,

ഒരു 5 = ഒരു 4 + ഡി. ◄

ഒരു എൻ = ഒരു എൻ-കെ + kd,

ഒരു എൻ = ഒരു n+k - kd,

അപ്പോൾ വ്യക്തമായി

ഒരു ഗണിത പുരോഗതിയിലെ ഏതൊരു അംഗവും, രണ്ടാമത്തേതിൽ നിന്ന് ആരംഭിക്കുന്നു, അതിൽ നിന്ന് തുല്യ അകലത്തിലുള്ള ഈ ഗണിത പുരോഗതിയിലെ അംഗങ്ങളുടെ പകുതി തുകയ്ക്ക് തുല്യമാണ്.

കൂടാതെ, ഏതൊരു ഗണിത പുരോഗതിക്കും, തുല്യത ശരിയാണ്:

a m + a n = a k + a l,

m + n = k + l.

ഉദാഹരണത്തിന്,

ഗണിത പുരോഗതിയിൽ

1) എ 10 = 28 = (25 + 31)/2 = (എ 9 + എ 11 )/2;

2) 28 = ഒരു 10 = ഒരു 3 + 7ഡി= 7 + 7 3 = 7 + 21 = 28;

3) ഒരു 10= 28 = (19 + 37)/2 = (a 7 + a 13)/2;

4) a 2 + a 12 = a 5 + a 9, കാരണം

a 2 + a 12= 4 + 34 = 38,

a 5 + a 9 = 13 + 25 = 38. ◄

എസ് എൻ= a 1 + a 2 + a 3 + . . .+ ഒരു എൻ,

ആദ്യം എൻ ഒരു ഗണിത പുരോഗതിയിലെ അംഗങ്ങൾ, പദങ്ങളുടെ എണ്ണം കൊണ്ട് അങ്ങേയറ്റത്തെ പദങ്ങളുടെ പകുതി തുകയുടെ ഗുണനത്തിന് തുല്യമാണ്:

ഇതിൽ നിന്ന്, പ്രത്യേകിച്ചും, നിബന്ധനകൾ സംഗ്രഹിക്കേണ്ടത് ആവശ്യമാണെങ്കിൽ അത് പിന്തുടരുന്നു

ഒരു കെ, ഒരു കെ +1 , . . . , ഒരു എൻ,

അപ്പോൾ മുമ്പത്തെ ഫോർമുല അതിന്റെ ഘടന നിലനിർത്തുന്നു:

ഉദാഹരണത്തിന്,

ഗണിത പുരോഗതിയിൽ 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, . . .

എസ് 10 = 1 + 4 + . . . + 28 = (1 + 28) · 10/2 = 145;

10 + 13 + 16 + 19 + 22 + 25 + 28 = എസ് 10 - എസ് 3 = (10 + 28 ) · (10 - 4 + 1)/2 = 133. ◄

ഒരു ഗണിത പുരോഗതി നൽകിയിട്ടുണ്ടെങ്കിൽ, അളവുകൾ എ 1 , ഒരു എൻ, ഡി, എൻഒപ്പംഎസ് എൻ രണ്ട് ഫോർമുലകളാൽ ബന്ധിപ്പിച്ചിരിക്കുന്നു:

അതിനാൽ, ഈ അളവുകളിൽ മൂന്നെണ്ണത്തിന്റെ മൂല്യങ്ങൾ നൽകിയിട്ടുണ്ടെങ്കിൽ, മറ്റ് രണ്ട് അളവുകളുടെ മൂല്യങ്ങൾ ഈ ഫോർമുലകളിൽ നിന്ന് രണ്ട് അജ്ഞാതങ്ങളുള്ള രണ്ട് സമവാക്യങ്ങളുടെ ഒരു സിസ്റ്റത്തിലേക്ക് സംയോജിപ്പിച്ച് നിർണ്ണയിക്കപ്പെടുന്നു.

ഒരു ഗണിത പുരോഗതി ഒരു ഏകതാന ശ്രേണിയാണ്. അതിൽ:

• എങ്കിൽ ഡി > 0 , അപ്പോൾ അത് വർദ്ധിക്കുന്നു;
• എങ്കിൽ ഡി < 0 , അപ്പോൾ അത് കുറയുന്നു;
• എങ്കിൽ ഡി = 0 , അപ്പോൾ ക്രമം നിശ്ചലമായിരിക്കും.

ജ്യാമിതീയ പുരോഗതി

ജ്യാമിതീയ പുരോഗതി ഒരു ശ്രേണിയെ വിളിക്കുന്നു, അതിന്റെ ഓരോ പദവും, രണ്ടാമത്തേതിൽ നിന്ന് ആരംഭിക്കുന്നത്, മുമ്പത്തേതിന് തുല്യമാണ്, അതേ സംഖ്യ കൊണ്ട് ഗുണിച്ചാൽ.

ബി 1 , ബി 2 , ബി 3 , . . . , ബി എൻ, . . .

ഏതെങ്കിലും സ്വാഭാവിക സംഖ്യയാണെങ്കിൽ ഒരു ജ്യാമിതീയ പുരോഗതിയാണ് എൻ വ്യവസ്ഥ പാലിക്കുന്നു:

ബി എൻ +1 = ബി എൻ · q,

എവിടെ q ≠ 0 - കുറച്ച് നമ്പർ.

അതിനാൽ, ഈ ജ്യാമിതീയ പുരോഗതിയുടെ അടുത്ത പദത്തിന്റെ അനുപാതം മുമ്പത്തേതിലേക്കുള്ള അനുപാതം ഒരു സ്ഥിര സംഖ്യയാണ്:

ബി 2 / ബി 1 = ബി 3 / ബി 2 = . . . = ബി എൻ +1 / ബി എൻ = q.

നമ്പർ q വിളിച്ചു ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ ഡിനോമിനേറ്റർ.

ഒരു ജ്യാമിതീയ പുരോഗതി സജ്ജീകരിക്കുന്നതിന്, അതിന്റെ ആദ്യ പദവും ഡിനോമിനേറ്ററും വ്യക്തമാക്കിയാൽ മതി.

ഉദാഹരണത്തിന്,

എങ്കിൽ ബി 1 = 1, q = -3 , തുടർന്ന് ക്രമത്തിന്റെ ആദ്യ അഞ്ച് നിബന്ധനകൾ ഇനിപ്പറയുന്ന രീതിയിൽ കാണാം:

ബി 1 = 1,

ബി 2 = ബി 1 · q = 1 · (-3) = -3,

ബി 3 = ബി 2 · q= -3 · (-3) = 9,

ബി 4 = ബി 3 · q= 9 · (-3) = -27,

ബി 5 = ബി 4 · q= -27 · (-3) = 81. ◄

ബി 1 ഡിനോമിനേറ്ററും q അവളുടെ എൻ -ആം പദം ഫോർമുല ഉപയോഗിച്ച് കണ്ടെത്താം:

ബി എൻ = ബി 1 · q n -1 .

ഉദാഹരണത്തിന്,

ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ ഏഴാമത്തെ പദം കണ്ടെത്തുക 1, 2, 4, . . .

ബി 1 = 1, q = 2,

ബി 7 = ബി 1 · q 6 = 1 2 6 = 64. ◄

bn-1 = ബി 1 · q n -2 ,

ബി എൻ = ബി 1 · q n -1 ,

ബി എൻ +1 = ബി 1 · q n,

അപ്പോൾ വ്യക്തമായി

ബി എൻ 2 = ബി എൻ -1 · ബി എൻ +1 ,

ജ്യാമിതീയ പുരോഗതിയിലെ ഓരോ അംഗവും, രണ്ടാമത്തേതിൽ നിന്ന് ആരംഭിക്കുന്നത്, മുമ്പത്തേതും തുടർന്നുള്ളതുമായ അംഗങ്ങളുടെ ജ്യാമിതീയ ശരാശരി (ആനുപാതികം) തുല്യമാണ്.

സംഭാഷണവും സത്യമായതിനാൽ, ഇനിപ്പറയുന്ന അവകാശവാദം നിലനിൽക്കുന്നു:

a, b, c എന്നീ സംഖ്യകൾ ചില ജ്യാമിതീയ പുരോഗതിയുടെ തുടർച്ചയായ അംഗങ്ങളാണ്, അവയിലൊന്നിന്റെ വർഗ്ഗം മറ്റ് രണ്ടിന്റെയും ഗുണനത്തിന് തുല്യമാണെങ്കിൽ മാത്രം, അതായത്, സംഖ്യകളിൽ ഒന്ന് മറ്റ് രണ്ടിന്റെയും ജ്യാമിതീയ ശരാശരിയാണ്.

ഉദാഹരണത്തിന്,

ഫോർമുല നൽകിയ ക്രമം തെളിയിക്കാം ബി എൻ= -3 2 എൻ , ഒരു ജ്യാമിതീയ പുരോഗതിയാണ്. മുകളിലുള്ള പ്രസ്താവന നമുക്ക് ഉപയോഗിക്കാം. നമുക്ക് ഉണ്ട്:

ബി എൻ= -3 2 എൻ,

ബി എൻ -1 = -3 2 എൻ -1 ,

ബി എൻ +1 = -3 2 എൻ +1 .

അതിനാൽ,

ബി എൻ 2 = (-3 2 എൻ) 2 = (-3 2 എൻ -1 ) (-3 2 എൻ +1 ) = ബി എൻ -1 · ബി എൻ +1 ,

ആവശ്യമായ ഉറപ്പ് തെളിയിക്കുന്നു. ◄

അതല്ല എൻ ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ പദം വഴി മാത്രമല്ല കണ്ടെത്താനാകും ബി 1 , മാത്രമല്ല ഏതെങ്കിലും മുൻ ടേമും ബി കെ , ഫോർമുല ഉപയോഗിച്ചാൽ മതി

ബി എൻ = ബി കെ · q n - കെ.

ഉദാഹരണത്തിന്,

വേണ്ടി ബി 5 എഴുതാം

b 5 = ബി 1 · q 4 ,

b 5 = ബി 2 · q 3,

b 5 = ബി 3 · q2,

b 5 = ബി 4 · q. ◄

ബി എൻ = ബി കെ · q n - കെ,

ബി എൻ = ബി എൻ - കെ · q k,

അപ്പോൾ വ്യക്തമായി

ബി എൻ 2 = ബി എൻ - കെ· ബി എൻ + കെ

ജ്യാമിതീയ പുരോഗതിയിലെ ഏതെങ്കിലും അംഗത്തിന്റെ ചതുരം, രണ്ടാമത്തേതിൽ നിന്ന് ആരംഭിക്കുന്നു, അതിൽ നിന്ന് തുല്യമായ ഈ പുരോഗതിയിലെ അംഗങ്ങളുടെ ഉൽപ്പന്നത്തിന് തുല്യമാണ്.

കൂടാതെ, ഏതെങ്കിലും ജ്യാമിതീയ പുരോഗതിക്ക്, തുല്യത ശരിയാണ്:

ബി എം· ബി എൻ= ബി കെ· ബി എൽ,

എം+ എൻ= കെ+ എൽ.

ഉദാഹരണത്തിന്,

വിസ്തൃതമായി

1) ബി 6 2 = 32 2 = 1024 = 16 · 64 = ബി 5 · ബി 7 ;

2) 1024 = ബി 11 = ബി 6 · q 5 = 32 · 2 5 = 1024;

3) ബി 6 2 = 32 2 = 1024 = 8 · 128 = ബി 4 · ബി 8 ;

4) ബി 2 · ബി 7 = ബി 4 · ബി 5 , കാരണം

ബി 2 · ബി 7 = 2 · 64 = 128,

ബി 4 · ബി 5 = 8 · 16 = 128. ◄

എസ് എൻ= ബി 1 + ബി 2 + ബി 3 + . . . + ബി എൻ

ആദ്യം എൻ ഒരു ഡിനോമിനേറ്റർ ഉള്ള ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ നിബന്ധനകൾ q ≠ 0 ഫോർമുല ഉപയോഗിച്ച് കണക്കാക്കുന്നു:

പിന്നെ എപ്പോൾ q = 1 - ഫോർമുല അനുസരിച്ച്

എസ് എൻ= എൻ.ബി. 1

നമുക്ക് നിബന്ധനകൾ സംഗ്രഹിക്കണമെങ്കിൽ ശ്രദ്ധിക്കുക

ബി കെ, ബി കെ +1 , . . . , ബി എൻ,

അപ്പോൾ ഫോർമുല ഉപയോഗിക്കുന്നു:

ഉദാഹരണത്തിന്,

വിസ്തൃതമായി 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, . . .

എസ് 10 = 1 + 2 + . . . + 512 = 1 · (1 - 2 10) / (1 - 2) = 1023;

64 + 128 + 256 + 512 = എസ് 10 - എസ് 6 = 64 · (1 - 2 10-7+1) / (1 - 2) = 960. ◄

ഒരു ജ്യാമിതീയ പുരോഗതി നൽകിയിട്ടുണ്ടെങ്കിൽ, അളവുകൾ ബി 1 , ബി എൻ, q, എൻഒപ്പം എസ് എൻ രണ്ട് ഫോർമുലകളാൽ ബന്ധിപ്പിച്ചിരിക്കുന്നു:

അതിനാൽ, ഈ അളവുകളിൽ ഏതെങ്കിലും മൂന്ന് മൂല്യങ്ങൾ നൽകിയിട്ടുണ്ടെങ്കിൽ, മറ്റ് രണ്ട് അളവുകളുടെ മൂല്യങ്ങൾ ഈ ഫോർമുലകളിൽ നിന്ന് രണ്ട് അജ്ഞാതങ്ങളുള്ള രണ്ട് സമവാക്യങ്ങളുടെ ഒരു സിസ്റ്റത്തിലേക്ക് സംയോജിപ്പിച്ച് നിർണ്ണയിക്കപ്പെടുന്നു.

ആദ്യ ടേമിനൊപ്പം ഒരു ജ്യാമിതീയ പുരോഗതിക്ക് ബി 1 ഡിനോമിനേറ്ററും q ഇനിപ്പറയുന്നവ നടക്കുന്നു monotonicity പ്രോപ്പർട്ടികൾ :

• ഇനിപ്പറയുന്ന വ്യവസ്ഥകളിൽ ഒന്ന് പാലിക്കുകയാണെങ്കിൽ പുരോഗതി വർദ്ധിക്കുന്നു:

ബി 1 > 0 ഒപ്പം q> 1;

ബി 1 < 0 ഒപ്പം 0 < q< 1;

• ഇനിപ്പറയുന്ന വ്യവസ്ഥകളിൽ ഒന്ന് പാലിക്കുകയാണെങ്കിൽ പുരോഗതി കുറയുന്നു:

ബി 1 > 0 ഒപ്പം 0 < q< 1;

ബി 1 < 0 ഒപ്പം q> 1.

എങ്കിൽ q< 0 , അപ്പോൾ ജ്യാമിതീയ പുരോഗതി ചിഹ്ന-ആൾട്ടർനേറ്റിംഗ് ആണ്: അതിന്റെ ഒറ്റ-അക്ക പദങ്ങൾക്ക് അതിന്റെ ആദ്യ പദത്തിന്റെ അതേ ചിഹ്നവും ഇരട്ട-സംഖ്യയുള്ള പദങ്ങൾക്ക് വിപരീത ചിഹ്നവുമാണ്. ഒരു ഇതര ജ്യാമിതീയ പുരോഗതി ഏകതാനമല്ലെന്ന് വ്യക്തമാണ്.

ആദ്യത്തേതിന്റെ ഉൽപ്പന്നം എൻ ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ നിബന്ധനകൾ ഫോർമുല ഉപയോഗിച്ച് കണക്കാക്കാം:

പി എൻ= ബി 1 · ബി 2 · ബി 3 · . . . · ബി എൻ = (ബി 1 · ബി എൻ) എൻ / 2 .

ഉദാഹരണത്തിന്,

1 · 2 · 4 · 8 · 16 · 32 · 64 · 128 = (1 · 128) 8/2 = 128 4 = 268 435 456;

3 · 6 · 12 · 24 · 48 = (3 · 48) 5/2 = (144 1/2) 5 = 12 5 = 248 832.◄

ജ്യാമിതീയ പുരോഗതി അനന്തമായി കുറയുന്നു

ജ്യാമിതീയ പുരോഗതി അനന്തമായി കുറയുന്നു ഡിനോമിനേറ്റർ മോഡുലസിനേക്കാൾ കുറവുള്ള അനന്തമായ ജ്യാമിതീയ പുരോഗതി എന്ന് വിളിക്കുന്നു 1 , അതാണ്

|q| < 1 .

അനന്തമായി കുറയുന്ന ജ്യാമിതീയ പുരോഗതി കുറയുന്ന ഒരു ശ്രേണി ആയിരിക്കണമെന്നില്ല. ഇത് കേസിന് അനുയോജ്യമാണ്

1 < q< 0 .

അത്തരമൊരു ഡിനോമിനേറ്റർ ഉപയോഗിച്ച്, ക്രമം അടയാളം-ആൾട്ടർനേറ്റിംഗ് ആണ്. ഉദാഹരണത്തിന്,

1, - 1 / 2 , 1 / 4 , - 1 / 8 , . . . .

അനന്തമായി കുറയുന്ന ജ്യാമിതീയ പുരോഗതിയുടെ ആകെത്തുക ആദ്യത്തേതിന്റെ ആകെത്തുക വരുന്ന സംഖ്യയ്ക്ക് പേര് നൽകുക എൻ എണ്ണത്തിൽ പരിധിയില്ലാത്ത വർദ്ധനയോടെയുള്ള പുരോഗതിയുടെ നിബന്ധനകൾ എൻ . ഈ സംഖ്യ എല്ലായ്പ്പോഴും പരിമിതമാണ്, ഇത് ഫോർമുലയാൽ പ്രകടിപ്പിക്കുന്നു

ഉദാഹരണത്തിന്,

10 + 1 + 0,1 + 0,01 + . . . = 10 / (1 - 0,1) = 11 1 / 9 ,

10 - 1 + 0,1 - 0,01 + . . . = 10 / (1 + 0,1) = 9 1 / 11 . ◄

ഗണിതവും ജ്യാമിതീയവുമായ പുരോഗതികൾ തമ്മിലുള്ള ബന്ധം

ഗണിതവും ജ്യാമിതീയ പുരോഗതിഅടുത്ത ബന്ധമുള്ളവയാണ്. നമുക്ക് രണ്ട് ഉദാഹരണങ്ങൾ മാത്രം പരിഗണിക്കാം.

എ 1 , എ 2 , എ 3 , . . . ഡി , അത്

ബി എ 1 , ബി എ 2 , ബി എ 3 , . . . ബി ഡി .

ഉദാഹരണത്തിന്,

1, 3, 5, . . . - വ്യത്യാസത്തോടുകൂടിയ ഗണിത പുരോഗതി 2 ഒപ്പം

7 1 , 7 3 , 7 5 , . . . ഒരു ഡിനോമിനേറ്ററുള്ള ഒരു ജ്യാമിതീയ പുരോഗതിയാണ് 7 2 . ◄

ബി 1 , ബി 2 , ബി 3 , . . . ഒരു ഡിനോമിനേറ്ററുള്ള ഒരു ജ്യാമിതീയ പുരോഗതിയാണ് q , അത്

ലോഗ് എ ബി 1, ലോഗ് എ ബി 2, ലോഗ് എ ബി 3, . . . - വ്യത്യാസത്തോടുകൂടിയ ഗണിത പുരോഗതി ലോഗ് എq .

ഉദാഹരണത്തിന്,

2, 12, 72, . . . ഒരു ഡിനോമിനേറ്ററുള്ള ഒരു ജ്യാമിതീയ പുരോഗതിയാണ് 6 ഒപ്പം

lg 2, lg 12, lg 72, . . . - വ്യത്യാസത്തോടുകൂടിയ ഗണിത പുരോഗതി lg 6 . ◄

നമുക്ക് ഒരു പരമ്പര പരിഗണിക്കാം.

7 28 112 448 1792...

അതിന്റെ ഏതെങ്കിലും മൂലകങ്ങളുടെ മൂല്യം മുമ്പത്തേതിനേക്കാൾ നാലിരട്ടി കൂടുതലാണെന്ന് തികച്ചും വ്യക്തമാണ്. അതിനാൽ ഈ പരമ്പര ഒരു പുരോഗതിയാണ്.

സംഖ്യകളുടെ അനന്തമായ ശ്രേണിയാണ് ജ്യാമിതീയ പുരോഗതി പ്രധാന ഗുണംഅതായത് ചില പ്രത്യേക സംഖ്യ കൊണ്ട് ഗുണിച്ചാൽ മുമ്പത്തേതിൽ നിന്ന് അടുത്ത സംഖ്യ ലഭിക്കുന്നു. ഇത് ഇനിപ്പറയുന്ന ഫോർമുല ഉപയോഗിച്ച് പ്രകടിപ്പിക്കുന്നു.

a z +1 =a z q, ഇവിടെ z എന്നത് തിരഞ്ഞെടുത്ത ഘടകത്തിന്റെ സംഖ്യയാണ്.

അതനുസരിച്ച്, z ∈ N.

സ്കൂളിൽ ഒരു ജ്യാമിതീയ പുരോഗതി പഠിക്കുന്ന കാലഘട്ടം ഗ്രേഡ് 9 ആണ്. ആശയം മനസ്സിലാക്കാൻ ഉദാഹരണങ്ങൾ നിങ്ങളെ സഹായിക്കും:

0.25 0.125 0.0625...

ഈ ഫോർമുലയെ അടിസ്ഥാനമാക്കി, പുരോഗതിയുടെ ഡിനോമിനേറ്റർ ഇനിപ്പറയുന്ന രീതിയിൽ കണ്ടെത്താം:

q അല്ലെങ്കിൽ b z എന്നിവ പൂജ്യമാകില്ല. കൂടാതെ, പുരോഗതിയുടെ ഓരോ ഘടകങ്ങളും പൂജ്യത്തിന് തുല്യമായിരിക്കരുത്.

അതനുസരിച്ച്, പരമ്പരയിലെ അടുത്ത സംഖ്യ കണ്ടെത്താൻ, നിങ്ങൾ അവസാനത്തേത് q കൊണ്ട് ഗുണിക്കേണ്ടതുണ്ട്.

ഈ പുരോഗതി വ്യക്തമാക്കുന്നതിന്, നിങ്ങൾ അതിന്റെ ആദ്യ ഘടകവും ഡിനോമിനേറ്ററും വ്യക്തമാക്കണം. അതിനുശേഷം, തുടർന്നുള്ള ഏതെങ്കിലും നിബന്ധനകളും അവയുടെ തുകയും കണ്ടെത്താൻ കഴിയും.

ഇനങ്ങൾ

q, a 1 എന്നിവയെ ആശ്രയിച്ച്, ഈ പുരോഗതിയെ പല തരങ്ങളായി തിരിച്ചിരിക്കുന്നു:

• ഒരു 1 ഉം q ഉം ഒന്നിൽ കൂടുതലാണെങ്കിൽ, അത്തരം ഒരു അനുക്രമം ഓരോ അടുത്ത ഘടകത്തിലും വർദ്ധിക്കുന്ന ഒരു ജ്യാമിതീയ പുരോഗതിയാണ്. അത്തരത്തിലുള്ള ഒരു ഉദാഹരണം ചുവടെ അവതരിപ്പിച്ചിരിക്കുന്നു.

ഉദാഹരണം: a 1 =3, q=2 - രണ്ട് പരാമീറ്ററുകളും ഒന്നിൽ കൂടുതലാണ്.

അപ്പോൾ സംഖ്യാ ക്രമം ഇതുപോലെ എഴുതാം:

3 6 12 24 48 ...

• എങ്കിൽ |q| ഒന്നിൽ താഴെ, അതായത്, അത് കൊണ്ട് ഗുണിക്കുന്നത് വിഭജനത്തിന് തുല്യമാണ്, തുടർന്ന് സമാനമായ അവസ്ഥകളുള്ള ഒരു പുരോഗതി കുറയുന്ന ജ്യാമിതീയ പുരോഗതിയാണ്. അത്തരത്തിലുള്ള ഒരു ഉദാഹരണം ചുവടെ അവതരിപ്പിച്ചിരിക്കുന്നു.

ഉദാഹരണം: a 1 =6, q=1/3 - a 1 ഒന്നിനെക്കാൾ വലുതാണ്, q എന്നത് കുറവാണ്.

അപ്പോൾ സംഖ്യാ ക്രമം ഇനിപ്പറയുന്ന രീതിയിൽ എഴുതാം:

6 2 2/3 ... - ഏത് മൂലകവും അതിനെ പിന്തുടരുന്ന മൂലകത്തേക്കാൾ 3 മടങ്ങ് വലുതാണ്.

• അടയാളം-വേരിയബിൾ. എങ്കിൽ q<0, то знаки у чисел последовательности постоянно чередуются вне зависимости от a 1 , а элементы ни возрастают, ни убывают.

ഉദാഹരണം: a 1 = -3 , q = -2 - രണ്ട് പരാമീറ്ററുകളും പൂജ്യത്തേക്കാൾ കുറവാണ്.

അപ്പോൾ ക്രമം ഇങ്ങനെ എഴുതാം:

3, 6, -12, 24,...

സൂത്രവാക്യങ്ങൾ

ജ്യാമിതീയ പുരോഗതിയുടെ സൗകര്യപ്രദമായ ഉപയോഗത്തിന്, നിരവധി സൂത്രവാക്യങ്ങൾ ഉണ്ട്:

• z-th അംഗത്തിന്റെ ഫോർമുല. മുമ്പത്തെ സംഖ്യകൾ കണക്കാക്കാതെ ഒരു നിർദ്ദിഷ്ട സംഖ്യയ്ക്ക് കീഴിലുള്ള ഘടകം കണക്കാക്കാൻ നിങ്ങളെ അനുവദിക്കുന്നു.

ഉദാഹരണം:q = 3, എ 1 = 4. പുരോഗതിയുടെ നാലാമത്തെ ഘടകം കണക്കാക്കേണ്ടത് ആവശ്യമാണ്.

പരിഹാരം:എ 4 = 4 · 3 4-1 = 4 · 3 3 = 4 · 27 = 108.

• സംഖ്യയായ ആദ്യ മൂലകങ്ങളുടെ ആകെത്തുക z. വരെയുള്ള ഒരു ശ്രേണിയിലെ എല്ലാ ഘടകങ്ങളുടെയും ആകെത്തുക കണക്കാക്കാൻ നിങ്ങളെ അനുവദിക്കുന്നുഒരു ഇസഡ്ഉൾപ്പെടെ.

മുതൽ (1-q) ഡിനോമിനേറ്ററിലാണ്, തുടർന്ന് (1 - q)≠ 0, അതിനാൽ q 1 ന് തുല്യമല്ല.

ശ്രദ്ധിക്കുക: q=1 ആണെങ്കിൽ, പുരോഗതി അനന്തമായി ആവർത്തിക്കുന്ന സംഖ്യയുടെ ഒരു ശ്രേണിയായിരിക്കും.

ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ ആകെത്തുക, ഉദാഹരണങ്ങൾ:എ 1 = 2, q= -2. എസ് 5 കണക്കാക്കുക.

പരിഹാരം:എസ് 5 = 22 - ഫോർമുല പ്രകാരം കണക്കുകൂട്ടൽ.

• എങ്കിൽ തുക |q| < 1 и если z стремится к бесконечности.

ഉദാഹരണം:എ 1 = 2 , q= 0.5. തുക കണ്ടെത്തുക.

പരിഹാരം:Sz = 2 · = 4

Sz = 2 + 1 + 0.5 + 0.25 + 0.125 + 0.0625 = 3.9375 4

ചില ഗുണങ്ങൾ:

• സ്വഭാവഗുണം. ഇനിപ്പറയുന്ന വ്യവസ്ഥയാണെങ്കിൽ ഏതെങ്കിലും വേണ്ടി നടത്തിz, അപ്പോൾ നൽകിയിരിക്കുന്ന സംഖ്യ ശ്രേണി ഒരു ജ്യാമിതീയ പുരോഗതിയാണ്:

ഒരു ഇസഡ് 2 = ഒരു ഇസഡ് -1 · എz+1

• കൂടാതെ, ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ ഏത് സംഖ്യയുടെയും വർഗ്ഗം, തന്നിരിക്കുന്ന ശ്രേണിയിലെ മറ്റേതെങ്കിലും രണ്ട് സംഖ്യകളുടെ വർഗ്ഗങ്ങൾ ഈ മൂലകത്തിൽ നിന്ന് തുല്യ ദൂരെയാണെങ്കിൽ, അവയെ ചേർത്തുകൊണ്ട് കണ്ടെത്തുന്നു.

ഒരു ഇസഡ് 2 = ഒരു ഇസഡ് - ടി 2 + ഒരു ഇസഡ് + ടി 2 , എവിടെടിഈ സംഖ്യകൾ തമ്മിലുള്ള ദൂരമാണ്.

• ഘടകങ്ങൾq ൽ വ്യത്യാസമുണ്ട്ഒരിക്കല്.
• പുരോഗതി മൂലകങ്ങളുടെ ലോഗരിതങ്ങളും ഒരു പുരോഗതി ഉണ്ടാക്കുന്നു, പക്ഷേ ഇതിനകം ഗണിതമാണ്, അതായത്, അവ ഓരോന്നും മുമ്പത്തേതിനേക്കാൾ ഒരു നിശ്ചിത സംഖ്യ കൊണ്ട് വലുതാണ്.

ചില ക്ലാസിക്കൽ പ്രശ്നങ്ങളുടെ ഉദാഹരണങ്ങൾ

ഒരു ജ്യാമിതീയ പുരോഗതി എന്താണെന്ന് നന്നായി മനസ്സിലാക്കാൻ, ഗ്രേഡ് 9-ന് പരിഹാരമുള്ള ഉദാഹരണങ്ങൾ സഹായിക്കും.

• വ്യവസ്ഥകൾ:എ 1 = 3, എ 3 = 48. കണ്ടെത്തുകq.

പരിഹാരം: തുടർന്നുള്ള ഓരോ മൂലകവും മുമ്പത്തേതിനേക്കാൾ വലുതാണ്q ഒരിക്കല്.ഒരു ഡിനോമിനേറ്റർ ഉപയോഗിച്ച് ചില ഘടകങ്ങൾ മറ്റുള്ളവരിലൂടെ പ്രകടിപ്പിക്കേണ്ടത് ആവശ്യമാണ്.

അതിനാൽ,എ 3 = q 2 · എ 1

പകരം വയ്ക്കുമ്പോൾq= 4

• വ്യവസ്ഥകൾ:എ 2 = 6, എ 3 = 12. എസ് 6 കണക്കാക്കുക.

പരിഹാരം:ഇത് ചെയ്യുന്നതിന്, ആദ്യത്തെ ഘടകമായ q കണ്ടെത്തി അതിനെ ഫോർമുലയിലേക്ക് മാറ്റിസ്ഥാപിച്ചാൽ മതി.

എ 3 = q· എ 2 , അതിനാൽ,q= 2

a 2 = q a 1,അതുകൊണ്ടാണ് a 1 = 3

എസ് 6 = 189

• · എ 1 = 10, q= -2. പുരോഗതിയുടെ നാലാമത്തെ ഘടകം കണ്ടെത്തുക.

പരിഹാരം: ഇത് ചെയ്യുന്നതിന്, നാലാമത്തെ ഘടകം ആദ്യത്തേതും ഡിനോമിനേറ്ററിലൂടെയും പ്രകടിപ്പിക്കാൻ മതിയാകും.

a 4 = q 3· a 1 = -80

ആപ്ലിക്കേഷൻ ഉദാഹരണം:

• ബാങ്കിന്റെ ക്ലയന്റ് 10,000 റുബിളിൽ ഒരു നിക്ഷേപം നടത്തി, അതിന്റെ നിബന്ധനകൾ പ്രകാരം എല്ലാ വർഷവും ക്ലയന്റ് അതിന്റെ 6% പ്രധാന തുകയിലേക്ക് ചേർക്കും. 4 വർഷത്തിനുശേഷം അക്കൗണ്ടിൽ എത്ര പണം വരും?

പരിഹാരം: പ്രാരംഭ തുക 10 ആയിരം റുബിളാണ്. അതിനാൽ, നിക്ഷേപം കഴിഞ്ഞ് ഒരു വർഷം കഴിഞ്ഞ്, അക്കൗണ്ടിന് 10,000 + 10,000 തുല്യമായ തുക ഉണ്ടായിരിക്കും. · 0.06 = 10000 1.06

അതനുസരിച്ച്, മറ്റൊരു വർഷത്തിനുശേഷം അക്കൗണ്ടിലെ തുക ഇനിപ്പറയുന്ന രീതിയിൽ പ്രകടിപ്പിക്കും:

(10000 1.06) 0.06 + 10000 1.06 = 1.06 1.06 10000

അതായത്, ഓരോ വർഷവും തുക 1.06 മടങ്ങ് വർദ്ധിക്കുന്നു. ഇതിനർത്ഥം, 4 വർഷത്തിനു ശേഷം അക്കൗണ്ടിലെ ഫണ്ടുകളുടെ തുക കണ്ടെത്തുന്നതിന്, പുരോഗതിയുടെ നാലാമത്തെ ഘടകം കണ്ടെത്തുന്നതിന് ഇത് മതിയാകും, അത് 10 ആയിരത്തിന് തുല്യമായ ആദ്യ ഘടകവും 1.06 ന് തുല്യമായ ഡിനോമിനേറ്ററും നൽകുന്നു.

എസ് = 1.06 1.06 1.06 1.06 10000 = 12625

തുക കണക്കാക്കുന്നതിനുള്ള ജോലികളുടെ ഉദാഹരണങ്ങൾ:

വിവിധ പ്രശ്നങ്ങളിൽ, ഒരു ജ്യാമിതീയ പുരോഗതി ഉപയോഗിക്കുന്നു. തുക കണ്ടെത്തുന്നതിനുള്ള ഒരു ഉദാഹരണം ഇനിപ്പറയുന്ന രീതിയിൽ നൽകാം:

എ 1 = 4, q= 2, കണക്കാക്കുകS5.

പരിഹാരം: കണക്കുകൂട്ടലിന് ആവശ്യമായ എല്ലാ ഡാറ്റയും അറിയാം, നിങ്ങൾ അവയെ ഫോർമുലയിലേക്ക് മാറ്റിസ്ഥാപിക്കേണ്ടതുണ്ട്.

എസ് 5 = 124

• എ 2 = 6, എ 3 = 18. ആദ്യത്തെ ആറ് മൂലകങ്ങളുടെ ആകെത്തുക കണക്കാക്കുക.

പരിഹാരം:

ജിയോം. പുരോഗതി, ഓരോ അടുത്ത മൂലകവും മുമ്പത്തേതിനേക്കാൾ q മടങ്ങ് കൂടുതലാണ്, അതായത്, തുക കണക്കാക്കാൻ, നിങ്ങൾ മൂലകം അറിയേണ്ടതുണ്ട്എ 1 ഡിനോമിനേറ്ററുംq.

എ 2 · q = എ 3

q = 3

അതുപോലെ, നമ്മൾ കണ്ടെത്തേണ്ടതുണ്ട്എ 1 , അറിയുന്നഎ 2 ഒപ്പംq.

എ 1 · q = എ 2

a 1 =2

എസ് 6 = 728.

ഒരു ജ്യാമിതീയ പുരോഗതി എന്നത് ഒരു സംഖ്യാ ശ്രേണിയാണ്, അതിന്റെ ആദ്യ പദം പൂജ്യമല്ല, കൂടാതെ ഓരോ അടുത്ത പദവും പൂജ്യമല്ലാത്ത സംഖ്യ കൊണ്ട് ഗുണിച്ച മുൻ പദത്തിന് തുല്യമാണ്.

ജ്യാമിതീയ പുരോഗതിയുടെ ആശയം

ജ്യാമിതീയ പുരോഗതിയെ സൂചിപ്പിക്കുന്നത് b1,b2,b3, ..., bn, ... .

ജ്യാമിതീയ പിശകിന്റെ ഏതെങ്കിലും പദത്തിന്റെയും അതിന്റെ മുൻ പദത്തിന്റെയും അനുപാതം അതേ സംഖ്യയ്ക്ക് തുല്യമാണ്, അതായത്, b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+ 1)/bn =…. ഇത് ഒരു ഗണിത പുരോഗതിയുടെ നിർവചനത്തിൽ നിന്ന് നേരിട്ട് പിന്തുടരുന്നു. ഈ സംഖ്യയെ ജ്യാമിതീയ പുരോഗതിയുടെ ഡിനോമിനേറ്റർ എന്ന് വിളിക്കുന്നു. സാധാരണയായി ഒരു ജ്യാമിതീയ പുരോഗതിയുടെ ഡിനോമിനേറ്റർ q എന്ന അക്ഷരത്താൽ സൂചിപ്പിക്കപ്പെടുന്നു.

|q| എന്നതിനായുള്ള അനന്തമായ ജ്യാമിതീയ പുരോഗതിയുടെ ആകെത്തുക<1

ഒരു ജ്യാമിതീയ പുരോഗതി സജ്ജീകരിക്കുന്നതിനുള്ള ഒരു മാർഗ്ഗം, അതിന്റെ ആദ്യ ടേം b1 ഉം ജ്യാമിതീയ പിശകിന്റെ ഡിനോമിനേറ്ററും സജ്ജീകരിക്കുക എന്നതാണ്. ഉദാഹരണത്തിന്, b1=4, q=-2. ഈ രണ്ട് അവസ്ഥകളും 4, -8, 16, -32, … ന്റെ ജ്യാമിതീയ പുരോഗതി നൽകുന്നു.

q>0 (q 1 ന് തുല്യമല്ല) എങ്കിൽ, പുരോഗതി ഒരു ഏകതാന ശ്രേണിയാണ്. ഉദാഹരണത്തിന്, 2, 4,8,16,32, ... എന്ന ക്രമം ഏകതാനമായി വർദ്ധിക്കുന്ന ഒരു ശ്രേണിയാണ് (b1=2, q=2).

ജ്യാമിതീയ പിശകിൽ ഡിനോമിനേറ്റർ q=1 ആണെങ്കിൽ, ജ്യാമിതീയ പുരോഗതിയിലെ എല്ലാ അംഗങ്ങളും പരസ്പരം തുല്യമായിരിക്കും. അത്തരം സന്ദർഭങ്ങളിൽ, പുരോഗതി സ്ഥിരമായ ഒരു ക്രമമാണെന്ന് പറയപ്പെടുന്നു.

സംഖ്യാ ക്രമം (bn) ഒരു ജ്യാമിതീയ പുരോഗതി ആകുന്നതിന്, അതിന്റെ ഓരോ അംഗവും, രണ്ടാമത്തേതിൽ നിന്ന് ആരംഭിക്കുന്നത്, അയൽ അംഗങ്ങളുടെ ജ്യാമിതീയ ശരാശരി ആയിരിക്കേണ്ടത് ആവശ്യമാണ്. അതായത്, ഇനിപ്പറയുന്ന സമവാക്യം നിറവേറ്റേണ്ടത് ആവശ്യമാണ്
(b(n+1))^2 = bn * b(n+2), ഏത് n>0 നും, ഇവിടെ n സ്വാഭാവിക സംഖ്യകളുടെ N ഗണത്തിൽ പെടുന്നു.

ഇനി നമുക്ക് (Xn) - ഒരു ജ്യാമിതീയ പുരോഗതി. |q|∞) ഉള്ള ജ്യാമിതീയ പുരോഗതി q ന്റെ ഡിനോമിനേറ്റർ.
അനന്തമായ ജ്യാമിതീയ പുരോഗതിയുടെ ആകെത്തുക എസ് കൊണ്ട് സൂചിപ്പിക്കുന്നുവെങ്കിൽ, ഇനിപ്പറയുന്ന ഫോർമുല പിടിക്കും:
S=x1/(1-q).

ഒരു ലളിതമായ ഉദാഹരണം പരിഗണിക്കുക:

അനന്തമായ ജ്യാമിതീയ പുരോഗതിയുടെ ആകെത്തുക കണ്ടെത്തുക 2, -2/3, 2/9, - 2/27, ... .

എസ് കണ്ടെത്തുന്നതിന്, അനന്തമായ ഗണിത പുരോഗതിയുടെ ആകെത്തുകയ്ക്കായി ഞങ്ങൾ ഫോർമുല ഉപയോഗിക്കുന്നു. |-1/3|< 1. x1 = 2. S=2/(1-(-1/3)) = 3/2.