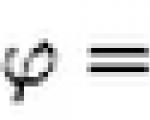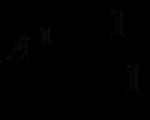हार्मोनिक कंपनांचे समीकरण कसे लिहायचे. हार्मोनिक कंपने आणि त्यांची वैशिष्ट्ये

oscillations सर्वात सोपा प्रकार आहेत हार्मोनिक कंपने- दोलन ज्यामध्ये समतोल स्थितीतून दोलन बिंदूचे विस्थापन साइन किंवा कोसाइनच्या नियमानुसार कालांतराने बदलते.

अशा प्रकारे, वर्तुळात बॉलच्या एकसमान रोटेशनसह, त्याचे प्रक्षेपण (प्रकाशाच्या समांतर किरणांमधील सावली) उभ्या पडद्यावर हार्मोनिक दोलन गती करते (चित्र 1).

हार्मोनिक कंपनांच्या दरम्यान समतोल स्थितीतून होणारे विस्थापन हे फॉर्मच्या समीकरणाद्वारे (याला हार्मोनिक मोशनचा किनेमॅटिक नियम म्हणतात) वर्णन केले आहे:

जेथे x हे विस्थापन आहे - समतोल स्थितीशी संबंधित आणि समतोल स्थितीपासून बिंदूच्या स्थानापर्यंतच्या अंतराने मोजले जाणारे एक परिमाण t वेळी दोलन बिंदूची स्थिती दर्शवते; ए - दोलनांचे मोठेपणा - समतोल स्थितीतून शरीराचे जास्तीत जास्त विस्थापन; टी - दोलनाचा कालावधी - एका संपूर्ण दोलनाचा काळ; त्या सर्वात कमी कालावधी ज्यानंतर दोलन दर्शविणारी भौतिक परिमाणांची मूल्ये पुनरावृत्ती केली जातात; - प्रारंभिक टप्पा;

दोलन टप्पा वेळी टी. दोलन टप्पा हा नियतकालिक कार्याचा एक युक्तिवाद आहे, जो दिलेल्या दोलन मोठेपणासाठी, शरीराच्या कोणत्याही वेळी दोलन प्रणालीची (विस्थापन, गती, प्रवेग) स्थिती निर्धारित करतो.

जर वेळेच्या सुरुवातीच्या क्षणी दोलन बिंदू समतोल स्थितीपासून जास्तीत जास्त विस्थापित झाला असेल, तर , आणि समतोल स्थितीपासून बिंदूचे विस्थापन कायद्यानुसार बदलते.

जर दोलन बिंदू स्थिर समतोल स्थितीत असेल, तर समतोल स्थितीपासून बिंदूचे विस्थापन कायद्यानुसार बदलते.

मूल्य V, कालावधीचा व्यस्त आणि 1 s मध्ये पूर्ण झालेल्या दोलनांच्या संख्येइतका, याला दोलन वारंवारता म्हणतात:

जर टी वेळेत शरीर N पूर्ण दोलन करते, तर

आकार शरीर s मध्ये किती दोलन करते हे दर्शविण्यास म्हणतात चक्रीय (परिपत्रक) वारंवारता.

हार्मोनिक मोशनचा किनेमॅटिक नियम खालीलप्रमाणे लिहिला जाऊ शकतो:

ग्राफिकदृष्ट्या, वेळेवर दोलन बिंदूच्या विस्थापनाचे अवलंबित्व कोसाइन वेव्ह (किंवा साइन वेव्ह) द्वारे दर्शविले जाते.

आकृती 2, a केससाठी समतोल स्थितीपासून दोलन बिंदूच्या विस्थापनाच्या वेळेच्या अवलंबनाचा आलेख दर्शवितो.

एका दोलन बिंदूचा वेग काळाबरोबर कसा बदलतो ते शोधूया. हे करण्यासाठी, आम्हाला या अभिव्यक्तीचा वेळ व्युत्पन्न सापडतो:

x-अक्षावर वेग प्रक्षेपणाचे मोठेपणा कुठे आहे.

हे सूत्र दर्शविते की हार्मोनिक दोलनांदरम्यान, शरीराच्या वेगाचा x-अक्षावर प्रक्षेपण देखील हार्मोनिक नियमानुसार समान वारंवारतेसह, भिन्न मोठेपणासह बदलतो आणि (चित्र 2, बी) टप्प्यात विस्थापनाच्या पुढे असतो. ).

प्रवेगाचे अवलंबित्व स्पष्ट करण्यासाठी, आम्हाला वेग प्रक्षेपणाचा वेळ व्युत्पन्न आढळतो:

एक्स-अक्षावर प्रवेग प्रक्षेपणाचे मोठेपणा कुठे आहे.

हार्मोनिक दोलनांसह, प्रवेग प्रक्षेपण k (Fig. 2, c) द्वारे फेज विस्थापनाच्या पुढे आहे.

त्याचप्रमाणे, तुम्ही अवलंबित्व आलेख तयार करू शकता

हार्मोनिक कंपनाचे समीकरण

हार्मोनिक ऑसीलेशनचे समीकरण वेळेवर शरीराच्या समन्वयांचे अवलंबित्व स्थापित करते

सुरुवातीच्या क्षणी कोसाइन आलेखाचे कमाल मूल्य असते आणि साइन आलेखाला सुरुवातीच्या क्षणी शून्य मूल्य असते. जर आपण समतोल स्थितीतून दोलन तपासण्यास सुरुवात केली, तर दोलन साइनसॉइडची पुनरावृत्ती करेल. जर आपण कमाल विचलनाच्या स्थितीतून दोलनाचा विचार करू लागलो, तर दोलन कोसाइनद्वारे वर्णन केले जाईल. किंवा अशा दोलनाचे वर्णन प्रारंभिक टप्प्यासह साइन सूत्राद्वारे केले जाऊ शकते.

हार्मोनिक दोलन दरम्यान गती आणि प्रवेग मध्ये बदल

सायन किंवा कोसाइनच्या नियमानुसार केवळ शरीराचे समन्वयच बदलत नाहीत. परंतु बल, वेग आणि प्रवेग यांसारखे प्रमाण देखील त्याचप्रमाणे बदलतात. जेव्हा विस्थापन जास्तीत जास्त असते तेव्हा दोलन शरीर अत्यंत स्थानांवर असते तेव्हा बल आणि प्रवेग कमाल असते आणि जेव्हा शरीर समतोल स्थितीतून जाते तेव्हा शून्य असते. याउलट, तीव्र स्थितीत गती शून्य असते आणि जेव्हा शरीर समतोल स्थितीतून जाते तेव्हा ते त्याच्या कमाल मूल्यापर्यंत पोहोचते.

जर दोलन कोसाइनच्या नियमाने वर्णन केले असेल

जर दोलन साइन नियमानुसार वर्णन केले असेल

कमाल गती आणि प्रवेग मूल्ये

अवलंबन v(t) आणि a(t) च्या समीकरणांचे विश्लेषण केल्यावर, त्रिकोणमितीय घटक 1 किंवा -1 च्या बरोबरीच्या असल्यास गती आणि प्रवेग कमाल मूल्ये घेतात असा अंदाज लावू शकतो. सूत्रानुसार ठरवले जाते

यांत्रिक कंपने. दोलन मापदंड. हार्मोनिक स्पंदने.

संकोच ही एक प्रक्रिया आहे जी स्वतःची अचूक किंवा अंदाजे ठराविक अंतराने पुनरावृत्ती होते.

दोलनांचे वैशिष्ठ्य म्हणजे प्रक्षेपणावर स्थिर समतोल स्थितीची अनिवार्य उपस्थिती, ज्यामध्ये शरीरावर कार्य करणार्‍या सर्व शक्तींची बेरीज शून्य इतकी असते याला समतोल स्थिती म्हणतात.

गणितीय पेंडुलम हा पातळ, वजनहीन आणि अगम्य धाग्यावर निलंबित केलेला एक भौतिक बिंदू आहे.

दोलन गतीचे मापदंड.

1. ऑफसेट किंवा समन्वय (x) - दिलेल्या समतोल स्थितीपासून विचलन

वेळेचा क्षण	[x ]=मी

2. मोठेपणा ( Xm) - समतोल स्थितीपासून जास्तीत जास्त विचलन.

[ एक्स मी ]=मी

3. दोलन कालावधी ( ट) - एक संपूर्ण दोलन पूर्ण करण्यासाठी लागणारा वेळ.

[ट ]=c

0 " style="margin-left:31.0pt;border-collapse:collapse">

गणिताचा पेंडुलम

स्प्रिंग पेंडुलम

मी

https://pandia.ru/text/79/117/images/image006_26.gif" width="134" height="57 src="> वारंवारता (रेखीय) ( n ) – 1 s मध्ये पूर्ण दोलनांची संख्या.

[n] = Hz

5. चक्रीय वारंवारता ( w ) – 2p सेकंदात पूर्ण दोलनांची संख्या, म्हणजे अंदाजे 6.28 सेकंदात.

w = 2pn ; [w] =0 " style="margin-left:116.0pt;border-collapse:collapse">

https://pandia.ru/text/79/117/images/image012_9.jpg" width="90" height="103">

पडद्यावरची सावली डगमगते.

हार्मोनिक कंपनांचे समीकरण आणि आलेख.

हार्मोनिक स्पंदने - हे दोलन आहेत ज्यामध्ये साइन किंवा कोसाइनच्या नियमानुसार समन्वय वेळोवेळी बदलतो.

https://pandia.ru/text/79/117/images/image014_7.jpg" width="254" height="430 src="> x=एक्समीपाप(w ट+j 0 )

x=एक्समीकारण(w ट+j 0 )

x - समन्वय,

Xm - कंपन मोठेपणा,

w - चक्रीय वारंवारता,

w t + j 0 = j - दोलन टप्पा,

j 0 - दोलनांचा प्रारंभिक टप्पा.

https://pandia.ru/text/79/117/images/image016_4.jpg" width="247" height="335 src=">

आलेख वेगळे आहेत फक्तमोठेपणा

आलेख फक्त कालावधीत भिन्न असतात (वारंवारता)

https://pandia.ru/text/79/117/images/image018_3.jpg" width="204" height="90 src=">

दोलनांचे मोठेपणा कालांतराने बदलत नसल्यास, दोलनांना म्हणतात undamped.

नैसर्गिक कंपने घर्षण विचारात घेत नाहीत, प्रणालीची एकूण यांत्रिक ऊर्जा स्थिर राहते: इ k + इ n = इफर = const.

नैसर्गिक दोलन अखंड आहेत.

सक्तीच्या दोलनांसह, बाह्य स्त्रोताकडून सतत किंवा अधूनमधून पुरवली जाणारी ऊर्जा घर्षण शक्तीच्या कार्यामुळे उद्भवलेल्या नुकसानाची भरपाई करते आणि दोलन निर्विवाद केले जाऊ शकतात.

शरीरातील गतिज आणि संभाव्य ऊर्जा कंपनांच्या वेळी एकमेकांमध्ये रूपांतरित होते. जेव्हा समतोल स्थितीपासून प्रणालीचे विचलन जास्तीत जास्त असते, तेव्हा संभाव्य ऊर्जा जास्तीत जास्त असते आणि गतिज ऊर्जा शून्य असते. समतोल स्थितीतून जात असताना, ते उलट आहे.

मुक्त दोलनांची वारंवारता दोलन प्रणालीच्या पॅरामीटर्सद्वारे निर्धारित केली जाते.

सक्तीच्या दोलनांची वारंवारता बाह्य शक्तीच्या वारंवारतेद्वारे निर्धारित केली जाते. सक्तीच्या दोलनांचे मोठेपणा देखील बाह्य शक्तीवर अवलंबून असते.

अनुनाद c

अनुनाद जेव्हा बाह्य शक्तीची वारंवारता सिस्टमच्या नैसर्गिक दोलनांच्या वारंवारतेशी जुळते तेव्हा सक्तीच्या दोलनांच्या मोठेपणामध्ये तीव्र वाढ म्हणतात.

जेव्हा शक्ती बदलाची वारंवारता w प्रणालीच्या दोलनांच्या नैसर्गिक वारंवारता w0 शी एकरूप होते, तेव्हा शक्ती संपूर्णपणे सकारात्मक कार्य करते, ज्यामुळे शरीराच्या दोलनांचे मोठेपणा वाढते. इतर कोणत्याही वारंवारतेवर, कालावधीच्या एका भागामध्ये शक्ती सकारात्मक कार्य करते आणि कालावधीच्या दुसर्या भागात, नकारात्मक कार्य करते.

अनुनाद दरम्यान, दोलनांच्या मोठेपणामध्ये वाढ झाल्यामुळे प्रणालीचा नाश होऊ शकतो.

1905 मध्ये, रक्षक घोडदळाच्या पथकाच्या खुराखाली, सेंट पीटर्सबर्गमधील फोंटांका नदीवरील इजिप्शियन पूल कोसळला.

स्व-दोलन.

सेल्फ-ऑसिलेशन्स ही प्रणालीमध्ये अखंडित दोलन असतात, ज्याला बाह्य शक्तीच्या प्रभावाच्या अनुपस्थितीत अंतर्गत ऊर्जा स्त्रोतांद्वारे समर्थित केले जाते.

सक्तीच्या दोलनांच्या विपरीत, स्वयं-दोलनांची वारंवारता आणि मोठेपणा दोलन प्रणालीच्या गुणधर्मांद्वारे निर्धारित केले जाते.

स्वयं-दोलन हे मुक्त दोलनांपेक्षा मोठेपणाच्या स्वतंत्रतेमुळे आणि सुरुवातीच्या अल्प-मुदतीच्या प्रभावापासून वेगळे असतात जे दोलन प्रक्रियेला उत्तेजित करतात. स्वयं-दोलन प्रणाली सहसा तीन घटकांमध्ये विभागली जाऊ शकते:

1) दोलन प्रणाली;

2) ऊर्जेचा स्त्रोत;

3) एक फीडबॅक डिव्हाइस जे स्त्रोतापासून ओसीलेटरी सिस्टममध्ये उर्जेचा प्रवाह नियंत्रित करते.

एका कालावधीत स्त्रोताकडून येणारी ऊर्जा त्याच वेळी दोलन प्रणालीमध्ये गमावलेल्या उर्जेइतकी असते.

आम्ही अनेक शारीरिकदृष्ट्या पूर्णपणे भिन्न प्रणालींचे परीक्षण केले आणि गतीची समीकरणे समान स्वरूपात कमी केली आहेत याची खात्री केली.

भौतिक प्रणालींमधील फरक केवळ परिमाणाच्या भिन्न व्याख्यांमध्ये दिसून येतो आणि व्हेरिएबलच्या वेगवेगळ्या भौतिक संवेदनांमध्ये x: हे समन्वय, कोन, शुल्क, विद्युत् प्रवाह इ. असू शकते. लक्षात घ्या की या प्रकरणात, समीकरणाच्या (1.18) रचनेवरून खालीलप्रमाणे, परिमाणामध्ये नेहमी व्यस्त वेळेचे परिमाण असते.

समीकरण (1.18) तथाकथित वर्णन करते हार्मोनिक कंपने.

हार्मोनिक कंपन समीकरण (1.18) हे द्वितीय श्रेणीचे रेखीय विभेदक समीकरण आहे (कारण त्यात व्हेरिएबलचे दुसरे व्युत्पन्न आहे. x). समीकरणाची रेखीयता म्हणजे

काही कार्य असल्यास x(t)या समीकरणाचे समाधान आहे, नंतर फंक्शन Cx(t)त्याचाही उपाय असेल ( सी- अनियंत्रित स्थिरांक);

कार्ये असल्यास x 1(t)आणि x 2(t)या समीकरणाचे उपाय आहेत, नंतर त्यांची बेरीज x 1 (t) + x 2 (t)त्याच समीकरणावर एक उपाय देखील असेल.

एक गणितीय प्रमेय देखील सिद्ध झाला आहे, त्यानुसार दुसऱ्या क्रमाच्या समीकरणाला दोन स्वतंत्र उपाय आहेत. इतर सर्व उपाय, रेखीयतेच्या गुणधर्मांनुसार, त्यांचे रेखीय संयोजन म्हणून मिळू शकतात. स्वतंत्र कार्ये करतात आणि समीकरण पूर्ण करतात हे थेट भिन्नतेद्वारे सत्यापित करणे सोपे आहे (1.18). याचा अर्थ असा की या समीकरणाच्या सामान्य समाधानाचे स्वरूप आहे:

कुठे C 1,C 2- अनियंत्रित स्थिरांक. हे समाधान दुसर्या स्वरूपात सादर केले जाऊ शकते. चला मूल्य प्रविष्ट करूया

आणि संबंधांद्वारे कोन निश्चित करा:

नंतर सामान्य समाधान (1.19) असे लिहिले आहे

त्रिकोणमिती सूत्रांनुसार, कंसातील अभिव्यक्ती समान आहे

आम्ही शेवटी येतो हार्मोनिक कंपन समीकरणाचे सामान्य समाधानजसे:

नॉन-नकारात्मक मूल्य एम्हणतात कंपन मोठेपणा, - दोलनाचा प्रारंभिक टप्पा. संपूर्ण कोसाइन युक्तिवाद - संयोजन - म्हणतात दोलन टप्पा.

अभिव्यक्ती (1.19) आणि (1.23) पूर्णपणे समतुल्य आहेत, म्हणून आम्ही साधेपणाच्या विचारांवर आधारित, त्यापैकी कोणतेही वापरू शकतो. दोन्ही सोल्यूशन्स ही काळाची नियतकालिक कार्ये आहेत. खरंच, साइन आणि कोसाइन हे कालखंडासह नियतकालिक असतात . म्हणून, हार्मोनिक दोलन करत असलेल्या प्रणालीच्या विविध अवस्था ठराविक कालावधीनंतर पुनरावृत्ती केल्या जातात ट*, ज्या दरम्यान दोलन टप्प्याला एक वाढ प्राप्त होते जी ची गुणाकार असते :

ते त्याचे पालन करते

यापैकी कमीत कमी वेळा

म्हणतात दोलन कालावधी (अंजीर 1.8), आणि - त्याचे वर्तुळाकार (चक्रीय) वारंवारता.

तांदूळ. १.८.

ते देखील वापरतात वारंवारता चढउतार

त्यानुसार, वर्तुळाकार वारंवारता प्रति दोलनांच्या संख्येइतकी असते सेकंद

त्यामुळे, वेळीच व्यवस्था असल्यास टव्हेरिएबलच्या मूल्याद्वारे वैशिष्ट्यीकृत x(t),नंतर व्हेरिएबलचे काही कालावधीनंतर समान मूल्य असेल (चित्र 1.9), म्हणजे

तोच अर्थ कालांतराने स्वाभाविकपणे पुनरावृत्ती होईल 2T, ZTइ.

तांदूळ. १.९. दोलन कालावधी

सामान्य समाधानामध्ये दोन अनियंत्रित स्थिरांक समाविष्ट असतात ( C 1, C 2किंवा ए, a), ज्याची मूल्ये दोन द्वारे निर्धारित करणे आवश्यक आहे प्रारंभिक परिस्थिती. सहसा (जरी अपरिहार्यपणे) त्यांची भूमिका व्हेरिएबलच्या प्रारंभिक मूल्यांद्वारे खेळली जाते x(0)आणि त्याचे व्युत्पन्न.

एक उदाहरण देऊ. हार्मोनिक दोलनांच्या समीकरणाचे समाधान (1.19) स्प्रिंग पेंडुलमच्या गतीचे वर्णन करू द्या. अनियंत्रित स्थिरांकांची मूल्ये आपण ज्या पद्धतीने पेंडुलमला समतोल बाहेर आणले त्यावर अवलंबून असतात. उदाहरणार्थ, आम्ही स्प्रिंगला अंतरावर ओढले आणि सुरुवातीच्या वेगाशिवाय चेंडू सोडला. या प्रकरणात

बदली t = 0(1.19) मध्ये, आपल्याला स्थिरांकाचे मूल्य सापडते C 2

अशा प्रकारे उपाय असे दिसते:

वेळेच्या संदर्भात फरक करून आम्ही लोडचा वेग शोधतो

येथे प्रतिस्थापन ट = 0, स्थिरांक शोधा क १:

शेवटी

(1.23) शी तुलना केल्यास, आम्हाला ते आढळते हे दोलनांचे मोठेपणा आहे आणि त्याचा प्रारंभिक टप्पा शून्य आहे: .

आता आपण पेंडुलमला आणखी एका मार्गाने असंतुलित करू या. चला लोड दाबू या जेणेकरून ते प्रारंभिक गती प्राप्त करेल, परंतु प्रभाव दरम्यान व्यावहारिकपणे हलणार नाही. त्यानंतर आमच्याकडे इतर प्रारंभिक अटी आहेत:

आमचे समाधान असे दिसते

लोडची गती कायद्यानुसार बदलेल:

चला येथे बदलूया:

युनिफाइड स्टेट एक्झामिनेशन कोडिफायरचे विषय: हार्मोनिक कंपन; मोठेपणा, कालावधी, वारंवारता, दोलनांचा टप्पा; मुक्त कंपने, सक्तीची कंपने, अनुनाद.

दोलन - हे प्रणालीच्या अवस्थेतील बदल आहेत जे कालांतराने पुनरावृत्ती होतात. दोलनांची संकल्पना घटनांच्या विस्तृत श्रेणीचा समावेश करते.

यांत्रिक प्रणालींचे कंपन, किंवा यांत्रिक कंपने- ही शरीराची किंवा शरीराच्या प्रणालीची यांत्रिक हालचाल आहे, जी वेळेत पुनरावृत्ती करता येते आणि समतोल स्थितीच्या परिसरात उद्भवते. समतोल स्थितीही प्रणालीची एक अवस्था आहे ज्यामध्ये ती बाह्य प्रभावांचा अनुभव न घेता अनिश्चित काळासाठी राहू शकते.

उदाहरणार्थ, जर पेंडुलम विचलित झाला आणि सोडला गेला तर ते दोलन सुरू होईल. समतोल स्थिती ही विचलनाच्या अनुपस्थितीत पेंडुलमची स्थिती आहे. पेंडुलम, अबाधित राहिल्यास, इच्छेनुसार या स्थितीत राहू शकतो. पेंडुलम दोलायमान होत असताना, तो त्याच्या समतोल स्थितीतून अनेक वेळा जातो.

विचलित पेंडुलम सोडल्यानंतर लगेचच, तो हलू लागला, समतोल स्थिती पार केला, विरुद्ध टोकाच्या स्थितीत पोहोचला, क्षणभर तिथे थांबला, विरुद्ध दिशेने सरकला, पुन्हा समतोल स्थिती पार केली आणि परत आली. एक गोष्ट घडली आहे पूर्ण स्विंग. मग ही प्रक्रिया वेळोवेळी पुनरावृत्ती होईल.

शरीर दोलन मोठेपणा समतोल स्थितीपासून त्याच्या सर्वात मोठ्या विचलनाचे परिमाण आहे.

दोलन कालावधी - हा एक संपूर्ण दोलनाचा काळ आहे. आपण असे म्हणू शकतो की एका कालावधीत शरीर चार मोठेपणाच्या मार्गाने प्रवास करते.

दोलन वारंवारता कालावधीचा परस्पर आहे: . वारंवारता हर्ट्झ (Hz) मध्ये मोजली जाते आणि एका सेकंदात किती पूर्ण दोलन होतात हे दर्शविते.

हार्मोनिक स्पंदने.

आम्ही असे गृहीत धरू की दोलन शरीराची स्थिती एकाच समन्वयाने निर्धारित केली जाते. समतोल स्थिती मूल्याशी संबंधित आहे. या प्रकरणात मेकॅनिक्सचे मुख्य कार्य असे कार्य शोधणे आहे जे कोणत्याही वेळी शरीराचे समन्वय देते.

दोलनांच्या गणितीय वर्णनासाठी, नियतकालिक कार्ये वापरणे स्वाभाविक आहे. अशी अनेक कार्ये आहेत, परंतु त्यापैकी दोन - साइन आणि कोसाइन - सर्वात महत्वाचे आहेत. त्यांच्याकडे अनेक चांगले गुणधर्म आहेत आणि ते भौतिक घटनांच्या विस्तृत श्रेणीशी जवळून संबंधित आहेत.

द्वारे युक्तिवाद हलवून साइन आणि कोसाइन फंक्शन्स एकमेकांकडून मिळवले जात असल्याने, आपण स्वतःला त्यापैकी फक्त एकापर्यंत मर्यादित करू शकतो. निश्चिततेसाठी, आम्ही कोसाइन वापरू.

हार्मोनिक स्पंदने- हे दोलन आहेत ज्यात समन्वय हा हार्मोनिक कायद्यानुसार वेळेवर अवलंबून असतो:

(1)

या सूत्रात समाविष्ट केलेल्या प्रमाणांचा अर्थ शोधूया.

धनात्मक मूल्य हे समन्वयाचे सर्वात मोठे मापांक मूल्य आहे (कोसाइन मॉड्यूलसचे कमाल मूल्य एकतेच्या बरोबरीचे असल्याने), म्हणजेच, समतोल स्थितीपासून सर्वात मोठे विचलन. म्हणून - oscillations च्या मोठेपणा.

कोसाइन युक्तिवाद म्हणतात टप्पासंकोच येथील फेज व्हॅल्यूच्या बरोबरीच्या मूल्याला प्रारंभिक टप्पा म्हणतात. प्रारंभिक टप्पा शरीराच्या प्रारंभिक समन्वयाशी संबंधित आहे: .

प्रमाण म्हणतात चक्रीय वारंवारता. दोलन कालावधी आणि वारंवारता यांच्याशी त्याचा संबंध शोधू. एक संपूर्ण दोलन रेडियनच्या बरोबरीच्या फेज वाढीशी संबंधित आहे: , कुठून

(2)

(3)

चक्रीय वारंवारता rad/s (रेडियन प्रति सेकंद) मध्ये मोजली जाते.

अभिव्यक्ती (2) आणि (3) नुसार, आम्हाला हार्मोनिक कायदा (1) लिहिण्याचे आणखी दोन प्रकार मिळतात:

फंक्शनचा आलेख (1), हार्मोनिक दोलन दरम्यान वेळेवर समन्वयाचे अवलंबित्व व्यक्त करतो, अंजीर मध्ये दर्शविला आहे. १.

प्रकार (1) चा हार्मोनिक नियम सर्वात सामान्य स्वरूपाचा आहे. उदाहरणार्थ, पेंडुलमवर दोन प्रारंभिक क्रिया एकाच वेळी केल्या गेल्या अशा परिस्थितींना ते प्रतिसाद देते: ते एका रकमेद्वारे विचलित होते आणि त्याला एक विशिष्ट प्रारंभिक गती दिली जाते. दोन महत्त्वाची विशेष प्रकरणे आहेत जेव्हा यापैकी एक क्रिया केली गेली नाही.

पेंडुलम विक्षेपित होऊ द्या, परंतु प्रारंभिक वेग नोंदविला गेला नाही (तो सुरुवातीच्या वेगाशिवाय सोडला गेला). हे स्पष्ट आहे की या प्रकरणात, म्हणून आम्ही ठेवू शकतो. आम्हाला कोसाइन कायदा मिळतो:

या प्रकरणात हार्मोनिक दोलनांचा आलेख अंजीर मध्ये दर्शविला आहे. 2.

तांदूळ. 2. कोसाइनचा नियम

आता आपण असे गृहीत धरू की पेंडुलम विचलित झाला नव्हता, परंतु समतोल स्थितीतून सुरुवातीचा वेग त्याला आघाताने दिला गेला होता. या प्रकरणात, म्हणून आपण लावू शकता. आम्हाला साइनचा नियम मिळतो:

दोलन आलेख अंजीर मध्ये दर्शविले आहे. 3.

तांदूळ. 3. साइनचा नियम

हार्मोनिक कंपनांचे समीकरण.

चला सामान्य हार्मोनिक कायद्याकडे परत जाऊया (1). चला ही समानता वेगळे करूया:

. (4)

आता आम्ही परिणामी समानतेमध्ये फरक करतो (4):

. (5)

समन्वयासाठी अभिव्यक्ती (1) आणि प्रवेग प्रक्षेपणासाठी (5) अभिव्यक्तीची तुलना करू. आम्ही पाहतो की प्रवेग प्रक्षेपण केवळ एका घटकाद्वारे समन्वयापेक्षा वेगळे आहे:

. (6)

या गुणोत्तराला म्हणतात हार्मोनिक समीकरण. हे या फॉर्ममध्ये देखील पुन्हा लिहिले जाऊ शकते:

. (7)

गणिताच्या दृष्टिकोनातून, समीकरण (7) आहे विभेदक समीकरण. विभेदक समीकरणांचे उपाय म्हणजे फंक्शन्स (सामान्य बीजगणिताप्रमाणे संख्या नव्हे).
तर, हे सिद्ध केले जाऊ शकते की:

समीकरणाचे समाधान (7) हे फॉर्मचे कोणतेही कार्य आहे (1) अनियंत्रित ;

इतर कोणतेही कार्य या समीकरणावर उपाय नाही.

दुसऱ्या शब्दांत, संबंध (6), (7) चक्रीय वारंवारतेसह हार्मोनिक दोलनांचे वर्णन करतात आणि फक्त त्यांचेच. दोन स्थिरांक प्रारंभिक स्थितींवरून निर्धारित केले जातात - समन्वय आणि वेगाच्या प्रारंभिक मूल्यांवरून.

स्प्रिंग पेंडुलम.

स्प्रिंग पेंडुलम स्प्रिंगला जोडलेला भार आहे जो क्षैतिज किंवा उभ्या दिशेने दोलायमान होऊ शकतो.

स्प्रिंग पेंडुलमच्या लहान क्षैतिज दोलनांचा कालावधी शोधूया (चित्र 4). स्प्रिंगच्या विकृतीचे प्रमाण त्याच्या परिमाणांपेक्षा खूपच कमी असल्यास दोलन लहान असतील. लहान विकृतींसाठी आम्ही हुकचा नियम वापरू शकतो. यामुळे दोलन हार्मोनिक होतील.

घर्षणाकडे आपण दुर्लक्ष करतो. लोडमध्ये वस्तुमान आहे आणि स्प्रिंग कडकपणा समान आहे.

समन्वय समतोल स्थितीशी संबंधित आहे ज्यामध्ये स्प्रिंग विकृत नाही. परिणामी, स्प्रिंग विकृतीची परिमाण लोडच्या निर्देशांकांच्या मॉड्यूलसच्या समान आहे.

तांदूळ. 4. स्प्रिंग पेंडुलम

क्षैतिज दिशेने, स्प्रिंगमधून फक्त लवचिक शक्ती लोडवर कार्य करते. अक्षावरील प्रक्षेपणातील भाराचा न्यूटनचा दुसरा नियम खालीलप्रमाणे आहे:

. (8)

जर (आकृतीप्रमाणे भार उजवीकडे हलविला गेला असेल), तर लवचिक बल उलट दिशेने निर्देशित केले जाते आणि . याउलट, जर, तर. चिन्हे आणि नेहमी विरुद्ध असतात, म्हणून हूकचा नियम खालीलप्रमाणे लिहिला जाऊ शकतो:

मग संबंध (8) फॉर्म घेते:

आम्ही फॉर्म (6) च्या हार्मोनिक दोलनांचे समीकरण प्राप्त केले आहे, ज्यामध्ये

स्प्रिंग पेंडुलमच्या दोलनाची चक्रीय वारंवारता अशा प्रकारे समान आहे:

. (9)

येथून आणि संबंधातून आम्हाला स्प्रिंग पेंडुलमच्या क्षैतिज दोलनांचा कालावधी सापडतो:

. (10)

जर तुम्ही स्प्रिंगवर भार टांगला तर तुम्हाला एक स्प्रिंग पेंडुलम मिळेल जो उभ्या दिशेने फिरतो. हे दर्शविले जाऊ शकते की या प्रकरणात, सूत्र (10) दोलन कालावधीसाठी वैध आहे.

गणिती पेंडुलम.

गणिताचा पेंडुलम वजनहीन अभेद्य धाग्यावर लटकलेले एक लहान शरीर आहे (चित्र 5). गणितीय पेंडुलम गुरुत्वाकर्षणाच्या क्षेत्रात उभ्या समतल मध्ये दोलन करू शकतो.

तांदूळ. 5. गणितीय पेंडुलम

चला गणितीय पेंडुलमच्या लहान दोलनांचा कालावधी शोधू. धाग्याची लांबी आहे. आम्ही हवेच्या प्रतिकाराकडे दुर्लक्ष करतो.

न्यूटनचा लोलकाचा दुसरा नियम लिहूया:

आणि ते अक्षावर प्रक्षेपित करा:

जर पेंडुलम आकृती प्रमाणे स्थान घेते (म्हणजे), तर:

जर पेंडुलम समतोल स्थितीच्या (म्हणजे) दुसऱ्या बाजूला असेल तर:

तर, पेंडुलमच्या कोणत्याही स्थितीसाठी आमच्याकडे आहे:

. (11)

जेव्हा पेंडुलम समतोल स्थितीत विश्रांती घेते तेव्हा समानता समाधानी असते. लहान दोलनांसाठी, जेव्हा समतोल स्थितीपासून पेंडुलमचे विचलन लहान असते (धाग्याच्या लांबीच्या तुलनेत), तेव्हा अंदाजे समानता समाधानी असते. चला ते सूत्र (११) मध्ये वापरू:

हे फॉर्म (6) च्या हार्मोनिक दोलनांचे समीकरण आहे, ज्यामध्ये

म्हणून, गणितीय पेंडुलमच्या दोलनांची चक्रीय वारंवारता समान आहे:

. (12)

म्हणून गणितीय पेंडुलमच्या दोलनाचा कालावधी:

. (13)

कृपया लक्षात घ्या की सूत्र (13) मध्ये लोडचे वस्तुमान समाविष्ट नाही. स्प्रिंग पेंडुलमच्या विपरीत, गणितीय पेंडुलमच्या दोलनाचा कालावधी त्याच्या वस्तुमानावर अवलंबून नाही.

मुक्त आणि सक्तीची कंपने.

ते म्हणतात की यंत्रणा करते मुक्त कंपने, जर ते एकदा समतोल स्थितीतून काढून टाकले गेले आणि नंतर स्वतःकडे सोडले गेले. नियतकालिक बाह्य नाही
या प्रकरणात, सिस्टमला कोणत्याही प्रभावाचा अनुभव येत नाही आणि सिस्टममध्ये दोलनांना समर्थन देणारे कोणतेही अंतर्गत ऊर्जा स्त्रोत नाहीत.

वर चर्चा केलेले स्प्रिंग आणि गणितीय पेंडुलमचे दोलन ही मुक्त दोलनांची उदाहरणे आहेत.

ज्या वारंवारतेने मुक्त कंपने होतात त्याला म्हणतात नैसर्गिक वारंवारतादोलन प्रणाली. अशा प्रकारे, सूत्रे (9) आणि (12) स्प्रिंग आणि गणितीय पेंडुलमच्या दोलनांची नैसर्गिक (चक्रीय) वारंवारता देतात.

घर्षणाच्या अनुपस्थितीत आदर्श परिस्थितीमध्ये, मुक्त दोलन बेबंद असतात, म्हणजेच त्यांच्याकडे स्थिर मोठेपणा असतो आणि अनिश्चित काळ टिकतो. वास्तविक दोलन प्रणालींमध्ये, घर्षण नेहमीच असते, त्यामुळे मुक्त कंपने हळूहळू नष्ट होतात (चित्र 6).

जबरी कंपने- हे बाह्य शक्तीच्या प्रभावाखाली प्रणालीद्वारे बनविलेले दोलन आहेत जे वेळोवेळी बदलतात (तथाकथित प्रेरक शक्ती).

आपण असे गृहीत धरू की प्रणालीच्या दोलनांची नैसर्गिक वारंवारता समान आहे, आणि प्रेरक शक्ती हार्मोनिक कायद्यानुसार वेळेवर अवलंबून असते:

काही काळानंतर, सक्तीचे दोलन स्थापित केले जातात: प्रणाली एक जटिल हालचाल करते, जी सक्तीची आणि मुक्त दोलनांची सुपरपोझिशन असते. मुक्त दोलन हळूहळू नष्ट होतात आणि स्थिर स्थितीत प्रणाली सक्तीने दोलन करते, जे हार्मोनिक देखील होते. स्थिर-स्थिती सक्तीच्या दोलनांची वारंवारता वारंवारतेशी जुळते
फोर्सिंग फोर्स (बाह्य शक्ती, जसे ते होते, सिस्टमवर त्याची वारंवारता लादते).

प्रस्थापित सक्तीच्या दोलनांचे मोठेपणा प्रेरक शक्तीच्या वारंवारतेवर अवलंबून असते. या अवलंबनाचा आलेख अंजीर मध्ये दर्शविला आहे. ७.

तांदूळ. 7. अनुनाद

आम्ही पाहतो की प्रतिध्वनी वारंवारता जवळ येते - सक्तीच्या दोलनांच्या मोठेपणामध्ये वाढ होण्याची घटना. रेझोनंट फ्रिक्वेंसी सिस्टमच्या दोलनांच्या नैसर्गिक वारंवारतेच्या अंदाजे समान असते: , आणि ही समानता अधिक अचूकपणे पूर्ण होते, सिस्टममध्ये कमी घर्षण. घर्षणाच्या अनुपस्थितीत, रेझोनंट वारंवारता दोलनांच्या नैसर्गिक वारंवारतेशी एकरूप होते आणि दोलनांचे मोठेपणा अनंतापर्यंत वाढते.