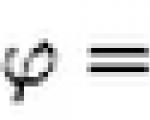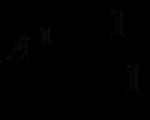समीकरणे सोडवण्यासारखी. उदाहरणांसह रेखीय समीकरणे सोडवणे

अंतिम चाचणीच्या तयारीच्या टप्प्यावर, हायस्कूलच्या विद्यार्थ्यांना “एक्सपोनेन्शियल इक्वेशन्स” या विषयावरील त्यांचे ज्ञान सुधारणे आवश्यक आहे. मागील वर्षांचा अनुभव सूचित करतो की अशा कार्यांमुळे शालेय मुलांसाठी काही अडचणी येतात. म्हणून, हायस्कूलच्या विद्यार्थ्यांना, त्यांच्या तयारीच्या पातळीकडे दुर्लक्ष करून, सिद्धांतामध्ये पूर्णपणे प्रभुत्व मिळवणे, सूत्रे लक्षात ठेवणे आणि अशा समीकरणांचे निराकरण करण्याचे तत्त्व समजून घेणे आवश्यक आहे. या प्रकारच्या समस्येचा सामना करण्यास शिकल्यानंतर, गणितातील युनिफाइड स्टेट परीक्षा उत्तीर्ण करताना पदवीधर उच्च गुणांवर अवलंबून राहू शकतात.

Shkolkovo सह परीक्षेच्या चाचणीसाठी सज्ज व्हा!

त्यांनी समाविष्ट केलेल्या सामग्रीचे पुनरावलोकन करताना, अनेक विद्यार्थ्यांना समीकरणे सोडवण्यासाठी आवश्यक सूत्रे शोधण्याच्या समस्येचा सामना करावा लागतो. शालेय पाठ्यपुस्तक नेहमीच हातात नसते आणि इंटरनेटवरील विषयावरील आवश्यक माहिती निवडण्यासाठी बराच वेळ लागतो.

Shkolkovo शैक्षणिक पोर्टल विद्यार्थ्यांना आमचा ज्ञान आधार वापरण्यासाठी आमंत्रित करते. अंतिम परीक्षेच्या तयारीसाठी आम्ही पूर्णपणे नवीन पद्धत लागू करत आहोत. आमच्या वेबसाइटवर अभ्यास करून, आपण ज्ञानातील अंतर ओळखण्यास सक्षम व्हाल आणि त्या कार्यांकडे लक्ष द्या ज्यामुळे सर्वात जास्त त्रास होतो.

श्कोल्कोवो शिक्षकांनी युनिफाइड स्टेट परीक्षा यशस्वीरित्या उत्तीर्ण होण्यासाठी आवश्यक असलेली सर्व सामग्री सर्वात सोप्या आणि सर्वात प्रवेशयोग्य स्वरूपात एकत्रित केली, व्यवस्थित केली आणि सादर केली.

मूलभूत व्याख्या आणि सूत्रे "सैद्धांतिक पार्श्वभूमी" विभागात सादर केली आहेत.

सामग्री चांगल्या प्रकारे समजून घेण्यासाठी, आम्ही शिफारस करतो की तुम्ही असाइनमेंट पूर्ण करण्याचा सराव करा. गणना अल्गोरिदम समजून घेण्यासाठी या पृष्ठावर सादर केलेल्या उपायांसह घातांकीय समीकरणांच्या उदाहरणांचे काळजीपूर्वक पुनरावलोकन करा. त्यानंतर, "निर्देशिका" विभागात कार्ये करण्यासाठी पुढे जा. तुम्ही सर्वात सोप्या कार्यांसह प्रारंभ करू शकता किंवा अनेक अज्ञातांसह जटिल घातांकीय समीकरणे सोडवण्यासाठी थेट जाऊ शकता किंवा . आमच्या वेबसाइटवरील व्यायामाचा डेटाबेस सतत पूरक आणि अद्यतनित केला जातो.

इंडिकेटर्स असलेली ती उदाहरणे ज्यामुळे तुम्हाला अडचणी येतात ते "आवडते" मध्ये जोडले जाऊ शकतात. अशाप्रकारे तुम्ही त्यांना त्वरीत शोधू शकता आणि तुमच्या शिक्षकांशी समाधानाची चर्चा करू शकता.

युनिफाइड स्टेट परीक्षा यशस्वीपणे उत्तीर्ण होण्यासाठी, दररोज श्कोल्कोव्हो पोर्टलवर अभ्यास करा!

सेवेचा उद्देश. मॅट्रिक्स कॅल्क्युलेटर मॅट्रिक्स पद्धतीचा वापर करून रेखीय समीकरणांची प्रणाली सोडवण्यासाठी डिझाइन केलेले आहे (समान समस्या सोडवण्याचे उदाहरण पहा).

सूचना. ऑनलाइन निराकरण करण्यासाठी, तुम्हाला समीकरणाचा प्रकार निवडणे आणि संबंधित मॅट्रिक्सचे परिमाण सेट करणे आवश्यक आहे. जेथे A, B, C निर्दिष्ट मॅट्रिक्स आहेत, X इच्छित मॅट्रिक्स आहे. (1), (2) आणि (3) ची मॅट्रिक्स समीकरणे व्यस्त मॅट्रिक्स A -1 द्वारे सोडवली जातात. जर A·X - B = C ही अभिव्यक्ती दिली असेल, तर प्रथम मॅट्रिक्स C + B जोडणे आवश्यक आहे आणि A·X = D या अभिव्यक्तीसाठी उपाय शोधणे आवश्यक आहे, जेथे D = C + B. जर अभिव्यक्ती A*X = B 2 दिली असेल, तर प्रथम मॅट्रिक्स B चा वर्ग करणे आवश्यक आहे.

मॅट्रिक्सवरील मूलभूत ऑपरेशन्ससह स्वतःला परिचित करण्याची देखील शिफारस केली जाते.

उदाहरण क्रमांक १. व्यायाम करा. मॅट्रिक्स समीकरणाचे निराकरण शोधा
उपाय. चला सूचित करूया:
मग मॅट्रिक्स समीकरण फॉर्ममध्ये लिहिले जाईल: A·X·B = C.
मॅट्रिक्स A चा निर्धारक detA=-1 च्या बरोबरीचा आहे
A हे नॉन-एकवचनी मॅट्रिक्स असल्याने, तेथे व्यस्त मॅट्रिक्स A -1 आहे. डावीकडील समीकरणाच्या दोन्ही बाजूंना A -1 ने गुणा: या समीकरणाच्या डावीकडील दोन्ही बाजूंना A -1 ने आणि उजवीकडील B -1 ने गुणा: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . A A -1 = B B -1 = E आणि E X = X E = X असल्याने X = A -1 C B -1

व्यस्त मॅट्रिक्स A -1:
चला व्यस्त मॅट्रिक्स B -1 शोधू.
ट्रान्सपोज्ड मॅट्रिक्स बी टी:
व्यस्त मॅट्रिक्स B -1:
आपण सूत्र वापरून मॅट्रिक्स X शोधतो: X = A -1 ·C·B -1

उत्तर:

उदाहरण क्रमांक २. व्यायाम करा.मॅट्रिक्स समीकरण सोडवा
उपाय. चला सूचित करूया:
मग मॅट्रिक्स समीकरण फॉर्ममध्ये लिहिले जाईल: A·X = B.
मॅट्रिक्स A चा निर्धारक detA=0 आहे
A हा एकवचन मॅट्रिक्स असल्यामुळे (निर्धारक 0 आहे), म्हणून समीकरणाला कोणतेही समाधान नाही.

उदाहरण क्रमांक 3. व्यायाम करा. मॅट्रिक्स समीकरणाचे निराकरण शोधा
उपाय. चला सूचित करूया:
मग मॅट्रिक्स समीकरण फॉर्ममध्ये लिहिले जाईल: X A = B.
मॅट्रिक्स A चा निर्धारक detA=-60 आहे
A हे नॉन-एकवचनी मॅट्रिक्स असल्याने, तेथे व्यस्त मॅट्रिक्स A -1 आहे. उजवीकडील समीकरणाच्या दोन्ही बाजूंना A -1 ने गुणाकार करू: X A A -1 = B A -1, जिथून आपल्याला X = B A -1 असे आढळते.
चला व्यस्त मॅट्रिक्स A -1 शोधू.
ट्रान्सपोज्ड मॅट्रिक्स ए टी:
व्यस्त मॅट्रिक्स A -1:
आम्ही सूत्र वापरून मॅट्रिक्स X शोधतो: X = B A -1


उत्तर: >

गणित सोडवण्यासाठी. पटकन शोधा गणितीय समीकरण सोडवणेमोडमध्ये ऑनलाइन. वेबसाइट www.site परवानगी देते समीकरण सोडवाजवळजवळ कोणतीही दिलेली बीजगणित, त्रिकोणमितीयकिंवा ट्रान्सेंडेंटल समीकरण ऑनलाइन. गणिताच्या जवळपास कोणत्याही शाखेचा वेगवेगळ्या टप्प्यांवर अभ्यास करताना तुम्हाला निर्णय घ्यावा लागतो ऑनलाइन समीकरणे. ताबडतोब उत्तर मिळवण्यासाठी आणि सर्वात महत्त्वाचे म्हणजे अचूक उत्तर मिळविण्यासाठी, तुम्हाला हे करण्याची परवानगी देणारे संसाधन आवश्यक आहे. साइट www.site धन्यवाद ऑनलाइन समीकरणे सोडवाकाही मिनिटे लागतील. गणित सोडवताना www.site चा मुख्य फायदा ऑनलाइन समीकरणे- ही प्रदान केलेल्या प्रतिसादाची गती आणि अचूकता आहे. साइट कोणत्याही निराकरण करण्यास सक्षम आहे ऑनलाइन बीजगणितीय समीकरणे, त्रिकोणमितीय समीकरणे ऑनलाइन, अतींद्रिय समीकरणे ऑनलाइन, आणि समीकरणेमोडमध्ये अज्ञात पॅरामीटर्ससह ऑनलाइन. समीकरणेएक शक्तिशाली गणितीय उपकरण म्हणून काम करा उपायव्यावहारिक समस्या. च्या मदतीने गणितीय समीकरणेपहिल्या दृष्टीक्षेपात गोंधळात टाकणारी आणि गुंतागुंतीची वाटणारी तथ्ये आणि संबंध व्यक्त करणे शक्य आहे. अज्ञात प्रमाण समीकरणेमध्ये समस्या तयार करून शोधली जाऊ शकते गणितीयफॉर्ममध्ये भाषा समीकरणेआणि ठरवामोडमध्ये कार्य प्राप्त झाले ऑनलाइनवेबसाइट www.site वर. कोणतीही बीजगणितीय समीकरण, त्रिकोणमितीय समीकरणकिंवा समीकरणेसमाविष्टीत अतींद्रियवैशिष्ट्ये आपण सहजपणे करू शकता ठरवाऑनलाइन आणि अचूक उत्तर मिळवा. नैसर्गिक विज्ञानाचा अभ्यास करताना, आपल्याला अपरिहार्यपणे गरज भासते समीकरणे सोडवणे. या प्रकरणात, उत्तर अचूक असणे आवश्यक आहे आणि मोडमध्ये त्वरित प्राप्त करणे आवश्यक आहे ऑनलाइन. म्हणून साठी ऑनलाइन गणितीय समीकरणे सोडवणेआम्ही www.site साइटची शिफारस करतो, जी तुमचा अपरिहार्य कॅल्क्युलेटर बनेल ऑनलाइन बीजगणितीय समीकरणे सोडवा, त्रिकोणमितीय समीकरणे ऑनलाइन, आणि अतींद्रिय समीकरणे ऑनलाइनकिंवा समीकरणेअज्ञात पॅरामीटर्ससह. विविध मुळे शोधण्याच्या व्यावहारिक समस्यांसाठी गणितीय समीकरणेसंसाधन www.. सोडवणे ऑनलाइन समीकरणेस्वतः, वापरून प्राप्त उत्तर तपासणे उपयुक्त आहे ऑनलाइन समीकरण सोडवणेवेबसाइट www.site वर. आपण समीकरण योग्यरित्या लिहिणे आवश्यक आहे आणि त्वरित मिळवा ऑनलाइन उपाय, ज्यानंतर उरते ते उत्तराची तुलना समीकरणाशी तुमच्या समाधानाशी करणे. उत्तर तपासण्यासाठी एका मिनिटापेक्षा जास्त वेळ लागणार नाही, ते पुरेसे आहे ऑनलाइन समीकरण सोडवाआणि उत्तरांची तुलना करा. हे आपल्याला मध्ये चुका टाळण्यास मदत करेल निर्णयआणि वेळेत उत्तर दुरुस्त करा ऑनलाइन समीकरणे सोडवणेएकतर बीजगणित, त्रिकोणमितीय, अतींद्रियकिंवा समीकरणअज्ञात पॅरामीटर्ससह.

या व्हिडिओमध्ये आम्ही समान अल्गोरिदम वापरून सोडवलेल्या रेखीय समीकरणांच्या संपूर्ण संचाचे विश्लेषण करू - म्हणूनच त्यांना सर्वात सोपा म्हटले जाते.

प्रथम, परिभाषित करूया: रेखीय समीकरण काय आहे आणि कोणते समीकरण सर्वात सोपे आहे?

रेखीय समीकरण हे असे असते ज्यामध्ये फक्त एकच चल असते आणि फक्त पहिल्या अंशापर्यंत.

सर्वात सोपा समीकरण म्हणजे बांधकाम:

अल्गोरिदम वापरून इतर सर्व रेषीय समीकरणे सर्वात सोपी केली जातात:

1. कंस विस्तृत करा, जर असेल तर;
2. समान चिन्हाच्या एका बाजूला व्हेरिएबल असलेल्या अटी आणि व्हेरिएबल नसलेल्या अटी दुसऱ्या बाजूला हलवा;
3. समान चिन्हाच्या डाव्या आणि उजव्या बाजूस समान संज्ञा द्या;
4. परिणामी समीकरण व्हेरिएबल $x$ च्या गुणांकाने विभाजित करा.

अर्थात, हा अल्गोरिदम नेहमीच मदत करत नाही. वस्तुस्थिती अशी आहे की काहीवेळा या सर्व युक्तिवादानंतर $x$ व्हेरिएबलचे गुणांक शून्याच्या बरोबरीचे होते. या प्रकरणात, दोन पर्याय शक्य आहेत:

1. समीकरणाला अजिबात उपाय नाही. उदाहरणार्थ, जेव्हा $0\cdot x=8$ सारखे काहीतरी निघते, उदा. डावीकडे शून्य आहे आणि उजवीकडे शून्याशिवाय दुसरी संख्या आहे. खालील व्हिडिओमध्ये आम्ही ही परिस्थिती का शक्य आहे याची अनेक कारणे पाहू.
2. उपाय म्हणजे सर्व संख्या. जेव्हा हे समीकरण $0\cdot x=0$ वर कमी केले जाते तेव्हा हे शक्य होते. हे अगदी तार्किक आहे की आम्ही $x$ बदलले तरीही ते "शून्य म्हणजे शून्याच्या बरोबरीचे" असे निघेल, म्हणजे. योग्य संख्यात्मक समानता.

आता वास्तविक जीवनातील उदाहरणे वापरून हे सर्व कसे कार्य करते ते पाहू.

समीकरणे सोडवण्याची उदाहरणे

आज आपण रेखीय समीकरणे हाताळत आहोत, आणि फक्त सर्वात सोपी समीकरणे. सर्वसाधारणपणे, एक रेखीय समीकरण म्हणजे कोणतीही समानता ज्यामध्ये अगदी एक व्हेरिएबल असते आणि ते फक्त पहिल्या अंशापर्यंत जाते.

अशा बांधकामांचे निराकरण अंदाजे त्याच प्रकारे केले जाते:

1. सर्व प्रथम, आपल्याला कंस विस्तृत करणे आवश्यक आहे, जर काही असतील तर (आमच्या शेवटच्या उदाहरणाप्रमाणे);
2. नंतर समान एकत्र करा
3. शेवटी, व्हेरिएबल वेगळे करा, म्हणजे. व्हेरिएबलशी जोडलेली प्रत्येक गोष्ट—त्यामध्ये समाविष्ट असलेल्या अटी—एका बाजूला हलवा आणि त्याशिवाय राहिलेल्या सर्व गोष्टी दुसऱ्या बाजूला हलवा.

मग, नियमानुसार, तुम्हाला परिणामी समानतेच्या प्रत्येक बाजूला समान देणे आवश्यक आहे, आणि त्यानंतर जे काही उरले आहे ते "x" च्या गुणांकाने विभाजित करणे आहे आणि आम्हाला अंतिम उत्तर मिळेल.

सैद्धांतिकदृष्ट्या, हे छान आणि सोपे दिसते, परंतु व्यवहारात, अगदी अनुभवी हायस्कूल विद्यार्थी अगदी सोप्या रेखीय समीकरणांमध्ये आक्षेपार्ह चुका करू शकतात. सामान्यतः, कंस उघडताना किंवा "प्लस" आणि "वजा" ची गणना करताना त्रुटी केल्या जातात.

याव्यतिरिक्त, असे घडते की एका रेखीय समीकरणाला कोणतेही निराकरण नसते, किंवा समाधान संपूर्ण संख्यारेषा असते, उदा. कोणतीही संख्या. आजच्या धड्यात आपण या बारकावे पाहणार आहोत. परंतु आम्ही तुम्हाला आधीच समजल्याप्रमाणे, सर्वात सोप्या कार्यांसह प्रारंभ करू.

साधी रेखीय समीकरणे सोडवण्याची योजना

प्रथम, मी पुन्हा एकदा सर्वात सोपी रेषीय समीकरणे सोडवण्याची संपूर्ण योजना लिहितो:

1. कंस विस्तृत करा, असल्यास.
2. आम्ही व्हेरिएबल्स वेगळे करतो, म्हणजे. आम्ही "X's" असलेली प्रत्येक गोष्ट एका बाजूला आणि "X's" नसलेली प्रत्येक गोष्ट दुसरीकडे हलवतो.
3. आम्ही समान अटी सादर करतो.
4. आपण सर्व काही “x” च्या गुणांकाने विभाजित करतो.

अर्थात, ही योजना नेहमीच कार्य करत नाही; त्यात काही बारकावे आणि युक्त्या आहेत आणि आता आपण त्या जाणून घेऊ.

साध्या रेखीय समीकरणांची वास्तविक उदाहरणे सोडवणे

कार्य क्रमांक १

पहिल्या पायरीसाठी आम्हाला कंस उघडणे आवश्यक आहे. परंतु ते या उदाहरणात नाहीत, म्हणून आम्ही ही पायरी वगळतो. दुसऱ्या चरणात आपल्याला व्हेरिएबल्स वेगळे करणे आवश्यक आहे. कृपया लक्षात ठेवा: आम्ही फक्त वैयक्तिक अटींबद्दल बोलत आहोत. चला ते लिहूया:

आम्ही डावीकडे आणि उजवीकडे समान अटी सादर करतो, परंतु हे येथे आधीच केले गेले आहे. म्हणून, आम्ही चौथ्या चरणावर जाऊ: गुणांकाने विभाजित करा:

\[\frac(6x)(6)=-\frac(72)(6)\]

तर आम्हाला उत्तर मिळाले.

कार्य क्रमांक 2

आपण या समस्येतील कंस पाहू शकतो, तर चला त्यांचा विस्तार करूया:

दोन्ही डावीकडे आणि उजवीकडे आपल्याला अंदाजे समान डिझाइन दिसते, परंतु आपण अल्गोरिदमनुसार कार्य करूया, म्हणजे. व्हेरिएबल्स वेगळे करणे:

येथे काही समान आहेत:

हे कोणत्या मुळांवर काम करते? उत्तरः कोणत्याहीसाठी. म्हणून, आपण असे लिहू शकतो की $x$ ही कोणतीही संख्या आहे.

कार्य क्रमांक 3

तिसरे रेखीय समीकरण अधिक मनोरंजक आहे:

\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]

येथे अनेक कंस आहेत, परंतु ते कोणत्याही गोष्टीने गुणाकार केलेले नाहीत, ते फक्त वेगवेगळ्या चिन्हांनी आधी आहेत. चला त्यांना खंडित करूया:

आम्हाला आधीच माहित असलेली दुसरी पायरी आम्ही करतो:

\[-x+x+2x=15-6-12+3\]

चला गणित करूया:

आम्ही शेवटची पायरी पार पाडतो - प्रत्येक गोष्ट “x” च्या गुणांकाने विभाजित करा:

\[\frac(2x)(x)=\frac(0)(2)\]

रेखीय समीकरणे सोडवताना लक्षात ठेवण्याच्या गोष्टी

जर आपण खूप सोप्या कार्यांकडे दुर्लक्ष केले, तर मी पुढील गोष्टी सांगू इच्छितो:

• मी वर म्हटल्याप्रमाणे, प्रत्येक रेखीय समीकरणाचे समाधान नसते - काहीवेळा फक्त मुळे नसतात;
• जरी मुळे असली तरी त्यांच्यामध्ये शून्य असू शकते - त्यात काहीही चुकीचे नाही.

शून्य ही इतरांसारखीच संख्या आहे; आपण कोणत्याही प्रकारे त्याच्याशी भेदभाव करू नये किंवा असे गृहीत धरू नये की जर आपल्याला शून्य मिळाले तर आपण काहीतरी चुकीचे केले आहे.

आणखी एक वैशिष्ट्य कंस उघडण्याशी संबंधित आहे. कृपया लक्षात ठेवा: जेव्हा त्यांच्या समोर "वजा" असतो, तेव्हा आम्ही ते काढून टाकतो, परंतु कंसात आम्ही चिन्हे बदलतो विरुद्ध. आणि मग आपण ते मानक अल्गोरिदम वापरून उघडू शकतो: वरील गणनेत आपण जे पाहिले ते आपल्याला मिळेल.

ही साधी वस्तुस्थिती समजून घेतल्याने तुम्हाला हायस्कूलमध्ये मूर्खपणाच्या आणि दुखावणाऱ्या चुका टाळण्यास मदत होईल, जेव्हा अशा गोष्टी करणे गृहीत धरले जाते.

जटिल रेखीय समीकरणे सोडवणे

चला अधिक जटिल समीकरणांकडे जाऊया. आता बांधकामे अधिक जटिल होतील आणि विविध परिवर्तने करताना एक चतुर्भुज कार्य दिसून येईल. तथापि, आपण याची भीती बाळगू नये, कारण जर, लेखकाच्या योजनेनुसार, आपण एक रेखीय समीकरण सोडवत आहोत, तर परिवर्तन प्रक्रियेदरम्यान चतुर्भुज फंक्शन असलेले सर्व मोनोमियल नक्कीच रद्द होतील.

उदाहरण क्रमांक १

अर्थात, पहिली पायरी म्हणजे कंस उघडणे. चला हे अतिशय काळजीपूर्वक करूया:

आता गोपनीयतेकडे एक नजर टाकूया:

\[-x+6((x)^(2))-6((x)^(2))+x=-12\]

येथे काही समान आहेत:

अर्थात, या समीकरणाला कोणतेही उपाय नाहीत, म्हणून आम्ही हे उत्तरात लिहू:

\[\varnothing\]

किंवा मुळे नाहीत.

उदाहरण क्रमांक २

आम्ही समान क्रिया करतो. पहिली पायरी:

चला सर्व काही व्हेरिएबलसह डावीकडे हलवू या, आणि त्याशिवाय - उजवीकडे:

येथे काही समान आहेत:

अर्थात, या रेखीय समीकरणाला कोणतेही समाधान नाही, म्हणून आम्ही ते अशा प्रकारे लिहू:

\[\varnothing\],

किंवा मुळे नाहीत.

उपाय च्या बारकावे

दोन्ही समीकरणे पूर्णपणे सोडवली आहेत. उदाहरण म्हणून या दोन अभिव्यक्तींचा वापर करून, आम्हाला पुन्हा एकदा खात्री पटली की अगदी सोप्या रेखीय समीकरणांमध्येही, सर्वकाही इतके सोपे असू शकत नाही: एकतर एक, किंवा एकही नाही, किंवा अमर्यादपणे अनेक मुळे असू शकतात. आमच्या बाबतीत, आम्ही दोन समीकरणे विचारात घेतली, दोघांनाही मुळीच नाही.

परंतु मी तुमचे लक्ष आणखी एका वस्तुस्थितीकडे आकर्षित करू इच्छितो: कंसांसह कसे कार्य करावे आणि त्यांच्यासमोर उणे चिन्ह असल्यास ते कसे उघडायचे. या अभिव्यक्तीचा विचार करा:

उघडण्यापूर्वी, आपल्याला सर्वकाही "X" ने गुणाकार करणे आवश्यक आहे. कृपया लक्षात ठेवा: गुणाकार प्रत्येक वैयक्तिक पद. आत दोन संज्ञा आहेत - अनुक्रमे, दोन संज्ञा आणि गुणाकार.

आणि हे वरवरचे प्राथमिक, परंतु अत्यंत महत्वाचे आणि धोकादायक परिवर्तन पूर्ण झाल्यानंतरच, आपण ब्रॅकेट उघडू शकता की त्या नंतर एक वजा चिन्ह आहे. होय, होय: फक्त आता, जेव्हा परिवर्तने पूर्ण होतात, तेव्हा आम्हाला आठवते की कंसाच्या समोर एक वजा चिन्ह आहे, ज्याचा अर्थ असा आहे की खाली असलेली प्रत्येक गोष्ट फक्त चिन्हे बदलते. त्याच वेळी, कंस स्वतःच अदृश्य होतात आणि सर्वात महत्त्वाचे म्हणजे, समोरचा “वजा” देखील अदृश्य होतो.

आम्ही दुसऱ्या समीकरणासह तेच करतो:

मी या लहान, वरवर क्षुल्लक तथ्यांकडे लक्ष देणे योगायोगाने नाही. कारण समीकरणे सोडवणे हा नेहमीच प्राथमिक परिवर्तनाचा क्रम असतो, जेथे साध्या कृती स्पष्टपणे आणि सक्षमपणे करण्यास असमर्थतेमुळे हायस्कूलचे विद्यार्थी माझ्याकडे येतात आणि पुन्हा अशी साधी समीकरणे सोडवायला शिकतात.

अर्थात, असा दिवस येईल जेव्हा तुम्ही ही कौशल्ये आपोआप विकसित कराल. तुम्हाला यापुढे प्रत्येक वेळी इतके परिवर्तन करावे लागणार नाही; तुम्ही सर्व काही एका ओळीवर लिहाल. पण तुम्ही फक्त शिकत असताना, तुम्हाला प्रत्येक कृती स्वतंत्रपणे लिहायची आहे.

आणखी जटिल रेखीय समीकरणे सोडवणे

आता आपण जे सोडवणार आहोत त्याला क्वचितच सर्वात सोपे कार्य म्हणता येईल, परंतु अर्थ तोच आहे.

कार्य क्रमांक १

\[\left(7x+1 \right)\left(3x-1 \right)-21((x)^(2))=3\]

पहिल्या भागातील सर्व घटकांचा गुणाकार करूया:

चला काही गोपनीयता करूया:

येथे काही समान आहेत:

चला शेवटची पायरी पूर्ण करूया:

\[\frac(-4x)(4)=\frac(4)(-4)\]

येथे आमचे अंतिम उत्तर आहे. आणि, सोडवण्याच्या प्रक्रियेत आमच्याकडे चतुर्भुज फंक्शन असलेले गुणांक असूनही, त्यांनी एकमेकांना रद्द केले, जे समीकरण रेखीय बनवते आणि द्विघाती नाही.

कार्य क्रमांक 2

\[\left(1-4x \उजवे)\left(1-3x \right)=6x\left(2x-1 \उजवे)\]

चला पहिली पायरी काळजीपूर्वक पार पाडूया: पहिल्या कंसातील प्रत्येक घटकास दुसऱ्या घटकापासून प्रत्येक घटकाने गुणाकार करा. परिवर्तनानंतर एकूण चार नवीन संज्ञा असाव्यात:

आता प्रत्येक टर्ममध्ये गुणाकार काळजीपूर्वक करू:

चला “X” असलेल्या अटी डावीकडे हलवू आणि त्याशिवाय - उजवीकडे:

\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]

येथे समान अटी आहेत:

पुन्हा एकदा आम्हाला अंतिम उत्तर मिळाले आहे.

उपाय च्या बारकावे

या दोन समीकरणांबद्दलची सर्वात महत्वाची नोंद खालीलप्रमाणे आहे: आपण एकापेक्षा जास्त पद असलेल्या कंसाचा गुणाकार करण्यास सुरुवात केल्यावर, हे खालील नियमानुसार केले जाते: आपण पहिल्यापासून प्रथम पद घेतो आणि प्रत्येक घटकासह गुणाकार करतो. दुसरा; मग आपण पहिल्यापासून दुसरा घटक घेतो आणि त्याचप्रमाणे दुसऱ्या घटकासह गुणाकार करतो. परिणामी, आमच्याकडे चार पद असतील.

बीजगणितीय बेरीज बद्दल

या शेवटच्या उदाहरणासह, मी विद्यार्थ्यांना बीजगणितीय बेरीज काय असते याची आठवण करून देऊ इच्छितो. शास्त्रीय गणितात, $1-7$ ने आमचा अर्थ एक साधा रचना आहे: एकातून सात वजा करा. बीजगणितामध्ये, आपल्याला याचा अर्थ खालीलप्रमाणे आहे: “एक” क्रमांकावर आपण दुसरी संख्या जोडतो, ती म्हणजे “वजा सात”. अशाप्रकारे बीजगणितीय बेरीज सामान्य अंकगणिताच्या बेरजेपेक्षा वेगळी असते.

सर्व परिवर्तने, प्रत्येक बेरीज आणि गुणाकार करताना, तुम्हाला वर वर्णन केलेल्या प्रमाणेच रचना दिसू लागतात, बहुपदी आणि समीकरणांसह कार्य करताना तुम्हाला बीजगणितात कोणतीही अडचण येणार नाही.

शेवटी, आणखी काही उदाहरणे पाहू या जी आपण नुकतीच पाहिली त्यापेक्षा अधिक गुंतागुंतीची असतील आणि त्यांचे निराकरण करण्यासाठी आपल्याला आपला मानक अल्गोरिदम किंचित वाढवावा लागेल.

अपूर्णांकांसह समीकरणे सोडवणे

अशी कार्ये सोडवण्यासाठी, आम्हाला आमच्या अल्गोरिदममध्ये आणखी एक पाऊल जोडावे लागेल. पण प्रथम, मी तुम्हाला आमच्या अल्गोरिदमची आठवण करून देतो:

1. कंस उघडा.
2. वेगळे व्हेरिएबल्स.
3. समान आणा.
4. गुणोत्तराने भागा.

अरेरे, हे आश्चर्यकारक अल्गोरिदम, त्याच्या सर्व प्रभावीतेसाठी, जेव्हा आपल्यासमोर अपूर्णांक असतात तेव्हा ते पूर्णपणे योग्य नसते. आणि आपण खाली पाहणार आहोत, दोन्ही समीकरणांमध्ये डावीकडे आणि उजवीकडे अपूर्णांक आहे.

या प्रकरणात कसे कार्य करावे? होय, हे खूप सोपे आहे! हे करण्यासाठी, आपल्याला अल्गोरिदममध्ये आणखी एक पाऊल जोडणे आवश्यक आहे, जे पहिल्या क्रियेपूर्वी आणि नंतर दोन्ही केले जाऊ शकते, म्हणजे, अपूर्णांकांपासून मुक्त होणे. तर अल्गोरिदम खालीलप्रमाणे असेल:

1. अपूर्णांकांपासून मुक्त व्हा.
2. कंस उघडा.
3. वेगळे व्हेरिएबल्स.
4. समान आणा.
5. गुणोत्तराने भागा.

"अपूर्णांकांपासून मुक्त होणे" म्हणजे काय? आणि हे पहिल्या मानक चरणानंतर आणि आधी दोन्ही का केले जाऊ शकते? खरं तर, आमच्या बाबतीत, सर्व अपूर्णांक त्यांच्या भाजकात संख्यात्मक आहेत, म्हणजे. सर्वत्र भाजक फक्त एक संख्या आहे. म्हणून, जर आपण समीकरणाच्या दोन्ही बाजूंना या संख्येने गुणाकार केला तर आपण अपूर्णांकांपासून मुक्त होऊ.

उदाहरण क्रमांक १

\[\frac(\left(2x+1 \right)\left(2x-3 \right))(4)=(x)^(2))-1\]

चला या समीकरणातील अपूर्णांकांपासून मुक्त होऊ या:

\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \right)\cdot ४\]

कृपया लक्षात ठेवा: प्रत्येक गोष्ट एकदा "चार" ने गुणाकार केली जाते, म्हणजे. तुमच्याकडे दोन कंस आहेत याचा अर्थ असा नाही की तुम्हाला प्रत्येकाला "चार" ने गुणावे लागेल. चला खाली लिहू:

\[\left(2x+1 \right)\left(2x-3 \right)=\left((x)^(2))-1 \right)\cdot 4\]

आता विस्तार करूया:

आम्ही व्हेरिएबल वेगळे करतो:

आम्ही समान अटी कमी करतो:

\[-4x=-1\left| :\left(-4 \right) \right.\]

\[\frac(-4x)(-4)=\frac(-1)(-4)\]

आम्हाला अंतिम समाधान मिळाले आहे, चला दुसऱ्या समीकरणाकडे जाऊया.

उदाहरण क्रमांक २

\[\frac(\left(1-x \right)\left(1+5x \right))(5)+(x)^(2))=1\]

येथे आम्ही सर्व समान क्रिया करतो:

\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]

\[\frac(4x)(4)=\frac(4)(4)\]

समस्या सुटली आहे.

खरं तर, आज मला तुम्हाला एवढंच सांगायचं होतं.

महत्त्वाचे मुद्दे

मुख्य निष्कर्ष आहेत:

• रेखीय समीकरणे सोडवण्यासाठी अल्गोरिदम जाणून घ्या.
• कंस उघडण्याची क्षमता.
• तुमच्याकडे कुठेतरी चतुर्भुज कार्ये असतील तर काळजी करू नका; बहुधा, पुढील परिवर्तनाच्या प्रक्रियेत ते कमी केले जातील.
• रेखीय समीकरणांमध्ये तीन प्रकारची मुळे असतात, अगदी सोपी: एकच मूळ, संपूर्ण संख्यारेषा ही मूळ असते आणि मुळीच मुळी नसते.

मला आशा आहे की हा धडा तुम्हाला सर्व गणिताच्या अधिक समजून घेण्यासाठी एका सोप्या, परंतु अतिशय महत्त्वाच्या विषयावर प्रभुत्व मिळवण्यास मदत करेल. काहीतरी स्पष्ट नसल्यास, साइटवर जा आणि तेथे सादर केलेली उदाहरणे सोडवा. संपर्कात रहा, आणखी अनेक मनोरंजक गोष्टी तुमची वाट पाहत आहेत!