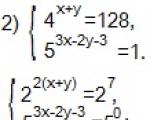Løse homogene eksponentielle ulikheter. Løse eksponentielle ligninger og ulikheter
Det er obligatorisk når du løser et system med eksponentialligninger? Sikkert, transformasjon dette systemet inn i et system av enkle ligninger.
Eksempler.
Løs ligningssystemer:
La oss uttrykke på gjennom X fra (2) systemligningen og erstatte denne verdien med (1) systemligningen.
Vi løser (2) ligningen til det resulterende systemet:
2 x +2 x +2 =10, bruk formelen: en x + y=en x∙ et y.
2 x +2 x ∙2 2 =10, la oss ta fellesfaktoren 2 x ut av parentes:
2 x (1+2 2)=10 eller 2 x ∙5=10, derav 2 x =2.
2 x =2 1, herfra x=1. La oss gå tilbake til ligningssystemet.

Svar: (1; 2).
Løsning.
Vi representerer venstre og høyre side av (1) likning i form av potenser med en base 2 , og høyre side av (2) ligningen som null potens av tallet 5 .
Hvis to potenser med samme base er like, så er eksponentene til disse potensene like - vi setter likhetstegn mellom eksponentene med basene 2 og eksponenter med baser 5 .
Vi løser det resulterende systemet med lineære ligninger med to variabler ved å bruke addisjonsmetoden.
Vi finner x=2 og vi erstatter denne verdien i stedet X inn i systemets andre ligning.
Vi finner på.
Svar: (2; 1,5).

Løsning.
Hvis vi i de to foregående eksemplene flyttet til et enklere system ved å likestille indikatorene for to grader med de samme basene, er denne operasjonen umulig i det tredje eksemplet. Det er praktisk å løse slike systemer ved å introdusere nye variabler. Vi vil introdusere variabler u Og v, og uttrykk deretter variabelen u gjennom v og vi får en ligning for variabelen v.
Vi løser (2) systemets likning.
v 2 +63v-64=0. La oss velge røttene ved å bruke Vietas teorem, vel vitende om at: v 1 +v 2 = -63; v 1 ∙v 2 =-64.
Vi får: v 1 =-64, v 2 =1. Vi går tilbake til systemet og finner u.

Siden verdiene til eksponentialfunksjonen alltid er positive, er ligningene 4 x = -1 og 4 år = -64 har ingen løsninger.
Metoder for å løse ligningssystemer
Til å begynne med, la oss kort huske hvilke metoder som generelt finnes for å løse ligningssystemer.
Eksistere fire hovedmåter løsninger på ligningssystemer:
Substitusjonsmetode: ta hvilken som helst av de gitte ligningene og uttrykk $y$ i form av $x$, deretter erstattes $y$ inn i systemligningen, hvorfra variabelen $x.$ finnes. Etter dette kan vi enkelt beregne variabelen $y.$
Addisjonsmetode: I denne metoden må du multiplisere en eller begge ligningene med slike tall at når du legger begge sammen, "forsvinner en av variablene."
Grafisk metode: begge likningene til systemet er avbildet på koordinatplanet og skjæringspunktet deres er funnet.
Metode for å introdusere nye variabler: i denne metoden erstatter vi noen uttrykk for å forenkle systemet, og bruker deretter en av metodene ovenfor.
Systemer av eksponentielle ligninger
Definisjon 1
Likningssystemer som består av eksponentielle ligninger kalles systemer med eksponentielle ligninger.
Vi vil vurdere å løse systemer med eksponentielle ligninger ved å bruke eksempler.
Eksempel 1
Løs ligningssystem
Bilde 1.
Løsning.
Vi vil bruke den første metoden for å løse dette systemet. La oss først uttrykke $y$ i den første ligningen i form av $x$.

Figur 2.
La oss erstatte $y$ i den andre ligningen:
\ \ \[-2-x=2\] \ \
Svar: $(-4,6)$.
Eksempel 2
Løs ligningssystem

Figur 3.
Løsning.
Dette systemet tilsvarer systemet

Figur 4.
La oss bruke den fjerde metoden for å løse likninger. La $2^x=u\ (u >0)$ og $3^y=v\ (v >0)$, vi får:

Figur 5.
La oss løse det resulterende systemet ved å bruke addisjonsmetoden. La oss legge sammen ligningene:
\ \
Så fra den andre ligningen får vi det
Tilbake til erstatningen, fikk jeg et nytt system med eksponentielle ligninger:
Figur 6.
Vi får:
Figur 7.
Svar: $(0,1)$.
Systemer med eksponentielle ulikheter
Definisjon 2
Systemer av ulikheter som består av eksponentielle ligninger kalles systemer med eksponentielle ulikheter.
Vi vil vurdere å løse systemer med eksponentielle ulikheter ved å bruke eksempler.
Eksempel 3
Løs ulikhetssystemet

Figur 8.
Løsning:
Dette systemet med ulikheter er ekvivalent med systemet

Figur 9.
For å løse den første ulikheten, husk følgende teorem om ekvivalensen av eksponentielle ulikheter:
Teorem 1. Ulikheten $a^(f(x)) >a^(\varphi (x)) $, hvor $a >0,a\ne 1$ tilsvarer samlingen av to systemer
\}